Решения уравнений – Решить уравнение

Решение уравнений (Вольфсон Г.И.). Видеоурок. Математика 6 Класс

На этом уроке вы узнаете, какие свойства уравнений можно применять при их решении. Вы познакомитесь с определением линейного уравнения и уравнения, сводящегося к линейному. Разобранные примеры и упражнения проиллюстрируют применение рассмотренных правил и позволят связать новый и ранее изученный материал в единое целое.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Уравнения и неравенства»

Рассмотрим решение уравнения:

Уравнение (2) можно получить из уравнения (1), разделив обе части уравнения на 5.

Число 8 – это корень уравнения (1) и корень уравнения (2).

Сформулируем первое свойство уравнения.

Обе части уравнения можно умножить или разделить на одно и то же число, не равное нулю, и корни уравнения не изменятся.

Пример 1.

Умножим обе части уравнения на 9. Тогда коэффициент перед  станет целым.

Ответ:

Пример 2.

Умножим обе части уравнения на 10. Тогда коэффициенты перед  станут целыми.

Ответ:

Пример 3.

Разделим обе части уравнения на 20.

Ответ:

Пример 4.

Разделим обе части уравнения на 2,1.

Ответ:

Рассмотрим решение уравнения:

Число 4 – это корень уравнения (1) и корень уравнения (2).

Заметим, что уравнение (2) можно было получить, перенеся число +5 из левой части в правую с противоположным знаком:

Сформулируем второе свойство уравнения:

Любое слагаемое можно перенести из одной части уравнения в другую, изменив при этом его знак на противоположный.

Рассмотрим решение еще одного уравнения: .

Вычтем из левой и правой части уравнения . Тогда  останется только в левой части.

Число 4 – это корень уравнения (3) и корень уравнения (4).

Второе свойство уравнений можно сформулировать иначе.

Если к обеим частям уравнения прибавить одно и то же число, то корни уравнения не изменятся. Если из левой и правой части уравнения вычесть одно и то же число, то корни уравнения не изменятся.

Пример 1.  

Воспользуемся вторым свойством уравнений. Принято слагаемые, которые содержат неизвестное, собирать в левой части уравнения, а остальные в правой.

Пример 2.  

Перенесем слагаемые, которые содержат неизвестное, в левую часть, а известные слагаемые в правую часть.

Пример 1.  

Сначала раскроем скобки.

Перенесем слагаемые, которые содержат неизвестное, в левую часть, а известные слагаемые в правую часть.

Пример 2.

Воспользуемся основным свойством пропорции. Произведение средних равно произведению крайних.

Раскроем скобки в левой и в правой части уравнения.

Перенесем неизвестное влево, а известное вправо.

Во всех рассмотренных примерах мы приводили уравнение к виду

Уравнения такого вида называют линейными уравнениями с одним неизвестным. Уравнения, которые можно с помощью преобразований привести к такому виду, называют сводящимися к линейным.

При каких значениях переменной  значение выражения  равно значению выражения ?

Составим уравнение и решим уравнение.

Перенесем неизвестное влево, а известное вправо.

Ответ: при

Условие. Рост мальчика – 75 см и еще половина его роста. Найдите рост мальчика.

Решение.

1. Пусть  (см) – половина роста.

Тогда весь рост равен  (см),

с другой стороны, весь рост –  (см).

Составим уравнение:

75 см – половина роста

2.  – весь рост мальчика

Ответ: 150 см.

 

Список литературы

1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. – М.: Мнемозина, 2012.
2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. – Гимназия. 2006.
3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. – М.: Просвещение, 1989.
4. Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5–6 класс. – М.: ЗШ МИФИ, 2011.
5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5–6. Пособие для учащихся 6-х классов заочной школы МИФИ. – М.: ЗШ МИФИ, 2011.
6. Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5–6 классов средней школы. – М.: Просвещение, Библиотека учителя математики, 1989.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Математика (Источник).
2. Интернет-портал Math-portal.ru (Источник).

 

Домашнее задание

1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. – М.: Мнемозина, 2012: № 1333, № 1342 (а, г, ж, л), № 1343.
2. Другие задания: № 1345, № 1347.

interneturok.ru

Решения уравнений по алгебре онлайн

Применение квадратных уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Квадратные уравнения человек использовал еще в древности и с тех пор их применение только возрастает.Неполными квадратными уравнениями принято называть квадратные уравнения, у которых один из коэффициентов будет равен нулю. Например:

\[ax^2+ bx + 0= 0\]

Его мы может легко преобразовать к следующему виду:

\[ax^2 +bx = 0\]

Для решения такого уравнения нам необходимо применить формулу решения неполного квадратного уравнения, суть которой заключается в том, чтобы левую часть разложить на множители и далее применить условие равенства произведения \[0.\]

Так же читайте нашу статью «Решить уравнение 5 класса онлайн решателем»

Допустим, у нас такое уравнение:

\[5x^2 — 20x = 0\]

Выполним разложение левой части с выносом общего множителя за скобки:

\[5x (x — 4) = 0\]

Применим условие:

\[5x = 0\] или \[x — 4 = 0\]

\[x = \frac {0}{5}, x = 4\]

\[x = 0\]

Как видно из вышеописанных результатов, то первый корень — 0, второй корень — 4.

Главное помнить, если коэффициент с будет равен \[0, а b \ne 0,\] то \[ax^2 + bx + 0= 0\] преобразуется к виду \[ax^2 + bx= 0\]. Если \[b = 0,\] а свободный член не равен \[0,\] то к виду \[ax^2 + с= 0 \]

Где можно решить неполное квадратное уравнение онлайн?

Решить уравнение онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

www.pocketteacher.ru

Решение уравнения — это… Что такое Решение уравнения?



Решение уравнения

Уравне́ние — равенство вида или , где f и g — функции (в общем случае — векторные) одного или нескольких аргументов, а также задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.).

Аргументы заданых функций (иногда называются «переменными») в случае уравнения называются «неизвестными».

Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения.

Про корни говорят, что они удовлетворяют данному уравнению.

Решить уравнение означает найти множество всех его решений (корней) или доказать, что корней нет.

Равносильными называются уравнения, множества корней которых совпадают.

Примеры уравнений

• x = 1
• e^{x + y} = x + y
• aⁿ + bⁿ = cⁿ, где a,b,c,n — натуральные числа.

Свойства

Если уравнение задано на множестве [[Вещественное чис== Свойства == Если уравнение задано на множестве вещественных чисел, то любое из следующих преобразований приведёт заданое уравнение к равносильному: [Вещественприбавить

1. К обеим частям уравнения можно прибавить любое число.
2. Из обеих частей уравнения можно вычесть любое число.
3. Обе части уравнения можно умножить на любое число, кроме нуля.
4. Обе части уравнения можно разделить на любое число, кроме нуля.

К обпреобразование не всегда является равносильным. ло|вещественных чисел]], то любое из следующих преобразований приведёт заданое уравнение к равносильному:

1. К обеим частям уравнения можно прибавить любое число.
2. Из обеих частей уравнения можно вычесть любое число.
3. Обе части уравнения можно умножить на любое число, кроме нуля.
4. Обе части уравнения можно разделить на любое число, кроме нуля.

К обеим частям уравнения можно применить любую функцию, но это может привести к появлению сторонних корней, поэтому такое преобразование не всегда является равносильным. γПолужирное начертание²

См. также

Ссылки

• EqWorld — Мир математических уравнений. Содержит обширную информацию о математических уравнениях и системах уравнений (алгебраических, дифференциальных, интегральных, функциональных и др.).

Wikimedia Foundation. 2010.

• Решение судебное
• Решенц

Смотреть что такое «Решение уравнения» в других словарях:

• Уравнения Гамильтона — Якоби — В физике и математике, уравнение Гамильтона Якоби Здесь S обозначает классическое действие, классический гамильтониан, qi обобщенные координаты. Непосредственно относится к классической (не квантовой) механике, однако хорошо приспособлено для… …   Википедия

• Уравнения Гамильтона-Якоби — В физике и математике, уравнение Гамильтона Якоби Здесь S обозначает классическое действие, классический гамильтониан, qi обобщенные координаты. Непосредственно относится к классической (не квантовой) механике, однако хорошо приспособлено для… …   Википедия

• Уравнения Навье — Стокса — Механика сплошных сред Сплошная среда Классическая меха …   Википедия

• Решение треугольников — (лат. solutio triangulorum) исторический термин, означающий решение главной тригонометрической задачи: по известным данным о треугольнике (стороны, углы и т. д.) найти остальные его характеристики[1]. Треугольник может располагаться на… …   Википедия

• РЕШЕНИЕ — (solution) Такое значение, при котором уравнение (equations) становится тождеством (или такое множество значений аргументов, что все уравнения системы становятся тождествами). Для уравнения от одной переменной, записанным как f(x)=0, решением… …   Экономический словарь

• Уравнения Эйлера — Лагранжа — Уравнения Эйлера  Лагранжа (в физике также уравнения Лагранжа Эйлера или уравнения Лагранжа) являются основными формулами вариационного исчисления, c помощью которых ищутся стационарные точки и экстремумы функционалов. В частности, эти… …   Википедия

• Уравнения Эйлера-Лагранжа — Уравнения Эйлера  Лагранжа являются основными формулами вариационного исчисления, c помощью которых ищутся экстремумы функционалов. В частности, эти уравнения широко используются в задачах оптимизации, и, совместно с принципом действия,… …   Википедия

• Уравнения Фаддеева — Уравнения Фаддеева  это уравнения, которые описывают все возможные взаимодействия в системе трёх частиц в полной квантовомеханической формулировке. Установлены Л. Д. Фаддеевым. Уравнения могут быть решены итерационным способом. В… …   Википедия

• Уравнения Лагранжа (гидромеханика) — Уравнения Лагранжа (в гидромеханике) дифференциальные уравнения движения частиц несжимаемой идеальной жидкости в переменных Лагранжа, имеющие вид: где время …   Википедия

• РЕШЕНИЕ — (1) математическое определение искомого ответа, удовлетворяющего условиям поставленной задачи, а также процесс его нахождения; (2) Р. графическое один из способов отыскания ответа задачи, выраженный в графической форме; (3) Р. неравенства… …   Большая политехническая энциклопедия

dic.academic.ru

Решение уравнений

Содержание статьи:

Уравнения второй степени

Существуют ли методы решения уравнений любого типа? Краткий ответ: нет, их не существует. Подробный ответ займет несколько томов, в которых также будет излагаться история математики, так как решение уравнений было и продолжает оставаться одним из важнейших стимулов развития этой науки. Далее мы поговорим об уравнениях, известных каждому школьнику. Для их решения существует алгоритм и даже конкретная формула. Уравнение второй степени — это уравнение вида $ax^2+bx+c=0$.

Египтянам удалось решить некоторые особые случаи подобных уравнений. Их заметно превзошли вавилоняне, которые умели решать большинство видов квадратных уравнений. Греки использовали геометрические методы. Четвертая теорема книги II евклидовых «Начал» описывает геометрический метод решения уравнений второй степени. Общий метод решения квадратных уравнений встречается в книге Михаэля Штифеля Aritm?tica integra — одном из важнейших трудов по алгебре, написанном в XVI веке. В этой книге уже используются знаки + и -,а также упоминаются корни из отрицательных чисел, хотя сам Штифель называл их абсурдными числами.

Формула, позволяющая напрямую найти решения уравнения второй степени, выглядит следующим образом: $x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$.

Знак ±, который использован в числителе, применяется для одновременной записи двух решений. Чтобы получить одно решение, мы должны сложить выражения в числителе, а для нахождения второго корня — вычислить их разность. Если мы обозначим одно решение уравнения за $x_{1}$, а другое за $x_{2}$, то получим $x_{1}=\frac{-b — \sqrt{b^2-4ac}}{2a}$, $x_{2}=\frac{-b +\sqrt{b^2-4ac}}{2a}$.

Уравнения второй степени могут иметь два разных решения или одно решение, в этом случае говорят, что уравнение имеет кратный корень. Уравнение также может не иметь решений, если для нахождения его корней нужно вычислить квадратный корень из отрицательного числа.

Важно отметить, что в последнем случае, когда мы говорим, что уравнение не имеет решений, мы имеем в виду отсутствие вещественных корней. В действительности уравнение имеет два комплексных решения.

Уравнения и функции

Графическое представление функций может оказаться полезным при решении уравнений. С его помощью не всегда получится найти точные решения, но можно определить количество корней и примерный интервал, в котором они располагаются. Рассмотрим простейший случай — линейное уравнение, например х-3=0. Ему будет соответствовать функция f(х) = х — 3. Это уравнение прямой. Точка, в которой эта прямая пересекает ось X, х=3, является решением уравнения. Если мы представим уравнение графически, его решениями будут точки, в которых график пересекает ось абсцисс.

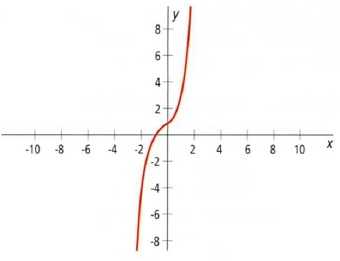
Например, если мы построим график функции $f(x) =x^3+x^2+x+1$,то увидим, что график пересекает ось абсцисс всего в одной точке x=-1. Это значение является решением уравнения $x^3+x^2+x+1$. Так как график функции не пересекает ось абсцисс в других точках, уравнение имеет единственное решение.

Уравнения второй степени и параболы

Графическое представление уравнений можно использовать при изучении уравнений второй степени. Графиком функции вида $f(x)=ax^2+bx+c$ всегда является парабола. Ее форма будет зависеть от значений а, b и с. Знак параметра а определяет, куда направлены ветви параболы, вверх или вниз.

Существует всего три возможных расположения параболы. Если она пересекает ось X в двух точках, это означает, что уравнение имеет два решения. Если она пересекает ось X в одной точке, то есть касается оси, в этом случае уравнение имеет один корень. Наконец, если парабола не пересекает ось X, то уравнение не имеет вещественных решений.

Конечно, не все эти знания пригодятся в реальной жизни, если она не будет связана с математикой.

Материалы по теме:

Поделиться с друзьями:

Загрузка…

matemonline.com