Решить систему линейных уравнений и вычислить невязку – Решение системы линейных уравнений (СЛАУ) онлайн

Содержание

Система линейных уравнений. Абсолютная погрешность и невязка решения системы линейных уравнений

Система уравнений вида:

(2.1)

или в сокращенной записи:

называется линейной алгебраической системой из n уравнений с n-неизвестными x_i (i=1,…,n). В матричной форме она записывается следующим образом:

(2.2)

где A — квадратная матрица, и — векторы столбцы вида:

Методы Рунге — Кутты второго порядка точности для решения задачи Коши

расчетам формулы метода Рунге-Кутты второго порядка точности имеют следующий вид:

(2.12)

Данный метод является двух этапным. Вначале вычисляется значение k⁽¹⁾, а затем значения k⁽²⁾.

При a=1 формулы (2.12) дают метод Эйлера-Коши, при a=1/2 — усовершенствованный метод Эйлера.

Экзаменационный билет №

12

Приближение функций. Среднеквадратичное и равномерное приближение
Версия
Аппроксимация состоит в том, что данную функцию f(x) приближенно заменяют (аппроксимируют) некоторой другой функцией, так, чтобы отклонение (x) от f(x) в заданной области [a,b] было минимально возможным, при этом функцию f(x) называют аппроксимируемой, а функцию (x) аппроксимирующей.
При приближении на непрерывном множестве точек отрезка [a,b] аппроксимацию называют непрерывной (или интегральной). Если приближение строится на заданном дискретном множестве точек {x_i} i=0,1,… отрезка [a,b], то аппроксимацию называют точечной.
Если аппроксимирующая функция (x) строится для всего отрезка [a,b] на котором задана функция f(x), то говорят о глобальной аппроксимации, если же весь отрезок [a,b] разбит на частичные отрезки и на каждом используется своя аппроксимирующая функция, то говорят о локальной аппроксимации.

Равномерное и среднеквадратичное приближения. Если приближение строится таким образом, что величина отклонения (модуль разности двух функций f(x) и (x)) удовлетворяет условию
(2.2)
то такое приближение (2.2) называют равномерным приближением.
Часто используется среднеквадратичное приближение функции f(x) функцией (x). Здесь стараются получить минимальную величину среднеквадратичного значения модуля разности аппроксимируемой и аппроксимирующей функций на всем отрезке [a,b]:
(2.3)
Первая формула используется при непрерывной аппроксимации, а вторая при дискретной аппроксимации.
Версия

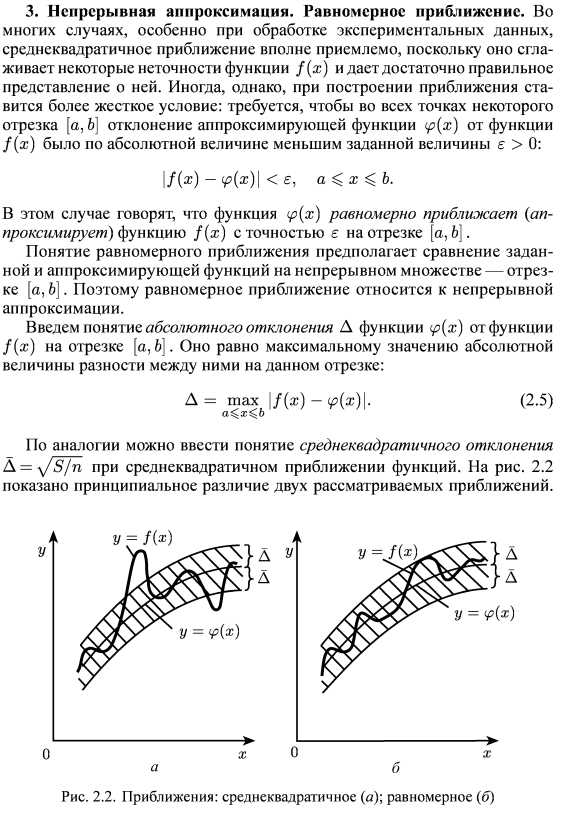
Норма вектора в линейном вещественном пространстве. Норма матрицы в линейном вещественном пространстве
Методы Рунге-Кутты четвертого порядка точности для системы дифференциальных уравнений

метод Рунге-Кутты четвертого порядка точности.Наиболее известным из методов Рунге-Кутты является классический 4-этапный метод четвертого порядка точности:
(2.13)
Этот метод прост и эффективен, когда отрезок [x₀,x_n] не очень велик.
метод Рунге-Кутты четвертого порядка точности для системы из 2-х уравнений.
Имеется система из двух дифференциальных уравнений:
Расчетные формулы для вычисления значений функции y(x) и z(x) имеют следующий вид:
(2.15)
где

Экзаменационный билет № 13

cyberpedia.su
2. Численные методы решения системы линейных уравнений
2.1. Постановка задачи
Рассмотрим систему линейных алгебраических уравнений: , где матрица m×m, — искомый вектор, — заданный вектор. Будем предполагать, что определитель матрицы отличен от нуля, т.е. решение системы существует.
Методы численного решения системы делятся на две группы: прямые методы («точные») и итерационные методы. Прямыми методами называются методы, позволяющие получить решение системы за конечное число арифметических операций. К этим методам относятся метод Крамера, метод Гаусса, LU-метод и т.д. Итерационные методы (методы последовательных приближений) состоят в том, что решение системы находится как предел последовательных приближений при , где — номер итерации. При использовании методов итерации обычно задается некоторое малое число и вычисления проводятся до тех пор, пока не будет выполнена оценка . К этим методам относятся метод Зейделя, Якоби, метод верхних релаксаций и т.д.

Следует заметить, что реализация прямых методов на компьютере приводит к решению с погрешностью, т.к. все арифметические операции над переменными с плавающей точкой выполняются с округлением. В зависимости от свойств матрицы исходной системы эти погрешности могут достигать значительных величин.
В нашем случае необходимо решить следующую систему линейных алгебраических уравнений.

2.2. Метод Гаусса
Запишем систему в развернутом виде:
Метод Гаусса состоит в последовательном исключении неизвестных из этой системы. Предположим, что . Последовательно умножая первое уравнение на и складывая сi-м уравнением, исключим из всех уравнений кроме первого. Получим систему:
где , , .
Аналогичным образом из полученной системы исключим . Последовательно, исключая все неизвестные, получим систему треугольного вида:
Описанная процедура называется прямым ходом метода Гаусса. Заметим, что ее выполнение было возможно при условии, что все , не равны нулю.
Выполняя последовательные подстановки в последней системе, (начиная с последнего уравнения) можно получить все значения неизвестных.
,
Эта процедура получила название обратный ход метода Гаусса.
Метод Гаусса может быть легко реализован на компьютере. При выполнении вычислений, как правило, не интересуют промежуточные значения матрицы . Поэтому численная реализация метода сводится к преобразованию элементов массива размерности (×()), где столбец содержит элементы правой части системы.

Для контроля ошибки реализации метода используются так называемые контрольные суммы. Схема контроля основывается на следующем очевидном положении. Увеличение значения всех неизвестных на единицу равносильно замене данной системы контрольной системой, в которой свободные члены равны суммам всех коэффициентов соответствующей строки. Создадим дополнительный столбец, хранящий сумму элементов матрицы по строкам. На каждом шаге реализации прямого хода метода Гаусса будем выполнять преобразования и над элементами этого столбца, и сравнивать их значение с суммой по строке преобразованной матрицы. В случае не совпадения значений счет прерывается.
Один из основных недостатков метода Гаусса связан с тем, что при его реализации накапливается вычислительная погрешность. Для больших систем порядка число действий умножений и делений близко к .
Для того, чтобы уменьшить рост вычислительной погрешности применяются различные модификации метода Гаусса. Например, метод Гаусса с выбором главного элемента по столбцам, в этом случае на каждом этапе прямого хода строки матрицы переставляются таким образом, чтобы диагональный угловой элемент был максимальным. При исключении соответствующего неизвестного из других строк деление будет производиться на наибольший из возможных коэффициентов и следовательно относительная погрешность будет наименьшей.

Существует метод Гаусса с выбором главного элемента по всей матрице. В этом случае переставляются не только строки, но и столбцы . Использование модификаций метода Гаусса приводит к усложнению алгоритма увеличению числа операций и соответственно к росту времени счета.
Алгоритм Гауссовских преобразований с выбором главного элемента по всей матрице:
Выберем ведущий элемент в какой-либо строке (для простоты расчетов лучше, если он будет равен 1).
Разделим ведущую строчку на ведущий элемент.

Обнулим элементы ведущего столбца
Остальные элементы пересчитаем по правилу прямоугольника
Столбец-контроль используется для контроля правильности вычислений. В первой таблице в нем собираются суммы по строкам. Пересчитывается, он также как и все остальные элементы. Если после пересчета в нем все равно остались суммы по строкам, значит, вычисления были проведены верно.

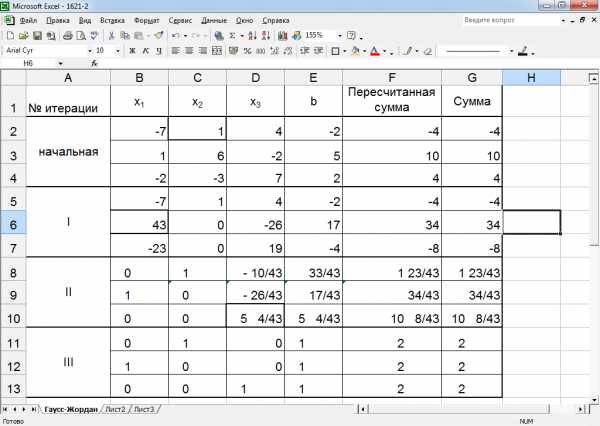
Рисунок 13 – Реализация алгоритма методом Жордана-Гаусса
Опишем механизм создания листа Excel с реализацией метода Гаусса.
На лист Excel занесем значения на начальной итерации. При столбцах х1, х2, х3 запишем основную матрицу системы. В столбце bзапишем столбец свободных коэффициентов. В столбцах «пересчитанная сумма» и «сумма» (они пока не отличаются способом расчета) автосуммируем все значения по строкам исходной матрицы.

На следующих итерациях «пересчитанная сумма» будет пересчитываться так же, как и все остальные элементы, а в «сумме» по-прежнему будут автосуммы по строкам. Если значения в 2 этих столбцах будут равны, значит, вычисления проведены верно.
Приведем пример пересчета элемента 1 (ячейка B3)
В ячейку D3 будет записано значение 43.
Чтобы эффективно использовать формулы Excel, создавая их только один раз, и затем копируя их, будем использовать абсолютные и относительные адреса ячеек. Если в адресе ячейки проставить знаки $ перед строкой или перед столбцом, то имя столбца или номер строки не будут смещаться в направлении копирования при копировании. Используем это свойство для создания рабочих формул Excel. Для перехода между относительными и абсолютными адресами ячеек используем клавишу F4.

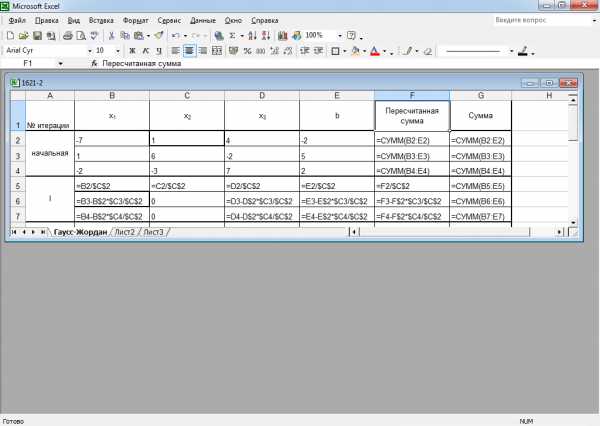
Рисунок 14 – Рабочие формулы реализации метода Жордана-Гаусса
Если ведущий элемент не равен 1, то при пересчете возникают дробные значения, поэтому выделим ячейки, содержащие дробные значения и в меню Формат, команда Ячейки выберем вкладку Число и применим Дробный форма. Выберем тип «Дробями до двух цифр» поскольку именно столько цифр было в ведущем элементе, на который делились элементы (в нашем случае ведущий элемент на первой итерации был равен 43).
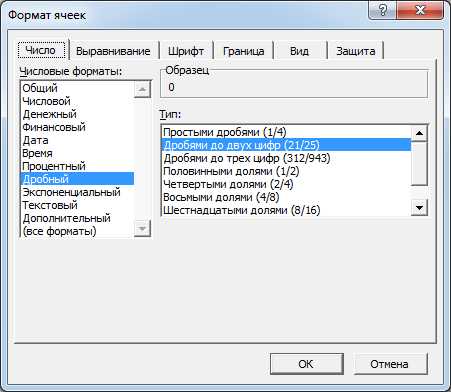
Рисунок 15 –установка дробного формата.
Продолжаем итерации пока не получим матрицу с единичными столбцами. Снова выпишем преобразованную систему линейных алгебраических уравнений.
Фактически, на последней итерации получаем точное решение.
Жордано-Гауссовские преобразования избавляют от необходимости ведения обратного хода Гаусса.
studfiles.net
Методы решения систем линейных уравнений
Методы решения систем линейных уравнений
1. Решение системы линейных уравнений методом Гаусса
Задачи аппроксимации функции, а также множество других задач прикладной математики м вычислительной физики сводятся к задачам о решении систем линейных уравнений. Самым универсальным методом решения системы линейных уравнений является метод последовательного исключения неизвестных, называемый методом Гаусса.
Для иллюстрации смысла метода Гаусса рассмотрим систему линейных уравнений:
(1)
Эту систему запишем в матричном виде:
(2)
Как известно, обе части уравнения можно умножить на ненулевое число, а также можно из одного уравнения вычесть другое. Используя эти свойства, постараемся привести матрицу системы (2) к треугольному виду, т.е. к виду, когда ниже главной диагонали все элементы – нули. Этот этап решения называется прямым ходом.
На первом шаге прямого хода умножим первое уравнение на
и вычтем из второго, тогда исключится переменная из второго уравнения. Затем, умножим первое уравнение на и вычтем из третьего, тогда система (2) преобразуется в систему вида:
(3)
На втором шаге прямого хода из третьего уравнения исключаем
, т.е. из третьего уравнения вычитаем второе, умноженное, на , что приводит систему (3) к треугольному виду (4) (4)
Систему (4) переписываем в привычном виде:
(5)
Теперь, из системы (5) можем находить решение в обратном порядке, т.е. сначала находим из третьего уравнения
, далее, подставляя во второе уравнение, находим . Подставляя и в первое уравнение системы (5), находим . Нахождение решения из системы (5) называют обратным ходом.
Теперь, на основе рассмотренного примера, составим общий алгоритм метода Гаусса для системы:

(6)
Метод Гаусса состоит из двух этапов:
а) прямой ход – когда матрица системы (6) приводится к треугольному виду;
б) обратный ход – когда последовательно вычисляются неизвестные в обратном порядке, т.е. в последовательности:
.
а) Прямой ход: для приведения системы (6) к треугольному виду, уравнения с ненулевыми коэффициентами при переменной
переставляются таким образом, чтобы они были выше, чем уравнения с нулевыми коэффициентами . Далее, вычитаем первое уравнение, помноженное на , из второго уравнения, вычитаем первое уравнение, помноженное на , из третьего уравнения и т.д. В общем, вычитаем первое уравнение, помноженное на , из — го уравнения при , если . Вследствие этой процедуры, мы обнулили все коэффициенты при переменной в каждом из уравнений, начиная со второго, т.е. система (6) принимает вид: (7)
Далее, применяем туже самую процедуру, для уравнений системы (7), начиная со второго уравнения, т.е. первое уравнение исключается из «игры». Теперь стараемся обнулить коэффициенты при переменной
, начиная с третьего уравнения и т.д., пока не приведём систему к треугольному виду. Если , то система всегда приводима (теоретически) к треугольному виду. Общий алгоритм прямого хода можно представить в виде: (8)
б) Обратный ход: Вычисляем неизвестные по формулам:
(9)
Замечание: для вычисления определителя системы можно использовать треугольную форму полученной матрицы, тогда определитель этой матрицы равен произведению диагональных элементов, т.е.
(10)
2. Метод Гаусса с выбором главного элемента
Метод Гаусса настолько универсален, что для некоторых систем получаются практически «плохие» результаты, поэтому разрабатываются различные хитрые выходы из ситуации. В случае, когда некоторые коэффициенты матрицы системы близки между собой, как известно относительные погрешности сильно возрастают при вычитании, поэтому классический метод Гаусса даёт большие погрешности. Чтобы обойти эту трудность, стараются в прямом ходе Гаусса выбрать то уравнение, у которого коэффициент при
максимален и в качестве основного «игрока» выбирают именно это уравнение, тем самым обходя трудности вычитания близких чисел (если это возможно). Далее, когда нужно обнулить все коэффициенты переменной , кроме одного уравнения – этим особым уравнением опять выбирают то уравнение, у которого коэффициент при максимальный и т.д., пока не получим треугольную матрицу.
Обратный ход происходит так же, как и в классическом методе Гаусса.
3. Оценка погрешности при решении системы линейных уравнений
Для того, чтобы оценить погрешности вычислений решения системы линейных уравнений, нам нужно ввести понятия соответствующих норм матриц.
Прежде всего, вспомним три наиболее часто употребляемые нормы для вектора
: (11) (Евклидова норма) (12) (Чебышевская норма) (13)
Для всякой нормы векторов можно ввести соответствующую норму матриц:
(14)
которая согласована с нормой векторов в том смысле, что
(15)
Можно показать, что для трёх приведённых выше случаев нормы матрицы
mirznanii.com
Решение СЛАУ с помощью надстройки «Поиск решения»

⇐ ПредыдущаяСтр 10 из 18Следующая ⇒
Систему линейных алгебраических уравнений можно также решить, используя надстройку «Поиск решения». При использовании данной надстройки строится последовательность приближений , i=0,1,…n.
Назовем вектором невязок следующий вектор:
Задача Excel заключается в том, чтобы найти такое приближение , при котором вектор невязок стал бы нулевым, т.е. добиться совпадения значений правых и левых частей системы .
В качестве примера рассмотрим СЛАУ (3.27).
Последовательность действий:
1. Оформим таблицу, как показано на рис.3.4. Введем коэффициенты системы (матрицу А) в ячейки А3:С5.
Рис.3.4. Решение СЛАУ с помощью надстройки «Поиск решения»
2. В ячейках А8:С8 будет сформировано решение системы (х₁, х₂, х₃). Первоначально они остаются пустыми, т.е. равными нулю. В дальнейшем будем их называть изменяемыми ячейками.. Однако для контроля правильности вводимых далее формул, удобно ввести в эти ячейки какие-либо значения, например, единицы. Эти значения можно рассматривать как нулевое приближение решения системы, = (1, 1, 1).
3. В столбец D введем выражения для вычисления левых частей исходной системы. Для этого в ячейкуD3 введем и затем скопируем вниз до конца таблицы формулу:
D3=СУММПРОИЗВ (A3:C3;$A$8:$C$8).
Используемая функция СУММПРОИЗВ принадлежит категории Математические.
4. В столбец Е запишем значения правых частей системы (матрицу В).
5. В столбец F введем невязки в соответствии с формулой (3.29), т.е. введем формулу F3=D3-E3 и скопируем ее вниз до конца таблицы.
6. Будет не лишним проверить правильность вычислений для случая = (1, 1, 1).
7. Выберем команду Данные\Анализ\Поиск решения.
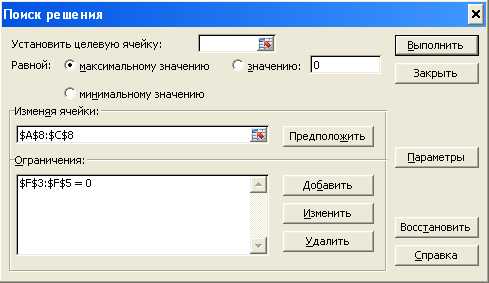
Рис. 3.5. Окно надстройки «Поиск решения»
В окне Поиск решения (рис.3.5) в поле Изменяемые ячейки укажем блок $А$8:$С$8, а в поле Ограничения – $F$3:$F$5=0. Далее щелкнем по кнопке Добавить и введем эти ограничения. И затем — кнопка Выполнить
Полученное решение систем (3.28) х₁=1; х₂=–1 х₃=2 записано в ячейках А8:С8, рис.3.4.
Реализация метода Якоби средствами приложения MS Excel
В качестве примера рассмотрим систему уравнений (3.19), решение которой методом Якоби получено выше (пример 3.2)

Приведем эту систему к нормальному виду:
Последовательность действий
1. Оформим таблицу, как показано на рис.3.6.:
• Матрицы и (3.15)введем в ячейки В6:Е8.
• Значение e–в Н5.
• Номер итерации k сформируем в столбце А таблицы с помощью автозаполнения.
• В качестве нулевого приближения выберем вектор
= (0, 0, 0) и введем его в ячейки В11:D11.
2. Используя выражения (3.29), в ячейки В12:D12 запишем формулы для вычисления первого приближения:
B12=$E$6+B11*$B$6+C11*$C$6+D11*$D$6,
C12=$E$7+B11*$B$7+C11*$C$7+D11*$D$7,
D12=$E$8+B11*$B$8+C11*$C$8+D11*$D$8.
Эти формулы можно записать иначе, используя функцию Excel СУММПРОИЗВ.
В ячейку Е12 введем формулу: E12=ABS(B11-B12) и скопируем ее вправо, в ячейки F12:G12.
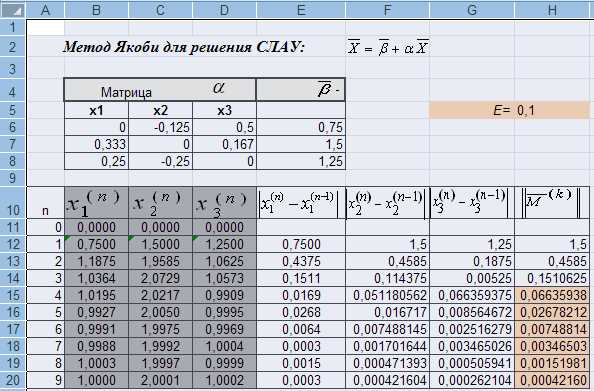
Рис.3.6. Схема решения СЛАУ методом Якоби
3. В ячейку Н12 введем формулу для вычисления M^(k), используя выражение (3.18): Н12 = МАКС(E12:G12). Функция МАКС находится в категории статистические.
4. Выделим ячейки В12:Н12 и скопируем их вниз до конца таблицы. Таким образом, получим k приближений решения СЛАУ.
5. Определим приближенное решение системы и количество итераций, необходимое для достижения заданной точности e.
Для этого оценим степень близости двух соседних итераций по формуле (3.18). Воспользуемся Условным форматированиемв ячейках столбца.
Результат такого форматирования виден на рис.3.6. Ячейки столбца Н, значения которых удовлетворяют условию (3.18), т.е. меньше e=0,1, тонированы.
Анализируя результаты, принимаем за приближенное решение исходной системы с заданной точностью e=0,1 четвертую итерацию, т.е.
Исследуем характер итерационного процесса. Для этого выделим блок ячеек А10:D20 и, используя Мастер диаграмм, построим графики изменения каждой компоненты вектора решения в зависимости от номера итерации,
Приведенные графики (рис.3.7) подтверждают сходимость итерационного процесса.

Рис. 3.7. Иллюстрация сходящегося итерационного процесса
Изменяя значение eв ячейке Н5, получим новое приближенное решение исходной системы с новой точностью.
Реализация метода прогонки средствами приложения Excel
Рассмотрим решение следующей системы линейных алгебраических уравнений методом «прогонки», используя таблицы Excel.
Векторы:
Последовательность действий
1. Оформим таблицу, как показано на рис.3.8. Исходные данные расширенной матрицы системы (3.30), т.е. вектора введем в ячейки B5:E10.
2. Про гоночные коэффициенты U₀=0 и V₀=0 введем в ячейки G4 и h5 соответственно.
3. Вычислим прогоночные коэффициенты L_i, U_i, V_i. Для этого в ячейках F5, G5, H5 вычислим L₁, U₁, V₁. по формуле (3.8). Для этого введем формулы:
F5 = B5*G4+C5; G5=-D5/F5, H5 = (E5-B5*h5)/F5, и затем скопируем их вниз.

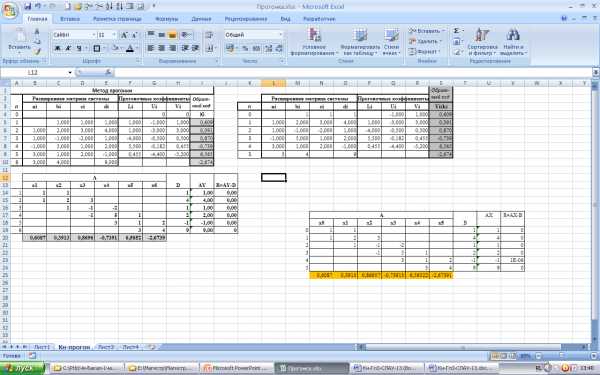
Рис.3.8. Расчетная схема метода «прогонки»

4. В ячейке I10 вычислим x₆ по формуле (3.10)
I10 = (E10-B10*H9)/(B10*G9+C10).
5. По формуле (3.7) вычислим все остальные неизвестные x₅ x₄, x₃, x₂, x₁. Для этого в ячейке I9 вычислим x₅ по формуле (3.6): I9=G9*I10+H9 . А далее копируем эту формуле вверх.
Контрольные вопросы
1. Система линейных алгебраических уравнений (СЛАУ). Что является решением СЛАУ. Когда существует единственное решение СЛАУ.
2. Общая характеристика прямых (точных) методов решения СЛАУ. Методы Гаусса и прогонки.
3. Общая характеристика итерационных методов решения СЛАУ. Методы Якоби (простых итераций) и Гаусса-Зейделя.
4. Условия сходимости итерационных процессов.
5. Что понимают под терминами обусловленности задач и вычислений, корректности задачи решения СЛАУ.

Глава 4.
Численное интегрирование
При решении достаточно большого круга технических задач приходится сталкиваться с необходимостью вычисления определенного интеграла:
Вычисление площадей, ограниченных кривыми, работы, моментов инерции, перемножение эпюр по формуле Мора и т.д. сводится к вычислению определенного интеграла.
Если непрерывная на отрезке [a, b] функция y = f(x) имеет на этом отрезке первообразную F(x), т.е. F^’(x) = f(x) , то интеграл (4.1) может быть вычислен по формуле Ньютона – Лейбница:
Однако, только для узкого класса функций y=f(x) первообразная F(x) может быть выражена в элементарных функциях. Кроме того, функция y=f(x) может задаваться графически или таблично. В этих случаях применяют различные формулы для приближенного вычисления интегралов.
Такие формулы называют квадратурными формулами или формулами численного интегрирования.
Формулы численного интегрирования хорошо иллюстрируются графически. Известно [1, 12], что значение определенного интеграла (4.1) пропорционально площади криволинейной трапеции, образованной подынтегральной функцией y=f(x), прямыми х=а и х=b, осью ОХ (рис.4.1).
Задачу вычисления определенного интеграла (4.1) заменяем задачей вычисления площади этой криволинейной трапеции. Однако задача нахождения площади криволинейной не является простой.
Отсюда идея численного интегрирования [3, 6] будет заключатся в замене криволинейной трапеции фигурой, площадь которой вычисляется достаточно просто.
Рис.4.1. Геометрическая интерпретация численного интегрирования
Для этого отрезок интегрирования [a, b] разобьем на n равных элементарных отрезков [x_i ,x_i₊₁] (i=0, 1, 2, …..,n-1), с шагом h=(b-a)/n. При этом криволинейная трапеция разобьется на n элементарных криволинейных трапеций с основаниями равными h (рис.4.1).
Каждая элементарная криволинейная трапеция заменяется фигурой, площадь которой вычисляется довольно просто. Обозначим эту площадь S_i. Сумма всех этих площадей называется интегральной суммой и вычисляется по формуле
Тогда приближенная формула вычисления определенного интеграла (4.1) имеет вид
Точность вычисления по формуле (4.4) зависит от шага h, т.е. от числа разбиений n. С увеличением n интегральная сумма приближается к точному значению интеграла
Это хорошо проиллюстрировано на рис.4.2.
Точное значение интеграла
Рис.4.2. Зависимость точности вычисления интеграла
от числа разбиений
В математике доказывается теорема: если функция y=f(x) непрерывна на [a, b], то предел интегральной суммы б_n существует и не зависит от способа разбиения отрезка [a,b] на элементарные отрезки.
Формулу (4.4) можно использовать, если известна степень точности такого приближения. Существуют различные формулы для оценки погрешности выражения (4.4), но, как правило, они достаточно сложны. Будем проводить оценку точности приближения (4.4) методом половинного шага.

Рекомендуемые страницы:
lektsia.com
Прямые методы решения систем линейных алгебраических уравнений
ч. 1
МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО
ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
им. Н. И. ЛОБАЧЕВСКОГО

Механико-математический факультет
Кафедра теоретической механики
Лабораторная работа
ПРЯМЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ
ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Нижний Новгород 2003
УДК 519.6

Прямые методы решения систем линейных алгебраических уравнений. Лабораторная работа для студентов дневного отделения. Специальность: 01.02  прикладная математика, системный программист; 01.03  механика. Библ. назв. 6.
Сост. А.Ф.Ляхов, Солдатов Е.В., Чернова Е.В.  Н.Новгород: ННГУ, 1999.16c.
Нижегородский государственный университет
им. Н.И. Лобачевского, 1997
Рассмотрим систему линейных алгебраических уравнений (СЛАУ) [1,2]
, (1)
где  матрица ,  искомый вектор,  заданный вектор. Будем предполагать, что определитель матрицы отличен от нуля, т.е. решение системы (1) существует.
Методы численного решения системы (1) делятся на две группы: прямые методы («точные») и итерационные методы.
Прямыми методами называются методы, позволяющие получить решение системы (1) за конечное число арифметических операций. К этим методам относятся метод Крамера, метод Гаусса, LU-метод и т.д.
Итерационные методы (методы последовательных приближений) состоят в том, что решение системы (1) находится как предел последовательных приближений при , где n номер итерации. При использовании методов итерации обычно задается некоторое малое число 0 и вычисления проводятся до тех пор, пока не будет выполнена оценка . К этим методам относятся метод Зейделя, Якоби, метод верхних релаксаций и т.д.
Следует заметить, что реализация прямых методов на компьютере приводит к решению с погрешностью, т.к. все арифметические операции над переменными с плавающей точкой выполняются с округлением. В зависимости от свойств матрицы исходной системы эти погрешности могут достигать значительных величин.

Метод Гаусса
Запишем систему Ax=f, в развернутом виде
Метод Гаусса состоит в последовательном исключении неизвестных из этой системы. Предположим, что . Последовательно умножая первое уравнение на и складывая с i-м уравнение, исключим из всех уравнений кроме первого. Получим систему
Аналогичным образом из полученной системы исключим . Последовательно, исключая все неизвестные, получим систему треугольного вида
Описанная процедура называется прямым ходом метода Гаусса. Заметим, что ее выполнение было возможно при условии, что все , не равны нулю.
Выполняя последовательные подстановки в последней системе, (начиная с последнего уравнения) можно получить все значения неизвестных.
.
Эта процедура получила название обратный ход метода Гаусса..
Метод Гаусса может быть легко реализован на компьютере. При выполнении вычислений, как правило, не интересуют промежуточные значения матрицы А. Поэтому численная реализация метода сводится к преобразованию элементов массива размерности (m×(m+1)), где m+1 столбец содержит элементы правой части системы.
Для контроля ошибки реализации метода используются так называемые контрольные суммы. Схема контроля основывается на следующем очевидном положении. Увеличение значения всех неизвестных на единицу равносильно замене данной системы контрольной системой, в которой свободные члены равны суммам всех коэффициентов соответствующей строки. Создадим дополнительный столбец, хранящий сумму элементов матрицы по строкам. На каждом шаге реализации прямого хода метода Гаусса будем выполнять преобразования и над элементами этого столбца, и сравнивать их значение с суммой по строке преобразованной матрицы. В случае не совпадения значений счет прерывается.
Один из основных недостатков метода Гаусса связан с тем, что при его реализации накапливается вычислительная погрешность. В книге [ Самарский , Гулин] показано, что для больших систем порядка m число действий умножений и делений близко к .
Для того, чтобы уменьшить рост вычислительной погрешности применяются различные модификации метода Гаусса. Например, метод Гаусса с выбором главного элемента по столбцам, в этом случае на каждом этапе прямого хода строки матрицы переставляются таким образом, чтобы диагональный угловой элемент был максимальным. При исключении соответствующего неизвестного из других строк деление будет производиться на наибольший из возможных коэффициентов и следовательно относительная погрешность будет наименьшей.
Существует метод Гаусса с выбором главного элемента по всей матрице. В этом случае переставляются не только строки, но и столбцы^¹. Использование модификаций метода Гаусса приводит к усложнению алгоритма увеличению числа операций и соответственно к росту времени счета. Поэтому целесообразность выбора того или иного метода определяется непосредственно программистом^².
Выполняемые в методе Гаусса преобразования прямого хода, приведшие матрицу А системы к треугольному виду позволяют вычислить определитель матрицы
.
Метод Гаусса позволяет найти обратную матрицу. Для этого необходимо решить матричное уравнение
,
где Е единичная матрица. Его решение сводится к решению m систем
у вектора j –я компонента равна единице, а остальные компоненты равны нулю.

LU–метод
LU-метод основан на том, что если главные миноры матрицы А отличны от нуля, тогда матрицу А можно представить, причем единственным образом, в виде произведения
А=LU,
где L–нижняя треугольная матрица с ненулевыми диагональными элементами и U–верхняя треугольная матрица с единичной диагональю.

Рассмотрим СЛАУ Ax=f.
A=LU
где

или

,
Окончательно запишем
Полагая получим следующие рекуррентные формулы для вычисления элементов матрицы L и U
Если найдены матрицы L и U, то решение исходной системы (1)ID_1 сводится к последовательному решению двух систем уравнений с треугольными матрицами
LU – метод позволяет вычислить определитель матрицы А
.
Метод квадратного корня
Метод квадратного корня по своему идейному содержанию близок к LU-методу. Основное отличие в том, что он дает упрощение для симметричных матриц.ID_1
Этот метод основан на разложении матрицы А в произведение
где S–верхняя треугольная матрица с положительными элементами на главной
Из условия (2) получаются уравнения
Так как матрица А симметричная, не ограничивая общности, можно считать, что в системе (3) выполняется неравенство i≤j. Тогда (3) можно переписать в виде
В частности, при i=j получится
(4)
Далее, при ij получим
По формулам (4) и (5) находятся рекуррентно все ненулевые элементы матрицы S.
Обратный ход метода квадратного корня состоит в последовательном решении двух систем уравнений с треугольными матрицами.
Решения этих систем находятся по рекуррентным формулам
Всего метод квадратного корня при факторизации A=S^тS требует примерно операций умножения и деления и m операций извлечения квадратного корня.[1]

Метод вращений решения линейных систем
Как и в методе Гаусса, цель прямого хода преобразований в этом методе–приведение системы к треугольному виду последовательным обнулением поддиагональных элементов сначала первого столбца, затем второго и т.д.
Умножим первое уравнение исходной системы (1) на с₁ ,второе на s₁ и сложим их ; полученным уравнением заменим первое уравнение системы. Затем первое уравнение исходной системы умножаем на –s₁ , второе на c₁ и результатом их сложения заменим второе уравнение . Таким образом, первые два уравнения (1) заменяются уравнениями
Отсюда . Эти числа можно интерпретировать как косинус и синус некоторого угла (отсюда название метод вращения, каждый шаг такого преобразования можно рассматривать как вращение расширенной матрицы системы в плоскости обнуляемого индекса).
В результате преобразований получим систему
где

Далее первое уравнение системы заменяется новым, полученным сложением результатов умножения первого и третьего уравнений соответственно на
а третье–уравнением, полученное при сложении результатов умножения тех же
где

Выполнив преобразование m-1 раз, придем к системе
Вид полученной системы такой же, как после первого этапа преобразований методом Гаусса. Эта система обладает следующим свойством: длина любого вектора-столбца (эвклидова норма) расширенной матрицы остается такой же, как у исходной матрицы. Следовательно, при выполнении преобразований не наблюдается рост элементов.

Далее по этому же алгоритму преобразуется матрица

и т.д.

В результате m-1 этапов прямого хода система будет приведена к треугольному виду.
Нахождение неизвестных не отличается от обратного хода метода Гаусса.
Всего метод вращения требует примерно операций умножения и деления.
Корректность постановки задачи и понятие обусловленности.
При использовании численных методов для решения тех или иных математических задач необходимо различать свойства самой задачи и свойства вычислительного алгоритма, предназначенного для ее решения.
Говорят, что задача поставлена корректно, если решение существует и единственно и если оно непрерывно зависит от входных данных. Последнее свойство называется также устойчивостью относительно входных данных.
Корректность исходной математической задачи еще не гарантирует хороших свойств численного метода ее решений и требует специального исследования.
Известно, что решение задачи (1) существует тогда и только тогда, когда . В этом случае можно определить обратную матрицу и решение записать в виде .
Исследование устойчивость задачи (1) сводится к исследованию зависимости ее решения от правых частей и элементов матрицы А. Для того чтобы можно было говорить о непрерывной зависимости вектора решений от некоторых параметров, необходимо на множестве — мерных векторов принадлежащих линейному пространству H, ввести метрику.
В линейной алгебре предлагается определение множества метрик  норма из которого легко получить наиболее часто используемые метрики
при р=1, ,
при , ,
при , .
Подчиненные нормы матриц определяемые как , соответственно запишутся в следующем виде:
, , .
Обычно рассматривают два вида устойчивости решения системы (1):первый  по правым частям, второй  по коэффициентам системы(1) и по правым частям..
Наряду с исходной системой (1) рассмотрим систему с «возмущенными» правыми частями
,
где  возмущенная правая часть системы, а возмущенное решение.
Можно получить оценку, выражающую зависимость относительной погрешности решения от относительной погрешности правых частей
,
где  число обусловленности матрицы А ( в современной литературе это число обозначают как ) Если число обусловленности велико (  ), то говорят, что матрица А плохо обусловлена. В этом случае малые возмущения правых частей системы (1), вызванные либо неточностью задания исходных данных, либо вызванные погрешностями вычисления существенно влияют на решение системы. Грубо говоря если погрешность правых частей , то погрешность решения будет . Более подробно о свойствах числа обусловленности и оценка его величины можно прочитать в [3].
Если возмущение внесено в матрицу А, то для относительных возмущений решения запишем
.
Экспериментальное исследование устойчивости решения.
При решении задач на практике часто бывает трудно оценить число обусловленности матрицы А. Поэтому существует ряд приемов, которые хотя и не дают строгий ответ об устойчивости применяемого метода и полученного решения, но все же позволяют сделать некоторые предположения о характере решения. Уточнить полученное решение и оценить его погрешность можно осуществить следующим образом.
Пусть получено приближенное решение системы (1) . Вычислим невязку уравнения . Если велико, то можно искать вектор-поправку такой, что точное решение системы . Следовательно
,
отсюда

.
Можно видеть, что для нахождения поправки можно использовать алгоритм метода и соответствующую программу, по которой находилось основное решение. После этого можно уточнить решение системы . Если относительная погрешность велика, то можно повторить процесс уточнения. Если процесс уточнения, повторенный два три раза, не приводит к повышению точности, то это говорит скорей всего о том, что данная система плохо обусловлена и ее решение не может быть найдено с требуемой точностью.

О вычислительных затратах.
Один из важных факторов предопределяющих выбор того или иного метода при решении конкретных задач, является вычислительная эффективность метода.
Учитывая, что операция сложения выполняется намного быстрее, чем операция умножения и деления, обычно ограничиваются подсчетом последних.
Для решения СЛАУ методом Гаусса без выбора главного элемента требуется
умножений и делений, решение СЛАУ методом квадратного корня требует и m операций извлечения корней. Метод вращения предполагает вчетверо больше операций умножения, чем в методе Гаусса. При больших значениях размерности m, можно сказать, что вычислительные затраты на операции умножения и деления в методе Гаусса составляют величину , в методе квадратных корней , в методе вращений .
Контрольные вопросы.

Дайте определения прямых и итерационных методов решения СЛАУ.

Опишите алгоритмы прямых методов приведенных в лабораторной работе.

Докажите, что подчиненные нормы матриц имеют вид, приведенный в лабораторной работе.

Что такое число обусловленности?

Покажите, что число умножений и делений при решении СЛАУ методом Гаусса равно .

Проведите качественное сравнение приведенных прямых методов решения СЛАУ.

Проведите качественное сравнение прямых и итерационных методов решения СЛАУ.
Задание1.
1. Привести систему уравнений к треугольному виду методом Гаусса (с выбором ненулевого элемента на главную диагональ).
2. Найти решение системы.
3. Вывести в файл результатов «rez.txt» полученную треугольную матрицу и вектор решения.
Задание2.
1. Привести систему уравнений к треугольному виду методом Гаусса (с выбором максимального элемента наглавную диагональ).
2. Найти решение системы.
3. Вывести в файл результатов «rez.txt» полученную треугольную матрицу и вектор решения.
Задание3.
1. Решить систему уравнений LU — методом.
2.Найти решение системы..
3. Вывести в файл результатов «rez.txt» полученную треугольную матрицу U и вектор решения.
Задание4.
1. Решить систему уравнений методом квадратного корня.
2. Найти решение системы.
3. Вывести в файл результатов «rez.txt» полученную матрицу S и вектор решения.
S-верхняя треугольная матрица с положительными элементами на главной диагонали.
Задание5.
1. Решить систему уравнений методом вращения.
2. Найти решение системы.
3. Вывести в файл результатов «rez.txt» полученную треугольную матрицу и вектор решения.

Этапы выполнения работы.

Провести исследование возможности применения прямых методов к решению данной задачи. Выполнить необходимые преобразования.

Выбрать способ преобразования матрицы к треугольному виду (для лабораторной работы).

Провести алгоритмизацию задачи и создать программу решения системы линейных алгебраических уравнений по методу, приложенному в задание. Программа должна учитывать структуру ввода и вывода исходных данных в соответствующий пакет программ лабораторной работы.

Запустить свою программу из программы лабораторной работы и сравнить результаты работы своей программы и программы, встроенной в пакет.

Провести анализ задачи, варьируя разным числом знаков округления. Как будет изменяться при этом решение.

Меняя способ приведения матрицы к треугольному виду, сравнить найденные при этом решения с вашим решением. Сделать вывод о полученных результатах.

Провести исследование на чувствительность найденного решения к погрешностям коэффициентов системы.

Используя полученную численную и графическую информацию, ответить на контрольные вопросы.

Оформить отчет, содержащий основные результаты работы.

В письменном отчете должны содержаться:

Постановка задачи. Исходные данные.

Обоснование возможности применения данного прямого метода к решению поставленной задачи.

Решение, невязка.

Матрица, приведенная к треугольному виду (указанному в задании).

Числа обусловленности в трех нормах.

Программа, реализующая данный прямой метод.
Структура интерфейса программы лабораторной работы.
Управление программой осуществляется с помощью команд меню и панели инструментов.

Меню Файл
Меню Файл содержит команды для создания новых систем уравнений, открытия существующих файлов с исходными данными, сохранения открытых файлов и выхода из лабораторной работы.

Новая система Открывает окно диалога “Ввод исходных данных”.
Открыть Открывает существующий файл с исходными данными(*mtr)
Сохранить Сохраняет изменения в открытом файле.
Сохранить как Сохраняет открытый файл под новым именем.
Выход Завершает работу приложения.
Меню Работа
Меню Работа содержит команды для иллюстрации исходных данных и их преобразования перед началом процесса решения, а также для выбора задания и выбора тестируемой программы.
Исходные данные Иллюстрация исходных данных
Рис1. Исходные данные.
Команда Выбрать задание открывает окно диалога в котором можно выбрать одно из пяти предложенных заданий.
Команда Генерация произвольных матриц открывает окно диалога в котором можно создать матрицы двух видов :симметричные и произвольные. Для этого изначально нужно указать размерность матрицы , а затем нажать кнопку ”Создать новую”. При этом запускается генератор случайных матриц.
Рис. 2. Генератор случайных матриц.

Команда Изменение начальных данных открывает окно диалога, в котором можно редактировать исходные данные задачи.
Рис. 3. Окно редактирования исходных данных.
Подменю Способ приведения матрицы к треугольному виду содержит две следующих команды:
1.С выбором ненулевого диагонального элемента. В этом случае реализуется обычный метод Гаусса.
2.С выбором главного диагонального элемента. В этом случае осуществляется метод Гаусса с выбором главного элемента по столбцам. Этот метод эквивалентен применению обычного метода Гаусса к системе, в которой на каждом шаге исключения проводится соответствующая перенумерация уравнений.
Пользователь должен выбрать один из вариантов и в дальнейшем сравнивать результаты своей программы с контрольными..
Во время просмотра результатов также можно изменять способ приведения матрицы к треугольному виду. Программа лабораторной работы немедленно произведет пересчет собственных результатов и изменит контрольные значения в таблице и на графиках. Это позволяет сравнить результаты применения разных методов к одной и той же системе.
Команда Тестируемая программа открывает окно диалога «Выбор тестируемой программы». В строке редактирования введите путь и имя Вашей программы или нажмите кнопку «Обзор» и выберете Ваше приложение среди других исполнимых файлов (*.exe, *.bat).
Имена 20-ти последних программ запоминаются и впоследствии могут выбираться из списка программ в этом же окне диалога.
В окне диалога ”Ввод исходных данных” имеется вкладка ”Дополнительно”. На ней можно ввести округление вычислений, а также установить диапазон значений и тип генерируемых коэффициентов матрицы. Благодаря этому, можно варьировать числом знаков округления и анализировать, как будет меняться при этом решение.
Рис.4.

Меню Сравнение результатов.
Меню Сравнение результатов содержит команду, которая запускает программу пользователя, а также служит для просмотра результатов его работы и сравнения их с контрольными значениями.
Рис.5. Результаты.
При этом оцениваются найденные решение, невязка.
Невязка вычисляется следующим образом:
В случае если студенту предложено решить задачу методом Гаусса, дополнительно сравнивается матрица, приведенная к треугольному виду.
Меню Дополнительно
содержит команды следующего вида:
Информация о системе уравнений Отображает дополнительную информацию о системе.
Рис. 6. Дополнительная информация о системе.
Выводится исходная система Ax=b и матрица обратная к левой части. Считаются определители обеих матриц и их нормы (||•||_1, ||•||_2, ||•||₃). По нормам находятся числа обусловленности системы. Информация сводится в таблицу.
Данные с вкладки «Информация о системе» полезны при исследовании устойчивости решения к возмущениям исходной системы
Влияние погрешностей коэффициентов Отображает влияние погрешностей коэффициентов системы на решение.
Исследование устойчивости проводится на вкладке «Погрешности». Производится теоретическая оценка относительной погрешности решения по формуле
,
которая верна при условии ||dA||A^-1||^-1 .
Теоретическая оценка сравнивается с практически полученным относительным отклонением. Полученные результаты сводятся в таблицу.
Непрерывные вычисления и вывод векторов решения в диаграммном виде позволяют увидеть динамику расходимости решений.

Рис. 7 Погрешности.
Команда Контрольные вопросы отображает список контрольных вопросов.
Команда Список студентов открывает окно диалога, в котором отображена информация о студентах и соответствующих им вариантах заданий.
Меню Вид.
Содержит команду отображения – скрытия Панели инструментов.
Меню Справка.
Меню Справка содержит команды для доступа к справочной системе и диалогу «О программе».
Описание работы Открытие справочного файла.
О программе Открытие окна диалога «О программе».
Литература
1.Самарский А.А., Гулин А.В. Численные методы: Учеб. пособие для вузов.—М.: Наука, 1989 г.
2.Бахвалов Н.С. Численные методы. – М.: Наука, 1975 г.
3.Д.Каханер, К.Моулер, С.Нэш. Численные методы и программное обеспечение.–М.:Мир,2001.–575с.
4. Вержбицкий В.М. Численные методы. (линейная алгебра и нелинейные уравнения). М.: Высшая школа, 2000. 266с.
5. Сборник задач по методам вычислений. (под ред. Монастырного П.И.)  М.: Наука, 1994.  320с.
ч. 1
izumzum.ru
Решение системы линейных уравнений
Министерство образования и науки Республики Беларусь
Белорусский государственный университет
информатики и радиоэлектроники
Факультет информационных технологий и управления
Кафедра Вычислительных Методов и Программирования
к курсовой работе
по программированию
на тему:
«Решение системы линейных уравнений»
Выполнил: Принял:
ст.гр.020603 Навроцкий А.А.
Червоный А.В.
Минск 2001г.
Содержание
Введение.
1. Анализ существующих методов решения задачи.
2. Описание используемого метода.
3. Анализ результатов.
Вывод.
Список использованной литературы.
Приложение (распечатка программы, результатов).
Введение
Применяемые на практике численные методы решения СЛАУ делятся на две группы — прямые и итерационные .
В прямых (или точных) методах решение системы получают за конечное число арифметических действий. К ним относятся известное правило Крамера нахождения решения с помощью определителей, метод последовательного исключения неизвестных (метод Гаусса) и его модификации, метод прогонки и другие. Сопоставление различных прямых методов проводится обычно по числу арифметический действий, необходимых для получения решения. Прямые методы являются универсальными и применяются для решения систем до порядка 10³ . Отметим, что вследствие погрешностей округления при решении задач на ЭВМ прямые методы на самом деле не приводят к точному решению системы.
Итерационные (или приближенные) методы являются бесконечными и находят решение системы как предел при k ® ¥ последовательных приближений x ⁽ ^k ⁾ , где k — номер итерации. Обычно задается точность e, и вычисления проводятся до тех пор, пока не будет выполнена оценка ºx ⁽ ^k ⁾ – x ⁽ ^k ^-1) º< e. Число итераций n (e), которое необходимо провести для получения заданной точности, для многих методов можно найти из теоретических рассмотрений. Качество различных итерационных методов можно сравнивать по необходимому числу итераций n (e). Эти методы особенно предпочтительны для систем с матрицами специального вида — симметричными, трехдиагональными, ленточными и большими разреженными матрицами.
Выбор среды программирования.
После проведенного обзора программных средств мы выбрали среду программирования наиболее подходящую нам как очень удобное средство для разработки данного программного продукта. DELPHI 5.0 является наиболее выгодной нам средой программирования.
1. Анализ существующих методов решения задачи
Прямые методы решения СЛАУ. К прямым (или точным) методам решения СЛАУ относятся алгоритмы, которые в предположении, что вычисления ведутся без округлений, позволяют получить точное решение системы за конечное число арифметических действий. Чаще всего решение задач такими методами осуществляется поэтапно: на первом этапе систему преобразуют к тому или иному простому виду, на втором — решают упрощенную систему и получают значения неизвестных.
Запишем систему линейных алгебраических уравнений в развернутом виде:
где x₁ , x₂ ,…, x_n — неизвестные величины, b₁ , b₂ ,…, b_n — элементы правой части. Если определитель системы отличен от нуля, то она имеет единственное решение. Для удобства дальнейших преобразований обозначим элементы правой части а _i ₍ _n ₊₁₎ и запишем расширенную матрицу размерами n ´ ( n +1) , которая содержит всю информацию о системе:
A =
.
С этой матрицей можно обращаться так же, как и с системой — переставлять строки, прибавлять кратное одной строки к другой, исключая неизвестные и приводя матрицу к треугольному или диагональному виду.
Приведем формальное описание схем некоторых прямых методов.
Метод Гаусса (схема единственного деления). Алгоритм метода состоит из двух этапов. Первый этап называется прямым ходом метода и заключается в последовательном исключении неизвестных из уравнений, т.е. в приведении матрицы А к верхнему треугольному виду (ниже главной диагонали все нули). Для этого на первом шаге разделим первое уравнение системы на а₁₁ (предположим, что коэффициент а₁₁ ¹ 0, в противном случае осуществляем перестановку уравнений системы). Обозначим коэффициенты полученного приведенного уравнения , домножим его на коэффициент а₂₁ и вычтем из второго уравнения системы, исключая тем самым х₁ из второго уравнения (обнуляя коэффициент а₁₂ матрицы). Поступим аналогично с остальными уравнениями и получим новую систему, матрица которой в первом столбце, кроме первого элемента, содержит только нули, т.е.
.
Первое уравнение в дальнейших преобразования не участвует. Описанный выше процесс исключения неизвестных применим к матрице
размерами (n -1) n . После k аналогичных шагов получим k приведенных уравнений с коэффициентами
и матрицу
размерами (n — k ) ( n — k +1), элементы которой вычисляются по формулам .
Элементы
, на которые осуществляется деление, называются ведущими элементами метода Гаусса и не должны равняться нулю. Прямой ход метода Гаусса заканчивается после n шагов определением .
Обратный ход метода Гаусса заключается в последовательном определении компонент решения, начиная с х_n и заканчивая х₁ , по следующим формулам:
Метод Гаусса с выбором главного элемента. Метод заключается в том, что при прямом ходе в алгоритме метода Гаусса на каждом шаге исключения производится выбор наибольшего по модулю элемента в качестве ведущего . Этого достигают перестановкой строк или столбцов матрицы коэффициентов. Наиболее распространённой в вычислительной практике является стратегия выбора главного элемента столбца — нахождение максимального по модулю элемента k — го столбца матрицы
и использование его в качестве ведущего элемента на k -м шаге исключения. В этом случае для невырожденных систем гарантируется, что ведущие элементы не равны нулю, и уменьшается погрешность при делении и последующем вычитании при преобразованиях. Рекомендуется также масштабировать предварительно каждое уравнение исходной системы, разделив на его наибольший по абсолютной величине коэффициент. Это делает рост элементов промежуточных матриц ограниченным.
Метод оптимального исключения. В целях экономии оперативной памяти (примерно в 4 раза) операции прямого и обратного хода метода Гаусса выполняются попеременно. На первом шаге после приведения первого уравнения исключается неизвестное x₁ из второго уравнения, а затем с помощью приведенного второго уравнения — неизвестное x₂ из первого. После ( k -1) таких шагов матрица системы имеет вид
.
На k — м шаге, используя первые k уравнений, исключаем неизвестные x₁ ,..,x _k из ( k +1) -го уравнения. Затем посредством этого уравнения исключается неизвестное x_k+1 из первых k
mirznanii.com
Решение систем линейных уравнений.

⇐ ПредыдущаяСтр 4 из 9Следующая ⇒
Системы линейных алгебраических уравнений (СЛАУ) в научно-исследовательской инженерной практике встречаются весьма часто. К решению систем линейных уравнений сводится многочисленные практические задачи с использованием численных методов.
Например:
Коэффициенты сплайнов находятся путем решения СЛАУ. К СЛАУ приводят уравнения частных производных.
Задачи по нахождению собственных значений также приводят к СЛАУ. Таким образом, решение СЛАУ – одна из самых распространенных и важных задач вычислительной математики.
Запишем СЛАУ в общем виде:

— номер уравнения
— номер неизвестной, на которую умножается коэффициент.
Коэффициенты образуют матрицу

Матрица системы столбец неизвестных величин столбец правых частей
Введя эти величины, мы можем записать СЛАУ в виде матричного решения
Важнейшей характеристикой квадратной матрицы является её определитель( )
Число возможных значений
В курсе высшей математики показывается, что система СЛАУ имеет единственное решение, если определитель системы не равен нулю. В этом случае решение может быть найдено с помощью формул Крамера:
,
где — определитель матрицы, которая получается после исключения в матрице А -го столбца и его замены столбцом свободных членов.
Если определитель системы равен нулю, то в этом случае матрица называется вырожденной, а система либо не имеет решения, либо имеет бесконечное множество решений. Для некоторых систем решение оказывается очень чувствительным к малым погрешностям в исходных данных . Такие системы называются плохо-обусловленными. Определитель плохо-обусловленных систем близок к нулю. При численных вычислениях всегда надо иметь ввиду эту особенность систем линейных уравнений.
Существуют методы улучшения обусловленности систем. Некоторые некорректные задачи приводят к плохо обусловленным системам уравнений. Эти задачи могут иметь важное практическое значение. Существуют методы решения таких задач.
Методы решения СЛАУ делятся на 2 группы:

1)прямые
используют готовые формулы для вычисления неизвестных, эти методы наиболее универсальны, пригодны для решения широкого класса СЛАУ. Но они обладают недостатками: они требуют хранения в оперативной памяти сразу всей матрицы. Существенным недостатком прямых методов является накапливание погрешности в процессе решения. Это особенно опасно для больших систем, а также для плохо-обусловленных , поэтому прямые методы используют обычно если нескольких сотен.
Итерационные
в итерационных методах решение находят путем последовательных приближений. Накапливание погрешности не происходит, и с помощью них решают систему с большим числом уравнений и для решения плохо-обусловленных систем. Однако сходимость итерации может быть очень медленной. Поэтому время счета может быть очень большим. Другим недостатком является то, что с их помощью решается ограниченный класс уравнений.
Например:
Уравнений с преобладанием диагональных элементов, либо системы со слабо заполненными матрицами.
Метод Крамера относится к прямому методу, однако на практике метод Крамера практически никогда не используется, так как он требует большого объёма вычислений. Оценим объём вычислений с помощью метода Крамера. Для применения этого необходимо вычислить определитель, а для вычисления каждого определителя необходимо сделать произведений, а число полученных слагаемых . Значит, число арифметических операций будет с ростом резко возрастает при
Наиболее распространенным среди прямых методов является метод Гаусса.
Метод 14
Метод Гаусса.
Метод Гаусса основан на приведении матрицы системы к треугольному виду. Метод Гаусса состоит из двух этапов: прямой ход и обратный. Прямой ход – матрица приводится к треугольному виду, при обратном последовательно находятся неизвестные величины.

Прямой ход состоит в следующем:
1)на первом шаге с помощью первого уравнения исключается из всех последних уравнений системы, в результате получается новая система, имеющая то же решение, но в первом столбце матрицы будет не нулевым только первый элемент.
2)на втором шаге с помощью второго уравнения исключается из всех уравнений. Этот процесс продолжается до тех пор, пока в левой части последнего — го уравнения не останется лишь один член с неизвестным .
Рассмотрим процесс исключения подробнее:
На -ом шаге исключается
Запишем -ое уравнение:
Исключим с помощью этого уравнения из уравнения с номером
Для исключения из -го уравнения вычитаем -ое , умноженное на .
После такого вычитания первые слагаемые сокращаются. Запишем значение коэффициенты перед , используем для него прежнее обозначение
При этом изменяется свободный член

По завершению прямого хода получается система с треугольной матрицей. Далее производится обратный ход метода Гаусса.
Обратный ход метода Гаусса состоит в последовательном вычислении искомых неизвестных, начиная с . Сначала находится . Далее, используя это значение, находится и так далее.
Например:
На — ом шаге обратного хода неизвестные находятся с помощью выражения.
В процессе исключения неизвестных приходится делить на диагональный элемент, который может оказаться равным нулю. Чтобы исключить эту ситуацию, необходимо на каждом шаге прямого хода менять расположение уравнений таким образом, чтобы диагональный элемент не был равным нулю, а лучше, чтобы он имел максимально возможное значение.
Перестановка уравнений должна быть предусмотрена в вычислительном алгоритме и метод Гаусса, в котором производится перестановка уравнений таким образом, чтобы диагональный элемент имел максимальное значение, называется метод Гаусса с выбором главного элемента.
В методе Гаусса объём вычислений пропорционален . Существует практически значимые случаи, когда объём вычислений при решении СЛАУ можно резко сократить.

Метод 15
Метод прогонки.
Метод прогонки является модификацией метода Гаусса для частного случая с трёхдиагональной матрицей. Такие системы возникают при численном решении уравнений математической физики.
Другой пример: коэффициенты сплайна третьей степени находятся путём решения систем с трёхдиагональной матрицей.
В методе прогонки объём вычислений растет пропорционально . Запишем систему уравнений, которая решается методом прогонки.

Общий вид уравнений с трёхдиагональной матрицей
Решение системы с трёхдиагональной матрицей, как и в методе Гаусса, состоит из двух этапов. Прямой прогонки и обратной прогонки.
Рассмотрим первый этап (прямой ход метода прогонки)
Для этого неизвестный выражаем через , таким образом:
,
где , — неизвестные пока (прогоночные) коэффициенты. На первом как раз и находится эти коэффициенты. Сравним это уравнение при с первым уравнением системы
И из сравнения находим, что
Заменим i-ое уравнение системы, выразив в нём с помощью
Сравнивая с
Получаем рекуррентные соотношения для нахождения прогоночных коэффициентов.
После того как найдены все прогоночные коэффициенты в результате прямого хода метода, находят . Для этого сравниваем последние уравнения системы с последним прогоночным соотношением. В результате получаем систему из двух уравнений с двумя неизвестными.
Отсюда
Это фактически начало обратного хода метода прогонки.
После этого последовательно находим …….и т.д. вплоть до .
Метод 16
Уточнение решения (итерационный метод).
Решения, получаемые с помощью прямых методов обычно содержат погрешности. В ряде случаев, особенно если объём системы велик, эти погрешности могут быть значительными.
Рассмотрим итерационный процесс позволяющий уточнить решения на следующем итерационном шаге. Пусть решается система
……………………………
Пусть на k-ом итерационном шаге получено решение в виде , ,…, , где k-это номер итерационного шага.
Подставим полученное решение в левые части уравнений системы, результат вычислений этих уравнений обозначим , , .
В результате получим систему

……………………………
Вычтем из каждого уравнения 1-ой системы уравнение 2-ой системы и получим систему вида
……………………………
Отсюда
Это невязка для уравнений с соответствующим номером.
Теперь мы получаем систему решением, которой будут соотношения уточняющие решение.
………………..
Преимуществом этого метода является то, что на каждом итерационном шаге решается система с одной и той же матрицей. Это позволяет оптимизировать вычислительный процесс, строить экономичные алгоритмы.
Метод 17
Метод Гаусса-Зейделя.
Является одним из самых распространённых итерационных методов. Это связано с простотой метода. Перепишем уравнение системы, выразив из первого уравнения, — из второго и т.д.
Получится система, которая имеет вид:
……………………………………….
Перед записью этой системы необходимо произвести проверку уравнений таким образом, чтобы диагональные элементы не были равны нулю, а ещё лучше, что бы на диагонали были максимальные элементы.
Сначала задаётся начальное приближение и на 1-ом итерационном шаге с помощью 1-го уравнения находится
и т.д. до .
Считаем пока не достигнем, заданной точности. Для сходимости итерационного процессадостаточно чтобы модули диагональных коэффициентов для каждого уравнения системы были не меньше суммы модулей всех не диагональных элементов.
, для любого i
И, по крайней мере, хотя бы в одном уравнении модуль должен быть большим.
Тема №5

Рекомендуемые страницы:
lektsia.com
No related posts.