§7. Решение систем n линейных уравнений с n неизвестными матричным методом и по формулам Крамера
I. Решение систем матричным методом (с помощью обратной матрицы)
Решение систем n линейных уравнений с n неизвестными матричным методом рассмотрим на примере системы трех линейных уравнений 1-ой степени с тремя неизвестными.
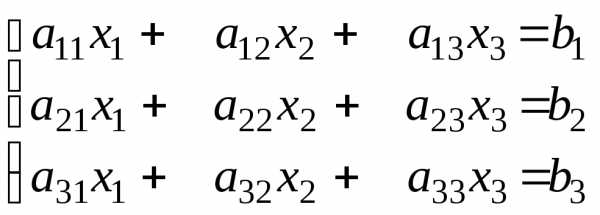 (1)
(1)
Обозначим: 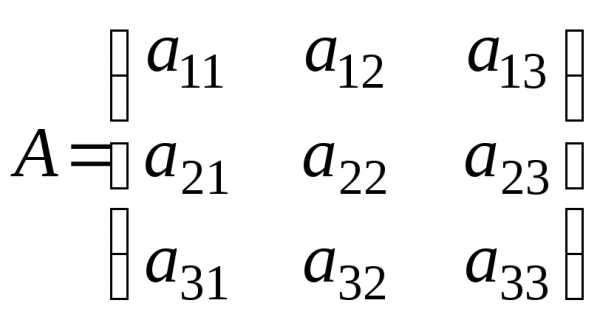 – матрица системы,
– матрица системы,
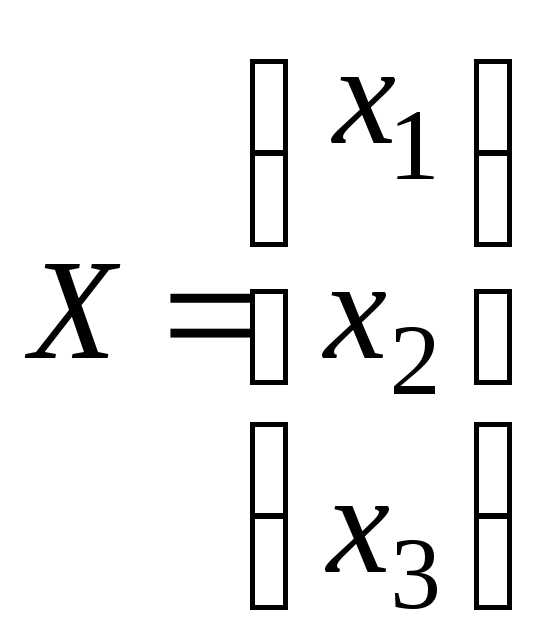
–матрица-столбец свободных членов
–матрица-столбец неизвестных,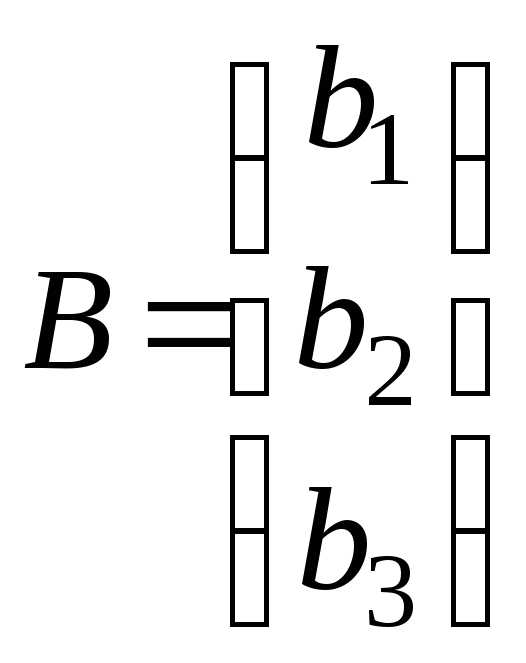
Найдем .
Тогда систему (1) можно записать используя свойство равенства матриц:
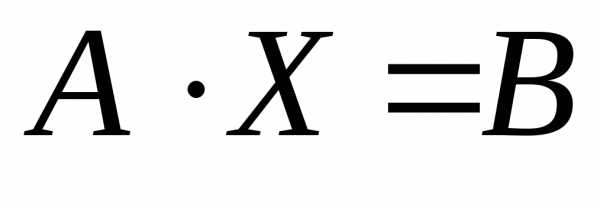 (2) – матричная
запись системы линейных уравнений.
(2) – матричная
запись системы линейных уравнений.
Найдем решение
этого матричного уравнения. Пусть А – невырожденная матрица,
т.е. 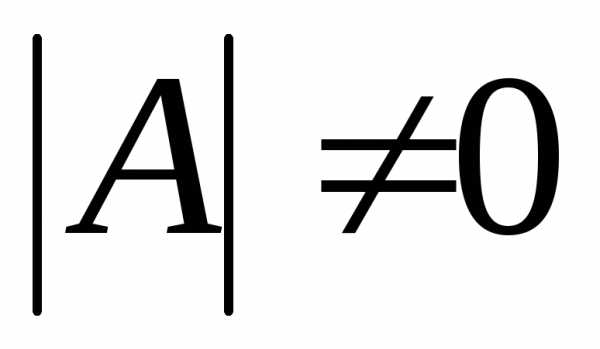 ,
значит
,
значит .
Умножим обе части (2) на
.
Умножим обе части (2) на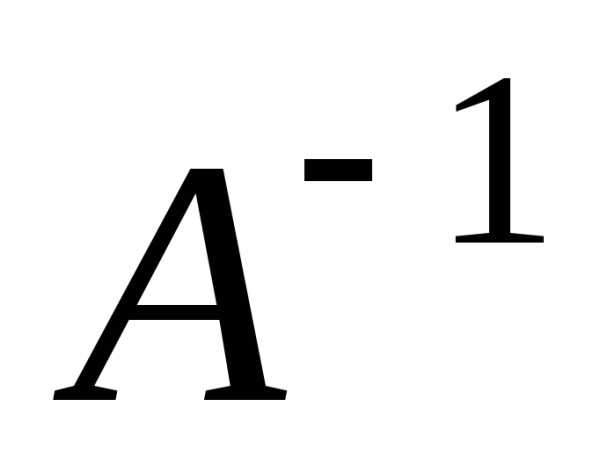
.
Поскольку 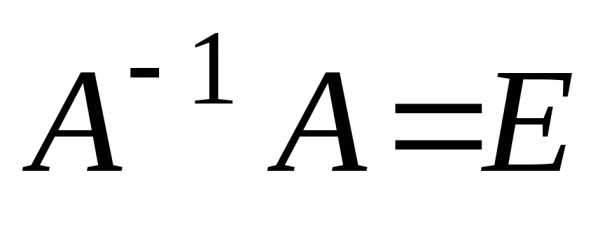
EX= X, значит
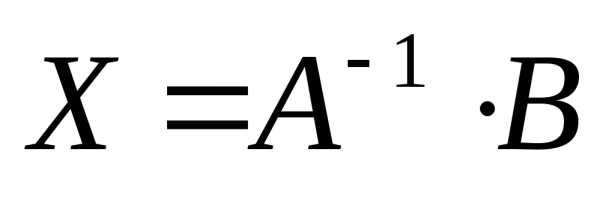 (3)
(3)
– решение (2) и системы (1).
Пример 7.1 Решить систему уравнений матричным методом.
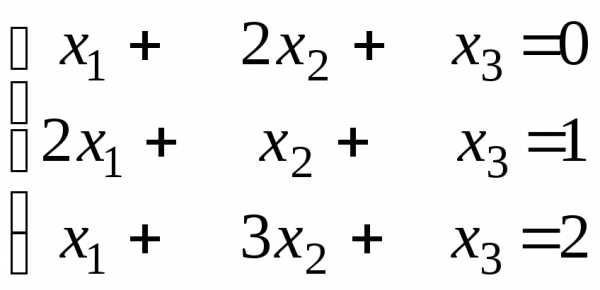
Решение:
–матричная запись системы.
–решение системы.
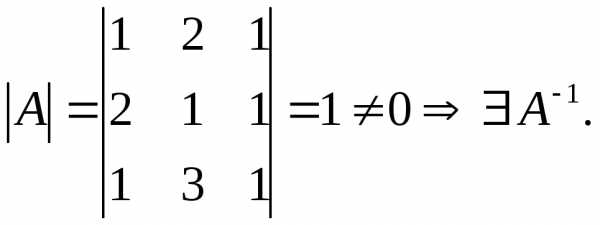
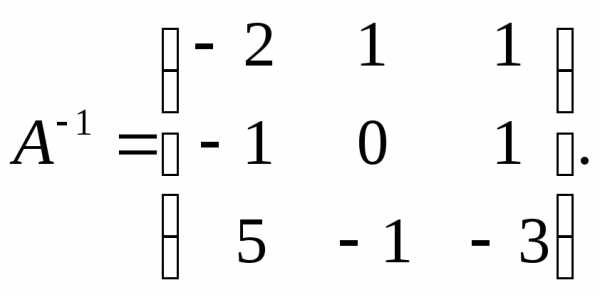
Пример 7.2
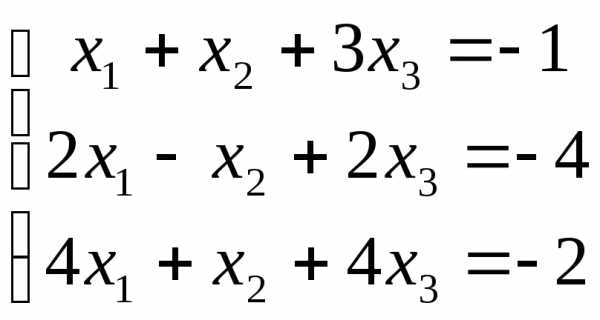 Ответ:
Ответ: 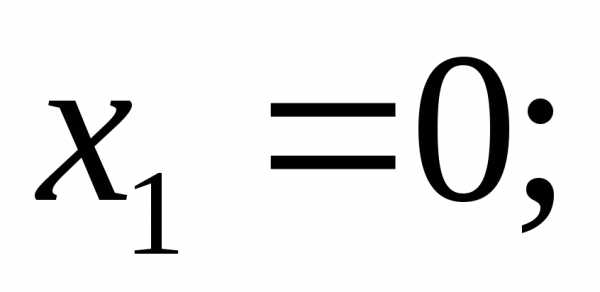
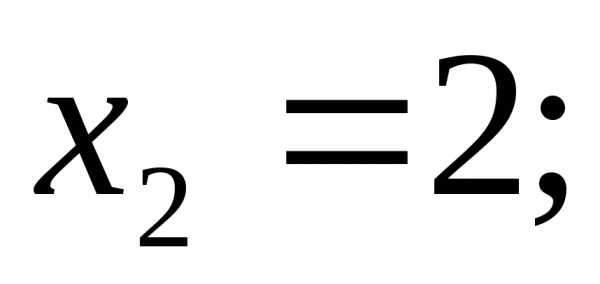
II. Правило Крамера
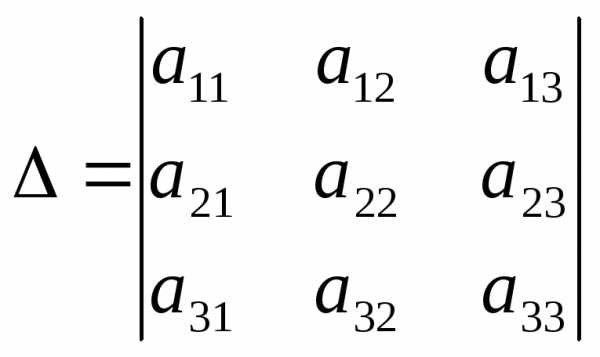 — определитель
системы, составленный из коэффициентов
при неизвестных
— определитель
системы, составленный из коэффициентов
при неизвестных
 ,
,  ,
,
 путем замены соответственно первого,
второго, третьего столбцов столбцом
свободных членов.
путем замены соответственно первого,
второго, третьего столбцов столбцом
свободных членов. 1. Если определитель
системы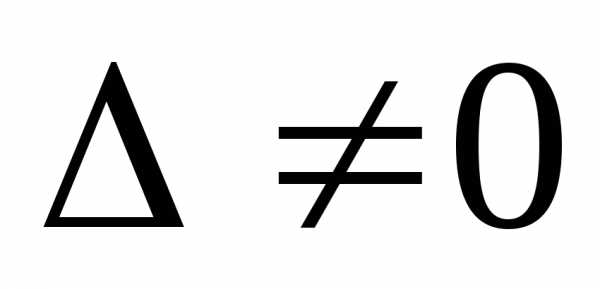 ,
то система имеетединственное
решение:
,
то система имеетединственное
решение: 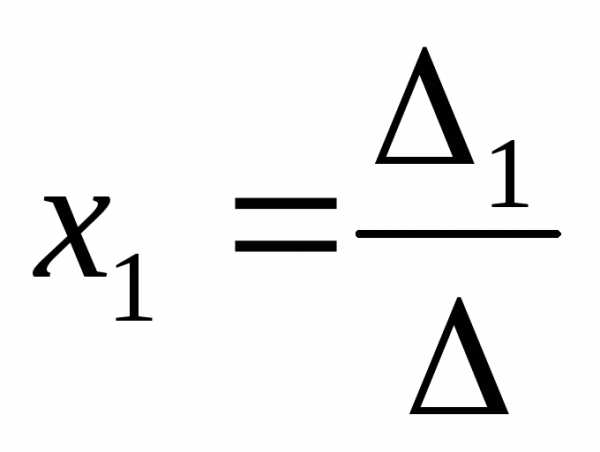 ,
,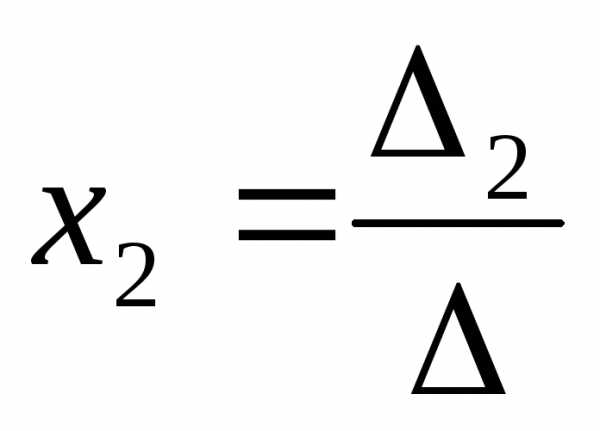 ,
,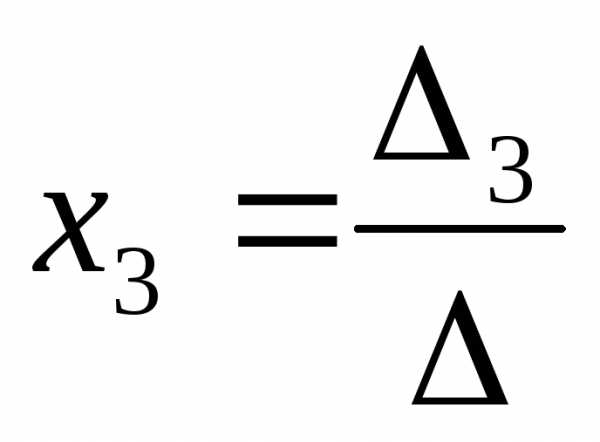 – формулы Крамера;
– формулы Крамера;
2. 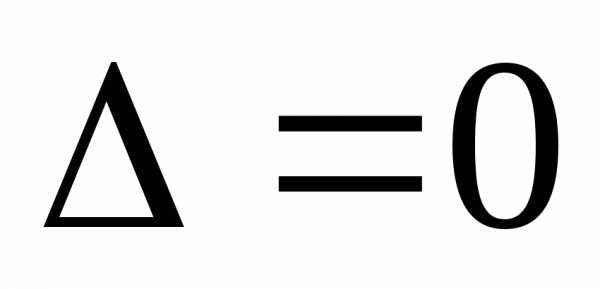
 или
или ,
или
,
или ,
то системане
имеет решений;
,
то системане
имеет решений; 3. 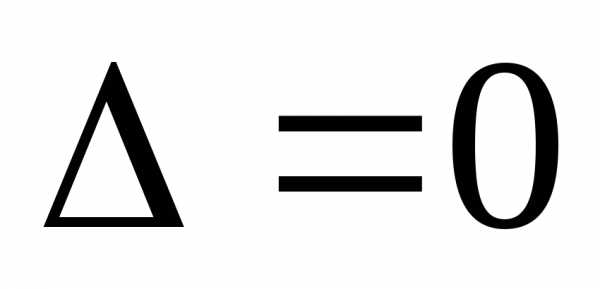 ,,
то система или не имеет решений или
имеет бесконечное множество решений.
,,
то система или не имеет решений или
имеет бесконечное множество решений.
Пример 7.3
Решить систему формулам Крамера.

Замечание. Система двух линейных уравнений с двумя неизвестными
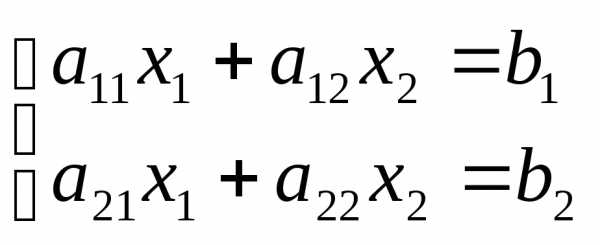
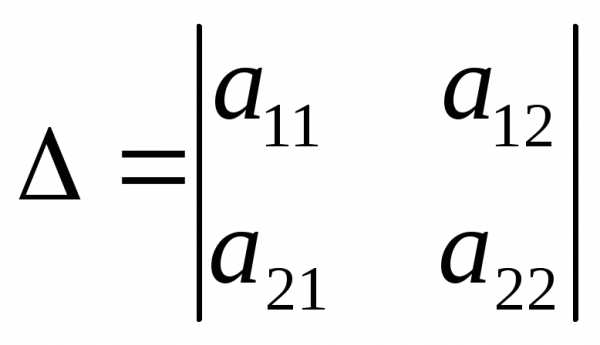
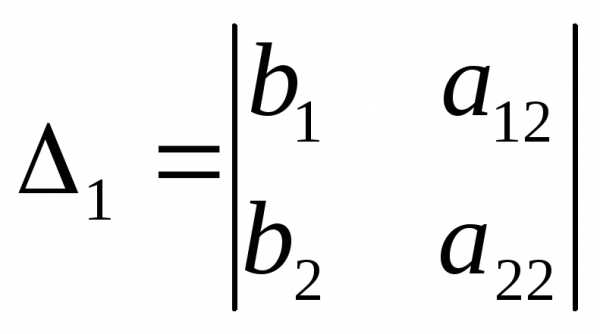
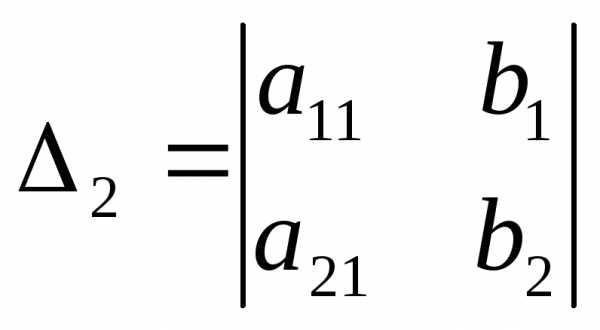
1. 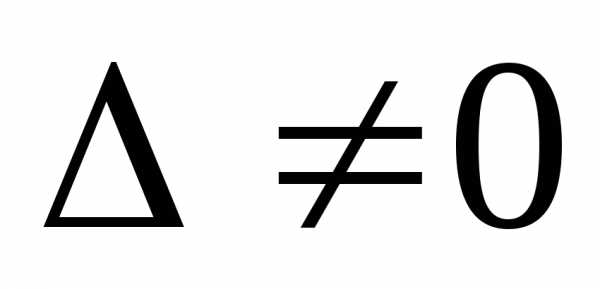 ,
то система имеетединственное
решение:
,
то система имеетединственное
решение: 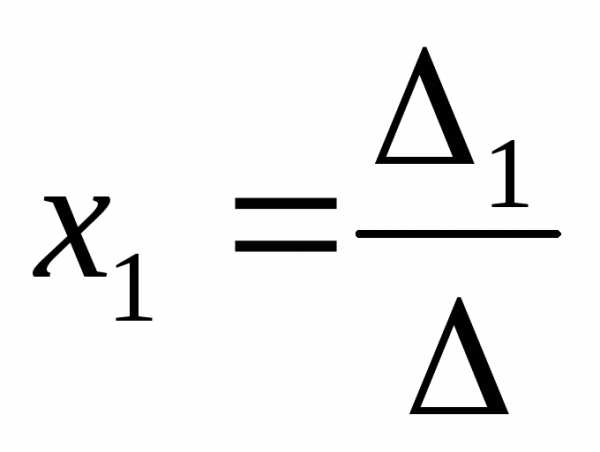 ,
,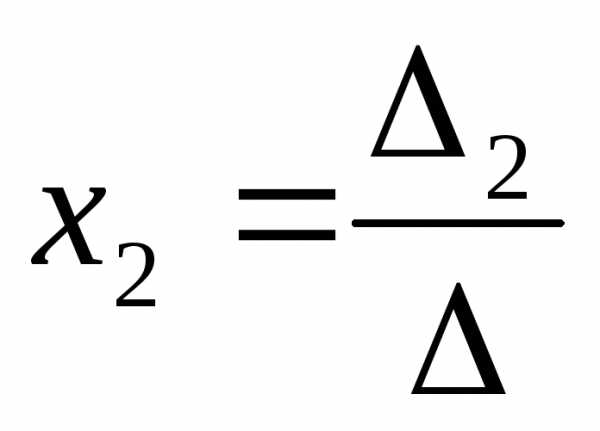 ;
;
2. 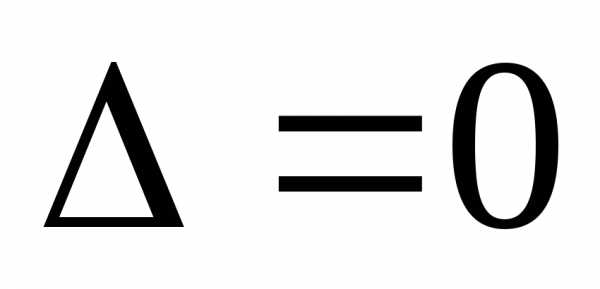
 или
или ,
то системане
имеет решений;
,
то системане
имеет решений; 3. 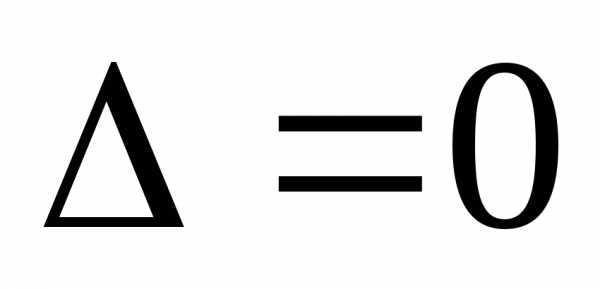 ,,
то система имеет бесконечное множество
решений.
,,
то система имеет бесконечное множество
решений.
§8. Метод Гаусса.
Рассмотрим систему m линейных уравнений с n неизвестными.
Матрицу системы и расширенную матрицу с помощью элементарных преобразований можно свести или к треугольному виду или к ступенчатому виду.
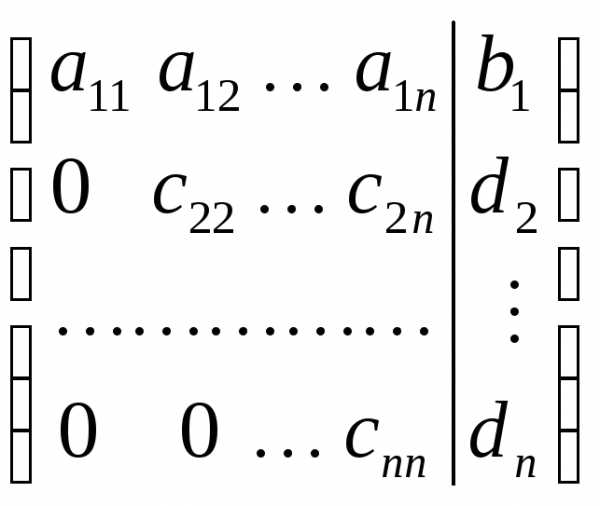 (1)
(1) 
Матрице (1) соответствует система:
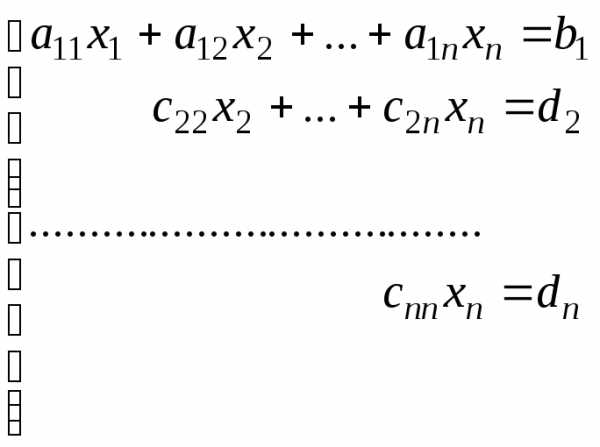
Если а11,
с22,
…сnn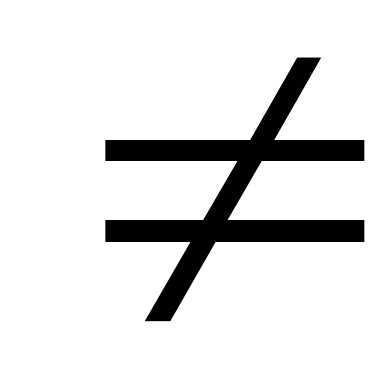 0, то начиная с последнего уравнения найти
единственное
0, то начиная с последнего уравнения найти
единственное
решение xn, xn-1,…,x1.
Если условие а11,
…, сnn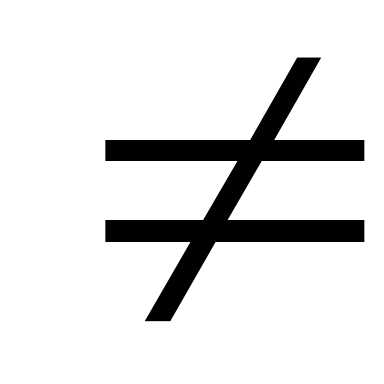 0 не выполняется, то переставить столбцы.
0 не выполняется, то переставить столбцы.
Матрице (2) соответствует система:
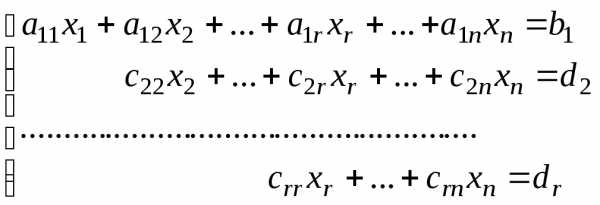
Если a11, c22,…,crr 0,
то r(A)= r(
0,
то r(A)= r( )
=r<n
)
=r<n бесконечное
множество решений.
бесконечное
множество решений.
r базисных неизвестных: x1, x2,…,xr,
где 
(n—r) свободных неизвестных: xr+1, …, xn
Выразить x1,…,xr через xr+1,…,xn.
Замечание. Если в матрице (1) или (2) есть такая i–я строка, у которой все
cij=0, а di0 (противоречивое уравнение), то система
несовместна, так как r(A) r(
r(
Данный метод называется методом Гаусса.
Метод Гаусса позволяет решить систему и исследовать ее на совместность.
Пример 8.1
Решить систему методом Гаусса.
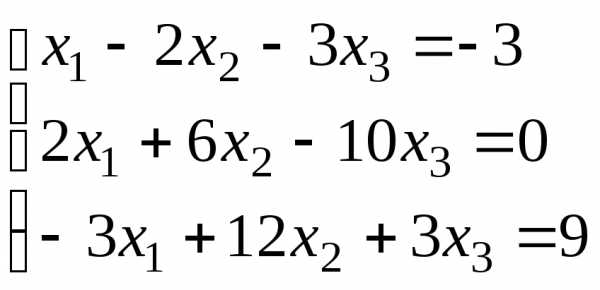
Ответ: 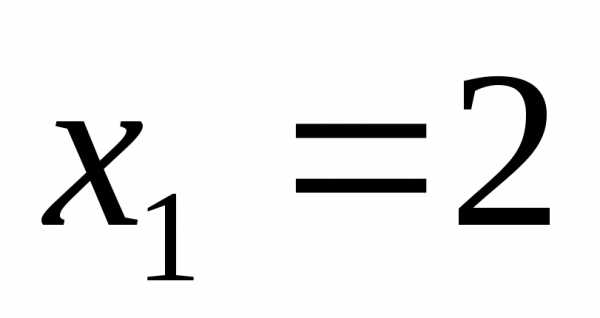 ,
,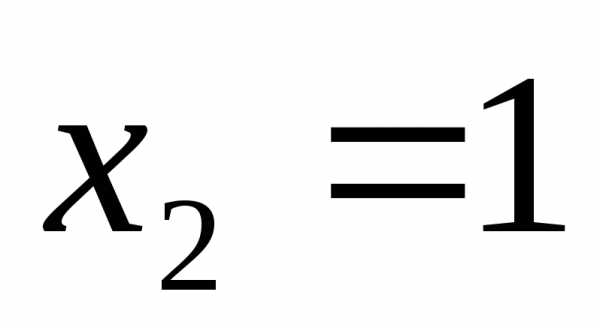 ,
,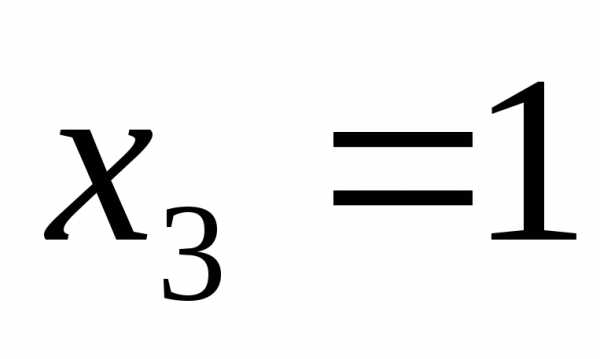
§9. Однородные системы уравнений.
Рассмотрим однородную систему уравнений.
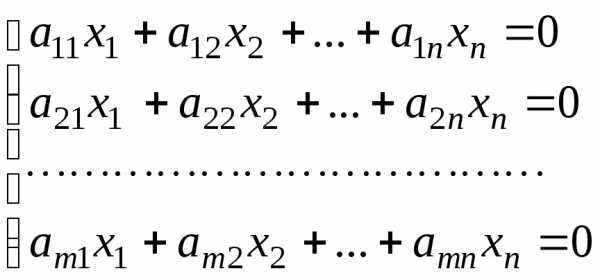
В матричном виде:
,
гдеА=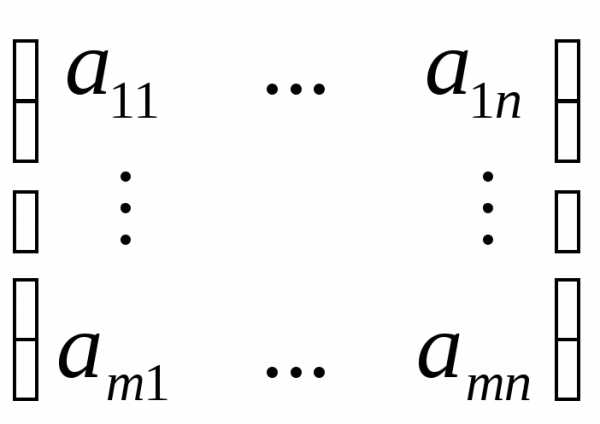 ;Х=
;Х=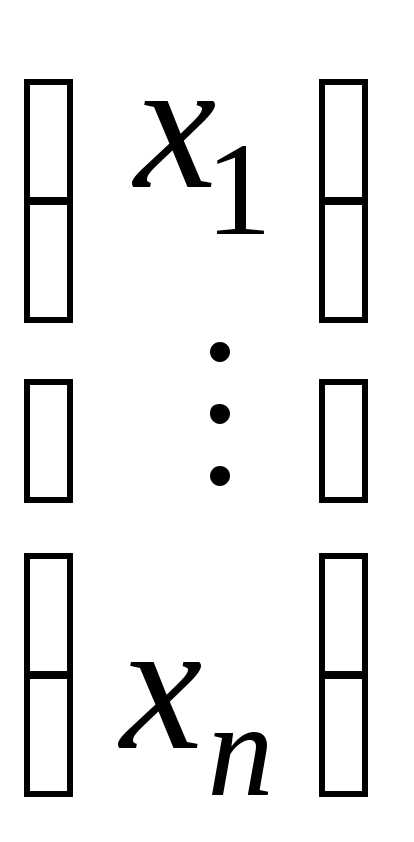 .
.
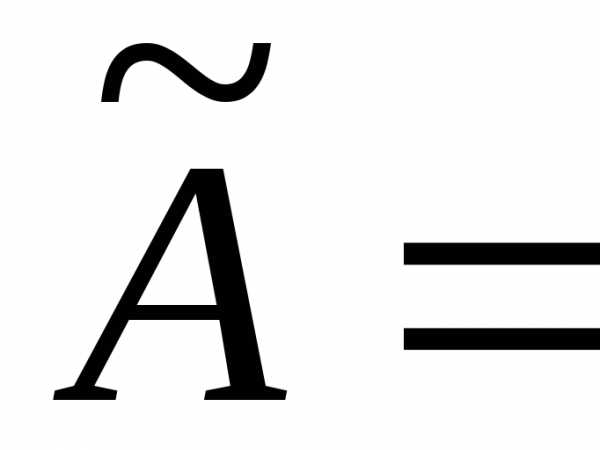
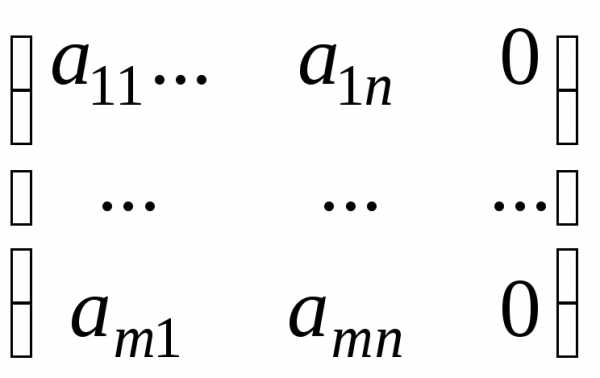 –расширенная
матрица
–расширенная
матрица
А~ (вычеркнув нулевой столбец)однородная система всегда
совместна.
(вычеркнув нулевой столбец)однородная система всегда
совместна.
Возможны два случая:
r = n ( когда
 единственное
решениеx1=…=xn=0
единственное
решениеx1=…=xn=0r<n (когда
 бесконечное
множество решенийx1,…,xr – базисные неизвестные; xr+1,…,xn– свободные
неизвестные.
бесконечное
множество решенийx1,…,xr – базисные неизвестные; xr+1,…,xn– свободные
неизвестные.
Пример 9.1 Исследовать и решить систему
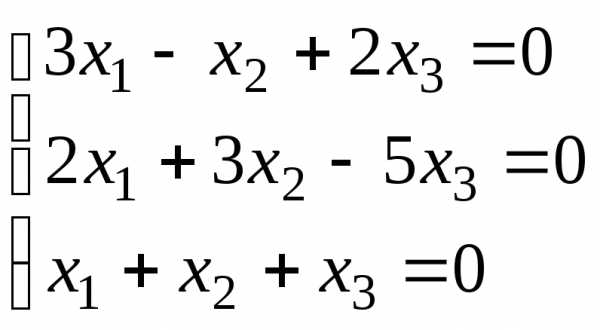
Ответ: 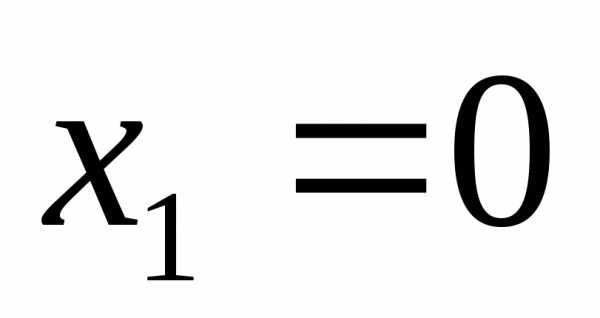 ,
,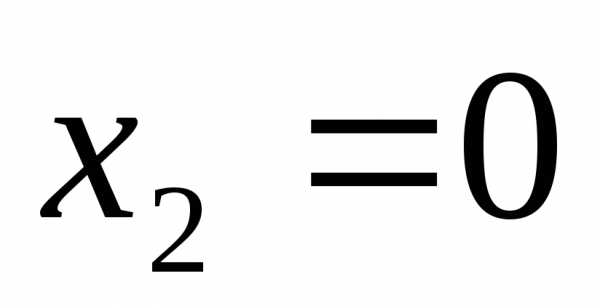 ,
,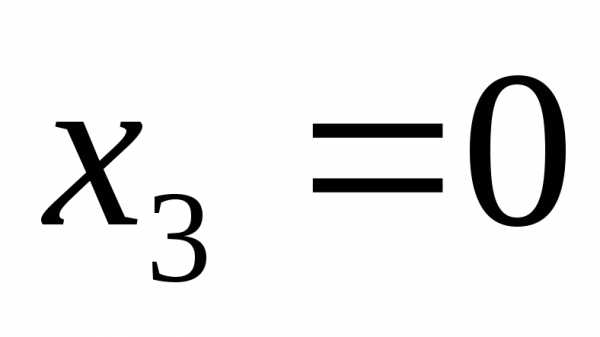
Пример 9.2 Исследовать и решить систему
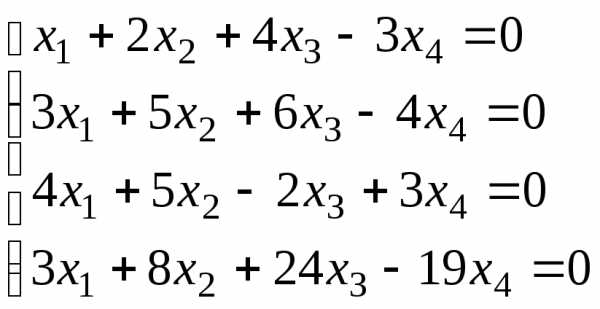
Ответ: бесконечное
множество решений вида ,,где 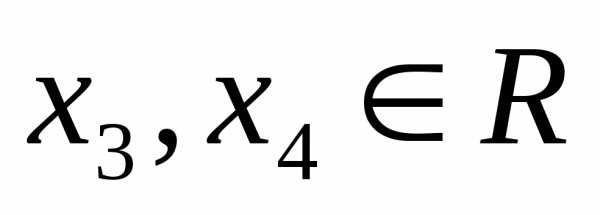
18
studfiles.net
§7. Решение систем n линейных уравнений с n неизвестными матричным методом и по формулам Крамера
матрица столбец определитель уравнение
I. Решение систем матричным методом (с помощью обратной матрицы)
Решение систем n линейных уравнений с n неизвестными матричным методом рассмотрим на примере системы трех линейных уравнений 1-ой степени с тремя неизвестными.
(1)
Обозначим: – матрица системы,
– матрица-столбец неизвестных, —
–матрица-столбец свободных членов
Найдем .
Тогда систему (1) можно записать используя свойство равенства матриц:
(2) – матричная запись системы линейных уравнений.
Найдем решение этого матричного уравнения. Пусть А – невырожденная матрица, т.е. , значит . Умножим обе части (2) на
.
Поскольку , то .
EX= X, значит
(3)
– решение (2) и системы (1).
Пример 7.1 Решить систему уравнений матричным методом.
Решение:
– матричная запись системы.
– решение системы.
Пример 7.2
Ответ:
II. Правило Крамера
— определитель системы, составленный из коэффициентов при неизвестных
, , — определители, полученные из путем замены соответственно первого, второго, третьего столбцов столбцом свободных членов.
1. Если определитель системы, то система имеет единственное решение: , , – формулы Крамера;
2. , или , или , то система не имеет решений;
3. , , то система или не имеет решений или имеет бесконечное множество решений.
Пример 7.3
Решить систему формулам Крамера.
Замечание. Система двух линейных уравнений с двумя неизвестными
1. , то система имеет единственное решение: , ;
2. , или , то система не имеет решений;
3. , , то система имеет бесконечное множество решений.
§8. Метод Гаусса
Рассмотрим систему m линейных уравнений с n неизвестными.
Матрицу системы и расширенную матрицу с помощью элементарных преобразований можно свести или к треугольному виду или к ступенчатому виду.
(1) (2)
Матрице (1) соответствует система:
Если а11, с22, …сnn0, то начиная с последнего уравнения найти единственное
решение xn, xn-1,…,x1.
Если условие а11, …, сnn0 не выполняется, то переставить столбцы.
Матрице (2) соответствует система:
Если a11, c22,…,crr0, то r(A)= r() =r<nбесконечное множество решений.
r базисных неизвестных: x1, x2,…,xr, где
(n-r) свободных неизвестных: xr+1, …, xn
Выразить x1,…,xr через xr+1,…,xn.
Замечание. Если в матрице (1) или (2) есть такая i–я строка, у которой все
cij=0, а di0 (противоречивое уравнение), то система несовместна, так как r(A)r().
Данный метод называется методом Гаусса.
Метод Гаусса позволяет решить систему и исследовать ее на совместность.
Пример 8.1
Решить систему методом Гаусса.
Ответ: , ,
§9. Однородные системы уравнений
Рассмотрим однородную систему уравнений.
В матричном виде: , где А=; Х=.
– расширенная матрица
А~ (вычеркнув нулевой столбец) однородная система всегда совместна.
Возможны два случая:
r = n ( когда единственное решение x1=…=xn=0
r<n (когда бесконечное множество решений x1,…,xr – базисные неизвестные; xr+1,…,xn – свободные неизвестные.
Пример 9.1 Исследовать и решить систему
Ответ: , ,
Пример 9.2 Исследовать и решить систему
Ответ: бесконечное множество решений вида , , где
studfiles.net
Система n линейных уравнений с n переменными. Метод обратной матрицы и формулы Крамера
Пусть m=n.
Тогда матрица системы является квадратной
, а ее определитель 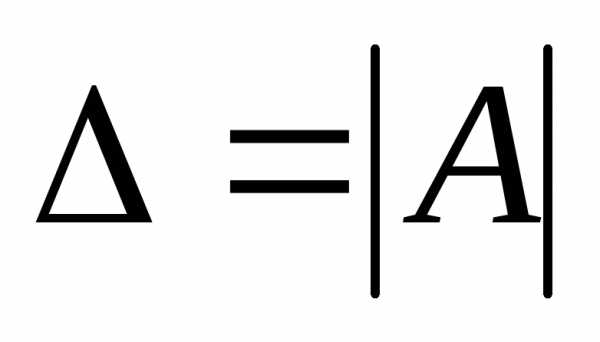 называетсяопределителем
системы.
называетсяопределителем
системы.
Предположим, что
квадратная матрица 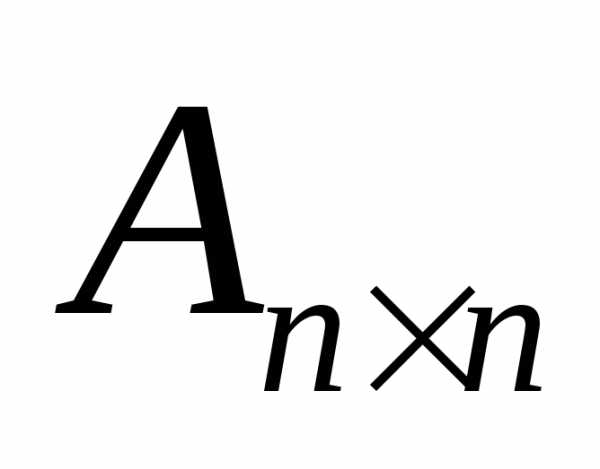 невырожденная, т.е.
невырожденная, т.е.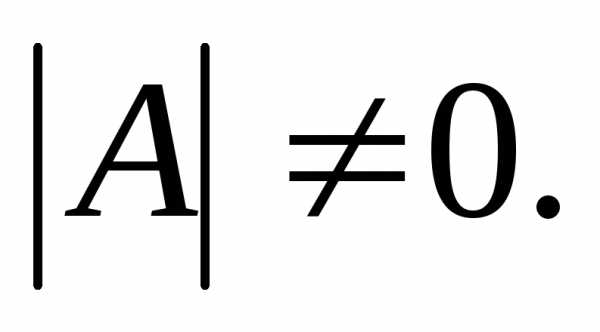
В этом случае
существует 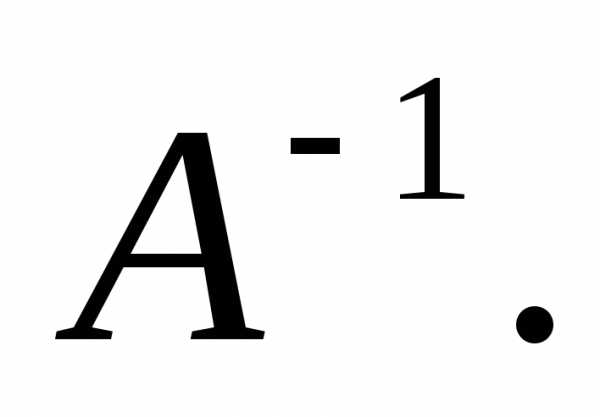
Умножим слева обе
части (3) на матрицу  получим
решение системы методом обратной
матрицы:
получим
решение системы методом обратной
матрицы:
Отсюда видно, что вектор решения системы уравнений получается, если вектор свободных членов умножить слева на матрицу, обратную к матрице системы. Поэтому в методе обратной матрицы главным является обращение матрицы.
Другим способом решения системы уравнений с квадратной матрицей является использование формул Крамера.
Теорема Крамера.
Пусть  -определитель
матрицы системы А, а
-определитель
матрицы системы А, а -определитель
матрицы, получаемый из А заменойj-го
столбца столбцом свободных членов.
Тогда, если
-определитель
матрицы, получаемый из А заменойj-го
столбца столбцом свободных членов.
Тогда, если  ,
то система имеет единственное решение,
определяемое по формулам:
,
то система имеет единственное решение,
определяемое по формулам:
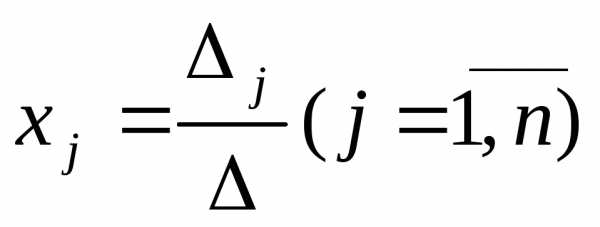 (5)
(5)
Формулы (5) называются формулами Крамера.
Недостаток формул Крамера и метода обратной матрицы- их большая трудоемкость, связанная с вычислением определителей и нахождением обратной матрицы. Эти методы представляют скорее теоретический интерес и на практике не могут быть использованы для решения реальных задач.
Пример. Решить по формулам Крамера и методом обратной матрицы следующую систему уравнений:
Для применения формул Крамера вычислим определитель системы :
2 -1 -1
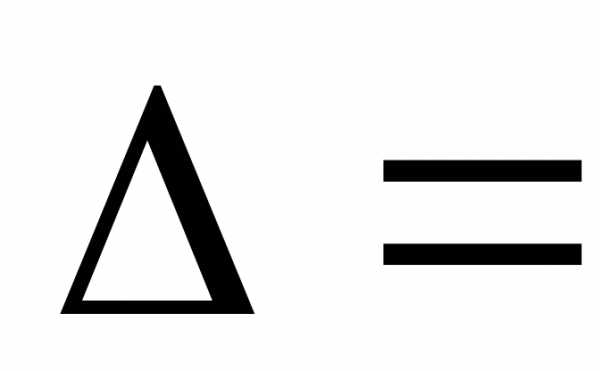 3 4 -2 = 60
3 4 -2 = 60
3 -2 4
Заменим в определителе системы первый столбец на столбец свободных членов, вычислим полученный определитель:
4 -1 -1
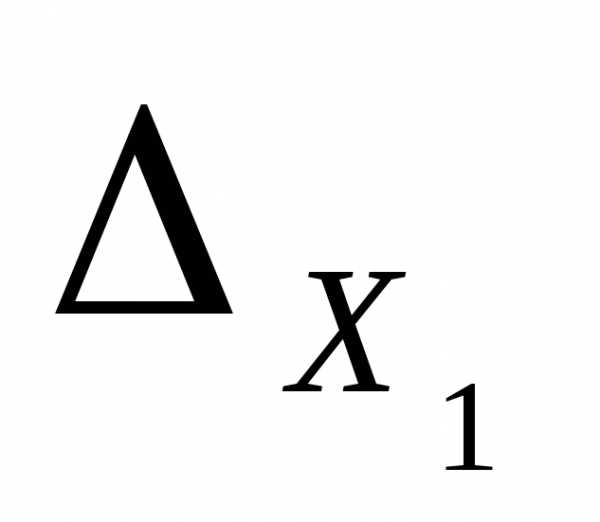 =11 4 -2 =180
=11 4 -2 =180
11 -2 4
Заменим в определителе системы второй столбец на столбец свободных членов, вычислим полученный определитель:
2 4 -1
3 11 -2
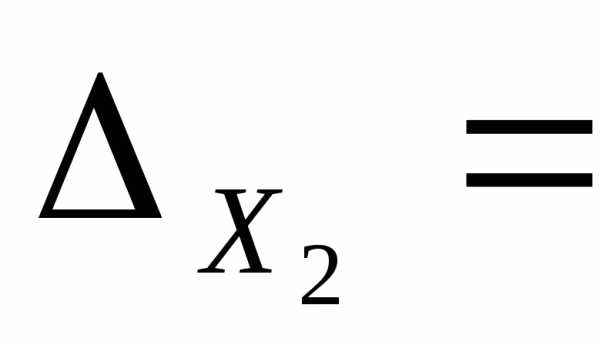 3 11 4 =60
3 11 4 =60
Заменим в определителе системы третий столбец на столбец свободных членов, вычислим полученный определитель:
2 -1 4
3 4 11
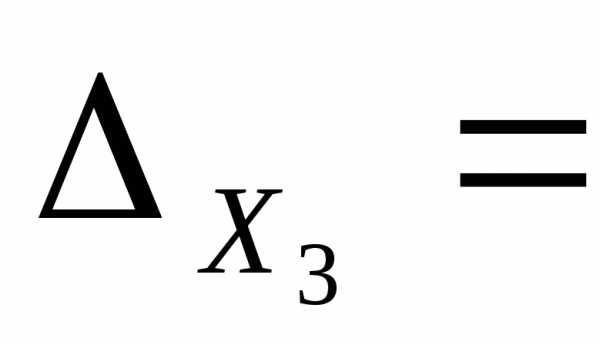 3 -2 11 =60.
3 -2 11 =60.
Вычислим значения неизвестных:
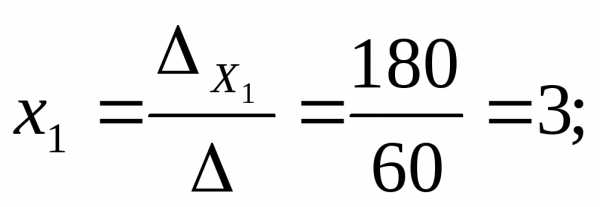
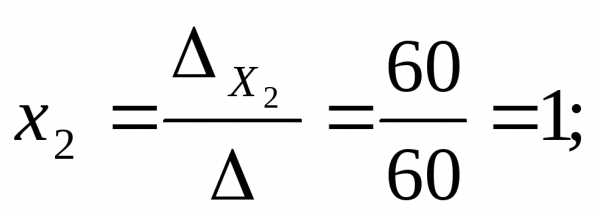
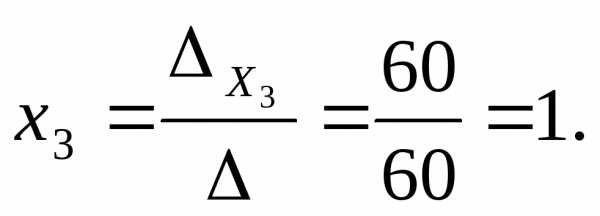
Для применения метода обратной матрицы представим систему уравнений в матричной форме:
2-1 -1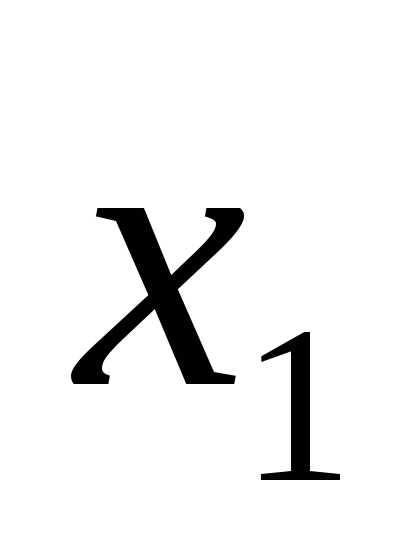 4
4
3
4 -2 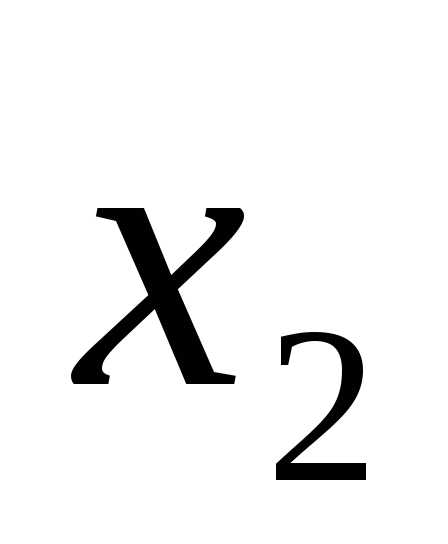 = 11
= 11
3 -2
4 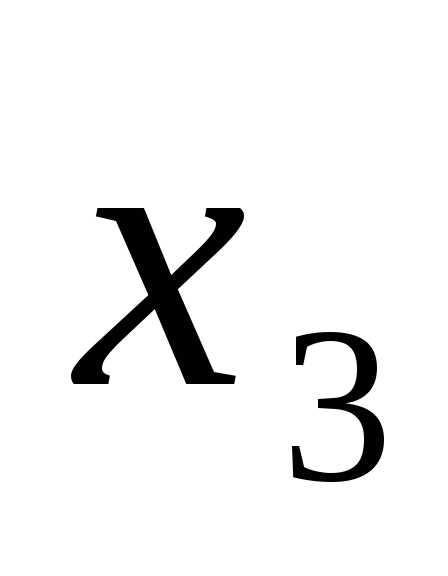 11
11
Далее рассчитываем обратную матрицу:
12 6 6

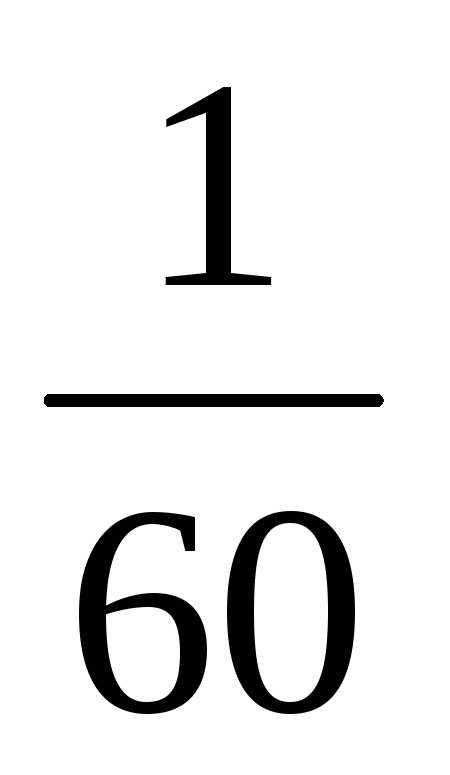 -18 11 1
-18 11 1
-18 1 11
По формуле (4) получаем решение:
12 6 6 4 3
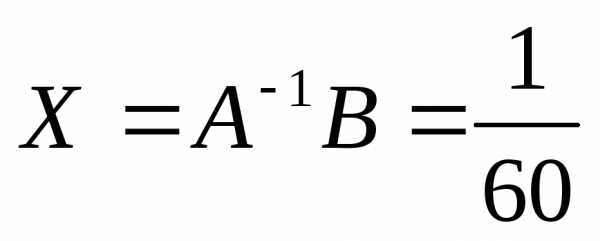 -18 11 1 11
= 1
-18 11 1 11
= 1
-18 1 11 11 1
Метод Гаусса
Метод Гаусса— метод последовательного исключения неизвестных- заключается в том, что с помощью элементарных преобразований система уравнений приводиться к равносильной системе ступенчатого или треугольного вида, из которой последовательно, начиная с последних переменных, находятся все остальные переменные.
Предположим, что
в системе (1) 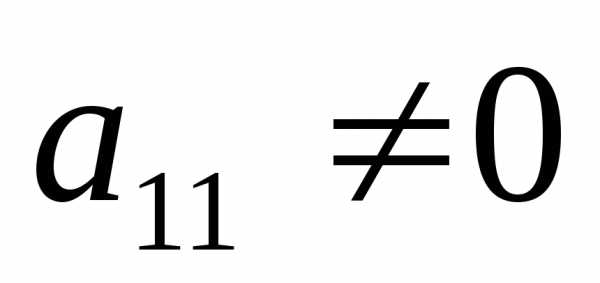 ( этого всегда можно добиться перестановкой
уравнений)
( этого всегда можно добиться перестановкой
уравнений)
Шаг
1. Умножим
1-ое уравнение на 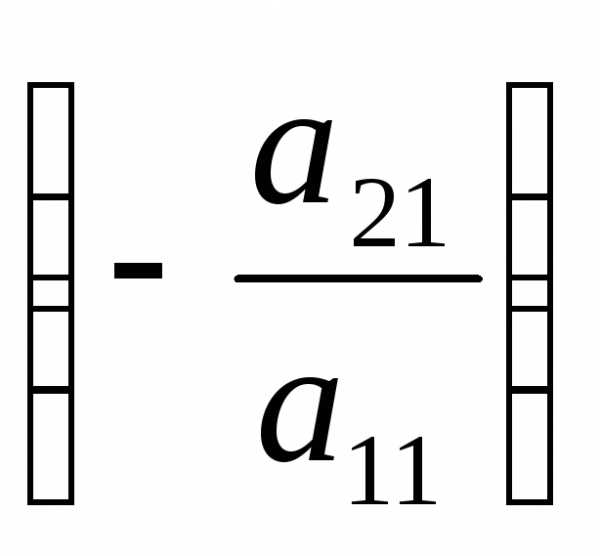 и прибавим ко второму; затем умножим
1-ое уравнение на
и прибавим ко второму; затем умножим
1-ое уравнение на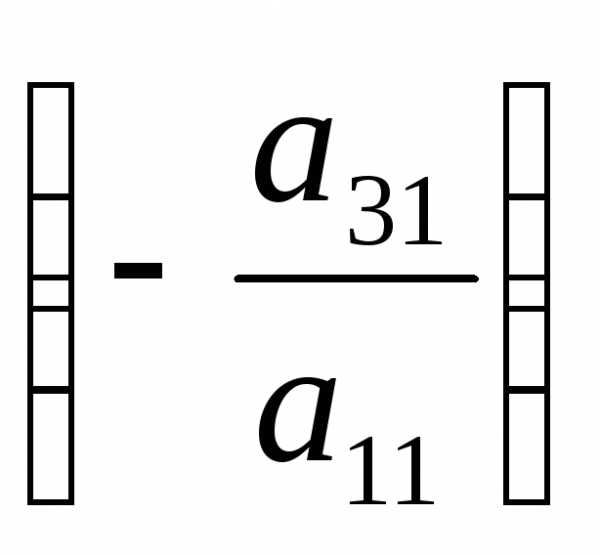 и прибавим к третьему, и т.д., и , наконец,
умножим 1-ое уравнение на
и прибавим к третьему, и т.д., и , наконец,
умножим 1-ое уравнение на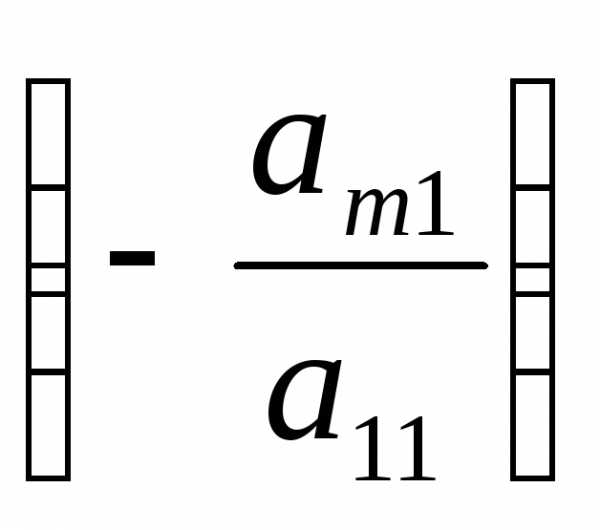 и прибавим кm-му
уравнению. Получим преобразованную
систему уравнений, в которой
и прибавим кm-му
уравнению. Получим преобразованную
систему уравнений, в которой 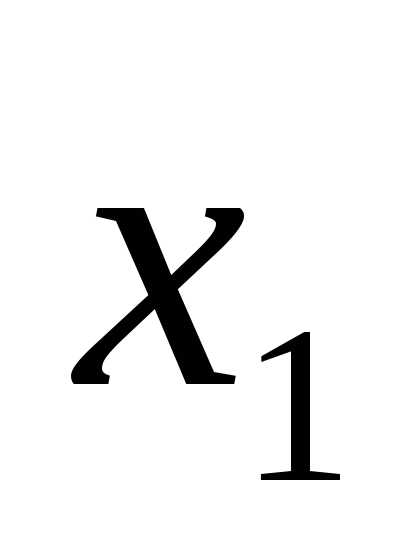 исключено
из всех уравнений, кроме первого:
исключено
из всех уравнений, кроме первого:
……………………….. ( 6)
Здесь коэффициенты с верхним индексом (1) получены после 1-ого шага.
Шаг
2. Предположим,
что 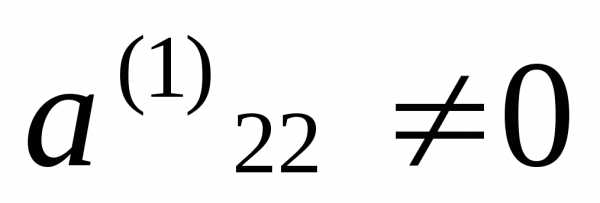 .(этого
всегда можно добиться перестановкой
уравнений с перенумерацией).
.(этого
всегда можно добиться перестановкой
уравнений с перенумерацией).
Умножаем
2-ое уравнение на числа —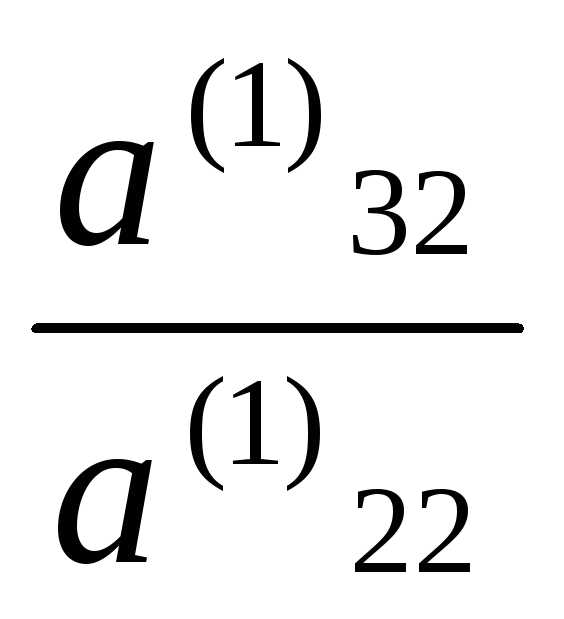 ,
, , …,
, …,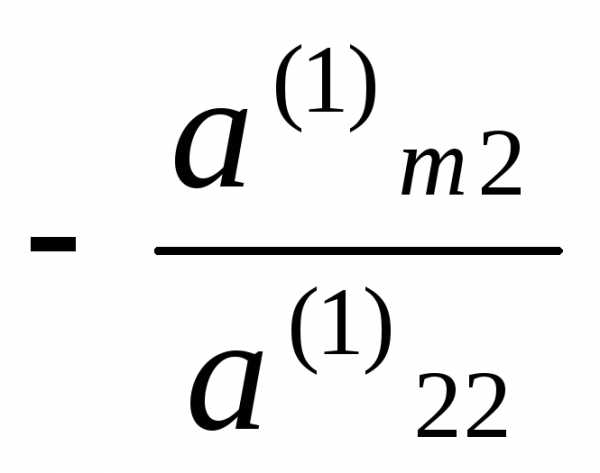 и прибавим полученные уравнения
соответственно к третьему, четвертому,
и прибавим полученные уравнения
соответственно к третьему, четвертому,
…,m-му
уравнению системы (6), исключая 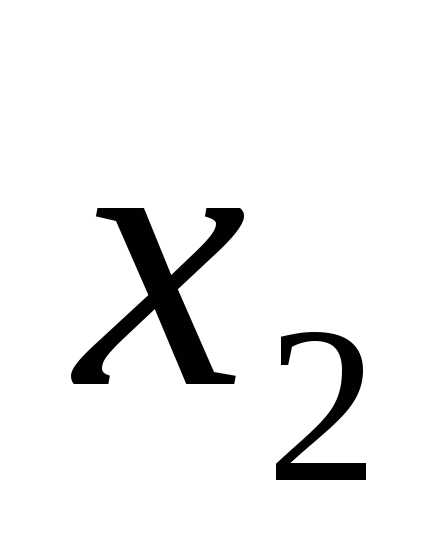 из всех уравнений, начиная с третьего.
из всех уравнений, начиная с третьего.
Продолжая процесс последовательного исключения переменных, после (r-1)- го шага получим систему:
………………………………….
(7)
…………
Если хотя бы одно из чисел не равно нулю, то соответствущее равенство противоречиво, и система (1) несовместна. Для любой совместной системы (m-r) уравнений в системе (7) являются тождествами, и их можно не принимать во внимание при решении системы (1). После отбрасывания « лишних» уравнений возможны два случая:
А) r=n , и в этом случае система (7) имеет треугольный вид;
Б) r<n, и система (7) имеет ступенчатый вид.
Переход системы (1) к равносильной системе (7) называется прямым ходом метода Гаусса, а нахождение переменных из системы (7)- обратным ходом .
Преобразования Гаусса удобно проводить не с самими уравнениями, а с расширенной матрицей системы (1), в которую, кроме матрицы А, дополнительно включен столбец свободных членов.
Пример. Решить методом Гаусса систему уравнений:
Расширенная матрица системы имеет вид:
12 3 -2 6
2 4 -2 -3 18
3 2 -1 2 4
2 –3 2 1 -8
Теперь
все действия над уравнениями будут
эквивалентны действиям над строками
матрицы. Умножаем 1-ую строку на —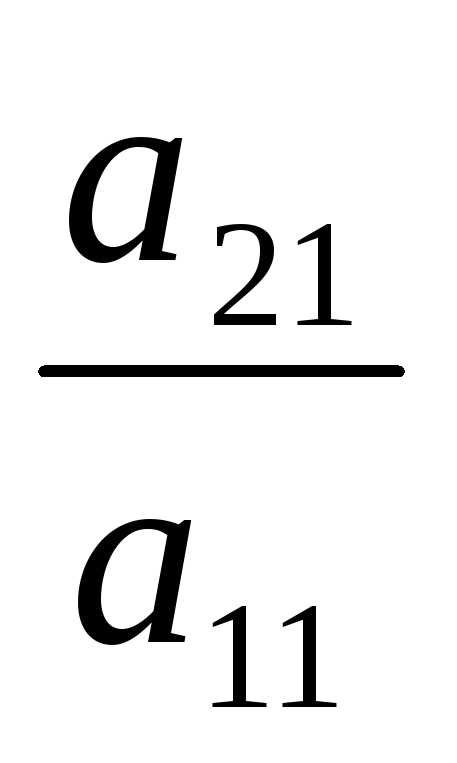 , т.е. на —
, т.е. на — = -2, получаем
= -2, получаем
(-2 -4 -6 4 -12)
эту строку прибавляем ко второй строке, получаем новую 2-ю строку:
0 -8 1 6).
Аналогично умножим 1-ую строку на (-3) и сложим с третьей строкой; умножим 1-ую строку на (-2) и сложим с 4-ой строкой. Расширенная матрица после 1-ого шага имеет вид:
23 -2 6
0 0 -8 1 6
-4 -10 8 -14
0 -7 -4 5 -20
Первая строка при преобразованиях Гаусса остается без изменений. Для дальнейшего хода необходимо переставить 2-ую и 3-ю строки ,чтобы
2 3 -2 6
0 -4 -10 8 -14
0 0 -8 1 6
0 -7 -4 5 -20
На
2-ом шаге, поскольку 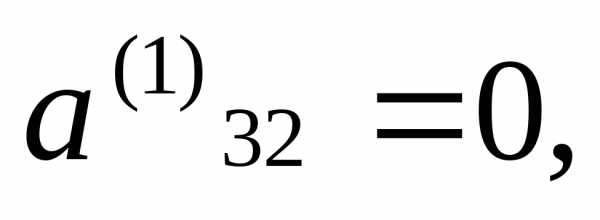 требуется
только обнулить элементДля
этого 2-ое уравнение умножим на
требуется
только обнулить элементДля
этого 2-ое уравнение умножим на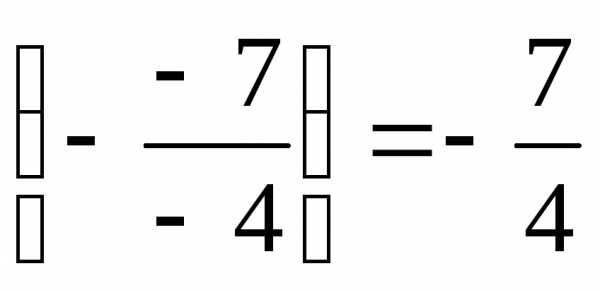 и сложим с 4-м уравнением. 2-ое уравнение
после умножения выглядит так:
и сложим с 4-м уравнением. 2-ое уравнение
после умножения выглядит так:
(
0 7 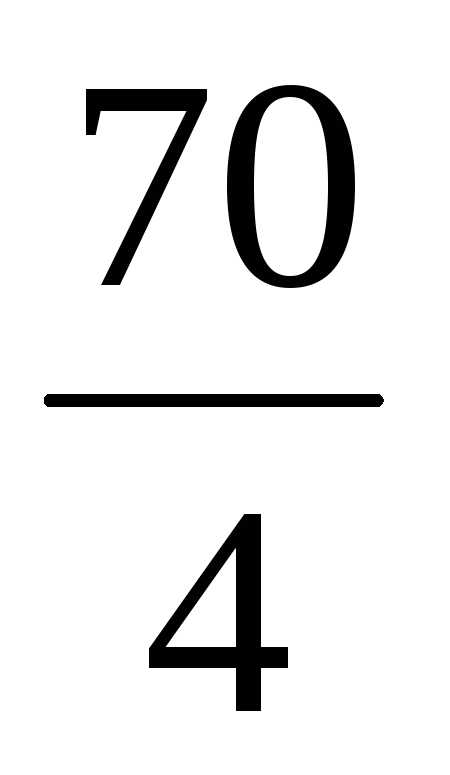 —
—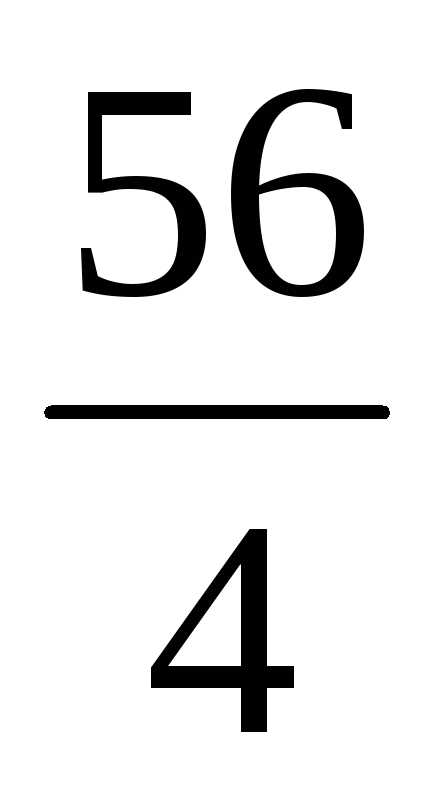
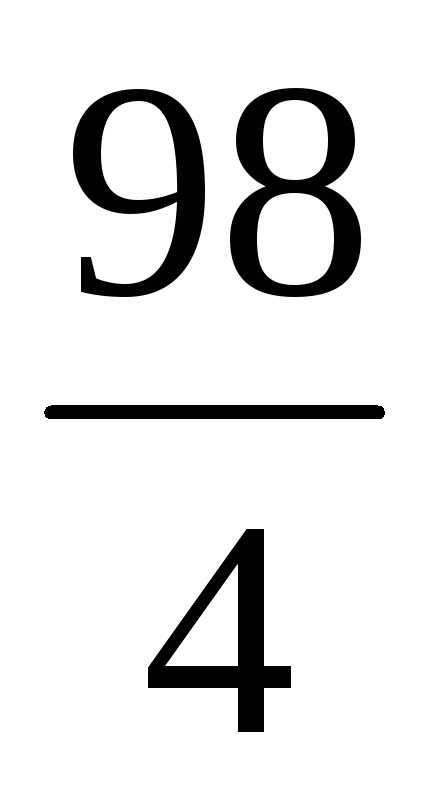 )
)
После 2-го шага матрица имеет вид:
12 3 -2 6
0 -4 -10 8 -14
0 0 -8 1 6
0 0 54/4 -36/4 -18/4
Поскольку в элементах последней строки одинаковый знаменатель, исключаем его; кроме того, можно сократить всю 4-ую строку на общий множитель 18:
12 3 -2 6
0 -4 -10 8 -14
0 0 -8 1 6
0 0 3 -2 1
На
3-м шаге исключаем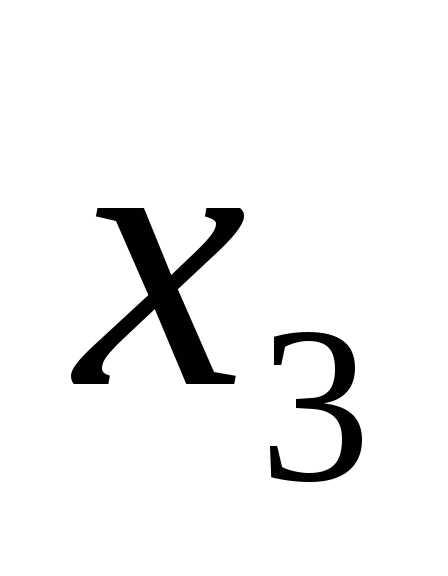 из 4-ого уравнения; для этого умножим
3-ю строку на 3/8 и сложим с 4-ой строкой:
из 4-ого уравнения; для этого умножим
3-ю строку на 3/8 и сложим с 4-ой строкой:
12 3 -2 6
0 -4 -10 8 -14
0 0 -8 1 6
0 0 0 -13/8 26
Теперь матрица системы имеет треугольный вид: все элементы ниже главной диагонали равны нулю.
Далее совершаем обратный ход метода Гаусса. 4-ое уравнение системы можно записать так:
оно
имеет решение: 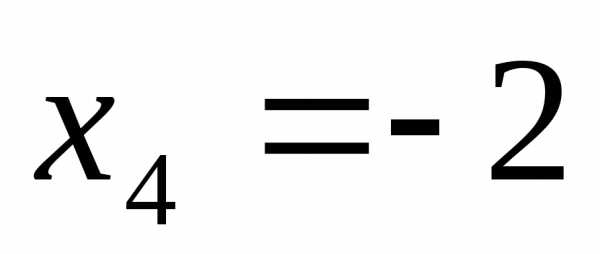 .
.
Подставляем полученное значение в 3-е уравнение:
Теперь
в 3-м уравнении только одно неизвестное 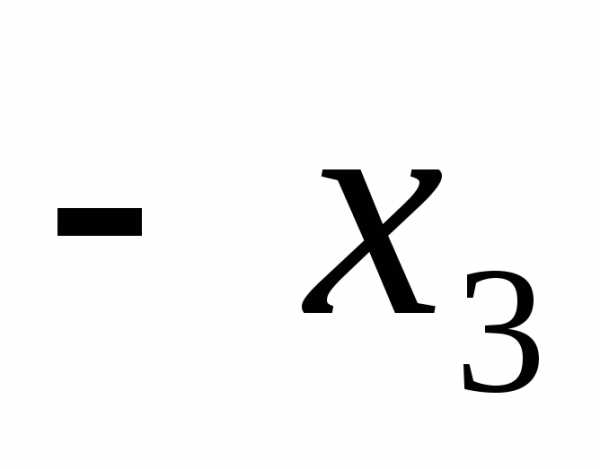 .Решаем
уравнение, получаем
.Решаем
уравнение, получаем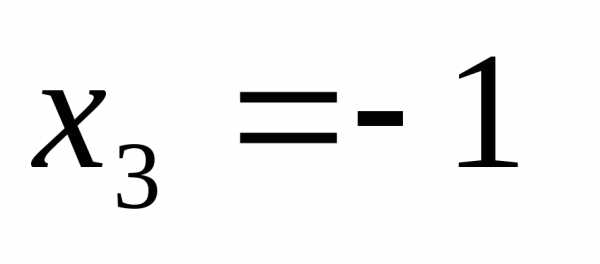 .
Далее подставим известные
.
Далее подставим известные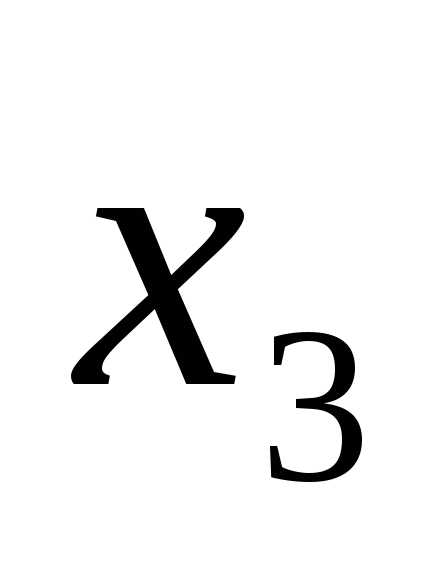 и
и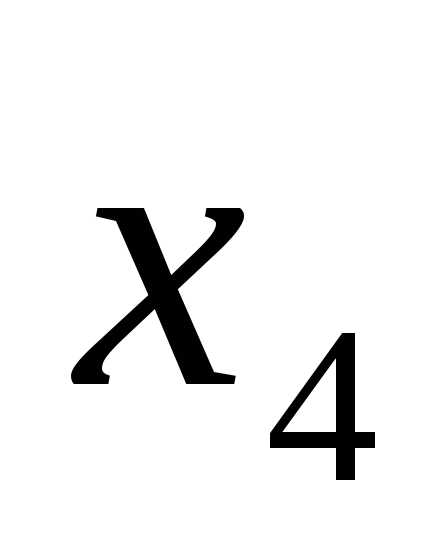 во
второе уравнение:
во
второе уравнение:
Отсюда 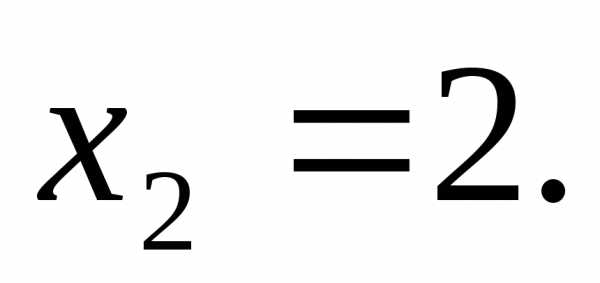
Подставляем
в 1-ое уравнение известные 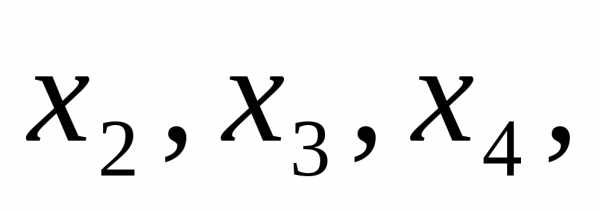 получаем
решение:
получаем
решение:
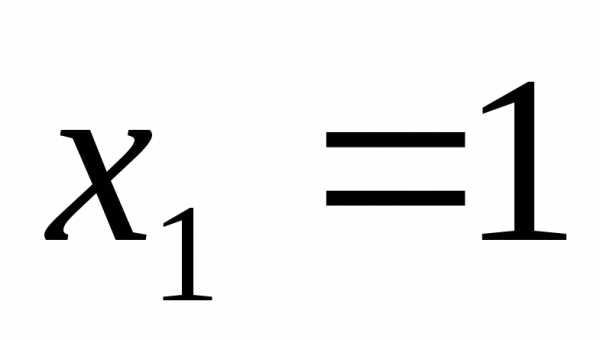
Вопросы для самоконтроля:
Чем отличается СЛАУ от систем произвольных уравнений?
Привести примеры определенной и неопределенной СЛАУ.
Какие основные методы решения СЛАУ?
studfiles.net

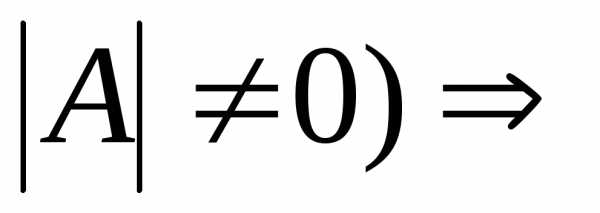 единственное
решениеx1=…=xn=0
единственное
решениеx1=…=xn=0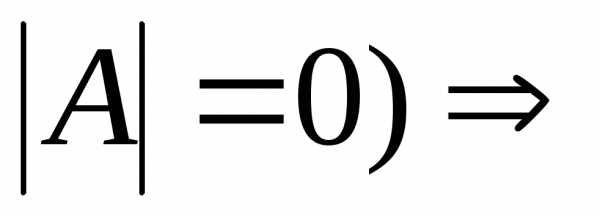 бесконечное
множество решенийx1,…,xr – базисные неизвестные; xr+1,…,xn– свободные
неизвестные.
бесконечное
множество решенийx1,…,xr – базисные неизвестные; xr+1,…,xn– свободные
неизвестные.