Формула площади выпуклого четырехугольника – Площадь выпуклого четырехугольника

Формулы площади выпуклого четырехугольника — Студопедия.Нет

Формулы площади треугольника

1. Формула площади треугольника по стороне и высоте
   Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты

1. Формула площади треугольника по трем сторонам

Формула Герона

S = √p(p — a)(p — b)(p — c)

1. Формула площади треугольника по двум сторонам и углу между ними
   Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

1. Формула площади треугольника по трем сторонам и радиусу описанной окружности

1. Формула площади треугольника по трем сторонам и радиусу вписанной окружности
   Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

1. где S — площадь треугольника,
   a, b, c — длины сторон треугольника,
   h — высота треугольника,
   γ — угол между сторонами a и b,
   r — радиус вписанной окружности,
   R — радиус описанной окружности,

p =	a + b + c	— полупериметр треугольника.
	2

 

Формулы площади квадрата

1. Формула площади квадрата по длине стороны
   Площадь квадрата равна квадрату длины его стороны.

S = a²

1. Формула площади квадрата по длине диагонали
   
   Площадь квадрата равна половине квадрата длины его диагонали.

где S — площадь квадрата,
a — длина стороны квадрата,
d — длина диагонали квадрата.

 

Формула площади прямоугольника

Площадь прямоугольника равна произведению длин двух его смежных сторон

S = a · b

где S — Площадь прямоугольника,
a, b — длины сторон прямоугольника.

 

 

Формулы площади параллелограмма

1. Формула площади параллелограмма по длине стороны и высоте
   Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.

S = a · h

1. Формула площади параллелограмма по двум сторонам и углу между ними
   Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.

S = a · b · sin α

1. Формула площади параллелограмма по двум диагоналям и углу между ними
   Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.

1. где S — Площадь параллелограмма,
   a, b — длины сторон параллелограмма,
   h — длина высоты параллелограмма,
   d₁, d₂ — длины диагоналей параллелограмма,
   α — угол между сторонами параллелограмма,
   γ — угол между диагоналями параллелограмма.

 

Формулы площади ромба

1. Формула площади ромба по длине стороны и высоте
   Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.

S = a · h

1. Формула площади ромба по длине стороны и углу
   
   Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.

S = a² · sin α

1. Формула площади ромба по длинам его диагоналей
   Площадь ромба равна половине произведению длин его диагоналей.

1. где S — Площадь ромба,
   a — длина стороны ромба,
   h — длина высоты ромба,
   α — угол между сторонами ромба,
   d₁, d₂ — длины диагоналей.

 

Формулы площади трапеции

1. Формула Герона для трапеции

S =	a + b	√(p-a)(p-b)(p-a-c)(p-a-d)
	|a — b|

1. Формула площади трапеции по длине основ и высоте
   Площадь трапеции равна произведению полусуммы ее оснований на высоту

где S — площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,

p =	a + b + c + d	— полупериметр трапеции.
	2

 

 

Формулы площади выпуклого четырехугольника

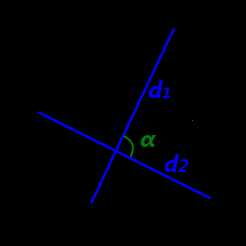
1. Формула площади четырехугольника по длине диагоналей и углу между ними Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:

где S — площадь четырехугольника,
d

1, d₂ — длины диагоналей четырехугольника,
α — угол между диагоналями четырехугольника.

1. Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
   Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности

S = p · r

3.

studopedia.net

Формулы площади. Площадь треугольника, квадрата, прямоугольника, ромба, параллелограмма, трапеции, круга, эллипса.

Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц. Формулы площади треугольника Формула площади треугольника по стороне и высоте Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты Формула площади треугольника по трем сторонам Формула Герона S = √p(p — a)(p — b)(p — c) Формула площади треугольника по двум сторонам и углу между ними Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними. S =  1 a · b · sin γ 2 Формула площади треугольника по трем сторонам и радиусу описанной окружности Формула площади треугольника по трем сторонам и радиусу вписанной окружности Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. где S — площадь треугольника, a, b, c — длины сторон треугольника, h — высота треугольника, γ — угол между сторонами a и b, r — радиус вписанной окружности, R — радиус описанной окружности, p =  a + b + c   — полупериметр треугольника. 2 Формулы площади квадрата Формула площади квадрата по длине стороны Площадь квадрата равна квадрату длины его стороны. S = a2 Формула площади квадрата по длине диагонали Площадь квадрата равна половине квадрата длины его диагонали. где S — Площадь квадрата, a — длина стороны квадрата, d — длина диагонали квадрата. Формула площади прямоугольника Площадь прямоугольника равна произведению длин двух его смежных сторон S = a · b где S — Площадь прямоугольника, a, b — длины сторон прямоугольника. Формулы площади параллелограмма Формула площади параллелограмма по длине стороны и высоте Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты. S = a · h Формула площади параллелограмма по двум сторонам и углу между ними Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними. S = a · b · sin α Формула площади параллелограмма по двум диагоналям и углу между ними Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними. где S — Площадь параллелограмма, a, b — длины сторон параллелограмма, h — длина высоты параллелограмма, d1, d2 — длины диагоналей параллелограмма, α — угол между сторонами параллелограмма, γ — угол между диагоналями параллелограмма. Формулы площади ромба Формула площади ромба по длине стороны и высоте Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты. S = a · h Формула площади ромба по длине стороны и углу Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба. S = a2 · sin α Формула площади ромба по длинам его диагоналей Площадь ромба равна половине произведению длин его диагоналей. где S — Площадь ромба, a — длина стороны ромба, h — длина высоты ромба, α — угол между сторонами ромба, d1, d2 — длины диагоналей. Формулы площади трапеции Формула Герона для трапеции S =  a + b √(p — a)(p — b)(p — a — c)(p — a — d) |a — b| Формула площади трапеции по длине основ и высоте Площадь трапеции равна произведению полусуммы ее оснований на высоту где S — Площадь трапеции, a, b — длины основ трапеции, c, d — длины боковых сторон трапеции, p =  a + b + c + d   — полупериметр трапеции. 2 Формулы площади выпуклого четырехугольника Формула площади четырехугольника по длине диагоналей и углу между ними Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними: где S — площадь четырехугольника, d1, d2 — длины диагоналей четырехугольника, α — угол между диагоналями четырехугольника. Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности) Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности S = p · r Формула площади четырехугольника по длине сторон и значению противоположных углов S = √(p — a)(p — b)(p — c)(p — d) — abcd cos2θ где S — площадь четырехугольника, a, b, c, d — длины сторон четырехугольника, p =  a + b + c + d   — полупериметр четырехугольника, 2 θ =  α + β  — полусумма двух противоположных углов четырехугольника. 2 Формула площади четырехугольника, вокруг которого можно описать окружность S = √(p — a)(p — b)(p — c)(p — d) Формулы площади круга Формула площади круга через радиус Площадь круга равна произведению квадрата радиуса на число пи. S = π r2 Формула площади круга через диаметр Площадь круга равна четверти произведения квадрата диаметра на число пи. где S — Площадь круга, r — длина радиуса круга, d — длина диаметра круга. Формулы площади эллипса Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи. S = π · a · b где S — Площадь эллипса, a — длина большей полуоси эллипса, b — длина меньшей полуоси эллипса. Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

0oq.ru

Формулы площадей

 На завтрак были круглая яичница, параллелепипедная булочка
и кофе в цилиндрической кружке.
Геометрия мне очень даже пригодилась в жизни, да.

       В стать «Есть ли у треугольника площадь» мы рассмотрели основные формулы для нахождения площади простейших геометрических фигур. Для решения большинства задач по нахождению площади плоских фигур эти формул вполне достаточно. Их обычно используют при решении типовых задач на контрольных или при сдаче ЕГЭ. Но вы должны понимать, это далеко не полный список формул для нахождения площади геометрических фигур. Более того, это лишь вершина айсберга. Взгляните что там, в глубине.

 

Формулы площади квадрата

      Всем хорошо известны формулы для нахождения площади квадрата с известной стороной или диагональю. Но как быть, если эти величины нам неизвестны? Все очень просто! Нам помогут формулы для нахождения площади квадрата через:

 

радиус вписанной окружности

     

радиус описанной окружности

линию выходящую из угла на
середину стороны квадрата

через периметр

Формулы площади прямоугольника

      Для прямоугольника помимо общеизвестной формулы нахождения площади перемножением длин двух его сторон существуют формулы для нахождения площади через:

известные диагонали и угол между ними

известную длину стороны и угол между этой стороной и диагональю

известный периметр и длину одной стороны

Формулы площади треугольника

    Все хорошо знают три основные формулы нахождения площади треугольника. Добавлю еще парочку: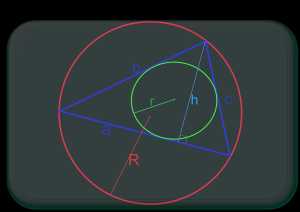

по трем сторонам и радиусу вписанной окружности

здесь p=(a+b+c) — полупериметр

по трем сторонам  и радиусу описанной окружности

Формулы площади параллелограмма

    Для нахождения площади параллелограмма также существует несколько дополнительных формул:

по известным диагоналям и углу между ними

по двум известным высотам и углу между ними

        Как вы могли заметить, некоторые формулы для нахождения площадей очень похоже. Строго говоря, квадрат, ромб, прямоугольник, трапеция и параллелепипед являются частными случаями другой геометрической фигуры — выпуклого четырехугольника. Поэтому, зная формулы для нахождения площади четырехугольника, всегда можно найти площадь любой другой фигуры.

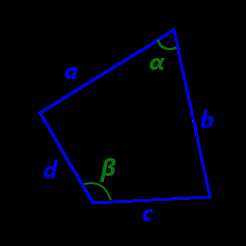
Формулы площади четырехугольника

формула площади выпуклого четырехугольника по известным длинам диагоналей и углу между ними

формула площади выпуклого четырехугольника по длине периметра и радиусу вписанной окружности

здесь p= (a+b+c+d)/2 — полупериметр

формула площади выпуклого четырехугольника по известным длинам сторон и значениям противоположных углов

здесь p=(a+b+c+d)/2 — полупериметр

Θ=(f1+f2)/2 — полусумма углов

формула площади выпуклого четырехугольника вокруг которого можно описать окружность

здесь p=(a+b+c+d)/2 — полупериметр

      Теперь вы знаете достаточно формул для нахождения площадей плоских фигур. Этого вполне достаточно для того спокойно чувствовать себя на экзамене и чтобы спокойно решать простейшие задачки по ЕГЭ. Но не надо думать, что способы нахождения площади ограничиваются этими формулами.  Ведь помимо уже известных вам треугольников и квадратов существует огромное множество самых разнообразных геометрических фигур, таких как вогнутые четырехугольники, выпуклые и вогнутые многоугольники, а также фигуры , вообще не имеющие какой-либо определенной формы. Кроме того, существуют способы нахождение площади по формулам аналитической геометрии (когда известны координаты вершин или вектора сторон), или с помощью интегрального исчисления.

Ну а в заключение хочу вам представить еще одну универсальную формулу − формулу для нахождения площади эллипса: площадь эллипса равна произведению длин большой и малой полуосей эллипса на число ∏

Комментирование и размещение ссылок запрещено.

df-dt.com

Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Планиметрия

      Фигуру называют выпуклой, если для любых двух точек этой фигуры соединяющий их отрезок полностью принадлежит фигуре.

      Правильными многоугольниками называют выпуклые многоугольники, у которых все углы равны и все стороны равны.

      Замечание 1. В любой правильный многоугольник можно вписать окружность.

      Замечание 2. Около любого правильного многоугольника можно описать окружность.

      Замечание 3. Центры вписанной в правильный многоугольник окружности и описанной около правильного многоугольника окружности совпадают. Эту точку называют центром правильного многоугольника.

      Используемые обозначения

Число вершин правильного многоугольника	Сторона правильного многоугольника	Радиус вписанной окружности	Радиус описанной окружности	Периметр	Площадь
n	a	r	R	P	S

Число вершин правильного многоугольника	n
Сторона правильного многоугольника	a
Радиус вписанной окружности	r
Радиус описанной окружности	R
Периметр	P
Площадь	S

Формулы для стороны, периметра и площади правильного n – угольника

Формулы для периметра правильного n – угольника

Выражение периметра через сторону P = an Выражение периметра через радиус вписанной окружности Выражение периметра через радиус описанной окружности

Формулы для площади правильного n – угольника

Выражение площади через сторону и радиус вписанной окружности Выражение площади через сторону Выражение площади через радиус вписанной окружности Выражение площади через радиус описанной окружности

Формулы для стороны правильного n – угольника

Выражение стороны через радиус вписанной окружности Выражение стороны через радиус описанной окружности

Формулы для стороны, периметра и площади правильного треугольника

Формулы для периметра правильного треугольника

Выражение периметра через сторону P = 3a Выражение периметра через радиус вписанной окружности Выражение периметра через радиус описанной окружности

Формулы для площади правильного треугольника

Выражение площади через сторону Посмотреть вывод формулы Выражение площади через сторону и радиус вписанной окружности Выражение площади через радиус вписанной окружности Посмотреть вывод формулы Выражение площади через радиус описанной окружности Посмотреть вывод формулы

Формулы для стороны правильного треугольника

Выражение стороны через радиус вписанной окружности Выражение стороны через радиус описанной окружности

Формулы для стороны, периметра и площади правильного шестиугольника

Формулы для периметра правильного шестиугольника

Выражение периметра через сторону P = 6a Выражение периметра через радиус вписанной окружности Выражение периметра через радиус описанной окружности P = 6R

Формулы для площади правильного шестиугольника

Выражение площади через сторон Выражение площади через сторону и радиус вписанной окружности S = 3ar Выражение площади через радиус вписанной окружности Выражение площади через радиус описанной окружности

Формулы для стороны правильного шестиугольника

Выражение стороны через радиус вписанной окружности Выражение стороны через радиус описанной окружности a = R

Формулы для стороны, периметра и площади квадрата

Формулы для периметра квадрата

Выражение периметра через сторону P = 4a Выражение периметра через радиус вписанной окружности P = 8r Выражение периметра через радиус описанной окружности

Формулы для площади квадрата

Выражение площади через сторону S = a2 Выражение площади через радиус вписанной окружности S = 4r2 Выражение площади через радиус описанной окружности S = 2R2

Формулы для стороны квадрата

Выражение стороны через радиус вписанной окружности a = 2r Выражение стороны через радиус описанной окружности

      На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10

      Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит

      У нас также для школьников организованы

МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»

www.resolventa.ru

Площадь четырёхугольника — ALL

Четырёхугольник

Площадь четырёхугольника — это число, характеризующее четырёхугольник в единицах измерения площади.

Рассмотрим плоские выпуклые четырёхугольники, т.е. такие, у которых все четыре точки лежат в одной плоскости и для любых его (четырёхугольника) двух точек все точки отрезка принадлежат четырёхугольнику.

Виды четырёхугольников:[править]

Введём обозначения:

a — первая сторона;

b — вторая сторона;

c — третья сторона;

d — четвёртая сторона;

α — угол между сторонами a и b;

β — угол между сторонами b и c;

γ — угол между сторонами c и d;

η — угол между сторонами a и d;

d₁ — диагональ, соединяющая вершины углов α и γ;

d₂ — диагональ, соединяющая вершины углов β и η;

l₁ — средняя линия, соединяющая середины сторон a и c;

l₂ — средняя линия, соединяющая середины сторон b и d;

φ — угол (острый) между диагоналями;

ψ — угол (острый) между средними линиями;

p — полупериметр четырёхугольника;

S_Δ — площадь треугольника;

S_четыр — площадь четырёхугольника.

Формулы в векторной и координатной форме[править]

Введём обозначения:

— радиус-вектор первой точки;

— радиус-вектор второй точки;

— радиус-вектор третьей точки;

— радиус-вектор четвёртой точки четырёхугольника, лежащей в плоскости первых трёх точек;

— нормаль к плоскости, проходящей через три заданные точки;

где

Формула Брахмагупты[править]

Рассмотрим четырёхугольники, вокруг которых можно описать окружность и у которых порядок следования вершин 1, 2, 3, 4. Для нахождения их площади можно использовать формулу Брахмагупты.

Введём обозначения:

a — сторона, расположенная между первой и второй точками;

b — сторона, расположенная между второй и третьей точками;

c — сторона, расположенная между третьей и четвёртой точками;

d — сторона, расположенная между первой и четвёртой точками;

p — полупериметр четырёхугольника.

где

• Когда одна из сторон четырёхугольника стремится к нулю, тогда формула Брахмагупты превращается в формулу Герона для площади треугольника.
• Когда четырёхугольник является прямоугольником и a≠b, тогда формула Брахмагупты превращается в формулу площади прямоугольника, S_{прямоуг}=ab, где c=a, d=b, p=a+b.
• Когда четырёхугольник является равнобедренной трапецией и b=d, тогда формула Брахмагупты превращается в формулу площади трапеции, S_{равн.трап}=h(a+c)/2, где h²=(p-a)(p-c), p-b=(a+c)/2.

• Бронштейн М. Н., Семендяев К. А., Справочник по математике. М., 1956, стр.167.
• Википедия. Четырёхугольник.
• Участник:Logic-samara

allll.net