Некоторые методы решения логарифмических уравнений
Рассмотрим некоторые типы логарифмических уравнений, которые не так часто рассматриваются на уроках математики в школе, но широко используются при составлении конкурсных заданий, в том числе и для ЕГЭ.
1. Уравнения, решаемые методом логарифмирования
При решении уравнений, содержащих переменную и в основании и в показателе степени, используют метод логарифмирования. Если, при этом, в показателе степени содержится логарифм, то обе части уравнения надо логарифмировать по основанию этого логарифма.
Пример 1.
Решить уравнение: хlog2х+2 = 8.
Решение.
Прологарифмируем левую и правую части уравнения по основанию 2. Получим
log2 (хlog2х+2) = log2 8,
(log2 х + 2) · log2 х = 3.
Пусть log2 х = t.
Тогда (t + 2)t = 3.
t2 + 2t – 3 = 0.
D = 16. t1 = 1; t2 = -3.
Значит log2 х = 1 и х1 = 2 или log2 х = -3 и х2 =1/8
Ответ: 1/8; 2.
2. Однородные логарифмические уравнения.
Пример 2.
Решить уравнение log23 (х2 – 3х + 4) – 3log3 (х + 5) log3 (х2 – 3х + 4) – 2log23 (х + 5) = 0
Решение.
Область определения уравнения
{х2 – 3х + 4 > 0,
{х + 5 > 0. → х > -5.
log3 (х + 5) = 0 при х = -4. Проверкой определяем, что данное значение х не является корнем первоначального уравнения. Следовательно можно разделить обе части уравнения на log2 3 (х + 5).
Получим log2 3 (х2 – 3х + 4) / log23 (х + 5) – 3 log3 (х2 – 3х + 4) / log3 (х + 5) + 2 = 0.
Пусть log3 (х2 – 3х + 4) / log3 (х + 5) = t. Тогда t 2– 3 t + 2 = 0. Корни данного уравнения 1; 2. Возвратившись к первоначальной переменной , получим совокупность двух уравнений
[log3 (х2 – 3х + 4) / log3 (х + 5) = 1
[log3 (х2 – 3х + 4) / log3 (х + 5) = 2. Отсюда
[log3 (х2 – 3х + 4) = log3 (х + 5),
[log3 (х2 – 3х + 4) = 2log3 (х + 5).
Выполнив потенцирование, получим
[х2 – 3х + 4 = х + 5,
[х2 – 3х + 4 = (х + 5)2 ;
[х2 – 4х – 1 = 0,
[-13х = 21.
[х = 2 – √5,
[х = 2 + √5, [х = -21/13. Все корни входят в область определения.
3. Уравнения, содержащие переменную и в основании логарифма и в выражении, стоящем под знаком логарифма
Пример 3.
Найдите среднее арифметическое корней уравнения log3х+7 (9 + 12х + 4х2) + log2х+3 (6х2 + 23х + 21) = 4.
Решение.
9 + 12х + 4х2 = (2х + 3)2; 6х2 + 23х + 21 = (2х + 3)(3х + 7).
Область определения уравнения
{2х + 3 > 0,
{2х + 3 ≠ 1,
{3х + 7 > 0,
{3х + 7 ≠ 1.
Следовательно х > -1,5 и х ≠ -1
Тогда log3х+7 (2х + 3)2 + log2х+3 (2х + 3)(3х + 7) = 4;
2log3х+7 (2х + 3) + log2х+3 (2х + 3)+ log2х+3 (3х + 7) = 4;
2log3х+7 (2х + 3) + 1 + log2х+3 (3х + 7) = 4;
2log3х+7
(2х + 3) + 1/log3х+7 (2х + 3) = 3;Введём новую переменную log3х+7 (2х + 3) = t. Получим 2t + 1/t = 3. 2t2 – 3t + 1 = 0. Корни уравнения 1/2; 1.
Возвращаемся к исходной переменной.
Получаем log3х+7 (2х + 3) = 1/2 или log 3х+7 (2х + 3) = 1
2х + 3 = (3х + 7)1/2;
(2х + 3)2 = 3х + 7;
4х2 + 9х + 2 = 0.
Корни уравнения -2; -0,25.
log3х+7 (2х+3) = 1.
2х + 3 = 3х + 7.
Х = -4.
В область определения уравнения входит только число -0,25.
Среднее арифметическое -0,25,
Ответ: -0,25.
4. Уравнения, требующие использования свойств логарифмических функций (т.е. решаемые функциональным методом).
Пример 4. Какой наибольший корень в уравнении log3 (8 + 2х – х2) = 2х-1 + 21-х
Решение.
Рассмотрим функцию у = 8 + 2х – х2. Её график – парабола, ветви которой направлены вниз. Координаты вершины (1; 9). Область значений функции (-∞; 9]. Но с учётом существования логарифма нужно рассматривать лишь значения (0; 9]. Значит выражение в левой части принимает наибольшее значение 2 при х = 1. Рассмотрим теперь функцию у = 2х-1 + 21-х . Если принять t = 2x-1,, то она примет вид у = t + 1/t, где t > 0. При таких условиях она имеет единственную критическую точку t = 1. Это точка минимума. Уvin = 2. И достигается он при х = 1.
Теперь очевидно, что графики рассматриваемых функций могут пересекаться лишь один раз в точке (1; 2). Получается, что х = 1 единственный корень решаемого уравнения.
Ответ: х = 1.
Пример 5. Решить уравнение log22 х + (х – 1) log2 х = 6 – 2х
Решение.
Решим данное уравнение относительно log2 х. Пусть log2 х = t. Тогда t2 + (х – 1) t – 6 + 2х = 0.
D = (х – 1)2 – 4(2х – 6) = (х – 5)2. t1 = -2; t2 = 3 – х.
Получим уравнение log2 х = -2 или log2 х = 3 – х.
Корень первого уравнения х1 = 1/4.
Корень уравнения log2 х = 3 – х найдём подбором. Это число 2. Этот корень единственный, так как функция у = log2 х возрастающая на всей области определения, а функция у = 3 – х – убывающая.
Проверкой легко убедится в том, что оба числа являются корнями уравнения
Ответ:1/4; 2.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
«Некоторые методы решения логарифмических уравнений»
Разделы: Математика
Некоторые методы решения логарифмических уравнений.
Настоящая статья содержит систематическое изложение методов решения логарифмических уравнений с одной переменной. Это поможет учителю, прежде всего в дидактическом смысле: подбор упражнений позволяет составить для учащихся индивидуальные задания с учетом их возможностей. Данные упражнения могут быть использованы для урока обобщения и для подготовки к ЕГЭ.
Краткие теоретические сведения и решения задач позволяют учащимся самостоятельно развивать умения и навыки решения логарифмических уравнений.
Решение логарифмических уравнений.
Логарифмические уравнения –
уравнения, содержащие неизвестное под знаком логарифма. При решении логарифмических уравнений часто используются теоретические сведения: Обычно решение логарифмических уравнений начинается с определения ОДЗ. В логарифмических уравнениях рекомендуется все логарифмы преобразовать так, чтобы их основания были равны. Затем уравнения либо выражают через один какой – либо логарифм, который обозначается новой переменной, либо уравнение преобразовывают к виду, удобному для потенцирования.
Преобразования логарифмических выражений не должны приводить к сужению ОДЗ, если же примененный метод решения сужает ОДЗ, выпуская из рассмотрения отдельные числа, то эти числа в конце задачи необходимо проверить подстановкой в исходное уравнение, т.к. при сужении ОДЗ возможна потеря корней.
1. Уравнения вида – выражение, содержащее неизвестное число, а число .
1) воспользоваться определением логарифма: ;
2) сделать проверку или найти область допустимых значений для неизвестного числа и отобрать соответствующие им корни (решения).
Если ) .
2. Уравнения первой степени относительно логарифма, при решении которых используются свойства логарифмов.
Для решения таких уравнений надо:
1) используя свойства логарифмов, преобразовать уравнение;
2) решить полученное уравнение;
3) сделать проверку или найти область допустимых значений для неизвестного числа и отобрать соответствующие им корни (решения).
).
3. Уравнение второй и выше степени относительно логарифма.
Для решения таких уравнений надо:
- сделать замену переменной;
- решить полученное уравнение;
- сделать обратную замену;
- решить полученное уравнение;
- сделать проверку или найти область допустимых значений для неизвестного числа и отобрать соответствующие им корни (решения).
4.Уравнения, содержащие неизвестное в основании и в показателе степени.
Для решения таких уравнений надо:
- прологарифмировать уравнение;
- решить полученное уравнение;
- сделать проверку или найти область допустимых значений для неизвестного числа и отобрать соответствующие им
корни (решения).
5. Уравнения, которые не имеют решения.
- Для решения таких уравнений надо найти ОДЗ уравнения.
- Проанализировать левую и правую часть уравнения.
- Сделать соответствующие выводы.
Примеры:
Исходное уравнение равносильно системе:
Доказать, что уравнение не имеет решения.
ОДЗ уравнения определяется неравенством х ≥ 0. На ОДЗ имеем
Сумма положительного числа и неотрицательного числа не равна нулю, поэтому исходное уравнение решений не имеет.
Ответ : решений нет.
В ОДЗ попадает только один корень х = 0. Ответ: 0.
Произведем обратную замену.
Найденные корни принадлежат ОДЗ.
ОДЗ уравнения – множество всех положительных чисел.
Поскольку
Аналогично решаются данные уравнения:
Задачи для самостоятельного решения:
Используемая литература.
- Бесчетнов В.М. Математика. Москва Демиург 1994
- Бородуля И.Т. Показательная и логарифмическая функции. ( задачи и упражнения). Москва «Просвещение» 1984
- Вавилов В.В., Мельников И.И., Олехник С.Н., Пасиченко П.И. Задачи по математике. Уравнения и неравенства. Москва «Наука» 1987
- Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер. Москва «Илекса»2007
- Саакян С.М., Гольдман А.М., Денисов Д.В.. Задачи по алгебре и началам анализа. Москва «Просвещение» 2003
Приложение 1
Приложение 2
26.03.2010
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
Решение логарифмического уравнения. Решение задания В5
Задание B7 (№ 26647) из Открытого банка заданий для подготовки к ЕГЭ по математике.
Найдите корень уравнения log5(4+x)=2
Решим это уравнение двумя способами.
1. Первый способ.
Чтобы решить это уравнение, вспомним определение логарифма:
Логарифмом числа b по основанию a (logab) называется показатель степени, в которую надо возвести a, чтобы получить b:
Т.е. если logab=х, то ax=b
Для нашего уравнения log5(4+x)=2, по определению логарифма получим:
52=4+x
Решим последнее уравнение:
х+4=25
х=21
Ответ: 21
2. Второй способ.
Рассмотрим логарифмическое уравнение вида:
logaf(x)=logag(x)
Заметим, что в левой и правой части уравнения стоят логарифмы с одинаковым основанием.
Два логарифма с одинаковым основанием равны, если равны выражения, стоящие под знаком логарифма.
Следовательно,
f(x)=g(x).
Внимание! Переход от логарифмов к выражениям, стоящим под знаком логарифма может привести к появлению посторонних корней. Поэтому, после того, как мы найдем корни, нужно сделать проверку: подставить найденные корни в исходное уравнение, и проверить, получится ли у нас верное равенство.
1. В правой части нашего уравнения log5(4+x)=2 стоит число 2. Представим это число в виде логарифма по основанию 5.
Так как logaa=1, то 2=2log55=log552=log525, и наше уравнение приводится к виду:
log5(4+х)=log525
Приравниваем выражения, стоящие под знаком логарифма:
4+х=25
х=21
Проверка: log5(4+21)=log525=2 — верно.
Ответ: 21
Вероятно, Ваш браузер не поддерживается. Попробуйте скачатьFirefox
ege-ok.ru
Методы решения логарифмических уравнений
Алгебра 11 класс
Тема: « Методы решения логарифмических уравнений »
Цели урока:
образовательная: формирование знаний о разных способах решения логарифмических уравнений, умений применять их в каждой конкретной ситуации и выбирать для решения любой способ;
развивающая: развитие умений наблюдать, сравнивать, применять знания в новой ситуации, выявлять закономерности, обобщать; формирование навыков взаимоконтроля и самоконтроля;
воспитательная: воспитание ответственного отношения к учебному труду, внимательного восприятия материала на уроке, аккуратности ведения записей.
Тип урока: урок ознакомления с новым материалом.
«Изобретение логарифмов, сократив работу астронома, продлило ему жизнь».
Французский математик и астроном П.С. Лаплас
Ход урока
I. Постановка цели урока
Изученные определение логарифма, свойства логарифмов и логарифмической функции позволят нам решать логарифмические уравнения. Все логарифмические уравнения, какой бы сложности они не были, решаются по единым алгоритмам. Эти алгоритмы рассмотрим сегодня на уроке. Их немного. Если их освоить, то любое уравнение с логарифмами будет посильно каждому из вас.
Запишите в тетради тему урока: «Методы решения логарифмических уравнений». Приглашаю всех к сотрудничеству.
II. Актуализация опорных знаний
Подготовимся к изучению темы урока. Каждое задание вы решаете и записываете ответ, условие можно не писать. Работайте в парах.
1) При каких значениях х имеет смысл функция:
а)
б)
в)
д)
(По каждому слайду сверяются ответы и разбираются ошибки)
2) Совпадают ли графики функций?
а) y = x и
б) и
3) Перепишите равенства в виде логарифмических равенств:
4) Запишите числа в виде логарифмов с основанием 2:
4 =
— 2 =
0,5 =
1 =
5) Вычислите:
6) Попытайтесь восстановить или дополнить недостающие элементы в данных равенствах.
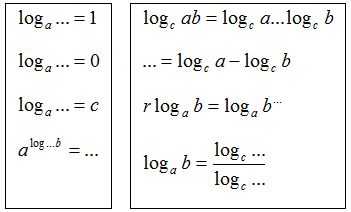
III. Ознакомление с новым материалом
Демонстрируется на экране высказывание:
«Уравнение – это золотой ключ, открывающий все математические сезамы».
Современный польский математик С. Коваль
Попробуйте сформулировать определение логарифмического уравнения. (Уравнение, содержащее неизвестное под знаком логарифма).
Рассмотрим простейшее логарифмическое уравнение: logа x = b (где а>0, a ≠ 1 ). Так как логарифмическая функция возрастает (или убывает) на множестве положительных чисел и принимает все действительные значения, то по теореме о корне следует, что для любого b данное уравнение имеет, и притом только одно, решение, причем положительное.
Вспомните определение логарифма. (Логарифм числа х по основанию а – это показатель степени, в которую надо возвести основание а, чтобы получить число х). Из определения логарифма сразу следует, что ав является таким решением.
Запишите заголовок: Методы решения логарифмических уравнений
1. По определению логарифма.
Так решаются простейшие уравнения вида .
Рассмотрим № 514(а): Решить уравнение
Как вы предлагаете его решать? (По определению логарифма)
Решение. , Отсюда 2х – 4 = 4; х = 4.
Ответ: 4.
В этом задании 2х – 4 > 0, так как > 0, поэтому посторонних корней появиться не может, и проверку нет необходимости делать. Условие 2х – 4 > 0 в этом задании выписывать не надо.
2. Потенцирование (переход от логарифма данного выражения к самому этому выражению).
Рассмотрим №519(г): log5(x2+8)-log5(x+1)=3log5 2
Какую особенность вы заметили? (Основания одинаковы и логарифмы двух выражений равны). Что можно сделать? (Потенцировать).
При этом надо учитывать, что любое решение содержится среди всех х, для которых логарифмируемые выражение положительны.
Решение: ОДЗ:
X2+8>0 лишнее неравенство
log5(x2+8) =log5 23+ log5(x+1)
log5(x2+8)= log5 (8 x+8)
Потенцируем исходное уравнение
x2+8= 8 x+8
получим уравнение x2+8= 8x+8
Решаем его: x2-8x=0
х=0, х=8
Ответ: 0; 8
В общем виде переходом к равносильной системе:
Уравнение
(Система содержит избыточное условие – одно из неравенств можно не рассматривать).
Вопрос классу: Какое из этих трех решений вам больше всего понравилось? (Обсуждение способов).
Вы имеете право решать любым способом.
3. Введение новой переменной.
Рассмотрим № 520(г). .
Что вы заметили? (Это квадратное уравнение относительно log3x) Ваши предложения? (Ввести новую переменную)
Решение. ОДЗ: х > 0.
Пусть , тогда уравнение примет вид:. Дискриминант D > 0. Корни по теореме Виета:.
Вернемся к замене: или .
Решив простейшие логарифмические уравнения, получим:
; .
Ответ: 27;
4. Логарифмирование обеих частей уравнения.
Решить уравнение:.
Решение: ОДЗ: х>0, прологарифмируем обе части уравнения по основанию 10:
. Применим свойство логарифма степени:
(lgx + 3) lgx =
(lgx + 3) lgx = 4
Пусть lgx = y, тогда (у + 3)у = 4
, (D > 0) корни по теореме Виета: у1 = -4 и у2 = 1.
Вернемся к замене, получим: lgx = -4,; lgx = 1, .
Ответ: 0,0001; 10.
5. Приведение к одному основанию.
№ 523(в). Решите уравнение:
Решение: ОДЗ: х>0. Перейдем к основанию 3.
или ;.
Ответ: 9.
6. Функционально-графический метод.
№ 509(г). Решить графически уравнение: = 3 – x.
Как вы предлагаете решать? (Строить по точкам графики двух функций у = log2x и y = 3 – x и искать абсциссу точек пересечения графиков).
Посмотрите ваше решение на слайде.
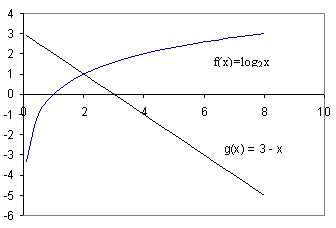
Есть способ, позволяющий не строить графики. Он заключается в следующем: если одна из функций у = f(x)возрастает, а другая y = g(x) убывает на промежутке Х, то уравнение f(x)= g(x) имеет не более одного корня на промежутке Х.
Если корень имеется, то его можно угадать.
В нашем случае функция возрастает при х>0, а функция y = 3 – x убывает при всех значениях х, в том числе и при х>0, значит, уравнение имеет не более одного корня. Заметим, что при х = 2 уравнение обращается в верное равенство, так как .
Ответ: 2
«Правильному применению методов можно научиться,
только применяя их на различных примерах».
Датский историк математики Г. Г. Цейтен
IV. Домашнее задание
П. 39 рассмотреть пример 3, решить № 514(б), № 529(б), №520(б), №523(б)
V. Подведение итогов урока
Какие методы решения логарифмических уравнений мы рассмотрели на уроке?
На следующих уроках рассмотрим более сложные уравнения. Для их решения пригодятся изученные методы.
Демонстрируется последний слайд:
«Что есть больше всего на свете?
Пространство.
Что мудрее всего?
Время.
Что приятнее всего?
Достичь желаемого».
Фалес
Желаю всем достичь желаемого. Благодарю за сотрудничество и понимание.
infourok.ru
Решение логарифмических уравнений на основании определения логарифма
ОБУЧАЮЩИЙ МАТЕРИАЛ ПО ТЕМЕ:
«Примеры решений логарифмических уравнений»
Логарифмическим уравнением называют уравнение, содержащее переменную под знаком логарифма.
Примеры логарифмических уравнений: =lg и т.д.
Решать логарифмическое уравнение – это значит найти все его корни или доказать, что их нет. Рассмотрим некоторые способы решения логарифмических уравнений.
Отметим, что в описанных ниже способах решения логарифмических уравнений применяются только такие преобразования, которые не приводят к потере корней, а могут лишь привести к приобретению посторонних корней. Поэтому проверка каждого из полученных корней обязательна, если нет уверенности в равносильности уравнений.
Решение логарифмических уравнений на основании определения логарифма.
Пример 1. Решите уравнение
Решение. По определению логарифма имеем: 2х+1=, 2х=8, х=4.
Проверка:
Ответ: 4.
Пример 2. Решите уравнение
Решение. По определению логарифма имеем: ,
Проверка: 1) Значение х=0 не может быть корнем данного уравнения, так как основание логарифма х+1 не должно равняться 1.
2)
Ответ: 2
Пример 3. Решите уравнение
Решение. Применяя последовательно определения логарифма, получим:
Проверка:
Ответ:
3
Задание 1. Решите уравнения: а) б) в)
Метод потенцирования.
Пример 4. Решите уравнение
Решение. Из равенства логарифмов чисел следует:
х=6-,
Проверка: 1) число -3 корнем данного уравнения быть не может, так как логарифмы отрицательных чисел не существует.
2)
Ответ: 2.
Пример 5. Решите уравнение:
Решение. Потенцируя данное равенство, получим:
Проверка: 1) -– корень.
2) – не существует.
Ответ: -1.
Пример 6. Решите уравнение
Решение.
Проверка: 1) – не существует, х=-4 – не корень.
2) – не существует, х=6 – не корень.
Ответ: уравнение решения не имеет.
Задание 2. Решите уравнения:
а)
б)
Приведение логарифмического уравнения к квадратному
Пример 7. Решите уравнение .
Решение. Обозначим lg х через y. Данное уравнение принимает вид:
lg х=-3,
lg х=1,
Проверка: 1) 3-21g0,001=9, х=0,001- корень.
2) , 3-21g10=1, х=10 – корень.
Ответ: 0,001; 10.
Задание 3. Решите уравнение: а)
б)
Уравнения, решаемые приведением логарифмов к одному и тому же основанию.
Пример 8. Решите уравнения:
а) б)
Решение.
а)
Проверка:
Ответ:
16
б) , 2,
Проверка:
Ответ: 3.
Задание 4. Решите уравнения: а) б)
Уравнения, решаемые логарифмированием его обеих частей.
Пример 9. Решите уравнение
Решение. Логарифмируя обе части уравнения (х˃0), получим:
(lg х+2)*lg х = lg 1000,
Заменим lg х=у. Уравнение принимает вид:
lg х=-3, lg х=1,
Проверка: 1)
Х=0,001 – корень данного уравнения.
2)
Ответ: 10; 0,001.
ПРОВЕРЬ СЕБЯ
Приведите примеры логарифмических уравнений.
Почему при решении логарифмических уравнений потенцированием возможно появление посторонних корней?
Назовите способы решения логарифмических уравнений.
Составьте план решения уравнения:
а) б)
5. Решите уравнения:
а) б)
в) г)
д) е)
ж)
6. Решите уравнения:
а)
б)
в)
г)
д)
е)
ж)
з) 0,5
7. Решите уравнения:
а) ;
б)
в)
г)
д) 3(
е) 0,1
8. Решите уравнения:
а)
б)
в)
г)
д)
е)
ж)
з)
и)
9. Решите уравнения:
а) =4 | б) 2 =5 |
в) | г) 3 |
д) |
10. Решите графические уравнения:
а) х+ | б) |
в) | г) |
д) 2 |
gigabaza.ru
Методика решения логарифмических уравнений
Разделы: Математика
Введение
Увеличение умственной нагрузки на уроках математики заставляет задуматься над тем как поддержать у студентов интерес к изучаемому материалу, их активность на протяжении всего урока. В связи с этим ведутся поиски новых эффективных методов обучения и таких методических приемов, которые активизировали бы мысль студентов, стимулировали бы их к самостоятельному приобретению знаний.
Возникновение интереса к математике у значительного числа студентов зависит в большей степени от методики ее преподавания, от того, на сколько умело будет построена учебная работа. Вовремя обращая внимание студентов на то, что математика изучает общие свойства объектов и явлений окружающего мира, имеет дело не с предметами, а с отвлеченными абстрактными понятиями, можно добиться понимания того, что математика не нарушает связи с действительностью, а, напротив, дает возможность изучить ее глубже, сделать обобщенные теоретические выводы, которые широко применяются в практике.
Участвуя в фестивале педагогических идей «Открытый урок» 2004-2005 учебного года, я представила урок-лекцию по теме «Логарифмическая функция» (диплом № 204044). Считаю этот метод наиболее удачным в данном конкретном случае. В результате изучения у студентов имеется подробный конспект и краткая схема по теме, что облегчит им подготовку к следующим урокам. В частности, по теме «Решение логарифмических уравнений», которая полностью опирается на изучение логарифмической функции и ее свойств.
При формировании основополагающих математических понятий важно создать у студентов представление о целесообразности введения каждого из них и возможности их применения. Для этого необходимо, чтобы при формулировке определения некоторого понятия, работе над его логической структурой, рассматривались вопросы об истории возникновения данного понятия. Такой подход поможет студентам осознать, что новое понятие служит обобщением фактов реальной действительности.
История возникновения логарифмов подробно представлена в работе прошлого года.
Учитывая важность преемственности при обучении математике в среднем специальном учебном заведении и в вузе и необходимость соблюдения единых требований к студентам считаю целесообразным следующую методику ознакомления студентов с решением логарифмических уравнений.
Уравнения, содержащие переменную под знаком логарифма (в частности, в основании логарифма), называются логарифмическими. Рассмотрим логарифмические уравнения вида:
(1)
Решение этих уравнений основано на следующей теореме.
Теорема 1. Уравнение равносильно системе
(2)
Для решения уравнения (1) достаточно решить уравнение
(3)
и его решения подставить в систему неравенств
(4),
задающую область определения уравнения (1).
Корнями уравнения (1) будут только те решения уравнения (3), которые удовлетворяют системе (4), т.е. принадлежат области определения уравнения (1).
При решения логарифмических уравнений может произойти расширение области определения (приобретение посторонних корней) или сужение (потеря корней). Поэтому подстановка корней уравнения (3) в систему (4), т.е. проверка решения, обязательна.
Пример 1: Решить уравнение
Решение:
Оба значения х удовлетворяют условиям системы.
Ответ:
Рассмотрим уравнения вида:
(5)
Их решение основано на следующей теореме
Теорема 2: Уравнение (5) равносильно системе
(6)
Корнями уравнения (5) будут только те корни уравнения , которые
принадлежат области определения, задаваемой условиями .
Логарифмическое уравнение вида (5) можно решить различными способами. Рассмотрим основные из них.
1. ПОТЕНЦИНИРОВАНИЕ (применение свойств логарифма).
Пример 2: Решить уравнение
Решение: В силу теоремы 2 данное уравнение равносильно системе:
Решим уравнение:
Всем условиям системы удовлетворяет лишь один корень. Ответ:
2. ИСПОЛЬЗОВАНИЕ ОПРЕДЕЛЕНИЯ ЛОГАРИФМА .
Пример 3: Найти х, если
Решение:
Значение х = 3 принадлежит области определения уравнения. Ответ х = 3
3. ПРИВЕДЕНИЕ К КВАДРАТНОМУ УРАВНЕНИЮ.
Пример 4: Решить уравнение
Оба значения х являются корнями уравнения.
Ответ:
4. ЛОГАРИФМИРОВАНИЕ.
Пример 5: Решить уравнение
Решение: Прологарифмируем обе части уравнения по основанию 10 и применим свойство «логарифм степени».
Оба корня принадлежат области допустимых значений логарифмической функции.
Ответ: х = 0,1; х = 100
5. ПРИВЕДЕНИЕ К ОДНОМУ ОСНОВАНИЮ.
Пример 6: Решить уравнение
Воспользуемся формулой и перейдем во всех слагаемых к логарифму по основанию 2:
Тогда данное уравнение примет вид:
Так как , то это корень уравнения.
Ответ: х = 16
6. ВВЕДЕНИЕ ВСПОМОГАТЕЛЬНОЙ ПЕРЕМЕННОЙ.
Решим способом введения вспомогательной переменной уравнение, заданное в примере 6.
Пусть ; тогда
Учитывая, что
Получим уравнение:
После проверки, проведенной устно, легко убеждаемся в правильности найденного ответа.
7. ГРАФИЧЕСКИЙ СПОСОБ.
Многие уравнения, содержащие переменную не только под знаком логарифма или в показателе степени, удобно решать графически.
Графически решением уравнения являются абсциссы точек пересечения графиков функций, заданных в уравнении.
Пример 7: Решить уравнение
Решение: Построим графики функций и y = x
Графики функций не пересекаются, и, значит, уравнение не имеет корней (см. рисунок).
Ответ: корней нет
8. МЕТОД ПОДБОРА.
Пример 8: Найти х, если
Решение: С помощью рассмотренных выше способов корни уравнения найти не удается. Найдем какой-нибудь корень методом подбора.
Пусть, например, х = 10. Проверкой убедимся в том, что 10 — корень уравнения. Действительно,
истинно
Докажем, что других корней данное уравнение не имеет.
Эти корни следует искать во множестве значений х.
Допустимые значения х находятся в промежутке
На этом промежутке функция убывает, а функция возрастает. И, значит, если уравнение имеет решение, то оно единственное.
Итак, получаем
Ответ: х = 10
Упражнения для закрепления:
26.02.2006
xn--i1abbnckbmcl9fb.xn--p1ai
Логарифмические уравнения
Введение
Логарифмы были придуманы для ускорения и упрощения вычислений. Идея логарифма, т. е. идея выражать числа в виде степени одного и того же основания, принадлежит Михаилу Штифелю. Но во времена Штифеля математика была не столь развита и идея логарифма не нашла своего развития. Логарифмы были изобретены позже одновременно и независимо друг от друга шотландским учёным Джоном Непером(1550-1617) и швейцарцем Иобстом Бюрги(1552-1632) Первым опубликовал работу Непер в 1614г. под названием «Описание удивительной таблицы логарифмов», теория логарифмов Непера была дана в достаточно полном объёме, способ вычисления логарифмов дан наиболее простой, поэтому заслуги Непера в изобретении логарифмов больше, чем у Бюрги. Бюрги работал над таблицами одновременно с Непером, но долгое время держал их в секрете и опубликовал лишь в 1620г. Идеей логарифма Непер овладел около1594г. хотя таблицы опубликовал через 20 лет. Вначале он называл свои логарифмы «искусственными числами» и уже потом предложил эти «искусственные числа» называть одним словом «логарифм», который в переводе с греческого- «соотнесённые числа», взятые одно из арифметической прогресси, а другое из специально подобранной к ней геометрической прогресси. Первые таблицы на русском языке были изданы в1703г. при участии замечательного педагога 18в. Л. Ф Магницкого. В развитии теории логарифмов большое значение имели работы петербургского академика Леонарда Эйлера. Он первым стал рассматривать логарифмирование как действие, обратное возведению в степень, он ввёл в употребление термины «основание логарифма» и «мантисса» Бригс составил таблицы логарифмов с основанием 10. Десятичные таблицы более удобны для практического употребления, теория их проще, чем у логарифмов Непера. Поэтому десятичные логарифмы иногда называют бригсовыми. Термин «характеристика» ввёл Бригс.
В те далекие времена, когда мудрецы впервые стали задумываться о равенствах содержащих неизвестные величины, наверное, еще не было ни монет, ни кошельков. Но зато были кучи, а также горшки, корзины, которые прекрасно подходили на роль тайников-хранилищ, вмещающих неизвестное количество предметов. В древних математических задачах Междуречья, Индии, Китая, Греции неизвестные величины выражали число павлинов в саду, количество быков в стаде, совокупность вещей, учитываемых при разделе имущества. Хорошо обученные науке счета писцы, чиновники и посвященные в тайные знания жрецы довольно успешно справлялись с такими задачами.
Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Однако ни в одном папирусе, ни в одной глиняной табличке не дано описания этих приемов. Авторы лишь изредка снабжали свои числовые выкладки скупыми комментариями типа: «Смотри!», «Делай так!», «Ты правильно нашел». В этом смысле исключением является «Арифметика» греческого математика Диофанта Александрийского (III в.) – собрание задач на составление уравнений с систематическим изложением их решений.
Однако первым руководством по решению задач, получившим широкую известность, стал труд багдадского ученого IX в. Мухаммеда бен Мусы аль-Хорезми. Слово «аль-джебр» из арабского названия этого трактата – «Китаб аль-джебер валь-мукабала» («Книга о восстановлении и противопоставлении») – со временем превратилось в хорошо знакомое всем слово «алгебра», а само сочинение аль-Хорезми послужило отправной точкой в становлении науки о решении уравнений.
Логарифмические уравнения и неравенства
1. Логарифмические уравнения
Уравнение, содержащее неизвестное под знаком логарифма или в его основании, называется логарифмическим уравнением.
Простейшим логарифмическим уравнением является уравнение вида
loga x = b . (1)
Утверждение 1. Если a > 0, a ≠ 1, уравнение (1) при любом действительном b имеет единственное решение x = ab .
Пример 1. Решить уравнения:
a) log2x = 3, b) log3x = -1, c)
Решение. Используя утверждение 1, получим a) x = 23 или x = 8; b) x = 3-1 или x = 1 /3 ; c)
или x = 1.Приведем основные свойства логарифма.
Р1. Основное логарифмическое тождество:
где a > 0, a ≠ 1 и b > 0.
Р2. Логарифм произведения положительных сомножителей равен сумме логарифмов этих сомножителей:
loga N 1 ·N 2 = loga N 1 + loga N 2 (a > 0, a ≠ 1, N 1 > 0, N 2 > 0).
Замечание. Если N 1 ·N 2 > 0, тогда свойство P2 примет вид
loga N 1 ·N 2 = loga |N 1 | + loga |N 2 | (a > 0, a ≠ 1, N 1 ·N 2 > 0).
Р3. Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя
(a > 0, a ≠ 1, N 1 > 0, N 2 > 0).Замечание. Если
, (что равносильно N 1N 2 > 0) тогда свойство P3 примет вид (a > 0, a ≠ 1, N 1N 2 > 0).P4. Логарифм степени положительного числа равен произведению показателя степени на логарифм этого числа:
loga N k = k loga N (a > 0, a ≠ 1, N > 0).
Замечание. Если k — четное число (k = 2s ), то
loga N 2s = 2s loga |N | (a > 0, a ≠ 1, N ≠ 0).
P5. Формула перехода к другому основанию:
(a > 0, a ≠ 1, b > 0, b ≠ 1, N > 0),в частности, если N = b , получим
(a > 0, a ≠ 1, b > 0, b ≠ 1). (2)Используя свойства P4 и P5, легко получить следующие свойства
(a > 0, a ≠ 1, b > 0, c ≠ 0), (3) (a > 0, a ≠ 1, b > 0, c ≠ 0), (4) (a > 0, a ≠ 1, b > 0, c ≠ 0), (5)и, если в (5) c — четное число (c = 2n ), имеет место
(b > 0, a ≠ 0, |a | ≠ 1). (6)Перечислим и основные свойства логарифмической функции f (x ) = loga x :
1. Область определения логарифмической функции есть множество положительных чисел.
2. Область значений логарифмической функции — множество действительных чисел.
3. При a > 1 логарифмическая функция строго возрастает (0 < x 1 < x 2 loga x 1 < loga x 2 ), а при 0 < a < 1, — строго убывает (0 < x 1 < x 2 loga x 1 > loga x 2 ).
4. loga 1 = 0 и loga a = 1 (a > 0, a ≠ 1).
5. Если a > 1, то логарифмическая функция отрицательна при x (0;1) и положительна при x (1;+∞), а если 0 < a < 1, то логарифмическая функция положительна при x (0;1) и отрицательна при x (1;+∞).
6. Если a > 1, то логарифмическая функция выпукла вверх, а если a (0;1) — выпукла вниз.
Следующие утверждения (см., например, [1]) используются при решении логарифмических уравнений.
Утверждение 2. Уравнение loga f (x ) = loga g (x ) (a > 0, a ≠ 1) равносильно одной из систем (очевидно, выбирается та система, неравенство которой решается проще)
Утверждение 3. Уравнение logh (x )f (x ) = logh (x )g (x ) равносильно одной из систем
Нужно подчеркнуть, что в процессе решения логарифмических уравнений часто используются преобразования, которые изменяют область допустимых значений (ОДЗ ) исходного уравнения. Следовательно, могут появиться «чужие» решения или могут быть потеряны решения. Например, уравнения
f (x ) = g (x ) иloga f (x ) = loga g (x )
или
loga [f (x )·g (x )] = b иloga f (x ) + loga g (x ) = b
вообще говоря, неравносильны (ОДЗ уравнений справа уже).
Следовательно, при решении логарифмических уравнений полезно использовать равносильные преобразования. В противном случае, проверка полученных решений является составной частью решения. Более того, необходимо учитывать и преобразования, которые могут привести к потере корней.
mirznanii.com
