Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Тригонометрия
Простейшими тригонометрическими уравнениями называют уравнения вида:
sin x = a , cos x = a ,
tg x = a , ctgx = a .
где a – произвольное число.
Решение уравнения sin x = a
| Обычная форма записи решения | |
| Более удобная форма записи решения | |
| Ограничения на число a | В случае, когда , уравнение решений не имеет |
Обычная форма записи решения:
Более удобная форма записи решения:
Ограничения на число a:
В случае, когда , уравнение решений не имеет.
Графическое обоснование решения уравнения sin x = a представлено на рисунке 1

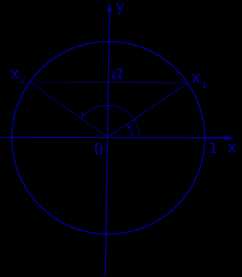
Рис. 1
Частные случаи решения уравнений sin x = a
Уравнение: sin x = – 1 Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: Решение: > |
Уравнение: sin x = 0 Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: sin x = 1 Решение: |
Решение уравнения cos x = a
| Обычная форма записи решения | |
| Более удобная форма записи решения | |
| Ограничения на число a | В случае, когда , уравнение решений не имеет |
Обычная форма записи решения:
Более удобная форма записи решения:
Ограничения на число a
В случае, когда , уравнение решений не имеет.
Графическое обоснование решения уравнения cos x = a представлено на рисунке 2
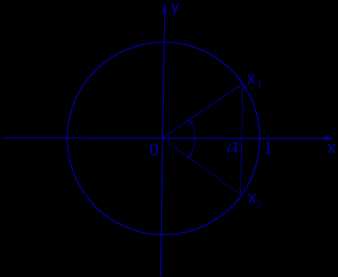
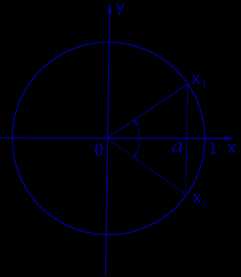
Рис. 2
Частные случаи решения уравнений cos x = a
Уравнение: cos x = – 1 Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: cos x = 0 Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: Решение: |
Уравнение: cos x = 1 Решение: |
Решение уравнения tg x = a
| Обычная форма записи решения: | |
| Более удобная форма записи решения | |
| Ограничения на число a | Ограничений нет |
Обычная форма записи решения:
Более удобная форма записи решения:
Ограничения на число a:
Ограничений нет.
Графическое обоснование решения уравнения tg x = a представлено на рисунке 3.
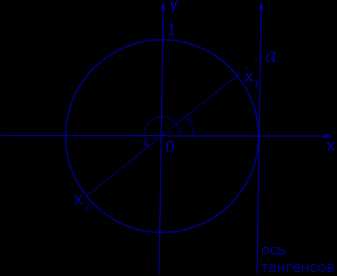
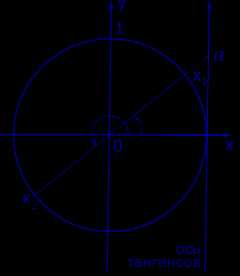
Рис. 3
Частные случаи решения уравнений tg x = a
Уравнение: Решение: |
Уравнение: tg x = – 1 Решение: |
Уравнение: Решение: |
Уравнение: tg x = 0 Решение: |
Уравнение: Решение: |
Уравнение: tg x = 1 Решение: |
Уравнение: Решение: |
Решение уравнения ctg x = a
| Обычная форма записи решения | |
| Более удобная форма записи решения | |
| Ограничения на число a | Ограничений нет |
Обычная форма записи решения:
Более удобная форма записи решения:
Ограничения на число a:
Ограничений нет.
Графическое обоснование решения уравнения ctg x = a представлено на рисунке 4.
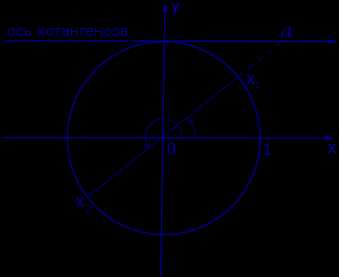
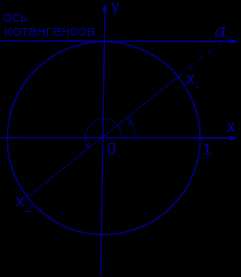
Рис. 4
Частные случаи решения уравнений ctg x = a
Уравнение: Решение: |
Уравнение: ctg x = – 1 Решение: |
Уравнение: Решение: |
Уравнение: ctg x = 0 Решение: |
Решение: |
Уравнение: ctg x = 1 Решение: |
Уравнение: Решение: |
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
sin 2x — sin x = 0 решение
Добрый вечер!
Вы обратились к нам с просьбой решить уравнение такого вида: sin 2x — sin x = 0.
На первый взгляд это кажется сложно. Но на самом деле, если Вы знаете формулы тригонометрии, то всё элементарно. Давайте разбираться на Вашем примере.
Итак, наше уравнение:
А теперь давайте рассуждать, что мы здесь можем сделать. Первое, что бросается в глаза — это sin двойного угла. И первое желание это как-то его заменить. К счастью, есть формула, которая может помочь нам это сделать. Вот как это будет:
Давайте использовать это в вашем уравнении:
Как видим, что в одной половине и во второй уравнения есть общий член — sin x. Чтоб ни на что не делить. Мы с Вами можем схитрить — вынести этот общий член за скобки и получить следующее:
По известным правилам математики, мы можем запишем как систему:
Попробуем по максимуму всё упростить, чтоб был понятный вид. Известно перенести вправо, неизвестные оставить слева:
Как видим, во втором нашем уравнении есть двоечка перед cos x, Давайте избавимся от неё, поделив две части уравнения на два:
решение данных уравнений будет происходить по общим правилам решения таких уравнений, а к тому же наши значения — нормальный табличные и не составит труда решить. По этим правилам мы получим следующие ответы:
И теперь итог — сам ответ, который будет таковым:
либо
ru.solverbook.com
sin x — cos x = 0 решение
Добрый вечер!
Вы попросили решить тригонометрическое уравнение. В нём нет ничего сложного, если иметь представление о базовых формулах и понятиях, которые здесь могут быть вовлечены.
Я считаю, что рациональней сразу показать шаги решения на конкретном примере, то есть Вашем: sin x — cos x = 0.
Итак, рассмотрим тригонометрическое уравнение:
Имея изначальный вид, мы сделать с этим уравнением ничего не можем. То есть надо как-то преобразовывать данное уравнение. Давайте разделим все члены уравнения на , так как на ноль делить нельзя. Из этого мы получаем, что:
Мы с Вами знаем, что:
И уже из этого получим преобразование такого вида:
Используя данные тригонометрических превращений, мы с Вами знаем, что:
Теперь можем выполнить полное преобразование:
Теперь дело за малым. Осталось использовать основные правила математики и получаем превращение в тангенс угла (tg x):
Теперь решаем обычным способом. Используя простое правило:
А сейчас применим общее правило на конкретном примере:
По таблице основных значений тригонометрических функций мы получим, что:
Подставим:
Вот и всё!
Ответ:
ru.solverbook.com
sin x + cos x = 0 решить уравнение
Добрый вечер!
Спасибо за обращение к нам!
Мы поможем Вам справиться с таким заданием: sin x + cos x = 0 решить уравнение.
Приступим к решению.
Нам дано уравнение такого вида:
На первый взгляд кажется, что решение невозможно, но это ошибочно, так как все забывают про такое свойство как деление на какой-то член. В нашем случае, мы можем поделить две части уравнения на cos x, который не должен равняться нулю, так как на ноль делить нельзя.
И получим следующее:
Так как если sin x поделить на cos x, мы получим tg x.
Теперь известные члены перенесём вправо с изменением знаков и получим:
У нас получилось простейшее тригонометрическое уравнение. Для решения этого уравнения есть определённое правило решения подобных уравнений, которое примет такой общий вид:
Как только мы разобрались с общим решением, то теперь можем преступить к решению именно Вашего уравнения:
Если бы у нас было классическое число из таблицы, которое нужно было бы найти, то мы бы с Вами воспользовались уже известной Вам таблицей. И уже исходя из этого получили бы какое-то значение, которое могли бы с Вами использовать.
И мы бы С вами продолжали решать наше уравнение. Но так как с этим не сложилось, то мы с Вами просто напросто ничего не меняем и записываем ответ в таком виде: :
Ответ:
Надеюсь, Вы поняли почему, зачем и как мы с Вами делали. Удачи Вам в решении подобных заданий. Удачи Вам!
ru.solverbook.com
Ответы@Mail.Ru: Как решить?=) sin3X-sinx=0
син 3х=син х 3х = х х = 0(если быть точным, то 2*пи*к) да, ступил на гочь глядя, неправильно это
я не согласен, что только в нулях ответ: лови график твоей функции, вишь, там куча пересечений, не отделенных периодом — <img src=»//otvet.imgsmail.ru/download/35a1a773ef004bb05a4547887e6240a4_i-19.jpg» > А прямо решать просто, полный стандарт, смори в любом учебнике по алгебре в разделе тригонометрические уравнения.touch.otvet.mail.ru
Решение тригонометрических уравнений
Мы уже познакомились с формулами корней более простых тригонометрических уравнений
cos x = a, sin x = a, tg x = a. К этим уравнениям сводятся другие тригонометрические уравнения. Для решения большей части таких уравнений необходимо использование формул преобразований тригонометрических выражений. Рассмотрим некоторые способы и примеры решения тригонометрических уравнений.
1. Уравнения, сводящиеся к квадратам
Задача 1.
Решить уравнение sin2 x + sin x – 2 = 0.
Решение.
Это уравнение является квадратным относительно sin x. Если мы обозначим sin x = у, то наше уравнение примет вид: у2 + у – 2 = 0. Решив это уравнение, мы получаем его корни: у1 = 1, у2 = -2. Таким образом, решение исходного уравнения свелось к решению простейших уравнений sin x = 1 и sin x = -2.
Корнем уравнения sin x = 1 является х = π/2 + 2πn, n € Z; уравнение sin x = -2 не имеет корней.
Ответ. х = π/2 + 2πn, n € Z.
Задача 2.
Решить уравнение 2 cos2x – 5 sin x + 1 = 0.
Решение.
Заменим cos2x на 1 – sin2 x и получим: 2(1 – sin2 x) – 5 sin x + 1 = 0, или 2 sin2 x + 5 sin x – 3 = 0.
Обозначив sin x = у, мы получили: 2у2 + 5у – 3 = 0, откуда у
1) sin x = -3 – уравнение не имеет корней, так как |-3|> 1.
2) sin x = 1/2, х = (-1)n arcsin 1/2 + πn = = (-1)n π/6 + πn, n € Z.
Ответ. х = (-1)n π/6 + πn, n € Z.
2. Уравнения вида а sin x + b cosx = c
Задача 3.
Решить уравнение 2 sin x – 3 cosx = 0.
Решение.
Разделим на cos x обе части уравнения и получим 2 tg x – 3 = 0, tg x = 3/2, х = arctg 3/2 + πn, n € Z.
Ответ. х = arctg 3/2 + πn, n € Z.
При решении этой задачи обе части уравнения 2 sin x – 3 cosx = 0 были разделены на cos x. Мы должны помнить, что в результате деления уравнения на выражение, которое содержит неизвестное, корни могут быть потеряны. Поэтому нужно проверить, не являются ли корни уравнения cos x = 0 корнями данного уравнения. Если cos x = 0, то из уравнения 2sin x – 3 cos x = 0 следует, что sin x = 0. Однако sin x и cos х одновременно не могут быть равными нулю, в силу того что они связаны равенством sin 2x + cos2x = 1. Следовательно, при делении уравнения а sin x + b cosx = 0, где а ≠ 0, b ≠ 0, на cos x (или sin x) корни этого уравнения не теряются.
3. Уравнения, решаемые разложением левой части на множители
Многие уравнения, в правой части которых располагается 0, решаются путем разложения на множители их левой части.
Задача 4.
Решить уравнение sin 2x – sinx = 0.
Решение.
Воспользуемся формулой синуса двойного аргумента и запишем уравнение в виде 2 sin x cosx – sin x = 0.
Общий множитель sin x вынесем за скобки и получим sin x(2 cosx – 1) = 0.
1) sin x = 0, х = πn, n € Z.
2) 2 cosx – 1 = 0, cosx = 1/2, х = +/-π/3 + 2πn, n € Z.
Ответ. х = +/-π/3 + 2πn, n € Z.
Задача 5.
Решить уравнение cos 3x + sin 5x = 0.
Решение.
Используя формулу приведения sin α = cos (π/2 – α), запишем уравнение в виде cos 3x + cos (π/2 – 5х)= 0.
Воспользуемся формулой для суммы косинусов и получим:
2 cos(π/4 – х) ∙ cos (4х – π/4)= 0.
1) cos(π/4 – х) = 0, х – π/4 = π/2 + πn, х = 3/4 π + πn, n € Z;
2) cos (4х – π/4)= 0, 4х – π/4 = π/2 + πn, х = 3/16 π + (πn)/4, n € Z.
Ответ. х = 3/4π + πn, х = 3/16π + (πn)/4, n € Z.
Задача 6.
Решить уравнение sin 7x + sin 3x = 3 cos 2х.
Решение.
Применим формулу суммы синусов и запишем уравнение в виде
2 sin 5x ∙ cos 2х = 3 cos 2х, или 2 sin 5x ∙ cos 2х – 3 cos 2х = 0,
откуда cos 2х(sin 5x – 3/2) = 0.
Уравнение cos 2х = 0 имеет корни х = π/4 + (πn)/2, а уравнение sin 5x = 3/2 не имеет корней.
Ответ. х = π/4 + (πn)/2, n € Z.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Помогите решить тригонометрическое уравнение sin3x-sinx=0
Всё решается очень просто. Применяется знаменитая формула разности синусов двух углов: sin a-sin b=2*sin (a-b)/2*cos(a+b)/2, и вот как эта формула применяется в решении уравнения: sin3x-sinx=0 2*sin х*cos 2х=0 Осталось решить два совсем простых тригонометрических уравнения: sin x=0 х=pi*n cos 2x=0 х=pi/4+pi*n/2 pi-это знаменитое число 3,14159 n-это любое целое число Вот и всё решение.
могу предположить, что х = 0
sin3x-sinx=0 3sinx-4(sinx)^3-sinx=0 2sinx-4(sinx)^3=0 sinx(1-2(sinx)^2)=0 sinx=0 или 1-2(sinx)^2=0 в первом случае x=pi*n во втором cos2x=0, 2x=pi/2+pi*n, x=pi/4+pi*n/2
Это же легко! Действуешь по формуле sin-sin. Решением будет: 2 sinx * cos2x = 0 А потом предполагаешь, что либо один множитель будет равен нулю, либо второй. sin x = 0, или сos 2x = 0 Если sin x = 0, x = Пn, n принадлежит Z Если cos 2x = 0, тогда 2x =П/2 + Пn, n принадлежит Z x = П/4 + Пn/2. n принадлежит Z
touch.otvet.mail.ru
