Система нормальных уравнений – 13. Система нормальных уравнений и явный вид ее решения при оценивании методом наименьших квадратов линейной модели парной регрессии

13. Система нормальных уравнений и явный вид ее решения при оценивании методом наименьших квадратов линейной модели парной регрессии

13. Система нормальных уравнений и явный вид ее решения при оценивании методом наименьших квадратов линейной модели парной регрессии

Предположим, что в ходе регрессионного анализа была установлена линейная взаимосвязь между исследуемыми переменными х и у, которая описывается моделью регрессии вида:

В результате оценивания данной эконометрической модели определяются оценки неизвестных коэффициентов. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).

Метод наименьших квадратов позволяет получить такие оценки параметров ?0 и ?1, при которых сумма квадратов отклонений фактических значений результативного признака y от расчетных (теоретических) ? минимальна:

В процессе минимизации функции (1) неизвестными являются только значения коэффициентов

?0 и ?1, потому что значения результативной и факторной переменных известны из наблюдений. Для определения минимума функции двух переменных вычисляются частные производные этой функции по каждому из оцениваемых параметров и приравниваются к нулю. Результатом данной процедуры будет стационарная система уравнений для функции (2):

.

Если разделить обе части каждого уравнения системы на (-2), раскрыть скобки и привести подобные члены, то получим систему нормальных уравнений для функции регрессии вида yi=?0+?1xi:

Если решить данную систему нормальных уравнений, то мы получим искомые оценки неизвестных коэффициентов модели регрессии ?0 и ?1:

где

– среднее значение зависимой переменной;

– среднее значение независимой переменной;

– среднее арифметическое значение произведения зависимой и независимой переменных;

– дисперсия независимой переменной;

Gcov (x, y) – ковариация между зависимой и независимой переменными.

Таким образом, явный вид решения системы нормальных уравнений может быть записан следующим образом:

Поделитесь на страничке

Следующая глава >

info.wikireading.ru

Система нормальных уравнений — Энциклопедия по экономике

Параметры уравнений регрессии находят решением системы нормальных уравнений, отвечающих требованию способа наименьших квадратов.  [c.390]
Величины указанных параметров были рассчитаны решением системы нормальных уравнений, получаемых способом наименьших квадратов  [c.24]

Это условие приводит к системе нормальных уравнений, решение которых позволяет определить параметры уравнения регрессии. Эти уравнения имеют вид  [c.99]

Считая формулу связи линейной (Y = a0 + aiX ), определяем зависимость рентабельности производства плащей в зависимости от рентабельности выпуска зонтов. Для этого решается система нормальных уравнений  [c.83]

Этап 3. Система нормальных уравнений для функции имеет вид  [c.223]

Считая формулу связи линейной (у = а0 + щх), определим зависимость выпуска промышленных изделий от их запуска. Для этого решается система нормальных уравнений  [c.160]

Для исчисления параметров я0 и я, используется система нормальных уравнений  [c.368]

В случае выравнивания по прямой способ наименьших квадратов приводит к следующей системе нормальных уравнений  [c.322]

По такому же принципу рассчитываются и параметры криволинейного уравнения. Так, в случае параболической зависимости параметры а0, аь а2 находятся по следующей системе нормальных уравнений  [c.322]

Вторым этапом является поиск значений параметров уравнения. Параметры трендовых моделей определяются с помощью системы нормальных уравнений. В случае применения линейного тренда используют следующую систему уравнений, которую решают способом наименьших квадратов  [c.612]

Величина k определяет гармонику ряда Фурье и определяется целым числом, как правило, в пределах от 1 до 4. Параметры уравнения находят с помощью системы нормальных уравнений способом наименьших квадратов.  [c.616]

Отсюда система нормальных уравнений имеет вид  [c.239]

Коэффициенты регрессии для представления (4.16) находятся с помощью системы нормальных уравнений (чтобы не загромождать запись, индекс k, по которому идет суммирование у результативного и факторных признаков, подразумевается, но не приводится k — 1,2,. .., п).  [c.125]

Параметры уравнения OQ, а и а находим из системы нормальных уравнений, при ] / = 0 значения параметров рассчитываются по формулам  [c.185]

Значения констант а0, а,, а2,. .. могут быть вычислены путем решения системы нормальных уравнений.  [c.126]

Анализ зависимости между ценой продукта и его количеством в динамике позволяет выбрать для функции спроса линейную форму связи вида Р= а0 + а[ + a(Q. По методу наименьших квадратов определяются неизвестные параметры ай и а[ на основе составления и решения системы нормальных уравнений вида  [c.74]

Анализ зависимости между издержками и количеством выпускаемой продукции в динамике позволяет для функции издержек выбрать также линейную форму связи вида С= Ь0 + b Q. Неизвестные параметры Ь0 и Ь( также находятся по методу наименьших квадратов на основе составления и решения системы нормальных уравнений вида  [c.75]

Уравнение прямой имеет вид у, = а0 + а t. В связи с этим система нормальных уравнений для оценивания параметров прямой имеет вид  [c.81]

Упрощенный расчет параметров уравнений заключается в переносе начала координат в середину ряда динамики. В этом случае упрощаются сами нормальные уравнения, а кроме того, уменьшаются абсолютные значения величин, участвующих в расчете. В самом деле, если до переноса начала координат / было равно 1,2,3,. .., п, то после переноса — t=. .. —4, — 3, —2, -1,0,1,2,3,4…, если число члена ряда нечетное. Когда же число ряда четное, то f =… —5, —3, — 1, 1,3,5… Следовательно, /и все f, у которых р нечетное число, равны 0. Таким образом, все члены уравнений, содержащие /с такими степенями, могут быть исключены. Системы нормальных уравнений теперь упрощаются для прямой  [c.82]

Система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов имеет следующий вид  [c.115]

В данном случае задача сводится к определению неизвестных параметров а0 а а2. Они определяются на основе системы нормальных уравнений  [c.115]

А, а, р и у — параметры производственной функции, которые определяются в результате решения системы нормальных уравнений.  [c.363]

При функциональной форме мультиколлинеарности по крайней мере одна из парных связей между объясняющими переменными является линейной функциональной зависимостью. В этом случае матрица Х Х особенная, так как содержит линейно зависимые векторы-столбцы и ее определитель равен нулю, т. е. нарушается предпосылка 6 регрессионного анализа. Это приводит к невозможности решения соответствующей системы нормальных уравнений и получения оценок параметров регрессионной модели.  [c.108]

Система нормальных уравнений 54 ——в матричной форме 85  [c.304]

Определение зависимости изменения затрат от изменения технико-экономических параметров изделий включает следующие основные этапы объединение изделий в параметрические ряды отбор параметров, в наибольшей степени влияющих на себестоимость изделий установление формы связи зависимости изменения себестоимости от изменения параметров построение системы нормальных уравнений в соответствии с принятой функцией и расчет коэффициентов.  [c.185]

Система нормальных уравнений будет выглядеть следующим образом  [c.158]

По данным, приведенным в табл. 5.7 (итоги гр. 2-6), построена система нормальных уравнений  [c.204]

Полученная система называется системой нормальных уравнений для нахождения параметров а0 и ах при выравнивании по прямой линии. -  [c.47]

Для получения конкретного математического выражения функциональной связи между двумя переменными у» is. х при гиперболической их взаимозависимости составлена система нормальных уравнений  [c.52]

Из системы нормальных уравнений находим параметры b и а  [c.29]

Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов (МНК). Для линейных уравнений и нелинейных уравнений, приводимых к линейным, строится следующая система нормальных уравнений, решение которой позволяет получить оценки параметров регрессии  [c.49]

Система нормальных уравнений составит  [c.115]

Для определения параметров а и Ь применяется МНК. Система нормальных уравнений следующая  [c.146]

Система нормальных уравнений будет иметь вид  [c.45]

Применение МНК для оценки параметров параболы второй степени приводит к следующей системе нормальных уравнений  [c.63]

Напомним, что в математической статистике для получения несмещенной оценки дисперсии случайной величины соответствующую сумму квадратов отклонений от средней делят не на число наблюдений я, а на число степеней свободы (degress of freedom) я — т, равное разности между числом независимых наблюдений случайной величины п и числом связей, ограничивающих свободу их изменения, т. е. число т уравнений, связывающих эти наблюдения. Поэтому в знаменателе выражения (3.26) стоит число степеней свободы п — 2, так как две степени свободы теряются при определении двух параметров прямой из системы нормальных уравнений (3.5).  [c.62]

Напомним, что согласно методу наименьших квадратов параметры прямой1 у, = /(0 = Ь0 + bit находятся из системы нормальных уравнений (3.5), в которой в качестве х, берем t  [c.141]

При применении метода наименьших квадратов для оценки параметров экспоненциальной, логистической функций или функции Гомперца возникают сложности с решением получаемой системы нормальных уравнений, поэтому предварительно, до получения соответствующей системы, прибегают к некоторым преобразованиям этих функций (например, логарифмированию и др.) (см. 5.5).  [c.143]

В этом модуле реализовано решение системы нормальных уравнений методом наименьших квадратов. Прогноз с использованием модуля М107 осуществляется на базе небольшого числа данных (N > 10) по упрощенной схеме, т. е. по трем наиболее распространенным функциям  [c.41]

На основе коэффициентов парной корреляции обра зуется система нормальных уравнений, однако, относящаяся ие к. самим коэффициентам уравнения О , а к таким же величинам в стандартизованном масштабе р  [c.45]

economy-ru.info

7.Решение системы нормальных уравнений

Существует несколько способов решения системы нормальных уравнений. Существует способ Гаусса [3,11]. Этот способ называют способом последовательного исключения неизвестных. Имеется способ последовательных приближений. В существующей практике для решения системы нормальных уравнений используют программы и алгоритмы, основанные на вычислении и дальнейшем использовании обратной матрицы системы нормальных уравнений. Повторим написанное в предшествующем разделе. На основании формул (6.7) – (6.10) можно утверждать, что в случае, если матрица коэффициентов системы нормальные уравнений является вырожденной, то есть определитель этой матрицы равен нулю, то решение этой системы уравнений отсутствует.

7.1. Вычисление вектора неизвестных с использованием обратной матрицы

Вернёмся к выражению (5.9). Умножим слева обе части этого выражения на обратную матрицу N^-1, получим:

(7.1)

В соответствии с выражением (6.4), произведение N^-1N равно единичной матрице Е. По аналогии с числами это означает, что в левой части (7.1) стоит только вектор Х определяемых неизвестных и (7.1) принимает окончательный вид:

(7.2)

Это и есть то выражение, которое позволяет вычислить вектор определяемых неизвестных. Выражение (7.2) аналогично выражению (2.2), к чему мы и стремились с самого начала. Но не так всё просто в геодезии. Следует не только определить вектор Х неизвестных. Необходимо оценить ошибки определяемых неизвестных, то есть ошибки элементов вектора X. Необходимо также определить, как ошибки определяемых неизвестных связаны между собой. Достоинство способа решения системы нормальных уравнений с использованием обратной матрицы в сравнении с другими способами решения этой системы состоит именно в том, что обратная матрица даёт возможность исчерпывающим образом оценить точность определения неизвестных в их совокупности.

7.2.Оценка точности элементов вектора определяемых неизвестных

В формулах (6.5) – (6.10) элементы обратной матрицы N^-1обозначены как q. В таком обозначении есть свой смысл. Каждый элемент q_ii обратной матрицы Q, смотри формулы (6.9), (6.10), расположенный на главной диагонали этой матрицы, представляет собой обратный вес неизвестного, которому приписан номер i. Поэтому матрицу N^-1 также обозначают Q:

(7.3)

и называют матрицей обратных весов. Хотя недиагональные элементы этой матрицы не являются обратными весами. Математический смысл недиагональных элементов пояснён далее.

Как один из результатов обработки и уравнивания геодезической сети, созданной спутниковым методом, наземными методами или сочетанием спутникового метода и наземных методов, программа позволяет получить ковариационную матрицу K определяемых неизвестных – координат пунктов геодезической сети:

(7.4)

В этой формуле σ² – дисперсия единицы веса определяемых неизвестных. Символ дан утолщенным шрифтом, чтобы отличить его от символа, обозначающего дисперсию σ² единицы веса измеренных величин, раздел 3.

Элемент , расположенный на главной диагонали матрицыK представляет собой дисперсию (практическую оценку дисперсии) соответствующего неизвестного, то есть, квадрат средней квадратической ошибки этого неизвестного. Элемент ,i≠j, расположенный вне главной диагонали (недиагональный элемент) матрицы K на пересечении строки с номером i и столбца с номером j характеризует взаимосвязь дисперсий неизвестных, которым приписаны номера i и j. Если представить написанное в терминах теории вероятностей, то недиагональный элемент матрицыK представляет собой математическое ожидание M произведения двух центрированных случайных величин и:

, где:. (7.5)

Под термином «случайная величина» понимают определяемое неизвестное. Величину ) называют функцией корреляции случайных величин и.

Вернёмся к математическому смыслу недиагональных элементов матрицы Q обратных весов. Повторим, что обратные веса определяемых неизвестных расположены только на главной диагонали этой матрицы. Недиагональный же элемент представляет собой коэффициент корреляции определяемых неизвестных с номерами i и j:

, (7.6)

Матрица Q симметричная, то есть q_ij= q_ji. Для получения матрицы Q обратных весов определяемых неизвестных в качестве исходной матрицы используют матрицу A коэффициентов параметрических уравнений. Значения элементов матрицы А зависят только от геометрии геодезической сети, от геометрии наблюдений, и не зависят от результатов наблюдений, от ошибок результатов этих наблюдений. Геометрию геодезической сети в форме навигационных координат пунктов этой сети можно знать уже после выполнения обследования и рекогносцировки геодезической сети, до этапа наблюдений. Координаты существующих пунктов внесены в каталог. Приближенные координаты пунктов можно снять с карты. Таким образом, оценку точности геодезической сети в форме матрицы Q обратных весов можно получить до выполнения измерений (наблюдений).

В результате уравнивания результатов измерений получают практическую оценку стандарта σ_ii определяемой величины в форме средней квадратической ошибки m_ii, то есть, в практических вычислениях σ_ii ≡ m_ii. Практическую оценку стандарта σ единицы веса определяемых величин обозначают μ, то есть, в практических вычислениях σ ≡ μ. В этих обозначениях среднюю квадратическую ошибку m_ii определяемой величины, которой приписан номер i, вычисляют по формуле:

, (7.7)

Где p_ii — вес определяемой величины, которой приписан номер i.

Значение μ ошибки единицы веса определяемых величин получают из результатов уравнивания. Такая процедура включена в стандартные программы обработки результатов измерений. На этапе проектирования геодезической сети возникает необходимость оценить ошибки определяемых величин координат пунктов до того, как измерения будут выполнены, то используют значение μ погрешности единицы веса, полученное ранее на других объектах из наблюдений того же состава, с использованием той же аппаратуры и при реализации аналогичной методики работ. Такую оценку точности называют предварительной (априорной) оценкой точности.

Практика обработки результатов измерений показывает, что проблемы создаёт именно определение погрешности единицы веса μ, значение которой, полученное из результатов уравнивания, является, как правило, преуменьшенным. Другими словами, точность определяемых из уравнивания величин получается завышенной. В связи с этим погрешности μ единицы веса определяемых величин придают значение, полученное на основе опыта предшествующих измерений.

Из практики создания геодезических сетей спутниковым методом известно также следующее. Недиагональные элементы ковариационной матрицы K всегда меньше элементов, расположенных на главной диагонали. Элементы, расположенные на главной диагонали, имеют значения в несколько единиц, умноженных на 10^-6, например, 9⋅10^-6. Это означает, что соответствующее неизвестное получено с ошибкой 3⋅10^-3 метра или 3 миллиметра. Такова обычная величина погрешности в определении координат пункта геодезической сети. При длительных сессиях наблюдений диагональные элементы ковариационной матрицы получаются равными нескольким единицам, умноженным на 10^-7.

Заключение

В учебном пособии в простейшем, по мнению автора, виде дано понятие матрицы применительно к параметрическому способу уравнивания результатов измерений. Возвращаясь к некоторым поставленным в тексте учебного пособия вопросам, напишем следующее.

В процессе производственной деятельности геодезист измеряет угловые и линейные величины. Эти величины физически существуют и их значения не зависят от выбранной системы координат. В ходе выполнения измерений геодезист вообще может не задумываться о том, какую именно систему координат он будет использовать для получения окончательного результата в виде координат пунктов опорной геодезической сети или в виде разностей этих координат. Но как только геодезист приступит к обработке результатов измерений – выбор конкретной системы координат становится его первоочередной задачей.

Геодезист измеряет те и только те угловые и линейные величины, которые функционально связаны с определяемыми величинами: с координатами пунктов геодезической сети и/или, чаще всего, с разностями координат этих пунктов. Корректным и полным результатом работы геодезиста являются полученные им измеряемые величины и определённые им координаты (разности координат) пунктов геодезической сети, сопровождённые оценкой точности. Мерой точности измеренной величины является её средняя квадратическая ошибка. Точность определения совокупности неизвестных, таких, как, опять же, координаты множества пунктов геодезической сети, характеризует ковариационная матрица K. Геометрию геодезической сети и геометрию наблюдений характеризует матрица обратных весов Q. Именно теория матриц позволяет наиболее эффективным и исчерпывающим образом изложить, понять и глубоко усвоить практикуемые в геодезии понятия и определения.

В ходе работы над учебным пособием автор стремился к тому, чтобы содержание учебного пособия было по возможности кратким, а восприятие содержания этого учебного пособия было по возможности лёгким для читателя. В частности, автор сделал попытку, за счёт математической строгости изложения, упростить структуру материала. В полной мере этого сделать не удалось. В частности, упоминание о ковариационной матрице встречается в начале текста учебного пособия, а понятие ковариационной матрицы дано ближе к концу текста. В связи с этим автор надеется, что читатель найдёт в себе желание и силы прочитать учебное пособие не менее двух раз. Автор надеется также, что учебное пособие будет скромным, но полезным дополнением к существующим методическим разработкам по высшей математике и по теории математической обработки результатов геодезических измерений.

Литература

1. Дроздов Н.Д. Теория матриц и решение систем линейных уравнений. Конспект лекций по курсу «Линейная алгебра». Москва. МИИГАиК. 1967 год. 68 с.

2. Дроздов Н.Д. Евклидовы пространства и линейные преобразования. Конспект лекций по курсу «Линейная алгебра». Москва. МИИГАиК. 1968 год. 53 с.

3. Дроздов Н.Д. Линейная алгебра в теории уравнивания измерений. Москва. Недра. 1972. 214 с.

4. Нейман Ю.М. К вопросу о математической обработке разнородных измерений. Москва, Известия ВУЗов. Геодезия и аэрофотосъёмка, №2, 2008, с. 7-21.

5. Боревич З.И. Определители и матрицы. Москва. Наука. 1970 год. 199 с.

6. Большаков В.Д., Деймлих Ф., Голубев А.Н., Васильев В.П. Радиогеодезические и электрооптические измерения. Москва. Недра. 1985 год. 303 с.

7. Шануров Г.А., Мельников С.Р. Геотроника. Учебное пособие. Москва. МИИГАиК. 2001 год. 136 с.

8. Купер Дж., Макгиллем К. Вероятностные методы анализа сигналов и систем. Москва. Мир. 1984 год. 376 с.

9. Свешников А.А. Прикладные методы теории случайных функций. Ленинград. Судпромгиз. 1961 год. 252 с.

10. Вентцель А.Д. Курс теории случайных процессов. Москва. Наука. 1975 год. 320 с.

11. Маркузе Ю.И., Бойко Е.Г., Голубев В.В. Геодезия. Вычисление и уравнивание геодезических построений. Москва. Картгеоцентр и Картгеоиздат. 1994 год.

12. Уралов С.С. Курс геодезической астрономии. Москва. Недра. 1980 год.

13. B. Hofmann-Wellenhoff, H. Lichtenegger, J. Collins. Global Positioning System. Theory and Practice. Second eddition. Springer-Verlag. Wien. New York. p. 326.

14. Phillips A.H. Geometrical determination of PDOP. Navigation (USA), 1984-1985, 31, #4, pp. 329-337.

studfiles.net

IV. Указания по выполнению контрольной работы

1. Построить график изменения объемов продаж.

При построении графика используется понятие временного ряда. Каждая точка из таблицы строится на координатном поле:

x = t (месяцы),

y = V (объём продаж).

2. Применить метод трёхчленной скользящей средней.

Метод скользящей средней используется для сглаживания эмпирических кривых. Метод основан на замене фактических показателей их усредненными величинами. В зависимости от периода усреднения различают скользящие средние, рассчитанные для нечетного и четного числа интервалов времени. Количество членов в скользящей средней определяется количеством усредняемых точек.

Кроме того, из-за сглаживания происходит выравнивание контура исходной кривой, что позволяет визуально определить тенденцию изменения показателя, т.е. по внешнему виду полученной кривой сделать предварительный прогноз.

Исходя из вышесказанного, значения трехчленных скользящих средних для трех членов ряда вычисляются по формуле:

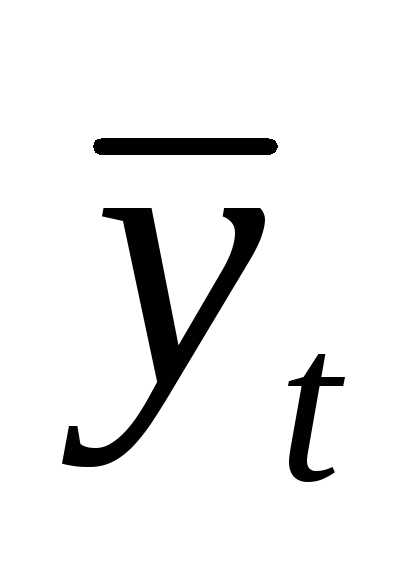=( y_t-1+ y_t+ y_t+1)/3, t = 2, 3,…, ( n — 1), (1.IV)

y_t-1, y_t , y_t+1 – выбираются из построенного графика п.1.

3. Построить систему нормальных уравнений и рассчитать константы прогнозирующей функции.

После построения исходной кривой и сглаживания её скользящей средней необходимо построить некую прогнозирующую функцию. Для этого применяется много разных методов, составляющих основу регрессионного анализа. В этом анализе одним из самых простых и наиболее применимым является метод наименьших квадратов. Особенность этого метода в том, что он позволяет подобрать параметры уравнения прогноза 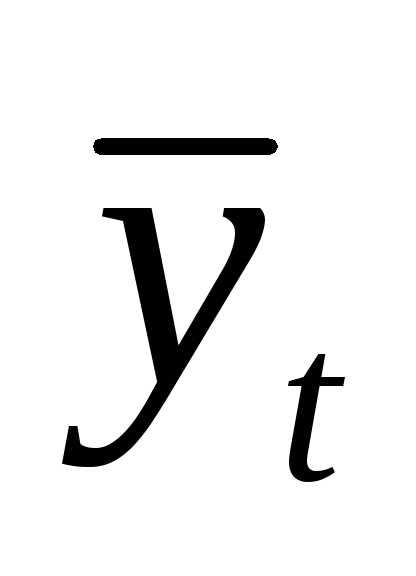=f (t) с таким расчетом, чтобы суммарные отклонения фактических значений ряда (y_t) от найденных по статистической модели 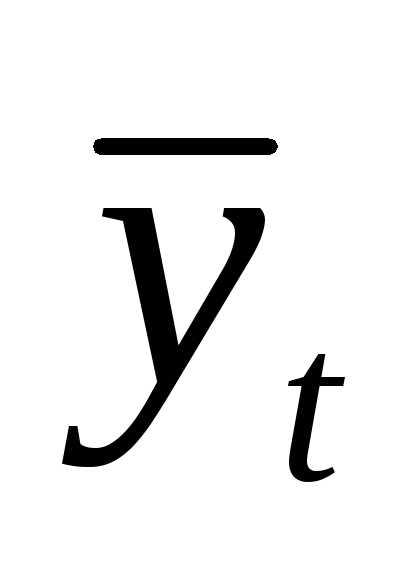были бы минимально возможными. При использовании метода наименьших квадратов для устранения возможности взаимного погашения величин, имеющих разные знаки, отклонения y_t –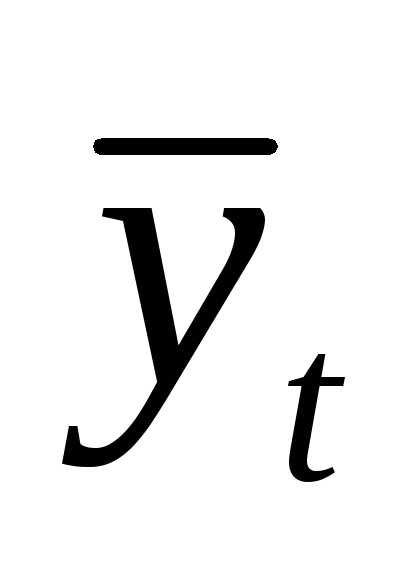сначала возводят в квадрат, после чего суммируют. Аналитическая функция 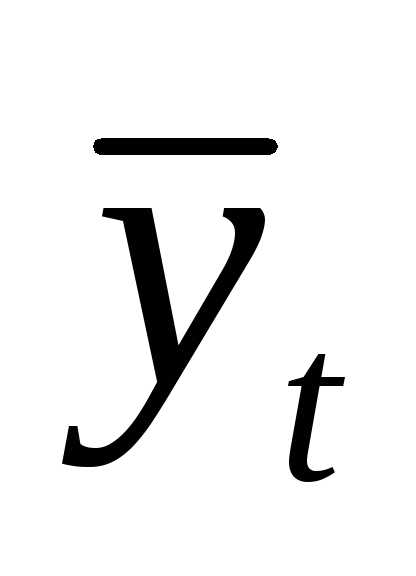=f (t) наиболее точно отображает исходную зависимость, если выполняется условие

 ( y_t – 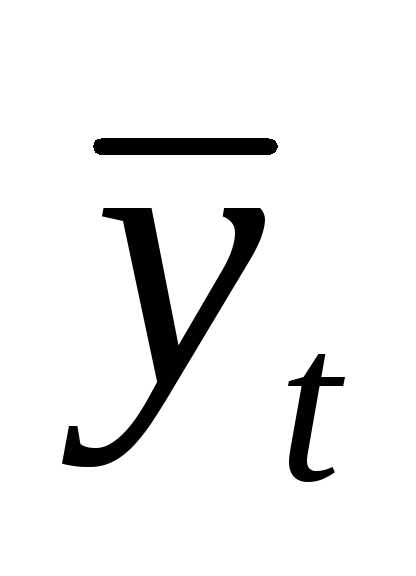)² = min (2.IV)

Для определения конкретного вида аналитической функции, используемой в качестве уравнения прогноза, необходимо определить параметры, определяющие её вид.

Например, если для прогноза выбирается линейная функция

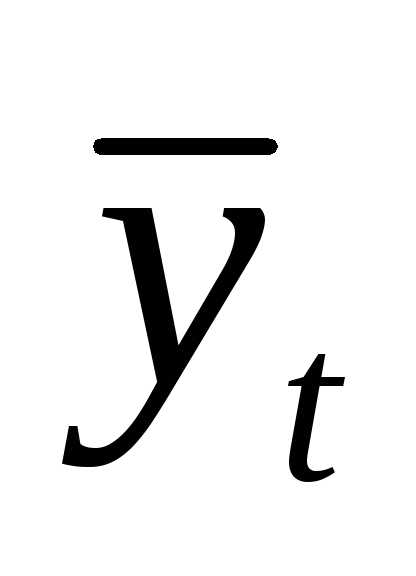= a + bt, (3.IV)

то для определения параметров a и b необходимо решить систему двух линейных уравнений с двумя неизвестными. Такая система получается из условия минимальности функции и называется системой нормальных уравнений. Подробно этот процесс описан в [1]. Здесь же просто отметим, что для уравнения тренда (3.IV) (называемого также уравнением регрессии) нормальные уравнения имеют вид:

(4.IV)

Подставив в систему уравнений, имеющуюся исходную информацию (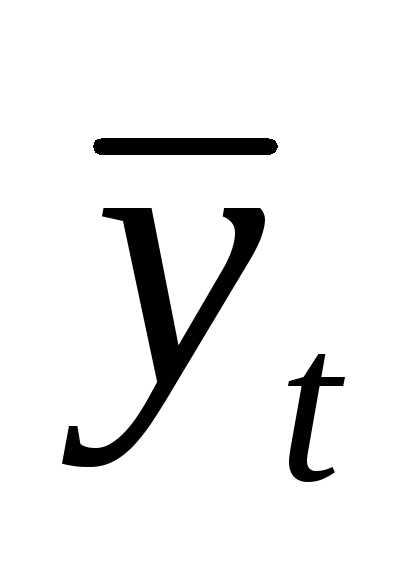и t), можно рассчитать параметры прогнозирующей функции a и b. Сомножитель n в первом нормальном уравнении обозначает длину временного ряда. Кроме того, ясно, что для решения этой системы необходимо посчитать все суммы, входящие в уравнения (4.IV).

Для нелинейных функций, например логарифмической, степенной, экспоненциальных и других (данных в настоящем задании в таблице исходных данных) процессу построения системы нормальных уравнений предшествует этап линеаризации кривой, предусматривающий переход от нелинейных связей к линейной зависимости изменения признака. С этой целью осуществляется замена переменных, исходя из соотношений, приведенных в таблице 2.IV .

Таблица 2.IV

Функция	Исходное уравнение	Способы замены переменных	Линеаризованное уравнение
Гиперболическая	yt = a + b/t	t1=1/t	yt=a+bt1
Логарифмическая	yt = a + bln t	t1= ln t	yt=a+bt1
Степенная	yt = atb	1. Логарифмируем ln yt = ln a + blnt 2. Обозначим yt1= ln yt a1 = ln a t1=lnt	yt1= a1 +b t1
Экспоненциальная	yt= a ebt	1. Логарифмируем ln yt = ln a + bt 2. Обозначим yt1= ln yt 3. a1 = ln a	yt1= a1 +b t

Для случая параболической прогнозирующей функции замена не производится. Системы нормальных уравнений для всех приведенных функций даны в таблице 3. IV.

Таблица 3. IV

Функция	Система нормальных уравнений
Гиперболическая yt = a + b/t	 yt = an + b t1  yt t1 = a t1 + b t12
Логарифмическая yt = a + bln t	 yt = an + b t1  yt t1 = a t1 + b t12
Степенная yt = atb	 yt1 = a1 n + b t1  yt1 t1 = a1 t1 + b t12
Экспоненциальная yt= a ebt	 yt1 = a1 n + b t  yt1t = a1 t + b t2
Параболическая yt = a + bt + ct2	 yt = an + b t + c t2  yt t = a t + b t2 + c t3  yt t2 = a t2 + b t3 + c t4

Как видно из таблицы 3.IV. все системы нормальных уравнений (кроме параболической функции) сводятся к системе (4.IV). Отличаются они только заменёнными переменными. В случае параболической функции необходимо решить систему из трёх уравнений, т.к. помимо параметров a и b появляется ещё параметр с.

studfiles.net

Нормальные уравнения — это… Что такое Нормальные уравнения?



Нормальные уравнения

        некоторая специальная система алгебраических или трансцендентных уравнений, решение которой даёт приближённые значения неизвестных величин, оцениваемых способом наименьших квадратов. См. Наименьших квадратов метод.

Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.

• Нормальные колебания
• Нормальные условия

Смотреть что такое «Нормальные уравнения» в других словарях:

• Нормальные колебания — Различные нормальные моды в 1D решётке. Нормальные колебания или нормальные моды  набор характерных для колебательной системы типов гармонических колебаний. Каждое из нормальных колебаний физической системы, например, колебаний атомов в… …   Википедия

• НАВЬЕ — СТОКСА УРАВНЕНИЯ — основные уравнения движения вязкой жидкости, представляющие математическое выражение законов сохранения импульса и массы. Для неустановившегося течения сжимаемой жидкости Н. С. у. в декартовой системе координат могут быть, записаны в виде где… …   Математическая энциклопедия

• Наименьшие квадраты — Под названием способа Н. квадратов разумеют прием, посредством которого вычисляются результаты из совокупности многих однородных наблюдений. Числа, получаемые из наблюдений, связаны с искомыми величинами уравнениями, вид которых определяется в… …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

• МНК — Метод наименьших квадратов один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. Метод наименьших квадратов применяется также для приближённого представления заданной функции… …   Википедия

• Уравнительные вычисления —         в геодезии, совокупность математических операций, выполняемых для получения вероятнейшего значения геодезических координат точек земной поверхности и для оценки точности результатов измерений. У. в. проводятся для устранения противоречий… …   Большая советская энциклопедия

• КОЕВКЛИДОВО ПРОСТРАНСТВО — пространство, получаемое из евклидова применением принципа двойственности проективного пространства такой же размерности. Обозначается R*n, где п размерность пространства. К. п. R*n является пространством с проективной метрикой, к рая задается в… …   Математическая энциклопедия

• Центральное многообразие — особой точки автономного обыкновенного дифференциального уравнения инвариантное многообразие в фазовом пространстве, проходящее через особую точку и касающееся инвариантного центрального подпространства линеаризации дифференциального уравнения.… …   Википедия

• Физическая кинетика — (др. греч. κίνησις  движение)  микроскопическая теория процессов в неравновесных средах. В кинетике методами квантовой или классической статистической физики изучают процессы переноса энергии, импульса, заряда и вещества в различных… …   Википедия

• Кинетика физическая — Физическая кинетика (др. греч. κίνησις  движение)  микроскопическая теория процессов в неравновесных средах. В кинетике методами квантовой или классической статистической физики изучают процессы переноса энергии, импульса, заряда и вещества в… …   Википедия

• Мода (физика) — Различные нормальные моды в 1D решётке. Нормальные колебания или нормальные моды  набор характерных для колебательной системы типов гармонических колебаний. Каждое из нормальных колебаний физической системы, например, колебаний атомов в молекулах …   Википедия

dic.academic.ru

система линейных нормальных уравнений — это… Что такое система линейных нормальных уравнений?



система линейных нормальных уравнений

1. normal equations

 

система линейных нормальных уравнений
(решение которых представляет собой среденеквадратическое приближение к желаемому сигналу)
[http://slovarionline.ru/anglo_russkiy_slovar_neftegazovoy_promyishlennosti/]

Тематики

• нефтегазовая промышленность

EN

Русско-английский словарь нормативно-технической терминологии. academic.ru. 2015.

• система легче воздуха (воздушные суда)
• система линейных уравнений с N неизвестными

Смотреть что такое «система линейных нормальных уравнений» в других словарях:

• система линейных нормальных уравнений — (решение которых представляет собой среденеквадратическое приближение к желаемому сигналу) [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN normal equations …   Справочник технического переводчика

• Нормальная форма дифференциальных уравнений — есть наипростейшая эквивалентная форма исходных уравнений. Нормальная форма получается с помощью специальных замен зависимых и независимых переменных задачи с целью максимального упрощения структуры уравнений. В математике эти замены переменных… …   Википедия

• Физика —         I. Предмет и структура физики          Ф. – наука, изучающая простейшие и вместе с тем наиболее общие закономерности явлений природы, свойства и строение материи и законы её движения. Поэтому понятия Ф. и сё законы лежат в основе всего… …   Большая советская энциклопедия

• НАИМЕНЬШИХ КВАДРАТОВ МЕТОД — один из методов ошибок теории для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. Н. к. м. применяется также для приближенного представления заданной функции другими (более простыми) функциями и часто оказывается …   Математическая энциклопедия

• Корреляция — (Correlation) Корреляция это статистическая взаимосвязь двух или нескольких случайных величин Понятие корреляции, виды корреляции, коэффициент корреляции, корреляционный анализ, корреляция цен, корреляция валютных пар на Форекс Содержание… …   Энциклопедия инвестора

• Наименьших квадратов метод —         один из методов ошибок теории (См. Ошибок теория) для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. Н. к. м. применяется также для приближённого представления заданной функции другими (более простыми)… …   Большая советская энциклопедия

• РАСШИРЕНИЕ — д и ф ф е р е н ц и а л ь н о г о п о л я F0 дифференциальное поле FЙF0. с таким множеством дифференцирований D, что ограничение D на F0 совпадает с множеством дифференцирований, заданных на F0. В свою очередь F0 будет д и ф ф ер е н ц и а л ь н… …   Математическая энциклопедия

• НЕСАМОСОПРЯЖЕННЫЙ ОПЕРАТОР — линейный оператор в гильбертовом пространстве, спектральный анализ которого не укладывается в рамки теории самосопряженных операторов и ее простейших обобщений: теории унитарных операторов и теории нормальных операторов. Н. о. возникают при… …   Математическая энциклопедия

• СИНТЕЗА ЗАДАЧИ — совокупность задач, концентрирующихся вокруг проблемы построения управляющей системы (у. с.), имеющей предписанное функционирование. У. с. строится из элементов, к рые обычно сами являются простыми у. с. При синтезе заранее заданы состав… …   Математическая энциклопедия

• Компьютерная томография — Запрос «КТ» перенаправляется сюда; см. также другие значения. Компьютерный томограф Компьютерная томография  метод неразрушающего послойного исследования внутренней стр …   Википедия

• АЛГЕБРА — часть математики, посвященная изучению алгебраических операций. Исторический очерк. Простейшие алгебраич. операции арифметич. действия над натуральными и положительными рациональными числами встречаются в самых ранних математич. текстах,… …   Математическая энциклопедия

normative_ru_en.academic.ru

19. Система нормальных уравнений для многофакторных моделей прогнозирования.

Параметры уравнения множественной регрессии оценивают­ся, как и в парной регрессии, методом наименьших квадратов (МНК). При его применении строится система нормальных уравнений, решение которой и позволяет получить оценки пара­метров регрессии.

Так, для уравнения

система нормальных уравнений составит

Ее решение может быть осуществлено методом определителей:

где Δ– определитель системы; Δа,Δb1,…,Δbp– частные определители.

20. Линейное уравнение множественной регрессии, вычисление статистических характеристик.

21. Оценка адекватности уравнения множественной регрессии.

Для оценки качества модели множественной регрессии вычисляют к-т монж.корреляции R и детерминации R².

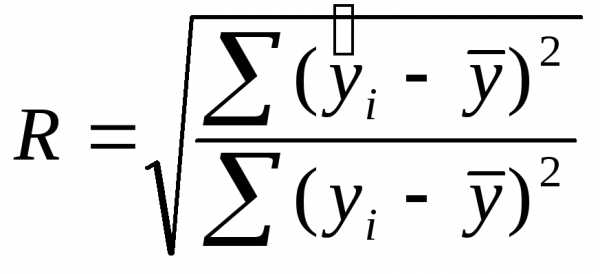;показывает долю вариации результативного признака, находящегося под воздействием изучаемых факторов, т.е. определяет, какая доля вариации признакаY учтена в модели и обусловлена влиянием на него факторов.

Чем ближе к 1 значение этих характеристик, тем выше качество модели. В многофакторной регрессии добавление дополнительных объясняющих переменных увеличивает к-т детерминации. Следовательно, к-т детерминации д.б. скорректирован с учетом числа независимых переменных. Скорректированный R² рассчитывается так:

, где n– число наблюдений, k– число независимых переменных.

Для проверки значимости модели регрессии исп-ся F-критерий Фишера: 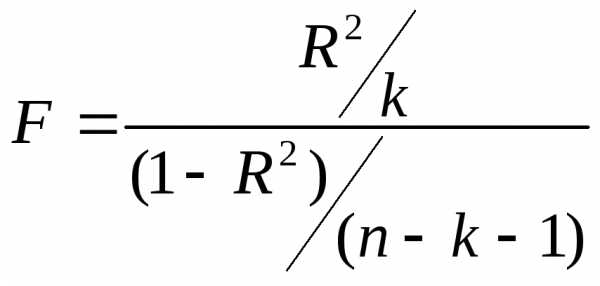Если расчетное значение сt₁=k и t₂=(n-k-1) степенями свободы, где k– количество факторов, включенных в модель, больше табличного при заданном уровне значимости, то модель считается значимой.

22. Оценка значимости факторов по к-там эластичности и к-там корреляции.

К-т эластичности: 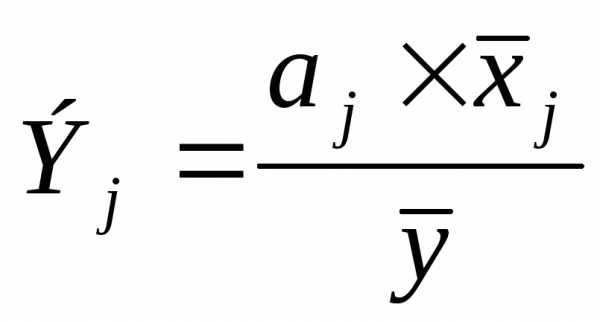. Он показывает, на сколько % изменяется зависимая переменная при изменении фактораj на 1%.

Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, или, иначе, оценивает тесноту совместного влияния факторов на результат. Независимо от формы связи показатель множ.корреояции м.б. найден как индекс множ.корреляции:

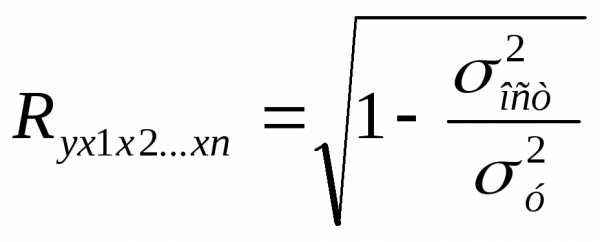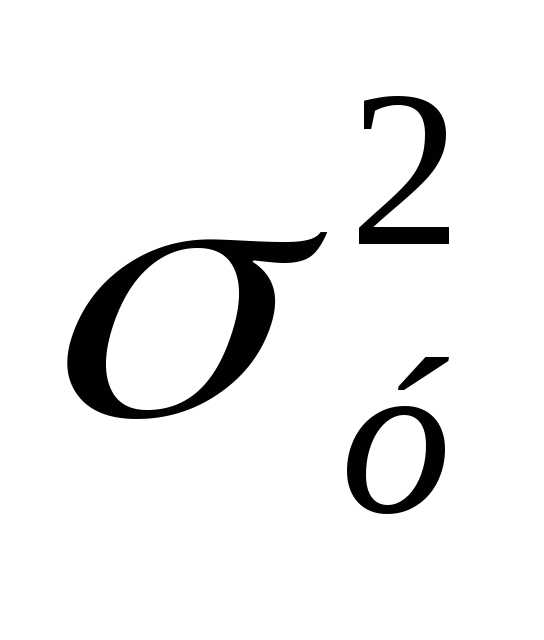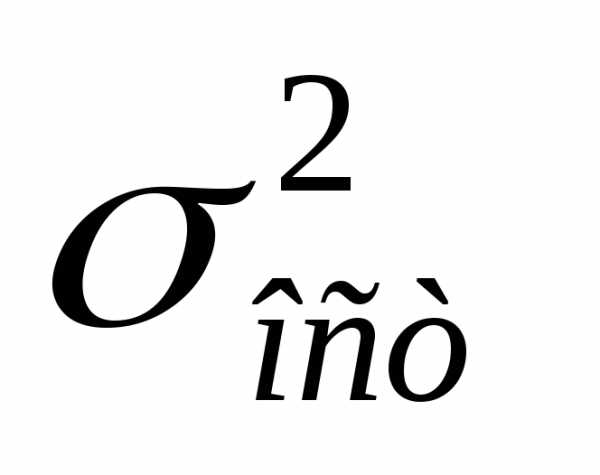где – общ.дисперсия результативн.признака,– остаточная досперсия для уравнения. Границы его измерения: от 0 до 1. Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов.

Частные к-ты (индексы) корреляции хар-т тесноту связи между результатом и соотв.фактором при устранении влияния др факторов, включенных в уравнение регрессии.

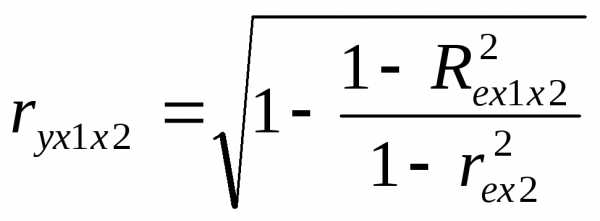
23. Построение точечного прогноза для многофакторных моделей.

Прогнозируемое значение переменной у получается при подстановке в уравнение регрессии ожидаемой величины фактора х. данный прогноз называется точечным. Значение независимой переменной х_прогн не должно значительно отличаться от входящих в исследуемую выборку, по которой вычислено уравнение регрессии.

Доверительный интервал прогноза рассчитывается след.образом:

studfiles.net