Непрерывные функции и их свойства
Поскольку f(a) принадлежит каждой окрестности Uf(a), то, учитывая определение предела функции f в точке a, получаем следующее определение, равносильное предыдущим.
Определение 3.3. Пустьf : X → R,a X,a — предельная точка множестваX. Функцияf называется непрерывной в точкеa, если существует предел функции в точкеa и он равен значению функцииf в точкеa.
Учитывая представление функции, имеющей в точке конечный предел, получаем: непрерывность функции f в точке a означает, что f имеет представление f(x) = f(a) + o(1), x → a.
Наконец, используя определение предела функции по Гейне, получаем определение, равносильное предыдущим
Определение 3.4 (по Гейне). Функция f : X → R называется непрерывной в точке a X, если для любой последовательности {xn} элементов множества X, сходящейся к a, соответствующая последовательность {f(xn)} образов сходится к f(a).
Замечание. По сравнению с определением Гейне предела функции в определении3.4 непрерывности функции снято требование, обязывающее все элементы последовательности {xn} быть отличными от a. (В случае, когда a — изолированная точка множества X, все элементы xn, начиная с некоторого, равны a.)
Определение 3.5. Функцияf называется непрерывной на множествеX, если она непрерывна в каждой точке этого множества.
Совокупность вещественнозначных функций, непрерывных на множестве X, обычно обозначается символом C(X).
Рассмотрим некоторые примеры.
Пример 3.1. Функция f(x) = C, x R, непрерывна на R.
Действительно, для любой точки a R, для x R |f(x) − f(a)| = 0. Поэтому ε > 0 δ > 0 имеем:
|x − a| < δ |f(x) − f(a)| < ε.
Последнее означает непрерывность функции в точке a, а значит и на множестве R.
Пример 3.2. Если f : R → R и f(x) = x, x R, то f C(R).
Зафиксируем произвольную точку a R и число ε > 0. Так как
|f(x) − f(a)| = |x − a|, x R,
то, полагая δ = ε, получим
|x − a| < δ |f(x) − f(a)| < ε.
studfiles.net
17. Свойства непрерывных функций.
1) Сумма, произведение и частное двух непрерывных функций есть функция непрерывная. (для частного кроме тех случаев, когда значение знаменателя равно нулю)
Пусть
функции 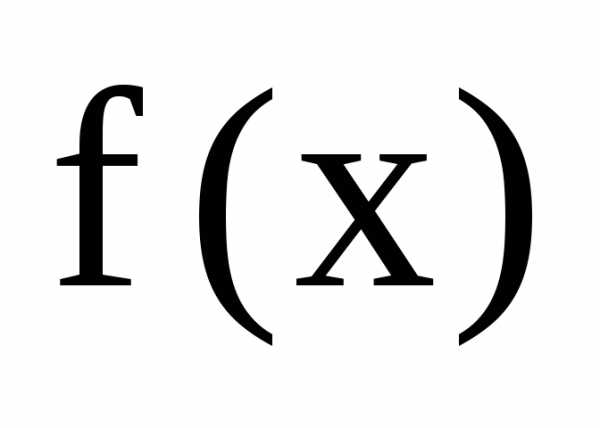 и
и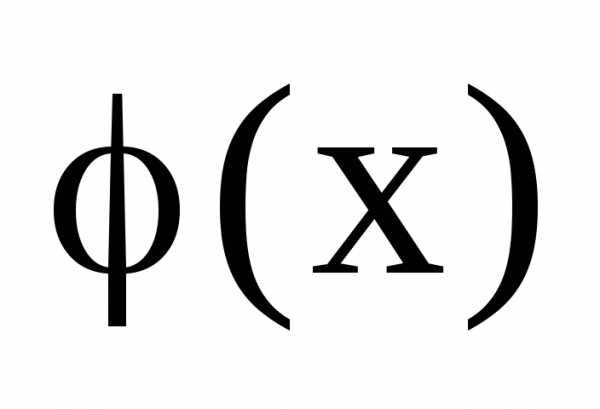 непрерывны на некотором множестве Х и
непрерывны на некотором множестве Х и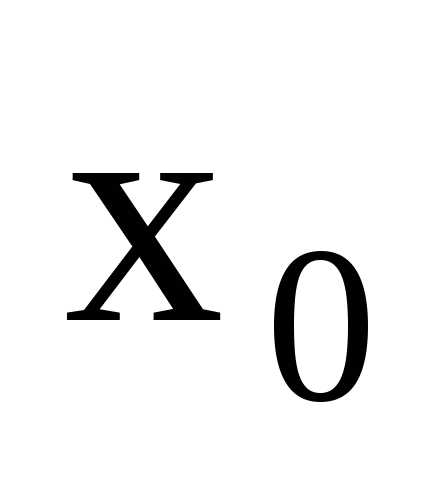 — любое значение из этого множества.
— любое значение из этого множества.
2) Пусть функции 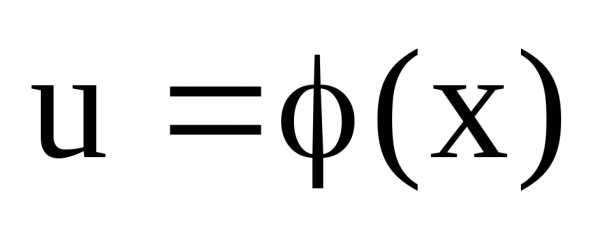 непрерывна в точке
непрерывна в точке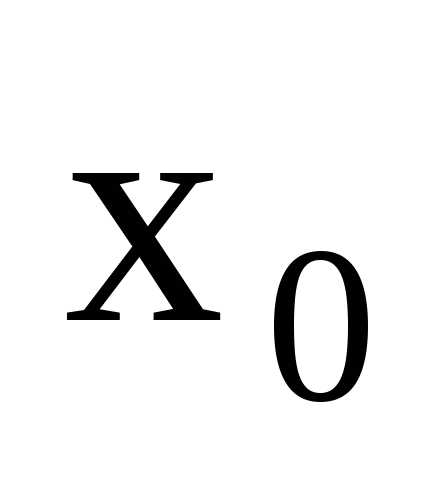 ,
а функция
,
а функция
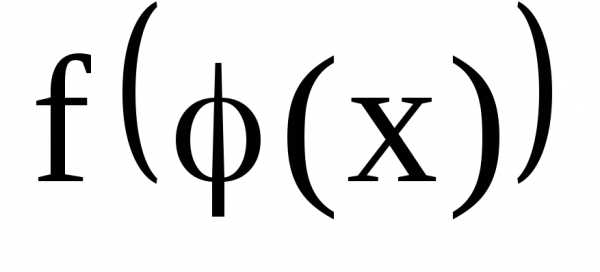 ,
состоящая из непрерывных функций,
непрерывна в точке
,
состоящая из непрерывных функций,
непрерывна в точке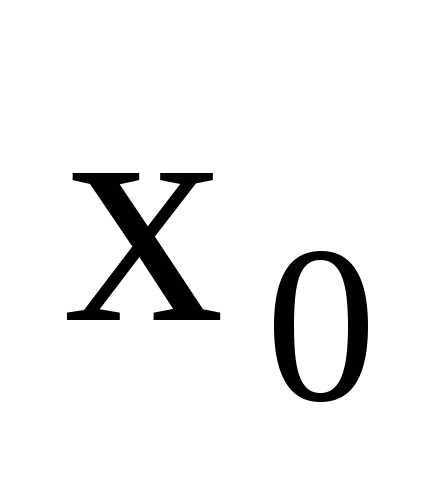 .
. В силу непрерывности
функции 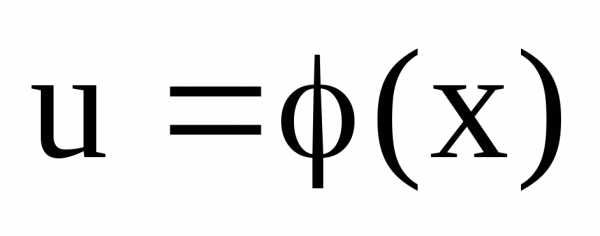 ,,
т.е. при
,,
т.е. при имеем
имеем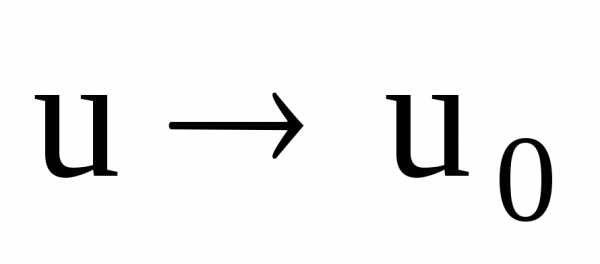 .
В следствии непрерывности функции
.
В следствии непрерывности функции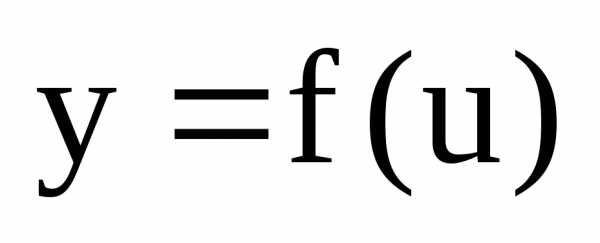 имеем :
имеем :
3) Если функция 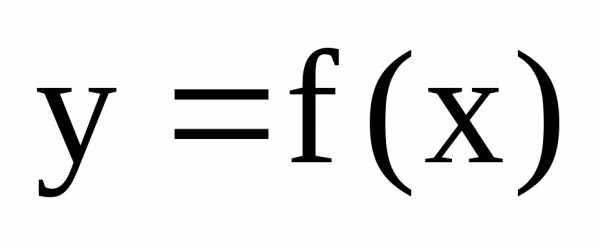 непрерывна и строго монотонна на [a;b]
оси Ох, то обратная функция
непрерывна и строго монотонна на [a;b]
оси Ох, то обратная функция 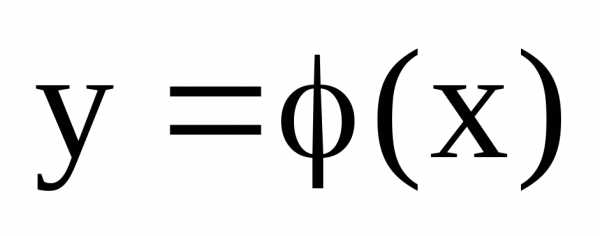 также непрерывна и монотонна на
соответствующем отрезке [c;d]
оси Oy.
также непрерывна и монотонна на
соответствующем отрезке [c;d]
оси Oy.
18. Точки разрыва и их классификация.
Точки,
в которых нарушается непрерывность
функции, называются точками
разрыва этой
функции. Если 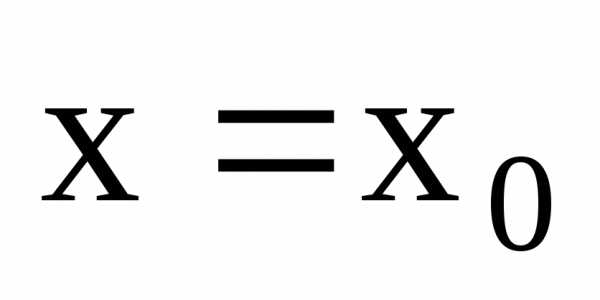 — точка разрыва функции
— точка разрыва функции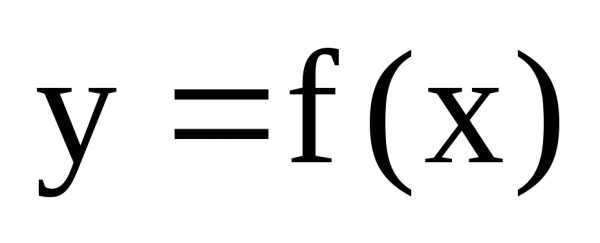 ,
то в ней не выполняется по крайней мере
одно из условий непрерывности функции.
,
то в ней не выполняется по крайней мере
одно из условий непрерывности функции.
Функция определена в окрестности точки
 ,
но не определена в самой точке
,
но не определена в самой точке .
.Функция
 определена в точке
определена в точке и в ее окрестности, но не существует
пределаf(x)
при
и в ее окрестности, но не существует
пределаf(x)
при 
Точка 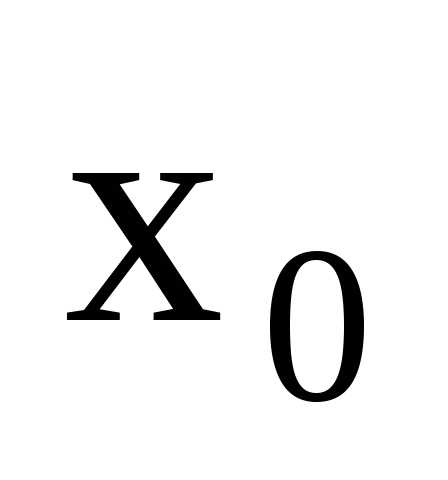 называетсяточкой
разрыва первого рода функции
называетсяточкой
разрыва первого рода функции 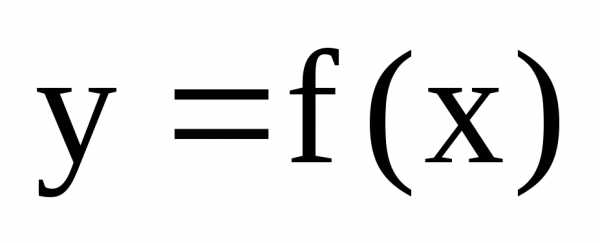 ,
если в этой точке существуют конечные
пределы слева и справа (односторонние
пределы), т.е.и.
При этом:
,
если в этой точке существуют конечные
пределы слева и справа (односторонние
пределы), т.е.и.
При этом:
Если
 ,
то точка
,
то точка называетсяточкой
устранимого разрыва.
называетсяточкой
устранимого разрыва.Если
 ,
то точка
,
то точка называетсяточкой
конечного разрыва
называетсяточкой
конечного разрыва
Величину  называютскачком
функции в
точке разрыва первого рода.
называютскачком
функции в
точке разрыва первого рода.
Точка 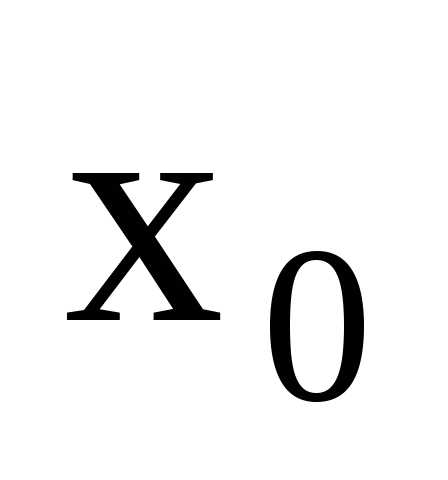 называетсяточкой
разрыва второго рода функции
называетсяточкой
разрыва второго рода функции 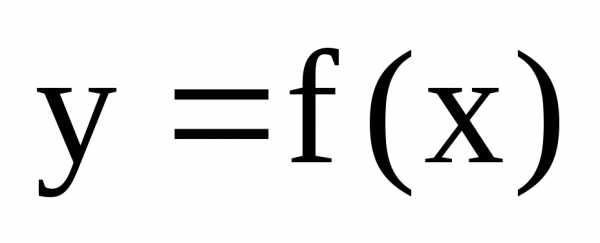 ,
если по крайней мере один из односторонних
пределов не существует или равен
бесконечности.
,
если по крайней мере один из односторонних
пределов не существует или равен
бесконечности.
19. Непрерывность функции на интервале и на отрезке.
Функция 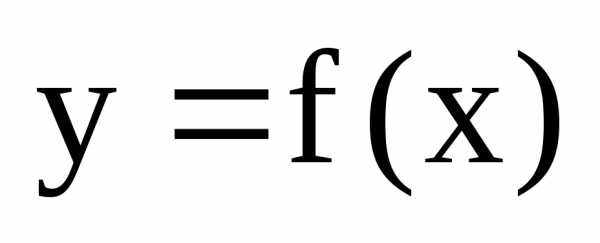 называетсянепрерывной
на интервале (a;b),
если она непрерывна в каждой точке
этого интервала.
называетсянепрерывной
на интервале (a;b),
если она непрерывна в каждой точке
этого интервала.
Функция 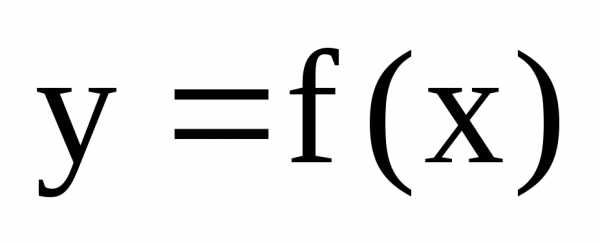 называетсянепрерывной
на отрезке [a;b],
если она непрерывна на отрезке (a;b)
и в точке
x
= a непрерывна справа ,
а в точкеx
= b непрерывна слева .
называетсянепрерывной
на отрезке [a;b],
если она непрерывна на отрезке (a;b)
и в точке
x
= a непрерывна справа ,
а в точкеx
= b непрерывна слева .
20. Свойства функций, непрерывных на отрезке.
1) Теорема Вейрштрасса. Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений.
1’) Следствие. Если функция непрерывна на отрезке, то она ограничена на этом отрезке.
2)
Теорема Больцано-Коши.
Если функция 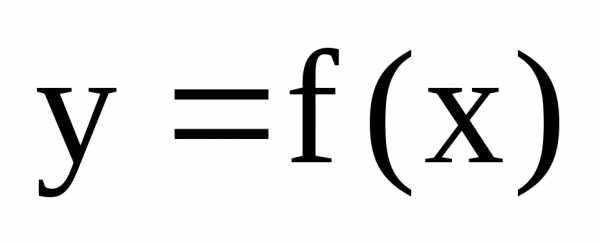 непрерывна на отрезке [a;b]
и принимает на его концах неравные
значения f(a)
= A
и f(b)
= B,
то на этом отрезке она принимает и все
промежуточные значения между А и В.
непрерывна на отрезке [a;b]
и принимает на его концах неравные
значения f(a)
= A
и f(b)
= B,
то на этом отрезке она принимает и все
промежуточные значения между А и В.
2’)
Следствие.
Если функция 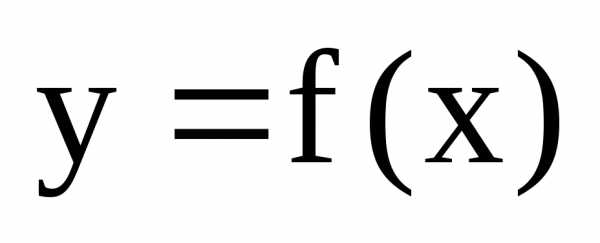 непрерывна на отрезке [a;b]
и принимает на его концах разные по
знаку значения, то внутри отрезка [a;b]
найдется хотя бы одна точка с, в которой
функция обращается в нуль. F(c)
= 0
непрерывна на отрезке [a;b]
и принимает на его концах разные по
знаку значения, то внутри отрезка [a;b]
найдется хотя бы одна точка с, в которой
функция обращается в нуль. F(c)
= 0
21. Дифференциальное исчисление функций одной переменной.
Производной
функции 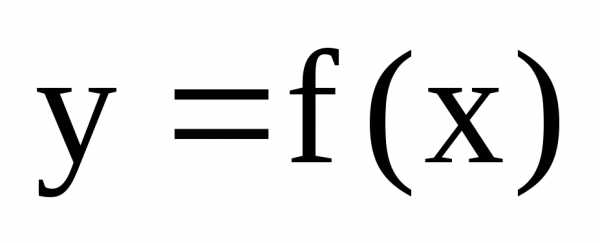 в точке
в точке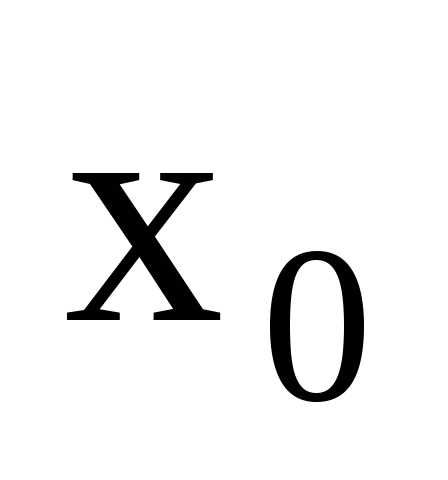
или
Функция 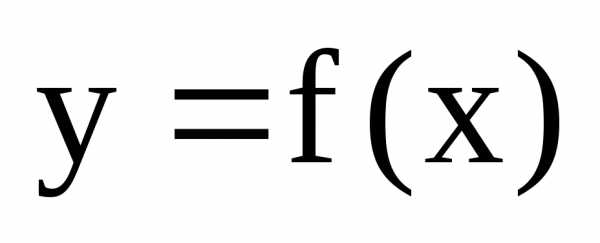 ,
имеющая производную в каждой точке
интервала (a;b),
называется дифференцируемой в этом интервале; операция нахождения
производной функции называется дифференцированием.
,
имеющая производную в каждой точке
интервала (a;b),
называется дифференцируемой в этом интервале; операция нахождения
производной функции называется дифференцированием.
22. Производная функции, ее геометрический и физический смысл.
Физический смысл. Производная – скорость протекания процесса.
Геометрический
смысл.
Производная 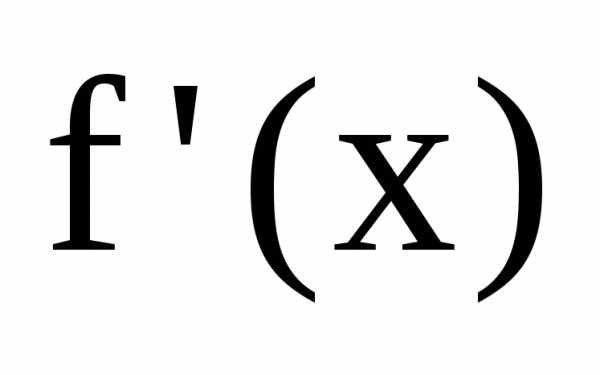 в точке х равна угловому коэффициенту
касательной (тангенсу угла наклона) к
графику функции
в точке х равна угловому коэффициенту
касательной (тангенсу угла наклона) к
графику функции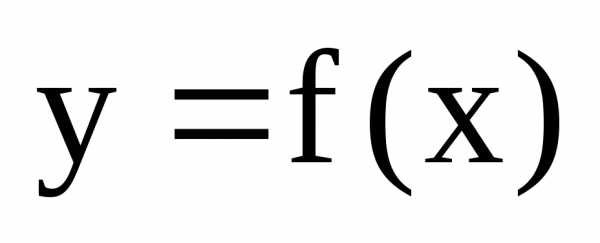
23. Уравнение касательной и нормали к кривой.
Уравнение касательной.
Уравнение нормали. 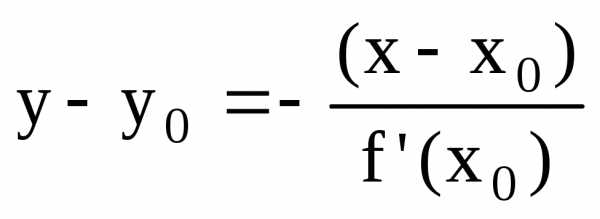
24. Односторонние производные функции в точке.
Возьмем
функцию y
= |x|
в точке х=0.  ,
,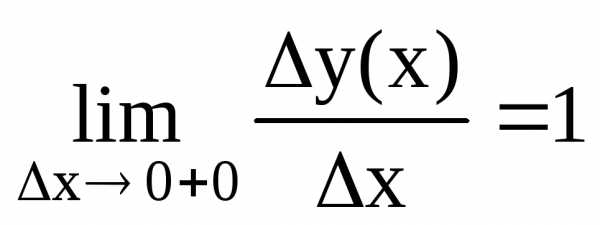 .
.
В
таких случаях говорят, что функция
имеет односторонние производные(или
«производные слева и справа»), и
обозначают соответственно 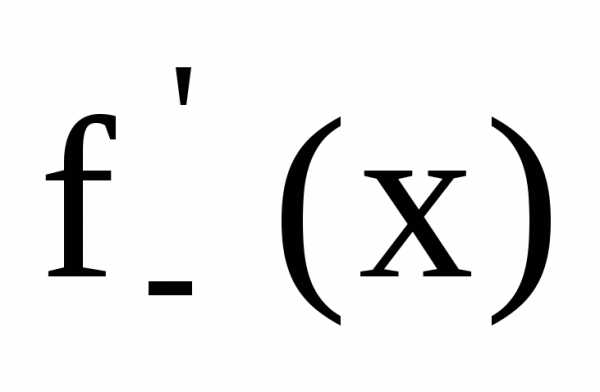 и
и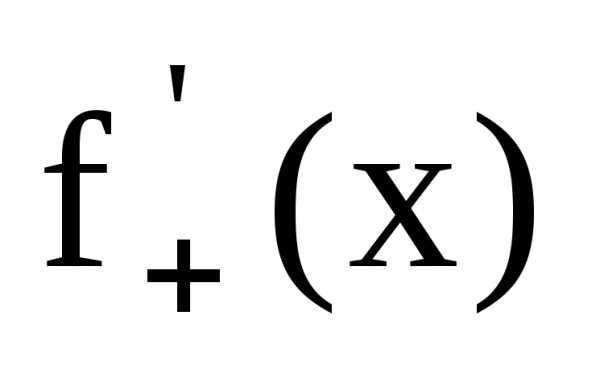 .
.
Если, значит, производная в точке не существует.
25. Основные правила дифференцирования.
Производная суммы (разности) двух функций равна сумме (разности) производных этих функций. .
Производная произведения двух функций равна произведению первого сомножителя на второй плюс произведение первого сомножителя на производную второго: .
Производная
частного двух функций равна дроби, числитель которой есть
разность произведения знаменателя
дроби на производную числителя и
числителя дроби на производную
знаменателя, а знаменатель есть квадрат
прежнего знаменателя: 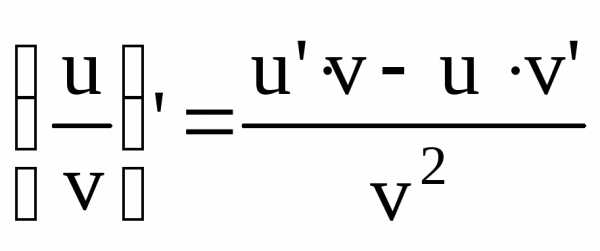 .
Выполняется, когда
.
Выполняется, когда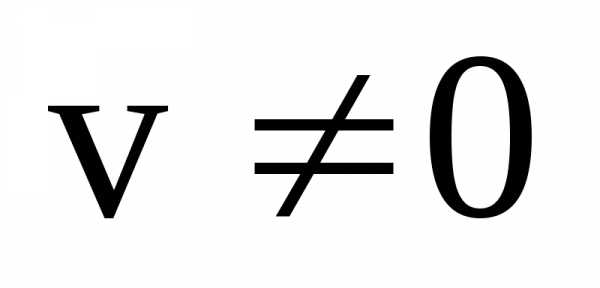 .
.
studfiles.net
Непрерывность функции на интервале и на отрезке.
При этом не требуется непрерывность функции на концах отрезка или интервала, необходима только односторонняя непрерывность на концах отрезка или интервала.
Свойства функций, непрерывных на отрезке.
Свойство 1: (Первая теорема Вейерштрасса (Вейерштрасс Карл (1815-1897)- немецкий математик)). Функция, непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке [a, b] выполняется условие –M f(x) M.
Доказательство этого свойства основано на том, что функция, непрерывная в точке х0, ограничена в некоторой ее окрестности, а если разбивать отрезок [a, b] на бесконечное количество отрезков, которые “стягиваются” к точке х0, то образуется некоторая окрестность точки х0.
Свойство 2: Функция, непрерывная на отрезке [a, b], принимает на нем наибольшее и наименьшее значения.
Т.е. существуют такие значения х1 и х2, что f(x1) = m, f(x2) = M, причем
m f(x) M
Отметим эти наибольшие и наименьшие значения функция может принимать на отрезке и несколько раз (например – f(x) = sinx).
Разность между наибольшим и наименьшим значением функции на отрезке называется колебанием функции на отрезке.
Свойство 3: (Вторая теорема Больцано – Коши). Функция, непрерывная на отрезке [a, b], принимает на этом отрезке все значения между двумя произвольными величинами.
Свойство 4: Если функция f(x) непрерывна в точке х = х0, то существует некоторая окрестность точки х0, в которой функция сохраняет знак.
Свойство 5: (Первая теорема Больцано (1781-1848) – Коши). Если функция f(x)- непрерывная на отрезке [a, b] и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где f(x) = 0.
Т.е. если sign(f(a)) sign(f(b)), то х0: f(x0) = 0.
Определение. Функция f(x) называется равномерно непрерывной на отрезке [a, b], если для любого >0 существует >0 такое, что для любых точек х1[a,b] и x2[a,b] таких, что
х2 – х1<
верно неравенство f(x2) – f(x1) <
Отличие равномерной непрерывности от “обычной” в том, что для любого существует свое , не зависящее от х, а при “обычной” непрерывности зависит от и х.
Свойство 6: Теорема Кантора (Кантор Георг (1845-1918)- немецкий математик). Функция, непрерывная на отрезке, равномерно непрерывна на нем.
(Это свойство справедливо только для отрезков, а не для интервалов и полуинтервалов.)
Пример. 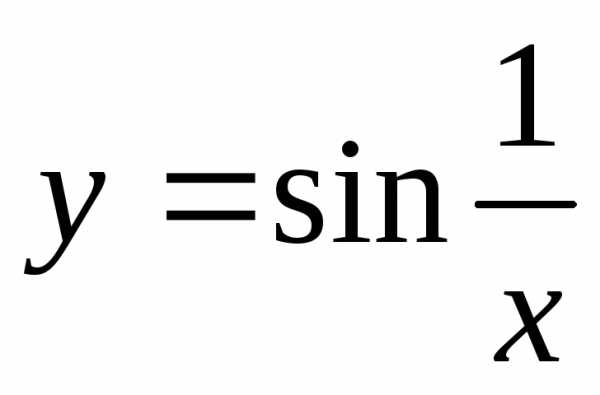
Функция 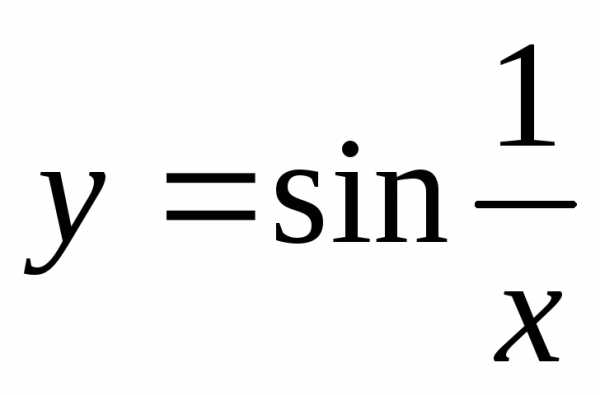 непрерывна на интервале (0, а), но не
является на нем равномерно непрерывной,
т.к. существует такое число >0
такое, что существуют значения х1 и х2 такие, чтоf(x1)
– f(x2)>,
— любое число при условии, что х1 и х2 близки к нулю.
непрерывна на интервале (0, а), но не
является на нем равномерно непрерывной,
т.к. существует такое число >0
такое, что существуют значения х1 и х2 такие, чтоf(x1)
– f(x2)>,
— любое число при условии, что х1 и х2 близки к нулю.
Свойство 7: Если функция f(x) определена, монотонна и непрерывна на некотором промежутке, то и обратная ей функция х = g(y) тоже однозначна, монотонна и непрерывна.
Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.
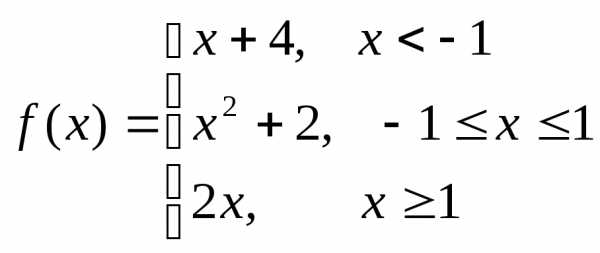
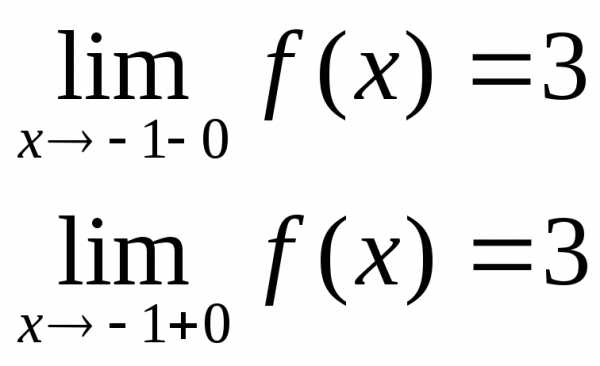

в точке х = -1 функция непрерывна в точке х = 1 точка разрыва 1 – го рода
у
3
2
-4 -1 0 1 х
Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.
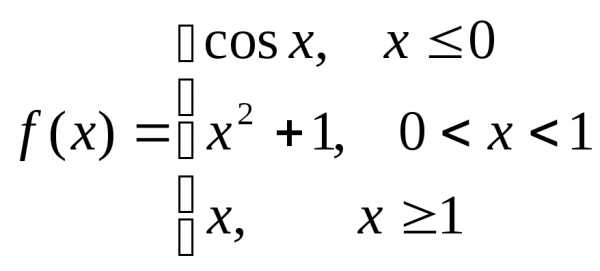
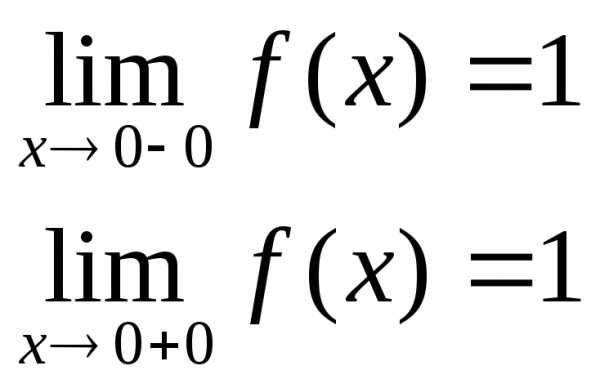
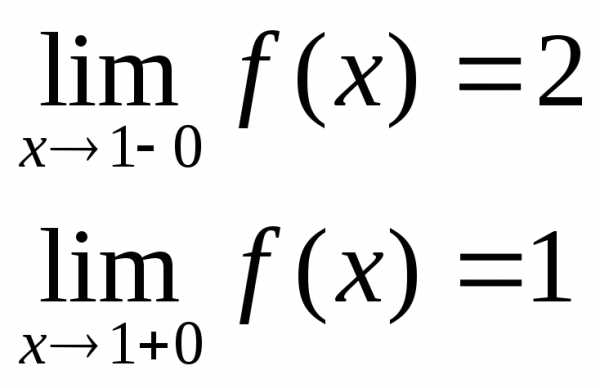
в точке х = 0 функция непрерывна в точке х = 1 точка разрыва 1 – го рода
у
2
1
- -/2 0 1 x
studfiles.net
(1)Понятие непрерывности функции.Свойства непрерывных функций.
Определение 1:
Функция называется непрерывной в точкеотносительно множества, если
Замечание 1:
Если в точке функция непрерывна, то в силу свойств предела она однозначна, поэтому в дальнейшем непрерывные функции будем считать однозначными.
Замечание 2:
Если понятно относительно какого множества непрерывность, то это множество не указываем.
Определение 2:
Функция называется непрерывной в точкеотносительно множества, если
Замечание:
В данном случае не обязательно требовать, чтобы , т.к. привыполняется автоматически.
Определение 3:
Функция называется непрерывной в точкеотносительно
множества , если
Пусть , обозначим,тогда
тогда по определению 1 функция непрерывна в точке относительно, когда
,
Если функция непрерывна в каждой точке множества , то говорят, что функция непрерывна на множестве
Свойства функций:
1) Общие свойства
1 св.) Пусть непрерывна в точкеотносительно множества,, тогданепрерывна в точкео тносительно множества
Доказательство:
2 св.) непрерывна в точкеотносительно множестваравносильно непрерывности функции в точкеотносительно
Доказательство:
По §3.4 св. 5
3 св.) Пусть ,, тогда непрерывность относительноравносильна непрерывности в точкекак относительно, так и
Замечание:
Если точка в св. 3 является предельной только для одного из множестви, то непрерывность относительноравносильна непрерывности относительно именно в этой точке.
4 св.) (предельный переход под знаком непрерывности функции)
1. Если непрерывна в точкеотносительно,
2. ,
тогда или
Следствие:
(теорема о непрерывности сложной функции)
1. Если непрерывна в точкеотносительно множества,,
2. непрерывна в точке,,
тогда непрерывна в точкеотносительно множества
5 св.) Если непрерывна в точкеотносительно множества,тоже непрерывная функция в точкеотносительно множества
Доказательство:
По §3.7 следствие теоремы о двух милиционерах
6 св.) (непрерывность результатов арифметических действий на непрерывных функциях)
Если инепрерывны в точкеотносительно множества, то:непрерывны в точке, относительно множества
(следует из §3.6 и определения непрерывности)
Следствие:
Многочлен и дробно-рациональные функции непрерывны во всех точках своей области определения.
Доказательство:
непрерывна непрерывеннепрерывен. Т.к. каждый многочлен – непрерывная функциятоже непрерывна
2) Односторонняя непрерывность
Определение:
называется непрерывной в точке относительно множествасправа (слева), еслинепрерывна в точкеотносительно множества
Теорема:
Пусть , тогда для того чтобы функция была непрерывна в точкеотносительно, необходимо и достаточно чтобы она была непрерывна в точкеи справа и слева
Доказательство:
По §3.4, св. 6
3) Непрерывность монотонной и обратной к строго монотонной функции
Теорема 1:
(о непрерывности монотонной функции)
Если: 1)монотонна на
2) область значений есть промежуток,
тогда непрерывна во всех точках предельной для нее
Доказательство:
, докажем непрерывность в точке слева и справа.
Слева (справа):
Пусть ,- возрастает. По теореме о пределе монотонной функции:(1). Т.к.возрастает(2). Покажем, что в неравенстве (2) знак «» не имеет места. Пусть, тогда для(а такие есть)(3) т.к. возрастает, а для(4). Из (3),(4) следует, что функция принимает значенияи не принимает значения на промежутке. Это противоречит тому, что по условию значение функции – промежутокв (2) меньше быть не может.
Лемма:
Функция обратная к строго монотонной (однозначная) однозначна и строго монотонна в том же направлении.
Доказательство:
Пусть строго возрастает на множестве. Рассмотрим обратную к ней
(- область значений)точка. Т.к.строго возрастает, то. Возьмёмиз,,. Если бы, тогда- функция строго возрастает
Теорема 2:
(о непрерывности функции обратной к строго монотонной)
Функция обратная к строго монотонной, определённой на промежутке непрерывна во всех точках своей области определения.
Доказательство:
Функция определена на промежутке и строго монотонна.по леммеоднозначна и монотонна на, а область значенийпо теореме 1непрерывна.
studfiles.net
Локальные свойства непрерывной функции
Больцано-Кошио промежуточном значении, получаем, что [mf , Mf ] f([a, b]). С другой стороны, по определениям точных верхней и нижней границ числового множества f([a, b]) [mf , Mf ]. Следовательно, f([a, b]) = [mf , Mf ]. Если же mf = Mf = M, то f(x) = M, x [a, b], а
поэтому f([a, b]) = {M}.
Cледствие. Если функция f непрерывна и не убывает (не возрастает) на отрезке [a, b], то f([a, b]) = [f(a), f(b)] (соответственно, f([a, b]) = [f(b), f(a)]).
Замечание 1. Если образом отрезка [a, b] при отображении f является отрезок f([a, b]), то отсюда, вообще говоря, не следует, что функция f является непрерывной. Подтверждением служит функция
f(x) = | sin | π | , | если x (0, 1], |
2x | ||||
|
|
|
|
|
|
| 0, | если x = 0, | |
|
|
|
|
|
|
|
|
|
|
которая терпит разрыв в точке x = 0, однако f([0, 1]) = [−1, 1]. Замечание 2. Можно доказать, что если функция f непрерывна
и не убывает (не возрастает) на интервале (a, b), то f((a, b)) = (A, B)
(соответственно, f((a, b)) = (B, A)), где |
|
|
|
| ||
A = lim f(x) = | inf | f(x), B = lim f(x) = | sup f(x). | |||
x→a | x (a,b) | x | → | b | x | (a,b) |
|
|
|
|
|
| |
Если функция f непрерывна и не убывает (не возрастает) на промежутке [a, b), то f([a, b)) = [f(a), B) (соответственно, f([a, b)) = (B, f(a)]).
Предлагаем читателю доказать эти утверждения самостоятельно.
Теорема 3.10 (o непрерывности монотонной функции). Если функция f монотонна на промежутке X и множество f(X) — промежуток, то функция f непрерывна на X.
Для определенности считаем, что функция f не убывает и X = (a, b). Прежде всего, заметим, что в силу теоремы о пределе монотонной функции, в каждой точке x (a, b) f(x − 0) ≤ f(x) ≤ f(x + 0).
Доказательство теоремы проведём методом «от противного». Предположим, что существует точка c (a, b), в которой функция f терпит разрыв. Тогда выполняется хотя бы одно из двух неравенств
f(c − 0) < f(c), f(c) < f(c + 0).
Пусть, например, f(c − 0) < f(c). Поскольку
f | ( | c | − 0) = sup | f | ( | x | , f | ( | c | inf f(x), |
|
|
| ) |
|
| + 0) = x (c,b) | ||||
|
|
| x (a,c) |
|
|
|
|
|
|
|
то на интервале (a, c) и (c, b) функция f не принимает значений, принадлежащих интервалу (f(c − 0), f(c)). Но этого не может быть, так
studfiles.net
Арифметические свойства непрерывных функций.
Теорема. Пусть и- непрерывные в точке, тогда:
1.)непрерывная в точке;
2.)непрерывная в точке;
3.)непрерывная в точке, если;
Проверим (2), используя определение 1.
.
Непрерывность сложной функции.
Пусть — непрерывна в точке;
непрерывна по в точке;
тогда сложная функция будет непрерывна в точке
Проверим используя определение 1.
Теорема. Все элементарные функции непрерывны в области своего определения.
Некоторые примеры разрывных функций.
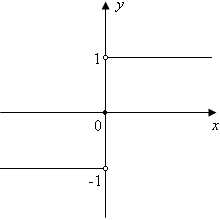
Скачок ”справа”: ;
;
Скачок ”слева”: ;
Скачок в точке :;
Для непрерывной функции скачки равны нулю.
Определение. Если в точке пределы слева и справа конечные, но условие непрерывности нарушено, то точканазывается точкой разрыварода, все остальные разрывырода.
Предел числовой последовательности.
Определение. Числовой последовательностью называется функция натурального аргумента.
Пусть дана последовательностью
общий член
1.)
2.)
Определение. Числовая является пределом числовой последовательности, есливыполняется неравенство
Предел числовой последовательности является частным случаем предела
для
При вычислении предела числовой последовательности можно применять все теоремы о пределах.
Примеры:
1.)Доказать
выполняется неравенство
целая часть числа.
Сравнение бесконечно малых функций.
и – бесконечно малые при;
Бесконечно малая называется бесконечно малой высшего порядка по сравнению с бесконечно малой, если;
при ;
Бесконечно малая называется бесконечно малой низшего порядка по сравнению с бесконечно малой, если;
Бесконечно малая называется бесконечно малой одного порядка с бесконечно малой, если, где– конечное число,;
Бесконечно малая называется эквивалентной бесконечно малой, если;
Бесконечно малая называется бесконечно малой-го порядка с бесконечно малой, если, где– конечное число,;
Таблица эквивалентностей.
При справедливы следующие эквивалентности:
Функция | Эквивалентность |
Свойства эквивалентных функций.
Теорема. Пусть ибесконечно малые функции при, тогда:
;
Доказательство.
1.)
а.)
при
б.)
при
Примеры:
Определить порядок бесконечно малой функции по сравнению с бесконечно малойпри
Составим предел:
Возможны 3 случая:
а.)тогдабесконечно малая порядка по сравнению с бесконечно малой;
б.) тогда бесконечно малая низшего порядка по сравнению с бесконечно малой ;
в.) тогдабесконечно малая высшего порядка по сравнению с бесконечно малой ;
Основные теоремы о непрерывных функциях.
Теорема1.”Об ограничении функции”(Вейерштрасс).
Если непрерывна на отрезке, то она ограничена на этом отрезке.
выполняется неравенство
Теорема2.”О наибольшем и наименьшем значениях функции на отрезке”(Вейерштрасс).
Еслинепрерывна на отрезке, то она достигает свои наибольшие и наименьшие значения на этом отрезке.
Теорема3.”О форме непрерывных функций”(Больцано — Коши).
Еслинепрерывна на отрезкеи на концах отрезка имеет значения разных знаков(, тогда
studfiles.net
Локальные свойства непрерывных функций — ПриМат
Локальными называют такие свойства функций, которые определяются поведением функции в сколь угодно малой окрестности точки области определения.
Теорема (формулировка)
Пусть $f: E \rightarrow \mathbb{R}$ — функция, непрерывная в точке $x_{0} \in R$ тогда справедливы следующие утверждения:
- Функция $f$ ограничена в некоторой окрестности $U_{E} (x_{0})$.
- Если $f(x_{0}) \neq 0$, то в некоторой окрестности $U_{E} (x_{0})$ точки $x_{0}$ функция $f(x)>0$
( или $f(x)<0$ ) вместе с $f(x_{0})$. - Если функция $g: U_{E} (x_{0})$ $ \rightarrow R$ также непрерывна в точке $x_{0}$, то следующие функции непрерывны в точке $x_{0}$:
- $f+g$
- $f \cdot g $
- $\Large \frac{f}{g}$
Если функция $g: Y$ $\rightarrow R$ непрерывна в точке $y_{0} \in Y$, а функция $f$ такова, что $f: E$ $\rightarrow R$, $f(x_{0})=y_{0}$, $f(E) \in Y$ и $f$ непрерывна в точке $x_{0}$, то композиция $g\circ f$ непрерывна в точке $x_{0}$.
Пример 1
Алгебраический многочлен $P_{n}(x)=a_{0}x^n+a_{1}x^{n-1}+…+a_{n}$ является непрерывной функцией для $x \in R$. Это следует из теоремы 1 и непрерывности функции $y=x$ и $y=k$.
Пример 2
Рациональная функция $\large R(x)=\frac{P_{n}(x)}{Q_{m}(x)}$ непрерывна всюду, кроме точек, в которых $Q_{m}(x)=0$.
Источники:
- А.М. Кытманов, Е.К. Лейнартас, О.Н. Черепанова «Математический анализ» / Сиб. федерал. ун-т. — Красноярск, 2010. — 50-53 стр.
- Конспект по математическому анализу Лысенко З.М.
Непрерывная функция
Лимит времени: 0
Информация
Тест на тему «непрерывные функции»
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
- С ответом
- С отметкой о просмотре
ib.mazurok.com

 ,
но не определена в самой точке
,
но не определена в самой точке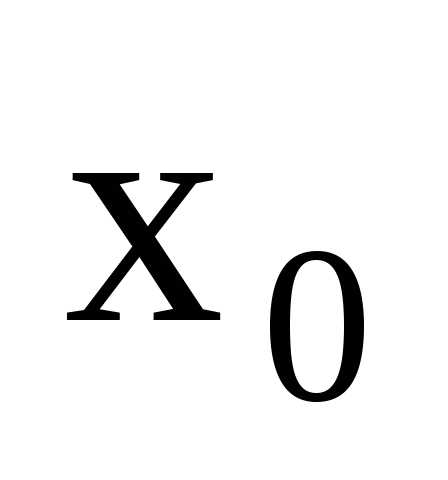 .
.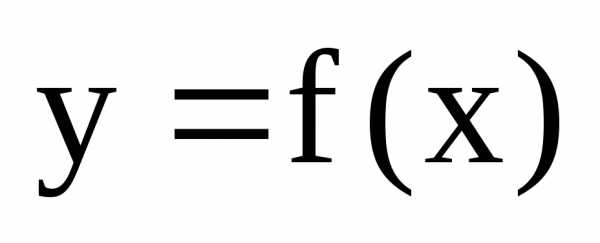 определена в точке
определена в точке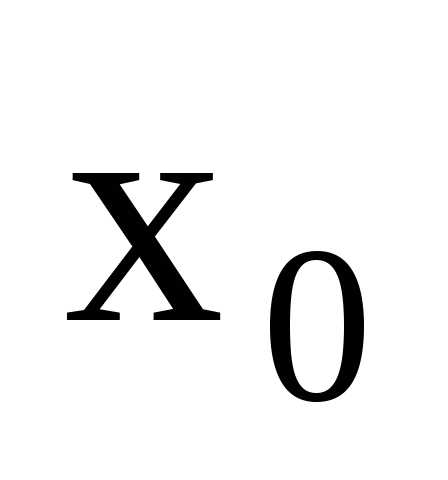 и в ее окрестности, но не существует
пределаf(x)
при
и в ее окрестности, но не существует
пределаf(x)
при 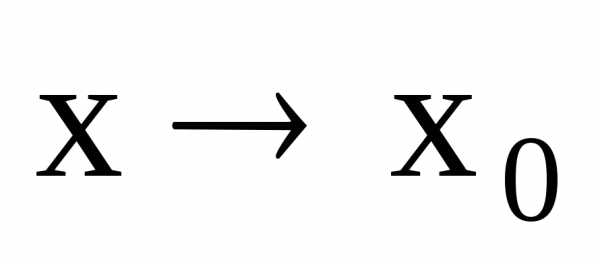
 ,
то точка
,
то точка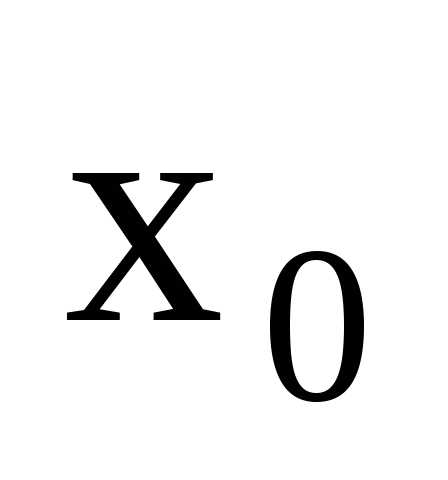 называетсяточкой
устранимого разрыва.
называетсяточкой
устранимого разрыва.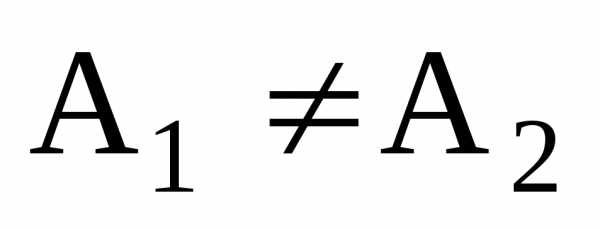 ,
то точка
,
то точка называетсяточкой
конечного разрыва
называетсяточкой
конечного разрыва