Линейные неравенства. Системы и совокупности неравенств
Мы часто сравниваем те или иные объекты по их числовым характеристикам: товары по их ценам, людей по их росту или возрасту, смартфоны по их диагонали или результаты команд по количеству забитых мячей в матче.
Соотношения вида или называют неравенствами. Ведь в них записано, что числа не равны, а больше или меньше друг друга.
Чтобы сравнивать натуральные числа в десятичной записи, мы упорядочили цифры: , а дальше чаще всего использовали преимущества десятичной записи: начинали сравнивать цифры чисел с крайних левых разрядов до первого несоответствия.
Но этот способ не всегда удобен.
Проще всего сравнивать положительные числа, т.к. они обозначают количества. Действительно, если число можно эквивалентно представить в виде суммы числа с каким-то другим числом , то больше : .
Эквивалентная запись: .
Это определение можно расширить не только на положительные числа, но и на любые два числа: .
Число больше числа
Например, сравним две дроби: и . Сразу так и не скажешь, какая из них больше. Поэтому обратимся к определению и рассмотрим разность :
Получили отрицательное число, значит, .
На числовой оси большее число всегда будет располагаться правее, меньшее – левее (Рис. 1).
Рис. 1. На числовой оси большее число располагается правее, меньшее – левее
Зачем нужны такие формальные определения? Одно дело – наше понимание, а другое – техника. Если сформулировать строгий алгоритм сравнения чисел, то его можно поручить компьютеру. В этом есть плюс – такой подход избавляет нас от выполнения рутинных операций. Но есть и минус – компьютер точно следует заданному алгоритму. Если компьютеру поставлена задача: поезд должен отправиться со станции в , то, даже если вы окажетесь на платформе в , на этот поезд вы уже не успеете. Поэтому алгоритмы, которые мы задаём компьютеру для выполнения различных вычислений или решения задач, должны быть очень точными и максимально формализованными.
Как и в случае равенств, с неравенствами можно совершать некоторые действия и получать эквивалентные неравенства.
Рассмотрим некоторые из них.
1. Если , то для любого числа . Т.е. можно прибавлять или вычитать одно и то же число к обеим частям неравенства.
У нас уже есть хороший образ – весы. Если одна из чашек весов перевешивала, то, сколько бы мы ни добавляли (или не забирали) к обеим чашам, эта ситуация не изменится (Рис. 2).
Рис. 2. Если чаши весов не уравновешены, то после добавления (убавления) к ним одинакового количества гирь они останутся в таком же неуравновешенном положении
Это действие можно сформулировать по-другому: можно переносить слагаемые из одной части неравенства в другую, изменяя их знак на противоположный: .
2.Если , то и для любого положительного . Т.е. обе части неравенства можно умножать или делить на положительное число и его знак не изменится.
Для понимания этого свойства можно опять воспользоваться аналогией с весами: если, к примеру, левая чаша перевешивала, то, если возьмём две левые чаши и две правые, перевес точно сохранится. Та же ситуация для , чаш и т.д. Даже если возьмём половины каждой из чаш, ситуация тоже не изменится (Рис. 3).
Рис. 3. Если чаши весов не уравновешены, то, после того как забрать половину каждой из них, они останутся в таком же неуравновешенном положении
Если же умножить или разделить обе части неравенства на отрицательное число, то знак неравенства изменится на противоположный. С аналогией для этой операции чуть сложнее – отрицательных количеств нет. Здесь поможет тот факт, что у отрицательных чисел всё наоборот (чем больше модуль числа, тем меньше само число): .
Для чисел разных знаков ещё легче: . Т.е., умножая на , мы должны изменить знак неравенства на противоположный.Что касается умножения на отрицательное число , то можно выполнить эквивалентную операцию из двух частей: сначала умножить на противоположное положительное число – как мы уже знаем, знак неравенства не изменится: .
А дальше умножить полученное неравенство на : .
Подробнее о сложении и умножении
В первом свойстве мы записали: , но при этом сказали, что можно не только прибавлять, но и вычитать. Почему? Потому что вычитание числа – это то же самое, что и прибавление противоположного числа: . Именно поэтому мы говорим не только о сложении, но и о вычитании.
Аналогично и со вторым свойством: деление – это умножение на обратное число: . Поэтому во втором свойстве мы говорим не только об умножении на число, но и о делении.
3. Для положительных чисел и , если , то .
Рис. 4. Четвёртая часть торта меньше третьей части того же торта
4.Если и , то .
Продолжая аналогию с весами: если на одних весах левая чаша перевешивает правую и на других – такая же ситуация, то, ссыпав отдельно содержимое левых и отдельно содержимое правых чаш, снова получим, что левая чаша перевешивает (Рис. 5).
Рис. 5. Если левые чаши двух весов перевешивают правые, то, ссыпав отдельно содержимое левых и отдельно содержимое правых чаш, получится, что левая чаша перевешивает
5. Для положительных , если и , то .
Здесь аналогия чуть более сложная, но тоже ясная: если левая чаша тяжелее правой и мы возьмём больше левых чаш, чем правых, то точно получим более массивную чашу (Рис. 6).
Рис. 6. Если левая чаша тяжелее правой, то если взять больше левых чаш, чем правых, то получится более массивная чаша
Последние два свойства интуитивно понятны: сложив или умножив числа побольше, мы в результате получим большее число.
Большинство из этих свойств можно строго доказать, используя различные алгебраические аксиомы и определения, но мы не будем этого делать. Для нас процесс доказательства представляет не такой интерес, как непосредственно полученный результат, который мы будем использовать на практике.
До сих пор мы говорили о неравенствах как о способе записи результата сравнения двух чисел: или . Но неравенства можно использовать и для записи различной информации об ограничениях для того или иного объекта. В жизни мы часто используем такие ограничения для описания, например: Россия – это миллионы людей от Калининграда до Владивостока; в лифте можно перевозить не больше кг, а в пакет – класть не больше кг. Ограничения могут быть использованы и для классификации объектов. Например, в зависимости от возра
interneturok.ru
что это такое, как решить
Тема совокупностей уравнений и др. систем, как правило, в рамках школьного курса представлена скупо. В 10-11 классе она изучается совсем недолго. Мы считаем, что это неверный подход, поскольку совокупности — прекрасный способ оформления привычных решений при работе с неравенствами и уравнениями, поэтому в рамках статьи мы раскроем этот вопрос.
В данной статье мы сформулируем общее понятие совокупностей неравенств, уравнений и их систем, а также их комбинации. Кроме определений здесь, как обычно, есть решения задач, наглядно поясняющие тот или иной фрагмент текста.
Yandex.RTB R-A-339285-1Понятие совокупности
Для того, чтобы хорошо понимать, что такое совокупность уравнений, нужно вспомнить еще одно понятие из школьного курса алгебры — система уравнений (аналогично неравенствам). Тогда определения совокупности покажутся вам знакомыми и легко усвоятся.Проанализировав несколько учебников, выберем наиболее удачное определение:
Определение 1Совокупность уравнений представляет собой несколько уравнений, записанных друг под другом и объединенных квадратной скобкой. Значение этой записи таково: совокупность объединяет такие значения переменных, при которых хотя бы одно из входящих в нее уравнений превращается в верное равенство.
Сравним между собой понятие совокупности и понятие системы:
- Запись совокупности, как мы уже говорили выше, осуществляется с помощью квадратной скобки, а системы записываются с фигурной.
- Совокупность включает в себя множество решений, которые относятся хотя бы одному из уравнений, входящих в ее состав. Система объединяет решения, которые подходят для каждого уравнения.
Вот примеры совокупности уравнений:
x+1=0,x2-1=-8 x+y2+z4=0,x·y·z=0,z=5
Иногда при записи совокупности можно обойтись и без квадратной скобки: так часто делают в школе. В таком случае уравнения можно просто указать через запятую. Для примера выше это может быть запись вида x+y2+z4=0, x·y·z=0, z=5.
Понятие совокупности неравенств формулируется схожим образом.
Определение 2Совокупность неравенств представляет собой несколько неравенств, записанных друг под другом и объединенных квадратн
zaochnik.com
Неравенства с одной переменной и их системы [wiki.eduVdom.com]
subjects:mathematics:неравенства_с_одной_переменной_и_их_системы
Общий способ сравнения чисел
Число а больше числа b (а>b), если их разность (а — b) — положительное число; число а меньше числа b, если их разность (а — b) — отрицательное число.
Свойства числовых неравенств:
Если a>b, то b<а; если a<b, то b>a;
Если a<b и b<c, то a<b<c;
Если a<b и $c\in\mathbb{R}$, то a+c<b+c;
Если а<b и с>0, то ас<bс; если а<b и с<0, то ac>bc;
Если a<b и c<d, то a+c<b+d;
Если a<b и c<d и а, b, с, d — положительные числа, то ac<bd.
Решить неравенство с одной переменной означает найти все его решения или доказать, что решений нет.
Решение системы неравенств с одной переменной — это значение переменной, при котором верно каждое из неравенств системы.
Решить систему означает найти все ее решения или доказать, что решений нет.
Решения неравенств с одной переменной метод интервалов
Если неравенство имеет вид $f(x) = (x — x_1)(x — x_2) \cdot \dots \cdot (x — x_n)>0 (<0)$ , то в каждом из промежутков, на которые область определения разбивается точками $x_1 x_2, \ldots, x_n$, знак функции сохраняется, а при переходе через каждую из точек $x_1, x_2, \ldots, x_n$ ее знак меняется.
Пример 1. Решите неравенства:
1.a) $\frac{4x-1}{2} — x > 3х + 2$
1.b) $\frac{4x-1}{2} — x \geq 3х + 2$..
Решение:
| 1.a | 1.b |
|---|---|
| $\frac{4x-1}{2} — x > 3х + 2$. | $\frac{4x-1}{2} — x \geq 3х + 2$. |
| $$ \frac{4x-1}{2} — x > 3х + 2 \\ \frac{4x-1-2x}{2} > 3х + 2 \,\,\,\,|\cdot 2 \\ 2x-1 > 6x+4 \\ 2x-6x > 4+1 \\ -4x > 5 \,\,\,\,|:(-4) \\ -4 < 0 \\ 4x < -5 \,\,\,\,|:4 \\ x < -\frac{5}{4} \\ \text{или} \\ (-\infty;\;-\frac{5}{4}) $$ | $$ \frac{4x-1}{2} — x \geq 3х + 2 \\ \frac{4x-1-2x}{2} \geq 3х + 2 \,\,\,\,|\cdot 2 \\ 2x-1 \geq 6x+4 \\ 2x-6x \geq 4+1 \\ -4x \geq 5 \,\,\,\,|:(-4) \\ -4 < 0 \\ 4x \leq -5 \,\,\,\,|:4 \\ x \leq- \frac{5}{4} \\ \text{или} \\ (-\infty;\;-\frac{5}{4}] $$ |
Ответы:
1.a) Ответ: $(-\infty;\;-\frac{5}{4})$
1.b) Ответ: $(-\infty;\;-\frac{5}{4}]$
Пример 2. Решите систему неравенств $$ \left\{\begin{matrix} (2x-3)-3(x-1)\geq 1 \\ 2(x+5)-x\leq 3 \end{matrix}\right. $$
Решение: $$ \left\{\begin{matrix} (2x-3)-3(x-1)\geq 1 \\ 2(x+5)-x\leq 3 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x\geq -1 \\ x\leq -7 \end{matrix}\right. \text{ — нет решений.} $$ Нельзя одновременно быть меньше -7 и больше -1.
Ответ: нет решений.
Пример 3. Решите неравенство $3x^2 — x — \frac{5}{4} \geq 0$.
Решение: Разложим квадратный трехчлен $3x^2 — x — \frac{5}{4}$ на множители.
Для этого найдем его корни: $D = 1 + 4• 3• \frac{5}{4} = 16$;
$$ x = \frac{1\pm 4}{6}; \\ x_1 = -\frac{1}{2} \\ x_2 = \frac{5}{6} \\ \\ 3x^2 — x — \frac{5}{4} = 3(x+\frac{1}{2})(x-\frac{5}{6}) \\ 3x^2 — x — \frac{5}{4} \geq 0 \\ 3(x+\frac{1}{2})(x-\frac{5}{6})\geq 0 $$
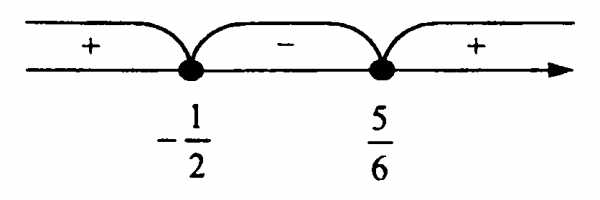
Ответ: $x\in(-\infty;\;-\frac{1}{2}]\cup [\frac{5}{6};\;+\infty)$
Пример 4. Решите неравенство $\frac{x^3-x}{x^2-4}\geq 0$.
Решение: $$ \frac{x^3-x}{x^2-4}\geq 0 \\ \\ \frac{x(x-1)(x+1)}{(x-2)(x+2)}\geq 0 $$ Находим, что смена знака происходит, при $x = 0, \pm 1, \pm 2$. При этом помним, что $x \neq \pm 2$, поскольку тогда знаменатель обратиться в ноль, а делить на ноль нельзя.
Ответ: $x\in(-2;\;-1]\cup [0;\;1]\cup (2;\;+\infty)$.
Пример 5. Под каким номером на каком рисунке верно указано решение системы неравенств? $$ \left\{\begin{matrix} 5x+13 \leq 0 \\ x+5 \geq 1 \end{matrix}\right. $$
Видео-решение:
subjects/mathematics/неравенства_с_одной_переменной_и_их_системы.txt · Последние изменения: 2013/09/14 19:46 — ¶
www.wiki.eduvdom.com
