Системы линейных ду – ?

Системы линейных дифференциальных уравнений с постоянными коэффициентами

Решить систему ДУ

$\left\{\begin{array}{c} {\frac{dy_{1} }{dx} =3\cdot y_{1} -y_{2} } \\ {\frac{dy_{2} }{dx} =4\cdot y_{1} -y_{2} } \end{array}\right. $.

Систему решаем исключением неизвестной функции $y_{2} $.

Шаг 1. Из первого уравнения находим $y_{2} $: $y_{2} =-\frac{dy_{1} }{dx} +3\cdot y_{1} $.

Шаг 2. Подставляем $y_{2} $ во второе уравнение:

\[\frac{dy_{2} }{dx} =4\cdot y_{1} +\frac{dy_{1} }{dx} -3\cdot y_{1} ; \frac{dy_{2} }{dx} =\frac{dy_{1} }{dx} +y_{1} .\]

Шаг 3. Дифференцируем первое уравнение по $x$: $\frac{d^{2} y_{1} }{dx^{2} } =3\cdot \frac{dy_{1} }{dx} -\frac{dy_{2} }{dx} $.

Шаг 4. Подставляем выражение, полученное на шаге 2, в выражение, полученное на шаге 3:

\[\frac{d^{2} y_{1} }{dx^{2} } =3\cdot \frac{dy_{1} }{dx} -\frac{dy_{1} }{dx} -y_{1} ; \frac{d^{2} y_{1} }{dx^{2} } -2\cdot \frac{dy_{1} }{dx} +y_{1} =0. \]

Шаг 5. Решаем линейное однородное ДУ второго порядка с постоянными коэффициентами:

1. характеристическое уравнение $k^{2} -2\cdot k+1=0$;
2. корни характеристического уравнения $k_{1} =1$, $k_{2} =1$ — действительные, равные;
3. искомая функция $y_{1} =C_{1} \cdot e^{x} +C_{2} \cdot x\cdot e^{x} $.

Шаг 6. Находим функцию $y_{2} $:

1. производная $\frac{dy_{1} }{dx} =C_{1} \cdot e^{x} +C_{2} \cdot \left(e^{x} +x\cdot e^{x} \right)$;
2. результат подстановки в выражение, полученное на шаге 1:

\[y_{2} =-C_{1} \cdot e^{x} -C_{2} \cdot \left(e^{x} +x\cdot e^{x} \right)+3\cdot \left(C_{1} \cdot e^{x} +C_{2} \cdot x\cdot e^{x} \right)=\] \[=-C_{1} \cdot e^{x} -C_{2} \cdot e^{x} -C_{2} \cdot x\cdot e^{x} +3\cdot C_{1} \cdot e^{x} +3\cdot C_{2} \cdot x\cdot e^{x} =\] \[=2\cdot C_{1} \cdot e^{x} -C_{2} \cdot e^{x} +2\cdot C_{2} \cdot x\cdot e^{x} .\]

Общее решение данной системы:

\[y_{1} =C_{1} \cdot e^{x} +C_{2} \cdot x\cdot e^{x} ; y_{2} =2\cdot C_{1} \cdot e^{x} -C_{2} \cdot e^{x} +2\cdot C_{2} \cdot x\cdot e^{x} .\]

spravochnick.ru

§6. Системы линейных ду с постоянными коэффициентами

Рассмотрим систему линейных, однородных ДУ с постоянными коэффициентами, т. е. систему вида

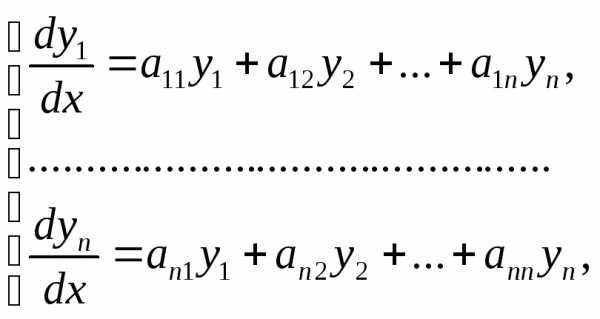
Для простоты ограничимся рассмотрением системы трех уравнений с тремя неизвестными функциями y₁, у₂и у₃.

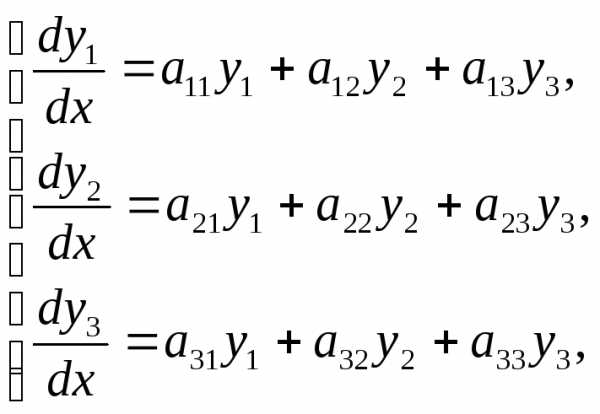(6.1)

где все коэффициенты a_ij(i,j = 1,2,3) — постоянные.

Будем искать частное решение системы (6.1) в виде

(6.2)

где α, β, γ, k — постоянные, которые надо подобрать (найти) так, чтобы функции (6.2) удовлетворяли системе (6.1).

Подставив эти функции в систему (6.1) и сократив на множитель e^kx≠ 0, получим:

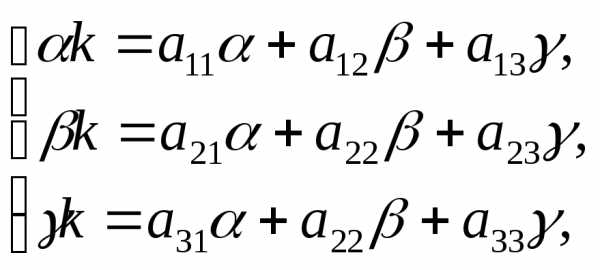
или

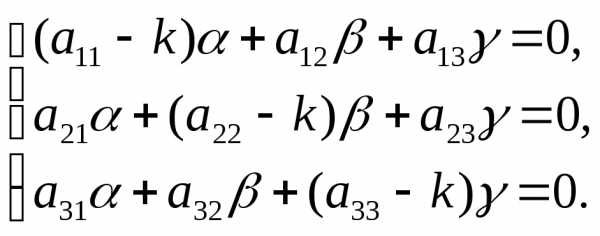(6.3)

Систему (6.3) можно рассматривать как однородную систему трех алгебраических уравнений с тремя неизвестными α, β, γ. Чтобы эта система имела ненулевое решение, необходимо и достаточно, чтобы определитель системы был равен нулю:

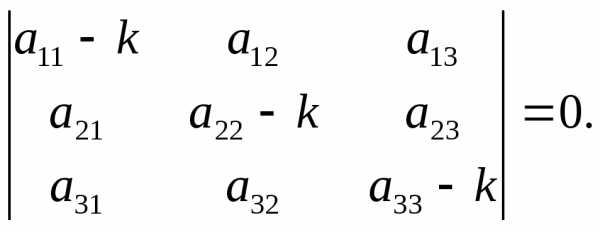(6.4)

Уравнение (6.4) называется характеристическим уравнением системы (6.2). Раскрыв определитель, получим уравнение третьей степени относительно. Рассмотрим возможные случаи.

Случай 1.Корни характеристического уравнения действительны и различны: k₁, k₂, k₃. Для каждого корня k

i(i = 1, 2, 3) напишем систему (6.3) и определим коэффициенты α_i, β_i, γ_i(один из коэффициентов можно считать равным единице). Таким образом, получаем:

для корня k₁частное решение системы (6.1):

для корня k₂—

для корня k₃—

Можно показать, что эти функции образуют фундаментальную систему общее решение системы (6.1) записывается в виде

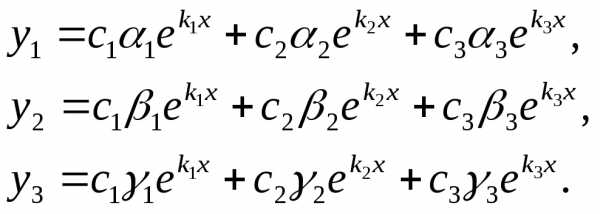(6.5)

Пример 6.3. Решить систему уравнений:

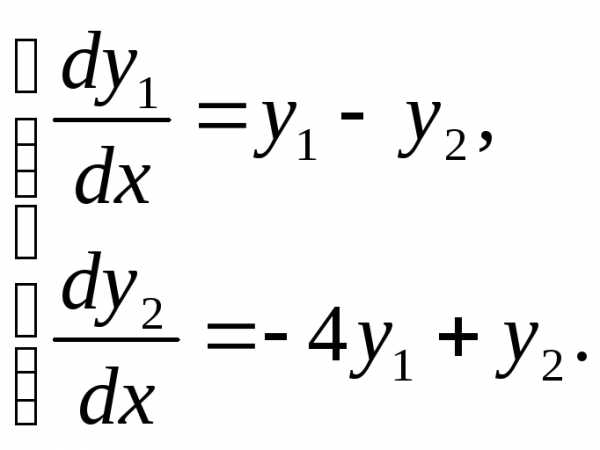
Решение:Характеристическое уравнение (6.4) данной системы имеет вид

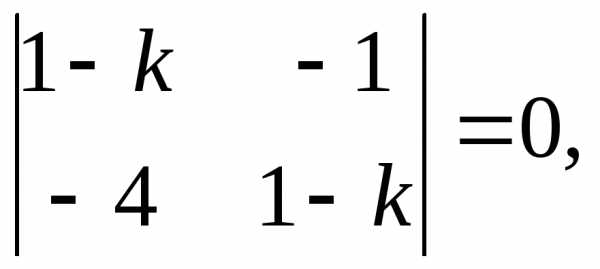
или 1 — 2k + k²— 4 = 0, k²– 2k — 3 = 0, k₁= -1, k

2= 3. Частные решения данной системы ищем в видеНайдем α_iи β_i(i = 1, 2).

При k₁= –1 система (6.3) имеет вид

т. е.

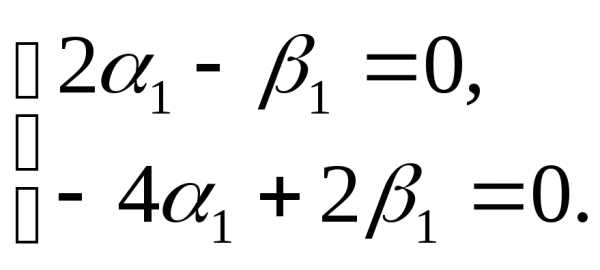
Эта система имеет бесчисленное множество решений. Положим α₁= 1, тогда- β₁= 2. Получаем частные решения

При k₂= 3 система (6.3) имеет вид

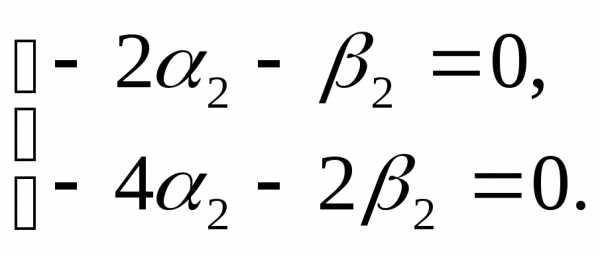
Положим α₂= 1, тогда β₂= -2. Значит, корню k₂= 3 соответствуют частные решения:

Общее решение исходной системы, согласно формуле (6.5), запишется в виде:

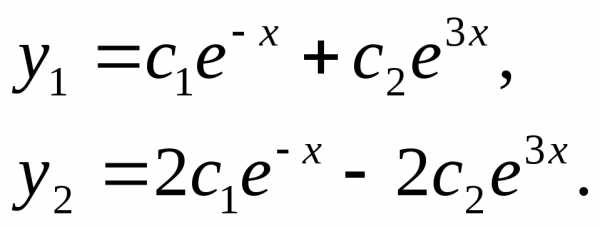
Случай 2.Корни характеристического уравнения различные, но среди них есть комплексные: k₁= a + ib, k

2= a — ib, k₃. Вид частных решений в этой ситуации определяют так же, как и в случае 1.

Замечание.Вместо полученных частных решений можно взять их линейные комбинации (п. 4.1, случай 3), применяя формулы Эйлера; в результате получим два действительных решения, содержащих функции вида е^αx∙cosbx, e^αx∙sinbx. Или, выделяя действительные и мнимые части в найденных комплексных частных решениях, получим два действительных частных решения (можно показать, что они тоже являются решениями уравнения). При этом понятно, что комплексно-сопряженный корень k₂= а — ib не даст новых линейно независимых действительных решений.

Вопросы

1. Что называется дифференциальным уравнением?

2. Что называется решением дифференциального уравнения?

3. Что такое интегральная кривая?

4. Почему при решении дифференциальных уравнений в них возникают произвольные постоянные константы?

5. Что такое начальные условия?

6. Решить дифференциальное уравнение первого порядка методом разделения переменных.

7. Сформулировать теорему Коши.

8. Что такое особые решения дифференциального уравнения первого порядка?

9. Привести пример дифференциального уравнения второго порядка с постоянными коэффициентами.

10. Что такое линейное, однородное дифференциальное уравнение с постоянными коэффициентами?

11. Какой вид имеют решения однородного, дифференциального уравнения второго порядка с постоянными коэффициентами?

12. Какой вид имеют решения неоднородного, дифференциального уравнения второго порядка с постоянными коэффициентами со специальной правой частью?

17

studfiles.net

16. Структура общего решения линейных систем ду

Структура общего решения линейных однородных систем ДУ: линейная комбинация _j x_j n – линейно независимых решений X₁ , X₂ , … , X_n линейной однородной системы L [X] = 0 с непрерывными на отрезке a ≤ t ≤ b коэффициентами a_ij (t) является общим решением этой линейной однородной системы на отрезке a ≤ t ≤ b.

Структура общего решения линейных неоднородных систем ДУ: общее решение на отрезке a ≤ t ≤ b линейной неоднородной системы ДУ с непрерывными на этом отрезке правыми частями равно сумме общего решения соответствующей линейной однородной системы ДУ и частного решения неоднородной системы ДУ.

17. Линейные однородные и неоднородные системы ду с постоянными коэффициентами

Линейные однородные системы ДУ с постоянными коэффициентами имеют вид:

В векторной форме: dY/dx = AY, где

Характеристическое уравнение:

или det (A – λE) = 0.

Общее решение этой системы имеет вид

если все корни характеристического уравнения простые, а решениями, соответствующими этим корням λ_k , будут

Линейные неоднородные системы ДУ с постоянными коэффициентами имеют вид:

dY/dx = AY + F, где

Общее решение неоднородной системы есть сумма общего решения однородной системы и некоторого частного решения неоднородной системы. Для нахождения общего решения неоднородной системы можно применить метод Лагранжа вариации произвольных постоянных.

18. Числовые ряды. Основные свойства

Числовым рядом (или просто рядом) называется выражение вида

_n = u₁ + u₂ + … + u_n + … , (1) где u₁ , u₂ , … , u_n , … — действительные или комплексные числа, называемые членами ряда, u_n – общим членом ряда.

Суммой первых n членов ряда (1) называется n-й частичной суммой ряда и обозначается через S_n , т.е. S

n = u₁ + u₂ + … + u_n.

Рассмотрим частичные суммы S₁ = u₁, S₂ = u₁ + u₂, S₃ = u₁ + u₂ + u₃, … Если существует конечный предел S = _n последовательности частичных сумм ряда (1), то этот предел называют суммой ряда (1) и говорят, что ряд сходится. Записывают: S = _n.

Если _nне существует или _n = ∞, то ряд (1) называют расходящимся. Такой ряд суммы не имеет.

Ряд u_{n + 1} + u_{n + 2} + … = _kназывается n-м остатком ряда (1). Он получается из ряда (1) отбрасыванием n первых его членов. Ряд (1) получается из остатка добавлением конечного числа членов.

Свойства:

1) Если ряд (1) сходится и его сумма равна S, то ряд

_n = cu₁ + cu₂ + … + cu_n + … , (2) где c – произвольное число, также сходится и его сумма равна cS. Если же ряд (1) расходится и c ≠ 0, то и ряд (2) расходится.

2) Если сходится ряд (1) и сходится ряд _n, а их суммы равны S₁ и S₂ соответственно, то сходятся и ряды

_n ± υ_n), причем сумма каждого равна соответственно S₁ ± S₂ .

3) Если к ряду (1) прибавить (или отбросить) конечное число членов, то полученный ряд и ряд (1) сходятся или расходятся одновременно.

studfiles.net

I. Решение систем линейных дифференциальных уравнений с постоянными коэффициентами.

Федеральное агентство по образованию

­­­­­­­­­­­­­­­­­­­­­­

Государственное образовательное учреждение высшего

профессионального образования

«МАТИ» – Российский государственный технологический

университет им. К.Э. Циолковского

Кафедра «Высшая математика»

Решение систем линейных дифференциальных уравнений с постоянными коэффициентами

Устойчивость решений

Методические указания для студентов и преподавателей

Составитель: Заварзина И.Ф.

Кулакова Р.Д.

Москва 2008

Методические указания предназначены для студентов второго курса, изучающих в рамках курса высшей математики тему «Дифференциальные уравнения». В них рассматривается решение систем линейных дифференциальных уравнений с постоянными коэффициентами. Кроме того, рассматривается устойчивость по Ляпунову, исследуются точки покоя. Приводятся примеры решения задач. Для закрепления материала студентам предлагается выполнить самостоятельную работу.

1. Общие понятия.

Во многих задачах математики, физики и техники требуется определить сразу несколько функций, связанных между собой дифференциальными уравнениями. Совокупность таких уравнений называется системой дифференциальных уравнений.

Рассмотрим неоднородную систему линейных дифференциальных уравнений с постоянными коэффициентами, которую называют нормальной системой:

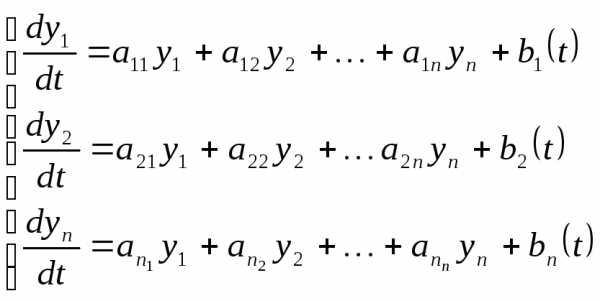(1.1),

где , – искомые функции; , ; – постоянные действительные коэффициенты, 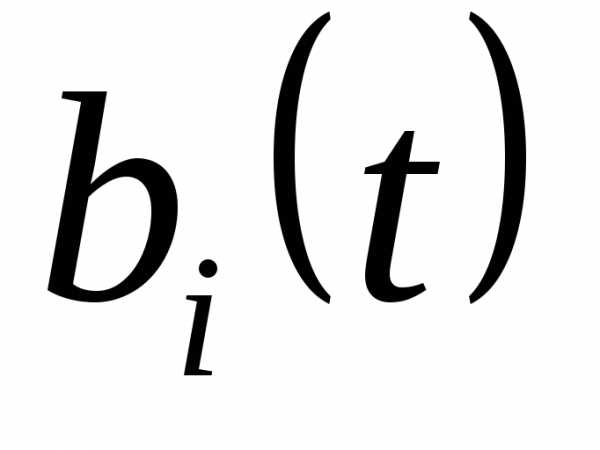, – заданные непрерывные функции.

Если 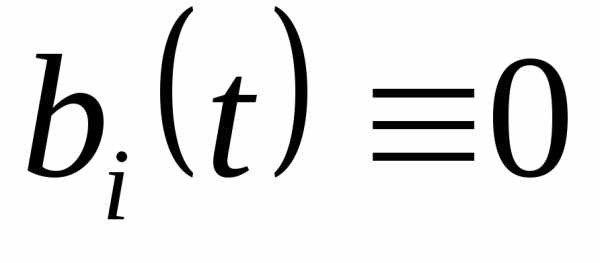, то система называется однородной.

Систему (1.1) можно зависать в векторной форме.

Введем обозначения:

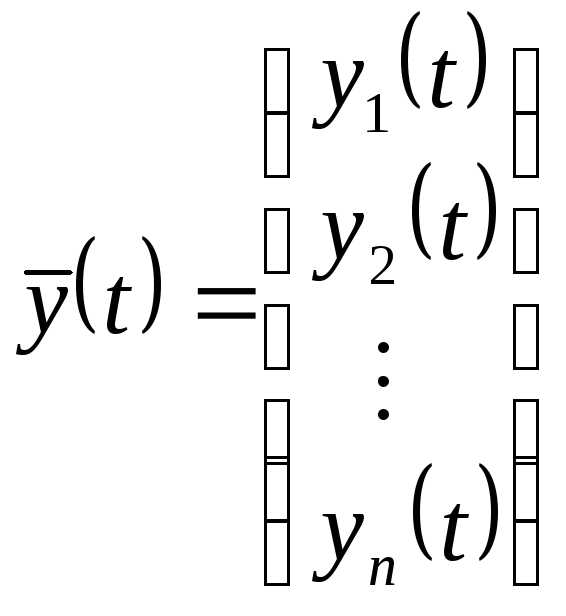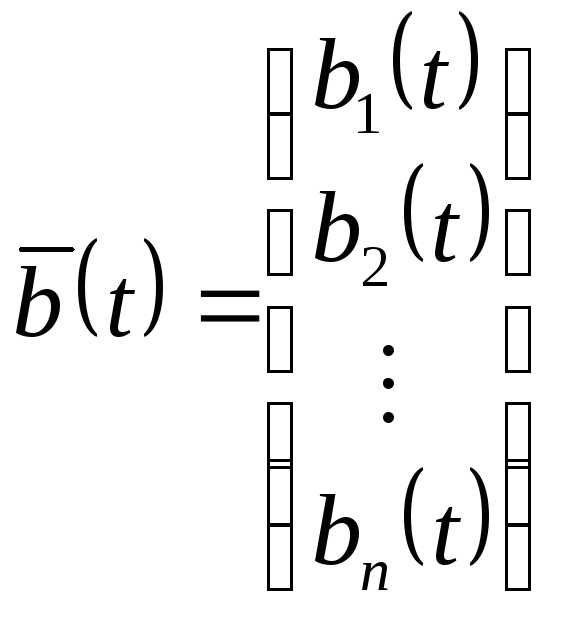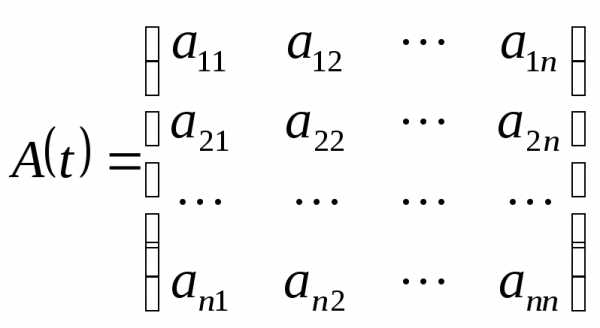; ; (1.2).

Система (1.1) принимает вид:

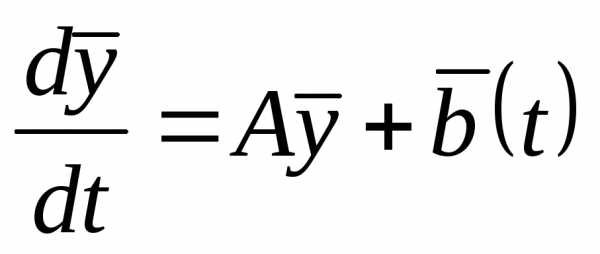(1.3).

Однородная система линейных уравнений в векторной форме имеет вид:

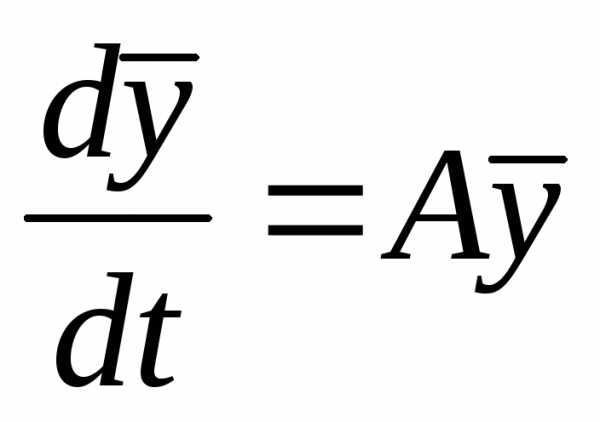(1.4).

Решение системы линейных дифференциальных уравнений представляется совокупностью функций: (1.5).

Система функций (1.5) называется фундаментальной системой решений. Линейная комбинация фундаментальной системы решений позволяет записать общее решение системы (1.4) в виде:

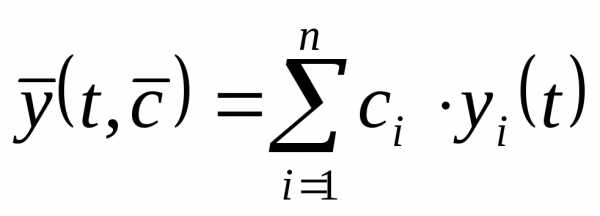(1.6).

Если при решении системы дифференциальных уравнений задаются начальные условия, которые в векторной форме имеют вид: 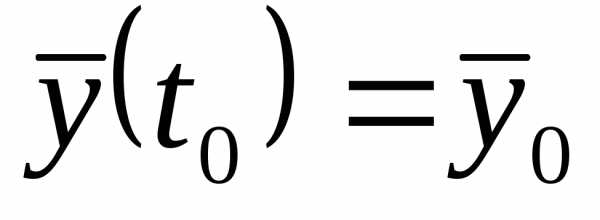(1.7), тогда определяется единственное решение системы дифференциальных уравнений, удовлетворяющее заданным начальным условиям.

В курсе лекций доказывается, что общее решение системы (1.3) представляется в виде суммы общего решения однородной системы дифференциальных уравнений (1.4), записанного в виде (1.6) и какого-нибудь частного решения неоднородной системы.

Рассмотрим получение решения однородной системы (1.4).

Будем искать частное решение системы в следующем виде:

(1.8),

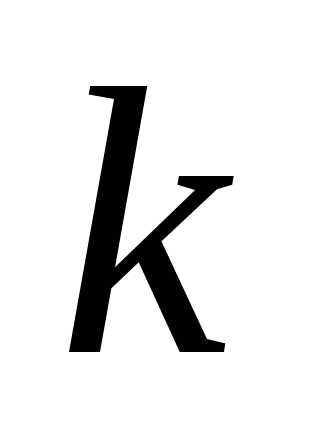, – константы, которые подлежат определению.

Подставим (1.8) в систему (1.4) и получим:

(1.9)

Упростим систему (1.9):

(1.10)

Система (1.4) – однородная система дифференциальных уравнений. Эта система имеет тривиальное решение:, если определитель системы (1.10)

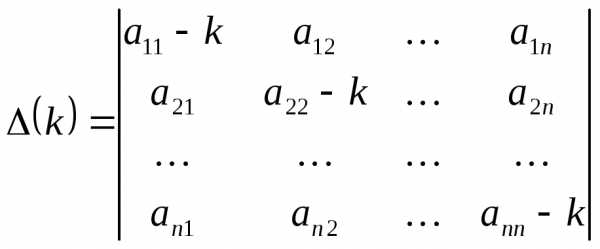(1.11)

отличен от нуля, а нас интересует частное решение системы (1.4), представленное в виде (1.8) и отличное от тривиального.

Нетривиальное решение (1.8) будет получено при условии равенства нулю определителя (1.11).

Приравнивая определитель (1.11) нулю, получим уравнение относительно 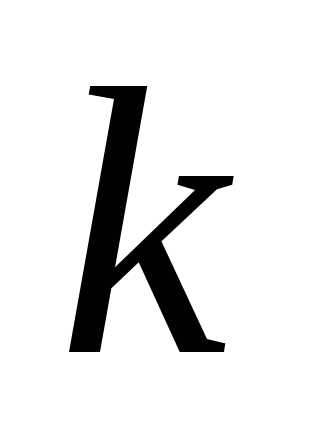, которое называется характеристическим уравнением:

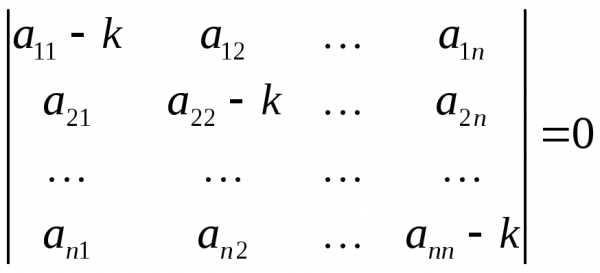(1.12)

корни характеристического уравнения (1.12) определяют вид решения (1.8).

2. Получение фундаментальной системы решений.

Характеристическое уравнение (1.12) системы (1.4) является уравнением 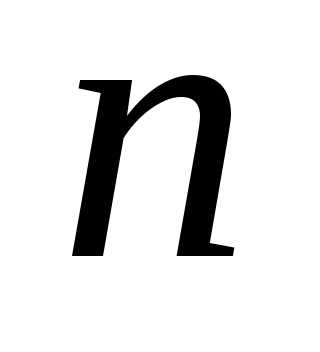-ой степени относительно.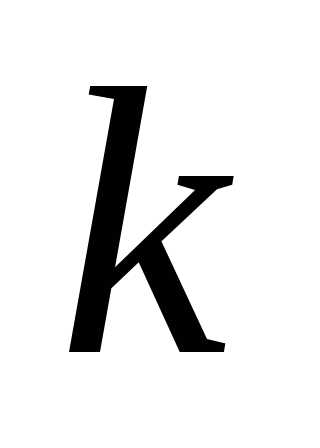

Предположим, что характеристическое уравнение имеет 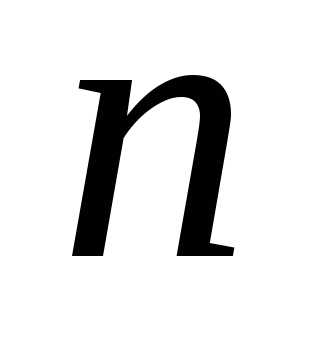различных корней, которые являются характеристическими числами матрицы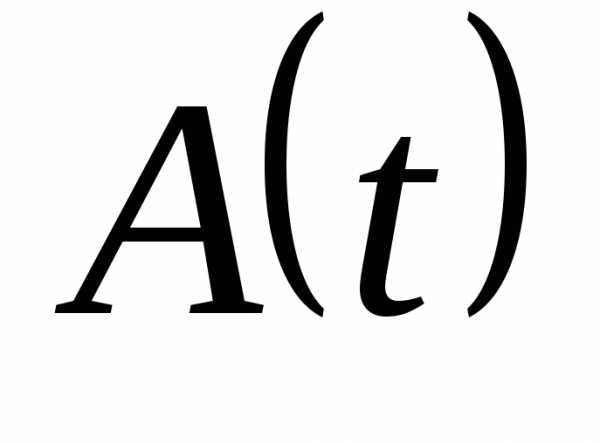. Каждому характеристическому числу соответствует свой собственный вектор. Для каждого характеристического числа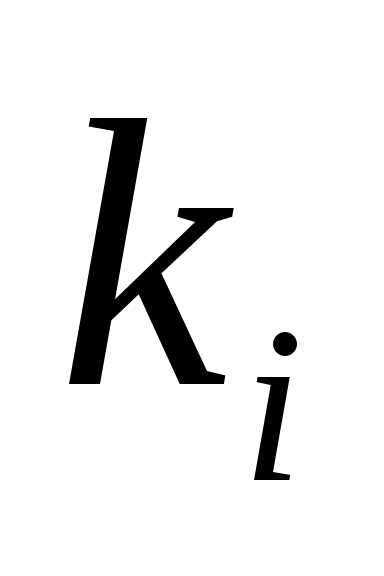напишем систему (1.10) и определим собственный вектор.

Тогда система дифференциальных уравнений имеет решений:

1-е решение, соответствующее корню :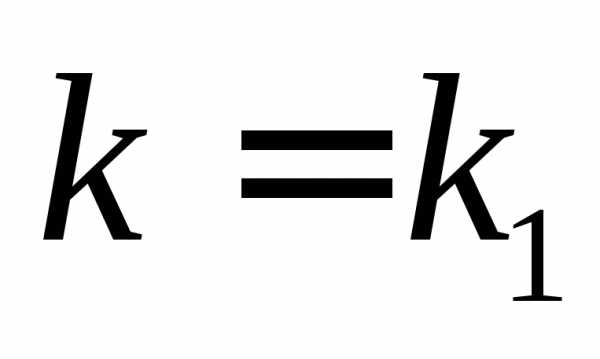

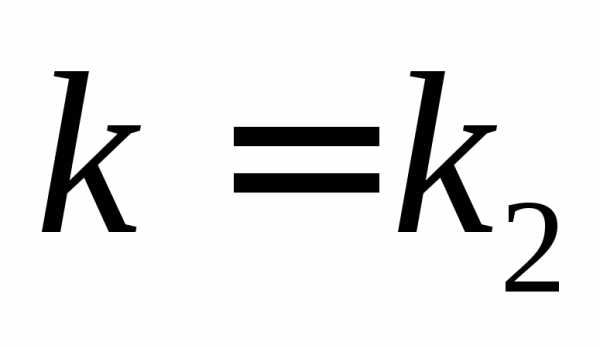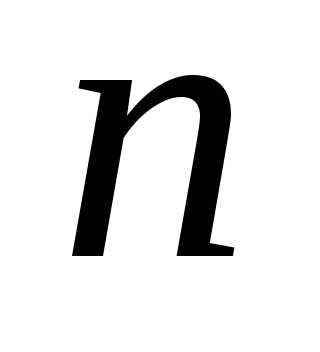2-е решение, соответствующее корню :

;

…………………………………………………

-е решение, соответствующее корню :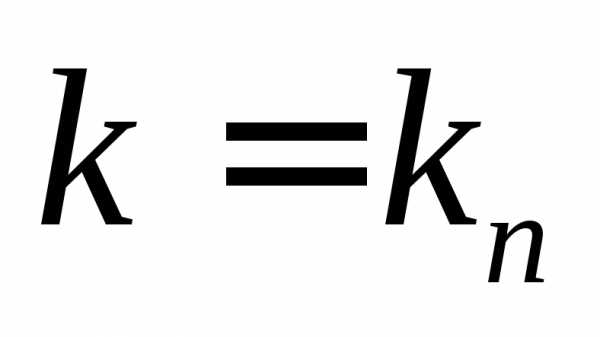

.

Мы получили фундаментальную систему решений. Общее решение системы (1.4) таково:

,

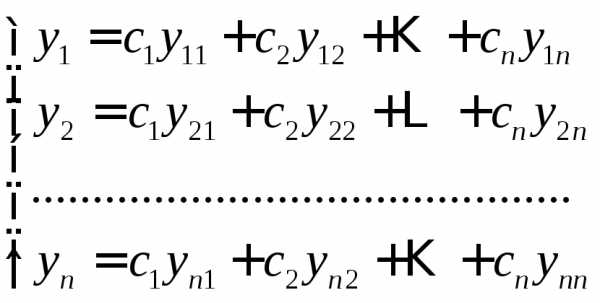где – произвольные постоянные.

Случаи комплексных и кратных корней рассмотрим на примерах.

studfiles.net

16 Системы линейных дифференциальных уравнений » СтудИзба

Лекция 16. Системы линейных дифференциальных уравнений.

Неоднородную систему линейных дифференциальных уравнений можно записать в виде

.

Однородную систему линейных дифференциальных уравнений можно записать в виде

.

Все теоремы для линейных систем аналогичны соответствующим теоремам для линейных дифференциальных уравнений высших порядков. Этого и следовало ожидать, так как система дифференциальных уравнений сводится к дифференциальному уравнению высшего порядка.

Теоремы о свойствах решений однородной и неоднородной системы.

Если — решения однородной системы, то — решения однородной системы.

Если  — решения однородной и неоднородной систем, то — решение  неоднородной системы.

Если — решения неоднородной системы, то — решение однородной системы.

Доказательство.

,

Теорема. Множество решений линейной однородной системы есть линейное пространство.

Из теорем о свойствах решений видно, что операции сложения и умножения на число на решениях однородной системы определены корректно.

Легко проверяется ассоциативность по сложению, существования «нуля» – тривиального решения , существование «противоположного элемента» , коммутативность по сложению. Отсюда следует, что решения однородной системы образуют коммутативную группу по сложению (абелев модуль) (4 аксиомы линейного пространства). Существует единица – число, справедлива ассоциативность по умножению на число (еще 2 аксиомы).

Наконец, справедлива дистрибутивность по сложению решений и чисел (последние 2 аксиомы). Таким образом, выполнены все 8 аксиом для корректно введенных операций сложения решений и умножения решения на число. Следовательно, множество решений однородной системы образует линейное пространство. Заметим, что точно так же доказывалась аналогичная теорема для дифференциального уравнения n-ого порядка.

Функции  называются линейно независимыми, если

.

Функции  называются линейно зависимыми, если

.

Введем определитель Вронского , по столбцам которого расположены векторы , введем также матрицу .

Теорема. Если функции  линейно зависимы, то .

Доказательство. Так как функции линейно зависимы, то одна из них линейно выражается (тождественно) через остальные, поэтому соответствующий столбец определителя Вронского линейно выражается через остальные. Тогда по свойству определителя .

Теорема. Пусть  — решения однородной системы и , тогда решения  линейно зависимы.

Доказательство. Т.к. , то его столбцы в  линейно зависимы, т.е. .

Рассмотрим решение  (с теми же коэффициентами).

 — решение однородной системы как линейная комбинация решений однородной системы (теоремы о свойствах решений). Начальные условия для этого решения в точке , как показано выше, нулевые. Но есть решение однородной системы (тривиальное решение ), имеющее те же начальные условия. Следовательно, по теореме Коши решение  и есть тривиальное решение. Тогда , следовательно, решения   линейно зависимы.

Следствие. Равенство определителя Вронского нулю  для решений однородной системы хотя бы в одной точке – критерий линейной зависимости решений, отличие определителя Вронского от нуля  для решений однородной системы хотя бы в одной точке – критерий линейной независимости решений.

Доказательство. Пусть , тогда решения  линейно зависимы. Если решения  линейно зависимы, то  по теореме о равенстве определителя Вронского нулю для системы линейно зависимых функций. Заметим, что тогда .

Пусть , если решения  линейно зависимы, то  (противоречие). Пусть решения линейно независимы. Если , тогда решения  линейно зависимы (противоречие).

Теорема. Размерность пространства решений однородной системы равна n.

Доказательство. Надо доказать 1) существуют n линейно независимых решений однородной системы, 2) любое решение однородной системы линейно выражается через эти линейно независимые решения.

1)      В любой точке  для однородной системы выполнены условия теоремы Коши, следовательно, через любую такую точку пройдет единственная интегральная кривая – график решения  однородной системы. Зададим такие точки – начальные условия, которые по теореме Коши определят решения .

Эти решения линейно независимы, так как .

Существование n линейно независимых решений однородной системы доказано.

2) Рассмотрим произвольное решение однородной системы . В точке  вектор  разлагается по естественному базису

.Поэтому  

Рассмотрим решение  — линейную комбинацию этих линейно независимых решений. Оно имеет те же начальные условия, что и выбранное произвольное решение . Следовательно, по теореме Коши выбранное произвольное решение  и есть (тождественно равно) . Поэтому произвольное решение линейно выражается через выбранные линейно независимые решения. Теорема доказана.

Любые n линейно независимых решений однородной системы представляют собой базис в пространстве решений и называются фундаментальной системой решений однородной системы.

Матрица , составленная из этих решений , называется фундаментальной матрицей однородной системы.

Теорема о структуре общего решения однородной системы.

Общее решение однородной системы представляет собой линейную комбинацию решений фундаментальной системы решений.

.

Доказательство.  Проверим, что  является общим решением, исходя из определения общего решения.

1)       — решение однородной системы как линейная комбинация ее решений (теорема о свойствах решений).

2)      Зададим произвольные начальные условия  и покажем, что можно единственным образом выбрать набор констант , при котором  . Запишем это соотношение покоординатно как систему уравнений относительно .

  ……………………………………

Определитель этой системы равен , так как решения линейно независимы. Поэтому набор констант  определяется из системы уравнений единственным образом. Теорема доказана.

Следствие. Общее решение однородной системы можно записать в виде

.

Матрица Коши (матрициант).

Пусть надо записать решение задачи Коши, удовлетворяющее начальным условиям .

Матрица  называется матрицей Коши. .

Теорема. Фундаментальная матрица удовлетворяет однородной системе, .

Доказательство. Столбцы фундаментальной матрицы являются решениями однородной системы. Объединяя запись в матрицу, получим утверждение теоремы.

Формула Остроградского – Лиувилля.

 

Выведем формулу Остроградского – Лиувилля.

Фундаментальная матрица системы является решением однородной системы. Запишем уравнение для k –го столбца фундаментальной матрицы – координат решения :

.

Отсюда .

Запишем определитель Вронского и продифференцируем его, подставляя вместо производных координат решений полученное соотношение.

 ,+…

++ =

+…+   +

=

(расписывая в сумму определителей, учитывая равенство нулю определителей с одинаковыми строками)

  …+=

.

Получено соотношение , где  — след матрицы системы. Отсюда имеем формулу Остроградского – Лиувилля.

.

Заметим, что эту формулу можно получить как следствие из теоремы Лиувилля о фазовом объеме.

Теорема о структуре общего решения неоднородной системы.

Общее решение неоднородной системы равно сумме общего решения однородной системы и частного решения неоднородной системы.

Доказательство. 1)  — решение неоднородной системы по теореме о свойствах решений.

2) Зададим произвольные начальные условия . Выберем какое-либо частное решение неоднородное системы и вычислим для него начальные условия в  . Составим систему уравнений  и запишем ее покоординатно.

………………………………………..

Определитель этой системы – определитель Вронского, он не равен нулю, так как составлен из линейно независимых решений, составляющих фундаментальную систему решений. Следовательно, набор констант из этой системы уравнений определяется однозначно. Теорема доказана.

Метод вариации произвольной постоянной.

Общее решение однородной системы можно записать в виде

, где — фундаментальная матрица системы, — вектор произвольных постоянных.

Будем искать решение неоднородной системы в том же виде, варьируя вектор произвольных постоянных:

.

Вычисляем производную и подставляем в уравнение неоднородной системы:

,    

,    

Так как фундаментальная матрица удовлетворяет уравнению однородной системы, то . Поэтому в предыдущем уравнении (как и всегда в методе вариации) сокращается пара слагаемых. Получаем уравнение

. Так как фундаментальная матрица не вырождена (), то отсюда получаем уравнение для определения вектора : 

.

Интегрируя, получаем

 (здесь предполагается, что при вычислении интеграла вектор констант не добавляется, он уже добавлен в виде вектора  ).

Подставляя в , имеем

().

Здесь в полном соответствии с теоремой о структуре общего решения неоднородной системы первое слагаемое представляет собой общее решение однородной системы, а второе слагаемое – частное решение неоднородной системы.

studizba.com

35.1. Нормальная система дифференциальных уравнений

Система вида

где функции определены в некотороймерной области переменныхназываетсянормальной системой дифференциальных уравнений первого порядкас неизвестными функциями

Число уравнений, входящих в систему, называется порядком нормальной системы. Решением нормальной системы в интервале называется совокупность функций

непрерывно дифференцируемых в интервале и обращающих вместе со своими производными каждое уравнение нормальной системы в тождество.

Задача Коши для системы дифференциальных уравнений первого порядка имеет следующую формулировку. Найти решение нормальной системы дифференциальных уравнений первого порядка, удовлетворяющее начальным условиямгдезаданные числа,

Теорема Коши о существовании и единственности решение задачи. Если функции непрерывны в окрестности точкии имеют непрерывные частные производныето всегда найдется некоторый интеграл с центромв котором существует единственное решение нормальной системы дифференциальных уравнений первого порядка, удовлетворяющее заданным начальным условиям.

Общим решением нормальной системы называется совокупность функций

зависящих от произвольных постоянныхи удовлетворяющих следующим условиям:

1. функции определены в некоторой области изменения переменных и имеют непрерывные частные производные

2. совокупность является решением нормальной системы дифференциальных уравнений первого порядка при любых значениях

3. для любых начальных условий из области где выполняются условия теоремы Коши, всегда найдутся такие значения произвольных постоянныхчто будут справедливы равенства

Частным решением нормальной системы дифференциальных уравнений первого порядка называется решение, полученное из общего при некоторых частных значениях произвольных постоянных.

Одним из методов решения нормальной системы дифференциальных уравнений первого порядка является сведение ее к решению одного или нескольких дифференциальных уравнений высших порядков – метод исключения.

35.2. Решение системы линейных дифференциальных уравнений с постоянными коэффициентами

Все сказанное выше верно и для частного случая нормальной системы дифференциальных уравнений, которая имеет вид

где функции предполагаются непрерывными в некотором интервалеЕсли всето рассматриваемая система называется однородной, в противном случае неоднородной. Еслито рассматриваемая системаназывается линейной с постоянными коэффициентами. Существуют методы, позволяющие проинтегрировать такую систему. Рассмотрим два из них.

Первый метод. Составляем характеристическое уравнение

где Раскрывая определитель, приходим к алгебраическому уравнению степениотносительнос действительными постоянными коэффициентами, которое имееткорней.

Если корни характеристического уравнения действительные и различные то каждому корню соответствует частное решение вида

где коэффициенты определяются из системы линейных алгебраических уравнений

Все частные решения вида

образуют фундаментальную систему решений.

Общее решение однородной системы с постоянными коэффициентами, получаемой из системы

при представляет собой следующую совокупность функций, являющихся линейной комбинацией решений

где произвольные постоянные.

Рассмотрим пример. Найти общее решение однородной системы

Характеристическое уравнение данной системы

имеет различные действительные корни Для каждого из них составляем систему

Так как определители этих систем равны нулю, то каждая из них имеет бесчисленное множество решений. В данном случае можно выбрать те решения, для которых Тогда получим следующие решения систем: еслито

если то

если то

Это приводит к фундаментальной системе решений

Линейная комбинация этих решений с учетом совокупности функций

дает общее решение исходной системы

Второй случай. Корни характеристического уравнения

различные, но среди них имеются комплексные. Известно, что в этом случае каждой паре комплексно – сопряженных корней характеристического уравнения соответствует пара частных решений

где Коэффициентыопределяются из системы

соответственно для иКоэффициентыоказываются, как правило, комплексными числами, а соответствующие им функциикомплексными функциями. Выделяя мнимую и действительную части функцийи пользуясь тем, что для линейных уравнений с действительными коэффициентами и мнимая, и действительная части решения также являются решениями, получаем пару частных действительных решений однородной системы.

Рассмотрим пример. Найти общее решение системы

Характеристическое уравнение системы

имеет корни Получаем

Корню соответствует система для вычисления

Согласно формуле получаем частное решение

Взяв в отдельности действительные и мнимые части в решении, получим два решения в действительной форме, образующих фундаментальную систему решений системы

Тогда общее решение системы имеет вид

Третий случай. Среди корней характеристического уравнения имеются кратные. В этом случае поступаем следующим образом. Пустькорень кратностихарактеристического уравнения. Тогда решение системы, для которойсоответствующее этомукратному корню, ищем в виде

……………………………………………………………………………

Числа находим, подставляя функциии их производныев исходную систему при указанных ограничениях наиа затем приравниваем коэффициенты при одинаковых степеняхв левых и правых частях полученных равенств. В результате проведенных действий из всех чиселвсегда остаются в качестве свободных параметров, которые принимаются за произвольные постоянные.

Рассмотрим пример. Найти общее решение системы

Характеристическое уравнение системы

имеет двукратный и однократныйкорни. Двукратному корнюсоответствует решение вида

Коэффициенты определяются из системы, полученной подстановкой выражений дляв исходную систему. После сокращения наимеем

Приравнивая коэффициенты при одинаковых степенях слева и справа, получаем систему

из которой находим, что

Числа можно считать произвольными параметрами. Обозначим их черезисоответственно. Тогда решение запишется в виде

Корню соответствует решение

где числа определяется из системы

Ее решение Следовательно, соответствующее корню

решение исходной системы имеет вид

где произвольная постоянная.

Общее решение исходной систему записывается в виде

Если система неоднородная, то, зная общее решение вида

соответствующей однородной системы, можно найти общее решение исходной неоднородной системы методом вариации произвольных постоянных в решении

Общее решение неоднородной системы всегда можно записать в данном виде, заменив произвольные постоянные соответственно функциямиЭти функции определяются с помощью данной неоднородной системы. В систему подставляютполучают линейную системуалгебраических уравнений относительнорешение которой всегда существует и представимо в виде

где известные функции. Интегрируя эти равенства, находим

где произвольные постоянные.

Рассмотрим пример. Решить задачу Коши

заданы начальные условия

Найдем общее решение соответствующей однородной системы

Корни ее характеристического уравнения общее решение ищем в виде

Пусть в данном решении иявляются неизвестными функциямииПотребуем, чтобыибыли решением исходной системы. Находим

Подставляем выражения для в исходную систему, приводим подобные члены и получаем систему

откуда

Проинтегрируем последние равенства

Подставляя ив равенствавместоиполучаем общее решение исходной неоднородной системы

Используя начальные условия, получим систему для определения постоянных и:

откуда

Решением задачи Коши будет следующее частное решение

Контрольные вопросы

1. Что называют порядком нормальной системы?

2. Дать определение решению нормальной системы в заданном интервале?

3. Дать формулировку Задачи Коши для системы дифференциальных уравнений первого порядка.

4. Что называют общим решением нормальной системы?

5. Дать определение частного решения нормальной системы дифференциальных уравнений первого порядка.

Лекция №36. Применение аппарата дифференциальных уравнений в механике

36.1. Особенности составления дифференциальных уравнений в прикладных задачах.

36.2. Задачи, приводящие к решению дифференциальных уравнений.

studfiles.net

Нормальные системы линейных однородных дифференциальных

уравнений с постоянными коэффициентами.

При рассмотрении систем дифференциальных уравнений ограничимся случаем системы трех уравнений (n = 3). Все нижесказанное справедливо для систем произвольного порядка.

Определение. Нормальная система дифференциальных уравнений c постоянными коэффициентами называется линейной однородной, если ее можно записать в виде:

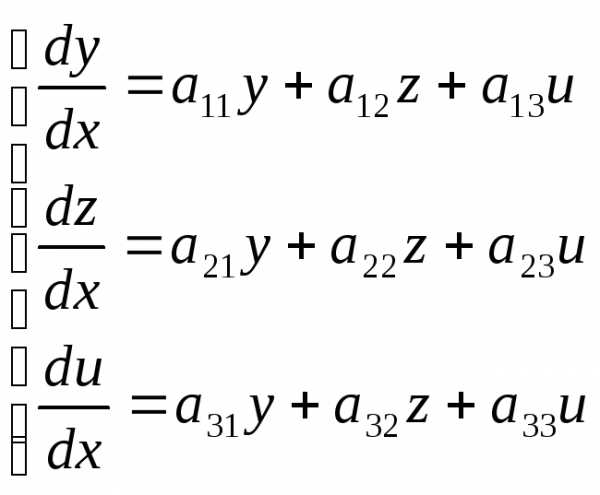(2)

Решения системы (2) обладают следующими свойствами:

1) Если y, z, u – решения системы, то Cy, Cz, Cu , где C = const – тоже являются решениями этой системы.

2) Если y₁, z₁, u₁ и y₂, z₂, u₂ – решения системы, то y₁ + y₂, z₁ + z₂, u₁ + u₂ – тоже являются решениями системы.

Решения системы ищутся в виде:

Подставляя эти значения в систему (2) и перенеся все члены в одну сторону и сократив на e^kx, получаем:

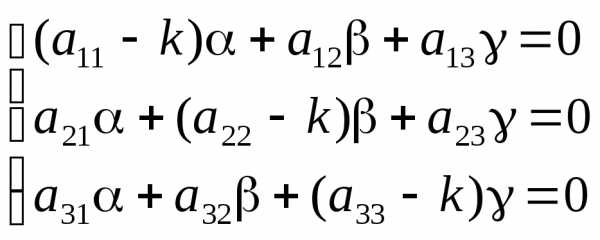
Для того, чтобы полученная система имела ненулевое решение необходимо и достаточно, чтобы определитель системы был равен нулю, т.е.:

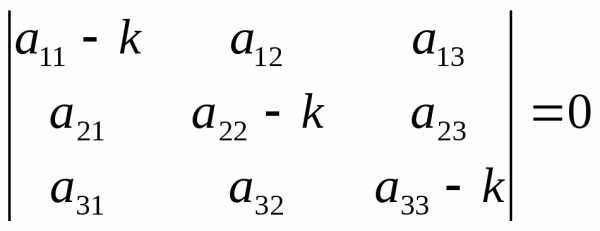
В результате вычисления определителя получаем уравнение третьей степени относительно k. Это уравнение называется характеристическим уравнением и имеет три корня k₁, k₂, k₃. Каждому из этих корней соответствует ненулевое решение системы (2):

Линейная комбинация этих решений с произвольными коэффициентами будет решением системы (2):

Пример. Найти общее решение системы уравнений:

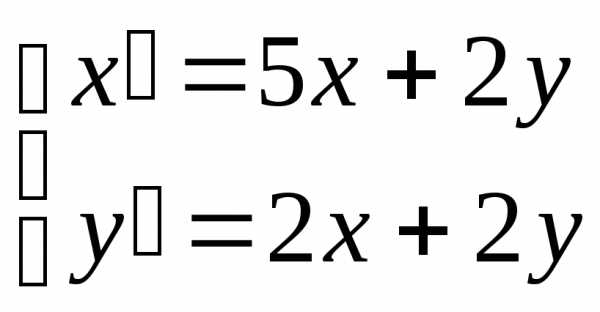
Составим характеристическое уравнение:

Решим систему уравнений:

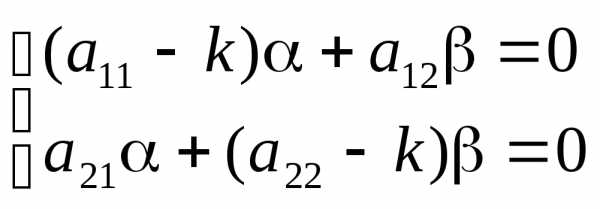
Для k₁:

Полагая 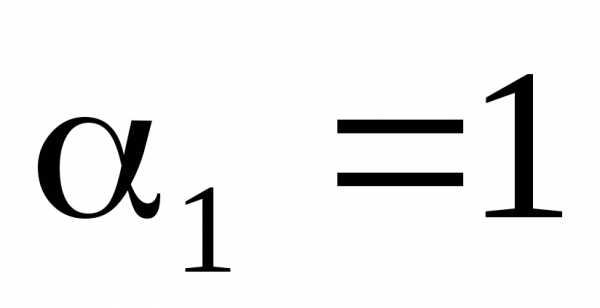(принимается любое значение), получаем: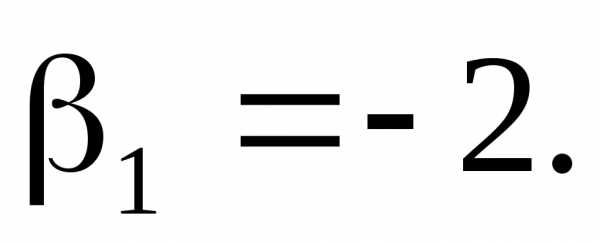

Для k₂:

Полагая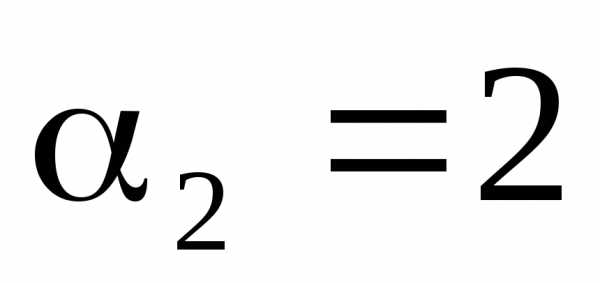(принимается любое значение), получаем: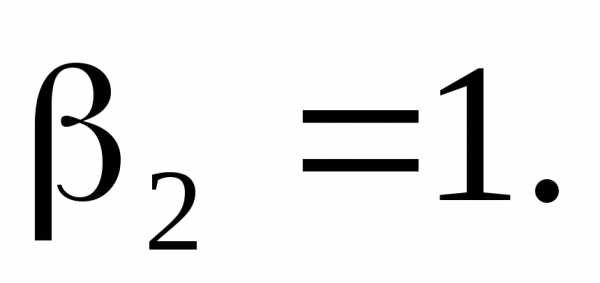

Общее решение системы: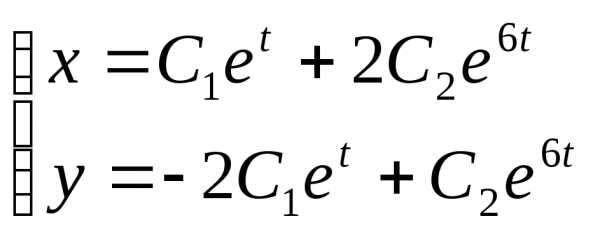

Этот пример может быть решен другим способом:

Продифференцируем первое уравнение:

Подставим в это выражение производную у =2x + 2y из второго уравнения.

Подставим сюда у, выраженное из первого уравнения:

Обозначив , получаем решение системы: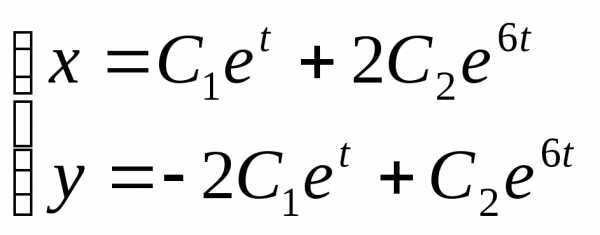

Пример. Найти решение системы уравнений

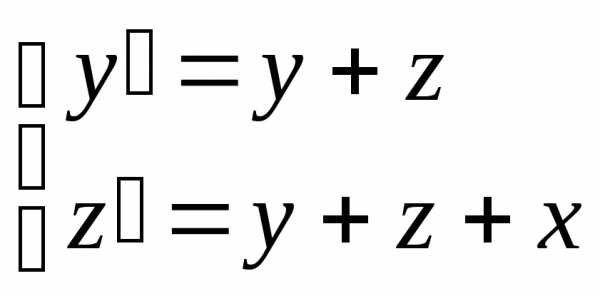
Эта система дифференциальных уравнений не относится к рассмотренному выше типу, т.к. не является однородным (в уравнение входит независимая переменная х).

Для решения продифференцируем первое уравнение по х. Получаем:

Заменяя значение z’ из второго уравнения получаем: .

С учетом первого уравнения, получаем:

Решаем полученное дифференциальное уравнение второго порядка.

Общее решение однородного уравнения:

Теперь находим частное решение неоднородного дифференциального уравнения по формуле

Общее решение неоднородного уравнения:

Подставив полученное значение в первое уравнение системы, получаем:

Пример. Найти решение системы уравнений:

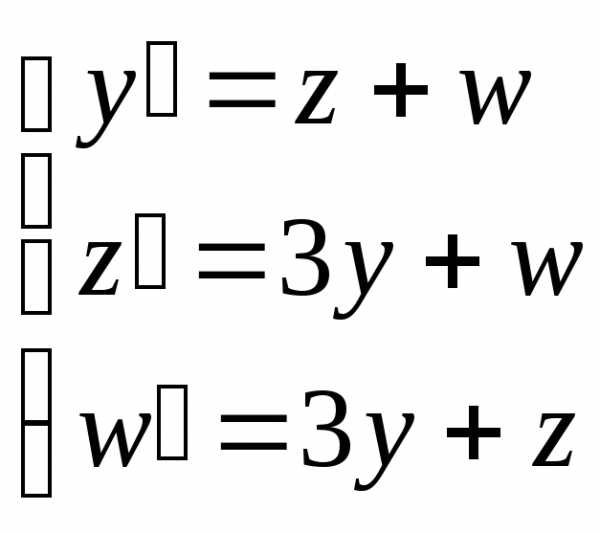
Составим характеристическое уравнение:

1. k = -1.

Если принять  = 1, то решения в этом случае получаем:

2. k₂ = -2.

Если принять  = 1, то получаем:

3. k₃ = 3.

Если принять  = 3, то получаем:

Общее решение имеет вид:

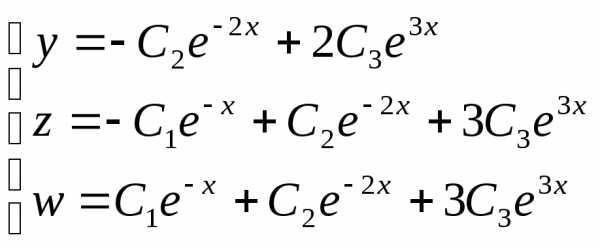
Элементы теории устойчивости.

Теория устойчивости решений дифференциальных уравнений является одним из разделов качественной теории дифференциальных уравнений, которая посвящена не нахождению какого – либо решения уравнения, а изучению характера поведения этого решения при изменении начальных условий или аргумента.

Этот метод особенно важен, т.к. позволяет делать вывод о характере решения без непосредственного нахождения этого решения. Т.е. даже в тех случаях, когда решение дифференциального уравнения вообще не может быть найдено аналитически.

Пусть имеется некоторое явление, описанное системой дифференциальных уравнений:

(1)

и начальные условия:

Для конкретного явления начальные условия определяются опытным путем и поэтому неточны.

Теорема. (о непрерывной зависимости решения от начальных условий)

Если правая часть дифференциального уравнения 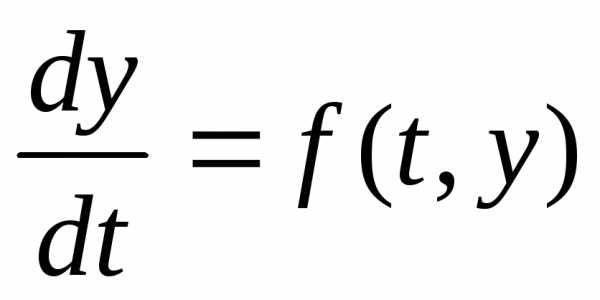непрерывна и по переменной у имеет ограниченную частную производную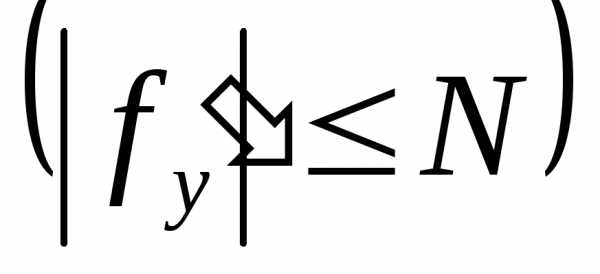на области прямоугольника, ограниченного, то решение

, удовлетворяющее начальным условиям 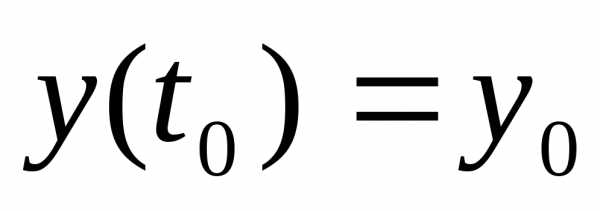, непрерывно зависит от начальных данных, т.е. для любого, при котором если

то при условии, что

где

Эта теорема справедлива как для одного дифференциального уравнения, так и для системы уравнений.

Определение. Если — решение системы дифференциальных уравнений, то это решение называетсяустойчивым по Ляпунову, если для любого , такое, что для любого решениятой же системы, начальные условия которого удовлетворяют неравенствам

справедливы неравенства

(Ляпунов Александр Михайлович (1857 – 1918) академик Петерб. АН)

Т.е. можно сказать, что решение (t) устойчиво по Ляпунову, если близкие к нему по начальным условиям решения остаются близкими и при t  t₀.

Если , то решение(t) называется асимптотически устойчивым.

Исследование на устойчивость по Ляпунову произвольного решения системы можно свести к исследованию на устойчивость равного нулю решения некоторой другой системы, которая получена из данной заменой неизвестных функций:

Тогда:

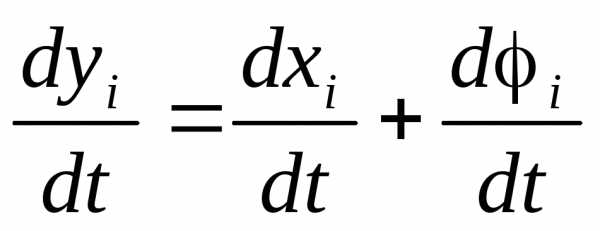
(2)

Система (2) имеет тривиальное (равное нулю) решение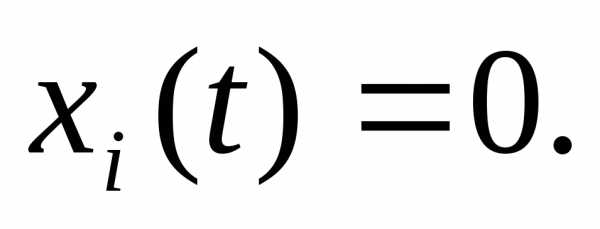

Теорема. Решение системы (1) устойчиво по Ляпунову тогда и только тогда, когда устойчиво по Ляпунову тривиальное решение системы (2).

Это тривиальное решение называется положением равновесия или точкой покоя.

Определение. Точка покоя 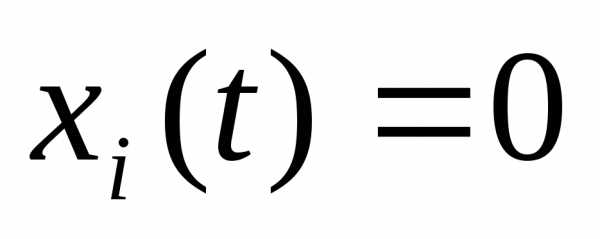системы (2) устойчива по Ляпунову, если для любоготакое, что из неравенства

следует

.

Теорема. (Теорема Ляпунова). Пусть задана система

имеющая тривиальное решение .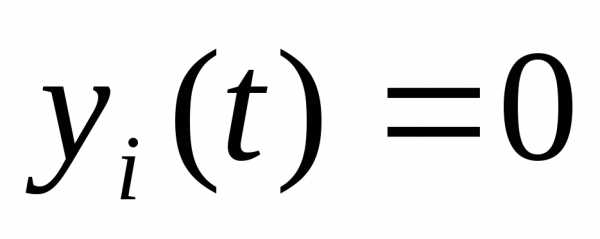

Пусть существует дифференцируемая функция , удовлетворяющая условиям:

1) 0 и v = 0 только при у₁ = у₂ = … = у_n =0, т.е. функция v имеет минимум в начале координат.

2) Полная производная функции v вдоль фазовой траектории (т.е. вдоль решения y_i(t) системы (1)) удовлетворяет условию:

при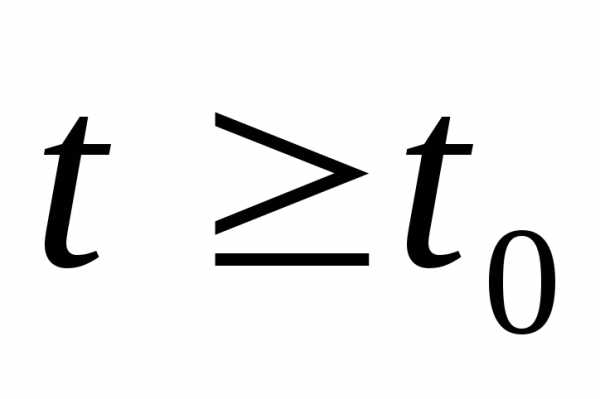

Тогда точка покоя устойчива по Ляпунову.

Если ввести дополнительное требование, чтобы вне сколь угодно малой окрестности начала координат выполнялось условие

где  — постоянная величина, то точка покоя асимптотически устойчива.

Функция v называется функцией Ляпунова.

Классификация точек покоя.

Рассмотрим систему двух линейных дифференциальных уравнений с постоянными коэффициентами

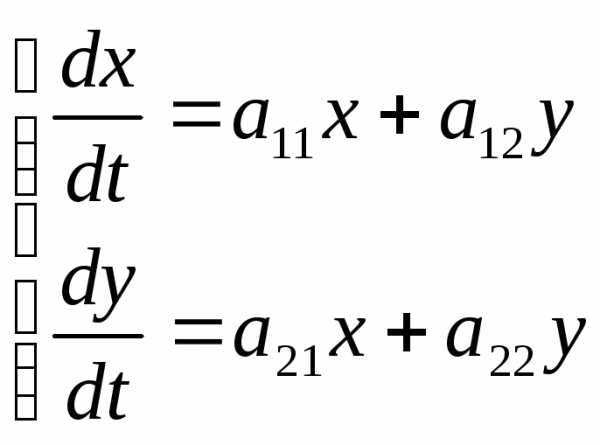
Характеристическое уравнение этой системы имеет вид:

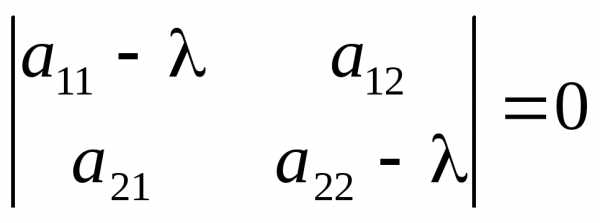
Рассмотрим следующие возможные случаи:

1) Корни характеристического уравнения действительные, отрицательные и различные.

Точка покоя будет устойчива. Такая точка покоя называетсяустойчивым узлом.

2) Корни характеристического уравнения действительны и

или .

В этом случае точка покоя также будет устойчива.

3) Хотя бы один из корней 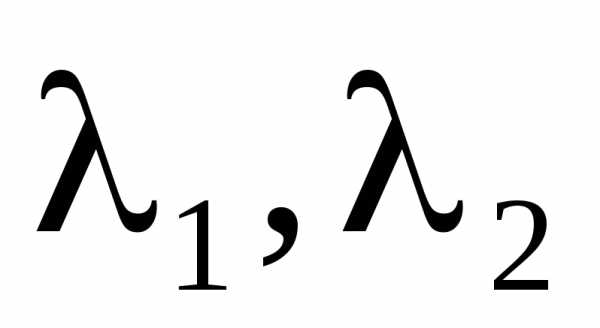положителен.

В этом случае точка покоя неустойчива, и такую точку называютнеустойчивым седлом.

4) Оба корня характеристического уравнения положительны .

В этом случае точка покоя неустойчива, и такую точку называютнеустойчивым узлом.

Если полученного решения системы исключить параметрt, то полученная функция 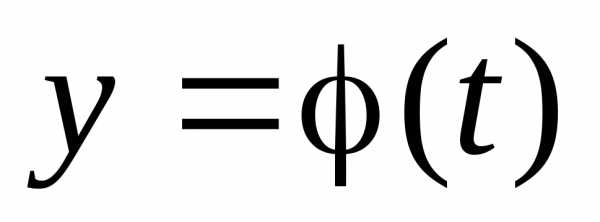дает траекторию движения в системе координатXOY.

Возможны следующие случаи:

 

 

Устойчивый узел. Неустойчивый узел. Седло.

5) Корни характеристического уравнения комплексные .

Если р = 0, т.е. корни чисто мнимые, то точка покоя (0, 0) устойчива по Ляпунову.

Такая точка покоя называется центром.

Если p< 0, то точка покоя устойчива и называется устойчивым фокусом.

Если p > 0, то точка покоя неустойчива и называется неустойчивым фокусом.

Уравнения математической физики.

Уравнения в частных производных.

Определение. Дифференциальным уравнением в частных производных называется уравнение относительно неизвестной функции нескольких переменных, ее аргументов и ее частных производных различных порядков.

Порядком дифференциального уравнения в частных производных называется порядок старшей производной, входящей в это уравнение. Решением уравнения будет некоторая функция , которая обращает уравнение в тождество.

studfiles.net