Логические операции и таблицы истинности
Основой цифровой техники служат три логические операции, лежащие в основе всех выводов компьютера. Это три логические операции: И, ИЛИ, НЕ, которые называют «тремя китами машинной логики».
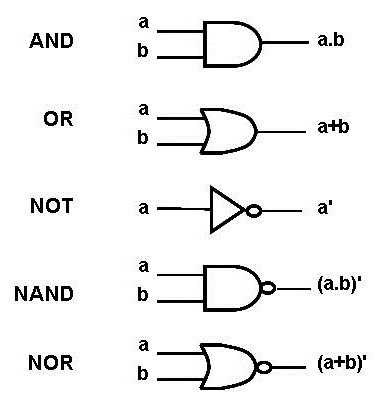
В компьютере логические функции реализуют логические элементы. Логический элемент (вентиль) – это часть электронной логической схемы, которая реализует элементарную логическую функцию, т.е. это электронная схема, которая формирует выходной сигнал в соответствии с простой булевой операцией преобразования сигналов, поданных на его входы.
Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И–НЕ, ИЛИ–НЕ и другие, а также триггер.
С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода.
Самой простой логической операцией является
Если А – истинно, то Ā – ложно и наоборот
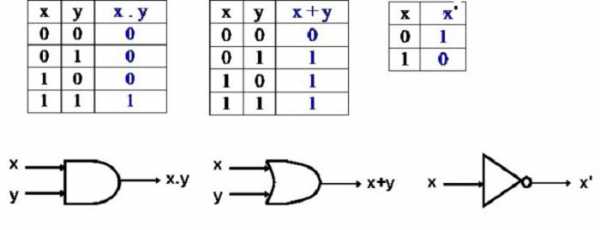
Таблица истинности:Результат отрицания всегда противоположен значению аргумента. Логическая операция НЕ является унарной, т.е. действие выполняются над одним операндом. В отличие от нее, операции И (AND) и ИЛИ (OR) являются бинарными, так как представляют собой результаты действий над двумя логическими величинами.
Например, A – идет дождь; Ā – не идет дождь (не(А) или not(A))
Логическое И еще часто называют конъюнкцией, или логическим умножением, Операция И (обозначается «И», «and», «&», А•В) имеет результат «истина» только в том случае, если оба ее операнда истинны.
Таблица истинности:
A | B | F |
0 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
Если F = A&B, то F истинно тогда и только тогда,
когда истинны и А и В
Например, A – пасмурно; B – идет дождь.
Можно записать: A&B (читается пасмурно и идет дождь)
Операция ИЛИ – дизъюнкция, или логическое сложение.
(обозначается «ИЛИ», «or», А+В) «менее привередлива» к исходным данным. Она дает «истину», если значение «истина» имеет хотя бы один из операндов. Разумеется, в случае, когда справедливы оба аргумента одновременно, результат по-прежнему истинный.
A | B | F |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 1 |
Если F = A+B, то F ложно тогда и только тогда, когда ложны и А и В.
Например, A – пасмурно; B – идет дождь.
Можно записать: A+B (читается пасмурно или идет дождь)
Операции И, ИЛИ, НЕобразуют полную систему логических операций, из которой можно построить сколь угодно сложное логическое выражение. В вычислительной технике также часто используется операции импликация и эквивалентность.
Логическое следование: импликация– связывает два простых логических выражения, из которых первое является условием (А), а второе (В) – следствием из этого условия. Результатом импликации является ЛОЖЬ только тогда, когда условие А истинно, а следствие В ложно. Обозначается символом «следовательно» и выражается словами ЕСЛИ … , ТО …
Таблица истинности:
A | B | F |
1 | 1 | 1 |
0 | 0 | |
0 | 1 | 1 |
0 | 0 | 1 |
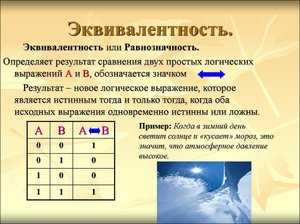
Логическая равнозначность: эквивалентность (конвергенция)– определяет результат сравнения двух простых логических выражений А и В. Результатом эквивалентности является новое логическое выражение, которое будет истинным тогда и только тогда, когда оба исходных выражения одновременно истинны или ложны. Обозначается символом «эквивалентности».
Таблица истинности:
A | B | F |
1 | 1 | 1 |
1 | 0 | 0 |
0 | 1 | 0 |
0 | 0 | 1 |
studfiles.net
11. Отношения между суждениями в сложных высказываниях. Таблица истинности
Билет № 11
Отношения между суждениями в сложных высказываниях. Таблица истинности.
Основу отношений между суждениями составляют их сходства по содержанию:
эквивалентность (p ≡ q, выражает одну и туже мысль в различной форме)
частичная совместимость (одновременно истины, но не могут быть одновременно ложными)
отношение подчинения (общий предикат, а субъекты суждения находятся в логическом подчинении, А-I ; E-O)
несовместимые (как противоположность, характерна для суждений, которые не могут быть одновременно истинными)
противоположность (контрарность)
противоречие (контрадикторность) A-O; E-I, такие суждения не могут быть одновременно ни истинными, ни ложными.
Сложные суждения могут быть истинными или ложными в соответствии с истинностью и ложностью, входящие в состав. Структуру сложных суждений образуют простые и логические связки (союзы).
p | q | 1. p /\ q | 2. p \/ q | 3. p \˙/q | 4. p → q | 5. p ≡ q |
И | И | И | И | Л | И | И |
И | Л | Л | И | И | Л | Л |
Л | И | Л | И | И | И | Л |
Л | Л | Л | Л | Л | И | И |
Соединительное или конъюнктивное суждение – сложное сужение, в котором простые суждения связаны логической связкой И (конъюнкция). Истинно тогда, когда истинны входящие в него суждения.
Разделительное или дизъюнктивное суждение – сложное суждение, в котором простые суждения связаны между собой логическим союзом ИЛИ. Суждение является ложным только тогда, когда входит в него простые суждения одновременно ложные.
Сильная дизъюнкция – разделительное суждение, содержащее союз ЛИБО … ЛИБО, является истинным при условию истинности одного и ложности другого.
Условные суждения или импликация – суждение, где простые соединяются логическим союзом ЕСЛИ ТО. Суждения, стоящие после слов ЕСЛИ, называется основанием, после ТО – следствием. Являются ложными, если основание – истинно, а следствие – ложно, из истинности ложь не следует.
Суждение эквивалентности – сложное суждение, где связь между простыми осуществляется с помощью логического союза ЕСЛИ И ТОЛЬКО ЕСЛИ, ТО. Одно из простых суждений является необходимым для другого. Истнинны тогда, когда входящие в него простые суждение имеют одинаковые истинные значения.
studfiles.net
Простейшие логические операции в информатике
Каждого, кто начинает изучать информатику, учат двоичной системе исчисления. Именно она используется для вычисления логических операций. Рассмотрим ниже все самые элементарные логические операции в информатике. Ведь если задуматься, именно они используются при создании логики вычислительных машин и приборов.
Отрицание
Перед тем как начать подробно рассматривать конкретные примеры, перечислим основные логические операции в информатике:

- отрицание;
- сложение;
- умножение;
- следование;
- равенство.
Также перед началом изучения логических операций стоит сказать, что в информатике ложь обозначается «0», а правда «1».
Для каждого действия, как и в обычной математике, используются следующие знаки логических операций в информатике: ¬, v, &, ->.
Каждое действие возможно описать либо цифрами 1/0, либо просто логическими выражениями. Начнём рассмотрение математической логики с простейшей операции, использующей всего одну переменную.
Логическое отрицание — операция инверсии. Суть заключается в том, что если исходное выражение — истина, то результат инверсии — ложь. И наоборот, если исходное выражение — ложь, то результатом инверсии станет — правда.
При записи этого выражения используется следующее обозначение «¬A».
Приведём таблицу истинности — схему, которая показывает все возможные результаты операции при любых исходных данных.
| А | х | о |
| ¬A | о | х |
То есть, если у нас исходное выражение — истина (1), то его отрицание будет ложным (0). А если исходное выражение — ложь (0), то его отрицание — истина (1).
Сложение
Оставшиеся операции требуют наличия двух переменных. Обозначим одно выражение —
 А, второе — В. Логические операции в информатике, обозначающие действие сложения (или дизъюнкция), при написании обозначаются либо словом «или», либо значком «v». Распишем возможные варианты данных и результаты вычислений.
А, второе — В. Логические операции в информатике, обозначающие действие сложения (или дизъюнкция), при написании обозначаются либо словом «или», либо значком «v». Распишем возможные варианты данных и результаты вычислений.- Е=1, Н=1 ,тогда Е v Н = 1. Если оба выражения истинны, тогда и их дизъюнкция также истинна.
- Е=0, Н=1 ,в итоге Е v Н = 1. Е=1, Н=0 , тогда Е v Н= 1. Если хотябы одно из выражений истинно, тогда и результат их сложения будет истиной.
- Е=0, Н=0 ,результат Е v Н = 0. Если оба выражения ложны, то их сумма также — ложь.
Для краткости создадим таблицу истинности.
| Е | х | х | о | о |
| Н | х | о | х | о |
| Е v Н | х | х | х | о |
Умножение
Разобравшись с операцией сложения, переходим к умножению (конъюнкции). Воспользуемся теми же обозначениями, которые были приведены выше для сложения. При письме логическое умножение обозначается значком «&», либо буквой «И».
- Е=1, Н=1 ,тогда Е & Н = 1. Если оба выражения истинны, тогда их конъюнкция — истина.
- Если хотя бы одно из выражений — ложь, тогда результатом логического умножения также будет ложь.
- Е=1, Н=0, поэтому Е & Н = 0.
- Е=0, Н=1, тогда Е & Н = 0.
- Е=0, Н=0, итог Е & Н = 0.
| Е | х | х | 0 | 0 |
| Н | х | 0 | х | 0 |
| Е & Н | х | 0 | 0 | 0 |
Следствие
Логическая операция следования (импликация) — одна из простейших в математической логике. Она основана на единственной аксиоме — из правды не может следовать ложь.
- Е=1, Н=, поэтому Е -> Н = 1. Если пара влюблена, то они могут целоваться — правда.
- Е=0, Н=1, тогда Е -> Н = 1. Если пара не влюблена, то они могут целоваться — также может быть истиной.
- Е=0, Н=0, из этого Е -> Н = 1. Если пара не влюблена, то они и не целуются — тоже правда.
- Е=1, Н=0, результатом будет Е -> Н = 0. Если пара влюблена, то они не целуются — ложь.
Для облегчения выполнения математических действий также приведём таблицу истинности.
| Е | х | х | о | о |
| Н | х | о | х | 0 |
| Е -> Н | х | о | х | х |
Равенство
Последней рассмотренной операцией станет логическое тождественное равенство или эквивалентность. В тексте оно может обозначаться как «…тогда и только тогда, когда…». Исходя из этой формулировки, напишем примеры для всех исходных вариантов.
- А=1, В=1, тогда А≡В = 1. Человек пьёт таблетки тогда и только тогда, когда болеет. (истина)
- А=0, В=0, в итоге А≡В = 1. Человек не пьёт таблетки тогда и только тогда, когда не болеет. (истина)
- А=1, В=0, поэтому А≡В = 0. Человек пьёт таблетки тогда и только тогда, когда не болеет. (ложь)
- А=0, В=1 ,тогда А≡В = 0. Человек не пьёт таблетки тогда и только тогда, когда болеет. (ложь)
| А | х | о | х | о |
| В | х | о | 0 | х |
| А≡В | х | х | о | о |
Свойства
Итак, рассмотрев простейшие логические операции в информатике, можем приступить к изучению некоторых их свойств. Как и в математике, у логических операций существует свой порядок обработки. В больших логических выражениях операции в скобках выполняются в первую очередь. После них первым делом подсчитываем все значения отрицания в примере. Следующим шагом станет вычисление конъюнкции, а затем дизъюнкции. Только после этого выполняем операцию следствия и, наконец, эквивалентности. Рассмотрим небольшой пример для наглядности.
А v В & ¬В -> В ≡ А
Порядок выполнения действий следующий.
- ¬В
- В&(¬В)
- А v(В&(¬В))
- (А v(В&(¬В)))->В
- ((А v(В&(¬В)))->В)≡А
Для того чтобы решить этот пример, нам потребуется построить расширенную таблицу истинности. При её создании помните, что столбцы лучше располагать в том же порядке, в каком и будут выполняться действия.
| А | В | ¬В | В&(¬В) | А v(В&(¬В)) | (А v(В&(¬В)))->В | ((А v(В&(¬В)))->В)≡А |
| х | о | х | о | х | х | х |
| х | х | о | о | х | х | х |
| о | о | х | о | о | х | о |
| о | х | о | о | о | х | о |
Как мы видим, результатом решения примера станет последний столбец. Таблица истинности помогла решить задачу с любыми возможными исходными данными.
Заключение
В этой статье были рассмотрены некоторые понятия математической логики, такие как информатика, свойства логических операций, а также — что такое логические операции сами по себе. Были приведены некоторые простейшие примеры для решения задач по математической логике и таблицы истинности, необходимые для упрощения этого процесса.
fb.ru
Построить таблицу истинности следующих логических выражений
Проблема определения истинности выражения встаёт перед многими науками. Любая доказательная дисциплина должна опираться на некоторые критерии истинности доказательств. Наука, изучающая эти критерии, называется алгеброй логики. Основной постулат алгебры логики заключается в том, что любое самое витиеватое утверждение может быть представлено в виде алгебраического выражения из более простых утверждений, истинность или ложность которых легко определить.
Для любого «алгебраического» действия над утверждением задаётся правило определения истинности или ложности измененного утверждения, исходя из истинности или ложности исходного утверждения. Эти правила записываются через таблицы истинности выражения. Прежде, чем составлять таблицы истинности, надо поближе познакомиться с алгеброй логики.
Алгебраические преобразования логических выражений
Любое логическое выражение, как и его переменные (утверждения), принимают два значения: ложь или истина. Ложь обозначается нулём, а истина — единицей. Разобравшись с областью определения и областью допустимых значений, мы можем рассмотреть действия алгебры логики.
Отрицание
Отрицание и инверсия — самое простое логическое преобразование. Ему соответствует частица «не.» Это преобразование просто меняет утверждение на противоположное. Соответственно, значение утверждения тоже меняется на противоположное. Если утверждение А истинно, то «не А» — ложно. Например, утверждение «прямой угол — это угол, равный девяносто градусов» — истина. Тогда его отрицание «прямой угол не равен девяноста градусам» — ложь.

Таблица истинности для отрицания будет такова:
Конъюнкция
Конъюнкция аналогична умножению и соответствует союзу «и». Такое выражение будет верно, только если верны все утверждения, объединённые конъюнкцией. То есть, утверждение «А и Б» будет истинным, только если А — истина и Б — истина. Во всех остальных случаях выражение «А и Б» ложно. Например, высказывание «Земля круглая и плоская» будет ложно, так как первая часть истина, а вторая — ложь.
Таблица истинности конъюнкции
| А | Б | А и Б |
| Л | Л | Л |
| Л | И | Л |
| И | Л | Л |
| И | И | И |
Дизъюнкция
Эта операция может быть обычной или строгой, их результаты будут различаться.
Обычная дизъюнкция или логическое сложение соответствует союзу «или». Она будет истинной если хотя бы одно из утверждений, входящих в неё — истина. Например, выражение «Земля круглая или стоит на трёх китах» будет истинным, так как первое утверждение — истинно, хоть второе и ложно.В таблице это будет выглядеть так:
| А | Б | А или Б |
| Л | Л | Л |
| Л | И | И |
| И | Л | И |
| И | И | И |
Строгую дизъюнкцию или сложение по модулю также называют «исключающим или». Эта операция может принимать вид грамматической конструкции «одно из двух: либо …, либо …». Здесь значение логического выражения будет ложным, если все утверждения, входящие в него, имеют одинаковую истинность. То есть, оба утверждения либо вместе истинны, либо вместе ложны.
Таблица значений исключающего или
| А | Б | либо А, либо Б |
| Л | Л | Л |
| Л | И | И |
| И | Л | И |
| И | И | Л |
Импликация и эквивалентность
Импликация представляет собой следствие и грамматически может быть выражена как «из А следует Б». Здесь утверждение А будет называться предпосылкой, а Б — следствием. Импликация может быть ложной, только в одном случае: если предпосылка истинна, а следствие ложно. То есть, ложь не может следовать из истины. Во всех остальных случаях импликация истинна. Варианты, когда оба утверждения имеют одинаковую истинность, вопросов не вызывают. Но почему верное следствие из неверной предпосылки — истина? Дело в том, что из ложной предпосылки может следовать что угодно. Это и отличает импликацию от эквивалентности.
В математике (и других доказательных дисциплинах) импликация используется для указания необходимого условия. Например, утверждение А — «точка О — экстремум непрерывной функции», утверждение Б — «производная непрерывной функции в точке О обращается в ноль». Если О, действительно, точка экстремума непрерывной функции, то производная в этой точке будет, и вправду, равна нулю. Если же О не является точкой экстремума, то производная в этой точке может быть нулевой, а может не быть. То есть Б необходимо для А, но не достаточно.

Таблица истинности для импликации выглядит следующим образом:
| А | Б | из А следует Б |
| Л | Л | И |
| Л | И | И |
| И | Л | Л |
| И | И | И |
Логическая операция эквивалентность, по сути, является взаимной импликацией. «А эквивалентно Б» означает, что «из А следует Б» и «из Б следует А» одновременно. Эквивалентность верна, когда оба утверждения либо одновременно верные, либо одновременно неверные.
| А | Б | А эквивалентно Б |
| Л | Л | И |
| Л | И | Л |
| И | Л | Л |
| И | И | И |
В математике эквивалентность используется для определения необходимого и достаточного условия. Например, утверждение А — «Точка О является точкой экстремума непрерывной функции», утверждение Б — «В точке О производная функции обращается в ноль и меняет знак». Эти два утверждения эквивалентны. Б содержит необходимое и достаточное условие для А. Обратите внимание, что в данном примере утверждений Б на самом деле является конъюнкцией двух других: «производная в точке О обращается в ноль» и «производная в точке О меняет знак».
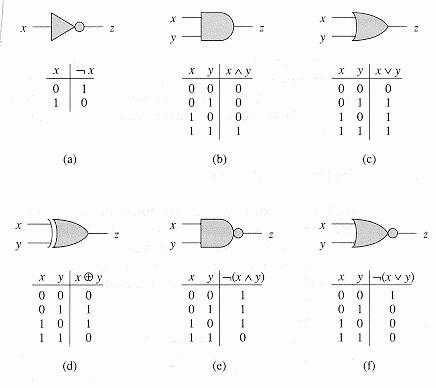
Прочие логические функции
Выше были рассмотрены основные логические операции, которые часто используются. Есть и другие функции, которые используются:
- Штрих Шеффера или несовместимость представляет собой отрицание конъюнкции А и Б
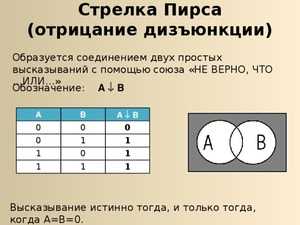
- Стрелка Пирса представляет сбой отрицание дизъюнкции.
Построение таблиц истинности
Чтобы построить таблицу истинности для какого-либо логического выражения, надо действовать в соответствии с алгоритмом:
- Разбить выражение на простые утверждения и обозначить каждое из них как переменную.
- Определить логические преобразования.
- Выявить порядок действий этих преобразований.
- Сосчитать строки в будущей таблице. Их количество равно два в степени N, где N — число переменных, плюс одна строка для шапки таблицы.
- Определить число столбцов. Оно равно сумме количества переменных и количества действий. Можно представлять результат каждого действия в виде новой переменной, если так будет понятней.
- Шапка заполняется последовательно, сначала все переменные, потом результаты действий в порядке их выполнения.
- Заполнение таблицы надо начать с первой переменной. Для неё количество строк делится пополам. Одна половина заполняется нулями, вторая — единицами.
- Для каждой следующей переменной нули и единицы чередуются вдвое чаще.
- Таким образом заполняются все столбцы с переменными и для последней переменной значение меняется в каждой строке.
- Потом последовательно заполняются результаты всех действий.
В итоге последний столбец отобразит значение всего выражения в зависимости от значения переменных.
Отдельно следует сказать о порядке логических действий. Как его определить? Здесь, как и в алгебре, есть правила, задающие последовательность действий. Они выполняются в следующем порядке:
- выражения в скобках;
- отрицание или инверсия;
- конъюнкция;
- строгая и обычная дизъюнкция;
- импликация;
- эквивалентность.
Примеры
Для закрепления материала можно попробовать составить таблицу истинности для ранее упомянутых логических выражений. Рассмотрим три примера:
- Штрих Шеффера.
- Стрелка Пирса.
- Определение эквивалентности.
Штрих Шеффера
Штрих Шеффера — это логическое выражение, которое можно записать в виде «не (А и Б)». Здесь две переменные, и два действия. Конъюнкция в скобках, значит, она выполняется первой. В таблице будет шапка и четыре строки со значениями переменных, а также четыре столбца. Заполним таблицу:
| А | Б | А и Б | не (А и Б) |
| Л | Л | Л | И |
| Л | И | Л | И |
| И | Л | Л | И |
| И | И | И | Л |
Отрицание конъюнкции выглядит как дизъюнкция отрицаний. Это можно проверить, если составить таблицу истинности для выражения «не А или не Б». Проделайте это самостоятельно и обратите внимание, что здесь будет уже три операции.
Стрелка Пирса
Рассматривая Стрелку Пирса, которая представляет собой отрицание дизъюнкции «не (А или Б)», сравним её с конъюнкцией отрицаний «не А и не Б». Заполним две таблицы:
| А | Б | А или Б | не (А или Б) |
| Л | Л | Л | И |
| Л | И | И | Л |
| И | Л | И | И |
| И | И | И | Л |
| А | Б | не А | не Б | не А и не Б |
| Л | Л | И | И | И |
| Л | И | И | Л | Л |
| И | Л | Л | И | И |
| И | И | Л | Л | Л |
Значения выражений совпали. Изучив два эти примера, можно прийти к выводу, как раскрывать скобки после отрицания: отрицание применяется ко всем переменным в скобках, конъюнкция меняется на дизъюнкцию, а дизъюнкция — на конъюнкцию.
Определение эквивалентности
Про утверждения А и Б можно сказать, что они эквивалентны, тогда и только тогда, когда из А следует Б и из Б следует А. Запишем это как логическое выражение и построим для него таблицу истинности. «(А эквивалентно Б) эквивалентно (из А следует Б) и (из Б следует А)».
Здесь две переменных и пять действий. Строим таблицу:
| А | Б | В = (из А следует Б) | Г = (из Б следует А) | Д = А эквивалентно Б | Е = В и Г | Д эквивалентно Е |
| Л | Л | И | И | И | И | И |
| Л | И | И | Л | Л | Л | И |
| И | Л | Л | И | Л | Л | И |
| И | И | И | И | И | И | И |
В последнем столбце все значения истинные. Это значит, что приведенное определение эквивалентности верно при любых значениях А и Б. Значит, оно всегда истинно. Именно так с помощью таблицы истинности можно проверить корректность любых определений и логических построений.
liveposts.ru
iMath Wiki — Алгебра логики. Основные логические операции и их таблицы истинности. Основные законы алгебры логики.
Мы выяснили, как информация представляется в памяти вычислительных устройств и установили алгоритмы проведения операций над этими представлениями.
Теперь, давайте попробуем разобраться, как именно реализуются операции над двоичными представлениями. Для этого, для начала, нам придется разобраться с алгеброй логики.
Алгебра логики является частью дискретной математики – раздела математики, изучающего свойства структур конечного характера.
Сама алгебра логики изучает свойства функций, у которых значения как аргументов, так и самих функций ограничены двумя значениями, например, \(\{0,1\}\).
Отцом алгебры логики считается английский математик Джордж Буль (1815-1864), поэтому алгебру логики иногда называют булевой алгеброй.
Долгое время алгебра логики была известна лишь узкому кругу специалистов, и только в 1938 году американский математик Клод Шеннон (1916-2001), стоявший у истоков современной информатики, показал, что алгебра логики применима для описания самых разных процессов, в том числе релейных и транзисторных схем.
Исследования в области алгебры логики связаны с формальной логикой, а точнее, с понятием высказывания. Высказывание – это некое лексическое образование, которое устанавливает свойства и взаимосвязи между объектами. Высказывания могут быть истинными, если они адекватно описывают объекты, или ложными в противном случае.
Так, примерами высказываний могут служить такие фразы, как “сегодня идет дождь”, или “завтра я не пойду в институт”.
Определение истинности высказывания не всегда тривиально. Так, например:
Великая теорема Ферма
Для любого натурального числа \(n>2\) уравнение \[ a^n + b^n = c^n\] Не имеет решений в целых ненулевых числах \(a,\,b,\,c\)
Как известно, сформулированная Пьером Ферма в 1637 году, была окончательно доказана только в 1994.
Введем не совсем формальное, но достаточное для наших целей определение
- Высказывание
- это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности.
Это определение было предложено Аристотелем.
Проблема языковых образований в рамках алгебры логики в том, что они могут иметь весьма своеобразную структуру. Например, фраза “это высказывание является ложным” не может считаться высказыванием, поскольку бессмысленно говорить о его истинности или ложности. Причиной парадокса является структура фразы: она ссылается сама на себя. Подобные парадоксы могут быть устранены введением следующего определения:
- Элементарное высказывание
- это такое высказывание, никакая часть которого не является высказыванием.
Следует заметить, что высказыванием в строгом смысле является только утверждение о конкретных объектах. Если речь идет о неких переменных, например, “x – рациональное число”, то мы говорим о неких функциях, имеющих значение “истина” или “ложь”. Такие функции называются предикатами.
Так же следует заметить, что алгебра логики отвлекается от смыслового содержания высказываний, и занимается скорее связями между высказываниями. Если мы договоримся считать за аксиому, что “солнце светит ночью”, то есть, договоримся что это высказывание истинно, то в рамках нашей аксиоматики сможем делать какие-то обоснованные выводы. Эти выводы, конечно, не будут иметь много общего с действительностью.
Примерами таких отвлеченных, на первый взгляд, систем, может служить, например, геометрия Лобачевского, которая имеет не слишком много общего с нашим псевдоевклидовым пространством.
Различные языковые связки, такие, как “не”, “если …, то …”, “или”, “и”, и т.п. позволяют строить из элементарных высказываний более сложные.
В алгебре логики существуют соответствующие подобным связкам операции.
Введем некоторые из них.
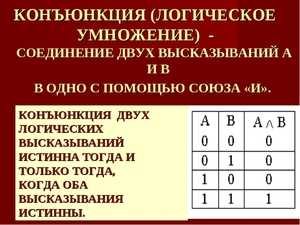
- Конъюнкция, или логическое умножение
- логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
Конъюнкция обозначается различными способами, в частности, амперсандом \(a \,\&\,b\), точкой \(a \cdot b\), или “крышкой” \(a \wedge b\), и соответствует языковой связке “и”. Мы будем в основном использовать амперсанд.
Поскольку оба исходных высказывания имеют по два возможных значения, и конъюнкция имеет два возможных значения, мы можем записать это определение в виде таблицы истинности:
- Дизъюнкция, или логическое сложение
- логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда хотя бы одно из исходных высказываний истинно.
Дизъюнкция соответствует союзу “или”, и обозначается плюсом \(a+b\), или “галочкой” \(a\vee b\). Мы будем использовать в основном второй вариант.
Таблица истинности дизъюнкции, по определению:
- Строгая дизъюнкция, или сложение по модулю 2
- логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда только одно из исходных высказываний истинно.
Строгая дизъюнкция соответствует связке “либо …, либо …”, и обозначается плюсом в кружочке \(a\oplus b\), или треугольником \(a\vartriangle b\). Будем в основном пользоваться первым обозначением.
Таблица истинности, по определению:
- Импликация
- логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся ложным тогда и только тогда, когда первое из исходных высказываний (условие) истинно, а второе (следствие) – ложно.
Импликация соответствует связке “если …, то …”, и обозначается стрелкой \(a \rightarrow b\), или \(a \Rightarrow b\)
Таблица истинности, по определению:
Импликация, на первый взгляд, имеет не очевидное определение: как вдруг из ложных условий получается истинное следствие. Однако, в математике это никакая не новость. Например, возьмем очевидно ложное утверждение “один равен двум”:
\[1 = 2\] \[2 = 1\]
Складывая эти равенства, получим очевидно истинный результат:
\[3=3.\]
С другой стороны, из заведомо истинных посылок формально нельзя вывести ложный результат (конечно, человеческий фактор никто не отменял, но человеческий фактор выходит за пределы рассмотрения формальной логики).
- Эквивалентность
- логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.
Эквивалентность соответствует связке “тогда и только тогда, когда”, и обозначается \(a \Leftrightarrow b\), или \(a \equiv b\), или \(a \sim b\), или \(a \leftrightarrow b\). Будем в основном пользоваться первыми двумя обозначениями.
Таблица истинности, по определению:
- Инверсия, или отрицание
- логическая операция, ставящая в соответствие элементарному высказыванию новое высказывание, являющееся истинным тогда и только тогда, исходное ложно.
Инверсия соответствует связке “не”, и обозначается \(\neg a\), или \(\;\overline{a}\;\), или \(!a\). Будем в основном пользоваться первыми двумя обозначениями.
Таблица истинности, по определению:
В заключение, таблица истинности основных логических операций:
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
Законы алгебры логики
Введем некоторые определения, аналогичные алгебре действительных чисел, для алгебры логики.
- Логическая переменная
- Переменная, значением которой может быть любое высказывание. Обозначать будем маленькими латинскими буквами.
- Логическая формула
- любая переменная, а так же любая из констант “0” (“ложь”) и “1” (“истина”)
- Любая комбинация логических формул, составленная с помощью логических операций.
- Эквивалентные формулы
- такие формулы, которые зависят от одного и того же набора переменных, и при одинаковых значениях этих переменных, формулы так же имеют одинаковые значения. Обозначать будем знаком равенства.
Существуют следующие “законы” алгебры логики, определяющие некий набор эквивалентных формул:
- Законы коммутативности
- \[x \,\&\,y = y \,\&\,x\] \[x \vee y = y\vee x\]
- Законы ассоциативности
- \[ (x \,\&\,y) \,\&\,z = x \,\&\,(y \,\&\,z)\] \[ (x \vee y) \vee z = x \vee(y \vee z)\]
- Законы поглощения
- \[x\vee 0 = x\] \[x\,\&\,1 = x\]
- Законы дистрибутивности
- \[ x\,\&\,(y\vee z) = (x\,\&\,y) \vee(x\,\&\,z)\] \[ x\vee(y\,\&\,z) = (x \vee y) \,\&\,(x\vee z)\]
- Закон противоречия
- \[ x \,\&\,\;\overline{x}\; = 0\]
- Закон исключения третьего
- \[ x \vee\;\overline{x}\; = 1\]
- Закон равносильности
- \[ x \,\&\,x = x\] \[ x \vee x = x \]
- Закон двойного отрицания
- \[\;\overline{\;\overline{x}\;}\; = x \]
- Законы де Моргана
- \[ \;\overline{x\,\&\,y}\; = \;\overline{x}\; \vee\;\overline{y}\; \] \[ \;\overline{x\vee y}\; = \;\overline{x}\; \,\&\,\;\overline{y}\; \]
- Законы поглощения
- \[ x\vee(x\,\&\,y) = x\] \[ x\,\&\,(x\vee y) = x\]
Все перечисленные законы элементарно доказываются составлением таблиц истинности.
Например, первый закон де Моргана:
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
3 и 6 столбец одинаковы, следовательно, соответствующие формулы эквивалентны.
Введем еще одно определение
- Тавтология
- логическая формула, которая всегда истинна.
Например, тавтологией является формула, выражающая закон исключения третьего.
Оказывается, алгебра логики хорошо подходит для решения логических задач. Решение логических задач, конечно, умеренно бессмысленное времяпрепровождение (исключая случаи, когда на их примере рассматриваются более сложные вопросы), однако это хороший способ поработать с алгеброй логики и осмыслить основные концепции.
Итак, формальный способ решения логических задач:
- Из условий задачи выделяются простые высказывания и обозначаются как логические переменные.
- Условия задачи записываются в виде логических формул
- Составляется единое логическое выражение, соответствующее условию задачи. По условию задачи оно является истинным.
- Полученное выражение упрощается, либо составляется таблица истинности для него (либо и то, и другое)
- Выбирается решение задачи (случаи, когда условие истинно)
- Решение формулируется в исходных терминах задачи.
Пример: (источник)
На весеннем фестивале, четыре садовника показывали выращенные ими розы.
Всего розы были четырех цветов и у каждого садовника было по две розы.
Известно, что
- У первого была желтая роза
- У второго не было красной розы
- У третьего была синяя роза, но не было зеленой
- У одного из садовников с зеленой розой не было красной
- Ни у одного из садовников с желтой розой не было зеленой
- Ни у кого нет роз двух одинаковых цветов
Введем переменные, в которых название переменной соответствует цвету, а индекс – садовнику (номеру). Это автоматически учитывает условие “Ни у кого нет роз двух одинаковых цветов”. Тогда условия задачи запишутся в виде:
- \(y_1\)
- \(\;\overline{r_2}\;\)
- \(b_3 \,\&\,\;\overline{g_3}\;\)
- \((g_1\rightarrow\;\overline{r_1}\;) \oplus(g_2\rightarrow\;\overline{r_2}\;)\oplus(g_3\rightarrow\;\overline{r_3}\;)\oplus(g_4\rightarrow\;\overline{r_4}\;)\)
- \((y_1\rightarrow\;\overline{g_1}\;) \,\&\,(y_2\rightarrow\;\overline{g_2}\;)\,\&\,(y_3\rightarrow\;\overline{g_3}\;)\,\&\,(y_4\rightarrow\;\overline{g_4}\;)\)
Дополнительно, у каждого садовника по условиям задачи по две розы: Поэтому, если у садовника есть розы двух цветов, то роз двух других цветов у него нет. Учтем подразумеваемые импликации постфактум.
Далее для простоты записи, амперсанды опускаются (если между переменными нет ничего – значит там амперсанд). В случае отсутствия скобок, сначала применяется конъюнкция, потом все остальное.
Рассматривая последнее условие:
\((y_1\rightarrow\;\overline{g_1}\;) (y_2\rightarrow\;\overline{g_2}\;)(y_3\rightarrow\;\overline{g_3}\;)(y_4\rightarrow\;\overline{g_4}\;)\)
Первая импликация истинна, только если \(\;\overline{g_1}\;\) истинно. Предпоследняя импликация истинна всегда, \(\;\overline{g_3}\;\). Можем переписать в виде:
\(y_1 \;\overline{g_1}\; (y_2\rightarrow\;\overline{g_2}\;) (y_4\rightarrow\;\overline{g_4}\;)\)
Рассмотрим предпоследнее условие
\[ (g_1 \rightarrow\;\overline{r_1}\;) \oplus(g_2 \rightarrow\;\overline{r_2}\;) \oplus(g_3 \rightarrow\;\overline{r_3}\;) \oplus(g_4 \rightarrow\;\overline{r_4}\;) \]
Первая импликация всегда истинна, поскольку \(\;\overline{g_1}\;\), вторая всегда истинна, поскольку \(\;\overline{r_2}\;\), третья всегда истинна, поскольку \(\;\overline{g_3}\;\). Получаем:
\[ 1 \oplus 1 \oplus 1 \oplus(g_4 \rightarrow\;\overline{r_4}\;) \]
\[ 1 \oplus(g_4 \rightarrow\;\overline{r_4}\;) \]
Легко показать, что \(1 \oplus x = \;\overline{x}\;\). Тогда условие принимает вид
\[ \;\overline{g_4 \rightarrow\;\overline{r_4}\;}\; \]
Импликацию можно представить в виде \(x \rightarrow y = \;\overline{x}\; \vee y\)
Применяя закон де Моргана,
\[ r_4 g_4 \]
Записывая все условия вместе:
\[ y_1 \;\overline{g_1}\; \;\overline{r_2}\; (\;\overline{y_2}\; \vee\;\overline{g_2}\;) (\;\overline{y_4}\; \vee\;\overline{g_4}\;) b_3 \;\overline{g_3}\; g_4 r_4 \]
Учитывая \(g_4 (\;\overline{y_4}\; \vee\;\overline{g_4}\;) = g_4 \;\overline{y_4}\;\),
\[ y_1 \;\overline{g_1}\; \;\overline{r_2}\; (\;\overline{y_2}\; \vee\;\overline{g_2}\;) b_3 \;\overline{g_3}\; \;\overline{y_4}\; g_4 r_4 \]
Известно, что зеленые розы должны быть у двух садовников:
\[ \;\overline{g_1}\; \;\overline{g_2}\; g_3 g_4 \vee\;\overline{g_1}\; g_2 \;\overline{g_3}\; g_4 \vee\;\overline{g_1}\; g_2 g_3 \;\overline{g_4}\; \vee g_1 \;\overline{g_2}\; \;\overline{g_3}\; g_4 \vee g_1 \;\overline{g_2}\; g_3 \;\overline{g_4}\; \vee g_1 g_2 \;\overline{g_3}\; \;\overline{g_4}\; \]
А так как \(\;\overline{g_3}\;\) и \(\;\overline{g_1}\;\)
\[ \;\overline{g_1}\; g_2 \;\overline{g_3}\; g_4 \]
Получаем \(g_2\), тогда \(g_2 (\;\overline{y_2}\; \vee\;\overline{g_2}\;) = g_2 \;\overline{y_2}\;\)
Аналогично для желтых:
\[ y_1 \;\overline{y_2}\; y_3 \;\overline{y_4}\; \]
Получаем \(y_3\). Поскольку \(y_3 b_3\), можно утверждать \(\;\overline{r_3}\; \;\overline{g_3}\;\)
Для красных тогда:
\[ r_1 \;\overline{r_2}\; \;\overline{r_3}\; r_4 \]
Получаем \(r_1\). Поскольку \(r_1 y_1\), можем утверждать \(\;\overline{b_1}\; \;\overline{g_1}\;\)
Для синих:
\[ \;\overline{b_1}\; b_2 b_3 \;\overline{b_4}\; \]
Получаем \(b_2\).
Итого
\[ y_1 r_1 g_2 b_2 b_3 y_3 g_4 r_4 \]
wiki.livid.pp.ru
Таблицы истинности логических операций
Глоссарий, определения логики
Высказывание — это повествовательное предложение, про которое можно определенно сказать истинно оно или ложно (истина (логическая 1), ложь (логический 0)).
Логические операции — мыслительные действия, результатом которых является изменение содержания или объема понятий, а также образование новых понятий.
Логическое выражение — устное утверждение или запись, в которое, наряду с постоянными величинами, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных величин (объектов) логическое выражение может принимать одно из двух возможных значений: истина (логическая 1) или ложь (логический 0).
Сложное логическое выражение — логическое выражение, состоящее из одного или нескольких простых логических выражений (или сложных логических выражений), соединенных с помощью логических операций.
Таблица истинности — это таблица, в которой отражены все значения логической функции при всех возможных значениях, входящих в неё логически
Под «логической функцией» в данном случае понимается функция, у которой значения переменных (параметров функции) и значение самой функции выражают логическую истинность. Например, в двузначной логике они могут принимать значения «истина» либо «ложь» (true либоfalse, 1 либо 0).
1) Логическое умножение или конъюнкция:
Конъюнкция — это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложеное выражение ложно.
Обозначение: F = A & B.
Таблица истинности для конъюнкции
2) Логическое сложение или дизъюнкция:
Дизъюнкция — это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженныя ложны.
Обозначение: F = A + B.
Таблица истинности для дизъюнкции
3) Логическое отрицание или инверсия:
Инверсия — это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
Таблица истинности для инверсии
4) Логическое следование или импликация:
Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. Тоесть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.
Таблица истинности для импликации
5) Логическая равнозначность или эквивалентность:
Эквивалентность — это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
Таблица истинности для эквивалентности
Порядок выполнения логических операций в сложном логическом выражении
1. Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.
Для изменения указанного порядка выполнения логических операций используются скобки.
Основные законы и постулаты алгебры логики и их реализация на логических элементах
Алгебра логики – раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.
Для преобразования функции в АЛ используется ряд законов и тождеств, основные из которых приведены ниже.(первое для ИЛИ, второе для И)
Коммутативные (переместительные) законы
Ассоциативные (сочетательные) законы:
Дистрибутивные (распределительные) законы
Законы повторения:
Законы инверсии (двойственности):
Законы отрицания:
Закон двойного отрицания:
Закон поглощения:
Закон склеивания:
Правила операций с константами:
Дополнительные тождества:
infopedia.su
Таблицы истинности
Значение истинности сложных суждений определяется с помощью таблиц истинности, где буквы a, b, c – переменные, обозначающие простые суждения; буква «и» обозначает истину, а «л» — ложь.
а | b | а ˄ b | а ˅ b | а b | a → b | a ↔ b | ~а | ~b |
и | и | и | и | л | и | и | л | л |
и | л | л | и | и | л | л | л | и |
л | и | л | и | и | и | л | и | л |
л | л | л | л | л | и | и | и | и |
Также возможно обозначать истину нулём «0», а ложь единицей «1».
а | b | а ˄ b | а ˅ b | а b | a → b | a ↔ b | ~а | ~b |
0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
1.КОНЪЮНКЦИЯ а ˄ b или а & b
Конъюнкция будет истинна в том и только в том случае, если суждения а и bоба истинны.
2.ДизъюнкциЯа ˅ b
Сложное суждение истинно, если истинно хотя бы одно из составляющих его простых суждений, и ложно, если оба простых суждения ложны.
3.Строгаядизъюнкция
Сложное суждение истинно, если истинно лишь одно из составляющих его простых суждений, так как элементы сложной дизъюнкции исключают друг друга.
4.Импликация a → b
Сложное суждение, соединённое импликацией, ложно только в одном случае: если основание (первое суждение) истинно, а следствие (второе суждение) ложно.
5.ЭКВИВАЛЕНЦИЯ a ↔ b или a ≡ b
Сложное суждение, соединённое эквиваленцией, истинно только в тех случаях, когда составляющие его простыtсуждения, либо оба истинны, либо оба ложны.
6.ОТРИЦАНИЕ~а или¬а или~b ;¬b ;
Если аистинно, то его отрицание ложно. Еслиаложно, тоне-а(~а) – истинно.
Если bистинно, то его отрицание ложно. Еслиbложно, тоне—b(~b) – истинно.
Если отрицание стоит внутри суждения перед связкой «есть», то мы имеем дело с простым отрицательным суждением типа «Черепахи не летают». Если же отрицание присоединяется к суждению снаружи – «Неверно, что черепахи летают», то мы имеем дело с логической связкой, преобразующей простое суждение в сложное.
Если знак отрицания стоит непосредственно перед аилиb, то есть~а; ~b, то отрицание применяется только к одному суждению.
Если знак отрицания стоит перед скобкой ~(a → b), то отрицанию будет подвержена операция, указанная в скобках. В данном примере, ̶ это отрицание импликации. Сначала выполняется импликация, затем результат подвергается отрицанию.
Выполнима та формула, которая может принимать по крайней мере одно значение «истина».
Тождественно-истинная формула та, которая при любых комбинациях значений для входящих в неё переменных принимают значение «истина» (иначе она называется законом логики).
Тождественно-ложная формулата, которая принимает только значение «ложь» (иначе ‒ противоречие).
!!! Следует помнить, что логику интересует не содержание, а исключительно форма мысли!
Устанавливать истинность сложных суждений в логике, опираясь на здравый смысл или жизненный опыт, или обращение к действительности, ̶ неправильно!
Формально-логические связки не в состоянии учитывать многих смысловых оттенков естественного языка. Значения истинности некоторых сложных суждений достаточно близки к здравому смыслу, но другие могут показаться странными. Поэтому то, то с точки зрения содержания может выглядеть непривычно, с точки зрения формы будет являться правильным.
studfiles.net
