1 Неопределенный интеграл, таблица интегралов » СтудИзба
Лекция 1 Неопределенный интеграл, таблица интегралов.
Функция называется первообразной для функции , если .
Теоремы о первообразных.
Теорема. Если — первообразная для функции , то (- константа) — тоже первообразная для функции .
Доказательство. .
Теорема. Пусть — две первообразных для функции , тогда они различаются на некоторую константу (- константа).
Рассмотрим функцию , она непрерывна и дифференцируема на всей числовой оси, как и функции . Тогда для любых конечных значений по формуле конечных приращений Лагранжа .
Следовательно,
Неопределенным интегралом (интеграл от функции по ) называется совокупность всех первообразных функций для функции .
.
Функция , стоящая под знаком интеграла, называется подинтегральной функцией, а выражение — подинтегральным выражением..
Свойства неопределенного интеграла.
Свойства неопределенного интеграла можно условно разделить на две группы. В первую группу собраны свойства, вытекающие из того, что интегрирование – операция, обратная дифференцированию. Во вторую группу собраны свойства линейности. Эти свойства вытекают из того, что интегрирование, как и дифференцирование – линейная операция и определяют линейную операцию.
Первая группа свойств.
1) .
2)
3)
4) .
Докажем первое свойство.
Так как
Здесь — первообразная для .
Докажем второе свойство.
Обозначим Тогда , а по первому свойству. Поэтому функции являются первообразными для функции . Следовательно, по теоремам о первообразных, они различаются на константу, т.е. или
Третье свойство следует из первого:
Четвертое свойство следует из второго, если вспомнить, что с дифференциалом первого порядка можно обращаться как с алгебраическим выражением (свойство инвариантности формы записи первого дифференциала).
Поэтому надо доказать два первых свойства.
Вторая группа свойств.
1) свойство суперпозиции
2) свойство однородности .
Доказательства того и другого свойств проводятся аналогично. Дифференцируем (по свойствам первой группы) левую и правую часть равенства, приходим к тождеству. Затем из теорем о первообразных заключаем, что левая и правая часть равенства, как первообразные одной и той же функции, различаются на константу. Эта константа может быть формально включена в неопределенный интеграл в левой или правой части равенства.
Для того, чтобы вычислить интеграл от функции, проще всего «угадать» первообразную для этой функции по таблице для производных, переписав эту таблицу в обратном порядке. Запишем интегралы для основных элементарных функций.
1) . Эти формулы лучше запомнить, они очень часто встречаются.
2)
3)
4)
Справедливость этих формул легко проверить, дифференцируя правую часть соотношения и получая подинтегральную функцию.
Основные формулы
Интегралы от рациональных функций (23 шт)
Интегралы от трансцендентных функций (15 шт)
Интегралы от иррациональных функций (27 шт)
Интегралы от тригонометрических функций (31 шт)
studizba.com
Тема 14. Первообразная и неопределенный интеграл. Свойства интеграла. Таблица неопределенных интегралов.
Понятие первообразной. Неопределенный интеграл как совокупность первообразных. Геометрическое понимание неопределенного интеграла. Свойства неопределенного интеграла. Таблица интегралов.
Тема 15. Основные методы интегрирования.
Основные методы интегрирования. Табличное. Метод подстановки. Известные подстановки для некоторых типов интегралов. Формула интегрирования по частям. Некоторые интегралы, не берущиеся в элементарных функциях.
Тема 16. Понятие определенного интеграла. Свойства и правила вычисления определенного интеграла.
Интегральная сумма. Определённый интеграл как предел интегральной суммы. Геометрический смысл определённого интеграла. Площадь криволинейной трапеции. Связь определённого и неопределённого интегралов. Теорема существования определенного интеграла. Формула Ньютона-Лейбница. Основные свойства определённого интеграла. Теорема о среднем. Определенный интеграл как функция переменного верхнего предела. Вычисление определенного интеграла. Интегрирование подстановкой. Формула интегрирования по частям. Интегрирование четных и нечетных функций в пределах симметричных относительно начала координат.
Тема 17. Приложения определенного интеграла. Несобственные интегралы.
Приложения определенного интеграла. Вычисление площадей плоских фигур. Вычисление длины дуги плоской кривой. Вычисление объемов тел вращения. Понятие несобственных интегралов. Их классификация. Определение сходимости. Методы решения несобственных интегралов.
Планы семинарских и практических занятий
Тема 1. Операции над матрицами. Определители третьего порядка. (2 часа)
Рассматриваемые вопросы:
Определение матрицы. Виды матриц.
Умножение матрицы на число. Алгебраическая сумма матриц.
Транспонирование матриц.
Умножение матриц. Некоммутативность произведения.
Определители второго и третьего порядков.
Задания для самостоятельного выполнения:
1. Транспонировать матрицы
2. Умножить матрицу на число
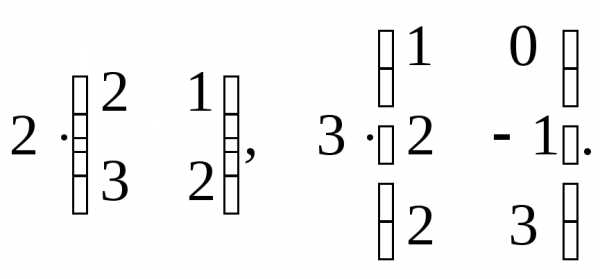
3. Сложение и вычитание матриц
4. Умножение матриц
5. Для заданной матрицы A вычислить E + A + A2 + A3:
а)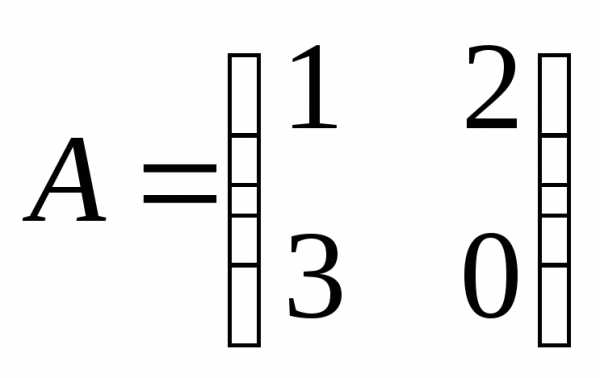 
б)
.
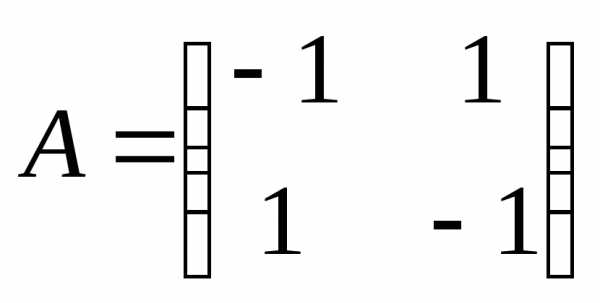6. Вычислить определители по определению:
7. Вычислить определители по правилу Саррюса:
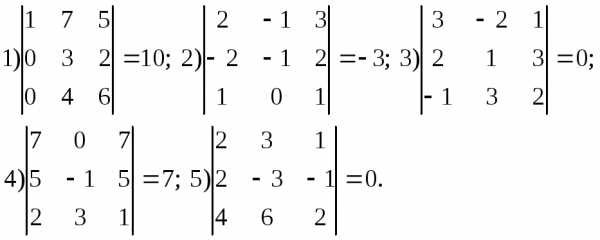
Тема 2. Определители четвертого и выше порядков. Элементарные преобразования определителей. Обратная матрица. (4 часа)
Рассматриваемые вопросы:
Определители четвертого порядка.
Применение основных свойств вычисления определителей для квадратных матриц произвольной размерности.
Алгебраические дополнения. Формула Лапласа.
Элементарные преобразования определителей.
Обратная матрица.
Задания для самостоятельного выполнения:
1. Вычислить определители при помощи разложения на по любой строке или столбцу:
2. Вычислить определитель, упростив его элементарными преобразованиями:
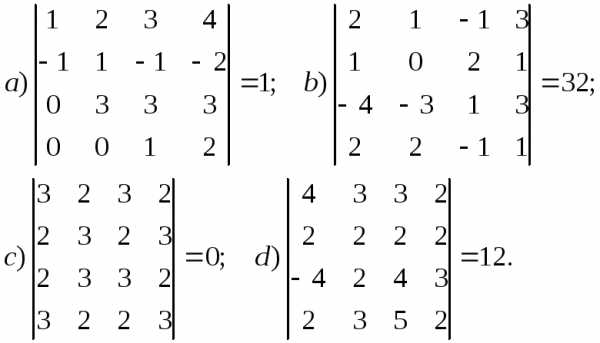
3. Найти обратные матрицы
4. Используя обратную матрицу, найти неизвестную матрицу Xиз матричного уравнения.
5. Найти обратные матрицы и проверить результат умножением на исходную.
studfiles.net
Глава 14. Неопределенный интеграл, структура интегрирования. Таблица неопределённых интегралов и правила интегрирования.
16
§14.1. Неопределенный интеграл
14.1.1. Основные определения
Определение. Пусть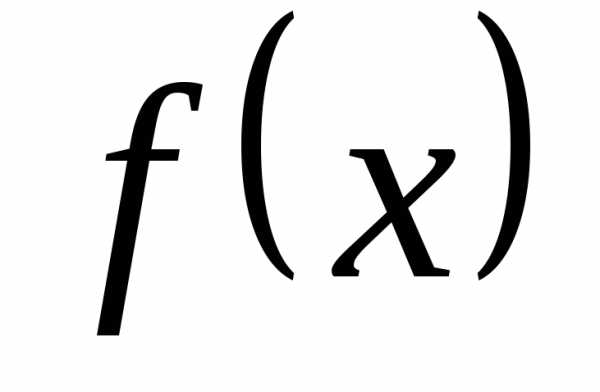 
определена в (конечном или бесконечном)
промежутке .Функция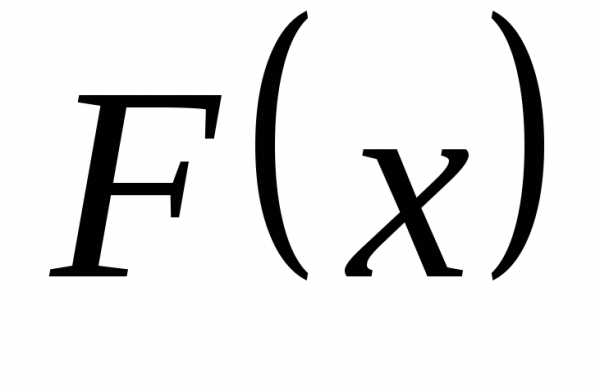 
называетсяпервообразной
функцией для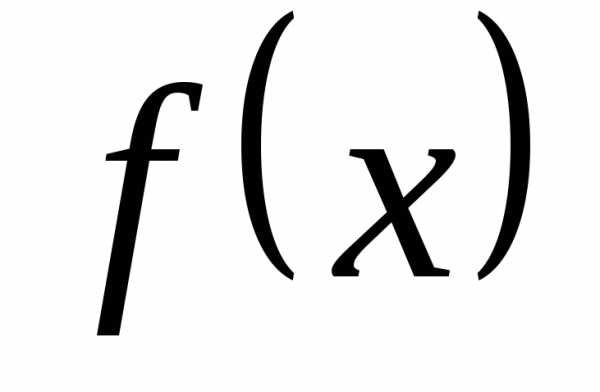 
, если для любого 
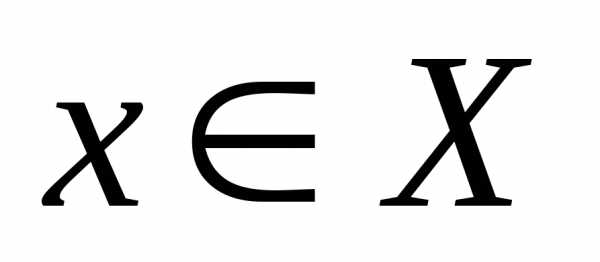выполняется равенство:.
Теорема
14.1.(Основная лемма интегрального
исчисления). Если в
некотором промежутке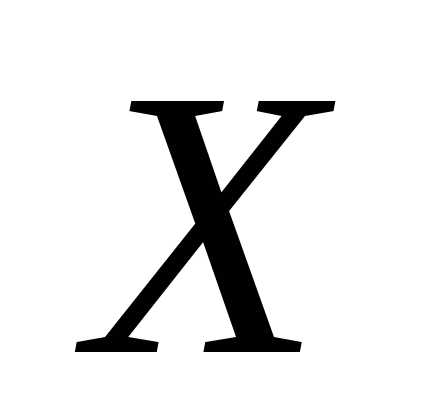 
(конечном или бесконечном) функция
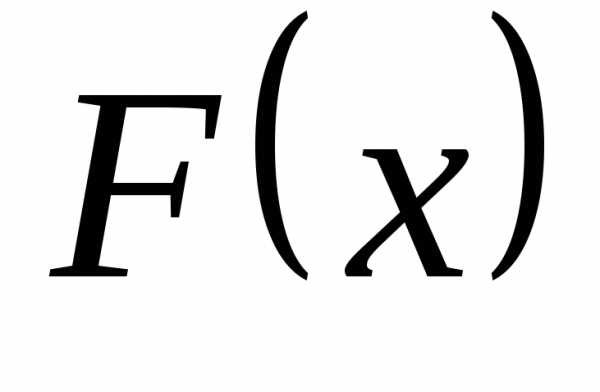является первообразной для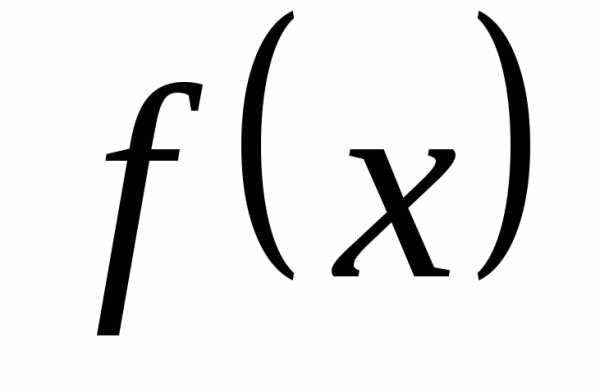
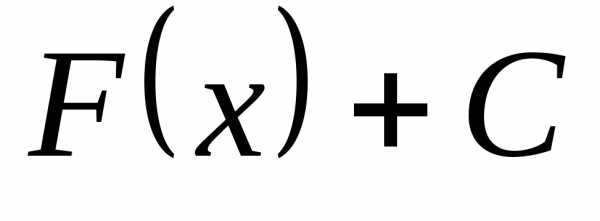— тоже является первообразной для
.
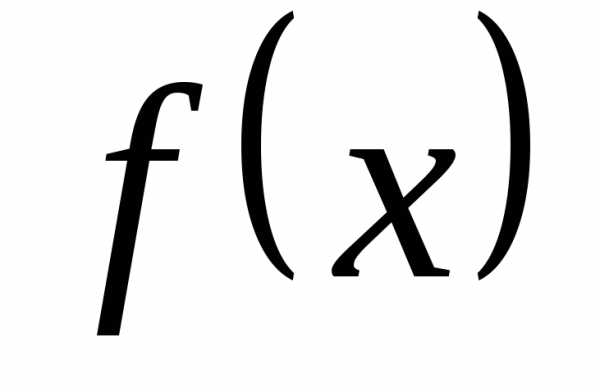Обратно, для любой другой первообразной
функции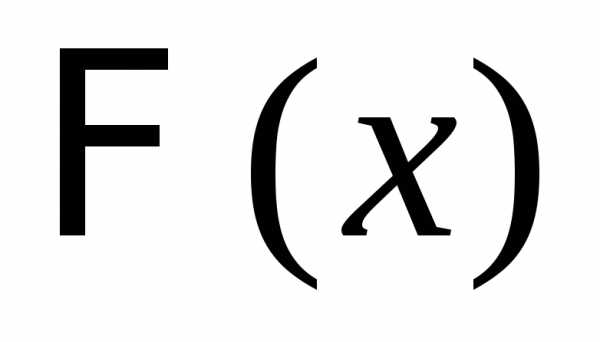 
найдётся постоянная 
такая, что. ►Очевидно, , и первая
часть теоремы доказана. Пусть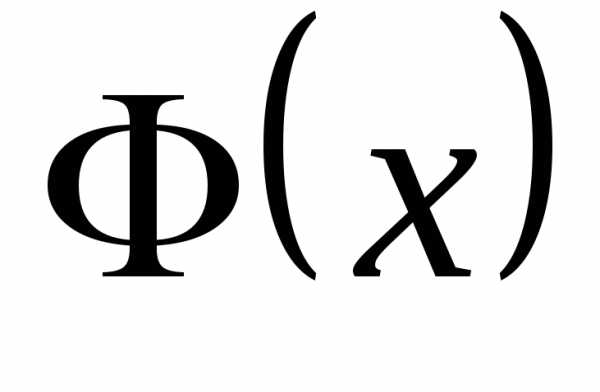 
— какая-либо первообразная для
.
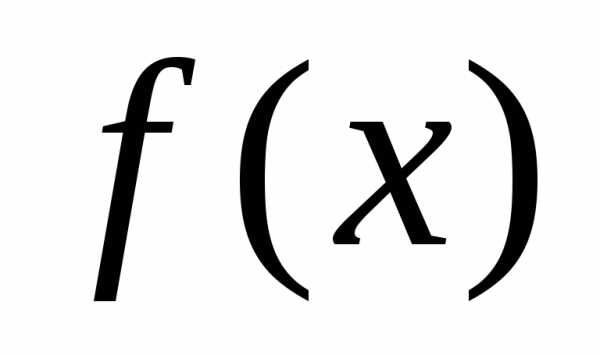Рассмотрим разность.
Производная этой функции. По следствию
из теоремы 7.3. Лагранжа (критерию
постоянства функции на промежутке)
получим, что
,
что и требовалось доказать. ◄
Определение. Множество первообразных функций для
функции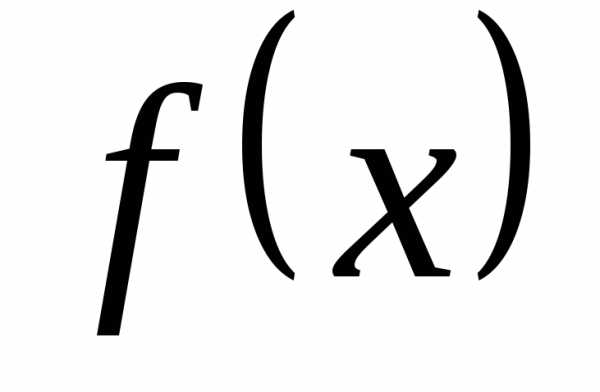 
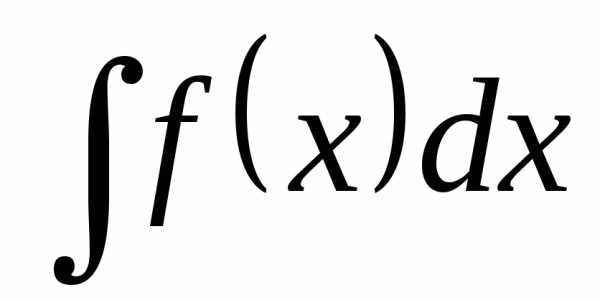. По доказанной
лемме, оно имеет следующую структуру:
,
где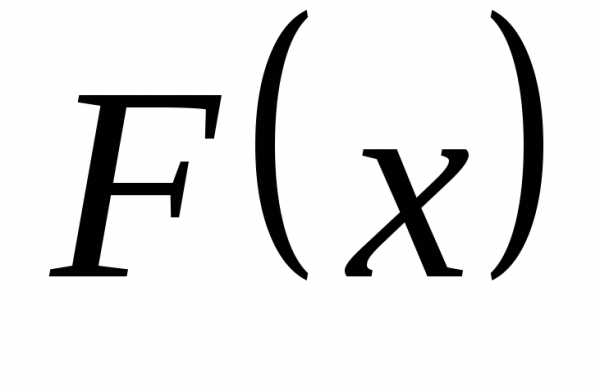
—
произвольная первообразная функция, а
—
произвольная постоянная. Обычно
используется обозначение,
в котором правая часть равенства
обозначает не одну из функций, а всё
семейство функций, образующих интеграл.
14.1.2.Таблица основных интегралов
Каждая формула сразу приводит к соответствующей формуле
.
Поэтому, используя формулы для производных элементарных функций, получим следующую таблицу:
1. 
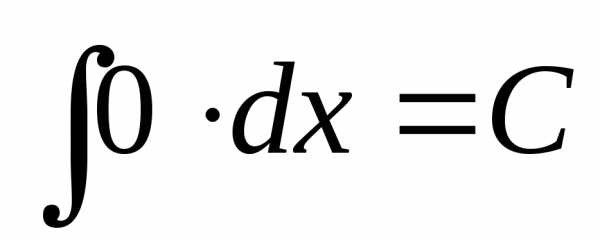
2.
3. 
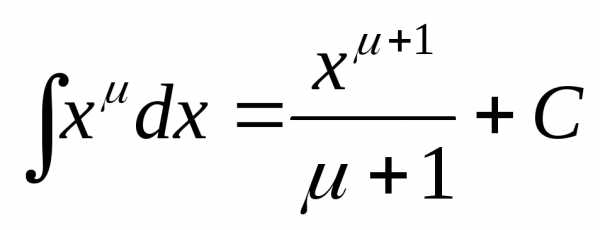
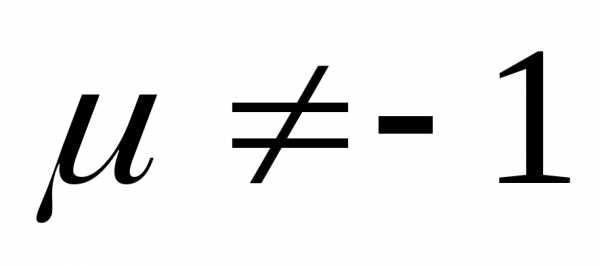. 4.
Эти
формулы часто соединяют в одну: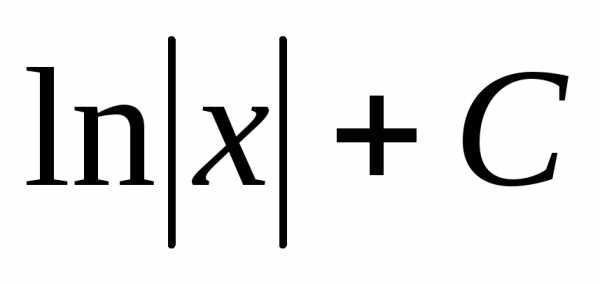 
.
При этом следует иметь в виду, что
множество, на котором определена функция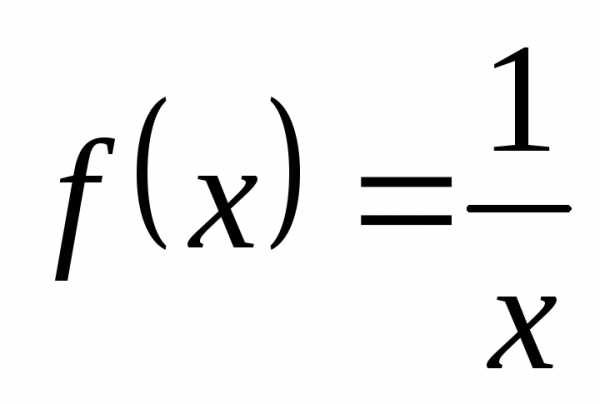
,
состоит из двух промежутков, задаваемых
неравенствами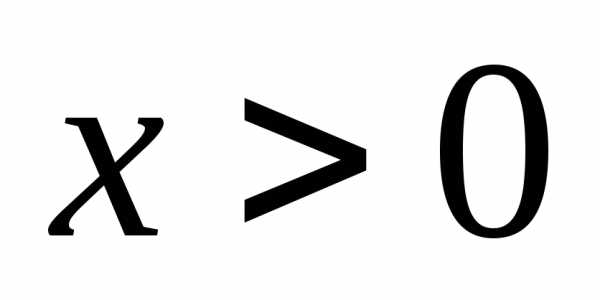
и,
соответственно. На каждом из этих
промежутков постоянную можно выбирать
независимо, что и отражено в формуле 4.
Так что формулу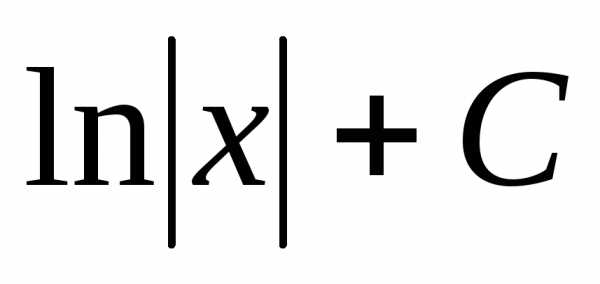
не следует понимать так, что к функции
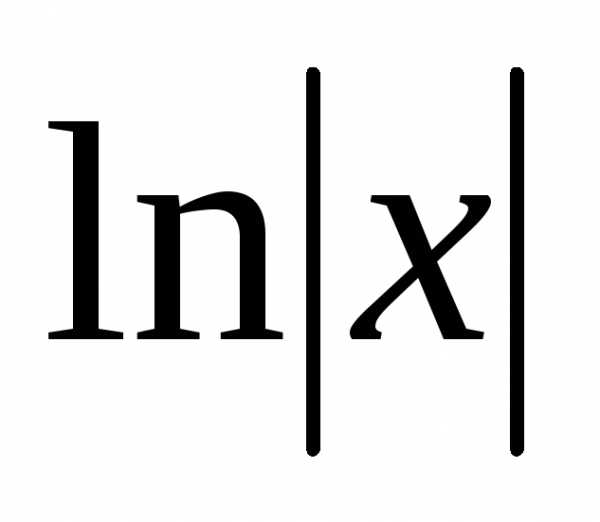прибавляется одна и та же постоянная
как при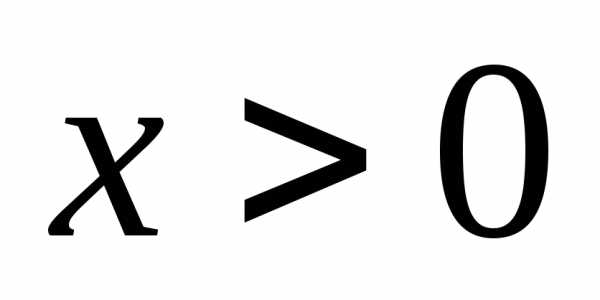 
.
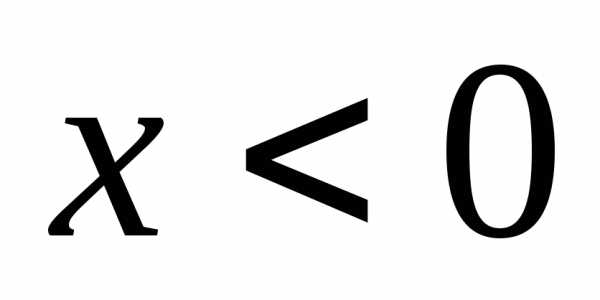Еще раз повторим – точный смысл дан
равенством 4. Это же замечание
можно сделать для формулы (3) при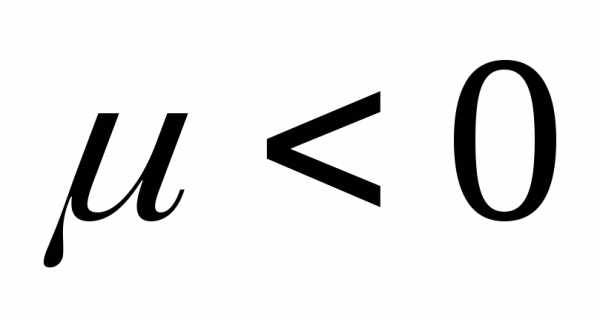 
и таком, что
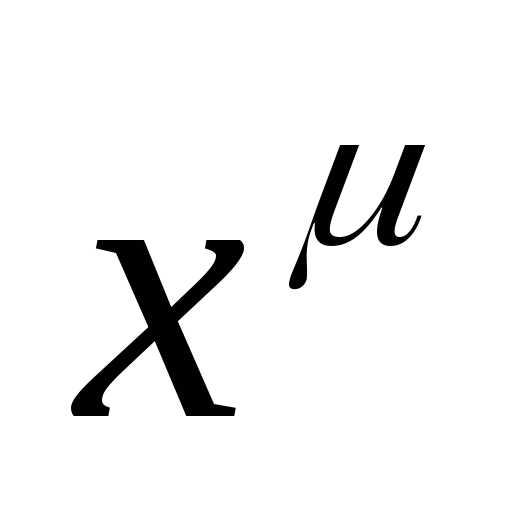определена как при
,
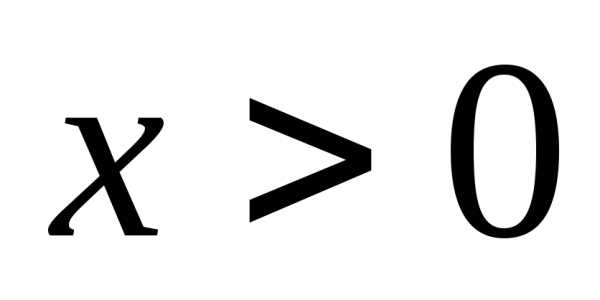так и при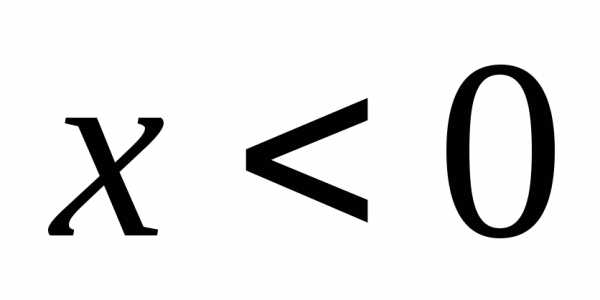
.
5. ,
6. ,
7. 
,
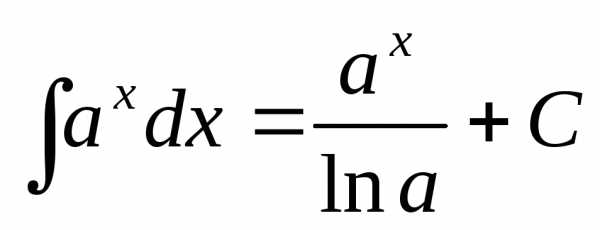в частности,
8. ,
9. ,
10. ,
точнее говоря, так
как функция определена на бесконечном
множестве промежутков
,
,
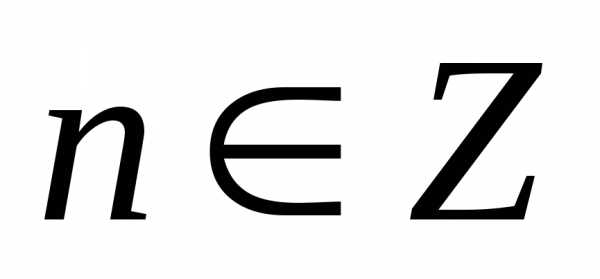для каждого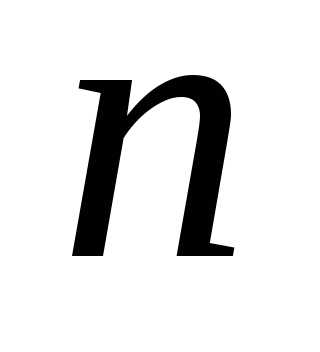
следует выбирать свою постоянную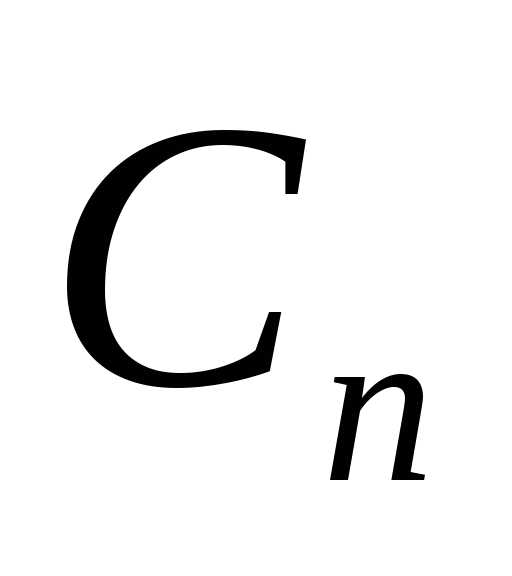
11. 
,
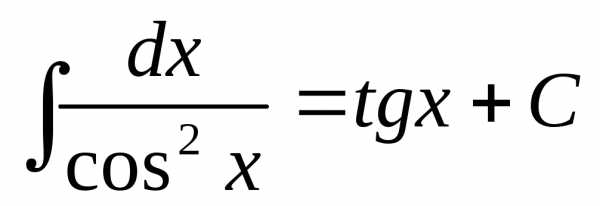разумеется, замечание, аналогичное сделанному в пункте 10, справедливо и здесь.
14.1.3.Правила интегрирования
Доказательства всех приведённых ниже утверждений получаются в результате вычисления производных от обеих частей доказываемых равенств.
1. Если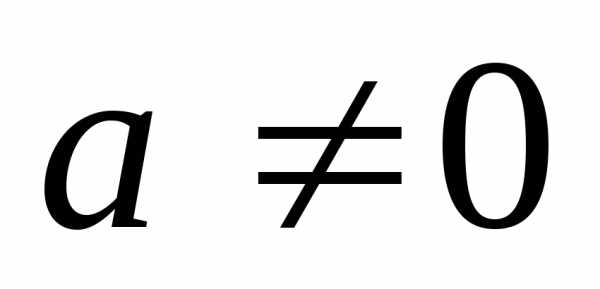
,
то
.
Замечание. Условие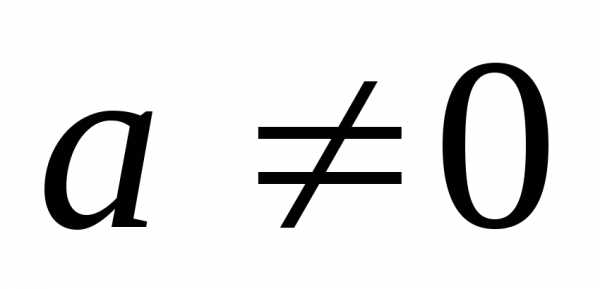 
существенно
для справедливости этого равенства.
При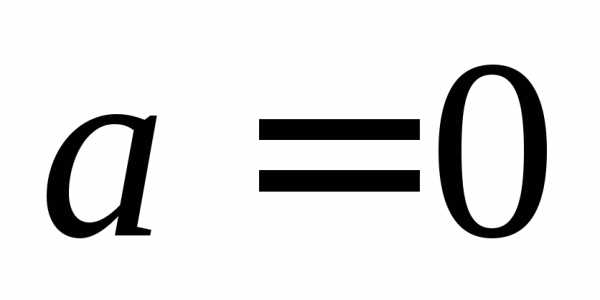
левая часть этого равенства представляет
собой множество постоянных функций, а
множество в правой части состоит только
из тождественно равной нулю функции,
притом при условии, что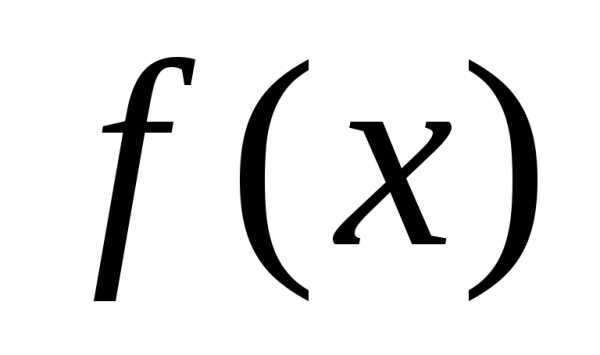
2. .
3. Если , где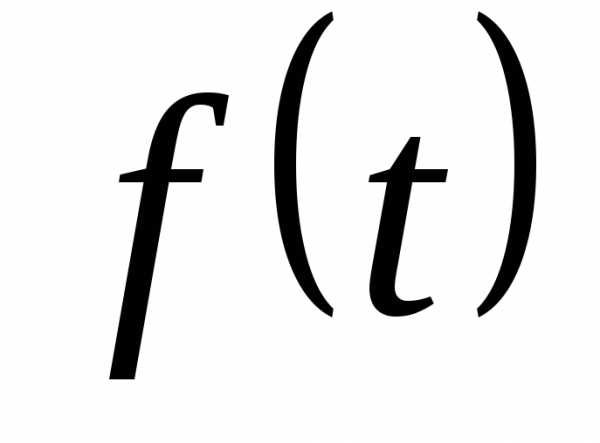 
— непрерывная функция, то для любой
функции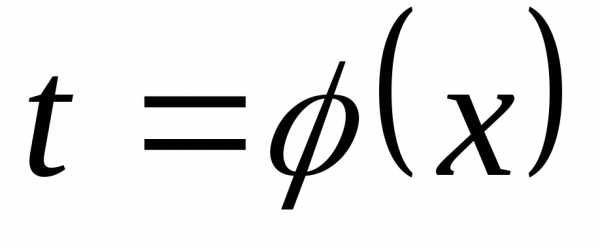
,
такой, что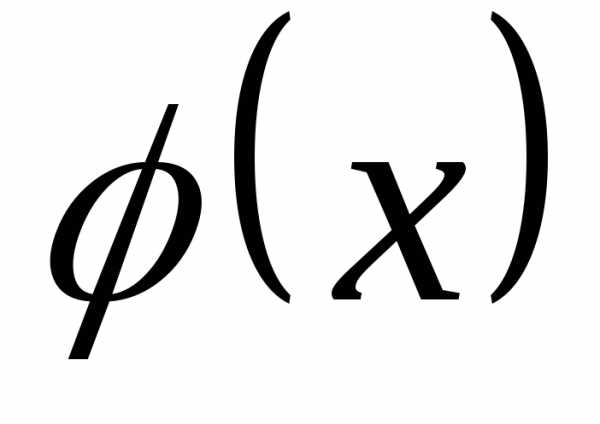
и
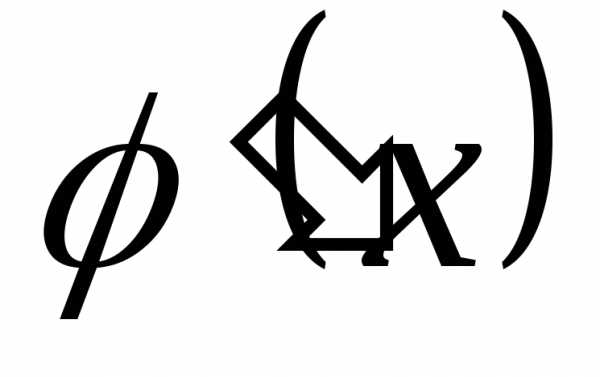— непрерывные функции, и такой, что
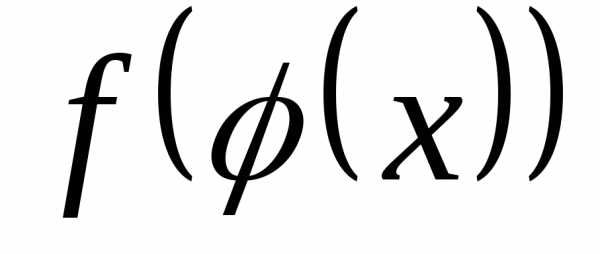— определена, имеет место равенство
.
Это правило замены переменной сразу следует из теоремы о производной сложной функции.
4. Пусть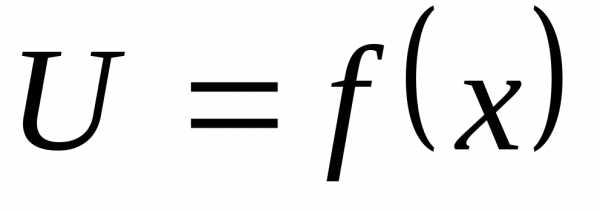 
и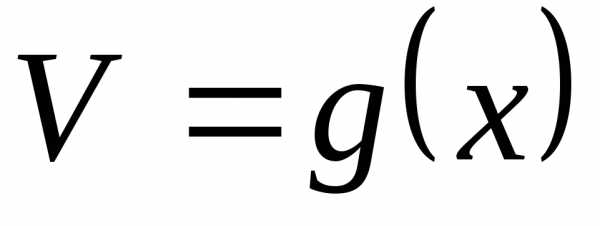
— непрерывные функции и пусть,
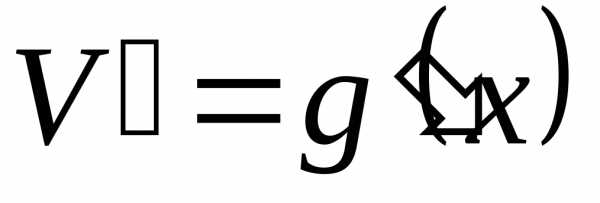— тоже непрерывные функции. Тогда
.
Формула, называемая формулой интегрирования по частям, вытекает из формулы для производной произведения.
studfiles.net
1. Первообразная. Неопределённый интеграл
Основные формулы интегрирования получаются путём обращения формул для производных, поэтому перед началом изучения рассматриваемой темы следует повторить формулы дифференцирования1основных функций (т.е. вспомнить таблицу производных).
Знакомясь с понятием первообразной, определением неопределённого интеграла и сравнивая операции дифференцирования и интегрирования, студенты должны обратить внимание на то, что операция интегрирования многозначна, т.к. дает бесконечное множество первообразных на рассматриваемом отрезке. Однако фактически решается задача нахождения только одной первообразной, т.к. все первообразные данной функции отличаются друг от друга на постоянную величину
, (1.1)
где C – произвольная величина2.
Вопросы для самопроверки.
Дайте определение первообразной функции.
Что называется неопределённым интегралом?
Что такое подынтегральная функция?
Что такое подынтегральное выражение?
Укажите геометрический смысл семейства первообразных функций.
6. В семействе найдите кривую, проходящую через точку
.
2. Свойства неопределённого интеграла.
ТАБЛИЦА ПРОСТЕЙШИХ ИНТЕГРАЛОВ
Здесь студенты должны изучить следующие свойства неопределённого интеграла.
Свойство 1. Производная от неопределённого интеграла равна подынтегральной3функции (по определению)
. (2.1)
Свойство 2. Дифференциал от интеграла равен подынтегральному выражению
, (2.2)
т.е. если знак дифференциала стоит перед знаком интеграла, то они взаимно уничтожаются.
Свойство 3. Если знак интеграла стоит перед знаком дифференциала, то они взаимно уничтожаются, а к функции добавляется произвольная постоянная величина
. (2.3)
Свойство 4. Разность двух первообразных одной и той же функции есть величина постоянная.
Свойство 5. Постоянный множитель можно выносить из-под знака интеграла
, (2.4)
где А – постоянное число.
Кстати, это свойство легко доказывается дифференцированием обеих частей равенства (2.4) с учётом свойства 2.
Свойство 6. Интеграл от суммы (разности) функции равен сумме (разности) интегралов от этих функций (если они порознь существуют)
. (2.5)
Это свойство также легко доказывается дифференцированием.
Естественное обобщение свойства 6
. (2.6)
Рассматривая интегрирование как действие, обратное дифферен-цированию, непосредственно из таблицы простейших производных можно получить таблицу следующую простейших интегралов.
Таблица простейших неопределённых интегралов
1. , где, (2.7)
2. , где, (2.8)
3. , (2.9)
4. , где,, (2.10)
5. , (2.11)
6. , (2.12)
7. , (2.13)
8. , (2.14)
9. , (2.15)
10. . (2.16)
Формулы (2.7) – (2.16) простейших неопределённых интегралов следует выучить наизусть. Знание их необходимо, но далеко не достаточно для того, чтобы научиться интегрировать. Устойчивые навыки в интегрировании достигаются только решением достаточно большого числа задач (обычно порядка 150 – 200 примеров различных типов).
Ниже приводятся примеры упрощения интегралов путём преобразования их к сумме известных интегралов (2.7) – (2.16) из вышеприведённой таблицы.
Пример 1.
.
Пример 2.
.
studfiles.net
20.Таблица основных неопределенных интегралов | spiruk
20.Таблица основных неопределенных интегралов
Пользуясь тем, что интегрирование есть действие, обратное дифференцированию. можно, получить таблицу основных интегралов путем обращения соответствующих формул дифференциального исчисления (таблица дифференциалов) и использования свойств неопределенного интеграла. Например, так как
d(sin u) = cos u*du, то Вывод ряда формул таблицы будет дан при рассмотрении основных методов интегрирования.
Интегралы в приводимой ниже таблице называются табличными. Их следует знать наизусть. В интегральном исчислении нет простых и универсальных правил отыскания первообразных от элементарных функций, как в дифференциальном исчислении. Методы нахождения первообразных (т. е. интегрирования функции) сводятся к указанию приемов, приводящих данный (искомый) интеграл к табличному. Следовательно, необходимо знать табличные интегралы и уметь их узнавать.
Отметим, что в таблице основных интегралов переменная интегрирования и может обозначать как независимую переменную, так и функцию от независимой переменной (согласно свойству инвариантности формулы интегрирования).
В справедливости приведенных ниже формул можно убедиться, взяв дифференциал правой части, который будет равен подынтегральному выражению в левой части формулы.
Докажем, например, справедливость формулы 2. Функция 1/u определена и непрерывна для всех значений u, отличных от нуля.
Если u > 0. то ln |u| = ln u, тогда d ln |u| = d ln u = du/u. Поэтому
Таблица основных интегралов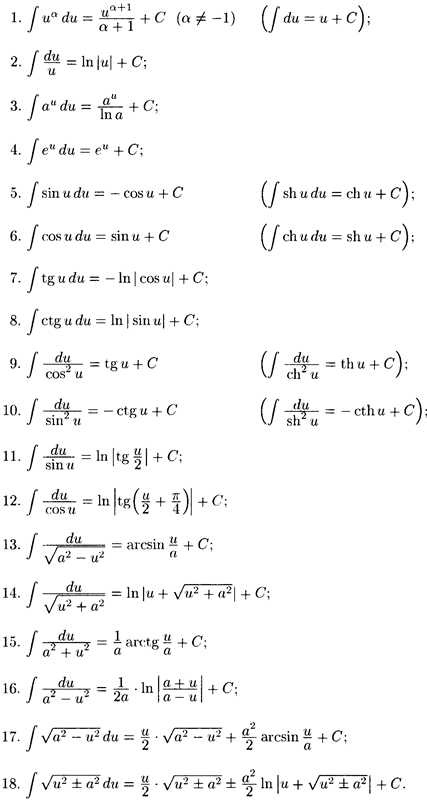
Понравилось это:
Нравится Загрузка…
Похожее
spiruk.wordpress.com