События несовместны в совокупности если – —

Независимость попарная и независимость в совокупности Определение попарной независимости

Пусть даны события А₁, А₂, … , А_n,они называются попарно независимыми, если для любой пары собитийA_i A_j (I,j=1..n,i≠j)выполняется равенство:

(3)

т.е. любая пара из nнезвисима.

Если это неравенство нарушется хотя бы для одной пары, то они попарно зависимы.

Определение независимости в совокупности.

Пусть даны события А₁, А₂, … , А_n,они называются независимыми в совокупности, если для любого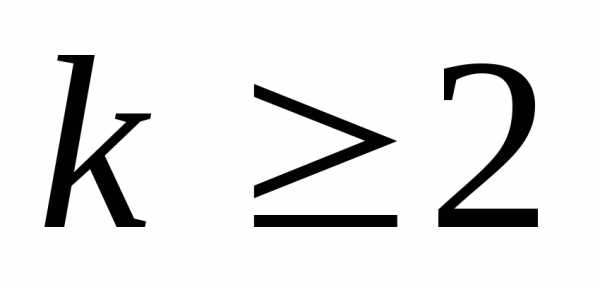иАi1, Ai2,…,Aik приi1≠i2≠…≠ik

выполняется равенство:

(4)

Если это неравенство нарушается хотя бы для одного подмножества событий, то они зависимы в совокупности.

Рассмотрим пример:

Пусть монету подбрасывают 2 раза. Рассмотрим события:

А1 – первый раз выпал герб

А2 – второй раз выпал герб

А3 – число гербов равно числу цифр

Проверим, будут ли они попарно независимы

,,

Выпишем вероятности:

Проверим 3):

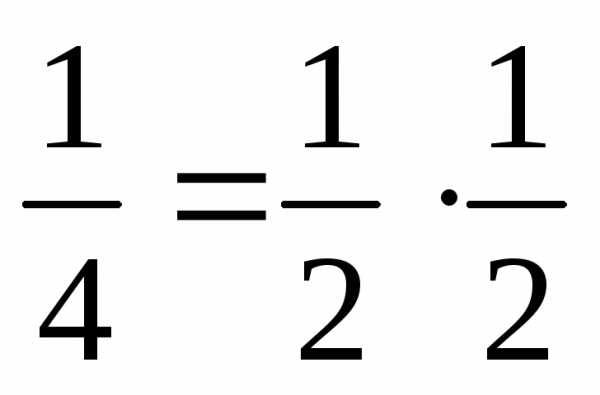— выполняется

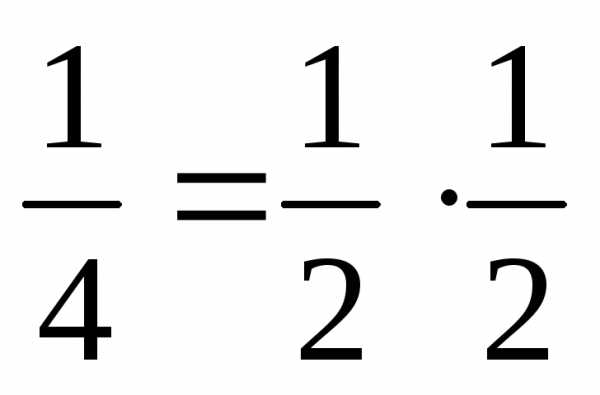— выполняется

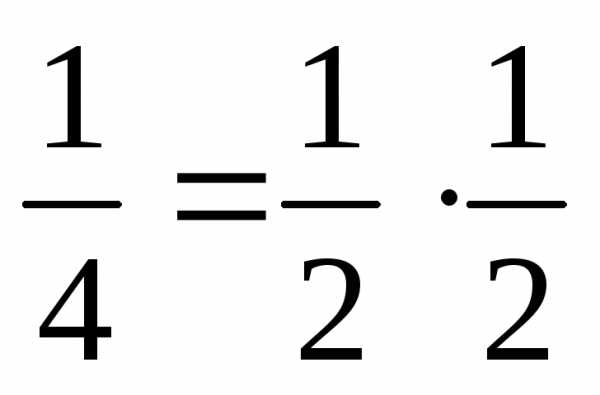— выполняется

Значит события А₁,А₂,А₃попарно независимы.

Проверим, будут ли они независимы в совокупности: надо проверить 4) для всех пар и для всех троек событий.

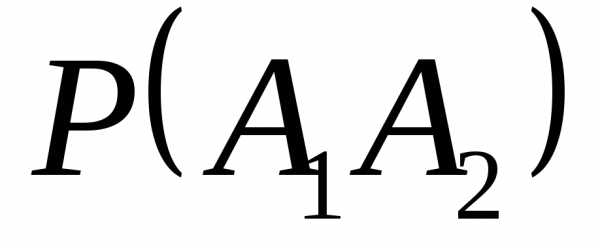
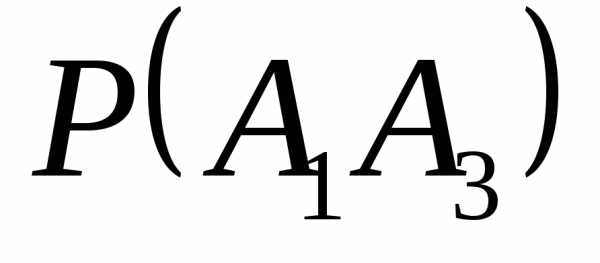
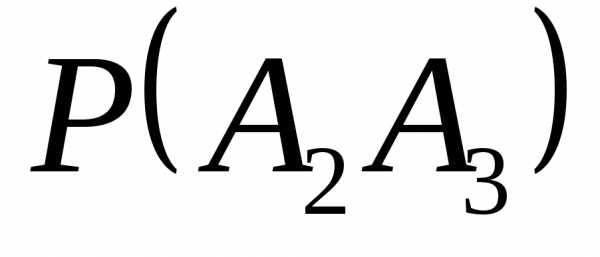уже проверялось и они выполнились

Осталось проверить для k=3, т.е. дляА₁А₂А₃

— совокупности зависимы.

Таким образом мы видим, что события А₁,А₂,А₃попарно независимы, но зависимы в совокупности, значит эти понятия не эквивалентны.

§6 Формула полной вероятности и формула Байеса. Формула полной вероятности

Пусть дано собятие А и собятие Н₁,Н₂,…,Н_n,причём выполняется следующее свойство:

(*) 1)

(**) 2)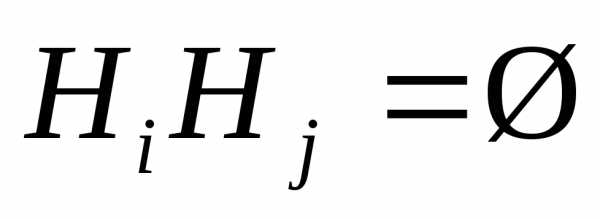

приi≠ j, i,j=1,2,…,n(Н₁,Н₂,…,Н_n, — образуют полную группу попарно несовместных событий)

Справедливо следующее утверждение:

(1)

Формула полной вероятности

Доказательство:

Теорема доказана.

Замечание: Часто события Н₁,Н₂,…,Н_n,называют гипотезами.

Замечание: Формула полной вероятности справедлива для счётного числа слагаемых.

Замечание: Формула полной вероятности справедлива при выполнении наиболее слабых условий.

1’) Н₁,Н₂,…,Н_n,— вместо 1)

Доказать самостоятельно

Пример: На заводе три цеха выпускающие одинаковые телевизоры

1 и 2 – одинаково

3 – в 2 раза больше чем 1ый

В 1-м цехе 1% брака

Во 2-м цехе – 2% брака

В 3-м цехе – 0% брака

Затем телевизоры проверяются.

Найти вероятность того, что случайно выбранный телевизор окажется небракован.

Решение: введём три дополнительные гипотезы:

Н₁– 1-й цех

Н₂– 2-й цех

Н₃– 3-й цех

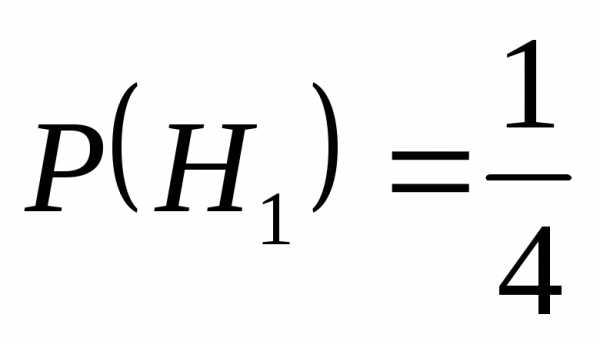
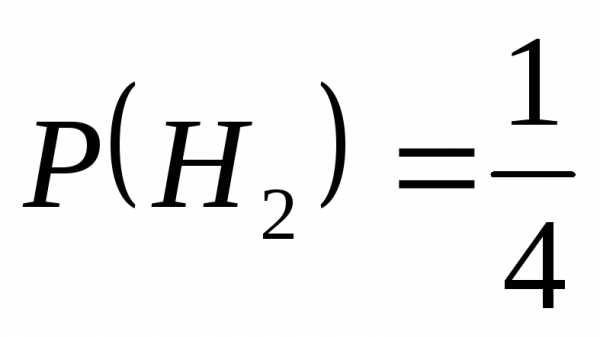
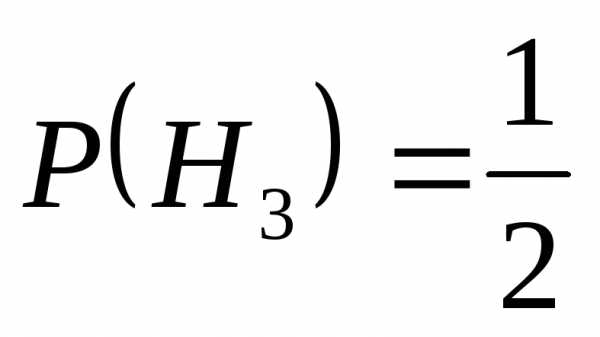
А – вероятность того, что случайно взятый телевизор небракован.

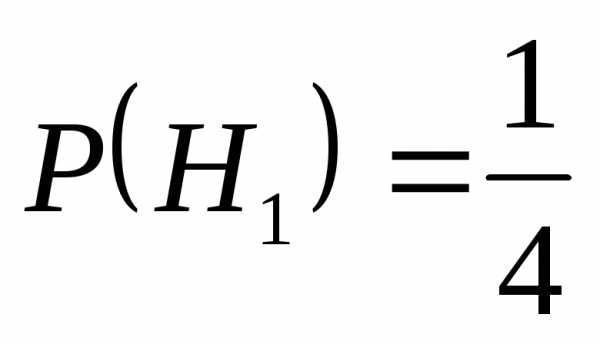
Пример: один студент выучил 20 вопросов из 30. на экзамене дают 1 вопрос (каждый билет содержит 1 вопрос). Каким лучше ему идти сдавать экзамен, т.е. когда больше вероятность вытянуть верный билет.

Решение:

А – вытянул выученный билет если идёт 1-м

Б — -||- 2-м

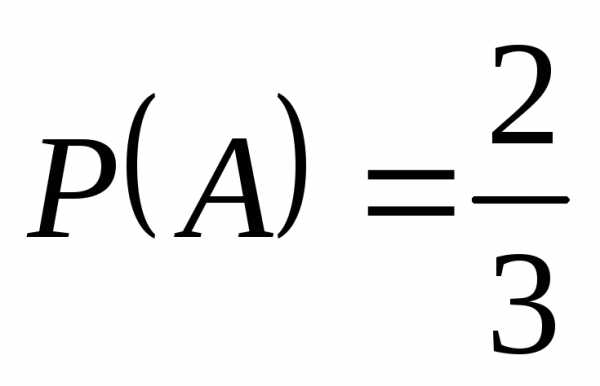
Найдём вероятность события Б.

Введём две гипотезы: Н1 – 1-й студент взял выученный «нашим» студентом билет

Н2 — 1-й студент взял невыученный «нашим» билет

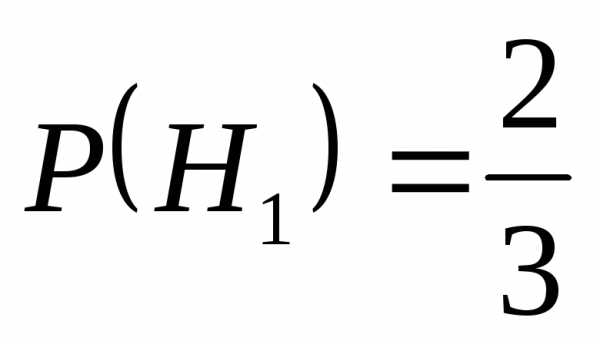
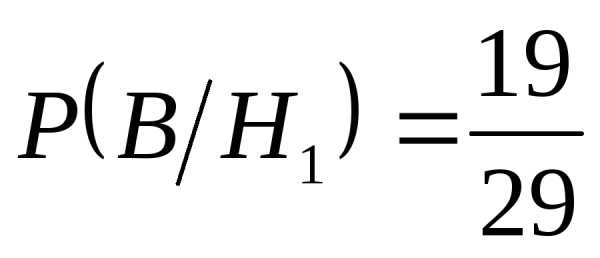
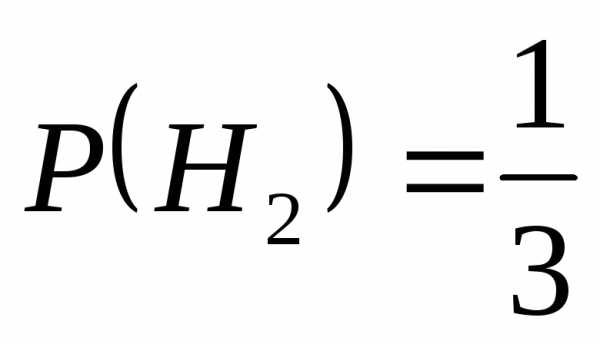
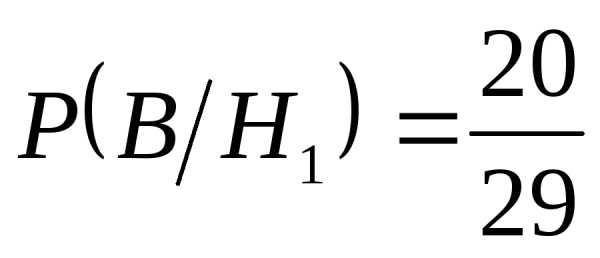
Замечание:

Ответ: вероятность вытащить выученный билет первым или вторым одинакова.

Формула Байеса

Пусть выполняются все условия Пункта 1, тогда справедливо равенство:

(2)

Hj– одно из событий из множества гипотезН

₁,Н₂,…,Н_n.

Доказательство:

Теорема доказана

Формула Байеса играет важную роль во многих технических приложениях и до сих пор её применение вызывает споры среди исследователей.

Задача 1:В учреждении два бухгалтера: главный и старший. Каждый из них составляет половину ведомости на зарплату, причём, главбух ошибается 1 раз на 1000, а старший 1 раз на 100 ведомостей. При выдаче зарплаты оказалось, что ведомость составлена с ошибкой, найти вероятность того, что её заполнил старший бухгалтер.

Решение:

А– ведомость (случайная) содержит ошибку

H₁– ведомость заполнил главный бухгалтер

H₂– ведомость заполнил старший бухгалтер

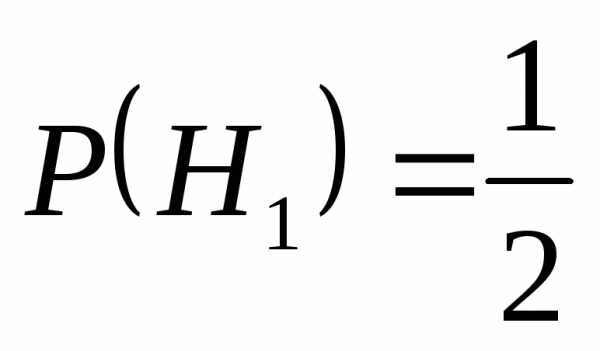
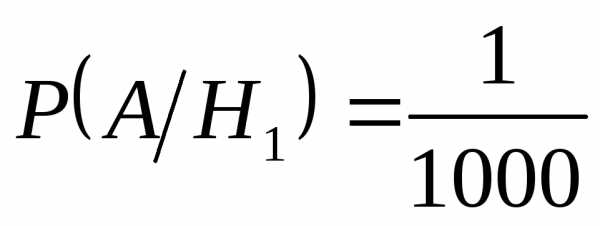
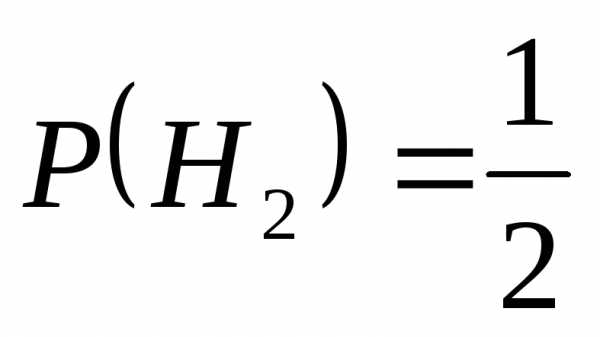
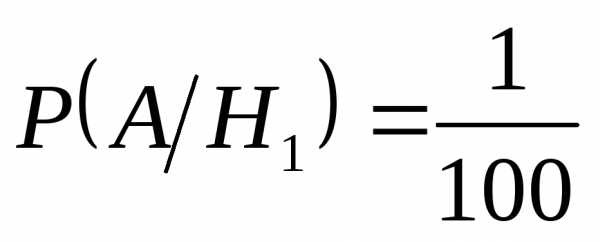
Подставляем в (2):

Найдём также вероятность, что ведомость составил главный бухгалтер

Задача 2:

В письменном столе 6 ящиков. Известно, что с вероятностью 0,9 ключ от сейфа находится в одном из ящиков. Некто в поисках ключа просмотрел 5 ящиков и ключ не нашёл. Найти вероятность того, что он найдёт его в 6-м ящике.

Решение:

А – ключ не найден в первых 5-ти ящиках

Введём следующие события:

Н₁– ключ в 1-м ящике

Н₂– ключ в 2-м ящике

Н₃– ключ в 3-м ящике

Н₄– ключ в 4-м ящике

Н₅– ключ в 5-м ящике

Н₆– ключ в 6-м ящике

Н₇– ключ в другом столе

Дома: найти вероятность «вытащить» выученный билет при условии что студент идёт 3-им и 4-м.

studfiles.net

Теория вероятности. Готовимся к егэ по математике

Продолжение статьи «Теория вероятности. Классическое определение».

В заданиях ЕГЭ по математике встречаются и более сложные задачи на вероятность (нежели мы рассматривали в части 1), где приходится применять правило сложения, умножения вероятностей, различать совместные и несовместные события.

Итак, теория.

Совместные и несовместные события

События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.

Например, бросая игральную кость, можно выделить такие события, как выпадение четного числа очков и выпадение нечетного числа очков. Эти события несовместны.

События называются совместными, если наступление одного из них не исключает наступления другого.

Например, бросая  игральную кость, можно выделить такие события, как выпадение нечетного числа очков и выпадение числа очков, кратных трем.   Когда выпадает три, реализуются оба события.

Сумма событий

Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.

При этом сумма двух несовместных событий  есть сумма  вероятностей этих событий:

Например, вероятность выпадения 5 или 6 очков на игральном кубике при одном броске, будет , потому что оба события (выпадение 5, выпадение 6) неовместны и вероятность реализации одного или второго события вычисляется следующим образом:

Вероятность же  суммы двух совместных событий равна сумме вероятностей этих событий без учета их совместного появления:

Например, в торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня  в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдем вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов (то есть или в одном, или в другом, или в обоих сразу).

Вероятность первого события «кофе закончится в первом автомате» также как и вероятность второго события «кофе закончится во втором автомате»  по условию равна 0,3. События являются совместными. 

Вероятность совместной реализации первых двух событий по условию равна 0,12.

Значит, вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов есть 

Зависимые и независимые события

Два случайных события А и В называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события А и В называют зависимыми.

Например,  при одновременном броске двух кубиков выпадение на одном из них, скажем 1, и на втором 5,  – независимые события.

Произведение вероятностей

Произведением (или пересечением) нескольких событий называется событие, состоящее в совместном появлении всех этих событий.

Если  происходят два независимых события А и В с  вероятностями  соответственно Р(А) и Р(В), то вероятность реализации событий А и В одновременно равна произведению вероятностей:

Например, нас интересует выпадение на игральном кубике два раза подряд шестерки. Оба события независимы и вероятность реализации каждого из них по отдельности – . Вероятность того, что произойдут оба эти события будет вычисляться по указанной выше формуле: .

 

Подборку задач на отработку темы смотрите здесь.

egemaximum.ru

25. Условная вероятность

Определение.Пусть при проведениииспытаний число наступлений события(то есть событиявместе с событием) равно, причемнаступилораз.Условной относительной частотой события при условии наступления событияназывается отношение.

Обозначение условной относительной частоты: . Таким образом,.

Теорема.Для условной относительной частоты справедлива формула:

. (10)

Определение.Пусть. Условной вероятностью событияпри условии наступления событияназывается отношение:

. (11)

26. Теорема умножения

Теорема (умножения).Если (так что существует условная вероятность ), то для вероятности произведения событий справедлива формула:

. (12)

Доказательство.Достаточно в формуле (11) обе части равенства умножить на. ▄

27. Независимость событий

I. Независимость двух событий.

Определение.Событияиназываютсянезависимыми, если вероятность произведения этих событий равна произведению их вероятностей:

. (14)

Таким образом, имеются две формы теоремы умножения:

1. Для произвольных событий:

.

2. Для независимыхсобытий:

.

Теорема (критерий независимости двух событий).Пусть . Для того, чтобы событияибыли независимы, необходимо и достаточно, чтобы условная вероятность событиясовпадала с его безусловной вероятностью:.

28.Теорема (независимость для противоположных событий).Если события инезависимы, то независимы также пары событий

и ,и,и.

Теорема (о независимости от и).Любое событиене зависит от достоверного события и от невозможного события.

Доказательство.1., так чтоинезависимы.

2. , так чтои независимы. ▄

II. Независимость событий в совокупности.

Для трех и более событий их взаимная независимость («независимость в совокупности») означает не только то, что любые два из них не влияют друг на друга (попарная независимость):

, (), (15)

но и что для любого подмножества из трех, четырех и т.д. событий этой совокупности вероятность произведения событий равна произведению их вероятностей:

, (), (16)

, (), (17)

и т. д. вплоть до условия

. (18)

Недостаточность попарных соотношений (15) для справедливости совокупности равенств (16)–(18) показывает

Пример С.Н.Бернштейна. Испытание: наугад бросается игральная кость, имеющая форму правильного тетраэдра, четыре грани которого имеют, соответственно, белую, синюю, красную и тройную бело-сине-красную (полосатую) окраску.

Рассмотрим события: — на выпавшей грани присутствует белый цвет,— на выпавшей грани присутствует синий цвет,— на выпавшей грани присутствует красный цвет. По схеме равновозможных исходов легко убедиться, что. Далее, произведение любых двух из них означает выпадение полосатой грани, так что. Значит, условие (15) выполняется. В то же время, и условие (16) не выполняется.

30. Формула полной вероятности

Определение.Событияобразуютполную группу, если выполняются два условия: 1)в результате испытания одно из них обязательно наступает, то есть их сумма есть достоверное событие:; 2) события попарно несовместны, то естьпри.

Теорема.Пусть выполняются два условия:

1. События («гипотезы») образуют полную группу.

2. События имеют ненулевые вероятности:.

Тогда для всякого события справедлива формула:

,

или в краткой записи:

. (19)

31. Формулы Бейеса

Теорема.Пусть для событий («гипотез») и событиявыполняются три условия:

1. Гипотезы образуют полную группу.

2. Гипотезы имеют ненулевые вероятности:

.

3. .

Тогда при справедливы формулы:

или в краткой записи:

. (20)

32. Схема независимых испытаний Бернулли

Определение.Испытанияобразуют относительно исходапоследовательность независимых испытаний по схеме Бернулли, если выполняются два условия:

1. Исходы испытаний независимы в совокупности.

2. Вероятность исхода во всех испытаниях одинакова и равна.

Терминология: — успех,— вероятность успеха,— неудача,— вероятность неудачи.

Теорема (о вероятности числа успехов).Справедлива формула:

. (21)

(Здесь – число сочетаний изпо; см. п. 1.5).

33. Локальная теорема Лапласа

I. Дифференциальная функция Лапласа.

Определение. Дифференциальной функцией Лапласаназывается функция.

График дифференциальной функции Лапласа («колокол») приведен на рис. 10.

Рис. 10.

Свойства функции .

1.при всех.

2. —чётная функция, то есть. График функции симметричен относительно оси ординат.

3..

Стремление к нулю в последнем пределе достаточно быстрое. Так, с точностью до четырех знаков после запятой .

Для отыскания значений функции имеются таблицы и стандартные компьютерные программы.

II. Предельное равенство.

Введём для испытаний по схеме Бернулли с вероятностью успехаобозначения:

, где – количество успехов (),.

Теорема. Пусть вероятность успеха в серии независимых испытаний по схеме Бернулли удовлетворяет условию. Тогда

. (24)

3.13. Интегральная теорема Лапласа

I. Интегральная функция Лапласа.

Определение. Интегральной функцией Лапласаназывается интеграл с переменным верхним пределом:

.

Для отыскания значений функции имеются таблицы и стандартные компьютерные программы.

График интегральной функции Лапласа приведен на рис. 11. Геометрически выражает площадь заштрихованной части криволинейной трапеции на рис. 12.

Рис. 11.

x

t

(x)

Рис. 12.

Свойства функции .

1.при всех .

2. – нечётная функция, то есть. График

функции симметричен относительно начала координат.

3. ; .

4. является производной для :.

5.Функция строго возрастает.

II. Предельное равенство.

Введём обозначение: — вероятность того, что в серии изиспытаний по схеме Бернулли число успеховлежит в пределах:.

Пусть, как и в п. 3.12: — количество испытаний по схеме Бернулли,— вероятность успеха,.

Теорема. Пусть для вероятности успеха в серии независимых испытаний по схеме Бернулли выполняется условие. Тогда для вероятности:

, (25)

или, учитывая определение функции:

. (26)

studfiles.net

2.3. Зависимые и независимые события

Определение. Два события называют независимыми, если вероятность появления одного из них не зависит от того, произойдет другое событие или нет.

Например, опыт состоит в бросании двух монет. Пусть А и В – события, состоящие в том, что герб появится соответственно на первой и второй монете. В данном случае вероятность события А не зависит от того, произошло событие В или нет. Следовательно, событие А независимо от события В.

Определение. Несколько событий называют попарно независимыми, если каждые два из них независимы.

Например, опыт состоит в бросании трех монет. Пусть А, В, С – события, состоящие в том, что герб появится соответственно на первой, второй и третьей монете. В данном случае каждые два из рассматриваемых событий (т.е. А и В, А и С, В и С) – независимы. Следовательно, события А, В и С – попарно независимые. ◄

Определение. Два события называют зависимыми, если вероятность появления одного из них меняется в зависимости от того, произойдет другое событие или нет.

Например, в урне 3 белых и 2 черных шара. Наудачу берут один шар, не возвращая его в урну. Если появился белый шар (событие А), то вероятность появления белого шара во втором испытании (событие В) Р(В) = 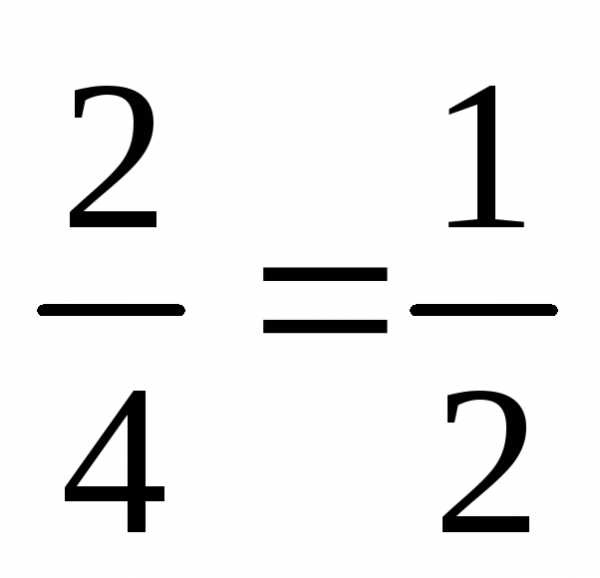. Если же в первом испытании появился черный шар (т.е. событиеА не произошло), то вероятность Р(В) = 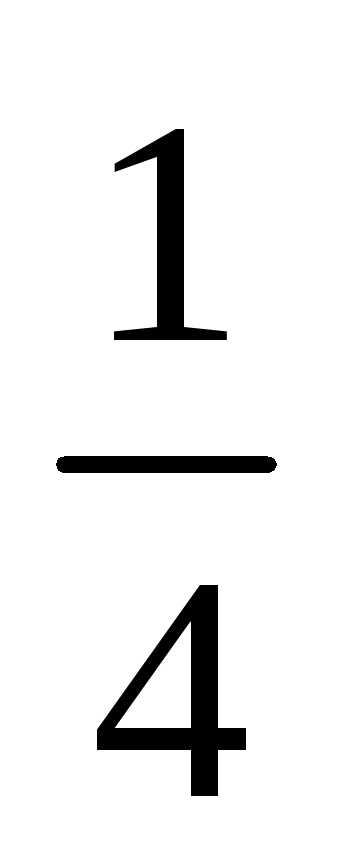. Т.е. вероятность событияВ зависит от того, произошло событие А или нет. Следовательно, события А и В – зависимые.

Отметим, что зависимость и независимость событий всегда взаимны, т.е. если событие В не зависит от события А, то и событие А не зависит от события В.

2.4. Теорема умножения вероятностей независимых событий

Сформулируем теорему умножения вероятностей независимых событий.

Теорема. Вероятность совместного появления двух независимых событий А и В равна произведению вероятностей этих событий:

Р(АВ) = Р(А)·Р(В).

(2.5)

Для того чтобы обобщить теорему умножения на несколько событий, введем понятие независимости событий в совокупности.

Определение. Несколько событий называют независимыми в совокупности, если каждое из них и любая комбинация остальных событий (содержащих либо все остальные события, либо часть из них) есть события независимые.

Например, если события А₁, А₂ и А₃ независимые в совокупности, то независимыми являются события: А₁ и А₂, А₁ и А₃, А₂ и А₃, А₁А₂ и А₃, А₁А₃ и А₂, А₂А₃ и А₁.

Подчеркнем, что если несколько событий независимы попарно, то из этого еще не следует их независимость в совокупности. В этом смысле требование независимости событий в совокупности сильнее требования их попарной независимости.

Теперь мы можем сформулировать следствие из теоремы умножения вероятностей, обобщающее теорему умножения на несколько событий.

Следствие. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий.

Р(А1А2…Аn) = Р(А1)·Р(А2) …·Р(Аn).

(2.6)

Пример 2.4. Имеется три урны, содержащих по 10 шаров. В первой урне 5 шаров красного цвета, во второй – 4, в третьей – 6. Из каждой урны наудачу вынимают по одному шару. Найти вероятность того, что все три шара окажутся красного цвета.

Решение. Вероятность того, что из первой урны вынут шар красного цвета (событие А) Р(А) = 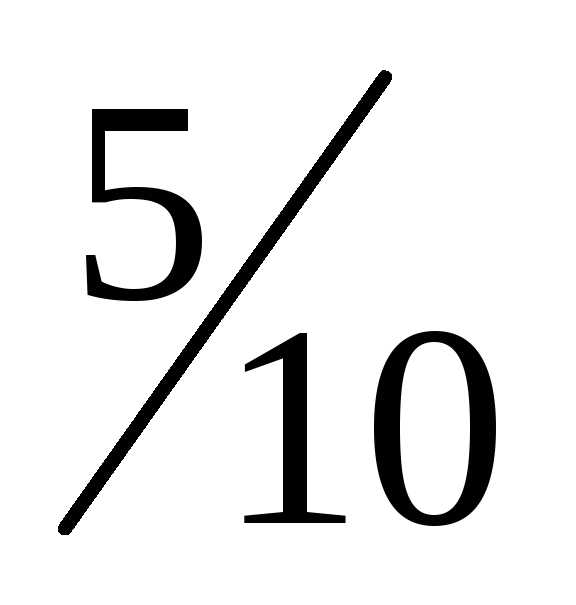= 0,5. Вероятность того, что из второй урны вынут шар красного цвета (событиеВ) Р(В) = 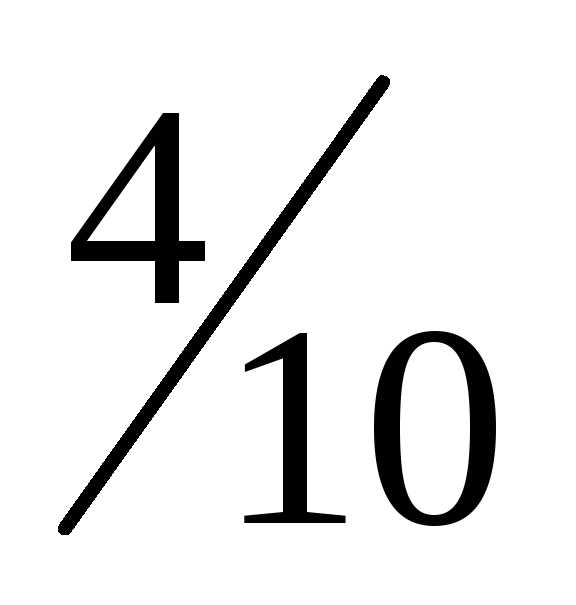= 0,4. Вероятность того, что из третьей урны вынут шар красного цвета (событиеС) Р(С) = 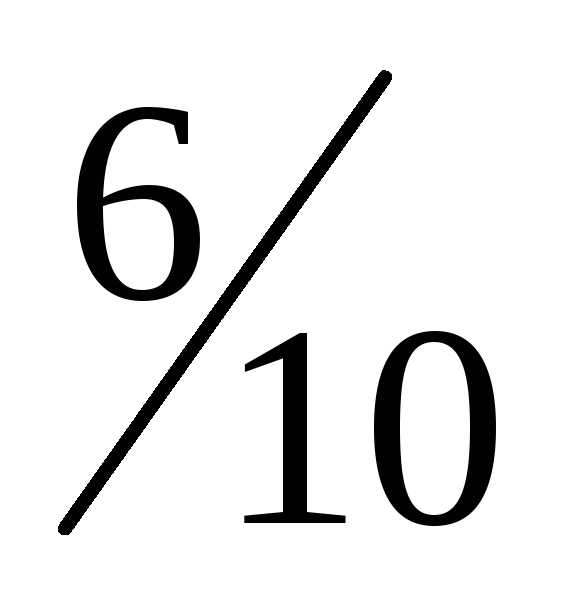= 0,6.

Так как события А, В и С независимые в совокупности, то искомая вероятность (по теореме умножения) равна

Р(АВС) = Р(А)·Р(В)·Р(С) = 0,5·0,4·0,6 = 0,12. ◄

studfiles.net

Зависимые и независимые события. Условная вероятность

Определения вероятности

Классическое определение

Классическое «определение» вероятности исходит из понятия равновозможности как объективного свойства изучаемых явлений. Равновозможность является неопределяемым понятием и устанавливается из общих соображений симметрии изучаемых явлений. Например, при подбрасывании монетки исходят из того, что в силу предполагаемой симметрии монетки, однородности материала и случайности (непредвзятости) подбрасывания нет никаких оснований для предпочтения «решки» перед «орлом» или наоборот, то есть выпадение этих сторон можно считать равновозможными (равновероятными).

Наряду с понятием равновозможности в общем случае для классического определения необходимо также понятие элементарного события (исхода), благоприятствующего или нет изучаемому событию A. Речь идет об исходах, наступление которых исключает возможность наступления иных исходов. Это несовместимые элементарные события. К примеру при бросании игральной кости выпадение конкретного числа исключает выпадение остальных чисел.

Классическое определение вероятности можно сформулировать следующим образом:

Вероятностью случайного события A называется отношение числа n несовместимых равновероятных элементарных событий, составляющих событие A, к числу всех возможных элементарных событий N:

Например, пусть подбрасываются две кости. Общее количество равновозможных исходов (элементарных событий) равно очевидно 36 (6 возможностей на каждой кости). Оценим вероятность выпадения 7 очков. Получение 7 очков возможно следующими способами: 1+6, 2+5, 3+4, 4+3, 5+2, 6+1. То есть всего 6 равновозможных исходов, благоприятствующих событию A — получению 7 очков. Следовательно, вероятность будет равна 6/36=1/6. Для сравнения вероятность получения 12 очков или 2 очков равна всего 1/36 — в 6 раз меньше.

Геометрическое определение

Несмотря на то, что классическое определение является интуитивно понятным и выведенным из практики, оно, как минимум не может быть непосредственно применено в случае, если количество равновозможных исходов бесконечно. Ярким примером бесконечного числа возможных исходов является ограниченная геометрическая область G, например, на плоскости, с площадью S. Случайно «подброшенная» «точка» с равной вероятностью может оказаться в любой точке этой области. Задача заключается в определении вероятности попадания точки в некоторую подобласть g с площадью s. В таком случая обобщая классическое определение можно прийти к геометрическому определению вероятности попадания в подобласть :

В виду равновозможности вероятность эта не зависит от формы области g, она зависит только от ее площади. Данное определение естественно можно обобщить и на пространство любой размерности, где вместо площади использовать понятие «объема». Более того, именно такое определение приводит к современному аксиоматическому определению вероятности. Понятие объема обобщается до понятия «меры» некоторого абстрактного множества, к которой предъявляются требования, которыми обладает и «объем» в геометрической интерпретации — в первую очередь, это неотрицательность и аддитивность.

Частотное (статистическое) определение

Классическое определение при рассмотрении сложных проблем наталкивается на трудности непреодолимого характера. В частности, в некоторых случаях выявить равновозможные случаи может быть невозможно. Даже в случае с монеткой, как известно существует явно не равновероятная возможность выпадения «ребра», которую из теоретических соображений оценить невозможно (можно только сказать, что оно маловероятно и то это соображение скорее практическое). Поэтому еще на заре становления теории вероятностей было предложено альтернативное «частотное» определение вероятности. А именно, формально вероятность можно определить как предел частоты наблюдений события A, предполагая однородность наблюдений (то есть одинаковость всех условий наблюдения) и их независимость друг от друга:

где — количество наблюдений, а — количество наступлений события .

Несмотря на то, что данное определение скорее указывает на способ оценки неизвестной вероятности — путем большого количества однородных и независимых наблюдений — тем не менее в таком определении отражено содержание понятия вероятности. А именно, если событию приписывается некоторая вероятность, как объективная мера его возможности, то это означает, что при фиксированных условиях и многократном повторении мы должны получить частоту его появления, близкую к (тем более близкую, чем больше наблюдений). Собственно, в этом заключается исходный смысл понятия вероятности. В основе лежит объективистский взгляд на явления природы. Ниже будут рассмотрены так называемые законы больших чисел, которые дают теоретическую основу (в рамках излагаемого ниже современного аксиоматического подхода) в том числе для частотной оценки вероятности.

Аксиоматическое определение

В современном математическом подходе вероятность задаётся аксиоматикой Колмогорова. Предполагается, что задано некоторое пространство элементарных событий . Подмножества этого пространства интерпретируются как случайные события. Объединение (сумма) некоторых подмножеств (событий) интерпретируется как событие, заключающееся в наступлении хотя бы одного из этих событий. Пересечение (произведение) подмножеств (событий) интерпретируется как событие, заключающееся в наступлении всех этих событий. Непересекающиеся множества интерпретируются как несовместные события (их совместное наступление невозможно). Соответственно, пустое множество означает невозможноесобытие.

Вероятностью (вероятностной мерой) называется мера (числовая функция) , заданная на множестве событий, обладющая следующими свойствами:

• Аддитивность: вероятность наступления хотя бы одного (то есть суммы) из попарно несовместных событий равна сумме вероятностей этих событий, то есть формально если т.е. при , то .

В случае если пространство элементарных событий X конечно, то достаточно указанного условия аддитивности для произвольных двух несовместных событий, из которого будет следовать аддитивность для любого конечного количества несовместных событий. Однако, в случае бесконечного (счетного или несчетного) пространства элементарных событий этого условия оказывается недостаточно. Требуется так называемая счетная или сигма- аддитивность, то есть выполнение свойства аддитивности для любого не более чем счетногосемейства попарно несовместных событий. Это необходимо для обеспечения «непрерывности» вероятностной меры.

Вероятностная мера может быть определена не для всех подмножеств множества . Предполагается, что она определена на некоторой сигма-алгебре подмножеств ^[6]. Эти подмножества называются измеримыми по данной вероятностной мере и именно они являются случайными событиями. Совокупность  — то есть множество элементарных событий, сигма-алгебра его подмножеств и вероятностная мера — называется вероятностным пространством.

   Непрерывные случайные величины.     Кроме дискретных случайных величин, возможные значения которых образуют конечную или бесконечную последовательность чисел, не заполняющих сплошь никакого интервала, часто встречаются случайные величины, возможные значения которых образуют некоторый интервал. Примером такой случайной величины может служить отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе. Такого рода, случайные величины не могут быть заданы с помощью закона распределения вероятностей р(х). Однако их можно задать с помощью функции распределения вероятностей F(х). Эта функция определяется точно так же, как и в случае дискретной случайной величины:   

   Таким образом, и здесь функция F(х) определена на всей числовой оси, и ее значение в точке х равно вероятности того, что случайная величина примет значение, меньшее чем х.     Формула (19) и свойства 1° и 2° справедливы для функции распределения любой случайной величины. Доказательство проводится аналогично случаю дискретной величины.     Случайная величина называется непрерывной, если для нее существует неотрицательная кусочно-непрерывная функция* , удовлетворяющая для любых значений x равенству

(22)

   Функция называется плотностью распределения вероятностей, или кратко, плотностью распределения. Если x₁<x₂, то на основании формул (20) и (22) имеем

(23)

   Исходя из геометрического смысла интеграла как площади, можно сказать, что вероятность выполнения неравенств равна площади криволинейной трапеции с основанием[x₁,x₂], ограниченной сверху кривой (рис. 6).

   Так как , а на основании формулы (22)   

   , то

(24)

   Пользуясь формулой (22), найдем как производную интеграла по переменной верхней границе, считая плотность распределения непрерывной**:

(25)

   Заметим, что для непрерывной случайной величины функция распределения F(х) непрерывна в любой точке х, где функция непрерывна. Это следует из того, что F(х) в этих точках дифференцируема.     На основании формулы (23), полагая x₁=x, , имеем   

   В силу непрерывности функции F(х) получим, что   

   Следовательно   

   Таким образом, вероятность того, что непрерывная случайная величина может принять любое отдельное значение х, равна нулю.     Отсюда следует, что события, заключающиеся в выполнении каждого из неравенств   

 , , , 

   Имеют одинаковую вероятность, т.е.   

   В самом деле, например,   

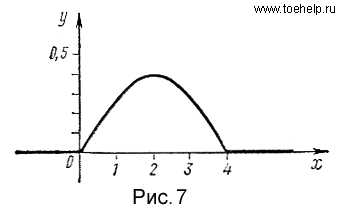
   так как     Замечание. Как мы знаем, если событие невозможно, то вероятность его наступления равна нулю. При классическом определении вероятности, когда число исходов испытания конечно, имеет место и обратное предложение: если вероятность события равна нулю, то событие невозможно, так как в этом случае ему не благоприятствует ни один из исходов испытания. В случае непрерывной случайной величины число возможных ее значений бесконечно. Вероятность того, что эта величина примет какое-либо конкретное значение x₁ как мы видели, равна нулю. Однако отсюда не следует, что это событие невозможно, так как в результате испытания случайная величина может, в частности, принять значение x₁. Поэтому в случае непрерывной случайной величины имеет смысл говорить о вероятности попадания случайной величины в интервал, а не о вероятности того, что она примет какое-то конкретное значение.     Так, например, при изготовлении валика нас не интересует вероятность того, что его диаметр будет равен номиналу. Для нас важна вероятность того, что диаметр валика не выходит из поля допуска.     Пример. Плотность распределения непрерывной случайной величины задана следующим образом:   

   График функции представлен па рис. 7. Определить вероятность того, что случайная величина примет значение, удовлетворяющее неравенствам .Найти функцию распределения заданной случайной величины. (Решение)

   Следующие два пункта посвящены часто встречающимся на практике распределениям непрерывных случайных величин — равномерному и нормальному распределениям. 

Дальше…

   * Функция называется кусочно-непрерывной на всей числовой оси, если она на любом сегменте или непрерывна, или имеет конечное число точек разрыва I рода.     ** Правило дифференцирования интеграла с переменной верхней границей, выведенное в случае конечной нижней границы, остается справедливым и для интегралов с бесконечной нижней границей. В самом деле,   

   Так как интеграл

   есть величина постоянная.

Различают события зависимые и независимые. Два события называются независимыми, если появление одного из них не изменяет вероятность появления другого. Например, если в цехе работают две автоматические линии, по условиям производства не взаимосвязанные, то остановки этих линий являются независимыми событиями.

Пример 3. Монета брошена два раза. Вероятность появления «герба» в первом испытании (событие ) не зависит от появления или не появления «герба» во втором испытании (событие ). В свою очередь, вероятность появления «герба» во втором испытании не зависит от результата первого испытания. Таким образом, события и независимые.

Несколько событий называются независимыми в совокупности, если любое из них не зависит от любого другого события и от любой комбинации остальных.

События называются зависимыми, если одно из них влияет на вероятность появления другого. Например, две производственные установки связаны единым технологическим циклом. Тогда вероятность выхода из строя одной из них зависит от того, в каком состоянии находится другая. Вероятность одного события , вычисленная в предположении осуществления другого события , называется условной вероятностью события и обозначается .

Условие независимости события от события записывают в виде , а условие его зависимости — в виде . Рассмотрим пример вычисления условной вероятности события.

Пример 4. В ящике находятся 5 резцов: два изношенных и три новых. Производится два последовательных извлечения резцов. Определить условную вероятность появления изношенного резца при втором извлечении при условии, что извлеченный в первый раз резец в ящик не возвращается.

Решение. Обозначим извлечение изношенного резца в первом случае, а — извлечение нового. Тогда . Поскольку извлеченный резец в ящик не возвращается, то изменяется соотношение между количествами изношенных и новых резцов. Следовательно, вероятность извлечения изношенного резца во втором случае зависит от того, какое событие осуществилось перед этим.

Обозначим событие, означающее извлечение изношенного резца во втором случае. Вероятности этого события могут быть такими:

Следовательно, вероятность события зависит от того, произошло или нет событие .

Пло́тность вероя́тности — один из способов задания вероятностной меры на евклидовом пространстве . В случае, когда вероятностная мера является распределением случайной величины, говорят о плотности случайной величины.

Плотность вероятности Пусть является вероятностной мерой на , то есть определено вероятностное пространство , где обозначает борелевскую σ-алгебру на . Пусть обозначает меру Лебега на .

Определение 1. Вероятность называется абсолютно непрерывной (относительно меры Лебега) (), если любое борелевское множество нулевой меры Лебега также имеет вероятность ноль:

Если вероятность абсолютно непрерывна, то согласно теореме Радона-Никодима существует неотрицательная борелевская функция такая, что

,

где использовано общепринятое сокращение , и интеграл понимается в смысле Лебега.

Определение 2. В более общем виде, пусть — произвольное измеримое пространство, а и — две меры на этом пространстве. Если найдется неотрицательная , позволяющая выразить меру через меру в виде

то такую функцию называют плотностью меры по мере , или производной Радона-Никодима меры относительно меры , и обозначают

.

studfiles.net

Независимость событий.

Если при наступлении события вероятность событияне меняется, то событияиназываютсянезависимыми.

Теорема: Вероятность совместного появления двух независимых событий и (произведения и) равна произведению вероятностей этих событий.

Действительно, так как событияинезависимы, то. В этом случае формула вероятности произведения событийипринимает вид.

События называютсяпопарно независимыми, если независимы любые два из них.

События называютсянезависимыми в совокупности (или просто независимыми), если независимы каждые два из них и независимы каждое событие и все возможные произведения остальных.

Теорема: Вероятность произведения конечного числа независимых в совокупности событий равна произведению вероятностей этих событий.

.

Проиллюстрируем различие в применении формул вероятности произведения событий для зависимых и независимых событий на примерах

Пример 1. Вероятность попадания в цель первым стрелком равна 0,85, вторым 0,8. Орудия сделали по одному выстрелу. Какова вероятность того, что в цель попал хотя бы один снаряд ?

Решение: P(A+B) =P(A) +P(B) –P(AB) Так как выстрелы независимы, то

P(A+B) = P(A) +P(B) –P(A)*P(B) = 0.97

Пример 2. В урне находится 2 красных и 4 черных шара. Из нее вынимают подряд 2 шара. Какова вероятность того, что оба шара красные.

Решение: 1 случай. Событие А – появление красного шара при первом вынимании, событие В – при втором. Событие С – появление двух красных шаров.

P(С) =P(A)*P(B/A) = (2/6)*(1/5) = 1/15

2 случай. Первый вынутый шар возвращается в корзину

P(С) =P(A)*P(B) = (2/6)*(2/6) = 1/9

Формула полной вероятности.

Пусть событие может произойти только с одним из несовместных событий , образующих полную группу. Например, в магазин поступает одна и та же продукция от трех предприятий и в разном количестве. Вероятность выпуска некачественной продукции на этих предприятиях различна. Случайным образом отбирается одно из изделий. Требуется определить вероятность того, что это изделие некачественное (событие). Здесь события – это выбор изделия из продукции соответствующего предприятия.

В этом случае вероятность события можно рассматривать как сумму произведений событий.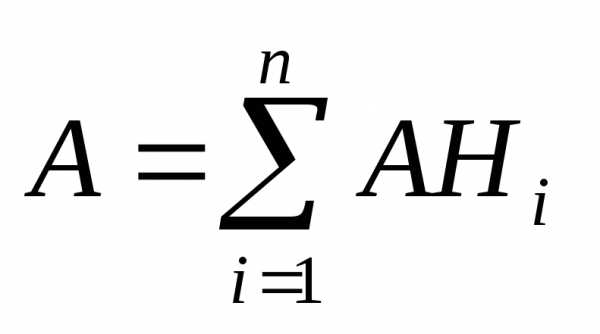

По теореме сложения вероятностей несовместных событий получаем 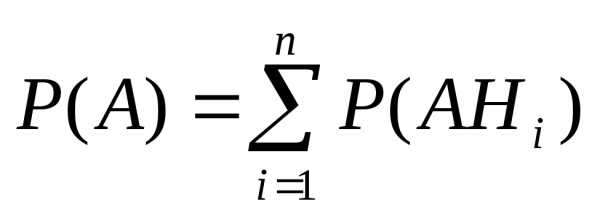. Используя теорему умножения вероятностей, находим

.

Полученная формула называется формулой полной вероятности.

Формула Байеса

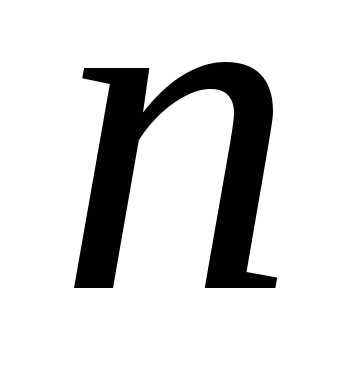Пусть событие происходит одновременно с одним изнесовместных событий , вероятности которых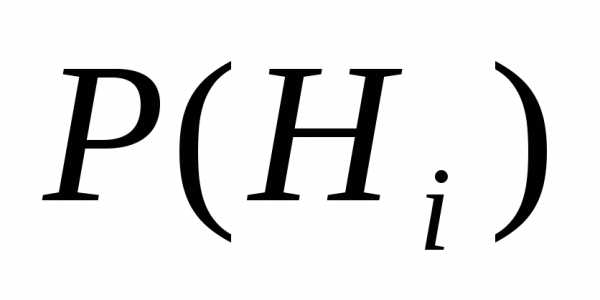() известны до опыта (вероятности априори). Производится опыт, в результате которого зарегистрировано появление события, причем известно, что это событие имело определенные условные вероятности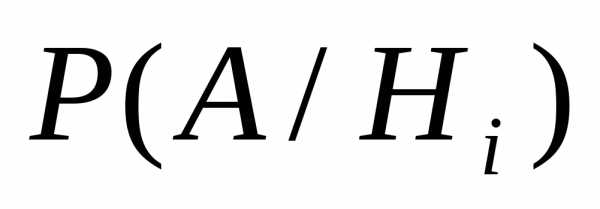(). Требуется найти вероятности событий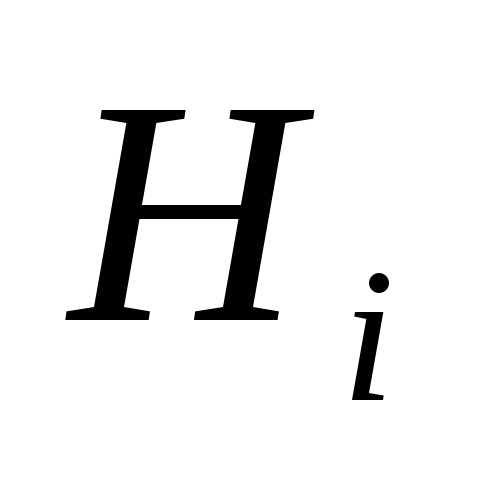если известно, что событиепроизошло (вероятности апостериори).

Задача состоит в том, что, имея новую информацию (событие Aпроизошло), нужно переоценить вероятности событий .

На основании теоремы о вероятности произведения двух событий

,

откуда

или

.

Полученная формула носит название формулы Байеса.

Основные понятия комбинаторики.

При решении ряда теоретических и практических задач требуется из конечного множества элементов по заданным правилам составлять различные комбинации и производить подсчет числа всех возможных таких комбинаций. Такие задачи принято называть комбинаторными.

При решении задач комбинаторики используют правила суммы и произведения.

studfiles.net

3.2.9. Вероятность суммы несовместных событий

3)

3.2.9. Вероятность суммы несовместных событий

Теорема. Вероятность суммы несовместных событий иравна сумме вероятностей этих событий:

(3.10)

Следствие 1. С помощью метода математической индукции формулу (3.10) можно обобщить на любое число попарно несовместных событий:

(3.11)

Следствие 2. Поскольку противоположные события являются несовместными, а их сумма – достоверным событием, то, используя (3.10), имеем:

(3.12)

Часто при решении задач формулу (3.12) используют в виде:

(3.13)

Пример 3.29. В опыте с бросанием игральной кости найти вероятности выпадения на верхней грани числа очков более 3 и менее 6.

Обозначим события, связанные с выпадением на верхней грани игральной кости одного очка, через U₁, двух очков через U₂,…, шести очков через U₆.

Пусть событие U – выпадение на верхней грани кости числа очков более 3 и менее 6. Это событие произойдет, если произойдет хотя бы одно из событий U₄ или U₅, следовательно, его можно представить в виде суммы этих событий: . Т. к. событияU₄ и U₅являются несовместными, то для нахождения вероятности их суммы используем формулу (3.11). Учитывая, что вероятности событий U₁, U₂,…,U₆ равны , получим:

Замечание. Ранее задачи такого типа решали с помощью подсчета числа благоприятствующих исходов. Действительно, событию U благоприятствуют два исхода, а всего шесть элементарных исходов, следовательно, используя классический подход к понятию вероятности, получим:

Однако классический поход к понятию вероятности, в отличие от теоремы о вероятности суммы несовместных событий, применим только для равновозможных исходов.

Пример 3.30. Вероятность попадания в цель стрелком равна 0,7. Какова вероятность того, что стрелок не попадет в цель?

Пусть событие − попадание стрелком в цель, тогда событие, состоящее в том, что стрелок не попадет в цель, является противоположным событиемсобытию, т. к. в результате каждого испытания всегда происходит одно и только одно из этих событий. Используя формулу (3.13), получим:

3.2.10. Вероятность произведения событий

Определение. Событие называетсязависимым от события если вероятность события зависит от того, произошло событиеили нет.

Определение. Вероятность события вычисленная при условии, что событиепроизошло, называетсяусловной вероятностью события и обозначается

Теорема. Вероятность произведения событий иравна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:

или (3.14)

Условие независимости события от события можно записать в виде Из этого утверждения следует, что для независимых событий выполняется соотношение:

(3.15)

т. е. вероятность произведения независимых событий и, равна произведению их вероятностей.

Замечание. Вероятность произведения нескольких событий равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляется при условии, что все предыдущие имели место:

Если события независимые, то имеем:

Пример 3.31. В ящике 5 белых и 3 черных шара. Из него наугад последовательно без возвращения вытаскивают два шара. Найти вероятность того, что оба шара белые.

Пусть событие − появление белого шара при первом вынимании,− появление белого шара при втором вынимании. Учитывая, что,(вероятность появления второго белого шара при условии, что первый вынутый шар был белым и его не возвратили в ящик). Так как событияизависимые, то вероятность их произведения найдем по формуле (3.15):

Пример 3.32. Вероятность попадания в цель первым стрелком 0,8; вторым – 0,7. Каждый стрелок выстрелил по мишени. Какова вероятность того, что хотя бы один стрелок попадет в цель? Какова вероятность того, что один стрелок попадет в цель?

Пусть событие – попадание в цель первым стрелком,– вторым. Все возможные варианты можно представить в видетаблицы 3.5, где «+» обозначает, что событие произошло, а «−» − не произошло.

Таблица 3.5

+	+
+	−
−	+
−	−

Пусть событие – попадание хотя бы одним стрелком в цель, Тогда событиеявляется суммой независимых событийиследовательно, применить теорему о вероятности суммы несовместных событий в данной ситуации нельзя.

Рассмотрим событие противоположное событиюкоторое произойдет тогда, когда ни один стрелок не попадет в цель, т. е. является произведением независимых событийИспользуя формулы (3.13) и (3.15), получим:

Пусть событие – попадание одним стрелком в цель. Это событие можно представить следующим образом:

События и– независимые, событияитакже являются независимыми. События, являющиеся произведениями событийи– несовместными. Используя формулы (3.10) и (3.15) получим:

Свойства операций сложения и умножения событий:

1.

2.

3.

4.

5.

6.

7.

Пусть событие может произойти только вместе с одним из попарно несовместных событий (гипотез),,…,, образующих полную группу, т. е.

Вероятность события находится по формулеполной вероятности:

(3.16)

Если событие уже произошло, то вероятности гипотез могут быть переоценены по формулеБайеса:

(3.17)

Пример 3.33. Имеются две одинаковых урны с шарами. В первой урне 5 белых и 10 черных шаров, во второй − 3 белых и 7 черных шаров. Выбирают наугад одну урну и вытаскивают из нее один шар.

studfiles.net