Решите неравенство cos(x)^2>0 (косинус от (х) в квадрате больше 0)
Дано неравенство:$$\cos^{2}{\left (x \right )} > 0$$
Чтобы решить это нер-во — надо сначала решить соотвествующее ур-ние:
$$\cos^{2}{\left (x \right )} = 0$$
Решаем:
Дано уравнение
$$\cos^{2}{\left (x \right )} = 0$$
преобразуем
$$\cos^{2}{\left (x \right )} = 0$$
$$\cos^{2}{\left (x \right )} = 0$$
Сделаем замену
$$w = \cos{\left (x \right )}$$
Это уравнение вида
a*w^2 + b*w + c = 0
Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:
$$w_{1} = \frac{\sqrt{D} — b}{2 a}$$
$$w_{2} = \frac{- \sqrt{D} — b}{2 a}$$
где D = b^2 — 4*a*c — это дискриминант.
Т.к.
$$a = 1$$
$$b = 0$$
$$c = 0$$
, то
D = b^2 - 4 * a * c =
(0)^2 - 4 * (1) * (0) = 0
Т.к. D = 0, то корень всего один.
w = -b/2a = -0/2/(1)
$$w_{1} = 0$$
делаем обратную замену
$$\cos{\left (x \right )} = w$$
Дано уравнение
$$\cos{\left (x \right )} = w$$
— это простейшее тригонометрическое ур-ние
Это ур-ние преобразуется в
$$x = \pi n + \operatorname{acos}{\left (w \right )}$$
$$x = \pi n + \operatorname{acos}{\left (w \right )} — \pi$$
Или
$$x = \pi n + \operatorname{acos}{\left (w \right )}$$
$$x = \pi n + \operatorname{acos}{\left (w \right )} — \pi$$
, где n — любое целое число
подставляем w:
$$x_{1} = \pi n + \operatorname{acos}{\left (w_{1} \right )}$$
$$x_{1} = \pi n + \operatorname{acos}{\left (0 \right )}$$
$$x_{1} = \pi n + \frac{\pi}{2}$$
$$x_{2} = \pi n + \operatorname{acos}{\left (w_{1} \right )} — \pi$$
$$x_{2} = \pi n — \pi + \operatorname{acos}{\left (0 \right )}$$
$$x_{2} = \pi n — \frac{\pi}{2}$$
$$x_{1} = \frac{\pi}{2}$$
$$x_{2} = \frac{3 \pi}{2}$$
$$x_{2} = \frac{3 \pi}{2}$$
Данные корни
$$x_{1} = \frac{\pi}{2}$$
$$x_{2} = \frac{3 \pi}{2}$$
являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки:
$$x_{0} Возьмём например точку
$$x_{0} = x_{1} — \frac{1}{10}$$
=
$$- \frac{1}{10} + \frac{\pi}{2}$$
=
$$- \frac{1}{10} + \frac{\pi}{2}$$
подставляем в выражение
$$\cos^{2}{\left (x \right )} > 0$$
$$\cos^{2}{\left (- \frac{1}{10} + \frac{\pi}{2} \right )} > 0$$
2
sin (1/10) > 0
значит одно из решений нашего неравенства будет при:
$$x
_____ _____
\ /
-------ο-------ο-------
x1 x2Другие решения неравенства будем получать переходом на следующий полюс
и т.д.
Ответ:
$$x $$x > \frac{3 \pi}{2}$$
Решите неравенство cos(x)^2-cos(x)
Дано неравенство:$$\cos^{2}{\left (x \right )} — \cos{\left (x \right )} Чтобы решить это нер-во — надо сначала решить соотвествующее ур-ние:
$$\cos^{2}{\left (x \right )} — \cos{\left (x \right )} = 0$$
Решаем:
Дано уравнение
$$\cos^{2}{\left (x \right )} — \cos{\left (x \right )} = 0$$
преобразуем
$$\left(\cos{\left (x \right )} — 1\right) \cos{\left (x \right )} = 0$$
$$\cos^{2}{\left (x \right )} — \cos{\left (x \right )} = 0$$
Сделаем замену
$$w = \cos{\left (x \right )}$$
Это уравнение вида
a*w^2 + b*w + c = 0
Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:
$$w_{1} = \frac{\sqrt{D} — b}{2 a}$$
$$w_{2} = \frac{- \sqrt{D} — b}{2 a}$$
где D = b^2 — 4*a*c — это дискриминант.
Т.к.
$$a = 1$$
$$b = -1$$
$$c = 0$$
, то
D = b^2 - 4 * a * c =
(-1)^2 - 4 * (1) * (0) = 1
Т.к. D > 0, то уравнение имеет два корня.
w1 = (-b + sqrt(D)) / (2*a)
w2 = (-b - sqrt(D)) / (2*a)
или
$$w_{1} = 1$$
$$w_{2} = 0$$
делаем обратную замену
$$\cos{\left (x \right )} = w$$
Дано уравнение
$$\cos{\left (x \right )} = w$$
— это простейшее тригонометрическое ур-ние
Это ур-ние преобразуется в
$$x = \pi n + \operatorname{acos}{\left (w \right )}$$
$$x = \pi n + \operatorname{acos}{\left (w \right )} — \pi$$
Или
$$x = \pi n + \operatorname{acos}{\left (w \right )}$$
$$x = \pi n + \operatorname{acos}{\left (w \right )} — \pi$$
, где n — любое целое число
подставляем w:
$$x_{1} = \pi n + \operatorname{acos}{\left (w_{1} \right )}$$
$$x_{1} = \pi n + \operatorname{acos}{\left (1 \right )}$$
$$x_{1} = \pi n$$
$$x_{2} = \pi n + \operatorname{acos}{\left (w_{2} \right )}$$
$$x_{2} = \pi n + \operatorname{acos}{\left (0 \right )}$$
$$x_{2} = \pi n + \frac{\pi}{2}$$
$$x_{3} = \pi n + \operatorname{acos}{\left (w_{1} \right )} — \pi$$
$$x_{3} = \pi n — \pi + \operatorname{acos}{\left (1 \right )}$$
$$x_{3} = \pi n — \pi$$
$$x_{4} = \pi n + \operatorname{acos}{\left (w_{2} \right )} — \pi$$
$$x_{4} = \pi n — \pi + \operatorname{acos}{\left (0 \right )}$$
$$x_{4} = \pi n — \frac{\pi}{2}$$
$$x_{1} = 0$$
$$x_{2} = \frac{\pi}{2}$$
$$x_{3} = \frac{3 \pi}{2}$$
$$x_{4} = 2 \pi$$
$$x_{1} = 0$$
$$x_{2} = \frac{\pi}{2}$$
$$x_{3} = \frac{3 \pi}{2}$$
$$x_{4} = 2 \pi$$
Данные корни
$$x_{1} = 0$$
$$x_{2} = \frac{\pi}{2}$$
$$x_{3} = \frac{3 \pi}{2}$$
$$x_{4} = 2 \pi$$
являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки:
$$x_{0} Возьмём например точку
$$x_{0} = x_{1} — \frac{1}{10}$$
=
$$- \frac{1}{10}$$
=
$$- \frac{1}{10}$$
подставляем в выражение
$$\cos^{2}{\left (x \right )} — \cos{\left (x \right )}
2 cos (-1/10) - cos(-1/10)2 cos (1/10) - cos(1/10)
значит одно из решений нашего неравенства будет при:
$$x_____ _____ _____ \ / \ / -------ο-------ο-------ο-------ο------- x1 x2 x3 x4
Другие решения неравенства будем получать переходом на следующий полюс
и т.д.
Ответ:
$$x $$x > \frac{\pi}{2} \wedge x $$x > 2 \pi$$
Решите уравнение cos(x)^2=1 (косинус от (х) в квадрате равно 1)
Дано уравнение$$\cos^{2}{\left (x \right )} = 1$$
преобразуем
$$- \sin^{2}{\left (x \right )} = 0$$
$$\cos^{2}{\left (x \right )} — 1 = 0$$
Сделаем замену
$$w = \cos{\left (x \right )}$$
Это уравнение вида
a*w^2 + b*w + c = 0
Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:
$$w_{1} = \frac{\sqrt{D} — b}{2 a}$$
$$w_{2} = \frac{- \sqrt{D} — b}{2 a}$$
где D = b^2 — 4*a*c — это дискриминант.
Т.к.
$$a = 1$$
$$b = 0$$
$$c = -1$$
, то
D = b^2 - 4 * a * c =
(0)^2 - 4 * (1) * (-1) = 4
Т.к. D > 0, то уравнение имеет два корня.
w1 = (-b + sqrt(D)) / (2*a)
w2 = (-b - sqrt(D)) / (2*a)
или
$$w_{1} = 1$$
$$w_{2} = -1$$
делаем обратную замену
$$\cos{\left (x \right )} = w$$
Дано уравнение
$$\cos{\left (x \right )} = w$$
— это простейшее тригонометрическое ур-ние
Это ур-ние преобразуется в
$$x = \pi n + \operatorname{acos}{\left (w \right )}$$
$$x = \pi n + \operatorname{acos}{\left (w \right )} — \pi$$
Или
$$x = \pi n + \operatorname{acos}{\left (w \right )}$$
$$x = \pi n + \operatorname{acos}{\left (w \right )} — \pi$$
, где n — любое целое число
подставляем w:
$$x_{1} = \pi n + \operatorname{acos}{\left (w_{1} \right )}$$
$$x_{1} = \pi n + \operatorname{acos}{\left (1 \right )}$$
$$x_{1} = \pi n$$
$$x_{2} = \pi n + \operatorname{acos}{\left (w_{2} \right )}$$
$$x_{2} = \pi n + \operatorname{acos}{\left (-1 \right )}$$
$$x_{2} = \pi n + \pi$$
$$x_{3} = \pi n + \operatorname{acos}{\left (w_{1} \right )} — \pi$$
$$x_{3} = \pi n — \pi + \operatorname{acos}{\left (1 \right )}$$
$$x_{3} = \pi n — \pi$$
$$x_{4} = \pi n + \operatorname{acos}{\left (w_{2} \right )} — \pi$$
$$x_{4} = \pi n — \pi + \operatorname{acos}{\left (-1 \right )}$$
$$x_{4} = \pi n$$
Решите уравнение cos(x)^2=cos(x) (косинус от (х) в квадрате равно косинус от (х))
Дано уравнение$$\cos^{2}{\left (x \right )} = \cos{\left (x \right )}$$
преобразуем
$$\left(\cos{\left (x \right )} — 1\right) \cos{\left (x \right )} = 0$$
$$\cos^{2}{\left (x \right )} — \cos{\left (x \right )} = 0$$
Сделаем замену
$$w = \cos{\left (x \right )}$$
Это уравнение вида
a*w^2 + b*w + c = 0
Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:
$$w_{1} = \frac{\sqrt{D} — b}{2 a}$$
$$w_{2} = \frac{- \sqrt{D} — b}{2 a}$$
где D = b^2 — 4*a*c — это дискриминант.
Т.к.
$$a = 1$$
$$b = -1$$
$$c = 0$$
, то
D = b^2 - 4 * a * c =
(-1)^2 - 4 * (1) * (0) = 1
Т.к. D > 0, то уравнение имеет два корня.
w1 = (-b + sqrt(D)) / (2*a)
w2 = (-b - sqrt(D)) / (2*a)
или
$$w_{1} = 1$$
$$w_{2} = 0$$
делаем обратную замену
$$\cos{\left (x \right )} = w$$
Дано уравнение
$$\cos{\left (x \right )} = w$$
— это простейшее тригонометрическое ур-ние
Это ур-ние преобразуется в
$$x = \pi n + \operatorname{acos}{\left (w \right )}$$
$$x = \pi n + \operatorname{acos}{\left (w \right )} — \pi$$
Или
$$x = \pi n + \operatorname{acos}{\left (w \right )}$$
$$x = \pi n + \operatorname{acos}{\left (w \right )} — \pi$$
, где n — любое целое число
подставляем w:
$$x_{1} = \pi n + \operatorname{acos}{\left (w_{1} \right )}$$
$$x_{1} = \pi n + \operatorname{acos}{\left (1 \right )}$$
$$x_{1} = \pi n$$
$$x_{2} = \pi n + \operatorname{acos}{\left (w_{2} \right )}$$
$$x_{2} = \pi n + \operatorname{acos}{\left (0 \right )}$$
$$x_{2} = \pi n + \frac{\pi}{2}$$
$$x_{3} = \pi n + \operatorname{acos}{\left (w_{1} \right )} — \pi$$
$$x_{3} = \pi n — \pi + \operatorname{acos}{\left (1 \right )}$$
$$x_{3} = \pi n — \pi$$
$$x_{4} = \pi n + \operatorname{acos}{\left (w_{2} \right )} — \pi$$
$$x_{4} = \pi n — \pi + \operatorname{acos}{\left (0 \right )}$$
$$x_{4} = \pi n — \frac{\pi}{2}$$
Решите неравенство cos(x)^2+3*cos(x)>0 (косинус от (х) в квадрате плюс 3 умножить на косинус от (х) больше 0)
Дано неравенство:$$\cos^{2}{\left (x \right )} + 3 \cos{\left (x \right )} > 0$$
Чтобы решить это нер-во — надо сначала решить соотвествующее ур-ние:
$$\cos^{2}{\left (x \right )} + 3 \cos{\left (x \right )} = 0$$
Решаем:
Дано уравнение
$$\cos^{2}{\left (x \right )} + 3 \cos{\left (x \right )} = 0$$
преобразуем
$$\left(\cos{\left (x \right )} + 3\right) \cos{\left (x \right )} = 0$$
$$\cos^{2}{\left (x \right )} + 3 \cos{\left (x \right )} = 0$$
Сделаем замену
$$w = \cos{\left (x \right )}$$
Это уравнение вида
a*w^2 + b*w + c = 0
Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:
$$w_{1} = \frac{\sqrt{D} — b}{2 a}$$
$$w_{2} = \frac{- \sqrt{D} — b}{2 a}$$
где D = b^2 — 4*a*c — это дискриминант.
Т.к.
$$a = 1$$
$$b = 3$$
$$c = 0$$
, то
D = b^2 - 4 * a * c =
(3)^2 - 4 * (1) * (0) = 9
Т.к. D > 0, то уравнение имеет два корня.
w1 = (-b + sqrt(D)) / (2*a)
w2 = (-b - sqrt(D)) / (2*a)
или
$$w_{1} = 0$$
$$w_{2} = -3$$
делаем обратную замену
$$\cos{\left (x \right )} = w$$
Дано уравнение
$$\cos{\left (x \right )} = w$$
— это простейшее тригонометрическое ур-ние
Это ур-ние преобразуется в
$$x = \pi n + \operatorname{acos}{\left (w \right )}$$
$$x = \pi n + \operatorname{acos}{\left (w \right )} — \pi$$
Или
$$x = \pi n + \operatorname{acos}{\left (w \right )}$$
$$x = \pi n + \operatorname{acos}{\left (w \right )} — \pi$$
, где n — любое целое число
подставляем w:
$$x_{1} = \pi n + \operatorname{acos}{\left (w_{1} \right )}$$
$$x_{1} = \pi n + \operatorname{acos}{\left (0 \right )}$$
$$x_{1} = \pi n + \frac{\pi}{2}$$
$$x_{2} = \pi n + \operatorname{acos}{\left (w_{2} \right )}$$
$$x_{2} = \pi n + \operatorname{acos}{\left (-3 \right )}$$
$$x_{2} = \pi n + \operatorname{acos}{\left (-3 \right )}$$
$$x_{3} = \pi n + \operatorname{acos}{\left (w_{1} \right )} — \pi$$
$$x_{3} = \pi n — \pi + \operatorname{acos}{\left (0 \right )}$$
$$x_{3} = \pi n — \frac{\pi}{2}$$
$$x_{4} = \pi n + \operatorname{acos}{\left (w_{2} \right )} — \pi$$
$$x_{4} = \pi n — \pi + \operatorname{acos}{\left (-3 \right )}$$
$$x_{4} = \pi n — \pi + \operatorname{acos}{\left (-3 \right )}$$
$$x_{1} = \frac{\pi}{2}$$
$$x_{2} = \frac{3 \pi}{2}$$
$$x_{3} = 2 \pi — \operatorname{acos}{\left (-3 \right )}$$
$$x_{4} = \operatorname{acos}{\left (-3 \right )}$$
Исключаем комплексные решения:
$$x_{1} = \frac{\pi}{2}$$
$$x_{2} = \frac{3 \pi}{2}$$
Данные корни
$$x_{1} = \frac{\pi}{2}$$
$$x_{2} = \frac{3 \pi}{2}$$
являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки:
$$x_{0} Возьмём например точку
$$x_{0} = x_{1} — \frac{1}{10}$$
=
$$- \frac{1}{10} + \frac{\pi}{2}$$
=
$$- \frac{1}{10} + \frac{\pi}{2}$$
подставляем в выражение
$$\cos^{2}{\left (x \right )} + 3 \cos{\left (x \right )} > 0$$
$$\cos^{2}{\left (- \frac{1}{10} + \frac{\pi}{2} \right )} + 3 \cos{\left (- \frac{1}{10} + \frac{\pi}{2} \right )} > 0$$
2
sin (1/10) + 3*sin(1/10) > 0
значит одно из решений нашего неравенства будет при:
$$x
_____ _____
\ /
-------ο-------ο-------
x1 x2Другие решения неравенства будем получать переходом на следующий полюс
и т.д.
Ответ:
$$x $$x > \frac{3 \pi}{2}$$
Функция «Косинус-квадрат» — исчисление
Эта статья посвящена конкретной функции от подмножества действительных чисел до действительных чисел. Информация о функции, включая ее домен, диапазон и ключевые данные, касающиеся построения графиков, дифференциации и интеграции, представлена в статье.
Посмотреть полный список конкретных функций в этой вики
Для функций, включающих углы (тригонометрические функции, обратные тригонометрические функции и т. Д.), Мы следуем соглашению, согласно которому все углы измеряются в радианах.Так, например, уголизмеряется как
.
Определение
Эта функция, обозначенная как 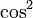 , определяется как сочетание функции квадрата и функции косинуса. Явно это карта:
, определяется как сочетание функции квадрата и функции косинуса. Явно это карта:
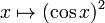
Для краткости запишем 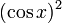 как
как 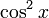 .
.
Основные данные
| Товар | Значение |
|---|---|
| Домен по умолчанию | все числа действительные, т.е. все 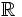 . . |
| диапазон | ![[0,1]](/800/600/https/calculus.subwiki.org/w/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) , т. Е. , т. Е. 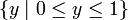 . . |
| период | 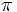 , т.е. , т.е. 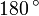 . . |
| локальные максимальные значения и точки достижения | Все локальные максимальные значения равны 1 и достигаются при целых кратных 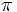 . . |
| местные минимальные значения и точки достижения | Все локальные минимальные значения равны 0 и достигаются при нечетных целых числах, кратных 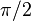 . . |
| точка перегиба (обе координаты) | нечетное число, кратное 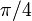 , со значением , со значением 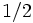 в каждой точке в каждой точке |
| производная | 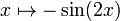 то есть отрицательная функция синусоиды двойного угла. то есть отрицательная функция синусоиды двойного угла. |
| вторая производная | 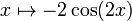 |
| высшие производные | 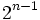 раз выражение, которое равно раз выражение, которое равно 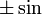 или или 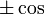 из из 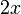 , в зависимости от остатка от , в зависимости от остатка от 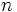 mod 4. mod 4. |
| первообразное | 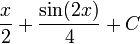 |
| среднее значение за период | 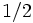 |
| выражение как синусоидальная функция плюс постоянная функция | 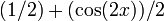 |
| важные симметрии | даже функция В более общем смысле, имеет зеркальную симметрию относительно всех вертикальных линий 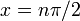 , , 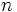 — целое число. — целое число. Также имеет симметрию полуоборота относительно всех точек формы 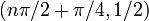 , т.е.е., все точки перегиба. , т.е.е., все точки перегиба. |
| на основе увеличения / уменьшения и вогнутости вверх / вниз | Для каждого целого числа 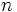 интервал от интервал от 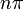 до до 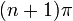 разделен на четыре части: разделен на четыре части: 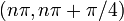 : убывающая и вогнутая вниз : убывающая и вогнутая вниз  : убывающая и вогнутая вверх : убывающая и вогнутая вверх 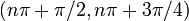 : увеличивающаяся и вогнутая вверх : увеличивающаяся и вогнутая вверх 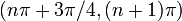 |
\ [\ frac {{dy}} {{dx}} = \ mathop {\ lim} \ limits _ {\ Delta x \ to 0} \ frac {{ \ left [{\ cos \ left ({x + \ Delta x} \ right) + \ cos x} \ right] \ left [{\ cos \ left ({x + \ Delta x} \ right) — \ cos x } \ right]}} {{\ Delta x}} \]
По формуле из тригонометрии \ [\ cos A — \ cos B = — 2 \ sin \ left ({\ frac {{A + B}} {2}} \ right) \ sin \ left ({\ frac {{ A — B}} {2}} \ right) \]
Пример : Найдите производную от \ [y = f \ left (x \ right) = {\ cos ^ 2} \ left ({{x ^ 2} + 8} \ right) \]
У нас есть заданная функция как
\ [y = {\ cos ^ 2} \ left ({{x ^ 2} + 8} \ right) \]
Дифференцируя по переменной $$ x $$, получаем
\ [\ frac {{dy}} {{dx}} = \ frac {d} {{dx}} {\ cos ^ 2} \ left ({ {x ^ 2} + 8} \ right) \]
Используя правило $$ \ frac {d} {{dx}} {\ cos ^ 2} x = — 2 \ cos x \ sin x $$, получаем
\ [\ begin {gather} \ frac {{dy }} {{dx}} = 2 \ cos \ left ({{x ^ 2} + 8} \ right) \ frac {d} {{dx}} \ cos \ left ({{x ^ 2} + 8} \ right) \\ \ frac {{dy}} {{dx}} = — 2 \ cos \ left ({{x ^ 2} + 8} \ right) \ sin \ left ({{x ^ 2} + 8 } \ right) \ frac {d} {{dx}} \ left ({{x ^ 2} + 8} \ right) \\ \ frac {{dy}} {{dx}} = — 2 \ cos \ left ({{x ^ 2} + 8} \ right) \ sin \ left ({{x ^ 2} + 8} \ right) \ left ({2x + 0} \ right) \\ \ frac {{dy}} {{dx}} = — 4x \ cos \ left ({{x ^ 2} + 8} \ right) \ sin \ left ({{x ^ 2} + 8} \ right) \\ \ end {собрано} \ ]
— cos (0) — Solumaths
Резюме:
Тригонометрическая функция cos вычисляет косинус угла в радианах, градусы или градианы.
Cos онлайнОписание:
Калькулятор позволяет использовать большинство тригонометрических функций , можно рассчитать косинус , синус и касательная угла через одноименные функции.,
Тригонометрическая функция косинус отмечена cos , позволяет вычислить косинус угла онлайн , можно использовать разные угловые единицы: градусы, градианы и радианы, которые являются угловыми единицами по умолчанию.
- Расчет косинуса
- Специальные значения косинуса
Косинус для вычисления угла в радианах
Калькулятор косинуса позволяет через функцию cos вычислить онлайн косинус угла в радианах, сначала необходимо выберите нужную единицу, нажав на кнопку параметров модуля расчета.После этого можно приступать к расчетам.
Чтобы вычислить косинус онлайн числа «пи / 6», введите cos (`pi / 6`), после вычисления результат sqrt (3) / 2 возвращается.
Обратите внимание, что функция косинуса может распознавать некоторые особые углы и делать расчеты со специальными связанными значениями в точной форме.
Вычислить косинус угла в градусах
Чтобы вычислить косинус угла в градусах, необходимо сначала выбрать нужные единицы нажав на кнопку опций модуля расчета.После этого вы можете приступить к расчету.
Чтобы вычислить косинус 90, введите cos (90), после вычисления restults 0 возвращается.
Вычислить косинус угла в градусах
Чтобы вычислить косинус угла в градусах, необходимо сначала выбрать желаемую единицу измерения. нажав на кнопку опций модуля расчета. После этого вы можете приступить к расчету.
Чтобы вычислить косинус 50, введите cos (50), после вычисления возвращается результат sqrt (2) / 2.
Обратите внимание, что функция косинуса способна распознавать некоторые особые углы и выполнять исчисление со специальными связанными точными значениями.
Косинус допускает некоторые особые значения, которые калькулятор может определять в точной форме. Вот список специальные значения косинуса :
Производная косинуса равна -sin (x).
Первообразная косинуса равна sin (x).
Функция косинуса является четной функцией для каждого действительного x: `cos (-x) = cos (x)`. Следствием для кривой, представляющей функцию косинуса, является то, что она допускает ось ординат как ось симметрии.
В калькуляторе есть решающая программа, позволяющая решать уравнение с косинусом в виде cos (x) = a .Расчеты для получения результата детализированы, поэтому можно будет решать уравнения вроде `Сов (х) = 1 / 2` или `2 * соз (х) = SQRT (2)` с шагами расчета.
Тригонометрическая функция cos вычисляет косинус угла в радианах, градусы или градианы.
Синтаксис:
cos (x), где x — мера угла в градусах, радианах или градианах.Примеры:
cos (`0`), возвращает 1Производный косинус:
Чтобы дифференцировать функцию косинуса онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции косинуса
Производная от cos (x) является производной (`cos (x)`) = `-sin (x)`
Первоначальный косинус:
Калькулятор первообразной позволяет вычислить первообразную функции косинуса.
Первообразная от cos (x) является первообразной (`cos (x)`) = `sin (x)`
Предельный косинус:
Калькулятор пределов позволяет вычислить пределы функции косинуса.
Предел для cos (x) является пределом (`cos (x)`)
Косинус обратной функции:
Обратная функция от косинуса — это функция арккосинуса, отмеченная как arccos.
Графический косинус:
Графический калькулятор может построить функцию косинуса в интервале ее определения.
Свойство функции косинус:
Функция косинуса является четной функцией.Рассчитать онлайн с помощью cos (косинус) ,
Функция Sinc в квадрате — Исчисление
Эта статья посвящена конкретной функции от подмножества действительных чисел до действительных чисел. Информация о функции, включая ее домен, диапазон и ключевые данные, касающиеся построения графиков, дифференциации и интеграции, представлена в статье.Посмотреть полный список конкретных функций в этой вики
Для функций, включающих углы (тригонометрические функции, обратные тригонометрические функции и т. Д.), Мы следуем соглашению, согласно которому все углы измеряются в радианах.Так, например, уголизмеряется как
.
Определение
Эта функция определяется как комбинация функции квадрата и функции sinc. Явно это дается как:
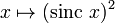
Как вариант:
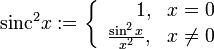
Основные данные
| Товар | Значение |
|---|---|
| домен по умолчанию | все числа действительные, т.е. все 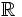 |
| диапазон | закрытый интервал ![[0,1]](/800/600/https/calculus.subwiki.org/w/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) , т.е.е., набор , т.е.е., набор 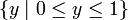 абсолютное максимальное значение: 1, абсолютное минимальное значение: 0 |
| период | нет; функция не периодическая |
| горизонтальные асимптоты | 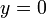 , т.е. ось , т.е. ось 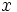 . Это потому, что . Это потому, что 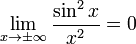 , что, в свою очередь, можно вывести из того факта, что числитель ограничен, а величина знаменателя приближается к , что, в свою очередь, можно вывести из того факта, что числитель ограничен, а величина знаменателя приближается к 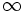 . . |
| локальные максимальные значения и точки достижения | Локальные максимальные значения встречаются во всех точках, где 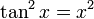 .Существует аномальный локальный максимум на уровне .Существует аномальный локальный максимум на уровне 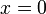 со значением 1. Все остальные локальные максимумы возникают в точках, близких к нечетным кратным со значением 1. Все остальные локальные максимумы возникают в точках, близких к нечетным кратным 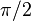 (, кроме самих (, кроме самих 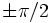 , хотя и не совсем в этих точках. , хотя и не совсем в этих точках. |
| местные минимальные значения и точки достижения | Локальные минимальные значения встречаются во всех точках, где 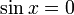 , кроме самой точки , кроме самой точки 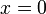 . Это в точности ненулевые целые числа, кратные . Это в точности ненулевые целые числа, кратные 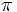 . Все значения равны нулю. . Все значения равны нулю. |
| производная | Заполните позже |
| вторая производная | Заполните позже |
| первообразное | 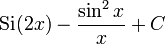 . См. # Первое первообразное. Здесь . См. # Первое первообразное. Здесь 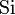 обозначает синусоидальный интеграл, первообразную для функции sinc. обозначает синусоидальный интеграл, первообразную для функции sinc. |
| степенная серия и серия Тейлора | Ряд степеней около 0 (который также является рядом Тейлора) — это Заполните его позже |
График
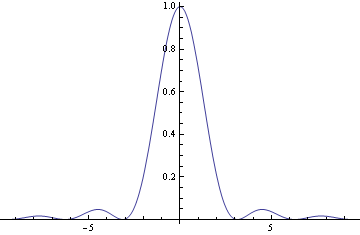
Вот график на интервале ![[-3\pi,3\pi]](/800/600/https/calculus.subwiki.org/w/images/math/7/1/a/71aa662f93de4c984d69940d031e3e7b.png) :
:

График немного нечеткий, вот альтернативная версия, в которой используются разные масштабы для оси 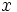 и оси
и оси 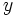 :
:
Интеграция
Первая первообразная
Обозначим 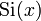 функцию
функцию 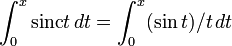 .Интегрируем
.Интегрируем 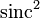 и получаем следующий ответ в терминах
и получаем следующий ответ в терминах 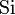 :
:
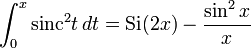
Для неопределенного интеграла можно поставить 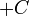 в конце.
в конце.
Делаем это с помощью интеграции по частям:
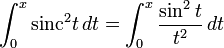
Возьмите 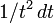 как часть для интеграции. Мы получили:
как часть для интеграции. Мы получили:
![\left[\sin^2t\left(\frac{-1}{t}\right)\right]_0^x - \int_0^x \sin(2t) \frac{-1}{t} \, dt](/800/600/https/calculus.subwiki.org/w/images/math/3/5/0/350763d748fe28f67b7e837e45d01db1.png)
Это становится:
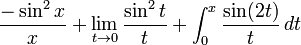
Предельное выражение равно нулю, потому что  имеет ноль порядка 2 в нуле. Для выражения интегрирования установите
имеет ноль порядка 2 в нуле. Для выражения интегрирования установите 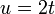 и получите
и получите 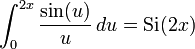 .Подключив снова, получаем желаемый ответ.
.Подключив снова, получаем желаемый ответ.
Неправильный определенный интеграл
Мы знаем, что:
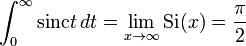
Используя это, получаем, что:
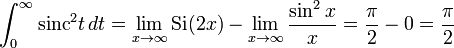
Аналогично:
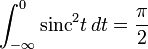
Всего:
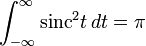
Обратите внимание, что неправильное интегральное значение — это , то же самое для функции sinc и ее квадрата. Грубо говоря, функция sinc больше, чем ее квадрат, когда оба положительны, но функция sinc также принимает отрицательные значения, а ее квадрат — нет, поэтому эти различия уравновешиваются в общей интеграции.
,
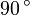 измеряется как
измеряется как