Все формулы средней линии трапеции
Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются — верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Средняя линия трапеции — отрезок соединяющий середины боковых сторон и расположен параллельно к основаниям. Длина средней линии, равна полу сумме оснований.
1. Формула средней линии трапеции через основания
b — верхнее основание
a — нижнее основание
m— средняя линия
Формула средней линии, (m ):
2. Формулы средней линии через основание, высоту и углы при нижнем основании
b — верхнее основание
a — нижнее основание
α, β — углы трапеции
h — высота трапеции
m — средняя линия
Формулы средней линии трапеции, (m):
3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями
α, β — углы между диагоналями
d1 , d2 — диагонали трапеции
h — высота трапеции
m — средняя линия
Формулы средней линии трапеции, (m ):
4. Формула средней линии трапеции через площадь и высоту
S — площадь трапеции
h — высота трапеции
m — средняя линия
Формула средней линии трапеции, (m):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
www-formula.ru
Средняя линия трапеции | Треугольники
Что такое средняя линия трапеции? Какими свойствами она обладает?
Определение
Средняя линия трапеции — это отрезок, соединяющий середины боковых сторон трапеции.
ABCD — трапеция,
AD ∥ BC,
M — середина AB,
N — середина CD,
MN — средняя линия трапеции ABCD.
Свойства средней линии трапеции
1) Средняя линия трапеции параллельна основаниям.
2) Средняя линия трапеции равна полусумме оснований.
В трапеции ABCD (AD ∥ BC)
Задача 1.
Основания трапеции относятся как 4:7, а средняя линия равна 55 см. Найти основания трапеции.
Дано: ABCD — трапеция,
AD ∥ BC, MN- средняя линия трапеции,
MN=55 см, BC:AD=4:7.
Найти: AD, BC.
Решение:
Пусть k — коэффициент пропорциональности.
Тогда BC=4k см, AD=7k см.
По свойству средней линии трапеции,
Составляем уравнение:
Отсюда BC=4∙10=40 см, AD=7∙10=70 см.
Ответ: 40 см, 70 см.
Задача 2.
Средняя линия трапеции равна 15 см, а одно из оснований на 6 см больше другого. Найти основания трапеции.
Дано: ABCD — трапеция,
AD ∥ BC, MN- средняя линия трапеции,
MN=15 см, AD на 6 см больше BC.
Найти: AD, BC.
Решение:
Пусть BC=x см, тогда AD=(x+6) см.
Так как средняя линия трапеции равна полусумме оснований,
Составим уравнение и решим его:
Значит, BC=12 см, AD=12+6=18 см.
Ответ:12 см, 18 см.
www.treugolniki.ru
чему равна, свойства, доказательство теоремы
Средняя линия трапеции, а особенно ее свойства, очень часто используются в геометрии для решения задач и доказательства тех или иных теорем.
Трапеция – это четырехугольник, у которого только 2 стороны параллельны друг другу. Параллельные стороны называют основаниями (на рисунке 1 — AD и BC), две другие – боковыми (на рисунке AB и CD).
Средняя линия трапеции – это отрезок, соединяющий середины ее боковых сторон (на рисунке 1 — KL).
Свойства средней линии трапеции
- Длина средней линии равна половине суммы длин ее оснований:
- Средняя линия всегда параллельна ее основаниям.
Доказательство теоремы о средней линии трапеции
Доказать, что средняя линия трапеции равна полусумме ее оснований и параллельна этим основаниям.
Дана трапеция ABCD со средней линией KL. Для доказательства рассматриваемых свойств требуется провести прямую через точки B и L. На рисунке 2 это прямая BQ. А также продолжить основание AD до пересечения с прямой BQ.
Рассмотрим полученные треугольники LBC и LQD:
- По определению средней линии KL точка L является серединой отрезка CD. Отсюда следует, что отрезки CL и LD равны.
- ∠ BLC = ∠ QLD, так как эти углы вертикальные.
- ∠ BCL = ∠ LDQ, так как эти углы накрест лежащие при параллельных прямых AD и BC и секущей CD.
Из этих 3 равенств следует, что рассмотренные ранее треугольники LBC и LQD равны по 1 стороне и двум прилежащим к ней углам (см. рис. 3). Следовательно, ∠ LBC = ∠ LQD, BC=DQ и самое главное — BL=LQ => KL, являющаяся средней линией трапеции ABCD, также является и средней линией треугольника ABQ. Согласно свойству средней линией треугольника ABQ получаем:
- KL = 1/2AQ = 1/2 (AD+DQ) = 1/2 (AD+BC)
- KL || AD по свойству средней линии треугольника. А так как AD || BC по определению трапеции, то KL || BC.
Для закрепления материала рекомендуем Вам просмотреть видео урок по данной теме:
Понравилась статья, расскажите о ней друзьям:
Скорее всего, Вам будет интересно:
Трапеция. Свойства и элементы трапеции
Виды трапеций
Равнобедренная трапеция — это вид трапеции с равными боковыми сторонами.
Также встречаются такие названия, как равнобокая или равнобочная.
Прямоугольная трапеция — это трапеция, у которой углы при боковой стороне прямые.
Элементы трапеции
a, b — основания трапеции (a параллельно b),
m, n — боковые стороны трапеции,
d1, d2 — диагонали трапеции,
h — высота трапеции (отрезок, соединяющий основания и при этом перпендикулярен им),
MN — средняя линия (отрезок, соединяющий середины боковых сторон).
Площадь трапеции
- Через полусумму оснований a, b и высоту h: S = \frac{a + b}{2}\cdot h
- Через среднюю линию MN и высоту h: S = MN\cdot h
- Через диагонали d1, d2 и угол (\sin \varphi) между ними: S = \frac{d_{1} d_{2} \sin \varphi}{2}
Свойства трапеции
Средняя линия трапеции
Средняя линия параллельна основаниям, равна их полусумме и разделяет каждый отрезок с концами, находящимися на прямых, которые содержат основания, (к примеру, высоту фигуры) пополам:
MN || a, MN || b, MN = \frac{a + b}{2}
Сумма углов трапеции
Сумма углов трапеции, прилежащих к каждой боковой стороне, равна 180^{\circ}:
\alpha + \beta = 180^{\circ}
\gamma + \delta =180^{\circ}
Равновеликие треугольники трапеции
Равновеликими, то есть имеющими равные площади, являются отрезки диагоналей и треугольники AOB и DOC, образованные боковыми сторонами.
Подобие образованных треугольников трапеции
Подобными треугольниками являются AOD и COB, которые образованы своими основаниями и отрезками диагоналей.
\triangle AOD \sim \triangle COB
Коэффициент подобия k находится по формуле:
k = \frac{AD}{BC}
Причем отношение площадей этих треугольников равно k^{2}.
Отношение длин отрезков и оснований
Каждый отрезок, соединяющий основания и проходящий через точку пересечения диагоналей трапеции, поделен этой точкой в отношении:
\frac{OX}{OY} = \frac{BC}{AD}
Это будет являться справедливым и для высоты с самими диагоналями.
Описанная около трапеции окружность
Каждая равнобокая трапеция может содержать описанную окружность. Только равнобокую трапецию возможно вписать в окружность.
Вписанная в трапецию окружность
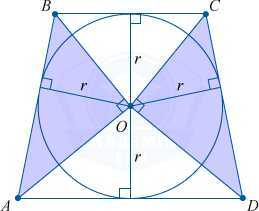
Треугольники AOB и DOC являются прямоугольными, если трапеция ABCD описана около окружности. Центром же вписанной окружности будет являться точка O.
Опущенные на гипотенузы, высоты этих треугольников, тождественны радиусу вписанной окружности, а высота трапеции тождественна диаметру вписанной окружности.
academyege.ru
Найдите среднюю линию трапеции
В этой статье для вас сделана очередная подборка задач с трапецией. Условия так или иначе связаны с её средней линией. Типы заданий взяты из открытого банка типовых задач. Если есть желание, то можете освежить свои теоретические знания связанные с трапецией. На блоге уже рассмотрены задачи условия которых связаны с площадью трапеции, а также с углами. Кратко о средней линии:
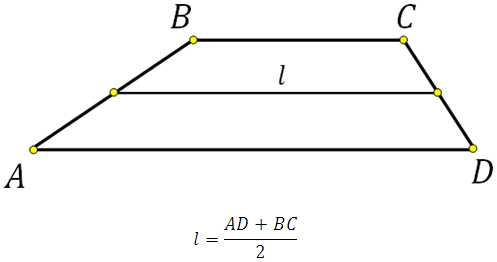
Средняя линия трапеции соединяет середины боковых сторон. Она параллельна основаниям и равна их полусумме.
Перед решением задач давайте рассмотрим теоретический пример.
Дана трапеция ABCD. Диагональ АС пересекаясь со средней линией образует точку К, диагональ BD точку L. Доказать, что отрезок KL равен половине разности оснований.
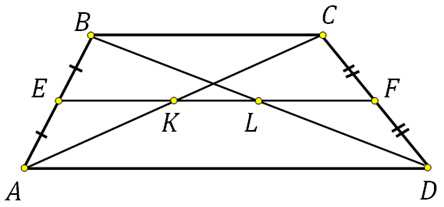
Давайте сначала отметим тот факт, что средняя линия трапеции делит пополам любой отрезок концы которого лежат на её основаниях. Этот вывод напрашивается сам собой. Представьте отрезок соединяющий две точки оснований, он разобьёт данную трапецию на две других. Получится, что отрезок параллельный основаниям трапеции и проходящий через середину боковой стороны на другой боковой стороне пройдёт через её середину.
Так же это основывается на теореме Фалеса:
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.
То есть в данном случае К середина АС и L середина BD. Следовательно EK есть средняя линия треугольника АВС, LF есть средняя линия треугольника DCB. По свойству средней линии треугольника:
Можем теперь выразить отрезок KL через основания:
Доказано!
Данный пример приведён не просто так. В задачах для самостоятельного решения имеется именно такая задача. Только в ней не сказано, что отрезок соединяющий середины диагоналей лежит на средней линии. Рассмотрим задачи:
27819. Найдите среднюю линию трапеции, если ее основания равны 30 и 16.
Вычисляем по формуле:
Ответ: 23
27820. Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.
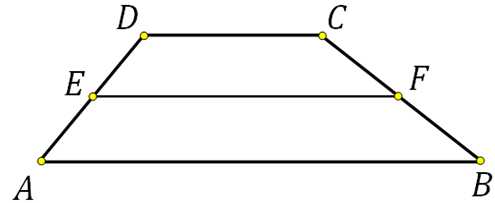
Выразим большее основание:
Таким образом:
Ответ: 38
27836. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.
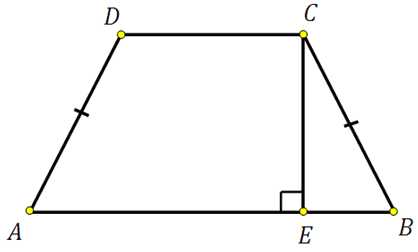
Для того, чтобы найти среднюю линию необходимо знать основания. Основание АВ найти просто: 10+4=14. Найдём DC.
Построим второй перпендикуляр DF:
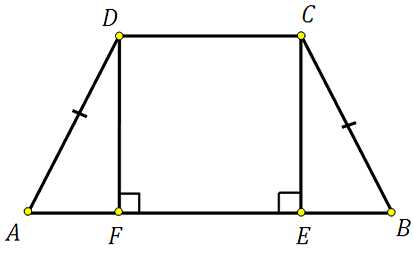
Отрезки AF, FE и EB будут равны соответственно 4, 6 и 4. Почему?
В равнобедренной трапеции перпендикуляры опущенные к большему основанию разбивают его на три отрезка. Два из них, являющиеся катетами отсекаемых прямоугольных треугольников, равны друг другу. Третий отрезок равен меньшему основанию, так как при построении указанных высот образуется прямоугольник, а в прямоугольнике противолежащие стороны равны. В данной задаче:
Таким образом DC=6. Вычисляем:
Ответ: 10
27839. Основания трапеции относятся 2:3, а средняя линия равна 5. Найдите меньшее основание.
Введём коэффициент пропорциональности х. Тогда АВ=3х, DC=2х. Можем записать:
Следовательно меньшее основание равно 2∙2=4.
Ответ: 4
27840. Периметр равнобедренной трапеции равен 80, ее средняя линия равна боковой стороне. Найдите боковую сторону трапеции.
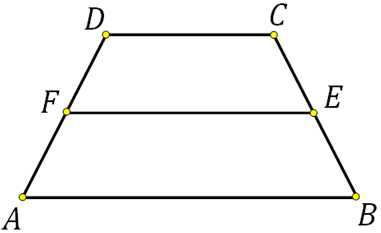
Исходя из условия можем записать:
Если обозначить среднюю линию через величину х, то получится:
Второе уравнение уже можно записать в виде:
Ответ: 20
27841. Средняя линия трапеции равна 7, а одно из ее оснований больше другого на 4. Найдите большее основание трапеции.
Обозначим меньшее основание (DC) как х, тогда большее (AB) будет равно х+4. Можем записать
Получили, что меньшее основание рано пяти, значит большее равно 9.
Ответ: 9
27842. Средняя линия трапеции равна 12. Одна из диагоналей делит ее на два отрезка, разность которых равна 2. Найдите большее основание трапеции.
Большее основание трапеции мы без труда найдём если вычислим отрезок ЕО. Он является средней линией в треугольнике ADB, и АВ=2∙ЕО.
Что имеем? Сказано что средняя линия равна 12 и разность отрезков ЕО и ОF равна 2. Можем записать два уравнения и решить систему:
Понятно, что в данном случае подобрать пару чисел можно без вычислений, это 5 и 7. Но, всё-таки, решим систему:
Значит ЕО=12–5=7. Таким образом, большее основание равно АВ=2∙ЕО=14.
Ответ: 14
27844. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.
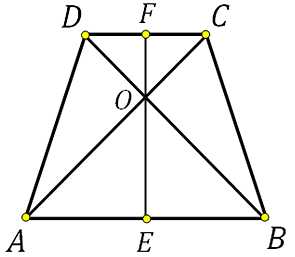
Сразу отметим, что высота проведённая через точку пересечения диагоналей в равнобедренной трапеции лежит на оси симметрии и разбивает трапецию на две равные прямоугольные трапеции, то есть основания этой высотой делятся пополам.
Казалось бы, для вычисления средней линии мы должны найти основания. Тут небольшой тупик возникает… Как зная высоту, в данном случае, вычислить основания? А ни как! Таких трапеций с фиксированной высотой и диагоналями пересекающимися по углом 90 градусов можно построить множество. Как быть?
Посмотрите на формулу средней линии трапеции. Ведь нам необязательно знать сами основания, достаточно узнать их сумму (или полусумму). Это мы сделать можем.
Так как диагонали пересекаются под прямым углом, то высотой EF образуются равнобедренные прямоугольные треугольники:
При чём:
Из выше сказанного следует, что FO=DF=FC, а OE=AE=EB. Теперь запишем чему равна высота выраженная через отрезки DF и AE:
Таким образом, средняя линия равна 12.
*Вообще это задачка, как вы поняли, для устного счёта. Но, уверен, представленное подробное объяснение необходимо. А так… Если взглянуть на рисунок (при условии, что при построении соблюдён угол между диагоналями), сразу в глаза бросается равенство FO=DF=FC, а OE=AE=EB.
Ответ: 12
В составе прототипов имеется ещё типы заданий с трапециями. Построена она на листе в клетку и требуется найти среднюю линию, сторона клетки обычно равна 1, но может быть другая величина.
27848. Найдите среднюю линию трапеции ABCD, если стороны квадратных клеток равны 1.
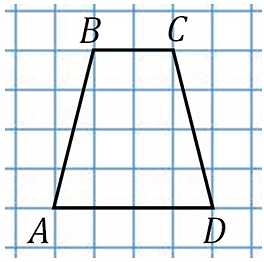
Всё просто, вычисляем основания по клеткам и используем формулу: (2+4)/2=3
Ответ: 3
Если же основания построены под углом к клеточной сетке, то есть два способа. Например!
28854.Найдите среднюю линию трапеции ABCD, если стороны квадратных клеток равны √2.
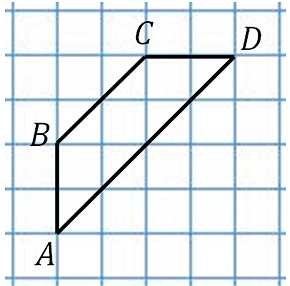
В данном случае видно, что средняя линия трапеции равна трём диагоналям клетки. Диагональ одной клетки по теореме Пифагора будет равна:
Значит средняя линия равна 2∙3=6.
Конечно, есть и другой путь решения.
Если допустить мысль, что основания трапеции могут лежать по отношению к сетке под углом не 45 градусов, а например 30, или другим, то вполне применим следующий метод (таких задач на ЕГЭ не предвидится):
Вычисляем основания используя теорему Пифагора, а далее используем формулу средней линии.
Основание AD при данных условиях это диагональ в прямоугольном треугольнике с катетами равными 4 сторонам клетки, вычисляем:
Основание BC это диагональ в прямоугольном треугольнике катетами равными 2 сторонам клетки, вычисляем:
Средняя линия будет равна (8+4)/2=6.
*То есть при данном подходе, как бы ни была построена трапеция всегда можно вычислить основания.
Ответ: 6
27853. Найдите высоту трапеции ABCD, опущенную из вершины B, если стороны квадратных клеток равны √2.

Высота трапеции равна диагонали клетки. Вычисляем по теореме Пифагора:
Ответ: 2
27821. Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
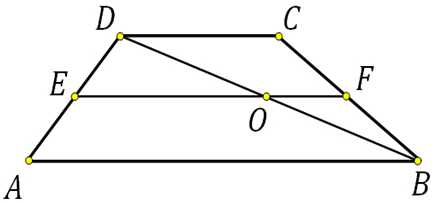
Посмотреть решение
27838.Периметр трапеции равен 50, а сумма непараллельных сторон равна 20. Найдите среднюю линию трапеции.
Посмотреть решение
27843. Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.
Посмотреть решение
На этом всё, успеха вам!
С уважением, Александр Крутицких.
P,S: Расскажите о сайте в социальных сетях.
matematikalegko.ru
