Прямоугольный треугольник
Дополнительное построение, ведущее к теореме о средней линии треугольника, трапеции и свойствам подобия треугольников.
Проводим из вершины прямого угла отрезок прямой, составляющий с катетом CA угол, равный углу CAB заданного прямоугольного треугольника ABC. В результате получим равнобедренный треугольник ACM с углами при основании . Но другой треугольник, получающийся при таком построении, также будет равнобедренным, поскольку каждый его угол при основании равен (по свойству углов прямоугольного треугольника и по построению — из прямого угла «вычли» угол ). В силу того, что треугольники BMC и AMC равнобедренные с общей стороной MC имеем равенство MB=MA=MC, т.е. MC – медиана, проведенная к гипотенузе прямоугольного треугольника, и она равна половине гипотенузы.Следствие 1. Середина гипотенузы является центром окружности, описанной вокруг этого треугольника, поскольку получилось, что середина гипотенузы равноудалена от вершин прямоугольного треугольника.
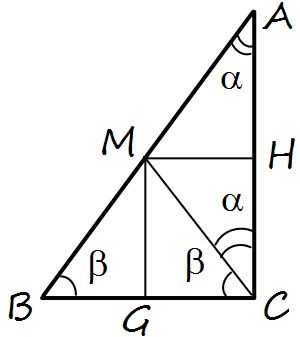Опустим в равнобедренных треугольниках BMC и AMC высоты MH и MG на основания. Поскольку в равнобедренном треугольнике, высота, опущенная на основание, является также и медианой (и биссектрисой), то MH и MG –линии прямоугольного треугольника, соединяющие середину гипотенузы с серединами катетов. По построению они оказываются параллельными противоположным катетам и равные их половинам, поскольку треугольники равны MHC и MGC равны (причем MHCG – прямоугольник). Этот результат является основанием для доказательства теоремы о средней линии произвольного треугольника и, далее, средней линии трапеции и свойства пропорциональности отрезков, отсекаемых параллельными прямыми на двух пересекающих их прямых. Все прямоугольные треугольники с одинаковым острым углом — подобны. Взгляд на тригонометрические функции.Пример дополнительного построения — высота, опущенная на гипотенузу. Вывод теоремы Пифагора на основе подобия треугольников.
basharov.me
Признаки подобия треугольников. Средняя линия.
Тестирование онлайн
Подобие треугольников
Пропорциональные отрезки в треугольнике
Определение
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
Теорема. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
Признаки подобия треугольников
Теорема.
Теорема. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Теорема. Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Средняя линия треугольника
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Теорема. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
fizmat.by
math-public:srednyaya_liniya_treugolnika [Президентский ФМЛ №239]
Определение
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.
Свойства средней линии треугольника
Средняя линия треугольника параллельна стороне треугольника и равна ее половине.
Доказательство
Рассмотрим $\triangle ABC$, с основанием $AC$ и средней линией $MN$.
Докажем, что $MN\parallel AC$ и $MN=\dfrac{1}{2}\cdot AC$.
На прямой $MN$ за точкой $N$ выберем точку $D$ так, чтобы выполнялось $MN=ND$.
Тогда $\triangle BMN=\triangle NDC$ по первому признаку равенства ($BN=NC, MN=ND$, $\angle BNM=\angle DNC$).
Тогда $\angle 1=\angle 2$, следовательно, $AB\parallel DC$.
Кроме того, из равенства треугольников следует, что $MB=DC$.
Но $MB=MA$, следовательно $MA=DC$.
Тогда $AMDC$ – параллелограмм ($DC=MA$, $MA\parallel DC$).
Следовательно, $MD\parallel AC$ и $AC=MD=2\cdot MN$.
Признаки средней линии треугольника
Если в треугольнике $ABC$ точка $M$ – середина стороны $AB$, а точка $N$ принадлежит стороне $BC$, и при этом $MN\parallel AC$, то $MN$ – средняя линия.
Если в треугольнике $ABC$ точки $M$ и $N$ принадлежат сторонам $AB$ и $BC$ соответственно, при этом $MN\parallel AC$ и $2|MN|=|AC|$, то $MN$ – средняя линия.
Доказательство
Докажем первый пункт теоремы.
Рассмотрим $\triangle ABC$, в котором $M$ – середина $AB$, $N$ лежит на стороне $BC$, $MN\parallel AC$.
Докажем, что $MN$ – средняя линия.
Выберем на прямой $MN$ за точкой $N$ такую точку $D$, что $MD=AC$.
Тогда $AMDC$ – параллелограмм ($AC=MD$, $AC\parallel MD$).
Следовательно, $\angle B=\angle 3, \angle 1=\angle 2$, так как $AM\parallel CD$.
Кроме того $AM=DC$, как противоположные стороны параллелограмма.
Следовательно, $BM=MA=DC$.
Тогда $\triangle BMN=\triangle NDC$ по второму признаку равенства.
Следовательно, $BN=NC$, то есть $MN$ – средняя линия.
Докажем второй пункт теоремы.
Рассмотрим треугольник $ABC$, в котором на сторонах $AB$ и $BC$ взяты точки $M$ и $N$ соответственно так, что $MN\parallel AC$ и $2\cdot MN=AC$.
Докажем, что тогда $MN$ – средняя линия треугольника $ABC$.
Пусть $D$ – это середина $AC$. Тогда $MNCD$ – параллелограмм ($MN=DC$, $MN\parallel DC$).
Следовательно, $MD\parallel NC$.
Тогда $\angle 1=\angle C=\angle 2$, как соответственные при параллельных прямых.
Кроме того $\angle A=\angle 3$.
Следовательно, $\triangle BMN=\triangle AMD$ по второму признаку равенства.
Тогда $BM=MA$ и $BN=MD=NC$, то есть $MN$ – средняя линия $\triangle ABC$.
Замечание
Третий признак средней линии неверен.
math-public/srednyaya_liniya_treugolnika.txt · Последние изменения: 2016/04/13 19:46 — labreslav
Треугольник — ov1098s Jimdo-Page!
1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то треугольники равны.
2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то треугольники равны.
3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то треугольники равны.
1. По двум катетам.
2. По катету и гипотенузе.
3. По гипотенузе и острому углу.
4. По катету и острому углу.
1. Сумма внутренних углов треугольника равна 180 градусов.
2. Внешний угол треугольника равен сумме двух внутренних не смежных с ним углов.
3. Сумма внутренних углов выпуклого n-угольника равна 180(n-2).
4. Сумма внешних углов n-угольника равна 360 градусов.
5. Угол между биссектрисами смежных углов равен 90.
6. Биссектрисы внутренних односторонних углов при параллельных прямых и секущей перпендикулярны.
1. Сумма двух сторон треугольника больше его третьей стороны.
2. Сумма звеньев ломаной больше отрезка, соединяющего начало первого звена с концом последнего.
3. Против большего угла треугольника лежит большая сторона.
4. Против большей стороны треугольника лежит больший угол.
5. Гипотенуза прямоугольного треугольника больше катета.
6. Если из одной точки проведены к прямой перпендикуляр м наклонные, то
1)перпендикуляр короче наклонных
2) большей наклонной соответствует большая проекция и наоборот.
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.
Средняя линия треугольника параллельна стороне треугольника и равна ее половине.
1. Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины.
2. Если медиана треугольника равна половине стороны, к которой она проведена, то треугольник прямоугольный.
3. Медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, которая является центром окружности, описанной около треугольника.
Прямые, содержащие высоты треугольника, пересекаются в одной точке.
Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в треугольник.
Биссектриса треугольника делит его сторону на отрезки пропорциональные двум другим сторонам.
1. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
2. Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами, равны, то треугольники подобны.
3. Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого, то треугольники подобны.
1. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
2. Если два треугольника имеют равные углы, то их площади относятся как произведения сторон, заключающих эти углы.
1. Катет прямоугольного треугольника равен произведению гипотенузы на синус противолежащего или косинус прилежащего к этому катету острого угла.
2. Катет прямоугольного треугольника равен другому катету, умноженному на тангенс противолежащего или котангенс прилежащего к этому катету острого угла.
3. Катет прямоугольного треугольника, лежащий против угла 30 градусов, равен половине гипотенузы.
4. R=c:2; r=(a+b-c):2=p-с, где a,b-катеты, а с-гипотенуза; R-радиус описанной окружности, r- радиус вписанной окружности, p- полупериметр.
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное проекций катетов на гипотенузу, а каждый катет есть среднее пропорциональное гипотенузы и своей проекции на гипотенузу.
Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
Стороны треугольника пропорциональны синусам противолежащих углов.
Отношение стороны треугольника к синусу противолежащего угла равно диаметру окружности, описанной около треугольника.
площадь треугольника.doc
Microsoft Word Document 17.5 KB
Параллелограммом называется четырехугольник, противолежащие стороны которого параллельны.
1. Диагональ разбивает параллелограмм на два равных треугольника.
2. Противоположные стороны параллелограмма попарно равны.
3. Противоположные углы параллелограмма попарно равны.
4. Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.
5. Если противоположные стороны четырехугольника попарно равны, то этот четырехугольник — параллелограмм.
6. Если две противоположные стороны четырехугольника равны и параллельны,то этот четырехугольник — параллелограмм.
7. Если диагонали четырехугольника делятся точкой пересечения пополам,то этот четырехугольник — параллелограмм.
Середины сторон любого четырехугольника являются вершинами параллелограмма, площадь которого равна половине площади четырехугольника.
Прямоугольником называется параллелограмм с прямым углом.
1. Диагонали прямоугольника равны.
2. Если диагонали параллелограмма равны, то этот параллелограмм — прямоугольник.
Квадратом называется прямоугольник, все стороны которого равны.
Ромбом называется параллелограмм, у которого все стороны равны.
1. Диагонали ромба перпендикулярны.
2. Диагонали ромба делят его углы пополам.
3. Если диагонали параллелограмма перпендикулярны, то это параллелограмм-ромб.
4. Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм-ромб.
Трапецией называется четырехугольник, у которого только две противоположные стороны ( основания) параллельны. Средней линией трапеции называется отрезок, соединяющий середины непараллельных сторон (боковых сторон).
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.
Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
1. Углы при основании равнобедренной трапеции равны.
2. Диагонали равнобедренной трапеции равны.
3. Если углы при основании трапеции равны, то она равнобедренная.
4. Если диагонали трапеции равны, то она равнобедренная.
5. Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали — полусумме оснований.
1. Площадь параллелограмма равна произведению основания на высоту.
2.Площадь параллелограмма равна произведению его соседних сторон на синус угла между ними.
3. Площадь прямоугольника равна произведению двух его соседних сторон.
4. Площадь ромба равна половине произведения его диагоналей.
5. Площадь трапеции равна произведению полусуммы оснований на высоту.
6. Площадь четырехугольника равна половине произведения его диагоналей на синус угла между ними.
7. Формула Герона для четырехугольника, около которого можно описать окружность
формула Герона.doc
Microsoft Word Document 16.0 KB
1. Отношение соответствующих линейных размеров подобных фигур равно коэффициенту подобия.
2. Отношение площадей подобных фигур равно квадрату коэффициента подобия.
правильный многоугольник.doc
Microsoft Word Document 16.0 KB
Окружностью называется множество точек плоскости, удаленных от данной точки, называемой центром окружности, на одно и то же расстояние.
1. Диаметр, перпендикулярный хорде, делит хорду и стягиваемые ею дуги пополам.
2. Диаметр, проходящий через середину хорды, не являющейся диаметром, перпендикулярен этой хорде.
3. Серединный перпендикуляр к хорде проходит через центр окружности.
4. Равные хорды удалены от центра окружности на равные расстояния.
5. Хорды окружности, удаленные от центра на равные расстояния, равны.
6. Окружность симметрична относительно любого своего диаметра.
7. Дуги окружности, заключенные между параллельными хордами, равны.
8. Из двух хорд больше та, которая менее удалена от центра.
9. Диаметр есть наибольшая хорда окружности.
Прямая, имеющая с окружностью единственную общую точку, называется касательной к окружности.
1. Касательная перепндикулярна радиусу, проведенному в точку касания.
2. Если прямая а, проходящая через точку на окружности, перпендикулярна радиусу, проведенному в эту точку, то прямая а-касательная к окружности.
3. Если прямые, проходящие через точку М, касаются окружности в точках А и В, то МА=МВ, и угол АМО равен углу ВМО, где О-центр окружности.
4. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.
Говорят, что две окружности касаются, если они имеют единственную общую точку (точку касания).
1. Точка касания двух окружностей лежит на их линии центров.
2. Окружности радиусов r и R с центрами А и В касаются внешним образом тогда и только тогда, когда r+R=AB.
3. Окружности радиусов r и R (r<R) с центрами А и В касаются внутренним образом тогда и только тогда, когда R-r=AB.
4. Окружности с центрами M и N касаютя внешним образом в точке К. Некоторая прямая касается этих окружностей в различных точках А и В и пересекается с общей касательной, проходящей через точку К, в точке С. Тогда углы АКВ и MCN равны по 90 градусов.
1. Величина дуги окружности равна величине центрального угла, на нее опирающегося.
2. Вписанный угол равен половине угловой величины дуги, на которую он опирается.
3. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
4. Угол между пересекающимися хордами равен полусумме противоположных дуг, высекаемых хордами.
5. Угол между двумя секущими, пересекающимися вне круга, равен полуразности дуг, высекаемых секущими на окружности.
6. Угол между касательной и хордой равен половине угловой величины дуги, заключенной между ними.
1. Линия центров двух пересекающихся окружностей перпендикулярна их общей хорде.
2. Произведения длин отрезков хорд АВ и CD окружности, пересекающихся в точке Е, равны, то есть АЕ*ЕВ=СЕ*ЕD.
1. Центры вписанной и описанной окружностей правильного треугольника совпадают.
2.Центр окружности, описанной около прямоугольного треугольника-середина гипотенузы.
3. Если в четырехугольник можно вписать окружность, то суммы его противоположных сторон равны.
4. Если четырехугольник можно вписать в окружность, то сумма его противоположных углов равна 180 градусов.
5. Если сумма противоположных улов четырехугольника равна 180 градусов, то около него можно описать окружность.
6. Если в трапецию можно вписать окружность, то боковая сторона трапеции видна из центра окружности под прямым углом.
7. Если в трапецию можно вписать окружность, то радиус окружности, есть среднее пропорциональное отрезков, на которые точка касания делит боковую сторону.
8. Если в многоугольник можно вписать окружность, то его площадь равна произведению полупериметра многоугольника на радиус этой окружности.
1. Если из одной точки проведены к окружности касательная и секущая, то произведение всей секущей на ее внешнюю часть равно квадрату касательной.
2. Произведение всей секущей на ее внешнюю часть для данной точки и данной окружности постоянно.
ov1098.jimdo.com