2.7. Предел показательно-степенной функции
Напомним, что функция y =u(x)v(x) ,u(x)> 0 , основание и показатель степени которой являются функциями, зависящими от переменнойx , называетсяпоказательно-степенной.Пользуясь тождествомeln N = N и свойст-
вом логарифмической функции ln (N n )= n lnN , представим показательно-
степенную функцию в виде u(x)v(x) = eln u(x)v( x) =ev(x) ln u(x) . В силу непрерывности показательной функции по формуле (2.6) получаем:
| lim v(x) lnu(x) | , a . | (2.10) |
lim u(x)v(x)= lim ev(x) lnu(x)= ex→a | |||
x→a | x→a |
|
|
Таким образом, нахождение исходного предела сводится к нахождению
предела lim v(x) lnu (x).Показательно-степенныевыражения в пределе мо-
x→a
гут порождать три типа неопределенности: 1∞, 00 ,∞0 . Для раскрытия неоп-
ределенности 1∞ можно использовать второй замечательный предел
1
lim (1+ x)x = e .
x→0
Правила вычисления lim u(x)v(x) :
x→a
1. Если функции u (x) иv(x) имеют приx →a конечные пределы, то
справедливо соотношение
lim u(x)v(x)
x→a
lim v(x)
= limu(x)x→a . (2.11)
x→a
2. Во всех остальных случаях рекомендуется перейти к основанию e по
формуле (2.10), вычислить предел lim v(x)lnu (x) и воспользоваться свойст-
x→a
вами показательной функции y = ex .
|
|
| 2 |
|
| sin x | |
|
| −2x +3 | x . | ||||
Пример 2.28. Вычислить | lim | x |
|
| |||
| 2 |
| |||||
| x→0 |
| −3x +2 |
|
| ||
| x |
|
|
| |||
| Решение. Так как основание и показатель степени имеют приx →0 ко- | |||||||||||||||||||||||
нечные пределы: | lim | x2 | −2x +3 | = | 3 | , | lim | sin x | =1, то по формуле (2.10) по- | |||||||||||||||
| −3x +2 | 2 |
| x |
| |||||||||||||||||||
|
|
|
|
|
|
| x→0x2 |
|
| x→0 |
|
|
|
|
|
| ||||||||
лучаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
| sin x |
|
|
|
|
|
|
|
|
|
|
| sin x |
|
|
| ||
| x2 | −2x +3 |
| x |
| x2 | −2x +3 | xlim→0 | x |
| 3 1 | 3 |
| |||||||||||
lim |
|
|
|
|
|
| = | lim |
|
|
|
|
|
|
|
|
|
|
| = | = |
| . | |
| 2 |
|
|
|
| 2 |
|
|
|
|
|
|
|
|
| |||||||||
x→0 |
| −3x +2 |
|
|
|
| −3x +2 |
|
|
|
| 2 | 2 |
| ||||||||||
x |
|
|
| x→0x |
|
|
|
|
|
| ||||||||||||||
| Пример 2.29. Вычислить | lim |
| 2x +1 | x |
|
|
|
|
| ||||||||||||||
|
|
|
|
|
| . |
|
|
|
| ||||||||||||||
|
|
|
|
|
|
|
|
|
|
| x→±∞ | x −1 |
|
|
|
|
| |||||||
| Решение. Согласно формуле (2.7) | lim | 2x +1 | = 2 . Пользуясь свойства- | ||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| x→±∞ |
| x −1 |
|
|
| ||
ми показательной функции с основанием, большим единицы: lim 2x =+∞ и
x→+∞
lim 2x = 0 , окончательно получаем:
x→−∞
lim |
| 2x +1 x | lim |
| 2x +1 x | ||
|
| = +∞ и |
|
| = 0 . | ||
x→+∞ | x −1 |
| x→−∞ | x −1 |
| ||
1
x −1 x−1
Пример 2.30. Вычислить lim . x→1 x2 −1
Решение. Найдем пределы основания и показателя степени приx →1:
lim | x −1 | = | 0 | = lim | x −1 | = lim | 1 |
| = | 1 | ; | lim | 1 |
| = ∞. |
| 0 | (x −1)(x +1) |
|
| 2 |
|
| ||||||||
x→1×2 −1 | x→1 | x→1x +1 |
|
| x→1x −1 |
| |||||||||
Однако поведение показательной функции на бесконечности существенно зависит от знака бесконечно удаленной точки. Для показательной функ-
ции с основанием, меньшим единицы, имеем: lim |
| 1 | x | |
| 2 |
| = 0 и | |
x→+∞ |
|
| ||
|
| 1 | x | 1 |
| при x →1. Если | ||
lim |
|
|
| = +∞. Проанализируем поведение функции |
|
| ||
2 | x −1 | |||||||
x→−∞ |
|
|
| |||||
x стремится к 1 справа, т. е. оставаясь все время больше 1, | то разность x −1 | |||
стремится | к нулю, также оставаясь положительной. | Следовательно, | ||
lim | 1 |
| = +∞. При стремленииx к 1 слеваx будет меньше 1, а разность | |
|
| |||
x→1+0x −1 |
|
| ||
x −1 | стремится | к | нулю, |
| оставаясь |
| отрицательной. В этом слу- | ||||||||||||||||
чае | lim |
|
|
| 1 |
|
|
| = −∞. Тогда предел исходнойпоказательно-степеннойфунк- | ||||||||||||||
|
|
|
|
|
|
| |||||||||||||||||
x→1−0x −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
ции будет зависеть от того, с какой стороны x приближается к 1: | |||||||||||||||||||||||
|
|
| x −1 |
|
| 1 |
|
|
|
| x −1 | 1 |
|
|
| ||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||
lim | x−1 | = 0 и | lim | x−1 | = +∞. | ||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
|
| 2 | −1 |
|
|
| 2 |
|
| ||||||||||||||
x→1+0x |
|
|
|
|
|
| x→1−0 | x |
| −1 |
|
| |||||||||||
Пример 2.31. Вычислить |
|
|
|
| 3x +1x | ||||||||||||||||||
| lim |
|
|
|
|
| . | ||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| x→∞ | 3x −2 | ||||||||
Решение. Неопределенность 1∞ можно раскрыть, не прибегая к формуле (2.10), а пользуясь вторым замечательным пределом. Воспользуемся свойст-
вом показательной функции (ax )y = ax y и преобразуем выражение, стоящее под знаком предела, следующим образом:
|
|
|
|
|
|
|
|
|
|
|
| 3x−2 | 3 | x | |
|
|
|
|
|
|
|
|
|
|
|
| ||||
| 3x +1 | x |
|
| 3 | x |
|
| 3 |
| 3x−2. | ||||
lim | = | lim 1 + | = | lim | 1 + |
| 3 | ||||||||
|
|
| |||||||||||||
x→∞ | 3x −2 |
| x→∞ | 3x −2 |
| x→∞ | 3x −2 |
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
По второму замечательному пределу (2.9) имеем:
|
| 3 |
| 3x−2 |
|
|
| 3 |
|
|
|
| 1 |
|
|
| 3 |
|
| y = | , y →0 |
|
| lim (1+ y) | y | ||
lim 1 | + |
|
| = |
|
|
| = |
| ||||
3x −2 |
| 3x −2 |
| ||||||||||
x→∞ |
|
|
|
|
|
|
| y→0 |
|
Кроме того, | lim |
| 3x |
| =1. Тогда по формуле (2.11) окончательно полу- | |||||||
|
|
| ||||||||||
|
|
|
| x→∞3x−2 |
|
|
|
|
| |||
чаем: |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| 3x−2 xlim→∞ | 3x |
| |
| 3x +1 | x |
|
|
| 3 |
| 3x−2 |
| |||
lim | = | lim 1 + |
|
| 3 | = e1 =e | ||||||
|
|
| ||||||||||
x→∞3x −2 |
|
| x→∞ |
| 3x −2 |
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
| ||
Список литературы
1.Письменный Д. Т. Конспект лекций по высшей математике: В 2 ч. М.: Айрис Пресс, 2006. Ч. 1.
2.Комплексные числа и многочлены: Методические указания к решению задач / Сост.: М. Н. Абрамова, Е. А. Толкачева, А. И. Куприянов. СПб.: Изд-воСПбГЭТУ «ЛЭТИ», 2007.
Содержание |
|
1. ПРЕДЕЛ ФУНКЦИИ……………………………………………………………………………… | 3 |
1.1. Окрестность точки ………………………………………………………………………………. | 3 |
1.2. Предел функции в точке. Непрерывность функции в точке ………………….. | 4 |
1.3. Предел функции на бесконечности………………………………………………………. | 5 |
1.4. Бесконечно большая и бесконечно малая функции ………………………………. | 6 |
1.5. Односторонние пределы………………………………………………………………………. | 7 |
1.6. Элементарные функции……………………………………………………………………….. | 7 |
2. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ………………………………………………………………… | 11 |
2.1. Правила предельного перехода ………………………………………………………….. | 11 |
2.2. Предел дробно-рациональнойфункции………………………………………………. | 14 |
2.3. Предел функций, содержащих иррациональные выражения……………….. | 18 |
2.4. Замечательные пределы. Эквивалентные бесконечно малые функции.. | 21 |
2.5. Пределы, содержащие тригонометрические функции…………………………. | 25 |
2.6. Пределы выражений, содержащих показательную, |
|
логарифмическую и степенную функции…………………………………………… | 27 |
2.7. Предел показательно-степеннойфункции ………………………………………….. | 29 |
Список литературы ………………………………………………………………………………….. | 31 |
Редактор И. Г. Скачек
__________________________________________________________________
Подписано в печать Формат 60×84 1/16. Бумага офсетная. Печать офсетная. Печ. л. 2.0.
Гарнитура «Times». Тираж 250 экз. Заказ
__________________________________________________________________
Издательство СПбГЭТУ «ЛЭТИ» 197376, С.-Петербург,Проф. Попова, 5
studfiles.net
Вычисление пределов степенно-показательных функций
Пусть функции изаданы на множествеи функцияна нем положительна. Функция
называется степенно — показательной.
Предположим, что – точка сгущения множестваи существуют конечные пределы
,,
где . Нужно найти
.
Воспользовавшись тождествами , запишем исходное выражение в виде
.
В силу теоремы 6.1 получим
.
При заданных значениях пределов будем иметь
.
Из проведенного рассуждения видно, что предположение о существовании конечных пределов иможно отбросить. Действительно, для нахождения предела выражениядостаточно знать предел произведения(конечный или бесконечный).
1) Пусть . Тогда.
2) Если , то.
3) Если , то.
Заметим, что произведение может оказаться неопределенностью типа. Тогда и исходное выражениепредставляет собой неопределенность. Перечислим возникающие здесь неопределенности.
1) Если , то вычисление пределаприводит к неопределенности типа.
2) Если , то вычисление пределаприводит к неопределенности типа.
3) Если , то вычисление пределаприводит к неопределенности типа.
Во всех указанных случаях (,,) можно раскрыть неопределенностьв показателе степени, преобразуя ее к типуи используя соответствующие эквивалентные бесконечно малые.
Замечание 8.3.Приведенные выше рассуждения справедливы и для вычисления предела степенно-показательной функции в бесконечно удаленной точке:.
Пример 8.2.Вычислить.
Решение.Здесь,, поэтому имеем неопределенность типа. Преобразуем выражение под знаком предела:
.
В показателе степени имеем неопределенность типа . Заменойприна эквивалентную бесконечно малуюраскрываем ее:
.
Таким образом,
.
Замечание 8.4.Аналогично доказывается равенство.
Пределы
,
образуют две формы одного и того же равенства, которое также является замечательным пределоми часто служат определением числа.
Задачи к §8
Задача 1.Вычислить.
Решение. Здесь имеем неопределенность типа. Преобразуем числитель дроби к форме произведения:
.
Затем заменим бесконечно малую в точке функциюэквивалентной бесконечно малой.
Тогда получим
.
Ответ:.
Задача 2.Вычислить.
Решение.Здесь возникает неопределенность типа. Преобразуем знаменатель, воспользовавшись свойствами логарифмической функции, и выделим в аргументе логарифма слагаемое, равное 1:
.
Заменим бесконечно малую в точке функциюэквивалентной бесконечно малой. Числитель разложим на множители:
.
Тогда получим:
.
Ответ: .
Задача 3.Вычислить.
Решение.Здесь возникает неопределенность типа. Представим числитель в виде:
.
Затем заменим его эквивалентной бесконечно малой в точке функцией.
Функцию в точкетоже заменим на эквивалентную бесконечно малую.
Тогда
.
Ответ: .
Задача 4.Вычислить.
Решение.Здесь возникает неопределенность типа. Представим числитель в виде:
.
Затем заменим его эквивалентной бесконечно малой в точке функцией.
Преобразуем знаменатель:
и заменим его на эквивалентную бесконечно малую . Тогда получим
.
Ответ: .
Задача 5.Вычислить.
Решение.Здесь возникает неопределенность типа. Числительможно заменить эквивалентной бесконечно малой.
Чтобы воспользоваться соотношением (8.4), преобразуем знаменатель:
и заменим его эквивалентной бесконечно малой .
Тогда
.
Ответ: .
Задача 6.Вычислить.
Решение.Здесь имеем неопределенность типа. Чтобы применить к выражениюсоотношение (8.3), представим его в виде:
,
и заменим бесконечно малую функцию эквивалентной бесконечно малой. Знаменатель же представим в виде:
и, используя соотношения (8.2) и (8.8), заменим его эквивалентной бесконечно малой . Учитывая проведенные выкладки и соотношение (8.4), получим:
.
Ответ: .
Задача 7.Вычислить.
Решение.Здесь имеем неопределенность типа. Используя ряд приемов, примененных в задачах 1–7, получим
.
Ответ: .
Задача 8.Вычислить.
Решение.Здесь имеем неопределенность типа. Используя ряд приемов, примененных в задачах 1–7 и формулы приведения для тригонометрических функций, получим
.
Ответ: .
Задача 9.Вычислить.
Решение.Здесь имеем неопределенность типа. Чтобы применить к числителю соотношение (8.2), преобразуем его следующим образом:
.
Теперь числитель согласно соотношению (8.2) можно заменить эквивалентной бесконечно малой .
Преобразуем знаменатель
.
Заменяем, используя соотношение (8.1), эквивалентной бесконечно малой.
Тогда
.
Ответ: .
Задача 10.Вычислить.
Решение.Здесь имеем неопределенность типа. Используя приемы, описанные выше, получим
.
.
Ответ:.
Задача 11.Вычислить.
Решение.Здесь имеем неопределенность типа. Используя теоремы 6.2 и 6.1, получим
.
Получили неопределенность типа . Преобразуем выражение с помощью формул приведения, затем переходим к эквивалентным бесконечно малым. В итоге получим
.
Ответ:.
Задача 12.Вычислить.
Решение.Здесь имеем неопределенность типа. Выделимв основании степени:
.
Заметим, что при.
Справедлива цепочка равенств
.
Заменяя логарифм эквивалентной бесконечно малой согласно соотношению (8.2) и используя замечание 6.4 для раскрытия неопределенности, получим
.
Ответ:.
Задача 134.Вычислить.
Решение.Здесь имеем неопределенность типа. Введем переменную. Если, то.
.
Выделим в основании степени:
,
тогда
.
Заметим, что при. Заменим функциюэквивалентной бесконечно малой, будем иметь
.
Используя теорему 7.3, окончательно получим
.
Ответ:.
Задача 14.Вычислить.
Решение.Здесь возникает неопределенность типа. Поскольку
,
вычислим сначала . Мы имеем дело с неопределенностью типа.
Воспользовавшись последовательно соотношениями (8.2) и (8.1), будем иметь
.
Ответ:.
Задача 15.Вычислить.
Решение.Здесь возникает неопределенность типа. Воспользуемся формулой
.
Вычислим предел, стоящий в показателе степени. Для этого требуется раскрыть неопределенность типа . Преобразуем ее в неопределенность типаи воспользуемся эквивалентностью бесконечно малых:
.
Ответ:.
Задача 16.Вычислить.
Решение.Здесь возникает неопределенность типа. Преобразуем исходное предельное выражение
.
Вычислим предел, стоящий в показателе степени.
.
Ответ:.
studfiles.net
предел показательной функции | Математика
Рассмотрим два следствия из 2-го замечательного предела, с помощью которых можно найти предел показательной функции, в том числе, предел экспоненты.
Эти формулы можно применять и для случаев, когда на месте x стоит f(x), при условии, что при x→0, f(x)→0:
Проиллюстрируем, как найти предел показательной функции, в частности, предел экспоненты, на примерах.
Найти предел функции:
Сокращаем дробь на x. Получаем в числителе выражение вида (Ia), а значит, можем применить это следствие из 2-го замечательного предела:
Здесь мы вычли и прибавили единицу, поэтому в итоге значение выражения, стоящего в числителе, не изменилось.
Выносим общий множитель x за скобки и сокращаем на него:
В числителе получили выражения вида (Ia) и (IIа)
В числителе — выражение вида (Ia), в знаменателе — 1й замечательный предел:
www.matematika.uznateshe.ru
|
Раскрытие неопределенностей вида , , Используя определение степенно – показательной функции и непрерывность экспоненты, раскрытие неопределённостей перечисленных видов можно привести к раскрытию неопределённостей стандартных видов , , . В самом деле : ; ; . Пример 1. . Пример 2. . Пример 3. Решение. . Пример 4. Решение. . Пример 5. Решение. . Пример 6. Решение. . Пример 7. Решение. .
|
matica.org.ua
15. Пределы степенно-показательных функций.
(x)=|(x-a)|p
(x)=|(x-a)|q
Если p>qто(x) б.м. более выс. пор-ка
Если (x) одного порядка с (x-a)n|(x) б.м. пор-каnв т.А
(x)=3x2-x5 б.м. в О
(x)=5x2+x7 б.м. в О
16. Рациональные, алгебраические, трансцендентные, элементарные функции. Гиперболические функции.
1) Рациональные ф-ции-ф-ции f(x),
представимые в виде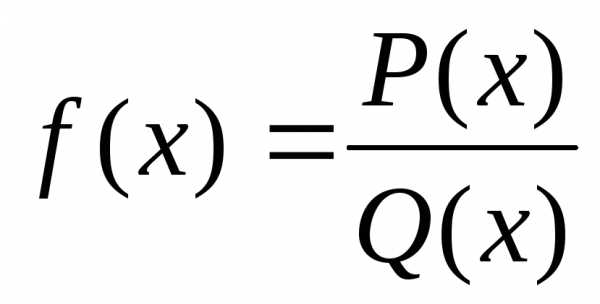 ,
гдеP(x) иQ(x) –
многочлены (Q(x)
не нулевой многочлен). Ф-цияf(x)
определена во всех точках числовой оси,
кроме тех её точек, в которых знаменательQ(x) обращается
в ноль.
,
гдеP(x) иQ(x) –
многочлены (Q(x)
не нулевой многочлен). Ф-цияf(x)
определена во всех точках числовой оси,
кроме тех её точек, в которых знаменательQ(x) обращается
в ноль.
Th. Многочлен непрерывен на всей числовой оси.
Th. Рациональная ф-ция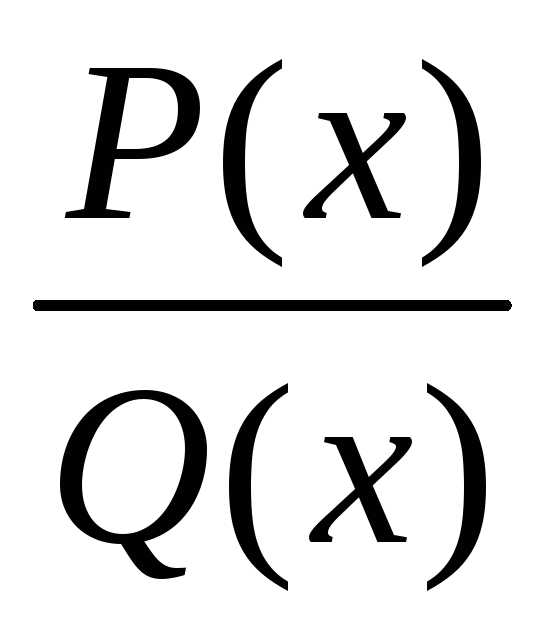 ,
гдеP(x) иQ(x) –
многочлены, непрерывна во всех точках
числовой оси, в которыхQ(x)0.
,
гдеP(x) иQ(x) –
многочлены, непрерывна во всех точках
числовой оси, в которыхQ(x)0.
Это следует из непр-ти многочленов P(x) иQ(x) на всей числовой оси и непрер-ти частного непрер-ых ф-ций во всех точках, в кот-х знам-ль не обр-ся в нуль.
2) Алгебраические ф-ции- ф-ции кот-е можно получить из констант, из +, -, *, /, обратной, суперпозиции.
Алгебр-е +sinx, +ex
элем-е ф-ции
3) Трансцедентные ф-ции- элем-ые ф-ции, не явл-ся рацион-ми или иррацион-ми. (не явл. алг-ми)
Иррац-е ф-ции, т.е. такие ф-ции, не явл-ся рацион-ми, кот-е могут быть заданы композицией конечного числа рациональных ф-ций, степ-х ф-ций с рацион-ми показателями и 4-х арифмет-х действий.
4) Элем-е. Ф-ция: линейная y=c(с-постоянная), степеннаяy=x,R, показательнаяy=ax,a>0, логарифмическаяy=logax,a>0,a1, тригонометрические ф-цииy=sinx,y=cosx,y=tgx,y=ctgxи обратные тригонометрические ф-цииy=arcsinx,y=arccosx,y=arctgx,y=arcctgxназываются основными элементарными ф-циями.
Всякая ф-ция f, кот-я может быть задана с пом-ю формулыy=f(x), содержащей лишь конечное число арифмет-х опер-й над основными элемент-ми ф-циями и композицией, называется элементарной ф-цией.
Th. Каждая элементарная ф-ция непр-на в обл-ти своего опред-я.
5) Нередко в мат. анализе встреч-ся ф-ции 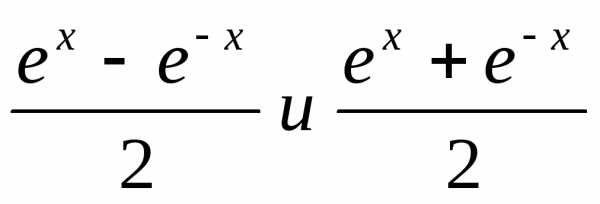 .
Они имеют специальные названия: первая
из них назыв-ся гиперболический синус
и обозначаетсяshx, а вторая
— гиперболический косинусchx.
Таким образом,
.
Они имеют специальные названия: первая
из них назыв-ся гиперболический синус
и обозначаетсяshx, а вторая
— гиперболический косинусchx.
Таким образом,
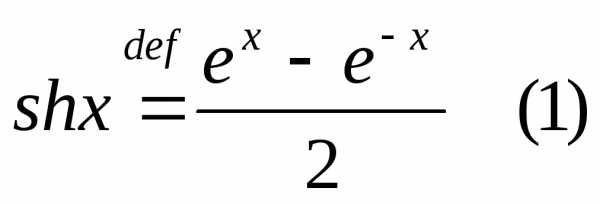
Эти ф-ции обладают некоторыми свойствами, похожими на св-ва обычных (круговых) синусов и косинусов, например,
Эпитет «гиперболический» в названии ф-ций (1) и (2) объясняется тем что, уравнения
x=acht,y=asht,a>0, -<t<+, явл-ся, в силу формулы (3), параметрическими уравнениями правой ветви гиперболыx2-y2=a2, подобно тому, как уравнения
x=acost,y=asint, 0t2, являются параметрическими уравнениями окружностиx2+y2=a2.
17. Дифференцируемость функции. Определение производной. Непрерывность дифференцируемой функции.
Опр1. Функцияf(x) называется дифференцируемой в данной точкеx , если приращениеyэтой функции в точкеx, соответствующее приращению аргументаx, может быть представлено в виде
,
где A– некоторое число, не зависящее отx,
а —
функция аргументаx,
являющаяся бесконечно малой приx0.
—
функция аргументаx,
являющаяся бесконечно малой приx0.
Т.к.
произведение двух бесконечно малых  x
является бесконечно малой более высокого
порядка, чем x,
то можно определение переписать
;(А
= f ’(x)).
x
является бесконечно малой более высокого
порядка, чем x,
то можно определение переписать
;(А
= f ’(x)).
Th. Чтобы f(x) была дифференцируема в т.x, необх. и дост., чтобы он в этой точке имела производную.
A=y’(x)
1) y’(x)-сущ-ет.
∆y(x)=y’(x)∙∆x+ (∆x)
(∆x)
2) Пусть ф-ция диф-ма
∆y=A∙∆x+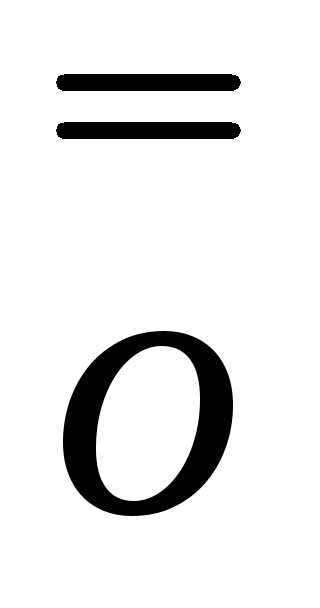 (∆x)
|:∆x
(∆x)
|:∆x
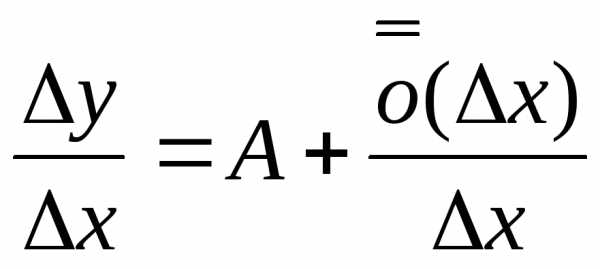
y’(x)=A
Опр2.Производной ф-иейy=f(x)
в точке х наз. предел при
наз. предел при х
х 0
отношения приращения ф-ии в этой точке
к приращению аргумента (при условии что
этот предел существует)
0
отношения приращения ф-ии в этой точке
к приращению аргумента (при условии что
этот предел существует)
Обозначение: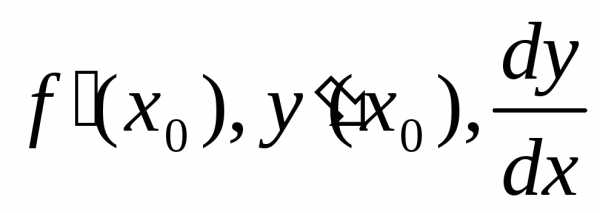 .
.
По определению =lim.
Ф-ия , имеющая производную в каждой точке интервала (а,в) наз. дифференцируемой в этом интервале. Операция нахождения производной ф-ии наз. дифференцированием.
Нахождение производной с помощью определения наз. непосредственным дифференцированием.
Предл. Если ф-ция y(x) дифф-а в т.х. то она непр-на
∆y=A∙∆x+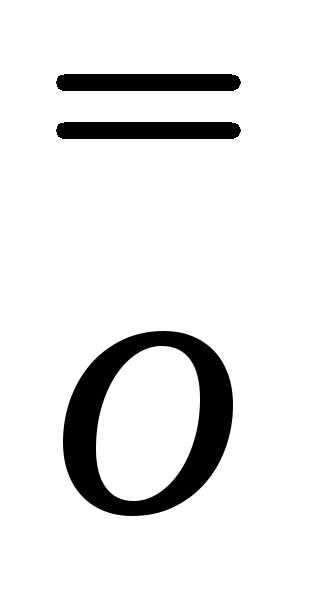 (∆x)
(∆x)
∆x→0
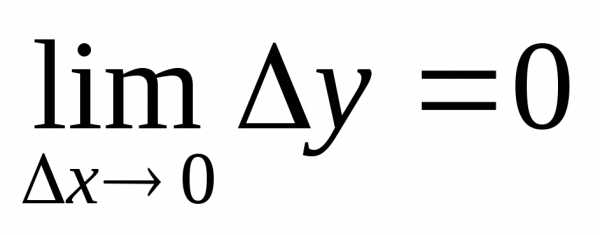
Замеч. Обратное утверждение не верно, ф-ция может быть непр-на, но не дифф-а.
y=|x| x=0
y(0)=0
∆y=|∆x|
∆y=y(0+∆x)-y(0)
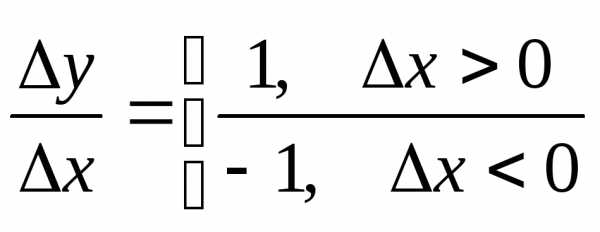
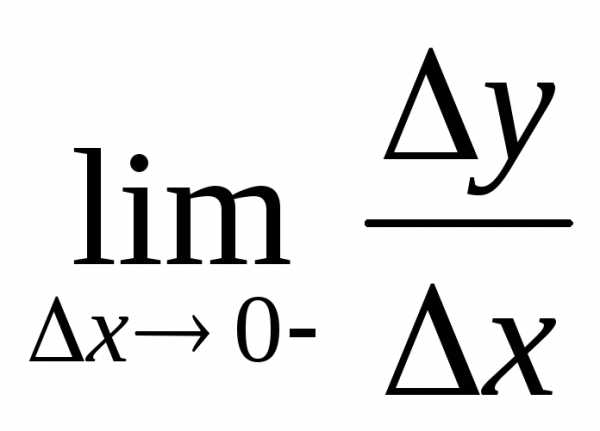 не=>
она не дифф-ма.
не=>
она не дифф-ма.
studfiles.net
15. Пределы степенно-показательных функций.
(x)=|(x-a)|p
(x)=|(x-a)|q
Если p>qто(x) б.м. более выс. пор-ка
Если (x) одного порядка с (x-a)n|(x) б.м. пор-каnв т.А
(x)=3x2-x5 б.м. в О
(x)=5x2+x7 б.м. в О
16. Рациональные, алгебраические, трансцендентные, элементарные функции. Гиперболические функции.
1) Рациональные ф-ции-ф-ции f(x),
представимые в виде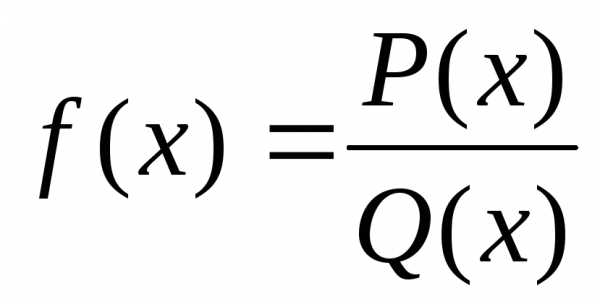 ,
гдеP(x) иQ(x) –
многочлены (Q(x)
не нулевой многочлен). Ф-цияf(x)
определена во всех точках числовой оси,
кроме тех её точек, в которых знаменательQ(x) обращается
в ноль.
,
гдеP(x) иQ(x) –
многочлены (Q(x)
не нулевой многочлен). Ф-цияf(x)
определена во всех точках числовой оси,
кроме тех её точек, в которых знаменательQ(x) обращается
в ноль.
Th. Многочлен непрерывен на всей числовой оси.
Th. Рациональная ф-ция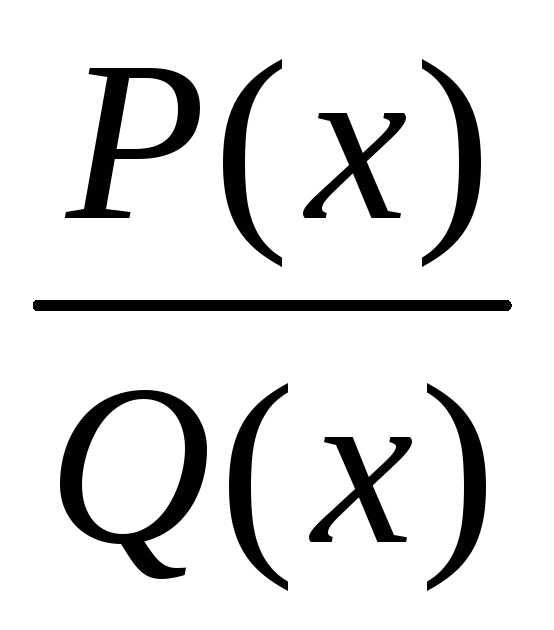 ,
гдеP(x) иQ(x) –
многочлены, непрерывна во всех точках
числовой оси, в которыхQ(x)0.
,
гдеP(x) иQ(x) –
многочлены, непрерывна во всех точках
числовой оси, в которыхQ(x)0.
Это следует из непр-ти многочленов P(x) иQ(x) на всей числовой оси и непрер-ти частного непрер-ых ф-ций во всех точках, в кот-х знам-ль не обр-ся в нуль.
2) Алгебраические ф-ции- ф-ции кот-е можно получить из констант, из +, -, *, /, обратной, суперпозиции.
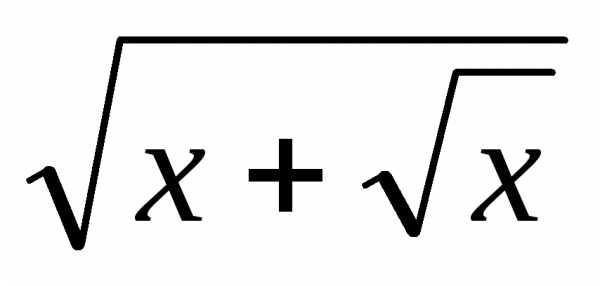
Алгебр-е +sinx, +ex
элем-е ф-ции
3) Трансцедентные ф-ции- элем-ые ф-ции, не явл-ся рацион-ми или иррацион-ми. (не явл. алг-ми)
Иррац-е ф-ции, т.е. такие ф-ции, не явл-ся рацион-ми, кот-е могут быть заданы композицией конечного числа рациональных ф-ций, степ-х ф-ций с рацион-ми показателями и 4-х арифмет-х действий.
4) Элем-е. Ф-ция: линейная y=c(с-постоянная), степеннаяy=x,R, показательнаяy=ax,a>0, логарифмическаяy=logax,a>0,a1, тригонометрические ф-цииy=sinx,y=cosx,y=tgx,y=ctgxи обратные тригонометрические ф-цииy=arcsinx,y=arccosx,y=arctgx,y=arcctgxназываются основными элементарными ф-циями.
Всякая ф-ция f, кот-я может быть задана с пом-ю формулыy=f(x), содержащей лишь конечное число арифмет-х опер-й над основными элемент-ми ф-циями и композицией, называется элементарной ф-цией.
Th. Каждая элементарная ф-ция непр-на в обл-ти своего опред-я.
5) Нередко в мат. анализе встреч-ся ф-ции 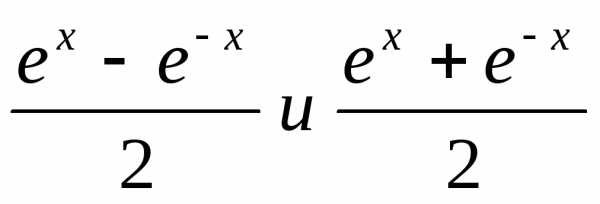 .
Они имеют специальные названия: первая
из них назыв-ся гиперболический синус
и обозначаетсяshx, а вторая
— гиперболический косинусchx.
Таким образом,
.
Они имеют специальные названия: первая
из них назыв-ся гиперболический синус
и обозначаетсяshx, а вторая
— гиперболический косинусchx.
Таким образом,
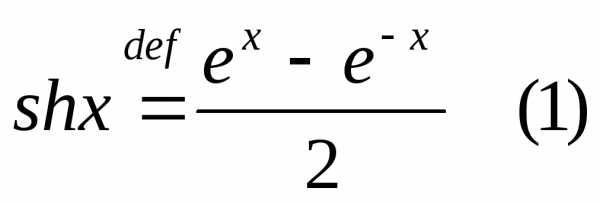
Эти ф-ции обладают некоторыми свойствами, похожими на св-ва обычных (круговых) синусов и косинусов, например,
Эпитет «гиперболический» в названии ф-ций (1) и (2) объясняется тем что, уравнения
x=acht,y=asht,a>0, -<t<+, явл-ся, в силу формулы (3), параметрическими уравнениями правой ветви гиперболыx2-y2=a2, подобно тому, как уравнения
x=acost,y=asint, 0t2, являются параметрическими уравнениями окружностиx2+y2=a2.
17. Дифференцируемость функции. Определение производной. Непрерывность дифференцируемой функции.
Опр1. Функцияf(x) называется дифференцируемой в данной точкеx , если приращениеyэтой функции в точкеx, соответствующее приращению аргументаx, может быть представлено в виде
,
где A– некоторое число, не зависящее отx,
а —
функция аргументаx,
являющаяся бесконечно малой приx0.
—
функция аргументаx,
являющаяся бесконечно малой приx0.
Т.к.
произведение двух бесконечно малых  x
является бесконечно малой более высокого
порядка, чем x,
то можно определение переписать
;(А
= f ’(x)).
x
является бесконечно малой более высокого
порядка, чем x,
то можно определение переписать
;(А
= f ’(x)).
Th. Чтобы f(x) была дифференцируема в т.x, необх. и дост., чтобы он в этой точке имела производную.
A=y’(x)
1) y’(x)-сущ-ет.
∆y(x)=y’(x)∙∆x+ (∆x)
(∆x)
2) Пусть ф-ция диф-ма
∆y=A∙∆x+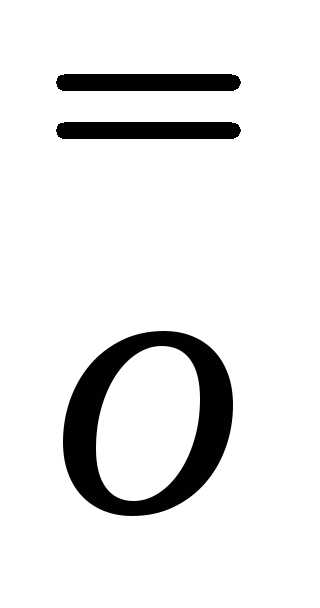 (∆x)
|:∆x
(∆x)
|:∆x
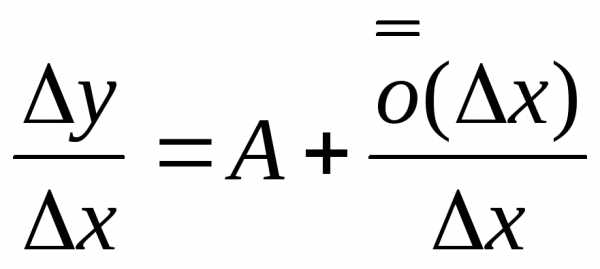
y’(x)=A
Опр2.Производной ф-иейy=f(x)
в точке х наз. предел при
наз. предел при х
х 0
отношения приращения ф-ии в этой точке
к приращению аргумента (при условии что
этот предел существует)
0
отношения приращения ф-ии в этой точке
к приращению аргумента (при условии что
этот предел существует)
Обозначение: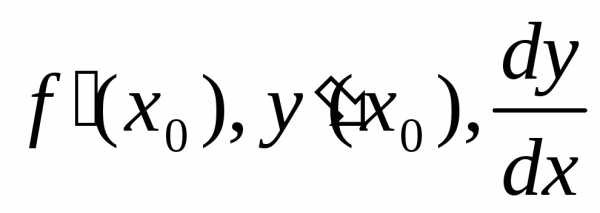 .
.
По определению =lim.
Ф-ия , имеющая производную в каждой точке интервала (а,в) наз. дифференцируемой в этом интервале. Операция нахождения производной ф-ии наз. дифференцированием.
Нахождение производной с помощью определения наз. непосредственным дифференцированием.
Предл. Если ф-ция y(x) дифф-а в т.х. то она непр-на
∆y=A∙∆x+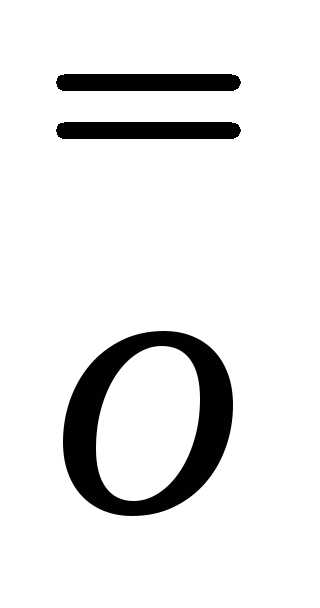 (∆x)
(∆x)
∆x→0
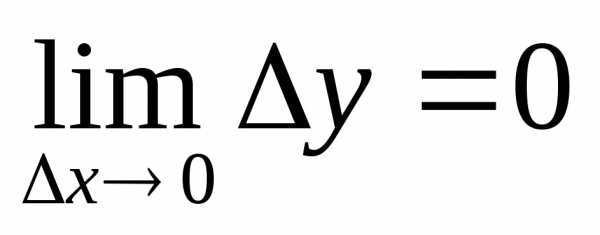
Замеч. Обратное утверждение не верно, ф-ция может быть непр-на, но не дифф-а.
y=|x| x=0
y(0)=0
∆y=|∆x|
∆y=y(0+∆x)-y(0)
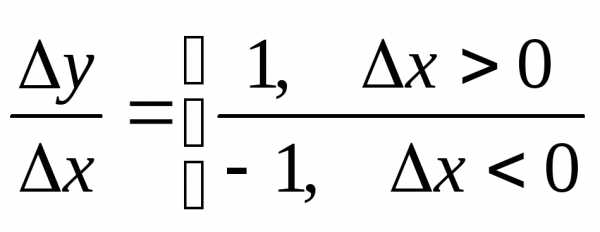
 не=>
она не дифф-ма.
не=>
она не дифф-ма.
studfiles.net
15. Пределы степенно-показательных функций.
(x)=|(x-a)|p
(x)=|(x-a)|q
Если p>q то (x) б.м. более выс. пор-ка
Если (x) одного порядка с (x-a)n | (x) б.м. пор-ка n в т.А
(x)=3x2-x5 б.м. в О
(x)=5x2+x7 б.м. в О
16. Рациональные, алгебраические, трансцендентные, элементарные функции. Гиперболические функции.
1) Рациональные
ф-ции-ф-ции f(x),
представимые в виде 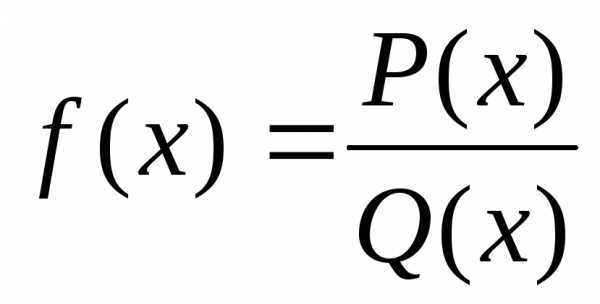 ,
гдеP(x)
и Q(x)
– многочлены (Q(x)
не нулевой многочлен). Ф-ция f(x)
определена во всех точках числовой оси,
кроме тех её точек, в которых знаменатель
Q(x)
обращается в ноль.
,
гдеP(x)
и Q(x)
– многочлены (Q(x)
не нулевой многочлен). Ф-ция f(x)
определена во всех точках числовой оси,
кроме тех её точек, в которых знаменатель
Q(x)
обращается в ноль.
Th. Многочлен непрерывен на всей числовой оси.
Th. Рациональная ф-ция, гдеP(x) и Q(x) – многочлены, непрерывна во всех точках числовой оси, в которых Q(x)0.
Это следует из непр-ти многочленов P(x) и Q(x) на всей числовой оси и непрер-ти частного непрер-ых ф-ций во всех точках, в кот-х знам-ль не обр-ся в нуль.
2) Алгебраические ф-ции- ф-ции кот-е можно получить из констант, из +, -, *, /, обратной, суперпозиции.
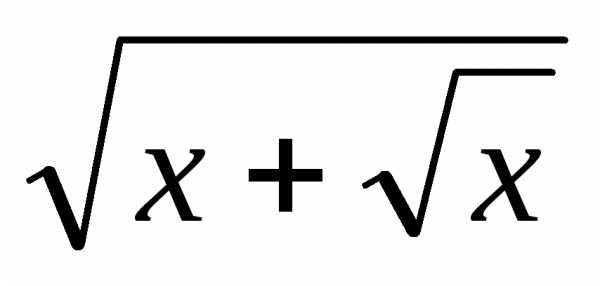
Алгебр-е +sinx, + ex
элем-е ф-ции
3) Трансцедентные ф-ции- элем-ые ф-ции, не явл-ся рацион-ми или иррацион-ми. (не явл. алг-ми)
Иррац-е ф-ции, т.е. такие ф-ции, не явл-ся рацион-ми, кот-е могут быть заданы композицией конечного числа рациональных ф-ций, степ-х ф-ций с рацион-ми показателями и 4-х арифмет-х действий.
4) Элем-е. Ф-ция: линейная y=c (с-постоянная), степенная y=x, R, показательная y=ax, a>0, логарифмическая y=logax, a>0, a1, тригонометрические ф-ции y=sinx, y=cosx, y=tgx, y=ctgx и обратные тригонометрические ф-ции y=arcsinx, y=arccosx, y=arctgx, y=arcctgx называются основными элементарными ф-циями.
Всякая ф-ция f, кот-я может быть задана с пом-ю формулы y=f(x), содержащей лишь конечное число арифмет-х опер-й над основными элемент-ми ф-циями и композицией, называется элементарной ф-цией.
Th. Каждая элементарная ф-ция непр-на в обл-ти своего опред-я.
5) Нередко в мат.
анализе встреч-ся ф-ции 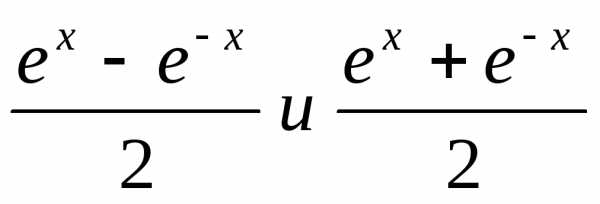 .
Они имеют специальные названия: первая
из них назыв-ся гиперболический синус
и обозначаетсяshx,
а вторая — гиперболический косинус chx.
Таким образом,
.
Они имеют специальные названия: первая
из них назыв-ся гиперболический синус
и обозначаетсяshx,
а вторая — гиперболический косинус chx.
Таким образом,
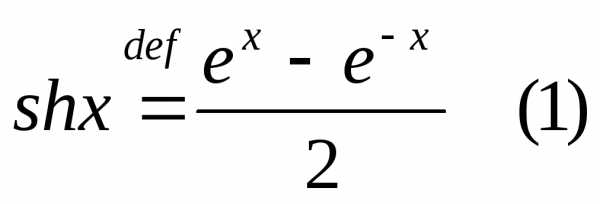
Эти ф-ции обладают некоторыми свойствами, похожими на св-ва обычных (круговых) синусов и косинусов, например,
Эпитет «гиперболический» в названии ф-ций (1) и (2) объясняется тем что, уравнения
x=a cht, y=a sht, a>0, -<t<+, явл-ся, в силу формулы (3), параметрическими уравнениями правой ветви гиперболы x2-y2=a2, подобно тому, как уравнения
x=a cost, y=a sint, 0t2, являются параметрическими уравнениями окружности x2+y2=a2.
17. Дифференцируемость функции. Определение производной. Непрерывность дифференцируемой функции.
Опр1. Функция f(x) называется дифференцируемой в данной точке x , если приращение y этой функции в точке x, соответствующее приращению аргумента x, может быть представлено в виде
,
где A – некоторое число, не зависящее от x,
а 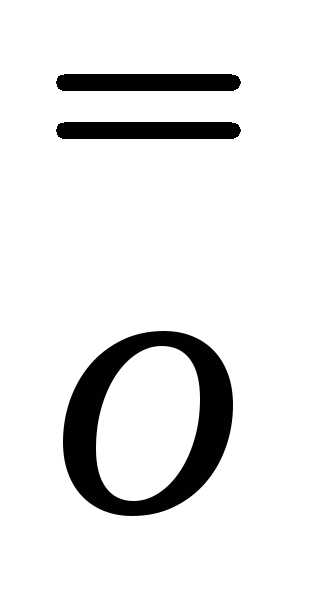 —
функция аргументаx,
являющаяся бесконечно малой при x
0.
—
функция аргументаx,
являющаяся бесконечно малой при x
0.
Т.к.
произведение двух бесконечно малых 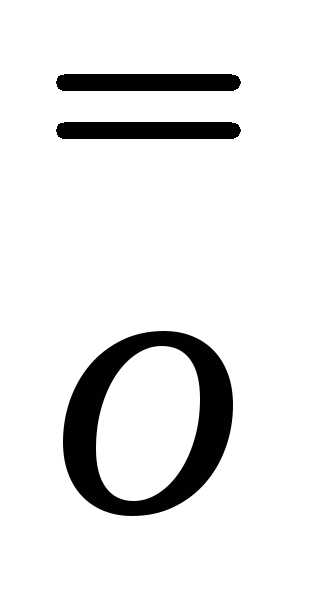 x
является бесконечно малой более высокого
порядка, чем x,
то можно определение переписать
;(А
= f ’(x)).
x
является бесконечно малой более высокого
порядка, чем x,
то можно определение переписать
;(А
= f ’(x)).
Th. Чтобы f(x) была дифференцируема в т.x, необх. и дост., чтобы он в этой точке имела производную.
A=y’(x)
1) y’(x)-сущ-ет.
∆y(x)=y’(x)∙∆x+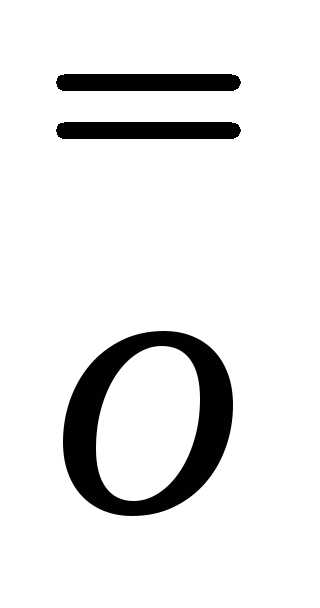 (∆x)
(∆x)
2) Пусть ф-ция диф-ма
∆y=A∙∆x+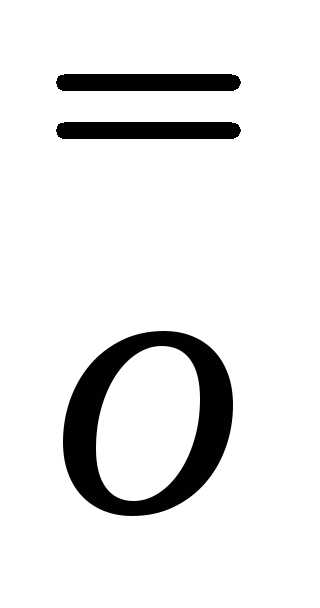 (∆x)
|:∆x
(∆x)
|:∆x
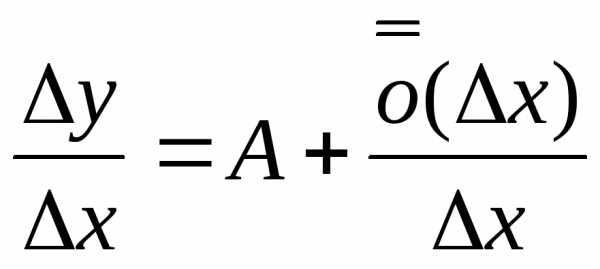
y’(x)=A
Опр2. Производной ф-ией y=f(x)
в точке х наз. предел при
наз. предел при х
х 0
отношения приращения ф-ии в этой точке
к приращению аргумента (при условии что
этот предел существует)
0
отношения приращения ф-ии в этой точке
к приращению аргумента (при условии что
этот предел существует)
Обозначение: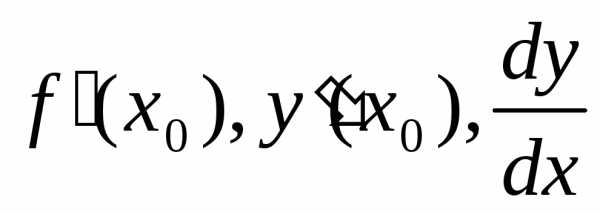 .
.
По определению =lim.
Ф-ия , имеющая производную в каждой точке интервала (а,в) наз. дифференцируемой в этом интервале. Операция нахождения производной ф-ии наз. дифференцированием.
Нахождение производной с помощью определения наз. непосредственным дифференцированием.
Предл. Если ф-ция y(x) дифф-а в т.х. то она непр-на
∆y=A∙∆x+ (∆x)
(∆x)
∆x→0
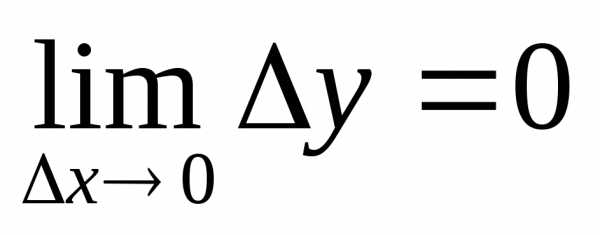
Замеч. Обратное утверждение не верно, ф-ция может быть непр-на, но не дифф-а.
y=|x| x=0
y(0)=0
∆y=|∆x|
∆y=y(0+∆x)-y(0)
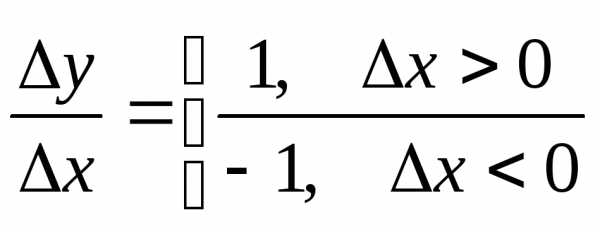
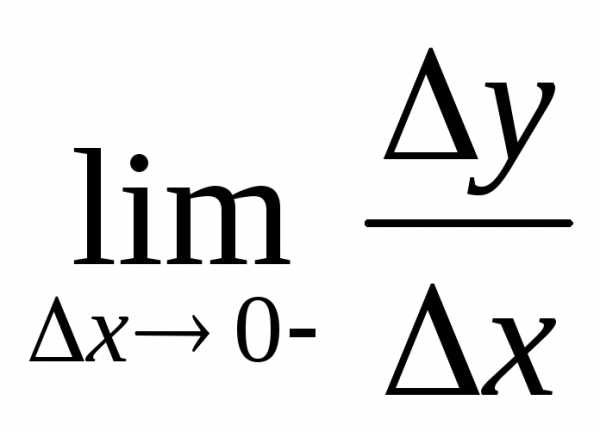 не
=> она не дифф-ма.
не
=> она не дифф-ма.
studfiles.net
