Урок геометрии в 8-м классе по теме «Признаки подобия треугольников»
Слайд 1 (Приложение 1)
Подобие двух существ того же вида,
но различных размеров имеет ту же самую
природу,
как и подобие геометрических фигур.
К.Гаусс
Сегодня на уроке мы повторим все признаки подобия треугольников, будем решать задачи, используя эти признаки, и рассмотрим применение подобных фигур в окружающем мире.
Любопытный отыскивает редкости только затем, чтобы им удивляться, любознательный же затем, чтобы узнать их и перестать удивляться. Так будьте же сегодня на уроке очень любознательными.
Какие виды треугольников вам известны?
Какие треугольники называются подобными?
Слайд 2
На этом слайде вы видите
различные треугольники. Найдите среди них
пары подобных и докажите почему они подобны.
А_Д Б_Е Г_Ж (рисунок 1)
Рисунок 1
Я предлагаю вам небольшой тест (См. стр. №4), проверьте каждый сам себя, как хорошо вы изучили эту тему. В тесте 5 вопросов, внимательно прочтите сначала вопрос, затем предложенные ответы и лишь потом подчеркните ответ, который вы считаете правильным.
Думаю, каждому интересно правильно ли он дал ответы на вопросы теста, вас ждёт самопроверка. Слайд 3-4
В геометрии подобными могут быть не только треугольники, но и совершенно произвольные фигуры. На этом слайде 5 мы видим подобные пятиугольники, фигуры похожие на звёзды, фигуры со стрелками, подобные параллелограммы.
Как вы думаете, какими свойствами все они обладают? У них одинаковые формы, но разные размеры.
Слайд 6 Рассмотрим подобные
трапеции (так как признаки подобных
трапеций похожи на признаки подобных
треугольников.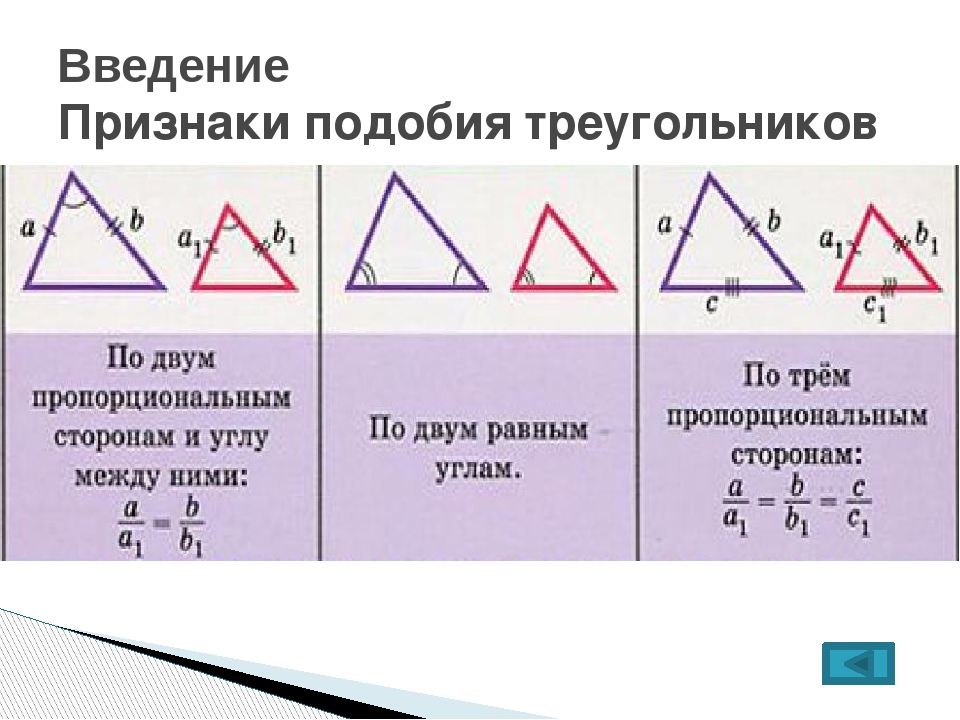
В трапеции АВСD провели отрезок MN, соединяющий боковые стороны и параллельный основанию. Найти длину отрезка MN, если AD = 32 см, ВС = 18 см, а трапеция AMND подобна трапеции MBCN.
Слайд 7 Подобные трапеции, которые мы сейчас рассматривали в задаче являются элементами паркетов
Паркетом называют заполнение плоскости одинаковыми фигурами, которые не перекрывают друг друга и не оставляют на плоскости пустого пространства. Тетрадный лист в клетку представляет собой простейший паркет, элементом которого является квадрат. Очень красивы те паркеты, которые составлены из разных геометрических фигур, подобных между собой и разных по цвету.
Слайд 8 Перед вами паркет
составленный из прямоугольных
треугольников.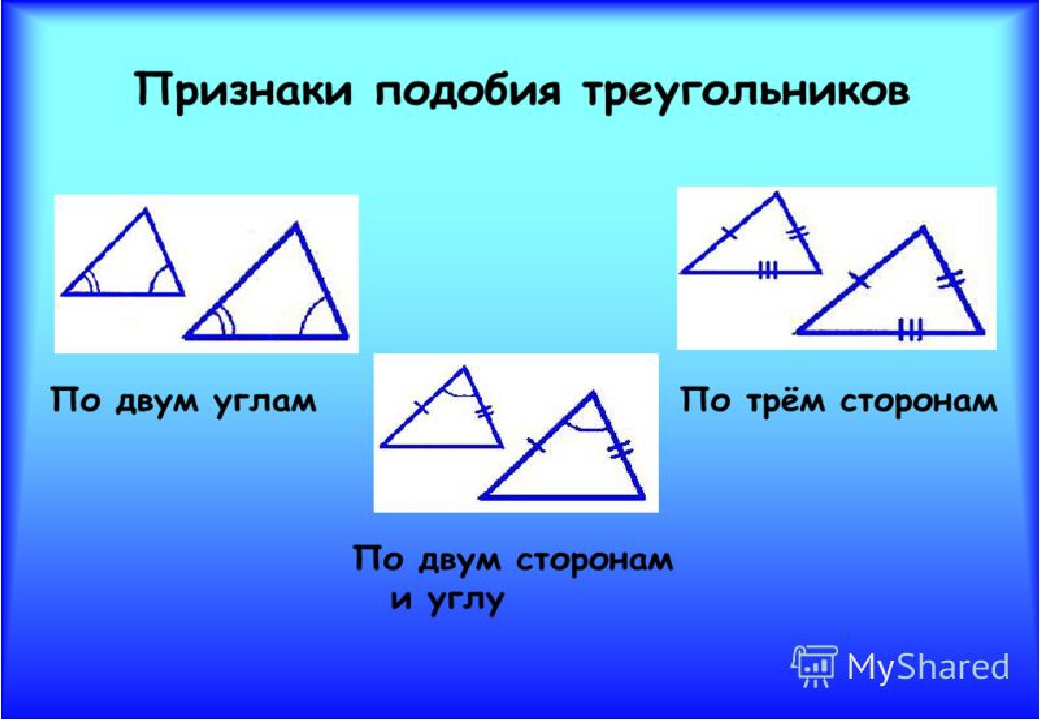
Сколько подобных треугольников вы видите на этом рисунке?
Сколько равных треугольников на этом рисунке?
Слайд 9 Уже в древности учёным были известны признаки подобия треугольников.
Однажды подобие прямоугольных треугольников помогло древнегреческому учёному Фалесу Милетскому измерить высоту Египетской пирамиды. В один из солнечных дней Фалес вместе с главным жрецом храма Изиды проходил мимо пирамиды Хеопса.
— Знает ли кто-либо, какова её высота? – спросил он.
— Нет, сын мой, — ответил жрец – Древние папирусы не сохранили нам этого, а наши знания не дают возможности судить о ней даже приблизительно.
— Но ведь это можно сказать совсем
точно и даже сейчас, — воскликнул Фалес –
Вот смотри, мой рост 3 царских вавилонских
локтя. А вот моя тень. Её длина такая же. И
какой бы ты предмет ни взял именно в это
время, тень от него, если ты поставишь его
вертикально, точно равна длине предмета. Этот предмет и его тень образуют
прямоугольный треугольник; знай же, что
такие треугольники подобны.
Этот предмет и его тень образуют
прямоугольный треугольник; знай же, что
такие треугольники подобны.
Фалес привёл в удивление жрецов, измерив высоту пирамиды без всяких приборов по отбрасываемой ею тени.
Решим и мы эту задачу.
Слайд 10 Домашнее задание:
- узнайте какова высота Египетской пирамиды, переведя царские вавилонские локти в метры и сантиметры, если 1 локоть = 462 мм.;
Всегда интересно проводить
эксперименты. Особенно важен конечный
результат. Проведём лабораторную
работу , которая поможет нам сделать
научное открытие. Для этого потребуются
карандаши, линейки, ручки и рабочие листы с
печатной основой (Приложение 3). Следуйте
указаниям чётко и быстро, и тогда у вас
обязательно всё получится, поможет вам наш
волшебный экран.
Слайд 11
- Измерьте основание АВ, результат запишите.
- Измерьте боковые стороны АС и ВС, результат запишите.
- В середине АС и ВС поставьте соответственно точки М и К.
- Проведите отрезок МК и измерьте его длину (вводится определение средней линии).
- Сравните длину отрезка МК и длину стороны АВ. Ответьте на вопрос: во сколько раз длина отрезка МК меньше длины стороны АВ.
- Сформулируйте гипотезу.
Проведённый эксперимент показывает, каков бы ни был треугольник его средняя линия всегда в два раза меньше основания. Я поздравляю, сейчас каждый открыл для себя новую теорему, которую теоретически докажет на следующем уроке.
Слайд 12 Сколько средних линий
может быть в треугольнике? Из подобных
треугольников, которые получены путём
разрезания по средним линиям, составим
новую геометрическую фигуру.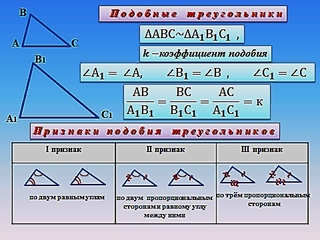 Получили
фигуру, части которой подобны целому
треугольнику. Учёные назвали такие фигуры автоподобными.
Получили
фигуру, части которой подобны целому
треугольнику. Учёные назвали такие фигуры автоподобными.
Чем так интересны автоподобные фигуры? Примером автоподобной фигуры является золотая спираль, геометрическим свойством этой спирали является то, что каждый следующий виток подобен предыдущему. В форме золотой спирали закручиваются раковины многих моллюсков, в виде этой спирали плетут свою паутину пауки и Слайд 13 даже галактика солнечной системы закручивается по золотой спирали.
Геометрия — это наука точная в рассуждениях, безупречная в доказательствах, ясная в ответах, гармонично сочетающая в себе прозрачность мысли и красоту человеческого разума.
Геометрия до конца не изученная наука, и может быть многие открытия ждут именно вас!
Итог урока: Слайд 14
Что вы узнали нового?
Чему научились?
Что показалось особенно трудным?
Слайд 19 Спасибо за урок!
Тесты
Урок»Контрольная работа по геометрии: Признаки подобия треугольников»
Контрольная работа по геометрии № 3.
Тема: «Признаки подобия треугольников»
Вариант 1
Напишите первый признак подобия треугольников
Какие из утверждений верны?
Углы подобных треугольников равны.
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники равны.
Отношение сходственных сторон подобных треугольников равно коэффициенту подобия.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=16, AC=20, NC=15.
Основания BC и AD трапеции ABCD равны соответственно 8 и 32,
BD =16 .Докажите, что треугольники CBD и BDA подобны.
Контрольная работа по геометрии № 3.
Тема: «Признаки подобия треугольников»
Вариант 2
Напишите второй признак подобия треугольников
Какие из утверждений верны?
Стороны подобных треугольников соответственно равны.

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Углы подобных треугольников пропорциональны.
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB = 18, DC = 54, AC = 48
Основания BC и AD трапеции ABCD равны соответственно 7 и 63,
BD =21 .Докажите, что треугольники CBD и BDA подобны.
Контрольная работа по геометрии № 3.
Тема: «Признаки подобия треугольников»
Вариант 3
Напишите третий признак подобия треугольников
Какие из утверждений верны?
Стороны одного из подобных треугольников пропорциональны сходственным сторонам другого треугольника.
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

У подобных фигур форма одинаковая, размеры одной фигуры отличаются от размеров другой в одно и то же число раз.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=14, AC=21, NC=10.
Основания BC и AD трапеции ABCD равны соответственно 3 и 12,
BD =6 .Докажите, что треугольники CBD и BDA подобны.
Контрольная работа по геометрии № 3.
Тема: «Признаки подобия треугольников»
Вариант 4
Напишите определение подобных треугольников.
Какие из утверждений верны?
Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
Любые два квадрата подобны.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, то такие треугольники подобны.

Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB = 11, DC = 22, AC = 27
Основания BC и AD трапеции ABCD равны соответственно 9 и 81, BD=27.Докажите, что треугольники CBD и BDA подобны.
Подобие геометрических фигур — презентация онлайн
2. Исследуемый вопрос:
3. План исследования:
Какиегеометрические
фигуры называются
подобными?
Какие из фигур
всегда подобны, а
какие нет?
Какие треугольники
подобны?
Какие фигуры
принято считать
похожими?
Используют ли в
геометрии это
понятие?
Полученные выводы!
Фигуры получаются
подобными в результате
преобразования, которое
называется ГОМОТЕТИЯ.
ЭТО как в кино, когда лучи
из проектора попадая на
экран, изображают
подобные фигуры.
У подобных фигур изменяются размеры сторон в одинаковое число раз,
но при этом все углы остаются без изменения.
О ТОМ как изменились стороны говорит нам их отношение, которое
называется коэффициентом подобия К.
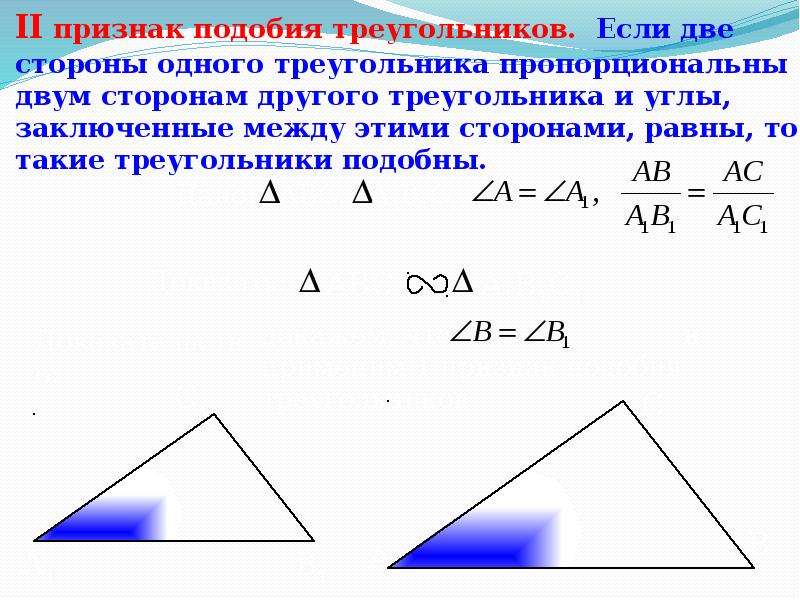
Два многоугольника ( ABCDEF и abcdef,
рис.37 ) подобны, если их углы равны:
A = a, B = b, …, F = f , а стороны
пропорциональны:
ЗНАЧИТ!
Если изменить ( увеличить или уменьшить ) все
размеры плоской фигуры в одно и то же
число раз ( отношение подобия ), то старая и
новая фигуры называются подобными.
Например, картина и её фотография – это
подобные фигуры.
Теперь понятно КАКИЕ ФИГУРЫ
НАЗЫВАЮТСЯ ПОДОБНЫМИ!
6. Какие фигуры всегда подобны а какие нет?
Эти всегдаподобны!
А эти нет!
Прямоугольники
Круги
Квадраты
Равносторонние
треугольники
Ромбы
Трапеции
Кубы
Шары
овалы
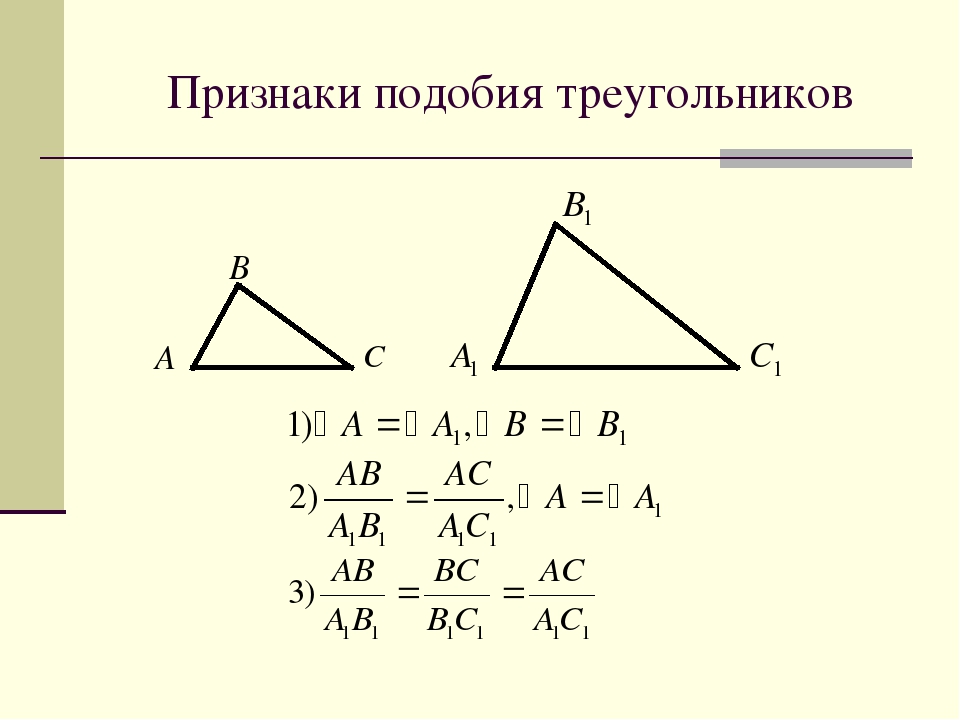
Для подобия многоугольников недостаточно только
пропорциональности сторон. Например, квадрат и ромб
имеют пропорциональные стороны: каждая сторона
квадрата вдвое больше, чем у ромба, однако их диагонали
не пропорциональны и углы не равны.
ЗНАЧИТ!
Чтобы фигуры были подобны надо
чтобы стороны их были
пропорциональны а углы равны!
Какие треугольники называются
подобными?
Два треугольника называются
подобными, если их углы равны, а
стороныпропорциональны.
AB
BC
CA
——— = ——- = ——— = k
ab
bc
ca
Выбери
подобные..
8. Признаки подобия треугольников:
Если два угла одного треугольника равныдвум углам другого треугольника, то такие
треугольники равны.
Если две стороны одного треугольника
пропорциональны сторонам другого
треугольника ауглы заключённые между
ними равны, то такие треугольники подобны.
Если три стороны одного треугольника
пропорциональны трём сторонам другого
треугольника, то такие треугольники
подобны.
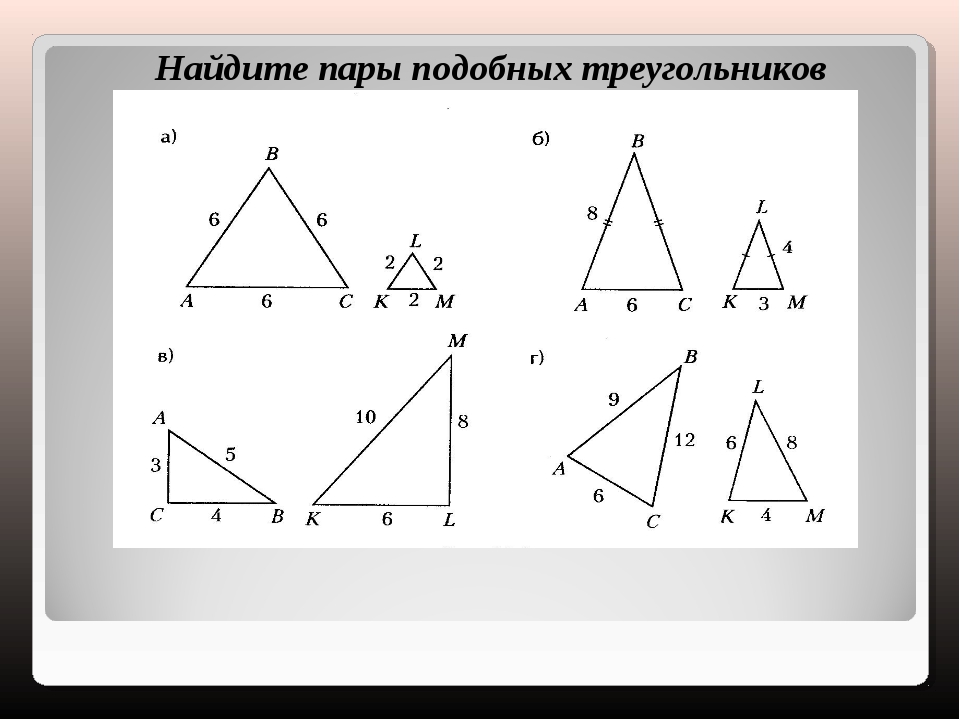
9. Признаки подобия прямоугольных треугольников:
Два прямоугольных треугольникаподобны, если:
1) их катеты пропорциональны;
2) катет и гипотенуза одного
треугольника пропорциональны катету
и гипотенузе другого;
3)два угла одного треугольника равны
двум углам другого.
10. Будут ли?
фигуры11. Я пришёл к выводу:
Если рассматривать похожесть и подобие,мы поймём, что это абсолютно разные вещи.
Если подобные фигуры можно назвать
похожими, то похожие подобными нет, и вот
почему. Два разных треугольника можно
назвать похожими, потому что например оба
треугольника имеют 3 угла, 3 стороны, но это
не означает, что они подобны. Так же у двух
ромбов 4 стороны, 4 угла и они не подобны.
Проанализировав всё это, мы приходим к
выводу, что похожие фигуры не подобны.
На практике постоянно встречаются
преобразования, при которых все
расстояния изменяются в одном и
том же отношении, т. е. умножаются
на одно и то же число. такое
преобразование называется
подобным (или подобием), а это
число называется коэффициентом
подобия.Например, при увеличении
фотографии все размеры
увеличиваются в одном и том же
отношении. т. е. происходит подобное
преобразование с фотопленки на
фотобумагу.
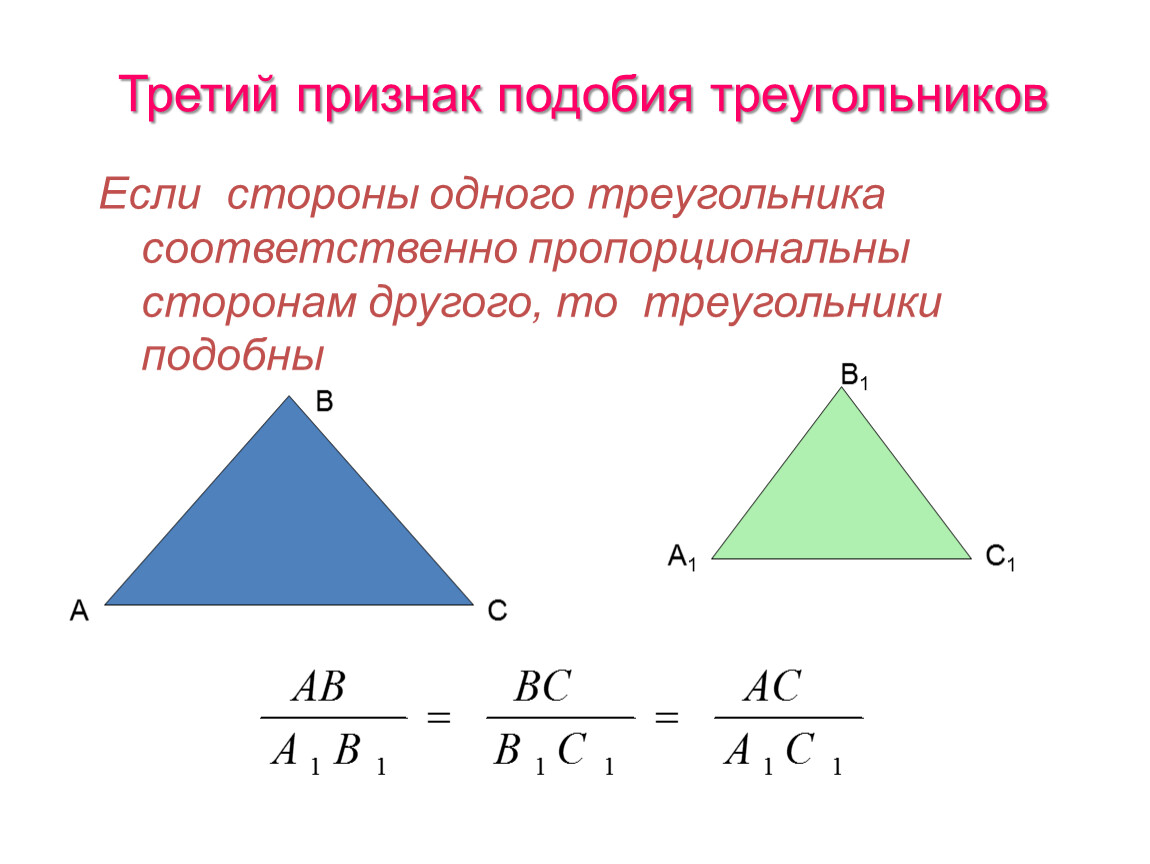 Подобное
Подобноепреобразование свершается и тогда,
когда делают уменьшенную копию
чертежа, рисунка и т. д. так,
например, вы поступаете, когда
срисовываете чертеж с доски в свою
тетрадь. Подобные фигуры имеют
одинаковую форму, но различные
размеры.
14. Конец
В создании проекта помогали:Поисковая система яндекс: www.ya.ru
Поисковая система Google: www.google.com
Сайт www.ru.wikipedia.org
Сайт www.bymath.net
Сделал:
Ученик школы №26 города Петропавловска-Камчатского
8 «Б» класса Гвенетадзе Вадим
Руководитель:Учитель Коробейникова А.И.
Подобие фигур. 8 класс — презентация онлайн
1. ПОДОБИЕ В ГЕОМЕТРИИ
ПОДОБНЫЕ ТРЕУГОЛЬНИКИ8 класс
2. ТЕМА «ПОДОБИЕ»
Теоретический материал.Задачи.
3. ПЛАН
Пропорциональные отрезки.Свойство биссектрисы
треугольника.
Определение подобных
треугольников.
Отношение периметров подобных
фигур.
Отношение площадей подобных
фигур.

Признаки подобия треугольников.
4. ЗАДАЧИ
Разминка.Решение задач.
Задачи на признаки подобия.
Тест
5. Пропорциональные отрезки
Отношениемотрезков называется
отношение их длин.
Отрезки AB и CD
пропорциональны
отрезкам A1B1 и
C1D1,, если
AB A1B1
CD C1D1
B
A
D
C
AB
CD
A
A1
B
С
D
B1 С1
ПРИМЕР
D1
6. ПРИМЕР
Даны два прямоугольных треугольникаСтороны ΒC и CA пропорциональны MN и MK,
так как
B
5
BC
3
MN 15
3
C
A
4
N
т.е.
?
15
M
K
20
и
AC
4
MK 20
BC AC 1
MN MK 5
НАЙДИТЕ ГИПОТЕНУЗУ БОЛЬШЕГО
ТРЕУГОЛЬНИКА.
7. Пропорциональность отрезков
Понятие пропорциональности вводитсядля любого числа отрезков.
B
например
5
3
C
A
BC AC AB
MN MK NK
4
N
25
15
M
K
20
8.
 Подобные фигуры Предметы
Подобные фигуры Предметыодинаковой формы,
но разных размеров
Фотографии, отпечатанные
с одного негатива, но с
разными увеличениями;
Здание и его макет
Планы,
географические
карты одного и того
же района,
выполненные в
разных масштабах.
9. Подобные фигуры
В геометрии фигуры одинаковой формы называют подобнымифигурами
Подобными
являются любые
два квадрата
Подобными
являются любые
два круга
два куба
два шара
10. Подобные треугольники
Даны два треугольника AΒC и A1Β1C1,у которых A = A1, Β = Β1, C = C1.
Стороны AΒ и A1Β1 , AC и A1C1 , ΒC и Β1C1,
лежащие против равных углов, называют
сходственными
Β1
Β
A
C
A1
C1
11. Определение
Два треугольника называются подобными,если их углы соответственно равны и
стороны одного треугольника
пропорциональны сходственным
сторонам другого.
Β
ΔAΒC ~ ΔA1Β1C1
A
C
A1
Β1
A = A1, Β = Β1, C = C1.

AB
BC
AC
A1 B1 B1C1 A1C1
C1
12. Коэффициент подобия
ΒΔAΒC ~ ΔA1Β1C1
AB
BC
AC
k
A1B1 B1C1 A1C1
A
Β1
C
A1
k – коэффициент подобия.
Число k , равное отношению сходственных
сторон, называется коэффициентом
подобия.
C1
13. Дополнительные свойства
Отношение высот подобных треугольников,проведенных к сходственным сторонам,
равно коэффициенту подобия.
Отношение медиан подобных треугольников,
проведенных к сходственным сторонам,
равно коэффициенту подобия.
Отношение биссектрис подобных
треугольников, проведенных к сходственным
сторонам, равно коэффициенту подобия.
14. Отношение периметров
ΒΒ1
ΔAΒC ~ ΔA1Β1C1
AB
BC
AC
k
A1B1 B1C1 A1C1
A
C
A1
PABC
k
PA1B1C1
ДОКАЗАТЕЛЬСТВО
Отношение периметров
подобных треугольников равно
коэффициенту подобия.

C1
15. Отношение периметров
ΔAΒC ~ ΔA1Β1C1Β
Β1
A
AB
BC
AC
k
A1B1 B1C1 A1C1
AB kA1B1
C
A1
C1
BC kB1C1
AC kA1C1
PABC
AB BC AC
kA1B1 kB1C1 kA1C1
PA1B1C1 A1B1 B1C1 A1C1
A1B1 B1C1 A1C1
Выносим общий множитель за скобку и
сокращаем дробь.
PABC
k
PA1B1C1
16. Отношение площадей
ΒΒ1
ΔAΒC ~ ΔA1Β1C1
AB
BC
AC
k
A1B1 B1C1 A1C1
A
Отношение площадей
подобных треугольников
равно квадрату
коэффициента подобия.
C
A1
SABC
2
k
SA1B1C1
ДОКАЗАТЕЛЬСТВО
C1
17. Отношение площадей
Пусть ΔAΒC ~ ΔA1Β1C1,коэффициент подобия k
AB
BC
AC
k
A1B1 B1C1 A1C1
Β
Β1
A
A = A1, по теореме об отношении
площадей треугольников, имеющих по
равному углу, имеем
C
A1
SABC
AB AC
AB AC
k k k2
SA1B1C1 A1B1 A1C1 A1B1 A1C1
C1
18.
 Свойство биссектрисы треугольника Биссектриса треугольника
Свойство биссектрисы треугольника Биссектриса треугольникаделит противоположную
сторону на отрезки,
пропорциональные
прилежащим сторонам
треугольника.
BD DC
AB AC
или
A
ПРИМЕР
B
BD AB
DC AC
ДОКАЗАТЕЛЬСТВО
D
C
19. Свойство биссектрисы треугольника
A2
1
H
B
ИМЕЕМ
D
BD AB
DC AC
C
ΔABD и ΔACD имеют
общую высоту AH
S ABD DB
S ACD DC
ΔABD и ΔACD имеют
равные углы 1 = 2
SABD AB AD AB
SACD AD AC AC
20. Свойство биссектрисы треугольника
Дано: ΔABCAD – биссектриса
A
AB = 14 см
BC = 20 см
1
2
AC = 21 см
Найти: BD,CD.
Решение:
B
D
20см
C
21. Свойство биссектрисы треугольника
A1
B
D
20см
2
Решение:
Пусть BD = x см,
тогда CD = (20 – x) см.
По свойству биссектрисы
треугольника BD DC
AB AC
имеем
x
20 x
C
14
21
Решая уравнение, получим х = 8
BD = 8 см, CD = 12 см.
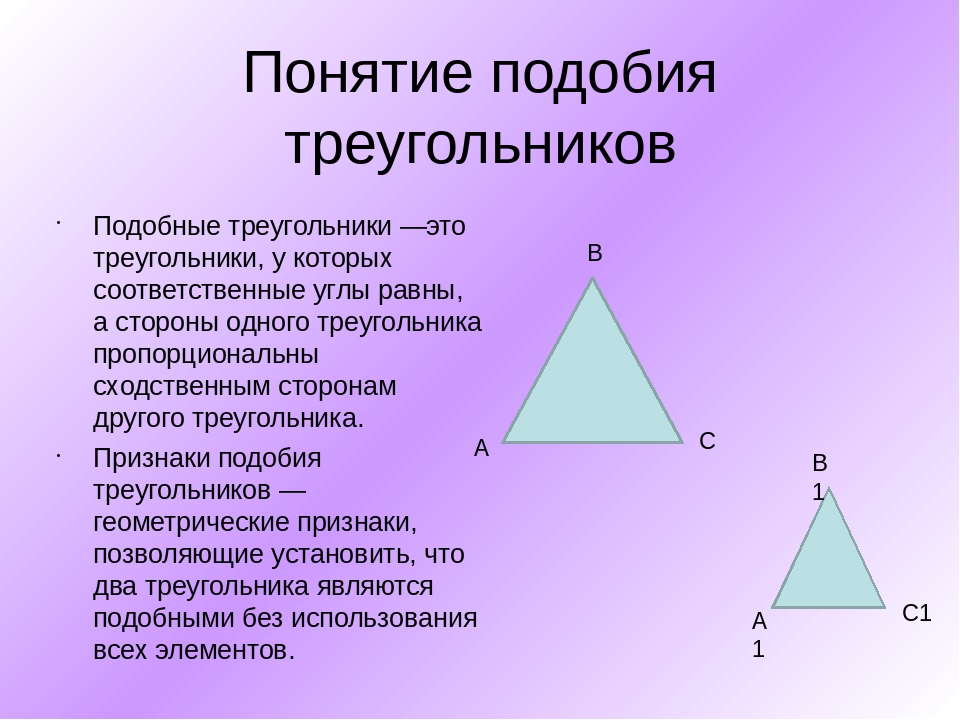
22. Признаки подобия треугольников
Первый признак подобия треугольников.(по двум углам)
Второй признак подобия треугольников.
(по углу и двум пропорциональным
сторонам)
Третий признак подобия треугольников.
(по трем пропорциональным сторонам)
23. Первый признак подобия треугольников.
Если два угла одного треугольникасоответственно равны двум углам другого
треугольника, то такие треугольники подобны.
C1
C
A
B
A1
B1
24. Первый признак подобия треугольников.
Дано:C
ΔABC и ΔA1B1C1, A = A1, B = B.
Доказать:
ΔABC ~ ΔA1B1C1
A
A1
B
C1
Доказательство:
B1
25. Первый признак подобия треугольников.
Доказательство:C
A = A1, B = B1.
C = 180º – A – B,
C1 = 180º – A1 – B1.
A
A1
C = C1
C1B
Таким образом углы треугольников
соответственно равны.
B1
26. Первый признак подобия треугольников.
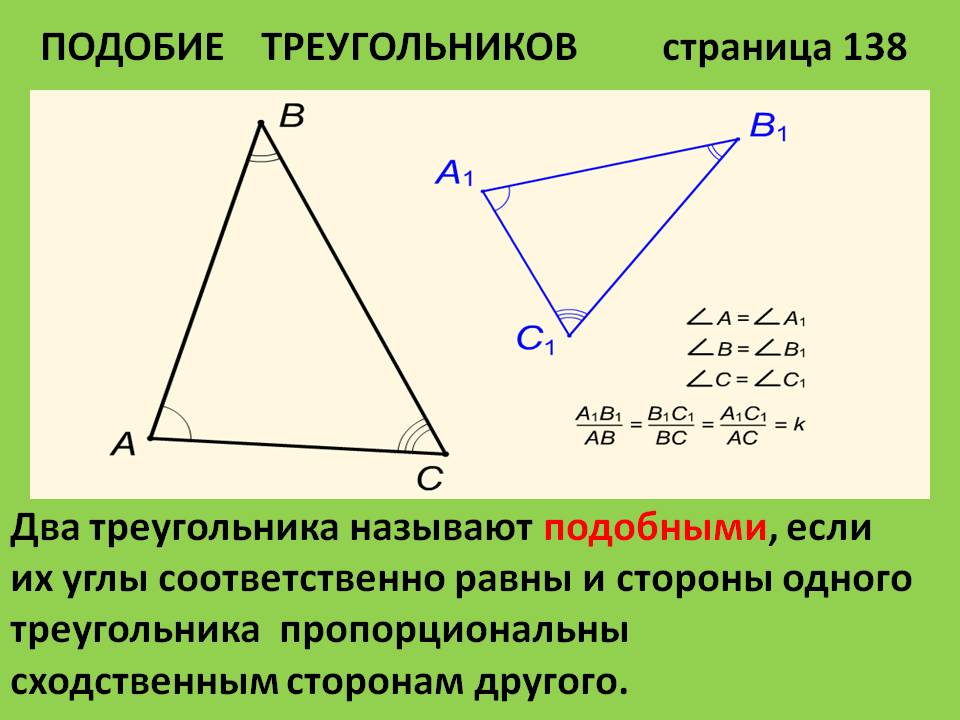 Доказательство:
Доказательство:A = A1,
B = B1.
SABC
AB AC
SA1B1C1 A1B1 A1C1
SABC
AB BC
SA1B1C1 A1B1 B1C1
C
A
B
Имеем BC
AC
B1C1 A1C1
Аналогично, рассматривая равенство углов
BC
AB
C= C1, A= A1, получим
B1C1 A1B1
Итак, сходственные стороны пропорциональны.
27. Второй признак подобия треугольников.
Если две стороны одного треугольникапропорциональны двум сторонам другого
треугольника и углы, заключенные между этими
сторонами, равны, то такие треугольники
подобны.
Β
A
A = A1
AB
AC
A1B1 A1C1
Β1
C
A1
C1
28. Второй признак подобия треугольников.
Дано:ΔABC и ΔA1B1C1,
Β
A = A1,
Доказать:
ΔABC ~ ΔA1B1C1
Β1
A
Доказательство:
C
A1
AB
AC
A1B1 A1C1
C1
29. Второй признак подобия треугольников.
СДоказательство:
Достаточно доказать, что B = B1.

A
1
2 B
C1
С2
A1
ΔABC2, 1= A1, 2= B1,
ΔABC2 ~ ΔA1B1C1 по двум углам.
AB
AC2
(из подобия).
A1B1 A1C1 AB
AC
По условию
A1B1 A1C1
AC=AC2.
B1
ΔABC=ΔABC2, т.е. B = B1.
30. Третий признак подобия треугольников.
Если три стороны одного треугольникапропорциональны трем сторонам другого
треугольника, то такие треугольники подобны.
Β1
Β
A1
A
C
AB
BC
AC
A1B1 B1C1 A1C1
C1
31. Третий признак подобия треугольников.
Дано:Β1
ΔABC и ΔA1B1C1,
AB
BC
AC
A1B1 B1C1 A1C1
A1
C1
Β
A
Доказать:
ΔABC ~ ΔA1B1C1
Доказательство:
C
32. Третий признак подобия треугольников.
СДоказательство:
Достаточно доказать, что A= A1
ΔABC2, 1= A1, 2= B1,
A
1
2 B ΔABC2 ~ ΔA1B1C1 по двум углам.
Отсюда
С2
A1
AB BC2 AC2
Β1
A1B1 B1C1 A1C1
По условию
AB
BC
AC
A1B1 B1C1 A1C1
ΔABC=ΔABC2 по трем
C1
сторонам,
т.
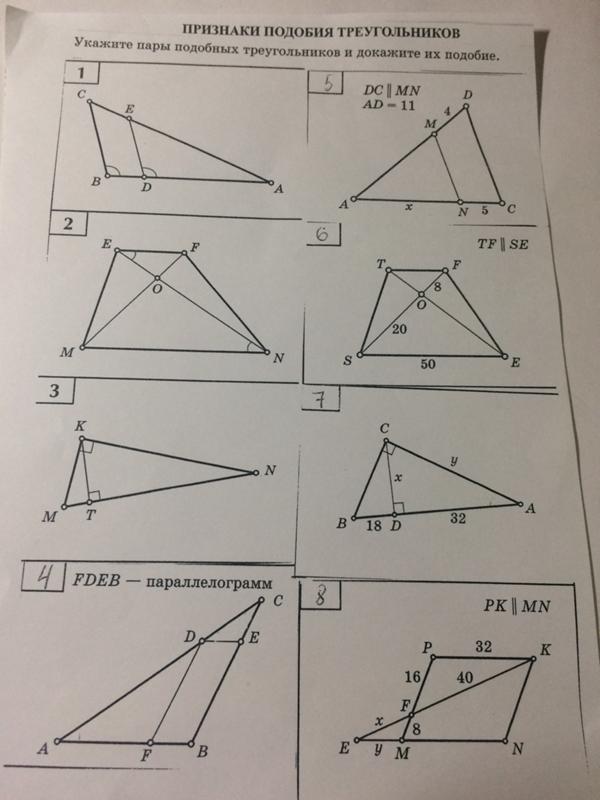 е. A = A1
е. A = A133. Разминка
1Отрезки AB и CD пропорциональны отрезкам MN и PK.
Найдите MN,
если AB = 3, CD = 4, PK = 2.
AB MN
CD PK
3 MN
4
2
MN = 1,5
34. Разминка
2• Даны два подобных прямоугольных
треугольника.
• Коэффициент подобия 1,5
• Стороны одного из них 3, 4 и 5.
• Найдите гипотенузу другого.
5 · 1,5 = 7,5
7,5
35. Разминка
3• По данным на
рисунке найдите х.
х
12
5
х
12
5
4
4
х = 15
36. Разминка
4• Длины двух окружностей 2π и 8π.
• Найдите отношение их радиусов.
2π : 8π = 1 : 4
0,25
37. Разминка
5• Отношение площадей двух квадратов
равно 9 : 1.
• Найдите сторону большего их них, если
сторона меньшего равна 2.
k2 = 9, k = 3
Коэффициент подобия
3·2=6
сторона большего квадрата
6
38. Решение задач
Пропорциональныеотрезки
1
2
3
Свойство
биссектрисы
4
5
6
7
8
9
10
11
12
13
14
15
Определение
подобных
треугольников
Отношение
периметров
подобных фигур
Отношение
площадей подобных
фигур
39.
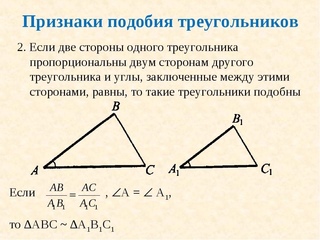 1 задача Отрезки AB и CD пропорциональны
1 задача Отрезки AB и CD пропорциональныотрезкам EF и MN.
Найдите EF,
если AB = 5 см, CD = 80 мм, MN = 1 дм.
40. 4 задача
BВ треугольнике АВС
АС = 6 см,
1
2
ВС = 7 см,
AB = 8 см,
A
D
C
BD – биссектриса.
Найдите, AD, CD.
41. 7 задача
Треугольник со сторонами 2 см, 3 см, 4 смподобен треугольнику
со сторонами 5 мм, 7,5 мм и 1 см.
Найдите коэффициент подобия.
42. 10 задача
Сходственные стороны подобныхтреугольников относятся как 1 : 3.
Найдите периметр большего
треугольника, если периметр
меньшего 15 см.
43. 13 задача
ΔABC ~ ΔA1B1C1 ,AB : A1B1 = k = 4
SΔABC= 48 м2.
Найдите площадь треугольника A1B1C1 .
44. 2 задача
BC
O
A
10
D
В параллелограмме
ABCD диагонали
пересекаются в точке О,
CD = 10 см.
Найдите периметр
параллелограмма, если
BC
AC
CD OC
45.
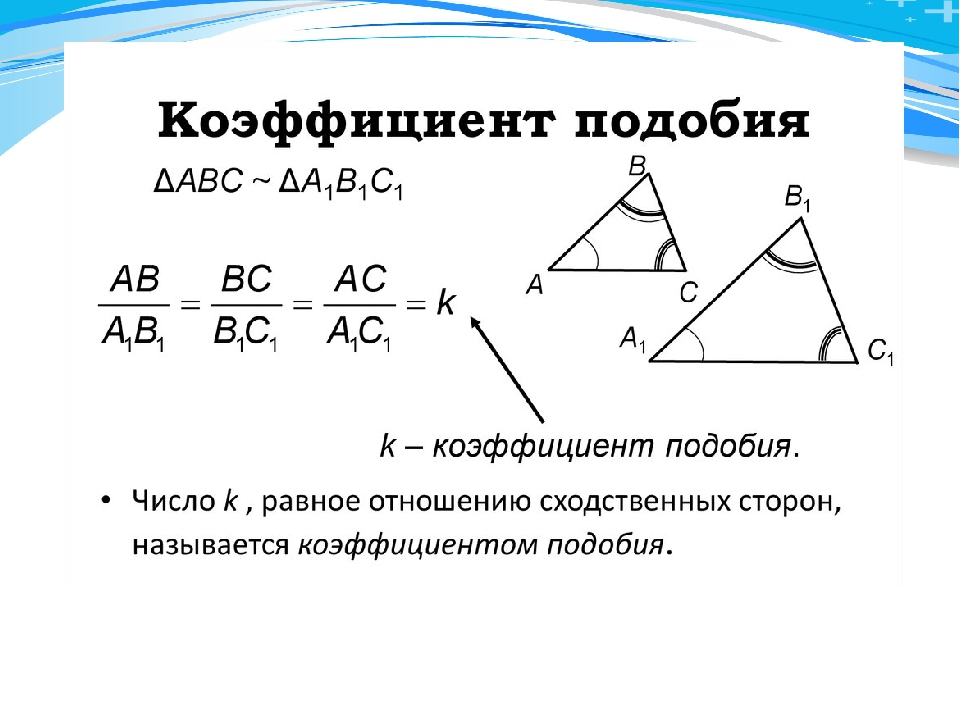 5 задача B
5 задача BM
12
A
18
C
Основание
равнобедренного
треугольника равно 18 мм,
а биссектриса делит
боковую сторону на
отрезки, из которых
прилежащий к основанию
равен 12 мм. Найдите
периметр треугольника
46. 8 задача
Треугольники KPF и ЕМТ подобны, причемT
M
40°
E
P
20°
F
K
KP
PF
KF
ME MT ET
F = 20°, E = 40°.
Найдите остальные
углы этих
треугольников.
47. 11 задача
Периметры подобных треугольников12 мм и 108 мм соответственно.
Стороны одного из них 3 мм, 4 мм и 5 мм.
Найдите стороны другого и
определите его вид.
48. 14 задача
Площади двух подобных треугольниковравны 16 см2 и 25 см2.
Одна из сторон первого треугольника
равна 2 см.
Найдите сходственную ей сторону
второго треугольника.
49. 3 задача
В треугольнике ABCB
точка K лежит на стороне
10
АС.
 Площади
Площадитреугольников АВK и
KВС относятся
.
A
K
C
как 1 : 3,
ВС = 10 см. Найдите AC ,
BC
AK
если
AC KC
50. 6 задача
BAD = 4
1
BC = 5
2
AB + DC = 12
Найти AB, DC, AC
4
A
D
C
51. 9 задача
На рисункеB
ΔВЕС ~ ΔАВС,
АЕ = 16 см,
A
C
16
E
9
СЕ = 9 см. Углы
ABC и ВЕС тупые.
Найдите ВС.
52. 12 задача
Масштаб плана 1 : 1000.Какова длина ограды участка,
если на плане размеры
прямоугольника,
изображающего участок 2 см х 5 см.
53. 15 задача
Периметры подобных треугольниковотносятся как 2 : 3,
сумма их площадей равна 260 см2.
Найдите площадь каждого
треугольника.
54. ЗАДАЧИ
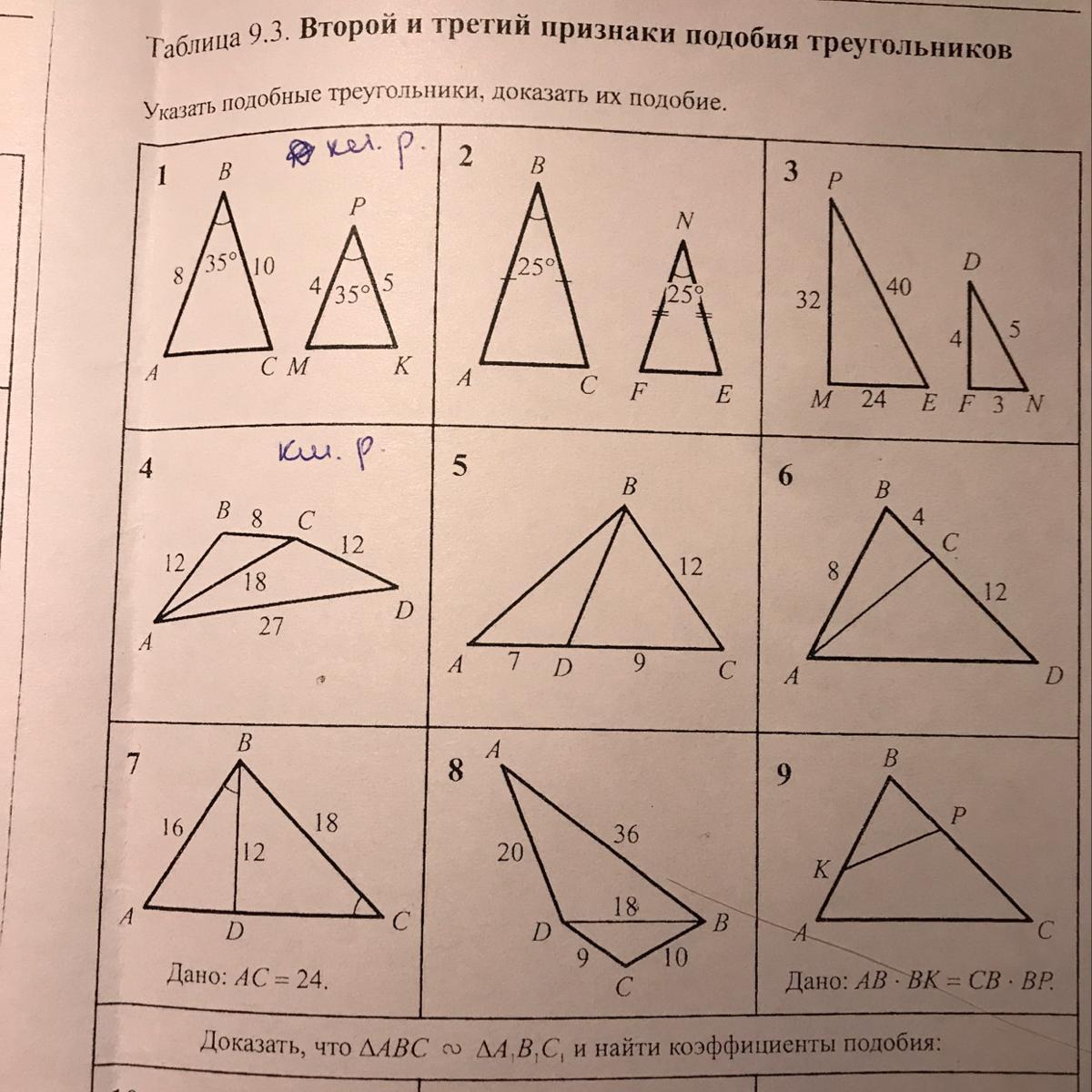
1.Диагонали трапеции ABCD пересекаются в точке O. Площади
треугольников BOC и AOD относятся как 1 : 9. Сумма оснований
BC и AD равна 4,8 см. Найдите основания трапеции.
Решение:
55. Решение
BC
2
4
3
O
1
A
Рассмотрим ΔAOD и
ΔBOC:
1= 2 (накрест
лежащие при AD ||
BC, и секущей AC;
3= 4 (вертикальные)
ΔAOD ~ ΔBOC (по двум
углам)
D
AO OD AD = k
OC OB BC
56. Решение
BC
2
4
3
S AOD
9
2
k
S BOC
1
.
k=3
O
AD + BC =
= 3BC + BC = 4BC
AD + BC = 4,8см
(по условию)
1
D
A
BC = 1,2 см
AD = 3,6 см
Ответ:
BC = 1,2 см AD = 3,6 см
57. ЗАДАЧИ
B2,5
4
20
A
2.
5
C
D
E
16
10
F
Докажите, что треугольники, изображенные на рисунке, подобны, и
выясните взаимное положение прямых CB и DF.
Решение:
58. Решение
B2,5
4
20
A
5
C
D
E
16
10
Отсюда
BС AC AB
DF DE EF
F
ΔABC~ΔDEF
по трем
пропорциональным
сторонам
Найдем
отношение
сходственных
сторон данных
треугольников
AB 2,5
0,25
EF 10
AC 5
0,25
ED 20
BС 4
0,25
DF 16
59.
 Решение B
Решение B.
E
1
A
C
D
2
ΔABC~ΔDEF
Соответственно
A = E
B = F
ACB = EDF
F
Рассмотрим
прямые BC и DF,
секущую AE
1 = 2
(внешние накрест
лежащие)
BC || DF.
60. ЗАДАЧИ
3.Отрезки AB и CD пересекаются
AO DO
в точке O, причем OB OC .
Докажите, что CBO = DAO.
Решение:
61. Решение
Рассмотрим ΔAOD иΔCOB
DOA = COB
(вертикальные).
D
A
O
B
C
AO DO
OB OC
.
ΔAOD ~ ΔCOB по углу и
двум пропорциональным
сторонам.
CBO = DAO (из
подобия).
62. ЗАДАЧИ
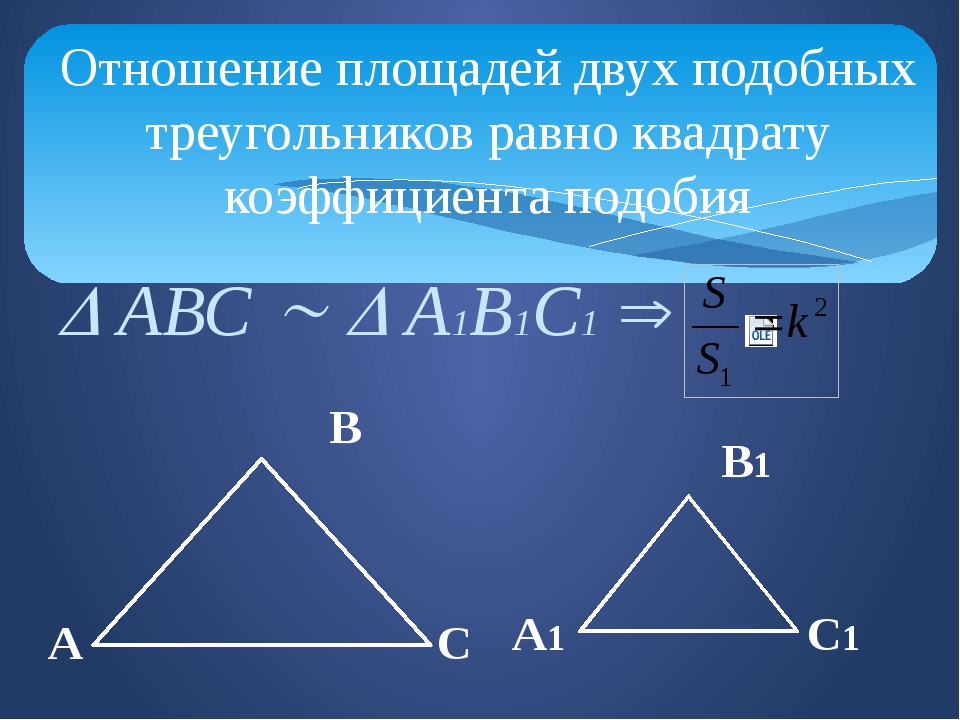
4.В треугольнике ABC
AB = 4, BC = 6, AC = 7.
Точка E лежит на стороне AB.
Внутри треугольника взята точка M так,
что MB = 5,25, ME = 4,5, AE = 1.
Прямая BM пересекает AC в точке P.
Докажите, что ΔAPB равнобедренный.
Решение:
63. Решение
.A
4 E
Рассмотрим ΔBEM и ΔABC
1
BE = AB − AE = 4 – 1 = 3
BE : AB = 3 : 4 = 0,75
B
4,5
5,25
M
EM : BC = 4,5 : 6 = 0,75
7
BM : AC = 5,25 : 7 = 0,75,
т.
 е. стороны треугольников
е. стороны треугольниковP
пропорциональны
6
C
Решение
ΔBEM ~ ΔABC по трем
пропорциональным сторонам.
Следовательно, BME = AСB
EBM = BAC
BEM = ABC.
Рассмотрим треугольник ABP:
EBM = BAC, т.е. ABP = BAP.
ΔABP – равнобедренный, что и
требовалось доказать.
65. ЗАДАЧИ
5.Диагональ AC параллелограмма ABCD равна 90.
Середина M стороны AB соединена с вершиной D.
Отрезок MD пересекает AC в точке O.
Найдите отрезки AО и CО.
Решение:
66. Решение
CB
M
A
O
D
Рассмотрим
ΔAOM и ΔCОD
AOM = CОD
(вертикальные),
MAO = ОCD
(накрест лежащие
при AB || DC и
секущей AC).
Отсюда ΔAOM ~
ΔCОD
по двум углам.
67. Решение
CB
M
A
O
D
AO OM AM
1
OC OD CD
2
.
AM = ½ AB (по условию)
AB = CD (ABCD параллелограмм),
AM : CD = 1 : 2
ΔAOM ~ ΔCОD
т.
 е. AO = 0,5CО
е. AO = 0,5CОAO = ⅓AC = ⅓·90 = 30
CO = ⅔AC = ⅔·90 = 60
68. ТЕСТ
Решите задачи, отметьте нужные ячейкиА
1
2
3
4
5
Б
В
Г
69. ТЕСТ
1. По данным рисунка х равенА) 7
7
Б) 14
В) 3,5
х
Г) 14/3
70. ТЕСТ
2) По данным рисунка периметрΔABC равен
В
А) 9
Б) 27
3
В) 36
2
А
4
Г) 18
С
71. ТЕСТ
3) По данным рисунка отрезок BCравен
В
А) 3,75
3
Б) 7,5
3
В) 5
2,5
Г) 4,5
А
4
0,5
С
72. ТЕСТ
BE
12
9
3
A
18
C
D
4
6
4) По данным рисунка площади данных
треугольников относятся
А) 3 : 1
Б) 9 : 1
В) 6 : 1
Г) 9 : 4
F
73. ТЕСТ
BE
12
9
3
A
18
C
D
4
6
F
5) По данным рисунка прямые AB и DE
А) нельзя ответить
Б) пересекаются
В) параллельны
74.
 ТЕСТ ОТВЕТЫ:
ТЕСТ ОТВЕТЫ:А
1
2
3
4
5
Б
В
Г
75. Помощь в управлении презентацией
• управление презентациейосуществляется с помощью левой
клавиши мыши
• переход от одного слайда к другому и на
гиперссылки по одиночному щелчку
• завершение презентации при нажатии
кнопки выход
Возврат в содержание
Переход по слайдам
Возврат к гиперссылке
Справка
| | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация / / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т.д. Градусы в радианы. / / Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. / / Признаки равенства треугольников. Признаки равенства прямоугольных треугольников. Признаки подобия треугольников. Признаки подобия прямоугольных треугольников. Треугольники, Прямоугольники и т.д. Градусы в радианы. / / Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. / / Признаки равенства треугольников. Признаки равенства прямоугольных треугольников. Признаки подобия треугольников. Признаки подобия прямоугольных треугольников.
| |||||||||
| Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||||||
| TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||
Доказательство признаков подобия треугольников
☰
Доказательство первого признака подобия треугольников
Первый признак подобия треугольников утверждает, что если у треугольников две стороны соответственно пропорциональны, а углы между ними равны, то такие треугольники подобны.
Рассмотрим треугольники ABC и DEF, у которых DE = kAB, EF = kBC и ∠B = ∠E.
Чтобы доказать подобие данных треугольников, требуется доказать, что DF = kAC, так как подобие треугольников определяется по трем пропорциональным сторонам.
Найдем стороны AC и DF по теореме косинусов (квадрат стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного произведения этих сторон, умноженному на косинус угла между ними):
AC2 = AB2 + BC2 – 2 · AB · BC · cos B
DF2 = DE2 + EF2 – 2 · DE · EF · cos E
Так как ∠B = ∠E и AB = kDE, BC = kEF, то мы можем выразить квадрат стороны DF через угол и стороны треугольника ABC:
DF2 = (kAB)2 + (kBC)2 – 2 · kAB · kBC · cos B
Вынесем k2 за скобку:
DF2 = k2(AB2 + BC2 – 2 · AB · BC · cos B)
Выражение в скобках равно ранее выраженному через теорему косинусов квадрату стороны AC. Поэтому можно записать так:
Поэтому можно записать так:
DF2 = k2AC2
Отсюда получаем, что DF = kAC, что и требовалось доказать. Таким образом, если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника и углы между этими сторонами каждого треугольника равны, то оказываются соответственно пропорциональными и третьи их стороны, а, следовательно, такие треугольника подобны.
Доказательство второго признака подобия треугольников
Второй признак подобия треугольников определяет подобие по наличию двух соответственно равных углов.
Пусть даны треугольники ABC и DEF, у которых ∠A = ∠D, ∠B = ∠E.
Если эти треугольники подобны, то их стороны будут пропорциональны друг другу, т. е. будут соблюдаться равенства AB = kDE, BC = kEF, AB = kDF.
Если в одном треугольнике два угла соответственно равны двум углам в другом треугольнике, то равными будут и третьи углы этих треугольников, т.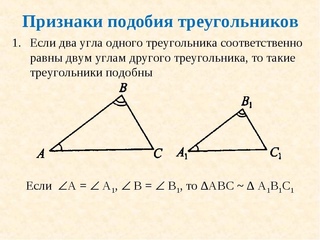 к. сумма углов любого треугольника равна 180°.
к. сумма углов любого треугольника равна 180°.
Как известно, у подобных треугольников углы соответственно равны. Т. е. если треугольники подобны, то их углы соответственно равны. Однако нельзя однозначно утверждать обратное: если углы соответственно равны, то треугольники подобны. Ведь можно предположить, что существую треугольники с соответственно равными углами, но у которых стороны не пропорциональны, а значит, такие треугольники не являются подобными.
Согласно теореме синусов, сторона треугольника равна произведению диаметра описанной окружности на синус противолежащего угла.
Если диаметр описанной около треугольника ABC окружности равен d, то мы можем выразить стороны этого треугольника так:
AB = d sin C, BC = d sin A, AC = d sin B
Если диаметр описанной около треугольника DEF окружности равен d1, то получим:
DE = d1 sin F, EF = d1 sin D, DF = d1 sin E
Так как углы A, B и C соответственно равны углам D, E и F, то мы можем заменить одни на другие. Сделаем это для сторон треугольника DEF:
Сделаем это для сторон треугольника DEF:
DE = d1 sin C, EF = d1 sin A, DF = d1 sin B
Найдем отношения сторон одного треугольника к соответствующим сторонам другого:
AB/DE = (d sin С) / (d1 sin С) = d/d1
BC/EF = (d sin A) / (d1 sin A) = d/d1
AC/DF = (d sin B) / (d1 sin B) = d/d1
То есть все три отношения равны одному и тому же значению (d/d1), а значит, равны между собой; т. е.
AB/DE = BC/EF = AC/DF
Таким образом, стороны одного треугольника пропорциональны сторонам другого треугольника. Значит, треугольники подобны.
Третий признак подобия треугольников
Нередко выделяют третий признак подобия треугольников: если все стороны одного треугольника соответственно пропорциональны сторонам другого, то такие треугольники подобны. Однако само определение подобных треугольников нередко ограничивается именно этим признаком, а равенство углов подобных треугольников доказывается в виде теоремы (Углы подобных треугольников).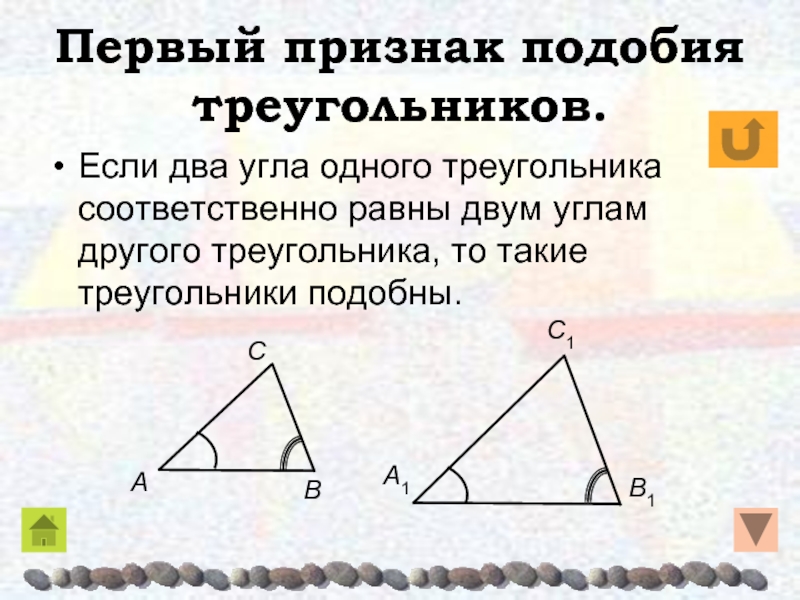
100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА
В 2021 году казахстанские школьники будут сдавать по-новому Единое национальное тестирование. Помимо того, что главный школьный экзамен будет проходить электронно, выпускникам предоставят возможность испытать свою удачу дважды. Корреспондент zakon.kz побеседовал с вице-министром образования и науки Мирасом Дауленовым и узнал, к чему готовиться будущим абитуриентам.
— О переводе ЕНТ на электронный формат говорилось не раз. И вот, с 2021 года тестирование начнут проводить по-новому. Мирас Мухтарович, расскажите, как это будет?
— По содержанию все остается по-прежнему, но меняется формат. Если раньше школьник садился за парту и ему выдавали бумажный вариант книжки и лист ответа, то теперь тест будут сдавать за компьютером в электронном формате. У каждого выпускника будет свое место, огороженное оргстеклом.
Зарегистрироваться можно будет электронно на сайте Национального центра тестирования. Но, удобство в том, что школьник сам сможет выбрать дату, время и место сдачи тестирования.
Но, удобство в том, что школьник сам сможет выбрать дату, время и место сдачи тестирования.
Кроме того, в этом году ЕНТ для претендующих на грант будет длиться три месяца, и в течение 100 дней сдать его можно будет два раза.
— Расскажите поподробнее?
— В марте пройдет тестирование для желающих поступить на платной основе, а для претендующих на грант мы ввели новые правила. Школьник, чтобы поступить на грант, по желанию может сдать ЕНТ два раза в апреле, мае или в июне, а наилучший результат отправить на конкурс. Но есть ограничение — два раза в один день сдавать тест нельзя. К примеру, если ты сдал ЕНТ в апреле, то потом повторно можно пересдать его через несколько дней или в мае, июне. Мы рекомендуем все-таки брать небольшой перерыв, чтобы еще лучше подготовиться. Но в любом случае это выбор школьника.
— Система оценивания останется прежней?
— Количество предметов остается прежним — три обязательных предмета и два на выбор. Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.
Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.
Самое главное — результаты теста можно будет получить сразу же после нажатия кнопки «завершить тестирование». Раньше уходило очень много времени на проверку ответов, дети и родители переживали, ждали вечера, чтобы узнать результат. Сейчас мы все автоматизировали и набранное количество баллов будет выведено на экран сразу же после завершения тестирования.
Максимальное количество баллов остается прежним — 140.
— А апелляция?
— Если сдающий не будет согласен с какими-то вопросами, посчитает их некорректными, то он сразу же на месте сможет подать заявку на апелляцию. Не нужно будет ждать следующего дня, идти в центр тестирования, вуз или школу, все это будет электронно.
— С учетом того, что школьникам не придется вручную закрашивать листы ответов, будет ли изменено время сдачи тестирования?
— Мы решили оставить прежнее время — 240 минут.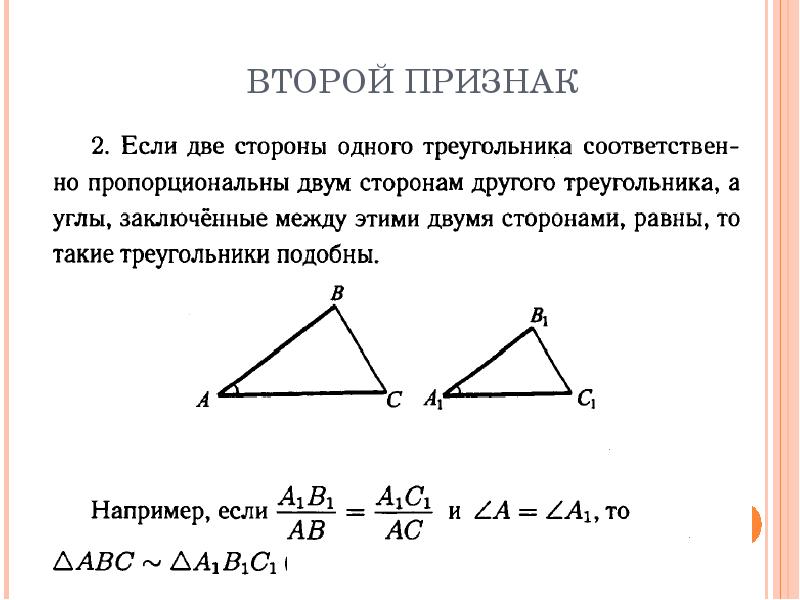 Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.
Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.
— Не секрет, что в некоторых селах и отдаленных населенных пунктах не хватает компьютеров. Как сельские школьники будут сдавать ЕНТ по новому формату?
— Задача в том, чтобы правильно выбрать время и дату тестирования. Центры тестирования есть во всех регионах, в Нур-Султане, Алматы и Шымкенте их несколько. Школьники, проживающие в отдаленных населенных пунктах, как и раньше смогут приехать в город, где есть эти центры, и сдать тестирование.
— На сколько процентов будет обновлена база вопросов?
— База вопросов ежегодно обновляется как минимум на 30%. В этом году мы добавили контекстные задания, то что школьники всегда просили. Мы уделили большое внимание истории Казахстана и всемирной истории — исключили практически все даты. Для нас главное не зазубривание дат, а понимание значения исторических событий. Но по каждому предмету будут контекстные вопросы.
Но по каждому предмету будут контекстные вопросы.
— По вашему мнению система справится с возможными хакерскими атаками, взломами?
— Информационная безопасность — это первостепенный и приоритетный вопрос. Центральный аппарат всей системы находится в Нур-Султане. Связь с региональными центрами сдачи ЕНТ проводится по закрытому VPN-каналу. Коды правильных ответов только в Национальном центре тестирования.
Кроме того, дополнительно через ГТС КНБ (Государственная техническая служба) все тесты проходят проверку на предмет возможного вмешательства. Здесь все не просто, это специальные защищенные каналы связи.
— А что с санитарными требованиями? Нужно ли будет школьникам сдавать ПЦР-тест перед ЕНТ?
— ПЦР-тест сдавать не нужно будет. Требование по маскам будет. При необходимости Центр национального тестирования будет выдавать маски школьникам во время сдачи ЕНТ. И, конечно же, будем измерять температуру. Социальная дистанция будет соблюдаться в каждой аудитории.
— Сколько человек будет сидеть в одной аудитории?
— Участники ЕНТ не за семь дней будут сдавать тестирование, как это было раньше, а в течение трех месяцев. Поэтому по заполняемости аудитории вопросов не будет.
— Будут ли ужесточены требования по дисциплине, запрещенным предметам?
— Мы уделяем большое внимание академической честности. На входе в центры тестирования, как и в предыдущие годы, будут стоять металлоискатели. Перечень запрещенных предметов остается прежним — телефоны, шпаргалки и прочее. Но, помимо фронтальной камеры, которая будет транслировать происходящее в аудитории, над каждым столом будет установлена еще одна камера. Она же будет использоваться в качестве идентификации школьника — как Face ID. Сел, зарегистрировался и приступил к заданиям. Мы применеям систему прокторинга.
Понятно, что каждое движение абитуриента нам будет видно. Если во время сдачи ЕНТ обнаружим, что сдающий использовал телефон или шпаргалку, то тестирование автоматически будет прекращено, система отключится.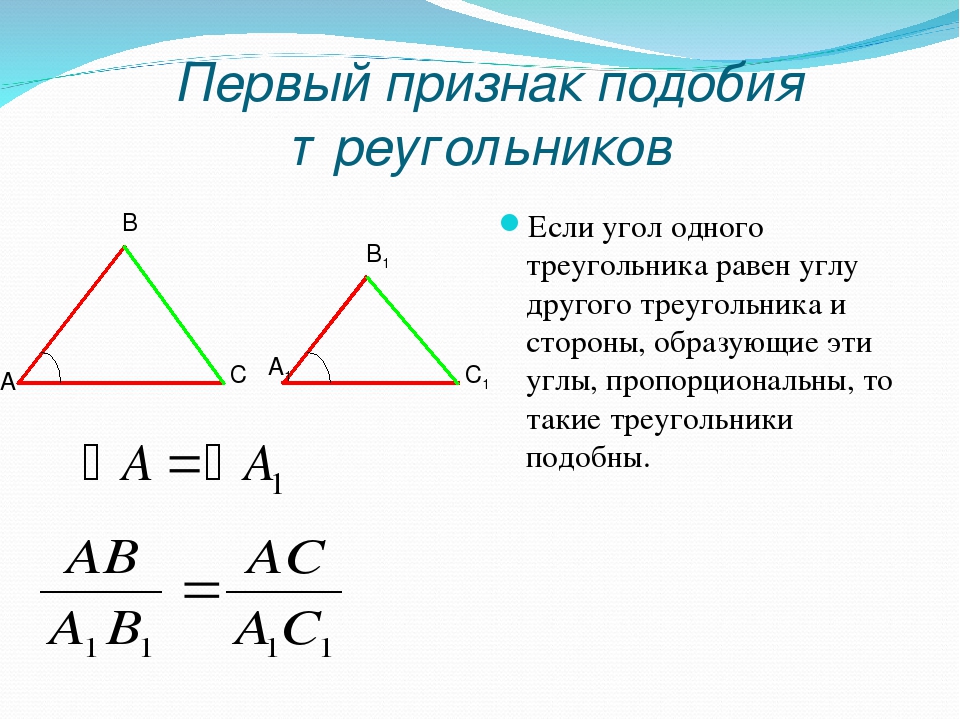
— А наблюдатели будут присутствовать во время сдачи тестирования?
— Когда в бумажном формате проводили ЕНТ, мы привлекали очень много дежурных. В одной аудитории было по 3-4 человека. При электронной сдаче такого не будет, максимум один наблюдатель, потому что все будет видно по камерам.
— По вашим наблюдениям школьники стали меньше использовать запрещенные предметы, к примеру, пользоваться телефонами?
— Практика показывает, что школьники стали ответственнее относиться к ЕНТ. Если в 2019 году на 120 тыс. школьников мы изъяли 120 тыс. запрещенных предметов, по сути у каждого сдающего был телефон. То в прошлом году мы на 120 тыс. школьников обнаружили всего 2,5 тыс. телефонов, и у всех были аннулированы результаты.
Напомню, что в 2020 году мы также начали использовать систему искусственного интеллекта. Это анализ видеозаписей, который проводится после тестирования. Так, в прошлом году 100 абитуриентов лишились грантов за то, что во время сдачи ЕНТ использовали запрещенные предметы.
— Сколько средств выделено на проведение ЕНТ в этом году?
Если раньше на ЕНТ требовалось 1,5 млрд тенге из-за распечатки книжек и листов ответов, то сейчас расходы значительно сокращены за счет перехода на электронный формат. Они будут, но несущественные.
— Все-таки почему именно в 2021 году было принято решение проводить ЕНТ в электронном формате. Это как-то связано с пандемией?
— Это не связано с пандемией. Просто нужно переходить на качественно новый уровень. Мы апробировали данный формат на педагогах школ, вы знаете, что они сдают квалификационный тест, на магистрантах, так почему бы не использовать этот же формат при сдаче ЕНТ. Тем более, что это удобно, и для школьников теперь будет много плюсов.
Похожие фигурки
Говорят, что две фигуры похожий если они одинаковой формы. Говоря более математическим языком, две фигуры похожи, если их соответствующие углы равны
конгруэнтный
, а отношения длин соответствующих сторон равны.
Это обычное отношение называется масштаб .
Символ ∼ используется для обозначения сходства.
Пример 1:
На рисунке ниже пятиугольник А B C D E ∼ пятиугольник V W Икс Y Z .
(Обратите внимание, что порядок, в котором вы пишете вершины, имеет значение; например, пятиугольник А B C D E является нет похож на пятиугольник V Z Y Икс W .)
Пример 2:
Два цилиндра похожи. Найдите коэффициент масштабирования и радиус второго цилиндра.
Высота цилиндра справа составляет
1
3
высота цилиндра слева.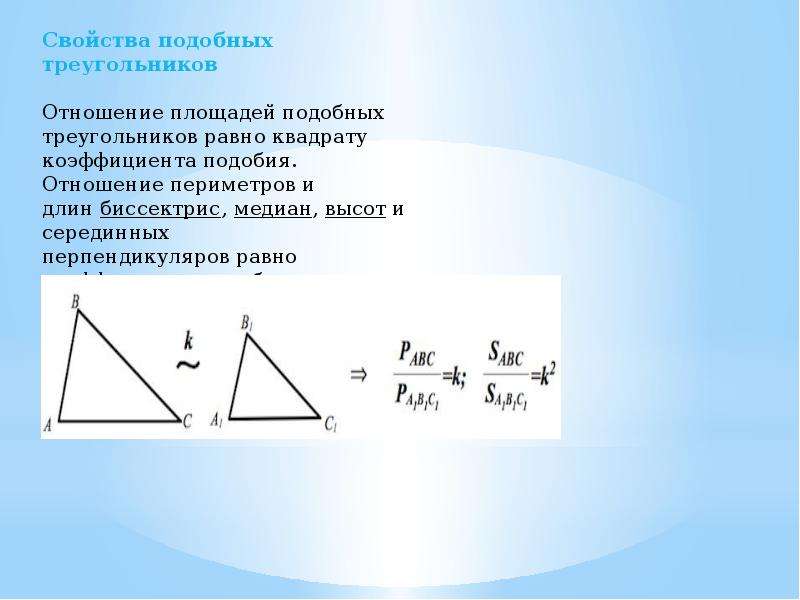 Итак, коэффициент масштабирования равен
1
3
.
Итак, коэффициент масштабирования равен
1
3
.
Чтобы получить радиус меньшего цилиндра, разделите 1,8 от 3 .
1,8 ÷ 3 знак равно 0,6
Итак, радиус меньшего цилиндра равен 0,6 см.
Обратите внимание, что двухмерная фигура похожа на другую, если вторая может быть получена из первой последовательностью вращения , размышления , переводы , а также дилатации .
Пример 3:
На рисунке выше шестиугольник
А
1
B
1
C
1
D
1
E
1
F
1
переворачивается по горизонтали, чтобы получить
А
2
B
2
C
2
D
2
E
2
F
2
.
Тогда шестиугольник А 2 B 2 C 2 D 2 E 2 F 2 переводится, чтобы получить А 3 B 3 C 3 D 3 E 3 F 3 .
Шестиугольник А 3 B 3 C 3 D 3 E 3 F 3 расширяется на коэффициент масштабирования 1 2 получить А 4 B 4 C 4 D 4 E 4 F .
Обратите внимание, что
А
1
B
1
C
1
D
1
E
1
F
1
∼
А
2
B
2
C
2
D
2
E
2
F
2
∼
А
3
B
3
C
3
D
3
E
3
F
3
∼
А
4
B
4
C
4
D
4
E
4
F
4
.
То есть все четыре шестиугольника похожи. (Фактически, первые три совпадают.)
Пример 4:
Рассмотрим пятиугольник п Q р S Т на координатной плоскости.
Ротация 180 ° о происхождении берет пятиугольник, чтобы п ‘ Q ‘ р ‘ S ‘ Т ‘ .
Теперь, расширение начала координат с помощью масштабного коэффициента. 2 занимает пятиугольник п ‘ Q ‘ р ‘ S ‘ Т ‘ к п ‘ ‘ Q ‘ ‘ р ‘ ‘ S ‘ ‘ Т ‘ ‘ .
Обратите внимание, что
п
Q
р
S
Т
∼
п
‘
Q
‘
р
‘
S
‘
Т
‘
∼
п
‘
‘
Q
‘
‘
р
‘
‘
S
‘
‘
Т
‘
‘
.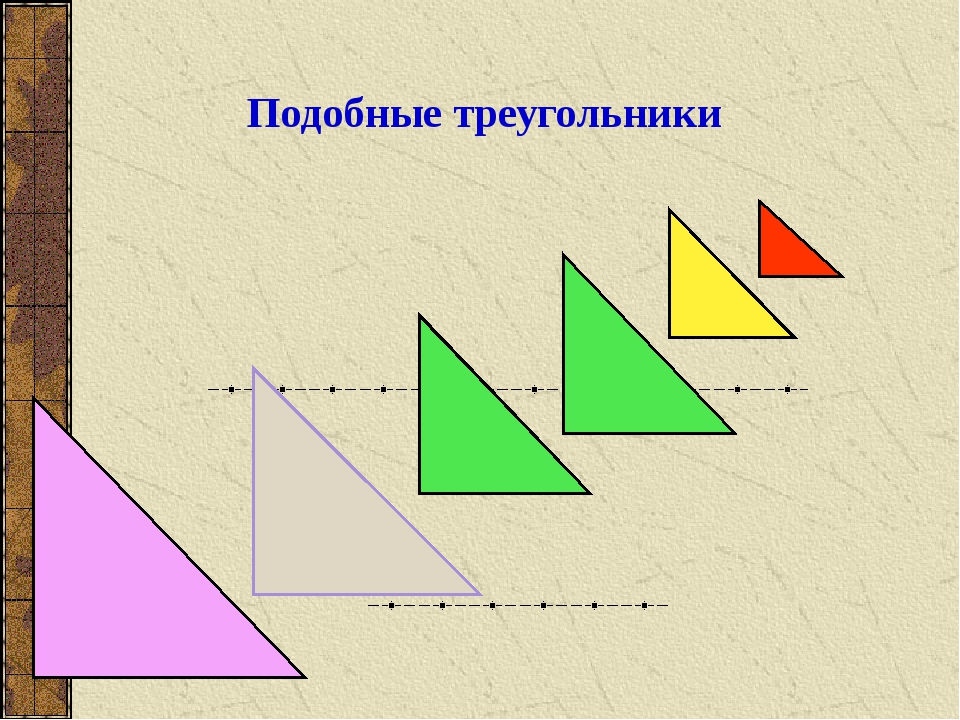 То есть все три пятиугольника похожи. (И первые два совпадают.)
То есть все три пятиугольника похожи. (И первые два совпадают.)
Сходство и соответствие
Два объекта на похожи , если они имеют одинаковую форму , так что один является увеличением другого.
Два объекта совпадают с , если они имеют одинаковую форму и размер .
Масштабные модели и факторы
В увеличении или уменьшении
- Соответствующие углы равны
- Соответствующие длины находятся в одинаковом соотношении — у них одинаковый масштабный коэффициент
- Масштабный коэффициент больше 1 для увеличения
- Коэффициент масштабирования меньше 1 для уменьшения
Треугольник A является увеличением буквы C с масштабным коэффициентом 2
Треугольник C — это уменьшение A с коэффициентом масштабирования ½
Треугольник B является увеличением C
, С масштабным коэффициентом 3
Треугольник B — это увеличение треугольника A,
с масштабным коэффициентом 1. 5
5
Его масштабный коэффициент можно записать как
Расчеты аналогичной формы
Две формы считаются подобными, если одна является масштабированной версией другой.
Это означает, что
- их соответствующие углы равны
- их соответствующие стороны находятся в таком же соотношении.
(т.е. у них одинаковый масштабный коэффициент)
Пример
Эти домино похожи?
- Убедитесь, что их соответствующие углы равны.
(все прямые углы, т. Е. Равны)
- Проверьте соотношение соответствующих сторон.
и
Домино похожи на
Недостающие стороны
Начните с формы, содержащей недостающую сторону.
Пример
Рассчитайте размер стороны x.
Подобные треугольники
Для любого треугольника
Если пары соответствующих углов равны,
тогда отношения длин соответствующих сторон равны и треугольники подобны.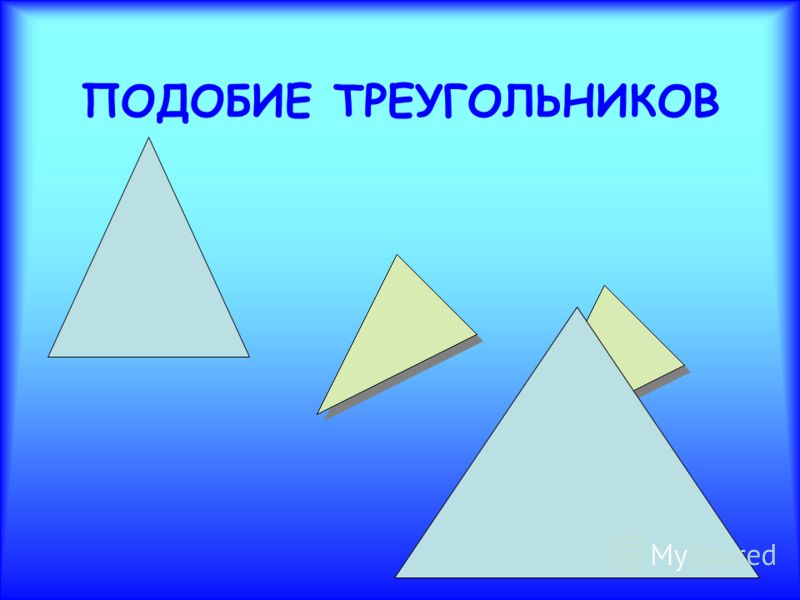
И наоборот, если отношения длин соответствующих сторон равны, то пары соответствующих углов равны, а треугольники подобны.
Пример
Если AD равно 15 см, AB равно 12 см, а DE 10 см, найдите длину BC.
BC параллельна DE, поэтому соответствующие углы равны.
Это означает, что треугольники ABC и ADE подобны.
Разделите треугольники на составляющие
Масштабированная площадь
Пример
Учитывая, что форма A увеличена в масштабе 2,
найдите размер области формы B.
Масштабированный объем
Пример
Дезодорант Wiffoff обычно продается в банках по 200 мл.
Изготовлена банка нового размера, вдвое меньшего размера старой.
Рассчитайте объем новой банки.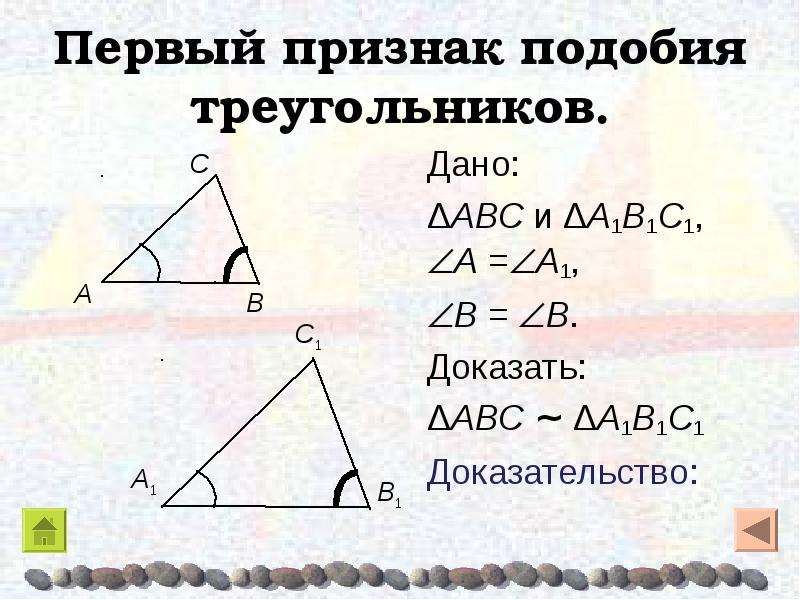
Новый баллончик объемом 25 мл.
© Александр Форрестпохожих многоугольников
Два многоугольника одинаковой формы называются аналогичными многоугольниками. Символ «похож на» — ∼. Обратите внимание, что это часть символа «соответствует» ≅. Когда два многоугольника похожи, эти два факта и должны быть верными:
- Соответствующие углы равны.
- Соотношение пар соответствующих сторон должно быть одинаковым.
На рисунке 1 четырехугольник ABCD ∼ четырехугольник EFGH.
Рисунок 1 Подобные четырехугольники.
Это означает: м ∠ A = м ∠ E , м ∠ B = м ∠ F , м ∠ C = м м м , м ∠ D = м ∠ H и
Для многоугольника один из вышеперечисленных фактов может быть истинным, а другой — истинным.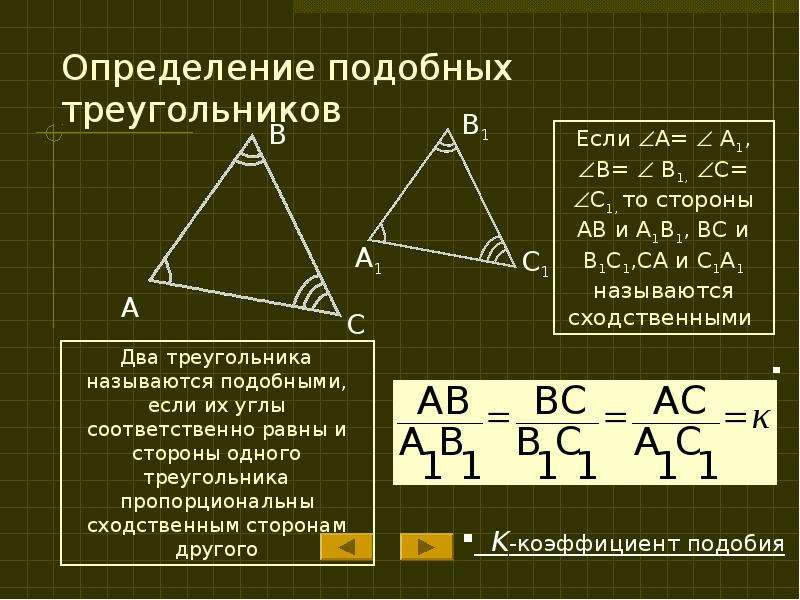 Следующие два примера показывают, как это возможно.
Следующие два примера показывают, как это возможно.
На рисунке 2 четырехугольник QRST не похож на четырехугольник WXYZ.
Рисунок 2 Четырехугольники не похожи друг на друга.
Даже если отношения соответствующих сторон равны, соответствующие углы не равны (90 ° ≠ 120 °, 90 ° ≠ 60 °).
На рисунке 3 четырехугольник FGHI не похож на четырехугольник JKLM.
Рисунок 3 Четырехугольники не похожи друг на друга.
Даже если соответствующие углы равны, отношения каждой пары соответствующих сторон не равны (3/3 ≠ 5/3).
Пример 1: На рисунке 4 четырехугольник ABCD ∼ четырехугольник EFGH. (a) Найдите m ∠ E. (b) Найдите x.
Рисунок 4 Подобные четырехугольники.
(a) м ∠ E = 90 ° (∠ E и ∠ A — соответствующие углы одинаковых многоугольников, а соответствующие углы одинаковых многоугольников равны.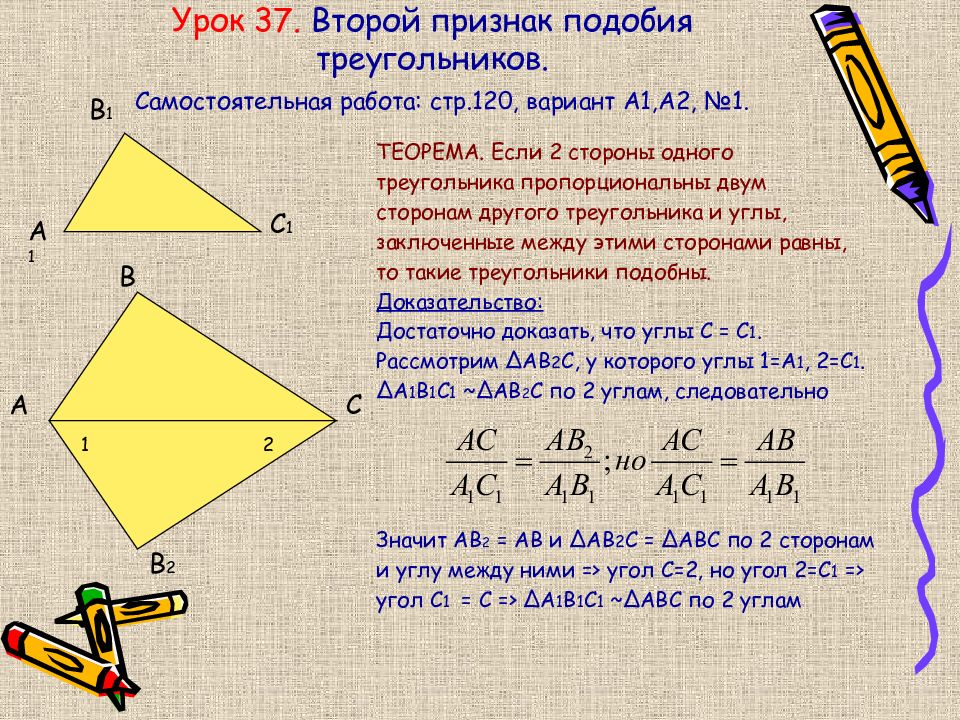 )
)
(b) 9/6 = 12/ x (Если два многоугольника похожи, то отношения каждой пары соответствующих сторон равны.)
Определение сходства | Texas Gateway
Коэффициенты могут использоваться для демонстрации мультипликативной связи между двумя величинами. Когда два соотношения эквивалентны, вы можете использовать пропорцию, чтобы связать соотношения.
Две фигуры считаются подобными, если они пропорционально связаны. В этом разделе вы исследуете взаимосвязь между соответствующими длинами сторон и соответствующими углами аналогичных фигур.На основании этого расследования вы дадите формальное определение аналогичным фигурам.
Используйте интерактив, чтобы начать исследование похожих фигур. В этом интерактиве треугольник ABC и треугольник DEF похожи на треугольники. Используйте флажки, чтобы показать или скрыть отношения длин соответствующих сторон, а также показать или скрыть размеры соответствующих углов.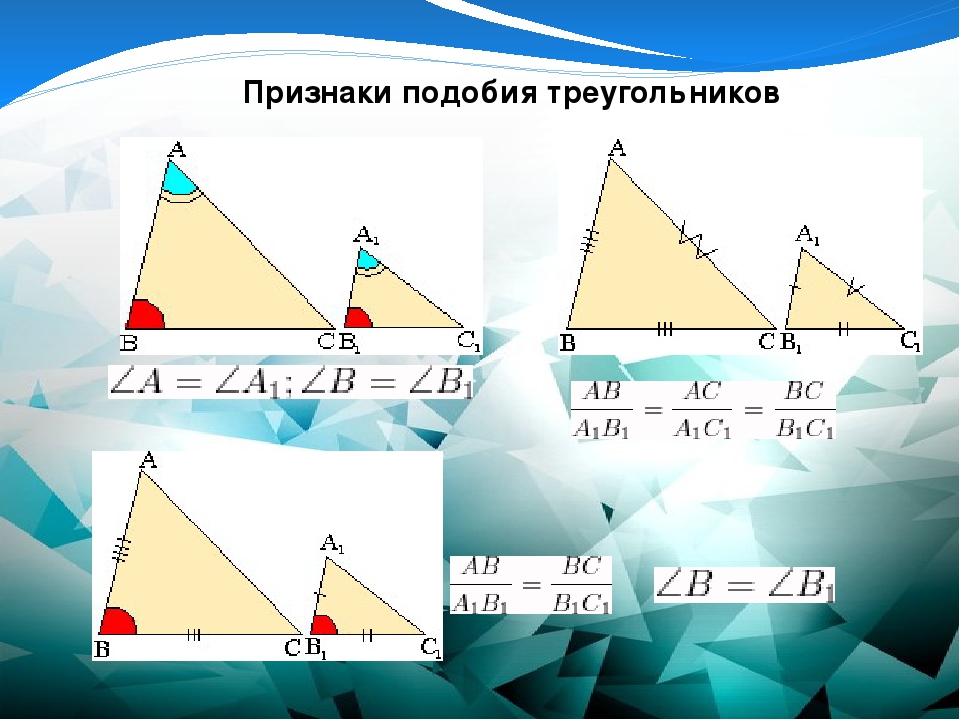 Переместите вершины треугольника ABC вокруг и обратите особое внимание на закономерности в соотношении длин соответствующих сторон и на образцы в размерах соответствующих углов.
Переместите вершины треугольника ABC вокруг и обратите особое внимание на закономерности в соотношении длин соответствующих сторон и на образцы в размерах соответствующих углов.
Исследование похожих фигур
Щелкните и перетащите на A , B или C , чтобы настроить размер треугольника ABC .
Щелкните поле «Показать / скрыть соотношения», чтобы показать или скрыть соотношения длин соответствующих сторон.
Щелкните поле «Показать / скрыть меры угла», чтобы отобразить или скрыть меры угла.
Нужны дополнительные направления?
Воспользуйтесь интерактивом, чтобы ответить на следующие вопросы.
1.Учитывая, что два треугольника похожи, что вы заметили в отношении длин соответствующих сторон треугольника ABC и треугольника DEF ?
2. Учитывая, что два треугольника похожи, что вы заметили о размерах соответствующих углов треугольника ABC и треугольника DEF ?
3. Используйте то, что вы заметили о соотношении длин соответствующих сторон и размеров соответствующих углов, чтобы написать определение подобных треугольников.
Используйте то, что вы заметили о соотношении длин соответствующих сторон и размеров соответствующих углов, чтобы написать определение подобных треугольников.
4. Как вы думаете, отношение, которое вы заметили для треугольников, будет верным для четырехугольника и других многоугольников?
7.3: Подобные многоугольники и коэффициенты масштабирования
Подобные многоугольники
Подобные многоугольники — это два многоугольника одинаковой формы, но разных размеров. Подобные многоугольники имеют соответствующие углы, равные конгруэнтным , и соответствующим сторонам, равным пропорциональным.
Рисунок \ (\ PageIndex {1} \)Эти многоугольники не похожи на :
Рисунок \ (\ PageIndex {2} \)Масштабный коэффициент
Думайте о похожих многоугольниках как об увеличении или уменьшении одной и той же формы.Символ \ sim \) используется для обозначения сходства. Определенные типы треугольников, четырехугольников и многоугольников всегда будут похожи. Например, все равносторонние треугольники и все квадраты одинаковы. . Если два многоугольника похожи, мы знаем, что длины соответствующих сторон пропорциональны. В подобных многоугольниках отношение одной стороны многоугольника к соответствующей стороне другой называется масштабным коэффициентом . Соотношение всех частей многоугольника (включая периметры, диагонали, медианы, средние сегменты, высоты) такое же, как и соотношение сторон.
Например, все равносторонние треугольники и все квадраты одинаковы. . Если два многоугольника похожи, мы знаем, что длины соответствующих сторон пропорциональны. В подобных многоугольниках отношение одной стороны многоугольника к соответствующей стороне другой называется масштабным коэффициентом . Соотношение всех частей многоугольника (включая периметры, диагонали, медианы, средние сегменты, высоты) такое же, как и соотношение сторон.
Что, если бы вам сказали, что два пятиугольника похожи, и дали бы длину сторон каждого пятиугольника. Как определить масштабный коэффициент от пятиугольника №1 до пятиугольника №2?
Пример \ (\ PageIndex {1} \)
\ (ABCD \) и \ (UVWX \) ниже. Эти два прямоугольника похожи?
Рисунок \ (\ PageIndex {3} \)Решение
Все соответствующие углы совпадают, потому что формы прямоугольные.
Посмотрим, пропорциональны ли стороны.\ (\ dfrac {8} {12} = \ dfrac {2} {3} \) и \ (\ dfrac {18} {24} = \ dfrac {3} {4} \). \ (\ dfrac {2} {3} \ neq \ dfrac {3} {4} \), поэтому стороны равны , а не в той же пропорции , а прямоугольники равны , а не аналогичный.
\ (\ dfrac {2} {3} \ neq \ dfrac {3} {4} \), поэтому стороны равны , а не в той же пропорции , а прямоугольники равны , а не аналогичный.
Пример \ (\ PageIndex {2} \)
\ (\ Delta ABC \ sim \ Delta MNP \). Периметр \ (\ Delta ABC \) равен 150, \ (AB = 32 \) и \ (MN = 48 \). Найдите периметр \ (\ Delta MNP \).
Решение
Из утверждения о подобии \ (AB \) и \ (MN \) являются соответствующими сторонами.Коэффициент масштабирования равен \ (\ dfrac {32} {48} = \ dfrac {2} {3} \) или \ (\ dfrac {3} {2} \). \ Delta ABC \) — меньший треугольник, поэтому периметр \ (\ Delta MNP \) равен \ (\ dfrac {3} {2} (150) = 225 \).
Пример \ (\ PageIndex {3} \)
Предположим, \ (\ Delta ABC \ sim \ Delta JKL \). Основываясь на утверждении о подобии, какие углы совпадают, а какие стороны пропорциональны?
Решение
Как и в заявлении о сопоставлении, конгруэнтные углы выстраиваются в соответствии с утверждением о подобии.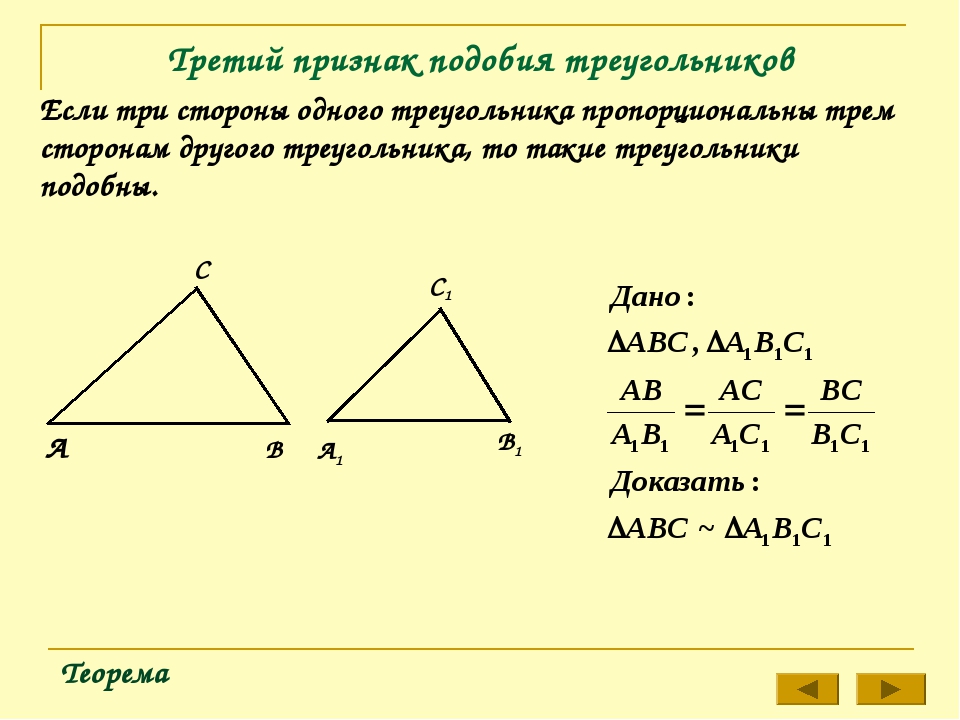 {\ circ} \).Для \ (x \) и \ (y \) установите пропорции.
{\ circ} \).Для \ (x \) и \ (y \) установите пропорции.
\ (\ dfrac {18} {30} = \ dfrac {x} {25} \ qquad \ dfrac {18} {30} = \ dfrac {15} {y} \)
\ (450 = 30x \ qquad 18y = 450 \)
\ (х = 15 \ qquad у = 25 \)
Пример \ (\ PageIndex {5} \)
\ (ABCD \ sim AMNP \). Найдите масштабный коэффициент и длину \ (BC \).
Рисунок \ (\ PageIndex {5} \)Решение
Выровняйте соответствующие стороны \ (AB \) и \ (AM = CD \), чтобы коэффициент масштабирования был \ (\ dfrac {30} {45} = \ dfrac {2} {3} \) или \ ( \ dfrac {3} {2} \).Поскольку \ (BC \) находится в большем прямоугольнике, мы умножим 40 на \ (\ dfrac {3} {2} \), потому что \ (\ dfrac {3} {2} \) больше 1. \ (BC = \ dfrac {3} {2} (40) = 60 \).
Геометрия: сходство в геометрии
Covid-19 привел мир к феноменальному переходу.
Электронное обучение — это будущее уже сегодня.
Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!!
В этом разделе мы обсудим сходство в геометрии.
Две геометрические фигуры одинаковой формы и размера называются конгруэнтными фигурами.Обратите внимание, что совпадающие числа во всех отношениях одинаковы.
Геометрические фигуры одинаковой формы, но разных размеров известны как подобных фигур.
Для обозначения аналогичной цифры мы используем этот знак ~ .
Например, если треугольник ABC и треугольник PQR подобны, то это можно представить следующим образом.
Δ ABC ~ ΔPQR.
Примеры:
1) Любые два отрезка линии всегда похожи, но они не обязательно должны совпадать. Они конгруэнтны, если их длины равны.
2) Любые два равносторонних треугольника подобны.
3) Любые два круга похожи, но не обязательно совпадают. Они конгруэнтны, если их радиусы равны.
Между частями двух одинаковых фигур всегда существует взаимно однозначное соответствие.
Q.1 Заполните пустые поля.
1) Все круги _________ (совпадают / похожи). (Ответ)
(Ответ)
2) Все _________ треугольники похожи (равнобедренные / равносторонние).(Ответ)
3) Все квадраты ________ (одинаковые / совпадающие). (Ответ)
Q.2 Сколько на рисунке похожих треугольников?
(Отв.)
Q.3 Определите пару, имеющую похожие треугольники.
(Ans)
Q.4 Приведите два разных примера пары
(i) Похожие цифры (Ans-i)
(ii) Не похожие цифры (Ans-ii)
Q.5 Укажите сходство или нет:
(i) Два круга радиусом 4 см и 5 см.
(ii) Два равносторонних треугольника со сторонами 5 см и 8 см каждый.
(iii) Два треугольника, один — прямоугольный, а другой — равнобедренный.
Сходство в треугольниках
• Сходство в геометрии
• Свойства подобных треугольников
• Основная теорема пропорциональности (теорема Фалеса)
• Противоположная основная теорема о пропорциональности
• Теорема о биссектрисе внутреннего угла
• Теорема о биссектрисе внешнего угла
• Доказательство теоремы о биссектрисе внешнего угла
• Базовая пропорциональность
• Критерии подобия треугольников
• Среднее геометрическое количество похожих треугольников
• Области двух одинаковых треугольников
Covid-19 повлиял на физическое взаимодействие между людьми.
Не позволяйте этому влиять на ваше обучение.
Как вычислить одинаковые треугольники в геометрии
Ключевые термины
o Преобразование
o Перевод
o Отражение
o Линия отражения
o Вращение
o Центр вращения
o Расширение
o Угловое состояние
o Условие соразмерности (пропорциональности)
o Боковой угол-сторона (пропорциональность)
Цели
o Понять, как преобразования могут использоваться как метод понимания соответствия и сходства
o Докажите, что два треугольника похожи, используя соответствующие критерии
Другой взгляд на совпадение и сходство
Давайте рассмотрим задачу доказательства того, что два треугольника подобны.Напомним, что сравнение означает, что размеры всех трех сторон и всех трех углов одинаковы для двух треугольников.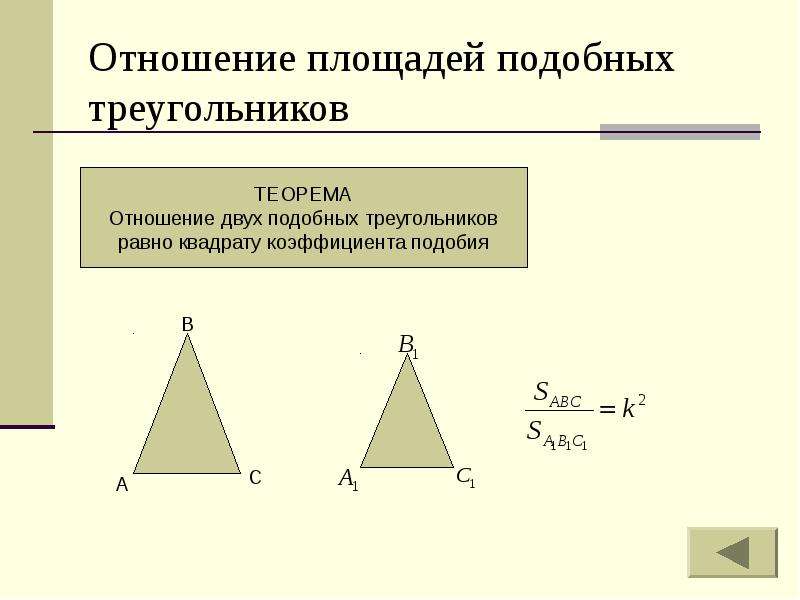 Все, что требуется для подобия, — это совпадение углов. Другой способ взглянуть на конгруэнтность и сходство — с помощью геометрических преобразований . С точки зрения непрофессионала трансформация — это просто движение или изменение фигуры. Четыре основных преобразования — это переводы, отражения, вращения и растяжения. Перенос — это просто перемещение всей фигуры на некоторое расстояние, при этом форма и ориентация фигуры остаются неизменными.Перевод показан ниже.
Все, что требуется для подобия, — это совпадение углов. Другой способ взглянуть на конгруэнтность и сходство — с помощью геометрических преобразований . С точки зрения непрофессионала трансформация — это просто движение или изменение фигуры. Четыре основных преобразования — это переводы, отражения, вращения и растяжения. Перенос — это просто перемещение всей фигуры на некоторое расстояние, при этом форма и ориентация фигуры остаются неизменными.Перевод показан ниже.
Еще одно преобразование — это отражение , которое создает зеркальное отображение фигуры. Линия отражения должна быть выбрана в качестве «зеркала» для создания отраженной фигуры. Отражение показано ниже.
Вращение , как следует из названия, просто включает в себя «вращение» фигуры вокруг некоторой точки (этот центр вращения может находиться внутри или вне фигуры). Ниже показаны два поворота: в крайнем левом примере центр вращения находится внутри рисунка, а в крайнем правом примере центр вращения находится за пределами рисунка.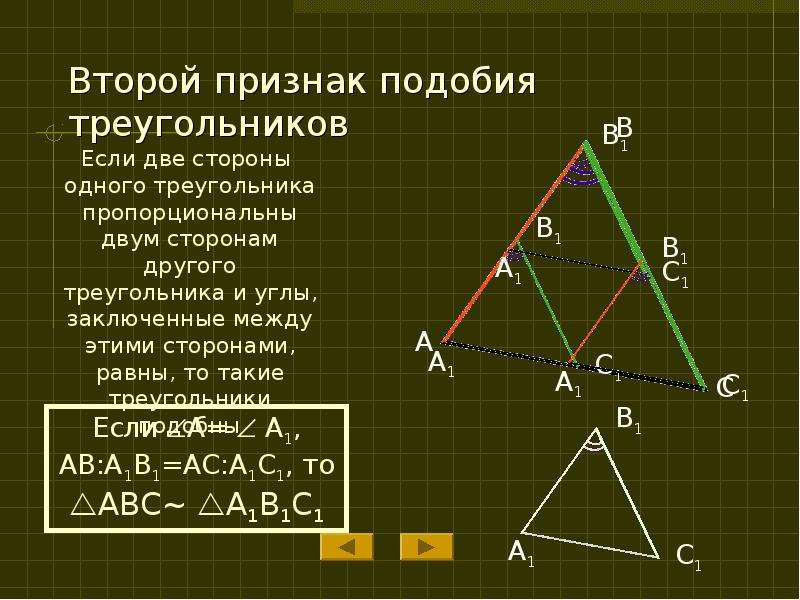
Наконец, расширение — это просто расширение или уменьшение фигуры, так что новая фигура пропорциональна во всех своих измерениях.
Если две фигуры совпадают, то одна фигура может быть наложена на другую посредством некоторой комбинации перемещений, отражений и вращений. Рассмотрим два конгруэнтных треугольника ниже.
Если мы повернем треугольник справа на четверть оборота (против часовой стрелки), а затем отразим его, то получится треугольник, который идеально совпадает с треугольником слева.
Эти математические манипуляции представляют собой более строгий способ сказать, что если мы вырежем из листа бумаги два треугольника совершенно одинаковой формы, то эти треугольники останутся такими же, независимо от того, как мы поворачиваем, переворачиваем или перемещаем эти листы бумаги. !
Если два треугольника (или другие фигуры) могут быть наложены посредством некоторой серии преобразований, включающих расширение, то треугольники подобны. Рассмотрим два подобных треугольника, показанных ниже.
Рассмотрим два подобных треугольника, показанных ниже.
Расширяя и перемещая меньший треугольник, мы можем создать идеальное перекрытие большого треугольника.Поскольку расширение необходимо, эти треугольники похожи, но не совпадают.
Практическая задача: Определите серию преобразований, которая показывает, что треугольники ниже совпадают.
Решение: Чтобы продемонстрировать, что два вышеупомянутых треугольника совпадают, нам нужно выполнить серию преобразований (сдвигов, вращений или отражений), чтобы один треугольник полностью перекрывал другой. Выполним наши преобразования в правом треугольнике.Осмотрев, мы видим, что нам нужно повернуть треугольник (180 °), а затем сдвинуть его влево.
Опять же, поскольку треугольники перекрываются, они конгруэнтны (мы также знаем, что треугольники конгруэнтны из данной диаграммы по условию SAS).
Практическая задача : Покажите серией преобразований, что треугольники ниже похожи.
Решение: Если мы сможем найти серию геометрических преобразований (перемещений, вращений, отражений или растяжений), которые позволят нам сделать треугольник справа, перекрывая треугольник слева, тогда треугольники будут похожи.По условию пропорциональности (пропорциональности) мы уже можем видеть, что треугольники подобны. Чтобы сделать их конгруэнтными, давайте сначала расширим треугольник справа (то есть мы увеличим его в три раза по сравнению с текущим размером).
Затем мы переместим треугольник влево, чтобы показать идеальное перекрытие, тем самым продемонстрировав, что треугольники похожи.
Доказательство подобия
Как и в случае с конгруэнцией, мы можем выделить несколько условий для доказательства сходства в треугольниках, которые не требуют от нас доказательства того, что все три угла конгруэнтны.Опять же, условием подобия является то, что внутренние углы одного треугольника совпадают с углами другого треугольника.
Первое условие, которое мы можем использовать для доказательства сходства, — это условие угол-угол . Напомним, что сумма всех углов в треугольнике всегда равна 180 °; таким образом, если два треугольника имеют два равных угла, они также должны иметь конгруэнтный третий угол, как показано ниже.
Остальные критерии подтверждают сходство через пропорциональность.Одним из этих критериев является условие side-side-side (пропорциональность) , которое просто гласит, что если соответствующие стороны двух треугольников пропорциональны (то есть имеют одну и ту же константу пропорциональности), то они похожи на треугольники. . Рассмотрим, например, два треугольника ниже.
Поскольку каждая сторона крайнего правого треугольника составляет половину длины соответствующей стороны крайнего левого треугольника, эти два треугольника подобны. Таким образом, мы также можем сделать вывод, что соответствующие углы для двух треугольников совпадают.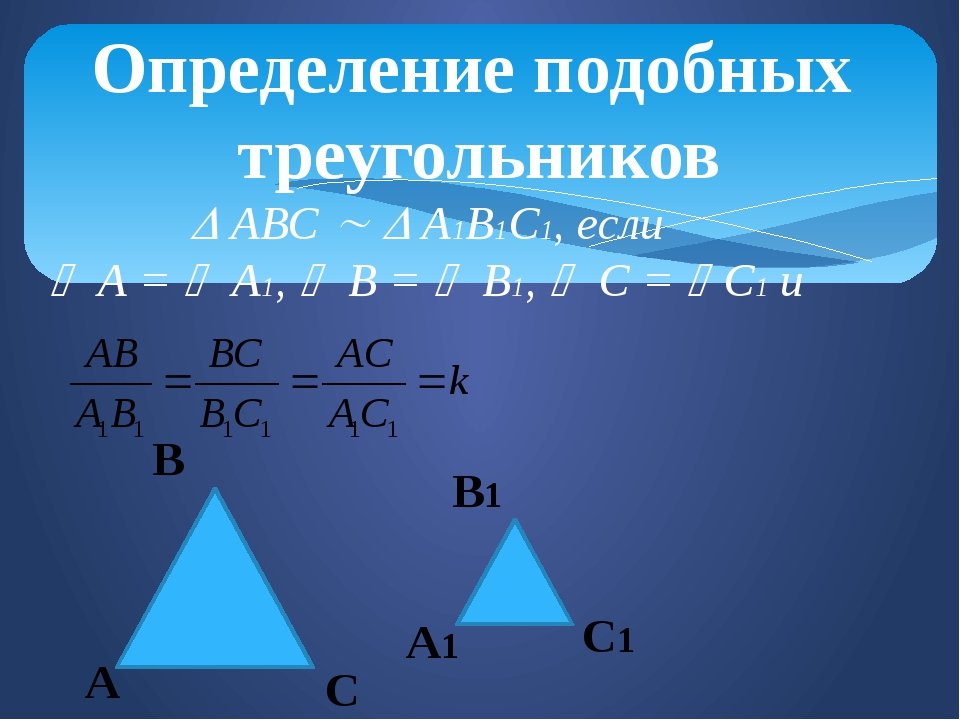
Последний критерий подобия, который мы обсудим, — это условие боковой угол-сторона (пропорциональность) . В этом случае два треугольника подобны, если две соответствующие стороны пропорциональны, а включенные углы совпадают. Рассмотрим два треугольника ниже.
Эти два треугольника подобны, потому что соответствующие помеченные стороны пропорциональны (длина сторон крайнего правого треугольника в 5/3 раз больше длины сторон крайнего левого треугольника), а соответствующие включенные углы конгруэнтны.Таким образом, используя любой из вышеперечисленных критериев, мы можем доказать, что два треугольника конгруэнтны.
Практическая задача: Докажите, что треугольники ABD и BCD подобны.
Решение : Давайте докажем, что треугольники похожи, используя формат доказательства с двумя столбцами. Обратите внимание, что треугольники имеют равные углы и . Мы также можем разделить треугольники для ясности.
1. Дано
2. Дано, 8 = 2 ∙ 4
3. Дано, 4 = 2 ∙ 2
4. Стороны BC и BD, а также утверждения 2 и 3
сторон BD и AB —
пропорциональный
5. Условие пропорциональности треугольников ABD и BCD Сторона, угол, сторона (пропорциональность)
похожи
Таким образом, мы показали, что два треугольника похожи.
Практическая задача : Докажите, что любые два равносторонних треугольника подобны.
Решение : Из нашего исследования треугольников мы знаем, что равносторонний треугольник содержит три совпадающих угла; таким образом, размер каждого угла в равностороннем треугольнике составляет 60 °. В результате по условию угол-угол все равносторонние треугольники должны быть похожи друг на друга.
Практическая задача : Два равнобедренных треугольника имеют внутренний угол 100 °. Докажите, что эти треугольники похожи.
Решение : Начнем с рисования диаграммы (не обязательно в масштабе).Назовем два равнобедренных треугольника ABC и XYZ.
Поскольку в треугольнике всего 180 °, сумма двух других углов в каждом треугольнике должна составлять 80 °; кроме того, поскольку треугольники равнобедренные, эти углы должны совпадать друг с другом. Давайте сделаем доказательство из двух столбцов, чтобы шаг за шагом показать наши рассуждения.
1. Дано
2. Равнобедренный треугольник
3. Равнобедренный треугольник
4. 180 ° в треугольнике
5.Треугольники ABC и XYZ соответствуют условию «Угол-угол
».аналогичный
В более общем плане мы можем сказать, что любые два равнобедренных треугольника, которые имеют равные тупые углы, должны быть подобны. (Применяются те же рассуждения — все, что требуется, — это то, что оба равнобедренных треугольника имеют тупой угол с одинаковой мерой.



 Признаки равенства прямоугольных треугольников.
Признаки равенства прямоугольных треугольников.