Сумма ряда натурального ряда – как сложить все натуральные числа и получить -1/12?

как сложить все натуральные числа и получить -1/12?

Вопрос ученому: — Я слышал, что сумма всех натуральных чисел равна −1/12. Это какой-то фокус, или это правда?

Ответ пресс-службы МФТИ — Да, такой результат можно получить при помощи приема, называемого разложением функции в ряд.

Вопрос, заданный читателем, достаточно сложный, и потому мы отвечаем на него не обычным для рубрики «Вопрос ученому» текстом на несколько абзацев, а некоторым сильно упрощенным подобием математической статьи.

В научных статьях по математике, где требуется доказать некоторую сложную теорему, рассказ разбивается на несколько частей, и в них могут поочередно доказываться разные вспомогательные утверждения. Мы предполагаем, что читатели знакомы с курсом математики в пределах девяти классов, поэтому заранее просим прощения у тех, кому рассказ покажется слишком простым — выпускники могут сразу обратиться к http://en.wikipedia.org/wiki/Ramanujan_summation.

Сумма всего

Начнем с разговора о том, как можно сложить все натуральные числа. Натуральные числа — это числа, которые используются для счета цельных предметов — они все целые и неотрицательные. Именно натуральные числа учат дети в первую очередь: 1, 2, 3 и так далее. Сумма всех натуральных чисел будет выражением вида 1+2+3+… = и так до бесконечности.

Ряд натуральных чисел бесконечен, это легко доказать: ведь к сколь угодно большому числу всегда можно прибавить единицу. Или даже умножить это число само на себя, а то и вычислить его факториал — понятно, что получится еще большая величина, которая тоже будет натуральным числом.

Детально все операции с бесконечно большими величинами разбираются в курсе математического анализа, но сейчас для того, чтобы нас поняли еще не сдавшие данный курс, мы несколько упростим суть. Скажем, что бесконечность, к которой прибавили единицу, бесконечность, которую возвели в квадрат или факториал от бесконечности — это все тоже бесконечность. Можно считать, что бесконечность — это такой особый математический объект.

И по всем правилам математического анализа в рамках первого семестра сумма 1+2+3+…+бесконечность — тоже бесконечна. Это легко понять из предыдущего абзаца: если к бесконечности что-то прибавить, она все равно будет бесконечностью.

Однако в 1913 году блестящий индийский математик-самоучка Сриниваса Рамануджан Айенгор придумал способ сложить натуральные числа несколько иным образом. Несмотря на то, что Рамануджан не получал специального образования, его знания не были ограничены сегодняшним школьным курсом — математик знал про существование формулы Эйлера-Маклорена. Так как она играет важную роль в дальнейшем повествовании, о ней придется тоже рассказать подробнее.

Формула Эйлера-Маклорена

Для начала запишем эту формулу:

Как можно видеть, она достаточно сложна. Часть читателей может пропустить этот раздел целиком, часть может прочитать соответствующие учебники или хотя бы статью в Википедии, а для оставшихся мы дадим краткий комментарий. Ключевую роль в формуле играет произвольная функция f(x), которая может быть почти чем угодно, лишь бы у нее нашлось достаточное число производных. Для тех, кто не знаком с этим математическим понятием (и все же решился прочитать написанное тут!), скажем еще проще — график функции не должен быть линией, которая резко ломается в какой-либо точке.

Производная функции, если предельно упростить ее смысл, является величиной, которая показывает то, насколько быстро растет или убывает функция. С геометрической точки зрения производная есть тангенс угла наклона касательной к графику.

Слева в формуле стоит сумма вида «значение f(x) в точке m + значение f(x) в точке m+1 + значение f(x) в точке m+2 и так до точки m+n». При этом числа m и n — натуральные, это надо подчеркнуть особо.

Справа же мы видим несколько слагаемых, и они кажутся весьма громоздкими. Первое (заканчивается на dx) — это интеграл функции от точки m до точки n. Рискуя навлечь на себя гнев всей кафедры математики за примитивность подхода к интегралам, скажем, что это площадь под кривой f(x) на графике от m до n; интегралы очень широко используются в самых разных науках.

На графике «по горизонтальной оси — время, по вертикальной — скорость» интеграл, то есть площадь под кривой, будет равен пройденному пути. На графике «ежемесячные платежи по вертикали, по горизонтали время» интегралом будет сумма, пришедшая на счет за все время.

Второе слагаемое, обозначенное как B₁(f(n) + f(m)), — это так называемое число Бернулли.

Третье слагаемое — сумма от чисел Бернулли (B_2k), поделенных на факториал удвоенного значения числа k и умноженных на разность производных функции f(x) в точках n и m. Причем, что еще сильнее усложняет дело, тут не просто производная, а производная 2k-1 порядка. То есть все третье слагаемое выглядит так:

Число Бернулли B

2 («2» так как в формуле стоит 2k, и мы начинаем складывать с k=1) делим на факториал 2 (это пока просто двойка) и умножаем на разность производных первого порядка (2k-1 при k=1) функции f(x) в точках n и m

+

Число Бернулли B₄ («4» так как в формуле стоит 2k, а k теперь равно 2) делим на факториал 4 (1×2х3×4=24) и умножаем на разность производных третьего порядка (2k-1 при k=2) функции f(x) в точках n и m

+

Число Бернулли B₆ (см.выше) делим на факториал 6 (1×2х3×4х5×6=720) и умножаем на разность производных пятого порядка (2k-1 при k=3) функции f(x) в точках n и m

+

…

Суммирование продолжается вплоть до k=p. Числа k и p получаются некоторыми произвольными величинами, которые мы можем выбирать по-разному, вместе с m и n — натуральными числами, которыми ограничен рассматриваемый нами участок с функцией f(x). То есть в формуле целых четыре параметра, и это вкупе с произвольностью функции f(x) открывает большой простор для исследований.

Оставшееся скромное R, увы, тут не константа, а тоже довольно громоздкая конструкция, выражаемая через уже упомянутые выше числа Бернулли. Теперь самое время пояснить, что это такое, откуда взялось и почему вообще математики стали рассматривать столь сложные выражения.

Числа Бернулли и разложения в ряд

В математическом анализе есть такое ключевое понятие как разложение в ряд. Это значит, что можно взять какую-то функцию и написать ее не напрямую (например y = sin(x^2) + 1/ln(x) + 3x), а в виде бесконечной суммы множества однотипных слагаемых. Например, многие функции можно представить как сумму степенных функций, умноженных на некоторые коэффициенты — то есть сложной формы график сведется к комбинации линейной, квадратичной, кубической… и так далее — кривых.

В теории обработки электрических сигналов огромную роль играет так называемый ряд Фурье — любую кривую можно разложить в ряд из синусов и косинусов разного периода; такое разложение необходимо для преобразования сигнала с микрофона в последовательность нулей и единиц внутри, скажем, электронной схемы мобильного телефона. Разложения в ряд также позволяют рассматривать неэлементарные функции, а ряд важнейших физических уравнений при решении дает именно выражения в виде ряда, а не в виде какой-то конечной комбинации функций.

В XVII столетии математики стали вплотную заниматься теорией рядов. Несколько позже это позволило физикам эффективно рассчитывать процессы нагрева различных объектов и решать еще множество иных задач, которые мы здесь рассматривать не будем. Заметим лишь то, что в программе МФТИ, как и в математических курсах всех ведущих физических вузов, уравнениям с решениями в виде того или иного ряда посвящен как минимум один семестр.

Якоб Бернулли исследовал проблему суммирования натуральных чисел в одной и той же степени (1^6 + 2^6 + 3^6 + … например) и получил числа, при помощи которых можно разложить в упомянутый выше степенной ряд другие функции — например, tg(x). Хотя, казалось бы, тангенс не очень-то похож хоть на параболу, хоть на какую угодно степенную функцию!

Полиномы Бернулли позже нашли свое применение не только в уравнениях матфизики, но и в теории вероятностей. Это, в общем-то, предсказуемо (ведь ряд физических процессов — вроде броуновского движения или распада ядер — как раз и обусловлен разного рода случайностями), но все равно заслуживает отдельного упоминания.

-1/12

Громоздкая формула Эйлера-Маклорена использовалась математиками для разных целей. Так как в ней, с одной стороны, стоит сумма значений функций в определенных точках, а с другой — есть и интегралы, и разложения в ряд, при помощи этой формулы можно (в зависимости от того, что нам известно) как взять сложный интеграл, так и определить сумму ряда.

Сриниваса Рамануджан придумал этой формуле иное применение. Он ее немного модифицировал и получил такое выражение:

В качестве функции f(x) он рассмотрел просто x — пусть f(x) = x, это вполне правомерное допущение. Но для этой функции первая производная равна просто единице, а вторая и все последующие — нулю: если все аккуратно подставить в указанное выше выражение и определить соответствующие числа Бернулли, то как раз и получится −1/12.

Это, разумеется, было воспринято самим индийским математиком как нечто из ряда вон выходящее. Поскольку он был не просто самоучкой, а талантливым самоучкой, он не стал всем рассказывать про поправшее основы математики открытие, а вместо этого написал письмо Годфри Харди, признанному эксперту в области как теории чисел, так и математического анализа. Письмо, кстати, содержало приписку, что Харди, вероятно, захочет указать автору на ближайшую психиатрическую лечебницу: однако итогом, конечно, стала не лечебница, а совместная работа.

Парадокс

Суммируя все сказанное выше, получим следующее: сумма всех натуральных чисел получается равной −1/12 при использовании специальной формулы, которая позволяет разложить произвольную функцию в некоторый ряд с коэффициентами, называемыми числами Бернулли. Однако это не значит, что 1+2+3+4 оказывается больше, чем 1+2+3+… и так до бесконечности. В данном случае мы имеем дело с парадоксом, который обусловлен тем, что разложение в ряд — это своего рода приближение и упрощение.

Можно привести пример намного более простого и наглядного математического парадокса, связанного с выражением чего-то одного через что-то другое. Возьмем лист бумаги в клеточку и нарисуем ступенчатую линию с шириной и высотой ступеньки в одну клетку. Длина такой линии, очевидно, равна удвоенному числу клеток — а вот длина спрямляющей «лесенку» диагонали равна числу клеток, умноженному на корень из двух. Если сделать лесенку очень мелкой, она все равно будет той же длины и практически не отличимая от диагонали ломаная линия окажется в корень из двух раз больше той самой диагонали! Как видите, для парадоксальных примеров писать длинные сложные формулы вовсе не обязательно.

Формула Эйлера-Маклорена, если не вдаваться в дебри математического анализа, является таким же приближением, как и ломаная линия вместо прямой. Используя это приближение можно получить те самые −1/12, однако это далеко не всегда бывает уместно и оправдано. В ряде задач теоретической физики подобные выкладки применяются для расчетов, но это тот самый передний край исследований, где еще рано говорить о корректном отображении реальности математическими абстракциями, а расхождения разных вычислений друг с другом — вполне обычное дело.

Так, оценки плотности энергии вакуума на основе квантовой теории поля и на основе астрофизических наблюдений различаются более чем на 120 порядков. То есть в 10^120 степени раз. Это одна из нерешенных задач современной физики; тут явно просвечивает пробел в наших знаниях о Вселенной. Или же проблема — в отсутствии подходящих математических методов для описания окружающего мира. Физики-теоретики совместно с математиками пытаются найти такие способы описать физические процессы, при которых не будет возникать расходящихся (уходящих в бесконечность) рядов, но это далеко не самая простая задача.

mipt.ru

Формулы сумм ряда натуральных чисел в целочисленной степени

 

Сумма натурального ряда

Это известная формула, открытая еще Гауссом  в шестилетнем возрасте.

 

Сумма натурального ряда где каждый элемент возведен во  вторую степень

 

 

Сумма натурального ряда где каждый элемент возведен в третью степень

 

 

Сумма натурального ряда где каждый элемент возведен в четвертую степень

 

 

Сумма натурального ряда где каждый элемент возведен в пятую степень

 

 

Сумма натурального ряда где каждый элемент возведен в шестую степень

 

 

Сумма натурального ряда где каждый элемент возведен в седьмую степень

 

 

Сумма натурального ряда где каждый элемент возведен в восьмую степень

 

 

Сумма натурального ряда где каждый элемент возведен в девятую степень

 

 

Сумма натурального ряда где каждый элемент возведен в десятую степень

 

Сумма натурального ряда где каждый элемент возведен в одинадцатую степень

 

Сумма натурального ряда где каждый элемент возведен в двенадцатую степень

 

 

• ФРС. Фундаментальное решение системы уравнений >>

abakbot.ru

Натуральный ряд

математика натуральный ряд чисел, натуральный ряд
Натуральный ряд — числовой ряд, члены которого являются последовательными натуральными числами: 1 + 2 + 3 + 4 + …; при этом n-ая сумма ряда является треугольным числом: ∑ k = 1 n k = n n + 1 2 ^k= ,

которое неограниченно растёт при стремлении n к бесконечности Из-за того, что последовательность частичных сумм ряда не имеет конечного предела, ряд расходится

Несмотря на расходимость в традиционном смысле, некоторые обобщённые операции над натуральным рядом позволяют получить выводы, находящие применение в компле́ксном анализе, квантовой теории поля и теории струн

Содержание

• 1 Сумма в обобщённом смысле
• 2 Частичные суммы
• 3 Суммируемость
  • 31 Эвристические предпосылки
  • 32 Регуляризация дзета-функцией
  • 33 Суммирование методом Рамануджана
  • 34 Несостоятельность устойчивых линейных методов суммирования
• 4 Применение в физике
• 5 Примечания
• 6 Список литературы
• 7 Ссылки

Сумма в обобщённом смыслеправить

Специальные методы суммирования, использующиеся в некоторых разделах математики, позволяют присвоить конечные значения расходящимся числовым рядам В частности, один из таких способов предоставляет метод, основанный на регуляризации аналитического продолжения дзета-функции Римана и суммирование по методу Рамануджана англ, позволяют сопоставить данному ряду некое конечное значение1:

1 + 2 + 3 + 4 + ⋯ = − 1 12 , ,

в обобщённом смысле суммы

Частичные суммыправить

Первые шесть треугольных чисел Основная статья: Треугольное число

Частичными суммами натурального ряда являются 1, 3, 6, 10, 15 и т д Таким образом, n-ая частичная сумма выражается формулой:

∑ k = 1 n k = n n + 1 2 ^k=

Это выражение было известно ещё Пифагору в VI веке до нашей эры2 Числа такого вида называются треугольными, так как они могут быть представлены в виде треугольника

Бесконечная последовательность треугольных чисел стремится к +∞ и, следовательно, бесконечная сумма натурального ряда также стремится к +∞ Такой результат является следствием невыполнения необходимого условия сходимости числового ряда

Суммируемостьправить

В сравнении с другими классическими расходящимися рядами, натуральному ряду сложнее приписать имеющее смысл некоторое конечное числовое значение Существует множество методов суммирования, некоторые из которых являются более устойчивыми и мощными Так, например, суммирование по Чезаро является широкоизвестным методом, который суммирует умеренно расходящийся Ряд Гранди 1 − 1 + 1 − 1 + … и приписывает ему конечное значение ½ Суммирование методом Абеля представляет собой более мощный метод, который, кроме ряда Гранди, позволяет также суммировать более сложный знакочередующийся натуральный ряд и присвоить ему значение ¼

В отличие от упомянутых выше рядов, как суммирование по Чезаро, так и метод Абеля неприменимы к натуральному ряду Эти методы работают только со сходящимися и гармоническими рядами, и не могут быть использованы для ряда, частичные суммы которого стремятся к +∞3 Большинство элементарных определений суммы расходящегося ряда являются линейными и устойчивыми, а любой линейный и устойчивый метод не может присвоить натуральному ряду конечное значение Следовательно, требуются более развитые методы, такие как регуляризация дзета-функцией или суммирование Рамануджана

Эвристические предпосылкиправить

Отрывок из первой заметки Рамануджана, описывающей конечное значение ряда

В главе 8 первого сборника своих трудов Рамануджан показал, что «1 + 2 + 3 + 4 + … = −1⁄12», используя два способа456 Ниже излагается более простой метод, состоящий из двух этапов

Первое ключевое наблюдение состоит в том, что ряд 1 + 2 + 3 + 4 + … похож на знакочередующийся натуральный ряд 1 − 2 + 3 − 4 + … Несмотря на то, что этот ряд также является расходящимся, с ним намного проще работать Существует несколько классических способов присвоить конечное значение этому ряду, известных ещё с XVIII века 7

Для того, чтобы привести ряд 1 + 2 + 3 + 4 + … к виду 1 − 2 + 3 − 4 + …, мы можем вычесть 4 из второго члена, 8 из четвёртого члена, 12 из шестого и т д Общая величина, которую нужно вычесть, выражается рядом 4 + 8 + 12 + 16 + …, который получается умножением исходного ряда 1 + 2 + 3 + 4 + … на 4 Данные выражения можно записать в алгебраической форме Что бы из себя ни представляла «сумма», введём для неё обозначение c = 1 + 2 + 3 + 4 + …, умножим полученное уравнение на 4 и вычтем второе из первого:

c = 1 + 2 + 3 + 4 + 5 + 6 + ⋯ , 4 c = 4 + 8 + 12 + ⋯ , − 3 c = 1 − 2 + 3 − 4 + 5 − 6 + ⋯ c&=&1+2&&+3+4&&+5+6+\cdots ,\\4c&=&4&&+8&&+12+\cdots ,\\-3c&=&1-2&&+3-4&&+5-6+\cdots \\\end

Второе ключевое наблюдение заключается в том, что ряд 1 − 2 + 3 − 4 + … является разложением в степенной ряд функции 1/1 + x2 при x, равном 1 Соответственно, Рамануджан заключает:

− 3 c = 1 − 2 + 3 − 4 + ⋯ = 1 1 + 1 2 = 1 4 =

Поделив обе части на −3, получаем c = −1/12

Строго говоря, существует неоднозначность при работе с бесконечными рядами в случае использования методов, предназначенных для конечных сумм наподобие тех методов, что были использованы выше, в особенности если эти бесконечные ряды расходятся Неоднозначность заключается в том, что если вставить ноль в любое место в расходящемся ряде, существует вероятность получить противоречивый результат Например, действие 4c = 0 + 4 + 0 + 8 + … противоречит свойствам сложения

Одним из способов обойти данную неопределённость и тем самым ограничить позиции, куда можно вставить ноль, является присвоение каждому члену ряда значения некоторой функции8 Для ряда 1 + 2 + 3 + 4 + …, каждый член n представляет собой натуральное число, которое может быть представлено в виде функции n−s, где s — некоторая комплексная переменная Используя данное представление, можно гарантировать, что все члены ряда последовательны Таким образом, присвоив s значение −1, можно выразить рассматриваемый ряд в строгом виде Реализация данного способа носит название регуляризации дзета-функцией

Регуляризация дзета-функциейправить

График функции ζs Для s > 1, ряд сходится и ζs > 1 Аналитическое продолжение в окрестности s = 1 приводит к отрицательным значениям, в частности ζ−1 = −1/12

В данном методе, ряд ∑ n = 1 ∞ n ^n заменяется рядом ∑ n = 1 ∞ n − s ^n^ Последний ряд является частным случаем ряда Дирихле Если реальная часть s больше 1, ряд Дирихле сходится и его сумма представляет собой дзета-функцию Римана ζs С другой стороны, если реальная часть s меньше или равна 1, ряд Дирихле расходится В частности, ряд 1 + 2 + 3 + 4 + · · ·, который получается подстановкой s = −1 не является сходящимся Преимущества перехода к дзета-функции Римана заключается в том, что, используя метод аналитического продолжения, она может быть определена для s меньше или равных 1 Следовательно, мы можем получить значение регуляризованной дзета-функции ζ−1 = −1/12

Существует несколько способов доказать, что ζ−1 = −1/12 Один из методов9 использует связь между дзета-функцией Римана и эта-функцей Дирихле англ ηs Эта-функция выражается знакопеременным рядом Дирихле, согласуясь тем самым с ранее представленными эвристическими предпосылками Тогда как оба ряда Дирихле сходятся, следующие тождества верны:

ζ s = 1 − s + 2 − s + 3 − s + 4 − s + 5 − s + 6 − s + ⋯ 2 ⋅ 2 − s ζ s = 2 ⋅ 2 − s + 2 ⋅ 4 − s + 2 ⋅ 6 − s + ⋯ 1 − 2 1 − s ζ s = 1 − s − 2 − s + 3 − s − 4 − s + 5 − s − 6 − s + ⋯ = η s \zeta s&=&1^+2^&&+3^+4^&&+5^+6^+\cdots &\\2\cdot 2^\zeta s&=&2\cdot 2^&&+2\cdot 4^&&+2\cdot 6^+\cdots &\\\left1-2^\right\zeta s&=&1^-2^&&+3^-4^&&+5^-6^+\cdots &=\eta s\\\end

Тождество 1 − 2 1 − s ζ s = η s \zeta s=\eta s остаётся справедливым если мы продолжим обе функции аналитически в область значений s, где вышезаписанные ряды расходятся Подставляя s = −1, получим −3ζ−1=η−1 Отметим, что вычисление η−1 является более простой задачей, так как значение эта-функции выражается значением суммы Абеля соответствующего ряда10 и представляет собой односторонний предел:

− 3 ζ − 1 = η − 1 = lim x ↗ 1 1 − 2 x + 3 x 2 − 4 x 3 + ⋯ = lim x ↗ 1 1 1 + x 2 = 1 4 \left1-2x+3x^-4x^+\cdots \right=\lim _=

Поделив обе части выражения на −3, получаем ζ−1 = −1/12

Суммирование методом Рамануджанаправить

Суммирование ряда 1 + 2 + 3 + 4 + · · · методом Рамануджана также позволяет получить значение −1/12 В своём втором письме к Х Г Харди, датированном 27 Февраля 1913, Рамануджан пишет:

«Уважаемый Сэр, я с большим удовольствием прочёл ваше письмо от 8го февраля 1913 Я ожидал, что вы ответите мне в том же стиле, что и профессор математики из Лондона, который посоветовал мне внимательно изучить „Бесконечные ряды“ Томаса Бромвича и не попадать в ловушку, которую таят расходящиеся ряды … Я ответил ему, что, согласно моей теории, сумма бесконечного числа членов ряда: 1 + 2 + 3 + 4 + · · · = −1/12 Узнав это, вы сию же минуту укажете в направлении психиатрической лечебницы Уверяю, вы не сможете проследить нить рассуждений в моём доказательстве этого факта, если я попытаюсь изложить их в единственном письме …»11

Метод суммирования Рамануджана заключается в изолировании постоянного члена в формуле Эйлера — Маклорена для частичных сумм ряда Для некоторой функции f, классическая сумма Рамануджана для ряда ∑ k = 1 ∞ f k ^fk определена как

c = − 1 2 f 0 − ∑ k = 1 ∞ B 2 k 2 k ! f 2 k − 1 0 , f0-\sum _^f^0,

где f2k−1 представляет собой 2k−1-ую производную функции f и B2k является 2k-ым числом Бернулли: B2 = 1/6, B4 = −1/30 и т д Принимая fx = x, первая производная f равна 1, а все остальные члены стремятся к нулю, поэтому:12

c = − 1 6 ⋅ 1 2 ! = − 1 12 \cdot =-

Для избежания противоречий, современная теория метода суммирования Рамануджана требует, чтобы функция f являлась «регулярной» в том смысле, что её производные высших порядков убывают достаточно быстро для того, чтобы оставшиеся члены в формуле Эйлера — Маклорена стремились к 0 Стоит отметить, что Рамануджан неявно подразумевал это свойство12 Требование регулярности помогает избежать использования метода суммирования Рамануджана для рядов типа 0 + 2 + 0 + 4 + · · · потому, что не существует регулярной функции, которая выражалась бы значениями такого ряда Такой ряд должен интерпретироваться с использованием регуляризацией дзета-функцией

Несостоятельность устойчивых линейных методов суммированияправить

Линейный и устойчивый метод суммирования не в состоянии присвоить конечное значение ряду 1 + 2 + 3 + … Устойчивый означает, что добавление члена в начало ряда увеличивает сумму ряда на величину данного члена Данное утверждение может быть продемонстрировано следующим образом Если

1 + 2 + 3 + …=x

тогда, добавляя 0 к обеим частям, получаем

0 + 1 + 2 + … = 0 + x = x исходя из свойства устойчивости

Вычитая нижний ряд из верхнего, получаем

1 + 1 + 1 + … = x — x = 0 исходя из свойства линейности

Добавляя 0 к обеим частям повторно, получаем

0 + 1 + 1 + 1 +… = 0

и вычитая два последних ряда приходим к

1 + 0 + 0 + … =0,

что противоречит свойству устойчивости

Методы, использованные выше, для суммирования 1 + 2 + 3 + … являются либо только устойчивыми, либо только линейными Например, существует два разных метода, называемых регуляризацией дзета-функцией Первый является устойчивым, но нелинейным и определяет сумму a+b+c+… множества чисел как значение аналитического продолжения выражения 1/as +1/bs +1/cs + при s=-1 Второй метод линейный, но неустойчивый и определяет сумму последовательности чисел как значение аналитического продолжения выражения a/1s +b/2s +c/3s при s=0 Оба метода присваивают ряду 1+2+3+… значение суммы ζ-1=-1/12

Применение в физикеправить

Значение − 1 12 встречается в теории бозонных струн при попытке рассчитать возможные энергетические уровни струны, а именно низший энергетический уровень

Регуляризация ряда 1 + 2 + 3 + 4 + ⋯ также встречается при расчёте эффекта Казимира для скалярного поля в одномерном пространстве13 Похожие вычисления возникают для трёхмерного пространства, однако в этом случае вместо дзета-функции Римана используются реальные аналитические ряды Эйзенштейна14

Примечанияправить

1. ↑ Lepowsky, J 1999, Naihuan Jing and Kailash C Misra, ed, Vertex operator algebras and the zeta function, vol 248, Contemporary Mathematics, сс 327–340 
2. ↑ Pengelley, David J 2002, Otto Bekken et al, ed, The bridge between the continuous and the discrete via original sources, National Center for Mathematics Education, University of Gothenburg, Sweden, с 3 
3. ↑ Hardy p10
4. ↑ Ramanujan’s Notebooks, <http://wwwimscresin/~rao/ramanujan/NoteBooks/NoteBook1/chapterVIII/page3htm> Проверено 26 января 2014 
5. ↑ Abdi, Wazir Hasan 1992, Toils and triumphs of Srinivasa Ramanujan, the man and the mathematician, National, с 41 
6. ↑ Berndt, Bruce C 1985, Ramanujan’s Notebooks: Part 1, Springer-Verlag, сс 135–136 
7. ↑ Euler, Leonhard; Lucas Willis; and Thomas J Osler Translation with notes of Euler’s paper: Remarks on a beautiful relation between direct as well as reciprocal power series The Euler Archive 2006 Проверено 22 марта 2007 Originally published as Euler, Leonhard 1768 «Remarques sur un beau rapport entre les séries des puissances tant directes que réciproques» Memoires de l’academie des sciences de Berlin 17: 83–106
8. ↑ Присвоение номеров функциям идентифицируется как один из двух широких классов методов суммирования, включая суммирование Абеля и суммирование Бореля: Konrad Knopp Theory and Application of Infinite Series — Dover, 1990 — P 475–476 — ISBN 0-486-66165-2
9. ↑ Stopple, Jeffrey 2003, A Primer of Analytic Number Theory: From Pythagoras to Riemann, с 202, ISBN 0-521-81309-3 
10. ↑ Knopp Konrad Theory and Application of Infinite Series — Dover, 1990 — P 490–492 — ISBN 0-486-66165-2
11. ↑ Berndt et al p53
12. ↑ 1 2 Berndt, Bruce C 1985, Ramanujan’s Notebooks: Part 1, Springer-Verlag, сс 13,134 
13. ↑ Zee pp65-67
14. ↑ Zeidler, Eberhard 2007, Quantum Field Theory I: Basics in Mathematics and Physics: A Bridge between Mathematicians and Physicists, Springer, сс 305–306, ISBN 9783540347644, <http://booksgooglecom/booksid=XYtnGl9enNgC&pg=PA305> 

Список литературыправить

• Berndt, Bruce C, Srinivasa Ramanujan Aiyangar, and Robert A Rankin Ramanujan: letters and commentary — American Mathematical Society, 1995 — ISBN 0-8218-0287-9
• Hardy GH Divergent Series — Clarendon Press, 1949 — ISBN LCC QA295 h39 1967
• Zee A Quantum field theory in a nutshell — Princeton UP, 2003 — ISBN 0-691-01019-6

Ссылкиправить

• This Week’s Finds in Mathematical Physics Week 124, Week 126, Week 147, Week 213
  • Euler’s Proof That 1 + 2 + 3 + · · · = −1/12 — By John Baez
  • John Baez My Favorite Numbers: 24 September 19, 2008
• The Euler-Maclaurin formula, Bernoulli numbers, the zeta function, and real-variable analytic continuation by Terence Tao
• A recursive evaluation of zeta of negative integers by Luboš Motl
• ASTOUNDING: 1 + 2 + 3 + 4 + 5 + … = −1/12 Numberphile video with over a million views
  • Sum of Natural Numbers second proof and extra footage includes demonstration of Euler’s method
  • What do we get if we sum all the natural numbers response to comments about video by Tony Padilla
  • Related article from New York TImes
• Divergent Series: why 1 + 2 + 3 + · · · = −1/12 by Brydon Cais from University of Arizona

Последовательности и ряды Последовательности Числовая последовательность • Фундаментальная последовательность • Линейная рекуррентная последовательность • Числа Фибоначчи • Последовательность Баркера • Последовательность де Брёйна Ряды, основное Сумма ряда • Остаток ряда • Условная сходимость • Мультисекция ряда Числовые ряды действия с числовыми рядами Гармонический ряд • Знакочередующийся ряд • Ряд Лейбница • Ряд Дирихле • Ряд Гранди • 1 − 2 + 3 − 4 + … • 1 + 2 + 3 + 4 + ⋯ Функциональные ряды Ряд Тейлора • Ряд Лорана • Ряд Фурье • Тригонометрический ряд Фурье • Тригонометрический ряд • Ряд Винера Другие виды рядов Ряд Неймана • Ряд Пюизё Признаки сходимости Признаки сходимости рядов Для всех рядов Необходимое условие · Критерий Коши ∑ n = 1 ∞ a n ^a_ Для знакоположительных рядов Основной критерий · Признак сравнения · Признак Куммера · Признак Гаусса · Радикальный признак Коши · Интегральный признак · Признак Д’Аламбера · Степенной признак · Логарифмический признак · Признак Раабе · Признак Бертрана · Признак Жамэ · Признак Ермакова · Признак Лобачевского · Признак Реткеса англ · Телескопический признак Для знакочередующихся рядов Признак Лейбница Для рядов вида ∑ n = 1 ∞ a n b n ^a_b_ Признак Абеля · Признак Дедекинда · Признак Дюбуа-Реймона · Признак Дирихле Для функциональных рядов Признак Вейерштрасса Для рядов Фурье Признак Дини · Признак Валле-Пуссена · Признак Жордана · Признак Юнга · Признак Салема · Признак Лебега · Признак Лебега–Гергена · Признак Марцинкевича

математика натуральный ряд чисел, натуральный ряд, натуральный ряд чисел

---

Натуральный ряд Информацию О

---

---

Натуральный ряд Комментарии

Натуральный ряд
Натуральный ряд
Натуральный ряд Вы просматриваете субъект

Натуральный ряд что, Натуральный ряд кто, Натуральный ряд описание

There are excerpts from wikipedia on this article and video

www.turkaramamotoru.com

Решение задач в Python. Сумма ряда натуральных чисел

Попробуем на практике разобрать работу циклов, про которые рассказано в одном из наших уроков. Выполним предложенное задание, использовав несколько разных методик и видов циклов.

Задача

Программа выводит сумму первых членов натурального ряда чисел до введённого n-числа включительно.

Решение задачи с помощью цикла while

Произведём расчёт, используя цикл с предусловием while.

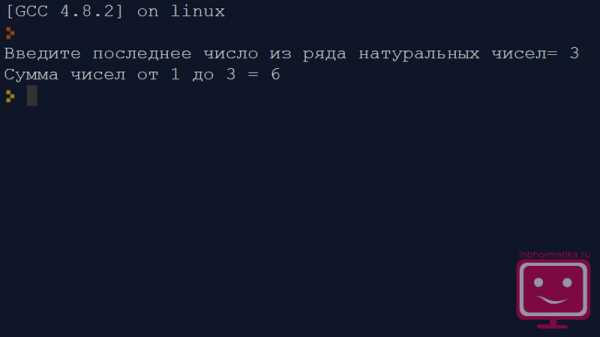
n=int(input(Введите последнее число из ряда натуральных чисел=))

i=1

s=0

while i	s=i+s

i=i+1

print (Сумма чисел от 1 до, n, =, s)

1. Сперва задаем в переменную n самое большое натуральное число (в пределах разумного).
2. Обнулим на входе сумму s.
3. Цикл будет выполняться до тех пор, пока внутренняя переменная не достигнет значения n.

Результат выполнения программы

Решение задачи с помощью цикла for

Быстрее происходит расчёт при помощи цикла for.

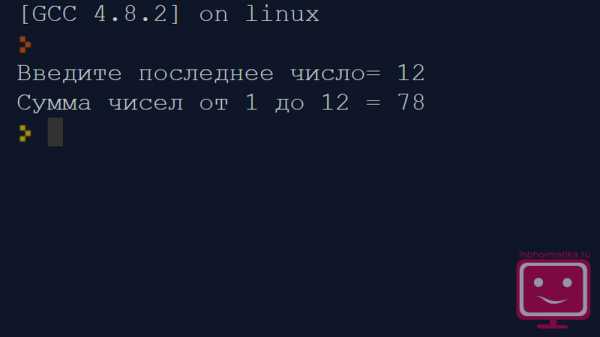
n=int(input(Введите последнее число=))

s=0

for i in range(1,n+1):

s=i+s

print (Сумма чисел от 1 до, n, =, s)

Посмотрите, в цикле записано максимальное число не n, а n+1. Это связано с тем, что цикл должен выполняться на один шаг больше, чтобы последнее значение промежуточной суммы было учтено.

Результат выполнения программы

Решение задачи с помощью списка

Ту же самую задачку можно решить, используя список. По сути, это ничего не меняет, но, как видите, код при этом занимает всего две строки:

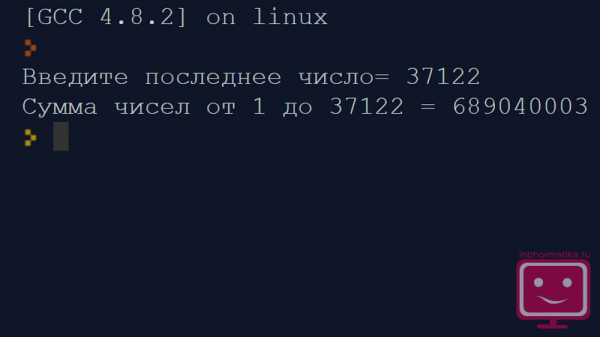
n=int(input(Введите последнее число=))

print (Сумма чисел от 1 до, n, =, sum([i for i in range(1,n+1)]))

Результат выполнения программы

Задача на последовательность Функция перевода целого двоичного числа в десятичное

inphormatika.ru

Тема 17 Числовые ряды

Тема 17. ЧИСЛОВЫЕ РЯДЫ

Выражение вида

называем рядом; — n-ый член ряда (1). Сумманазывается n-ой частичной суммой ряда (1).

Определение. Суммой ряда (1) называется предел частичных сумм, если. Итак, сумма ряда (1) есть число

т.е. такое число, что для любого найдется натуральноеначиная с которого, т.е. для любоговыполняется неравенство

Если существует предел (2), то ряд (1) называется сходящимся. В противном случае, ряд (1) называется расходящимся.

Ряд называется n-ым остатком ряда (1) и обозначается. Таким образом, неравенство (3) эквивалентно следующему неравенству

Задача о вычислении суммы ряда (1) с точностью 𝜺сводится к поиску такого натурального (по возможности наименьшего) числа n, что. Тогдас точностью.

Примеры. а) 0+0+0+… — сходящийся ряд;

б) 𝜺+𝜺+𝜺+… — расходящийся ряд, какое бы малое положительное число𝜺мы не взяли;

в) конечная сумма превращается в сходящийся ряд, если положитьпри; при этом сумма данного ряда равна исходной сумме;

г) 1+1/2+1/4+1/8+… сходится к числу 2, ибо имеет пределом 2 при n→∞ ;

д) .

Предложение.Дописывание или отбрасывание конечного числа слагаемых ряда не влияет на его сходимость (но влияет на его сумму).

Примеры. Найдем сумму ряда

Заметим, что , и поэтому, т.е. 1 — сумма ряда (4).

Теорема. Если рядсходится то n-ый членстремится к 0 .

Доказательство. .□

Пример.Гармоническим рядом называется ряд

Для этого ряда но этот ряд расходится, как показывает далее интегральный признак Коши.

— это ряд вида

Число q называется знаменателем геометрической прогрессии.

Теорема 2.Пусть. Тогда геометрическая прогрессия сходится тогда и только тогда, когда |q|<1. В этом случае сумма геометрической прогрессии равна.

Утверждение следует из равенства □

Определим сумму двух рядов икак ряд с n-ым слагаемым. Произведение рядана число- это ряд.

Теорема. Если рядыисходятся соответственно к s и t, то сумма этих рядов сходится к числу s+t, а произведение рядана числосходится к.

Доказательство вытекает из соответствующих свойств предела.

Лемма. Пусть дан ряд с неотрицательными слагаемыми. Тогда этот ряд сходится тогда и только тогда, когда его частичные суммы ограничены сверху.

Доказательство. Если — ряд с неотрицательными слагаемыми, то, частичные суммы ряда образуют возрастающую последовательность. Если она, к тому же еще и ограничена, то существование предела, т.е. сходимость рядаследует из теоремы о пределе монотонной ограниченной последовательности (см. главу «Введение в анализ» ). Обратное утверждение вытекает из ограниченности последовательности, имеющей предел.□

Теорема сравнения. Пустьдля любого натурального n начиная с некоторого номера. Если рядсходится, то и рядсходится. Если же рядрасходится, то рядтакже расходится.

Доказательство. Отбрасывая, если надо, первые несколько членов рядов и, сводим доказательство к случаю, когда неравенствовыполняется для всехОбозначим черезчастичные суммы ряда, а черезобозначим частичные суммы ряда. Тогда. Сходимость рядавлечет ограниченность сверху последовательности, что в свою очередь дает ограниченность последовательности. По лемме получаем сходимость ряда. Наоборот, если рядрасходится, то рядне может сходится, ибо в противном случае сходился бы и ряд, что противоречит доказанному выше.□

Следствие.Пустьдля любого натурального n, начиная с некоторого номера, и существует отличный от 0 предел отношения. Тогда рядыиведут себя одинаково в смысле сходимости (либо оба сходятся, либо оба расходятся).

Доказательство. Пусть . По условию. Предположим, что рядсходится. Выберем. Тогданачиная с некоторого. Отсюда вытекает неравенство. Из сходимости рядаследует сходимость ряда(см. «арифметические операции с рядами»). По теореме сравнения получаем тогда, что и рядсходится. Предположим теперь, что рядсходится. Так как(именно в этом месте нужно учесть, что), то мы можем в рассуждениях выше заменитьна, анаина. Получаем сходимость ряда.□

Теорема (интегральный признак сходимости Коши).Пусть- монотонно убывающая, непрерывная и неотрицательная функция при. Положимдля всех натуральныхn. Тогда ряди интегралведут себя одинаково в смысле сходимости. При этом имеет место следующая оценка остатка ряда:

Доказательство по сути вытекает из рисунка. Имеем (*). Если рядсходится, то и рядсходится по теореме сравнения. Отсюда следует, что интегралимеет предел при. Из этого вытекает (с учетом монотонности функции), что существует предел. Это доказывает сходимость интеграла. Наоборот, если последний интеграл сходится и равен, тодля любого. Отсюда и из неравенств (*) следует ограниченность частичных сумм ряда. По лемме из параграфа «теорема сравнения» вытекает сходимость ряда. Оценка остатка рядаследует из неравенства (*):

Следствие. Рядсходится тогда и только тогда, когда. В частности, гармонический ряд расходится.

Доказательство. Применим теорему, беря в качестве функции . Если, то

в силу того, что . Если, то

ибо неограниченно возрастающая функция. В случаеиз неравенстваи уже доказанной расходимости гармонического рядавытекает расходимость ряда(применяем теорему сравнения).□

Пример.Рядсходится, ибо. Так как рядсходится (здесь), то по следствию теоремы сравнения получаем сходимость исходного ряда.

Пусть для всех достаточно больших натуральных n и существует предел отношения, который мы обозначим через d. Если, то рядсходится; если же, то рядрасходится.

Доказательство. Пусть . Выберем. Тогданачиная с некоторого номера. Следовательно,

Так как геометрическая прогрессия сходится, то по теореме сравнения сходится и ряд. Заменяяполучаем сходимость ряда. Отсюда следует сходимость ряда.

Если , то иначиная с неокторого номера. Не выполнено необходимое условие сходимости, следовательно, ряд расходится.□

Пример.Исследуем рядна сходимость, применяя признак Даламбера. Имеем

Итак, в нашем случае и, следовательно, ряд сходится.

Ряд вида

где все , называется знакочередующимся.

Теорема Лейбница.Если последовательностьмонотонно убывает и стремится к 0, то ряд (1) сходится, причем его сумма меньше.

Доказательство. Последовательность четных частичных сумм

монотонно возрастает, ибо все слагаемые в скобках неотрицательны. С другой стороны,

По теореме о пределе монотонной ограниченной последовательности получаем существование предела четных частичных сумм. Так как и, то существует предел нечетных частичных сумм, и он совпадает с пределом четных частичных сумм. Отсюда следует существование предела последовательностии совпадении его с.□

Следствие.Остаток ряда (1) меньше первого отброшенного слагаемого.

Пример. Для того, что бы подсчитать

с точностью надо взять всего лишь 7 слагаемых, ибо. Итак

Более точное (калькуляторное) значение — 0,36787944

Дан ряд с произвольными слагаемыми. Рассмотрим ряд

составленный из абсолютных величин членов исходного ряда.

Теорема.Если ряд (1) сходится, то и исходный ряд сходится.

Доказательство. Так как и ряд (1) сходится, то по теореме сравнения получаем сходимость ряда. Арифметические операции с рядами показывают, что сходится ряд, равный разности сходящихся рядови.□

Определение.Рядтакой, что ряд (1), составленный из абсолютных величин сходится, называется абсолютно сходящимся. Если же ряд (1) расходится, а сам рядсходится, то рядназывают условно сходящимся.

Пример.Рядсходится условно, ибо сам он сходится по теореме Лейбница (см. параграф «Знакочередующиеся ряды»), а ряд, составленный из абсолютных величин есть гармонический ряд, который, как мы знаем расходится.

studfiles.net

Сумма ряда — это… Что такое Сумма ряда?

Сумма числового ряда определяется как предел, к которому стремятся суммы первых n слагаемых ряда, когда n неограниченно растёт. Если такой предел существует и конечен, то говорят, что ряд сходится, в противном случае — что он расходится^[1]. Элементы ряда представляют собой комплексные числа (в частности, вещественные).

Определение

Пусть  — числовой ряд. Число называется n-ой частичной суммой ряда .

Сумма (числового) ряда — это предел частичных сумм , если он существует и конечен. Таким образом, если существует число , то в этом случае пишут . Такой ряд называется сходящимся. Если предел частичных сумм не существует или бесконечен, то ряд называется расходящимся.

Сходимость числовых рядов

Свойство 1. Если ряд

  (1.1)

сходится и его сумма равна S, то ряд

 (1.2)

где c — произвольное число, также сходится и его сумма равна cS. Если же ряд (1.1) расходится и с ≠ 0, то ряд расходится.

Свойство 2. Если сходится ряд (1.1) и сходится ряд

,

а их суммы равны и соответственно, то сходятся и ряды

,

причём сумма каждого равна соответственно .

Необходимый признак сходимости ряда

Ряд   может сходиться лишь в том случае, когда член (общий член ряда) стремится к нулю:

Это необходимый признак сходимости ряда (но не достаточный!). Если же общий член ряда не стремится к нулю — это достаточный признак расходимости.

Примеры

См. также

Обобщения числовых рядов

Признаки сходимости

Литература

Примечания

dikc.academic.ru

Сумма ряда — это… Что такое Сумма ряда?

Сумма числового ряда определяется как предел, к которому стремятся суммы первых n слагаемых ряда, когда n неограниченно растёт. Если такой предел существует и конечен, то говорят, что ряд сходится, в противном случае — что он расходится^[1]. Элементы ряда представляют собой комплексные числа (в частности, вещественные).

Определение

Пусть  — числовой ряд. Число называется n-ой частичной суммой ряда .

Сумма (числового) ряда — это предел частичных сумм , если он существует и конечен. Таким образом, если существует число , то в этом случае пишут . Такой ряд называется сходящимся. Если предел частичных сумм не существует или бесконечен, то ряд называется расходящимся.

Сходимость числовых рядов

Свойство 1. Если ряд

  (1.1)

сходится и его сумма равна S, то ряд

 (1.2)

где c — произвольное число, также сходится и его сумма равна cS. Если же ряд (1.1) расходится и с ≠ 0, то ряд расходится.

Свойство 2. Если сходится ряд (1.1) и сходится ряд

,

а их суммы равны и соответственно, то сходятся и ряды

,

причём сумма каждого равна соответственно .

Необходимый признак сходимости ряда

Ряд   может сходиться лишь в том случае, когда член (общий член ряда) стремится к нулю:

Это необходимый признак сходимости ряда (но не достаточный!). Если же общий член ряда не стремится к нулю — это достаточный признак расходимости.

Примеры

См. также

Обобщения числовых рядов

Признаки сходимости

Литература

Примечания

brokgauz.academic.ru