Сумма ряда — это… Что такое Сумма ряда?
Сумма числового ряда определяется как предел, к которому стремятся суммы первых n слагаемых ряда, когда n неограниченно растёт. Если такой предел существует и конечен, то говорят, что ряд сходится, в противном случае — что он расходится[1]. Элементы ряда представляют собой комплексные числа (в частности, вещественные).
Определение
Пусть — числовой ряд. Число называется n-ой частичной суммой ряда .
Сумма (числового) ряда — это предел частичных сумм , если он существует и конечен. Таким образом, если существует число , то в этом случае пишут . Такой ряд называется сходящимся. Если предел частичных сумм не существует или бесконечен, то ряд называется расходящимся.
Сходимость числовых рядов
Свойство 1. Если ряд
- (1.1)
сходится и его сумма равна S, то ряд
- (1.2)
где c — произвольное число, также сходится и его сумма равна cS. Если же ряд (1.1) расходится и с ≠ 0, то ряд расходится.
Свойство 2. Если сходится ряд (1.1) и сходится ряд
- ,
а их суммы равны и соответственно, то сходятся и ряды
- ,
причём сумма каждого равна соответственно .
Необходимый признак сходимости ряда
Ряд может сходиться лишь в том случае, когда член (общий член ряда) стремится к нулю:
Это необходимый признак сходимости ряда (но не достаточный!). Если же общий член ряда не стремится к нулю — это достаточный признак расходимости.
Примеры
См. также
Обобщения числовых рядов
Признаки сходимости
Литература
Примечания
dic.academic.ru
1. Числовые ряды. Сходимость и сумма рядов. Необходимый признак сходимости.
Свойства сходящихся рядов
Определение. Выражение вида 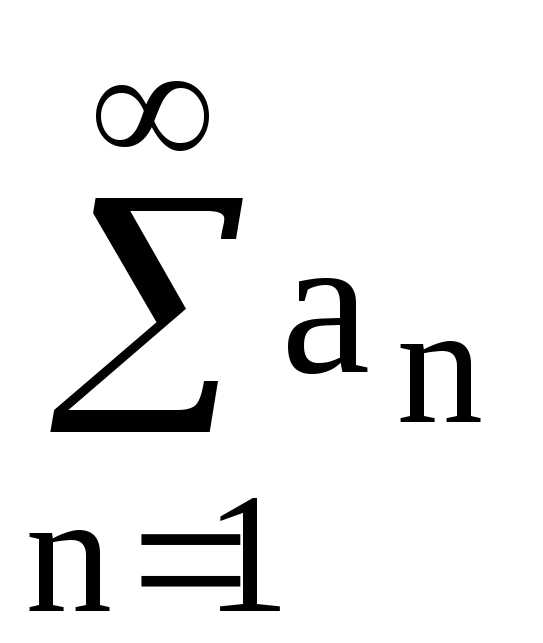 или, подробнее,(1)
или, подробнее,(1)
называется числовым рядом,
а числа 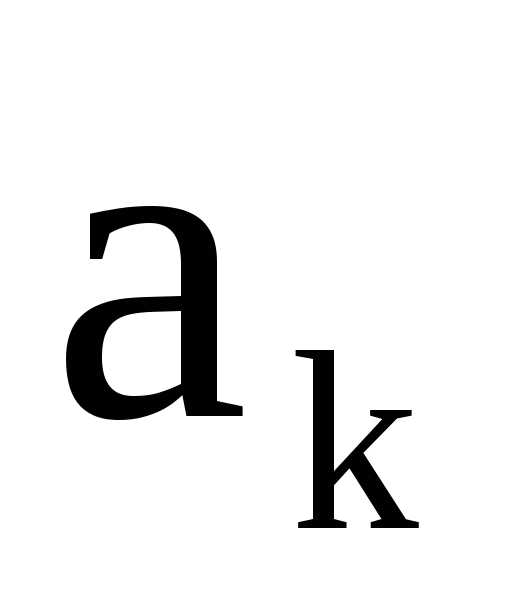 называются егочленами.
называются егочленами.
Для определенности будем считать  первым членом ряда, хотя ряд может
начинаться и с любого другого члена.
Сумма первых
первым членом ряда, хотя ряд может
начинаться и с любого другого члена.
Сумма первых слагаемых ряда (1) называется егочастичной
суммой, она обозначается через
слагаемых ряда (1) называется егочастичной
суммой, она обозначается через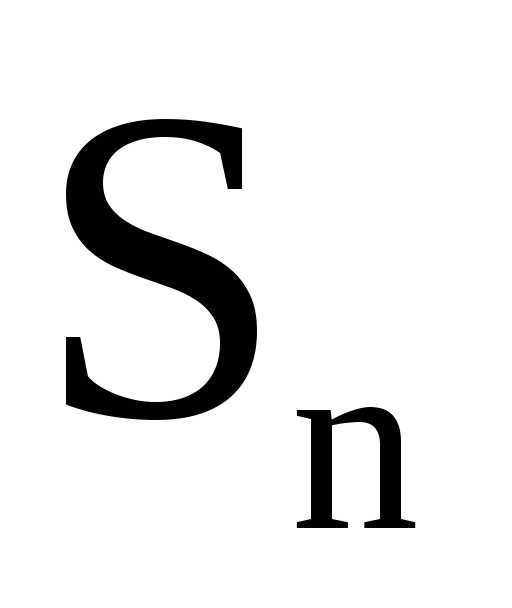 .
При этом
.
При этом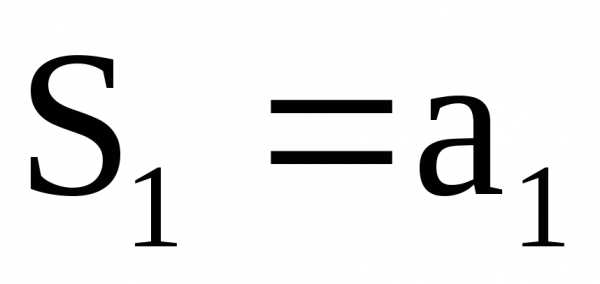 ,,,…
,,,…
.
Определение.Если существует
конечный предел частичных сумм ряда (1) при
,
то это число называетсясуммой
ряда  , а ряд в этом случае называется сходящимся:
, а ряд в этом случае называется сходящимся: 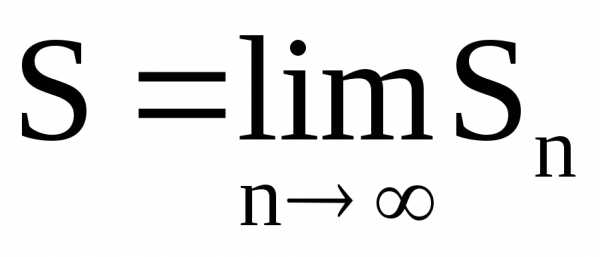
 ),то
ряд называется расходящимся.
У расходящегося ряда сумма не определена.
),то
ряд называется расходящимся.
У расходящегося ряда сумма не определена.Рассмотрим теперь простейшие свойства рядов.
1) Пусть числовые ряды 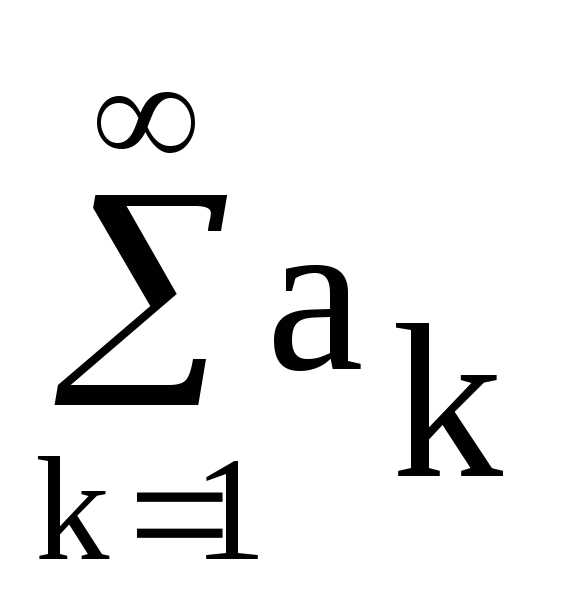 и
и 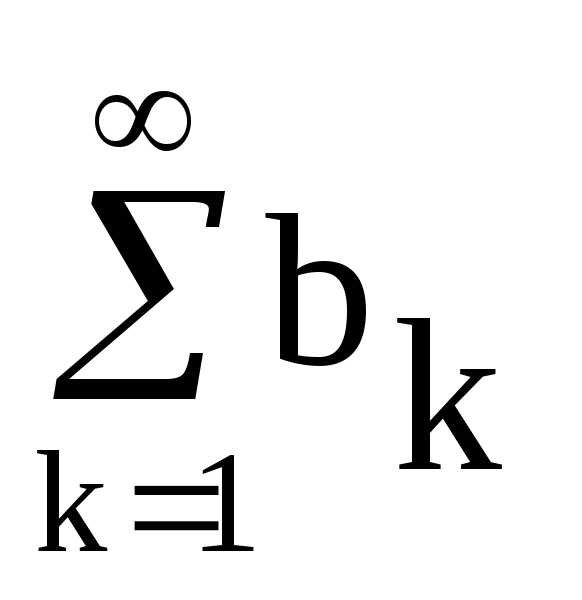 сходятся, и имеют суммы соответственно
сходятся, и имеют суммы соответственно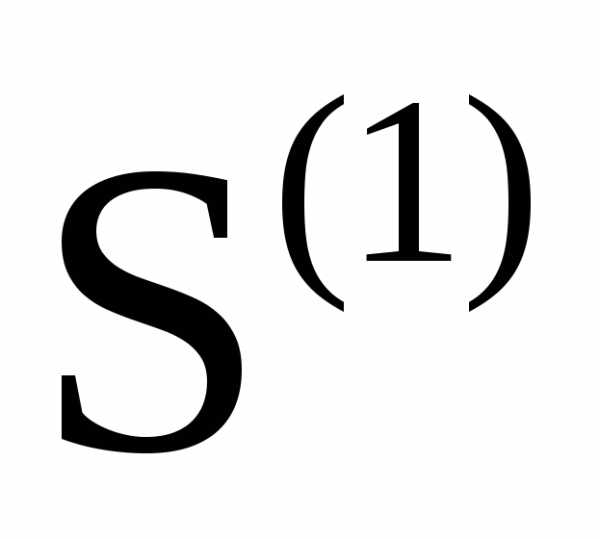 и
и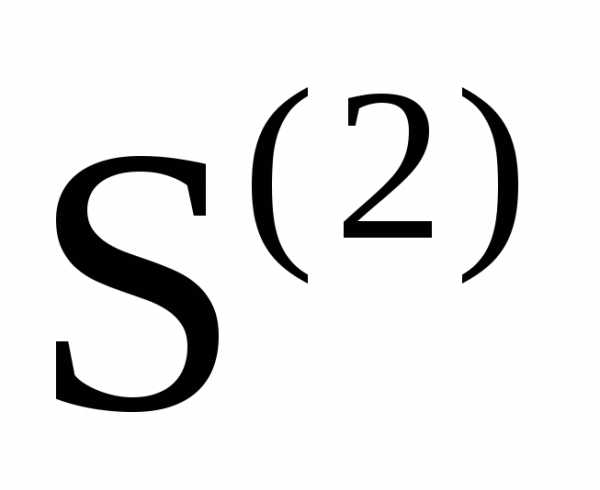 ,
тогда ряд
,
тогда ряд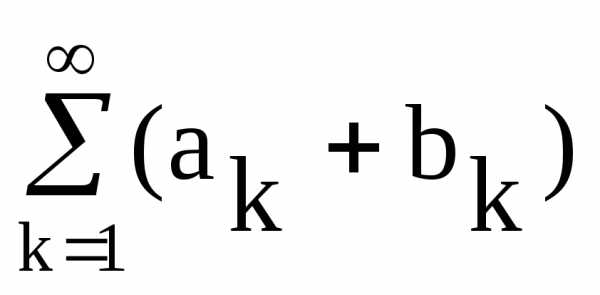 также сходится и его сумма равна
также сходится и его сумма равна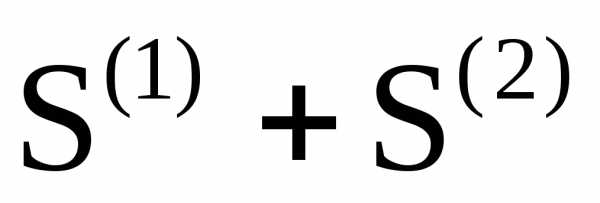 .
.
2) Если ряд (1) сходится, число 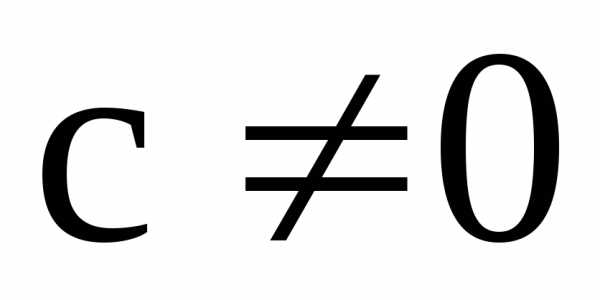 ,
то ряд
,
то ряд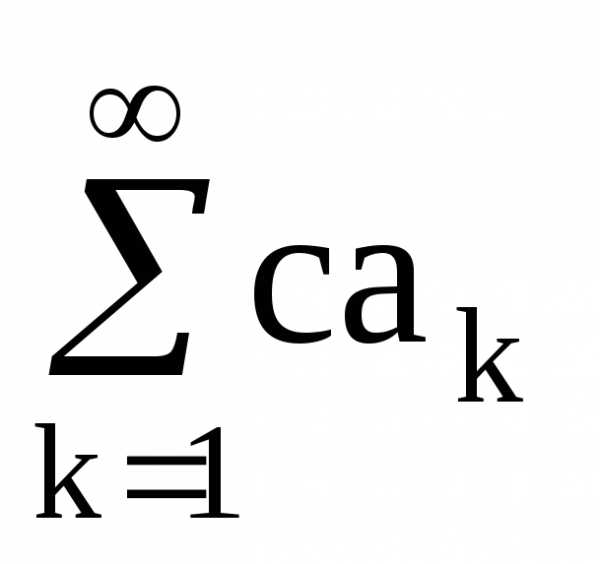 (1/) также сходится и его сумма
равна
(1/) также сходится и его сумма
равна 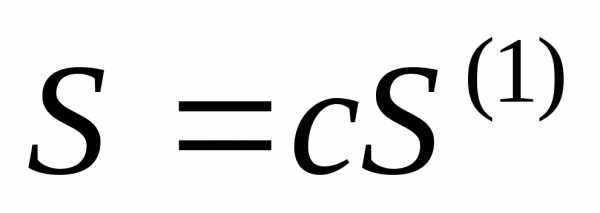 .
Если ряд(1) расходится и
.
Если ряд(1) расходится и 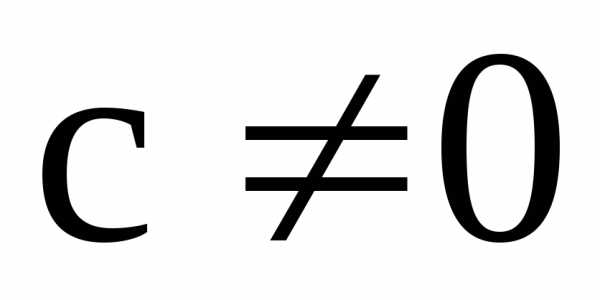 ,
то расходится и ряд(1/).
,
то расходится и ряд(1/).
3) Если в ряде(1) изменить, добавить или отбросить конечное число членов, то сходимость этого ряда не изменится, т.е. если ряд (1) сходился, то новый ряд также сходится, а если ряд (1) расходился, то новый ряд расходится.
Изменив конечное число членов сходящегося ряда, можно изменить его сумму, но сходимость ряда при этом не нарушится.
Теорема 1.(Необходимый признак
сходимости). Если ряд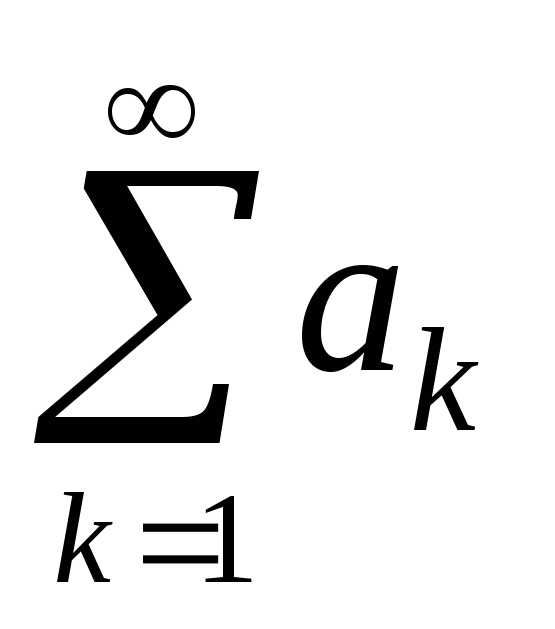 сходится,
то предел его членов при
сходится,
то предел его членов при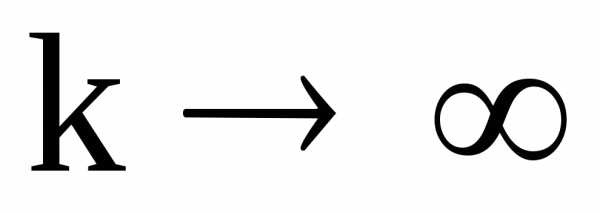 равен
равен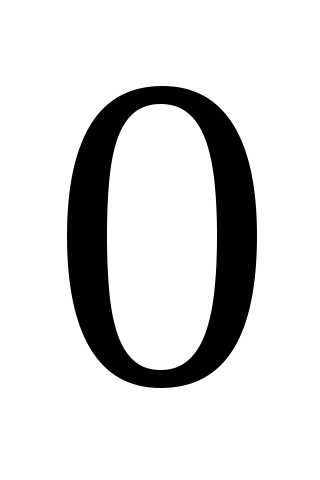 :
: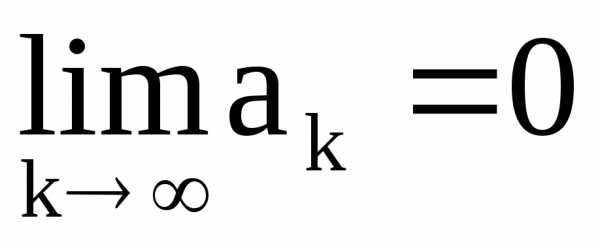 .
Условиеявляется
.
Условиеявляется
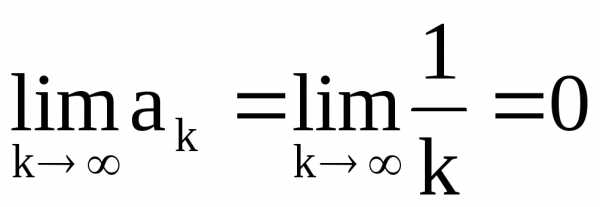 .
.
Следствие(Достаточное условие
расходимости).Если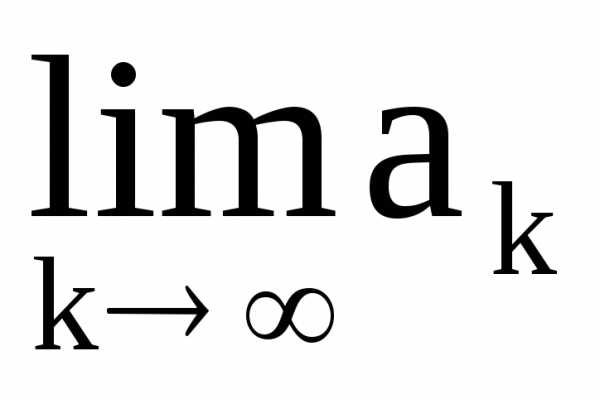 не равен нулю, то ряд (1) расходится.
не равен нулю, то ряд (1) расходится.
2. Достаточные признаки сходимости для рядов с положительными членами
Пусть имеются два ряда 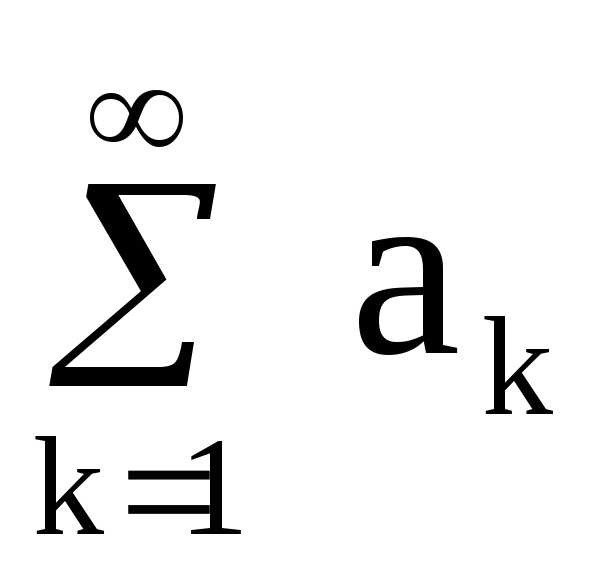 (1) и
(1) и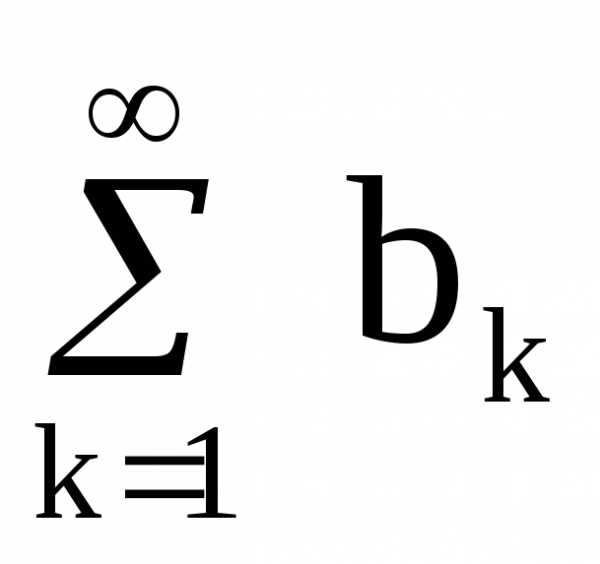 (2) с положительными членами,
удовлетворяющими неравенству
(2) с положительными членами,
удовлетворяющими неравенству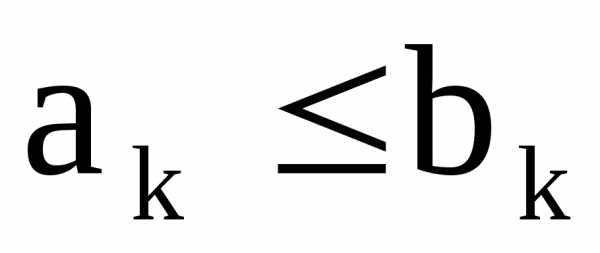 для всех, за исключением, быть может,
конечного числа членов рядов.
для всех, за исключением, быть может,
конечного числа членов рядов.
Теорема 2(Первый признак сравнения). Если ряд (2) сходится, то ряд (1)также сходится, если же ряд (1) расходится, то ряд (2) также расходится.
Пример. Исследуем сходимость ряда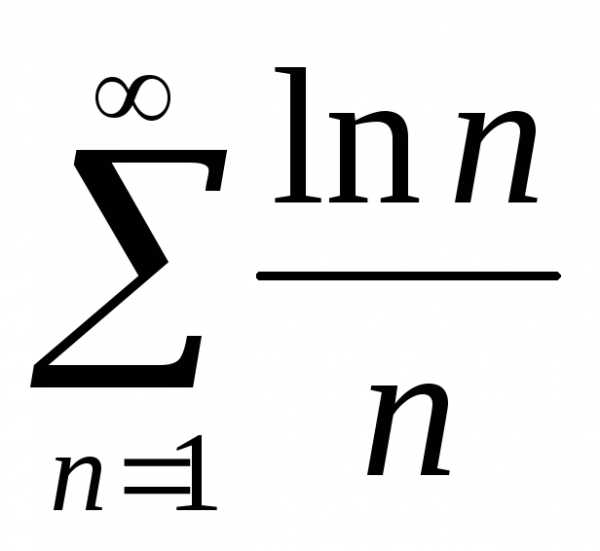 .
. Для сравнения используем расходящийся
гармонический ряд 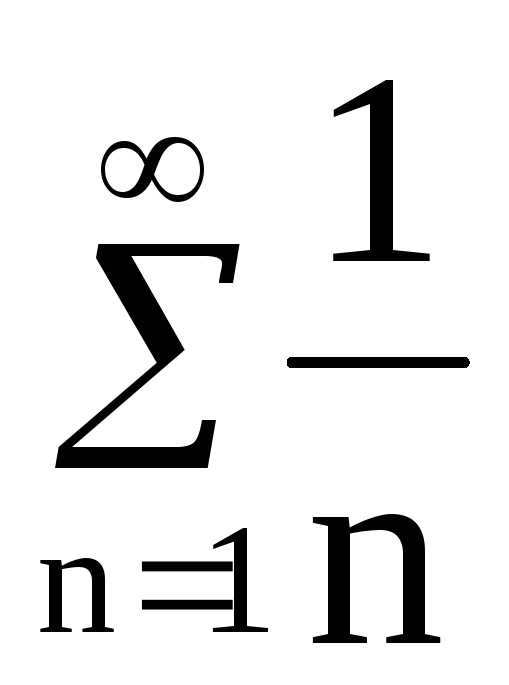 .
При
.
При и
и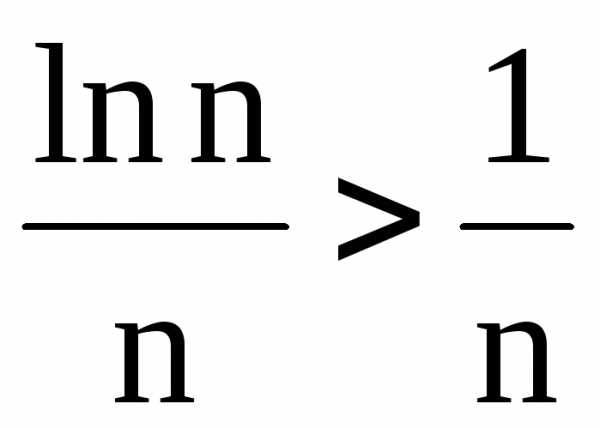 ,
поэтому, согласно первому признаку
сравнения, исследуемый ряд расходится.
,
поэтому, согласно первому признаку
сравнения, исследуемый ряд расходится.
Для сравнения обычно используют такие известные ряды как геометрическая прогрессия или ряд Дирихле.
Рядом Дирихле называется числовой ряд вида.
Ряд Дирихле при 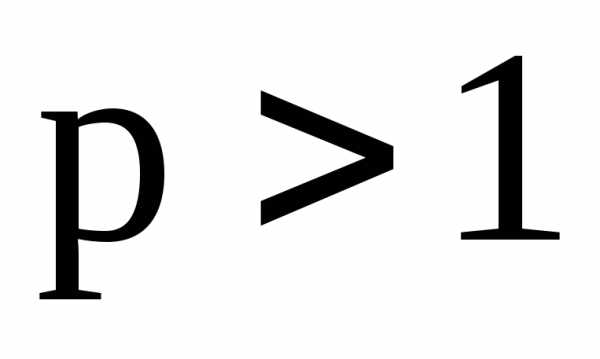 сходится, а при
сходится, а при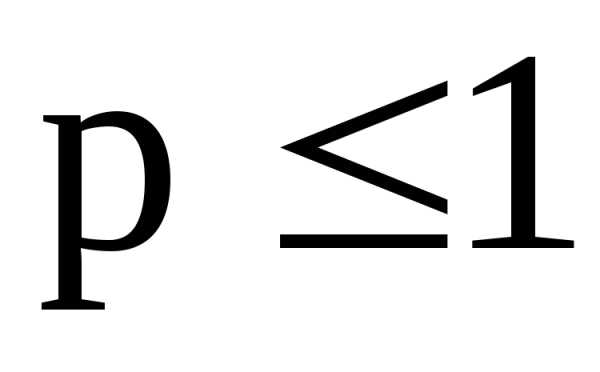 расходится. При
расходится. При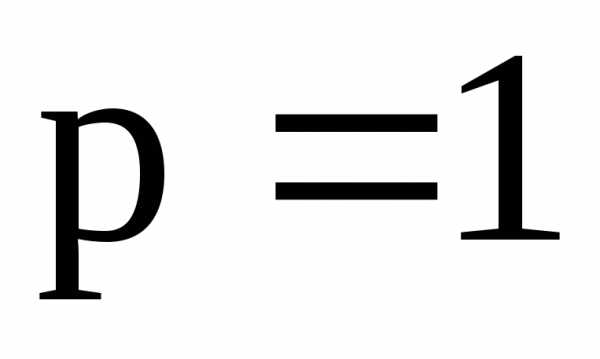 он превращается в гармонический ряд.
он превращается в гармонический ряд.
Теорема 3 (Предельный признак сравнения). Пусть ряды (1) и (2) с положительными
членами таковы, что существует конечный
ненулевой предел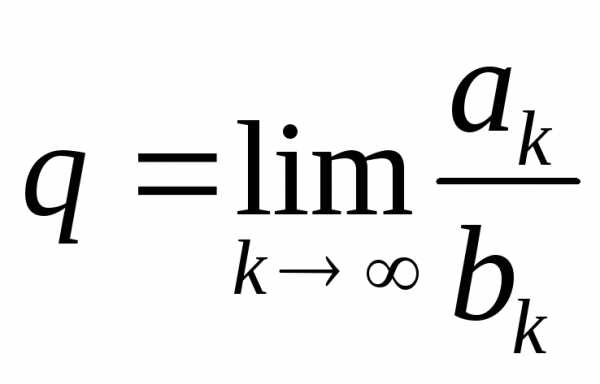
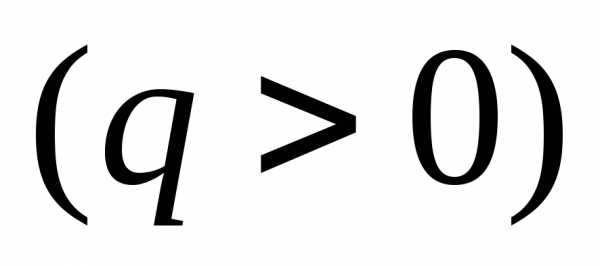 .
Тогда ряды (1) и (2) сходятся или расходятся
одновременно.
.
Тогда ряды (1) и (2) сходятся или расходятся
одновременно. Теорема 4 (Признак Даламбера). Пусть у ряда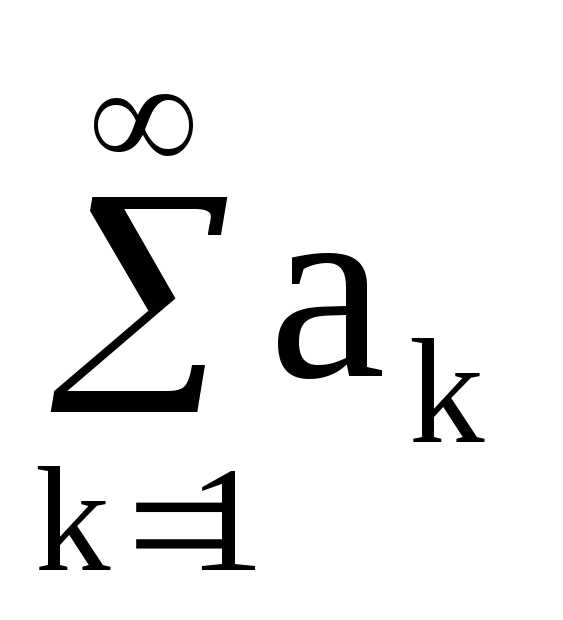 ,
где
,
где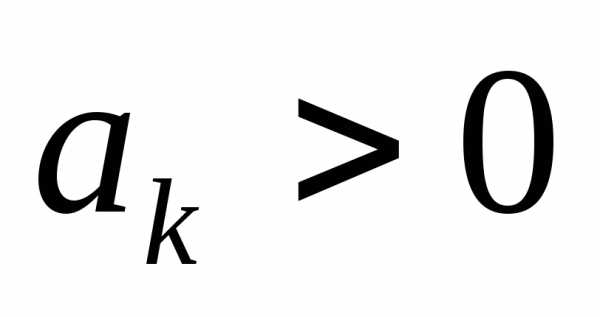 существует предел отношений
существует предел отношений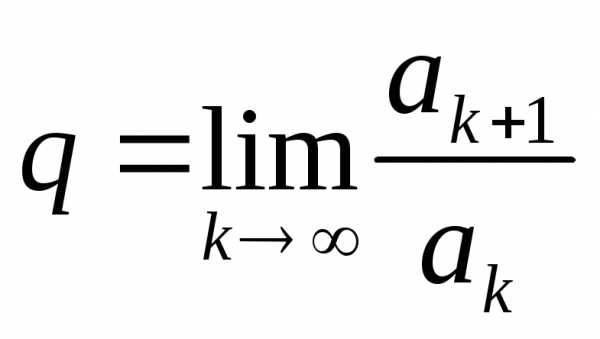 ,
тогда: а) если
,
тогда: а) если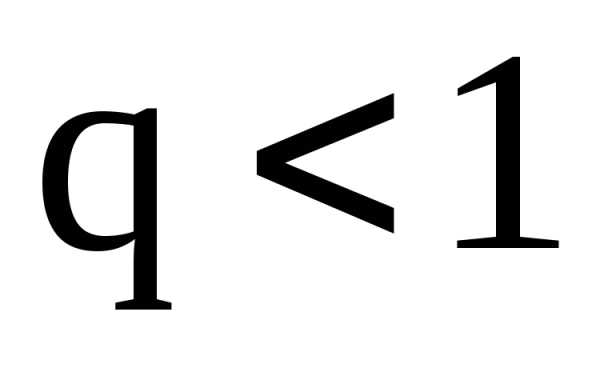 ,
то этот ряд сходится, в) если
,
то этот ряд сходится, в) если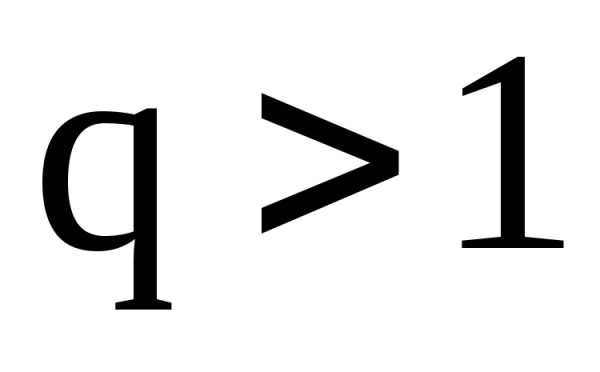 или
или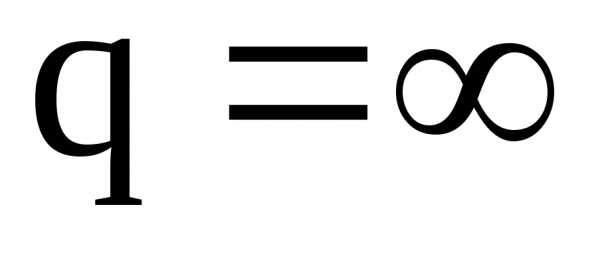 этот ряд расходится. При
этот ряд расходится. При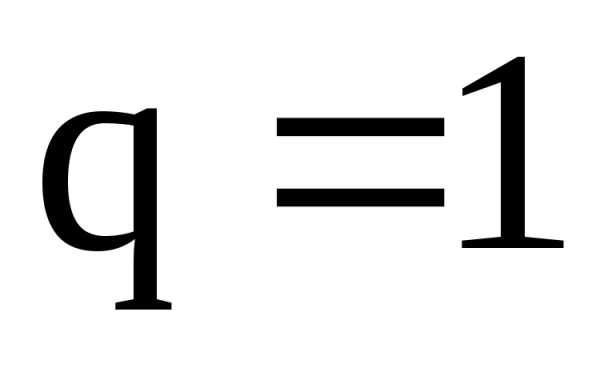 данный признак не применим.
данный признак не применим.
Признак Даламбера удобно применять в
тех случаях, когда выражения для членов 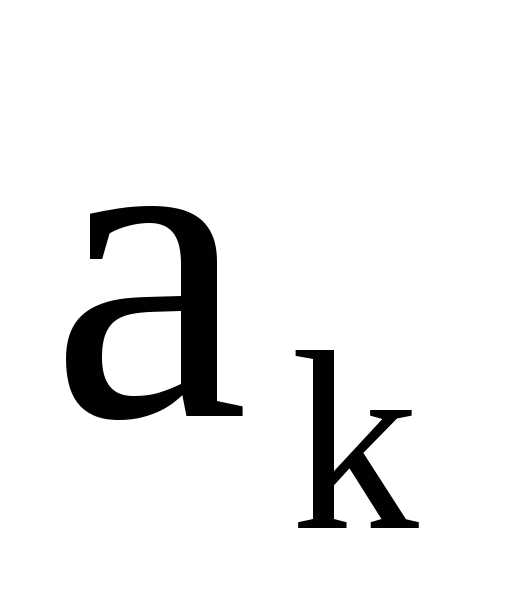 содержат факториалы и показательные,
относительно
содержат факториалы и показательные,
относительно
Теорема 5 (Радикальный признак
Коши). Пусть в ряде 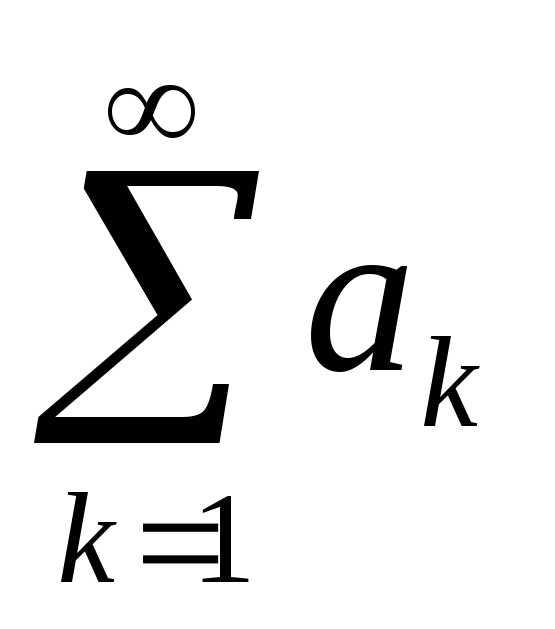 ,
где
,
где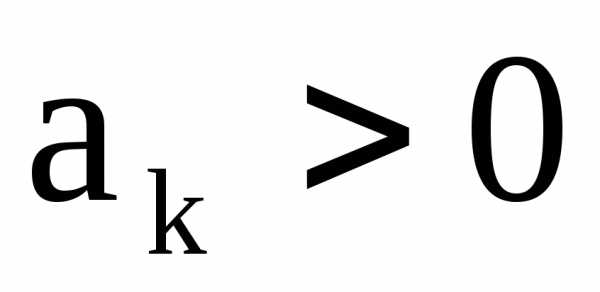 ,
существует предел
,
существует предел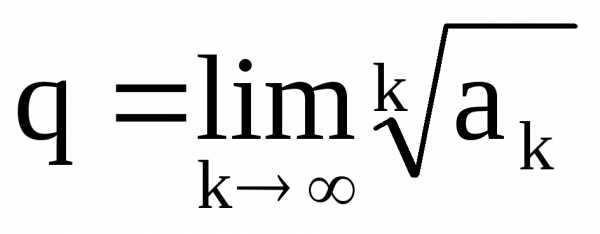 .
Тогда:а) если
.
Тогда:а) если 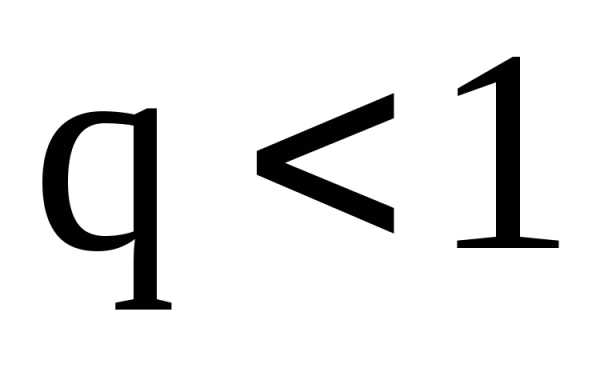 ,
то этот ряд сходится,в) если
,
то этот ряд сходится,в) если 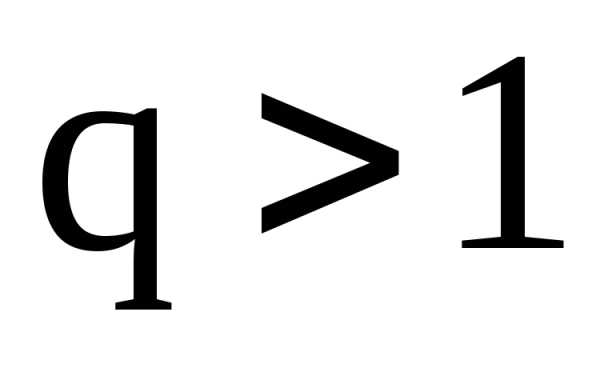 или
или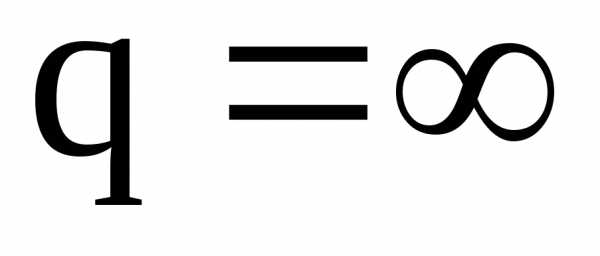 ,то
этот ряд расходится.При
,то
этот ряд расходится.При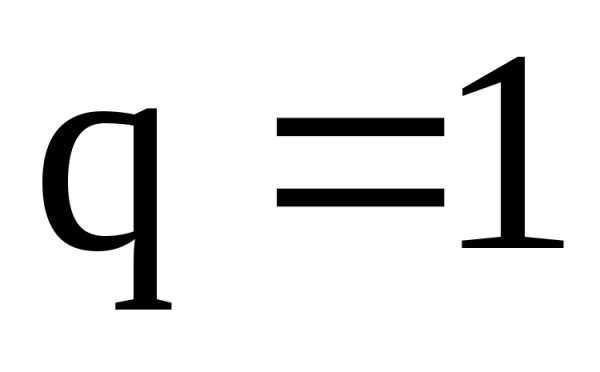 ,
признак Коши не применим.
,
признак Коши не применим.
Теорема 6 (Интегральный признак Коши).
Пусть имеется ряд 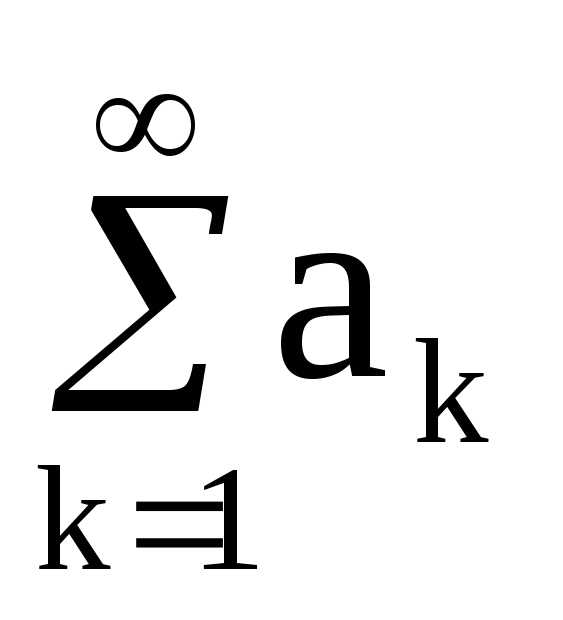 (1)и несобственный интеграл
(1)и несобственный интеграл 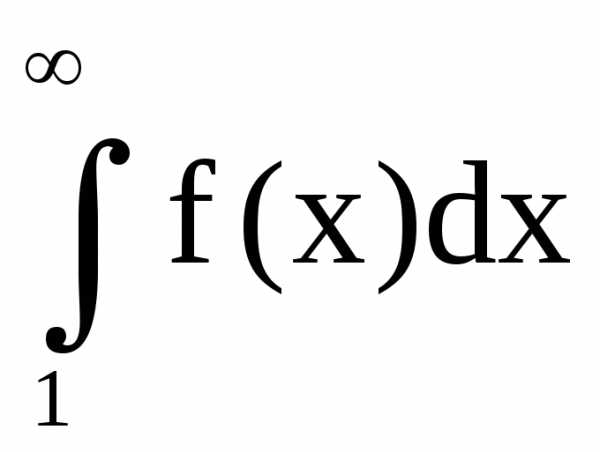 ,
(3)такие, что выполняются следующие
условия:
,
(3)такие, что выполняются следующие
условия:
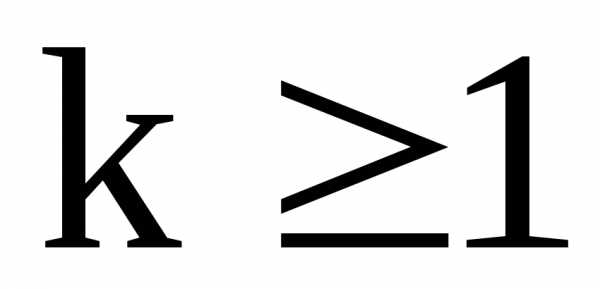 :
: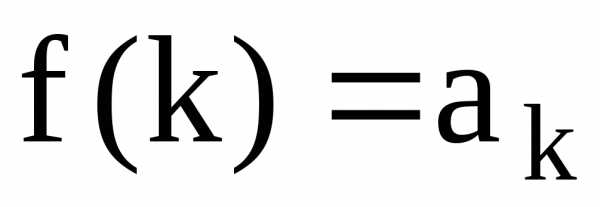 ;
б) функция
;
б) функция 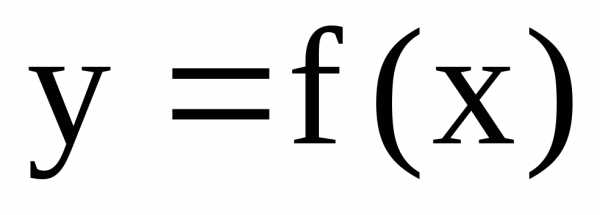 непрерывна, неотрицательна и не возрастает
на промежутке
непрерывна, неотрицательна и не возрастает
на промежутке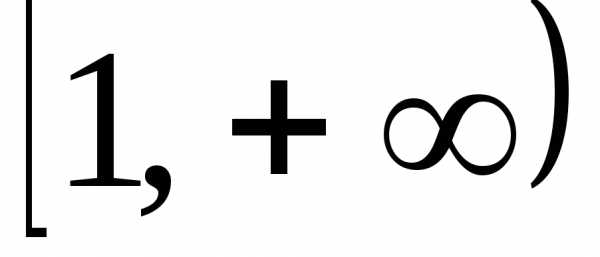 .
.Тогда ряд(1)и интеграл (3)сходятся или расходятся одновременно.
Интегральный признак следует применять
в тех случаях, когда возможно интегрирование
функции 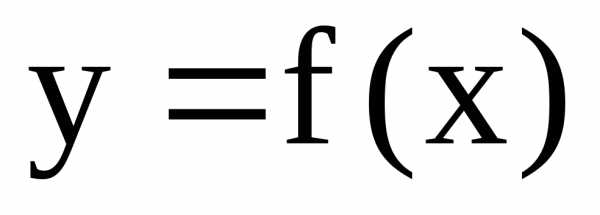 .
.
studfiles.net
37. Числовые ряды, частные суммы числовых рядов.
-числовой ряд.
Среди числ. рядов выделяют знакопостоянные, знакочередующиеся, знакопеременные.
Частичной суммой ряда соответсв. номеру n наз. сумма n первых его слагаемых.
— частичная сумма.
Ряд an наз. сходящимся, если последовательность частичных сумм для этого ряда имеет предел, т.е. если сущ-т число . Это число наз.суммой ряда.
38. Признаки сходимости ряда
Пусть задана бесконечная последовательность чисел . Выражение. наз-ют числовым рядом. При этом числа наз. членами ряда.
Числовой ряд часто записывают в виде. Теорема (необходимый признак сходимости ряда): если ряд сходится, то его n-й член стремится к нулю при неограниченном возрастании n.
Следствие. Если n-й член ряда не стремится к нулю при , то ряд расходится.
Признак Даламбера — признак сходимости числовых рядов, установлен Жаном д’Аламбером в 1768 г.
Если для числового ряда существует такое числоq, что 0<q<1, и что, начиная с некоторого номера, выполняется неравенство, то данный ряд абсолютно сходится; если же, начиная с некоторого номера – абсолютно расходится.
39. Теоремы о сходимости числовых рядов.
Определение. Частной суммой числового ряда называется сумма. Числовой ряд называетсясходящимся, если существует предел, при этомS называется суммой ряда.
Теорема. Числовой ряд сходится тогда и только тогда, когда для любого существует такое, что для всехm,n ><.
Доказательство.
Заметим, что . После этого утверждение превращается в критерий Коши сходимости последовательности .
Теорема.
Если ряд сходится, то.
Доказательство.
Из свойств пределов следует, что . Отсюда следует, что.
40. Эталонные ряды для установления сходимости
Геометрический ряд
Обобщеный гармонический ряд
В частности, при к=1 получаем гармонический ряд
Эталонные ряды, т.е. разложения элементарных функций, можно использовать для получения рядов тех же функций, но сложного аргумента.
41. Функциональные ряды, степенные ряды, ряды Тейлора и Маклорена
Пусть функции Un(x),n∈N, определены в области D. Выражение U1(x) + U2(x) +… + Un (x)+…= Un (x), где х∈D, наз. функциональным рядом. Каждому значению x0∈D соответствует числовой ряд Un (x0). Этот ряд может быть сходящимся или расходящимся. Если для x0∈D числовой ряд Un (x0) сходится, то говорят, чтo функциональный ряд сходится в точке x0, и точку x0 наз. точкой сходимости.Если функциональный ряд сходится в каждой точке x∈E⊂D, то этот ряд наз. сходящимся на множестве Е, а множество Е наз. областью сходимости ряда. Если множество Е пусто, то ряд расходится в каждой точке множества D.
Областью сходимости степенного ряда называется множество всех значений переменной х , при которых соответствующий числовой ряд сходится. Ряд вида а0 + а1 х + а2 х2 + … аn хn + … = называетсястепенным рядом, а – некот. числа, х – переменная.
Коэффициентами степенного ряда называются числа а0 , а1 , … , аn.
Формулой Тейлора для функции f(x) в окрестности точки х называется многочлен Рn(х) = f(х0) +Остаточным членом формулы Тейлора называется последнее слагаемое в формуле Тейлора
Rn(x)= =f(x) – Pn(x)
Т.о., многочлен Тейлора Рn(х) служит приближением функции f(х). Оценкой этого приближения служит остаточный член формулы Тейлора Rn(х).
Формулой Маклорена для функции f(х) называется ее формула Тейлора при х0 = 0: f(x)= f(0) +
где с – некоторая точка из интервала (0, х).
studfiles.net
Сумма ряда на практике
Вычислить сумму ряда можно только в случае, когда ряд сходится. Если ряд расходится то сумма ряда бесконечна и нет смысла что-то вычислять. Ниже приведены примеры из практики нахождения суммы ряда, которые задавали в Львовском национальном университете имени Ивана Франка. Задания на ряды подобраны так, что условие сходимости выполняется всегда, однако проверку на сходимость мы выполнять будем. Эта и следующие за ней статьи составляют решение контрольной работы по анализе рядов.
Пример 1.4 Вычислить сумму рядов:
а)
Вычисления: Поскольку граница общего члена ряда при номере следующему до бесконечности равна 0
то данный ряд сходится. Вычислим сумму ряда. Для этого преобразуем общий член, разложив его на простейшие дроби I и II типа. Методика разложения на простые дроби здесь приводиться не будет (хорошо расписана при интегрировании дробей), а лишь запишем конечный вид разложения
В соответствии с этим можем сумму расписать через сумму ряда образованного из простейших дробей, а дальше из разницы сумм рядов
Далее расписываем каждый ряд в явную сумму и выделяем слагаемые (подчеркивание), которые превратятся 0 после сложения. Таким образом сумма ряда упростится к сумме 3 слагаемых (обозначены черным), что в результате даст 33/40.
На этом базируется вся практическая часть нахождения суммы для простых рядов.
Примеры на сложные ряды сводятся к сумме бесконечно убывающих прогрессий и рядов, которые находят через соответствующие формулы, но здесь такие примеры рассматривать не будем.
б)
Вычисления: Находим границу n-го члена суммы
Она равна нулю, следовательно заданный ряд сходится и имеет смысл искать его сумму. Если граница отличная от нуля, то сумма ряда равна бесконечности со знаком «плюс» или «минус».
Найдем сумму ряда. Для этого общий член ряда который является дробью превратим методом неопределенных коэффициентов к сумме простых дробей I типа
Далее по инструкции которая приводилась ранее записываем сумму ряда через соответствующие суммы простейших дробей
Расписываем суммы и выделяем слагаемые, которые станут равными 0 при суммировании.
В результате получим сумму нескольких слагаемых (выделенные черным) которая равна 17/6.
Пример 1.9 Найти сумму ряда:
а)
Вычисления: Вычислениям границы
убеждаемся что данный ряд сходится и можно находить сумму. Далее знаменатель функции от номера n раскладываем на простые множители, а весь дробь превращаем к сумме простых дробей I типа
Далее сумму ряда в соответствии с расписанием записываем через два простые
Ряды записываем в явном виде и выделяем слагаемые, которые после добавления дадут в сумме ноль. Остальные слагаемые (выделенные черным) и представляет собой конечную сумму ряда
Таким образом, чтобы найти сумму ряда надо на практике свести под общий знаменатель 3 простых дроби.
б)
Вычисления: Граница члена ряда при больших значениях номера стремится к нулю
Из этого следует что ряд сходится, а его сумма конечна. Найдем сумму ряда, для этого сначала методом неопределенных коэффициентов разложим общий член ряда на три простейшего типа
Соответственно и сумму ряда можно превратить в сумму трех простых рядов
Далее ищем слагаемые во всех трех суммах, которые после суммирования превратятся в ноль. В рядах, содержащих три простых дроби один из них при суммировании становится равным нулю (выделен красным). Это служит своеобразной подсказкой в вычислениях
Сумма ряда равна сумме 3 слагаемых и равна единице.
Пример 1.15 Вычислить сумму ряда:
а)
Вычисления: При общем член ряда стремящемся к нулю
данный ряд сходится. Преобразуем общий член таким образом, чтобы иметь сумму простейших дробей
Далее заданный ряд, согласно формулам расписания, записываем через сумму двух рядов
После записи в явном виде большинство членов ряда в результате суммирования станут равны нулю. Останется вычислить сумму трех слагаемых.
Сумма числового ряда равна -1/30.
б)
Вычисления: Поскольку граница общего члена ряда равна нулю,
то ряд сходится. Для нахождения суммы ряда разложим общий член на дроби простейшего типа.
При разложении использовали метод неопределенных коэффициентов. Записываем сумму ряда из найденного расписание
Следующим шагом выделяем слагаемые, не вносящие никакого вклада в конечную сумму и остальные оставшиеся
Сумма ряда равна 4,5.
Пример 1.25 Вычислить сумму рядов:
а)
Вычисления: Находим границу общего члена ряда
Поскольку она равна нулю то ряд сходится. Можем найти сумму ряда. Для этого по схеме предыдущих примеров раскладываем общий член ряда через простейшие дроби
Это позволяет записать ряд через сумму простых рядов и, выделив в нем слагаемые, упростив при этом суммирование.
В этом случае останется одно слагаемое которое равен единице.
б)
Вычисления: Находим границу общего члена ряда
и убеждаемся что ряд сходится. Далее общий член числового ряда методом неопределенных коэффициентов раскладываем на дроби простейшего типа.
Через такие же дроби расписываем сумму ряда
Записываем ряды в явном виде и упрощаем к сумме 3 слагаемых
Сумма ряда равна 1/4.
На этом ознакомление со схемами суммирования рядов завершено. Здесь еще не рассмотрены ряды, которые сводятся к сумме бесконечно убывающей геометрической прогрессии, содержащие факториалы, степенные зависимости и подобные. Однако и приведенный материал будет полезен для студентов на контрольных и тестах.
yukhym.com
1 Понятие числового ряда и его суммы
Пусть задана бесконечная последовательность чисел u1, u2, u3…
Выражение u1+ u2+ u3…+ un (1) называется числовым рядом, а числа его составляющие- членами ряда.
Сумма конечно числа n первых членов ряда называется n-ной частичной суммой ряда: Sn = u1+..+un
Если
сущ. конечный предел: 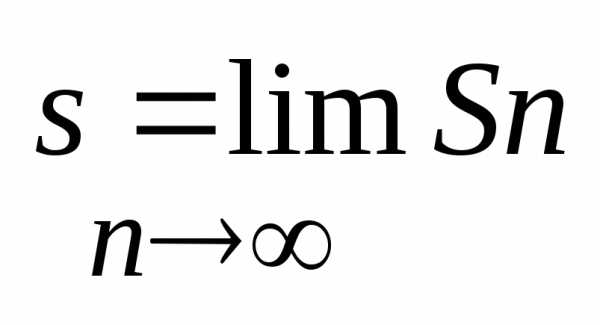 ,
то его называют суммой ряда и говорят,
что ряд сходится, если такого предела
не существует, то говорят что ряд
расходится и суммы не имеет.
,
то его называют суммой ряда и говорят,
что ряд сходится, если такого предела
не существует, то говорят что ряд
расходится и суммы не имеет.
2 Геометрический и арифметический ряды
Ряд состоящий из членов бесконечной геометрической прогрессии наз. геометрическим: или
а+ аq +…+aqn-1
a
0 первый член q
– знаменатель. Сумма ряда: 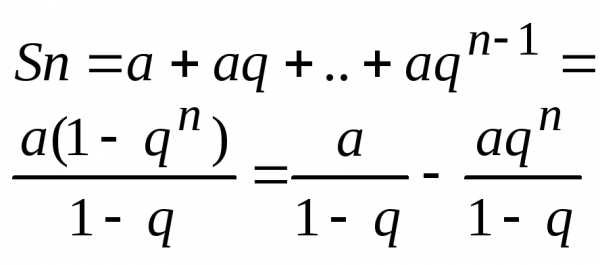
следовательно конечный предел последовательности частных сумм ряда зависит от величины q
Возможны случаи:
1
|q|<1 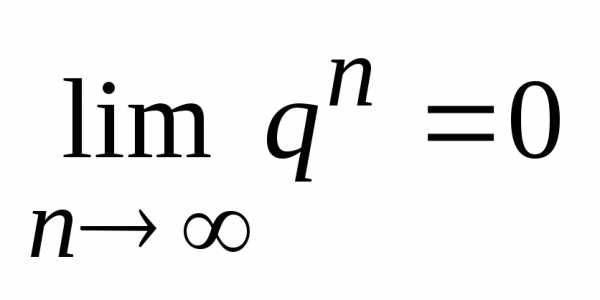
т.
е. ряд схд-ся и его сумма 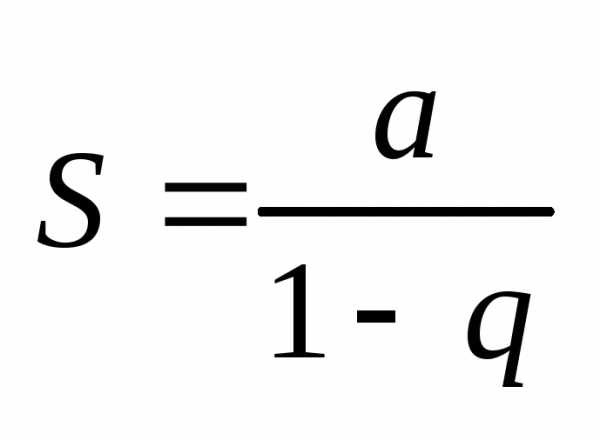 2
|q|>1
2
|q|>1 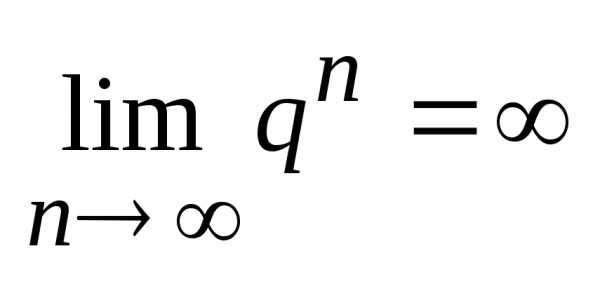 и предел суммы так же равен бесконечности
и предел суммы так же равен бесконечности
т. е. ряд расходится.
3 при q = 1 получается ряд: а+а+…+а… Sn = na ряд расходится
4 при q1 ряд имеет вид: а-а+а … (-1)n-1a Sn=0 при n четном, Sn=a при n нечетном предела частных суммы не существует. ряд расходится.
Рассмотрим ряд из бесконечных членов арифметической прогрессии:u – первый член, d – разность. Сумма ряда
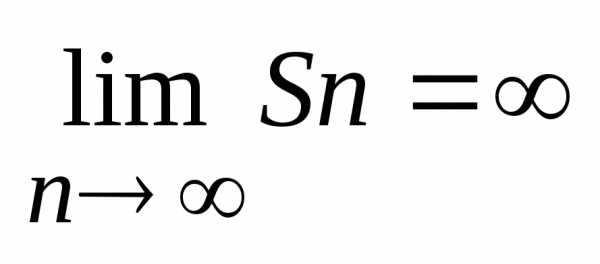 при
любых u1
и d
одновременно
0 и ряд всегда расходится.
при
любых u1
и d
одновременно
0 и ряд всегда расходится.
3 С-ва сходящихся рядов
Пусть
даны два ряда: u1+u2+…un
=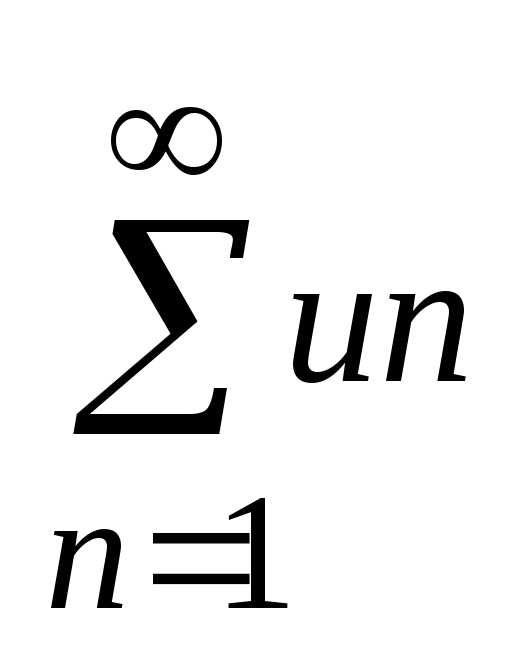 (1)
иv1+v2+…vn
=
(1)
иv1+v2+…vn
= 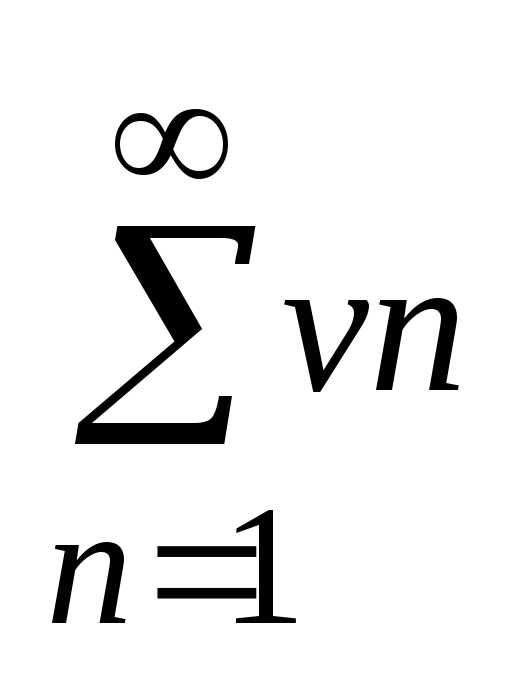 (2)
(2)
Произведением
ряда (1) на число
R
наз ряд: u1+u2+…un
=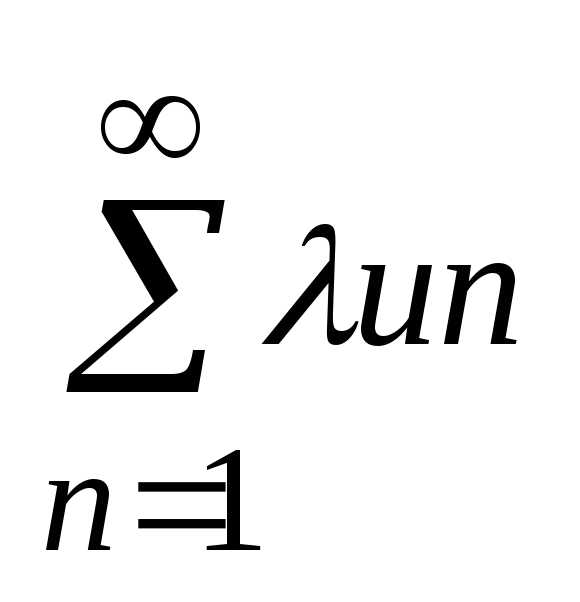 (3)
(3)
Суммой рядов (1) и (2) наз ряд:
(u1+v1)+(u2+v2)+…(un+vn)
= 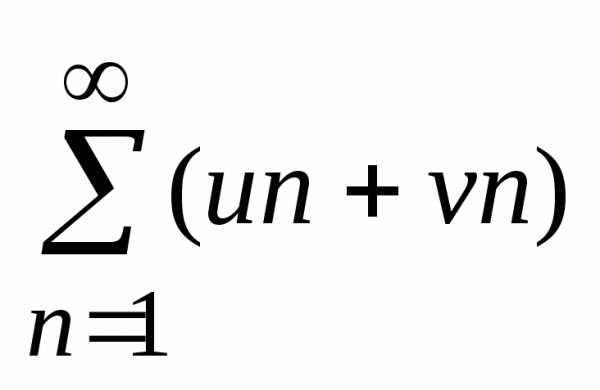 (для разности там только — появица)
(для разности там только — появица)
Т1 Об общем множителе
Если
ряд (1) сходится и его сумма = S,
то для любого числа
ряд 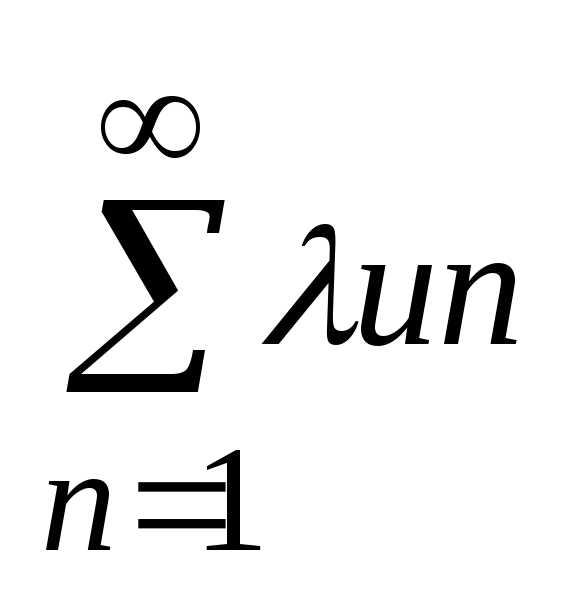 =
=
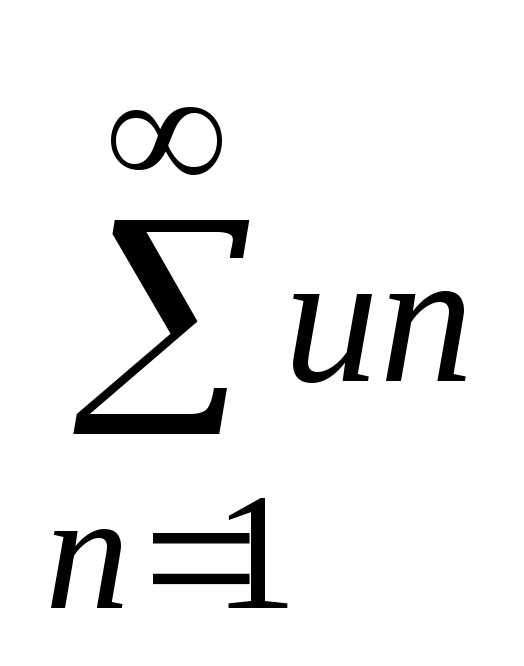 тоже сходится и его суммаS’
= S
Если ряд (1) расходится и
0, то и ряд
тоже сходится и его суммаS’
= S
Если ряд (1) расходится и
0, то и ряд 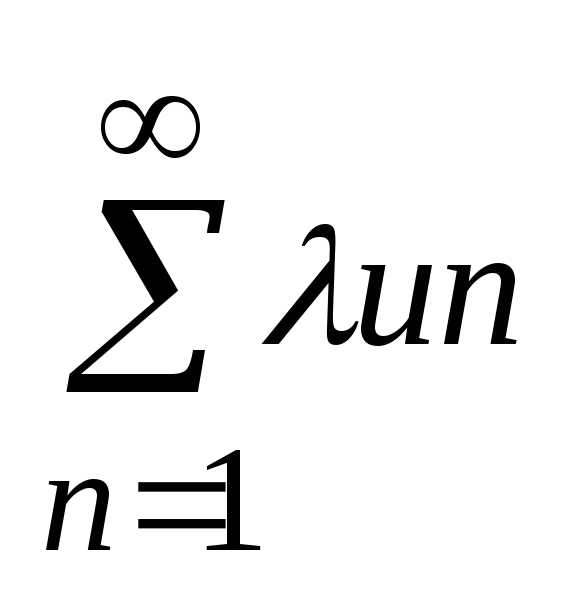 тоже расходится. Т. е. общий множитель
не влияет на расходимости ряда.
тоже расходится. Т. е. общий множитель
не влияет на расходимости ряда.
Т2
Если ряды (1) и (2) сходятся, а их суммы =
соотв S
и S’,
то и ряд: 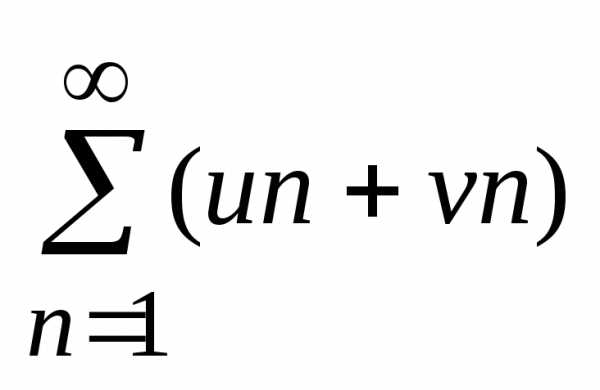 тоже сходится и если
его сумма, то
= S+S’.
Т. е. сходящиеся ряды можно почленно
складывать и вычитать. Если ряд (1)
сходится, а ряд (2) расходится, то их
сумма(или разность) тоже расходится. А
вот если оба ряда расходятся. то ихняя
сумма (или разность)может как расходится
(если un=vn)
так и сходиться (если un=vn)
тоже сходится и если
его сумма, то
= S+S’.
Т. е. сходящиеся ряды можно почленно
складывать и вычитать. Если ряд (1)
сходится, а ряд (2) расходится, то их
сумма(или разность) тоже расходится. А
вот если оба ряда расходятся. то ихняя
сумма (или разность)может как расходится
(если un=vn)
так и сходиться (если un=vn)
Для
ряда (1) ряд 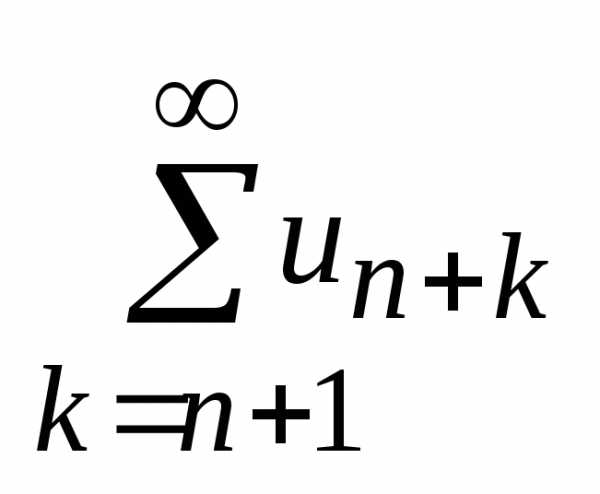 называетсяn
– ным остатком ряда. Если нный остаток
ряда сходится, то его сумму будем
обозначать: rn =
называетсяn
– ным остатком ряда. Если нный остаток
ряда сходится, то его сумму будем
обозначать: rn = 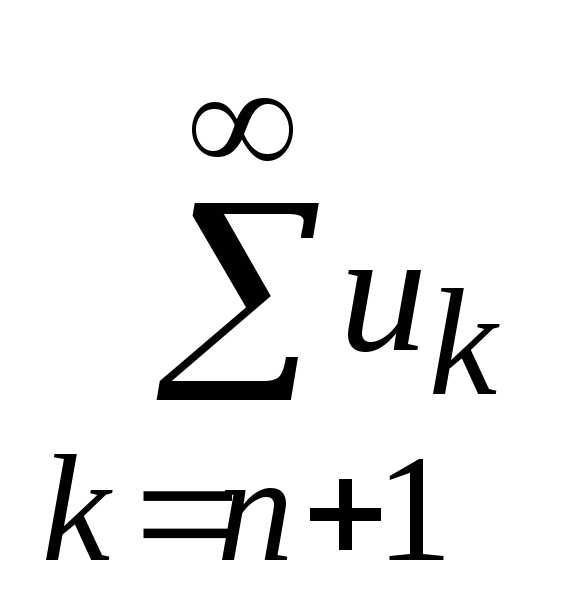
Т3 Если ряд сходится, то и любой его остаток сходится, если какой либо остаток ряда сходится, то сходится и сам ряд. Причем полная сумма = частичная сумма ряда Sn + rn
Изменение, а также отбрасывание или добавление конечного числа членов не влияет на сходимость (расходимость) ряда.
4 Необходимый признак сходимости рядов
Если
ряд сходится, то предел его общего члена
равен нулю: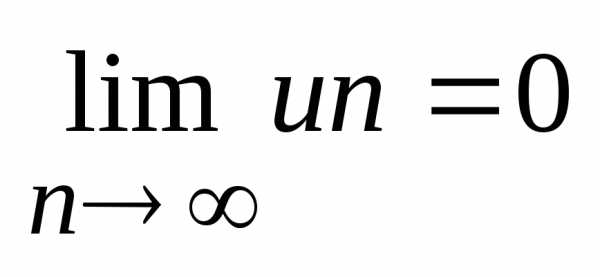
Док-во:
Sn=u1+u2+…+un
Sn-1\u1+u2+…+un-1
un=Sn-Sn-1, поэтому:
Сей признак является только необходимым, но не является достаточным., т. е. если предел общегоь члена и равен нулю совершенно необязательно чтобы ряд при этом сходился. Следовательно, вот сие условие при его невыполнении является зато достаточным условием расходимости ряда.
5 Интегральный признак сходимости ряда. Ряд Дирихле
Т1 Пущай дан рядт 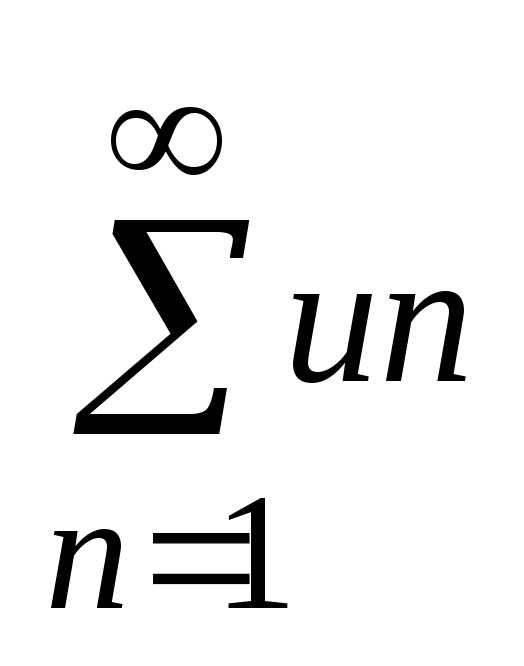 (1),
члены которого неотрицательны, и не
возрастают:u1>=u2>=u3…>=un
(1),
члены которого неотрицательны, и не
возрастают:u1>=u2>=u3…>=un
Если
существует ф-ция f(x) неотрицательная,
непрерывная и не возрастающая на [1,+]
такая, что f(n)
= Un,
n
N,
то для сходимости ряда (1) необходимо
унд достаточно, чтобы сходился
несобственный интеграл: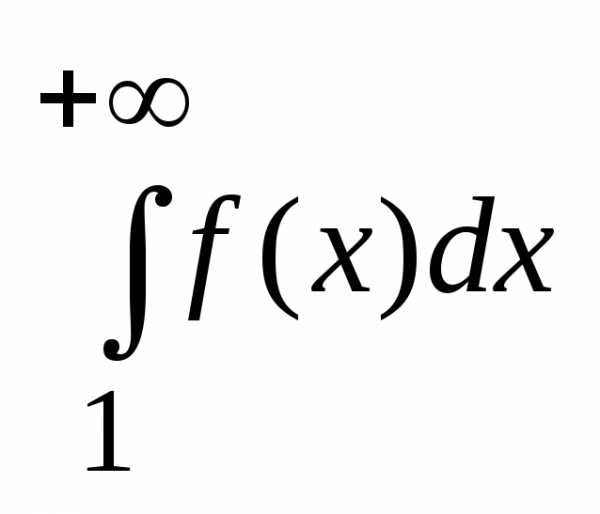 ,
а для расходимости достаточно и необходимо
чтобы сей интеграл наоборот расходился
(ВАУ!).
,
а для расходимости достаточно и необходимо
чтобы сей интеграл наоборот расходился
(ВАУ!).
Применим
сей признак для исследования ряда
Дирихле: Вот он: 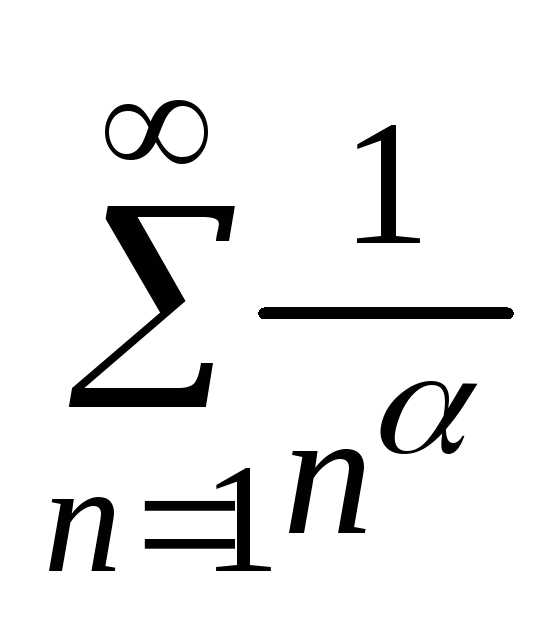 ,
R
Сей ряд называют обобщенным гармоническим
рядом, при
>0 общий член оного un=1/n 0
и убывает поэтому можно воспользоваться
интегральным признаком, функцией здеся
будет ф-ция f(x)=1/x (x>=1)сия
ф-ция удовлетворяет условиям теоремы
1 поэтому сходимость (расходимости) ряда
Дирихле равнозначна сходимости
расходимости интеграла:
,
R
Сей ряд называют обобщенным гармоническим
рядом, при
>0 общий член оного un=1/n 0
и убывает поэтому можно воспользоваться
интегральным признаком, функцией здеся
будет ф-ция f(x)=1/x (x>=1)сия
ф-ция удовлетворяет условиям теоремы
1 поэтому сходимость (расходимости) ряда
Дирихле равнозначна сходимости
расходимости интеграла: 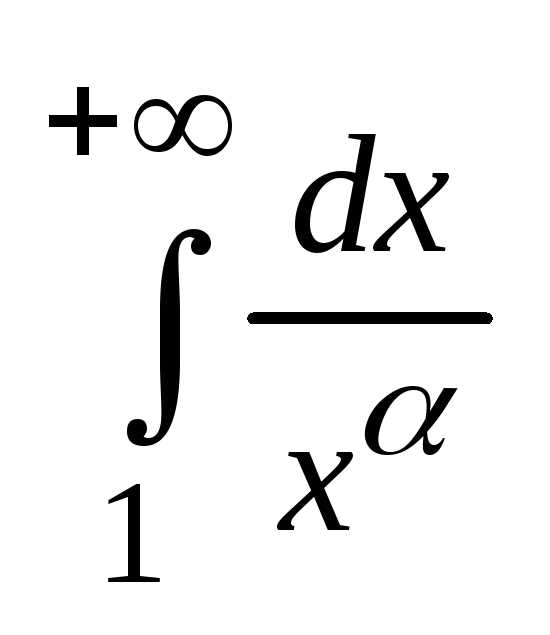
Возможны три случая:
1
>1, 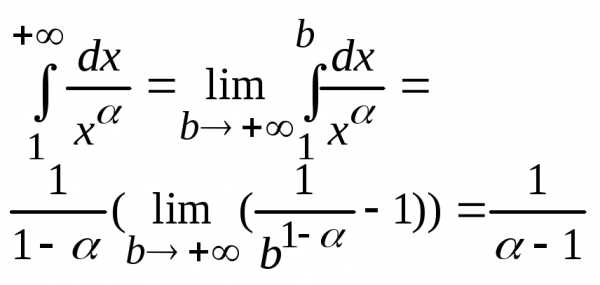
Интеграл а потому и ряд сходится.
2 0<<1,
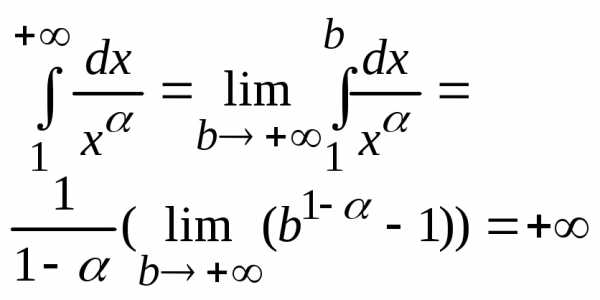
Интеграл и ряд расходится
3 =1,
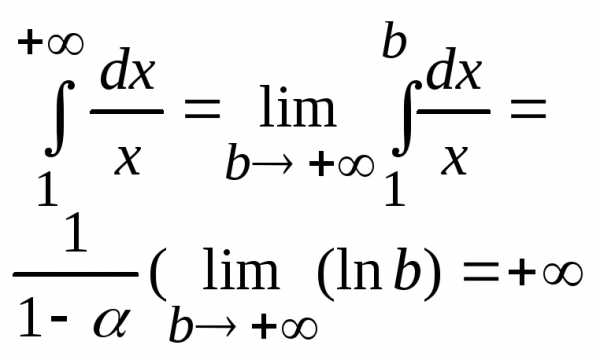
Интеграл и ряд расходится
studfiles.net
Сумма ряда — Циклопедия
Сумма ряда — значение бесконечной суммы [math]\sum_{i=1}^\infty a_i = a_1 + a_2 + … + a_n + …[/math] В математическом анализе определяется при каких условиях сумма ряда существует и как ее вычислять. Соответствующий раздел математического анализа называется теорией рядов.
[править] Опрделение сходимости ряда и суммы ряда
Предположим, что у нас есть бесконечная последовательность следующих (обычно, вещественных) чисел: [math]\ a_1[/math], [math]\ a_2[/math],.. [math]\ a_n[/math],… Тогда можно определить следующее выражение: [math]\ a_1 +a_2+[/math]…[math]\ +a_n+[/math]…=[math]\sum_{i=1}^\infty a_i[/math]. Этот символ называется числовым рядом.
Числовой ряд — символ, составленный из членов бесконечной числовой последовательности, соединённых формальным символом «+».
Если сложить k первых членов последовательности ряда, то полученное число будет называться частичной суммы k членов данного ряда.
Числовой ряд называется сходящимся, если существует предел частичных сумм при n стремящемся к бесконечности и говорят, что ряд сходится. В других случаях ряд называется расходящимся и ряд расходится.
Числовую последовательность можно задать не только перечислением членов этой последовательности, но и общей формулой, по которой можно получить член этой последовательности по его номеру n. В этом случае эта формула называется общим членом ряда и записывается перед заглавной греческой буквой «сигма», математическим знаком суммирования, сверху и снизу которой ставятся пределы суммирования.
Необходимым (но не достаточным) условием сходимости числового ряда является стремление общего члена к «0» при [math]n \rightarrow \infty[/math]. Так, например, ряд [math]1+1/2+1/3+1/4+..+1/n+..[/math] является расходящимся, несмотря на то, что общий член стремится к нулю.
Необходимым и достаточным условием сходимости числового ряда является существование верхней границы множества всех частичных сумм ряда. Супремум этого множества (или инфимум множества всех верхних границ) будет являться суммой этого ряда.
Существуют признаки сходимости числового ряда.
Так, из расходимости меньшего ряда с неотрицательными членами следует расходимость большего, а из сходимости большего с неотрицательными членами — сходимость меньшего. Обратное неверно.
Для определения большего и меньшего ряда достаточно сравнить n-ные члены двух рядов (найти их отношение).
cyclowiki.org
Сумма ряда — Википедия
Сумма числового ряда определяется как предел, к которому стремятся суммы первых n слагаемых ряда, когда n неограниченно растёт. Если такой предел существует и конечен, то говорят, что ряд сходится, в противном случае — что он расходится[1]. Элементы ряда представляют собой комплексные числа (в частности, вещественные).
Пусть — числовой ряд. Число называется n-ой частичной суммой ряда .
Сумма (числового) ряда — это предел частичных сумм , если он существует и конечен. Таким образом, если существует число , то в этом случае пишут . Такой ряд называется сходящимся. Если предел частичных сумм не существует или бесконечен, то ряд называется расходящимся.
Дальнейшим обобщением понятия суммы ряда является понятие суммирующей функции ряда.
Сходимость числовых рядов[править]
Свойство 1. Если ряд
- (1.1)
сходится и его сумма равна S, то ряд
- (1.2)
где c — произвольное число, также сходится и его сумма равна cS. Если же ряд (1.1) расходится и с ≠ 0, то ряд (1.2) расходится.
Свойство 2. Если сходится ряд (1.1) и сходится ряд
- ,
а их суммы равны и соответственно, то сходятся и ряды
- ,
причём сумма каждого равна соответственно .
Необходимый признак сходимости ряда[править]
Ряд может сходиться лишь в том случае, когда член (общий член ряда) стремится к нулю:
Это необходимый признак сходимости ряда (но не достаточный!). Если же общий член ряда не стремится к нулю — это достаточный признак расходимости.
Обобщения числовых рядов[править]
Признаки сходимости[править]
www.wiki-wiki.ru
