Свойства бинарных отношений
Пусть задано на множестве, .
1. Рефлексивность: .
Отношение на множествеXназываетсярефлексивным, если для любого имеет место, то есть каждый элемент находится в отношениик самому себе.
Матрица рефлексивного отношения имеет единичную главную диагональ, а граф рефлексивного отношения – имеет петлю возле каждого своего элемента.
Например:
,
,
,
.
На множестве людей: “быть родственником”, ”обучаться в одной студенческой группе ”.
На множестве множеств: A B, A=B.
2. Антирефлексивность: .
Матрица антирефлексивного отношения имеет нулевую главную диагональ, а граф – не имеет ни одной петли.
Например:
,
,
.
На множестве людей: “быть родителем”, ”быть ребенком”.
На множестве множеств: A B, AB.
3. Нерефлексивность: .
4. Симметричность: .
Отношение на множествеXназываетсясимметричным, если для всех и из Х, из принадлежности (x,y) отношению следует, чтои принадлежит отношению.
Матрица симметричного отношения симметрична относительно главной диагонали, а граф – для каждой дуги (x,y) существует обратная дуга(y,x).
Например:
,
,
.
На множестве людей: “быть родственником”, ”обучаться в одной студенческой группе ”. Отношение «брат» является симметричным на множестве мужчин и не является симметричным на множествевсех людей.
На множестве множеств: ,.
5. Антисимметричность: .
Отношение на множествеXназываетсяантисимметричным, если для всех и из Х, из принадлежности (x,y) и(y,x) отношению следует, что.
Матрица антисимметричного отношения не имеет ни одной симметричной единицы относительно главной диагонали, а граф – длякаждой дуги
Свойства симметричности и антисимметричности не являются взаимоисключающими, примером может служить отношения равенства на множестве натуральных чисел.
Например:
,
,
,
,
.
На множестве людей: “быть выше”, ”быть равным”.
На множестве множеств: ,,.
6. Транзитивность: .
Отношение на множественазываетсятранзитивным, если для всех из множества ,из принадлежности и отношению следует, что также принадлежит .
Например:
,
,
,
,
,
.
На множестве людей: “быть выше”, ”обучаться в одной студенческой группе”.
На множестве множеств: , , .
Отношение r на множестве Xнеявляется транзитивным,если существует, хотя бы один пример того,что для некоторых х,y,z множества Х из принадлежности (x,y) и(y,z) отношению r не следует,что (x,z) такжепринадлежит r.
Например.
1) .
Отношение неявляется транзитивным,потому что из принадлежности этому отношению пар и, неследует,что и парапринадлежит отношению .
2) Пусть задано двухэлементное множество определим все бинарные отношения на этом множестве: . Для всех отношений, заданных на множестве , определить наличие или отсутствие основных свойств.
Введем следующие обозначения:
а) рефлексивность– Р;
б) антирефлексивность– АР;
в) симметричность– С;
г) антисимметричность– АС;
д) транзитивность– Т.
№ | Р | АР | С | АС | Т | |
1 | — | + | + | + | + | |
2 | — | — | + | + | + | |
| 3 | — | + | — | + | + | |
4 | — | + | — | + | + | |
5 | — | — | + | + | + | |
6 | — | — | — | + | + | |
7 | — | — | — | + | + | |
8 | + | — | + | + | + | |
9 | — | + | + | — | — | |
10 | — | — | — | + | + | |
11 | — | — | — | + | + | |
12 | — | — | + | — | — | |
13 | + | — | — | + | + | |
14 | + | — | — | + | + | |
15 | — | — | + | — | — | |
16 | + | — | + | — | + |
Отношение порядка– антисимметрично, транзитивно.
Отношение нестрого порядка() – рефлексивно, антисимметрично, транзитивно.
Например:
,
.
На множестве множеств: ,.
Отношение строгого порядка() – антирефлексивно, антисимметрично, транзитивно.
Например:
,
.
— “x предшествует y в смысле отношения строгого порядка”,
— “x предшествует y в смысле отношения нестрогого порядка”.
Два элементаи некоторого упорядоченного множества (множества, на котором существует отношение порядка) сравнимы между собой, если предшествует , и/или предшествует в смыслеотношения порядка.
Если в упорядоченном множестве существует пара элементов x и y, для которойни непредшествует , ни не предшествует , тогда говорят, что эти два элементанесравнимы между собой в смысле этого.
В отношениях полногопорядка все элементы сравнимы между собой, а в отношенияхчастичногопорядка не все элементы сравнимы между собой.
Например:
Отношения полного порядка:
,
.
Отношения частичного порядка:
,
,
на множестве множеств: , ,.
Отношение эквивалентности( ) – рефлексивно, симметрично, транзитивно.
Класс эквивалентностидля элемента:.
Например:
,
.
На множестве людей: “иметь одно имя”, ”обучаться в одной студенческой группе”.
На множестве множеств: .
Отношение эквивалентности разбивает –множество, на котором задано отношение нанепересекающиеся, которые называют классами эквивалентности.
Элементы, принадлежащие одному классу, находятсямежду собой в отношении эквивалентности, элементы из разных классов в отношении эквивалентности между собой не находятся.
Например:
Отношение задано на множествесписком пар.
Область определения: .
Область значений: .
Отношение – рефлексивно, симметрично, транзитивно, следовательно, это отношение эквивалентности.
Классы эквивалентности:
.
Например:
Отношение .
Это отношение называют отношением сравнения по модулюна множестве натуральных чисел.
означает, чтоиимеют одинаковый остаток при делении на.
Отрезок натурального ряда .
Отношение сравнения по модулю 3 на :
.
Область определения и область значений: .
Отношение – рефлексивно, симметрично, транзитивно.
Отношение – отношение эквивалентности.
Классы эквивалентности: .
Пусть – некоторое бинарное отношение.
Обратным отношением называется отношение, которое определяется следующим образом:
Обратное отношение получается путём перестановки значений в парах исходного отношения.
Пусть и– произвольные бинарные отношения такие, чтогде– некоторые множества.
Композиция отношений и – это таке бинарное отношение которое состоит из упорядоченных пар для которых существует такой элемент, что выполняются условия:
Например.
.
.
.
.
studfiles.net
3.2. Свойства бинарных отношений.
Рассмотрим специальные свойства бинарных отношений на множестве A.
Свойства бинарных отношений.
1. Отношение на AA называется рефлексивным, если (a,a) принадлежит для всех a из A.
2. Отношение называется антирефлексивным, если из (a,b) следует ab.
3. Отношение симметрично, если для a и b, принадлежащих A, из (a,b) следует, что (b,a).
4. Отношение называется антисимметричным, если для a и b из A, из принадлежности (a,b) и (b,a) отношению следует, что a=b.
5. Отношение транзитивно, если для a, b и c из A из того, что (a,b) и (b,c), следует, что (a,c).
Пример ..
Отношения «=» и «£» являются рефлексивными отношениями на множестве N, но отношение «<» таковым не является.
Отношение «=» является симметричным, а «<» и «£» — нет.
Отношение на N «являются взаимно простыми» является симметричным.
Отношения «<», «£» и «=» являются транзитивными, а отношение = {(a,b): a,b ÎN и b = a+1} – нет, так как 34 и 45, но не 35.

Как по матрице представления определить свойства бинарного отношения
1. Рефлексивность: на главной диагонали стоят все единицы, звездочками обозначены нули или единицы.
 .
.
2. Антирефлексивность: на главной диагонали все нули.
3. Симметричность: если .
Антисииметричность:
Mij=1, i ≠j, Mji=0
Матрицы бинарных отношений
Рассмотрим два конечных множества A ={a1,a2,…,am} и B={b1,b2,…,bn} и бинарное отношение .
Определим
матрицу 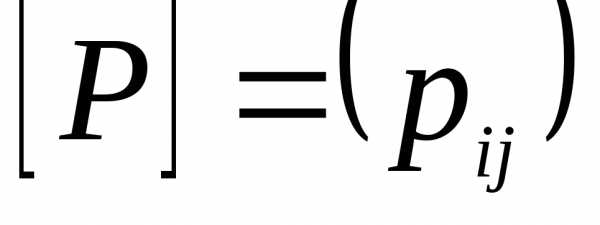 размераm×n
бинарного отношения Р по следующему
правилу:
размераm×n
бинарного отношения Р по следующему
правилу:
Полученная матрица содержит полную информацию о связях между элементами.Любая матрица, состоящая из 0 и 1, является матрицей некоторого бинарного отношения.
ПРИМЕР
1. Матрица бинарного отношения ,A={1,2,3},
заданного на рисунке
,A={1,2,3},
заданного на рисунке
имеет
вид 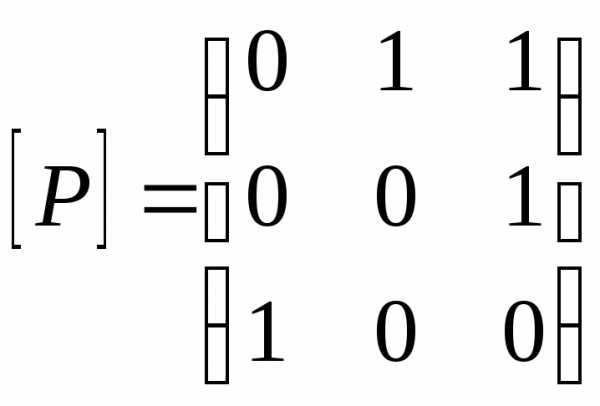
Основные свойства матриц бинарных отношений:
Если тои , где сложение осуществляется по правилам 0+0=0, 1+1=0+1=1+0=1, а умножение – обычным способом.
Итак,
Матрица
 получается перемножением соответствующих
элементов из
получается перемножением соответствующих
элементов из и
и :.
:.Если , то , где умножение матриц производится по обычному правилу умножения матриц, но произведение и сумма элементов – по определённым в свойстве 1 правилам.
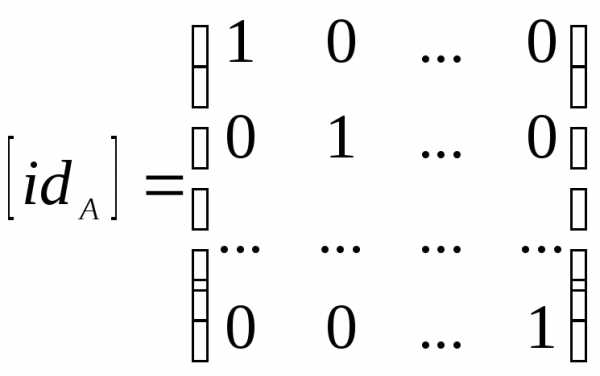
Матрица обратного отношения Р-1 равна транспонированной матрице отношения Р: .
Если , то
 .
.Матрица тождественного отношения idA единична:
ПРИМЕР
2. Пусть 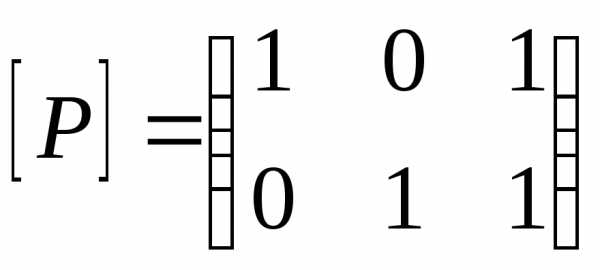
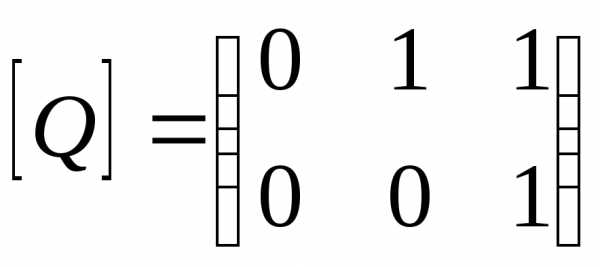 — матрицы отношений P и Q. Тогда
— матрицы отношений P и Q. Тогда
ПРИМЕР 3.
Если 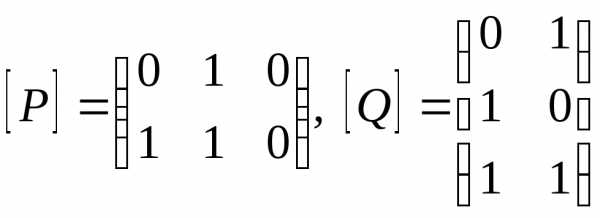 ,
то
,
то
Рассмотрим свойства отношений на языке матриц.
Пусть Р – бинарное отношение на множестве .
Отношение Р:
рефлексивно, если на главной диагонали матрицы отношения расположены только единицы;
симметрично, если матрица симметрична относительно главной диагонали;
антисимметрично, если в матрице
 все
элементы вне главной диагонали являются
нулевыми;
все
элементы вне главной диагонали являются
нулевыми;транзитивно, если выполнено соотношение .
ПРИМЕР
4. Проверим, какими свойствами обладает
отношение  ,
А={1,2,3}, изображённое на рисунке.
,
А={1,2,3}, изображённое на рисунке.
Составим
матрицу отношения Р: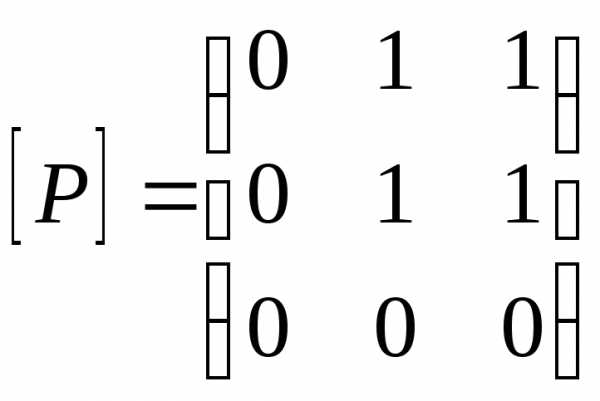
Так
как в матрице  на главной диагонали имеются нулевые
элементы, отношение Рне
рефлексивно.
на главной диагонали имеются нулевые
элементы, отношение Рне
рефлексивно.
Несимметричность
матрицы 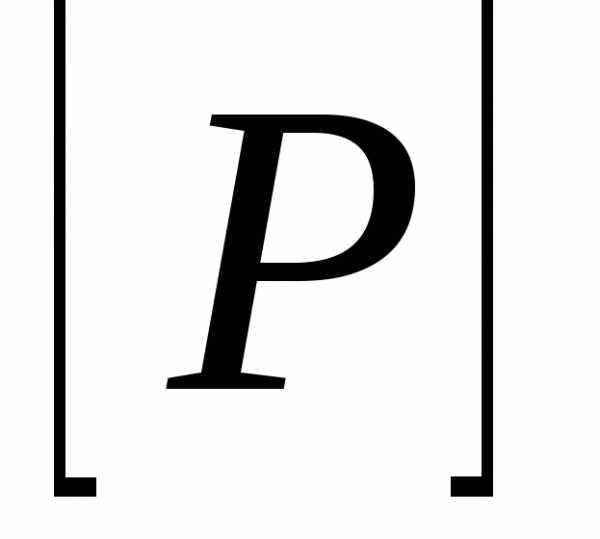 означает, что отношение Рне
симметрично.
означает, что отношение Рне
симметрично.
Для проверки антисимметричности вычислим матрицу .
Поскольку в полученной матрице все элементы, стоящие вне главной диагонали, нулевые, отношение Р антисимметрично.
Так как (проверьте!), то есть Р являетсятранзитивным отношением.
studfiles.net
3.2. Свойства бинарных отношений.
Рассмотрим специальные свойства бинарных отношений на множестве A.
Свойства бинарных отношений.
1. Отношение на AA называется рефлексивным, если (a,a) принадлежит для всех a из A.
2. Отношение называется антирефлексивным, если из (a,b) следует ab.
3. Отношение симметрично, если для a и b, принадлежащих A, из (a,b) следует, что (b,a).
4. Отношение называется антисимметричным, если для a и b из A, из принадлежности (a,b) и (b,a) отношению следует, что a=b.
5. Отношение транзитивно, если для a, b и c из A из того, что (a,b) и (b,c), следует, что (a,c).
Пример ..
Отношения «=» и «£» являются рефлексивными отношениями на множестве N, но отношение «<» таковым не является.
Отношение «=» является симметричным, а «<» и «£» — нет.
Отношение на N «являются взаимно простыми» является симметричным.
Отношения «<», «£» и «=» являются транзитивными, а отношение = {(a,b): a,b ÎN и b = a+1} – нет, так как 34 и 45, но не 35.

Как по матрице представления определить свойства бинарного отношения
1. Рефлексивность: на главной диагонали стоят все единицы, звездочками обозначены нули или единицы.
 .
.
2. Антирефлексивность: на главной диагонали все нули.
3. Симметричность: если .
Антисииметричность:
Mij=1, i ≠j, Mji=0
Матрицы бинарных отношений
Рассмотрим два конечных множества A ={a1,a2,…,am} и B={b1,b2,…,bn} и бинарное отношение .
Определим
матрицу 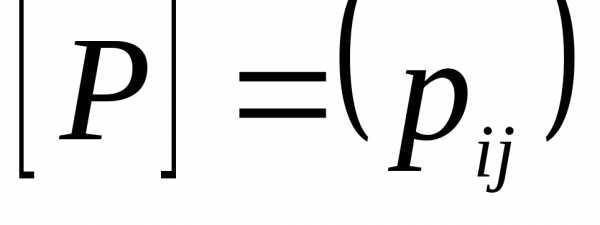 размераm×n
бинарного отношения Р по следующему
правилу:
размераm×n
бинарного отношения Р по следующему
правилу:
Полученная матрица содержит полную информацию о связях между элементами.Любая матрица, состоящая из 0 и 1, является матрицей некоторого бинарного отношения.
ПРИМЕР
1. Матрица бинарного отношения ,A={1,2,3},
заданного на рисунке
,A={1,2,3},
заданного на рисунке
имеет
вид 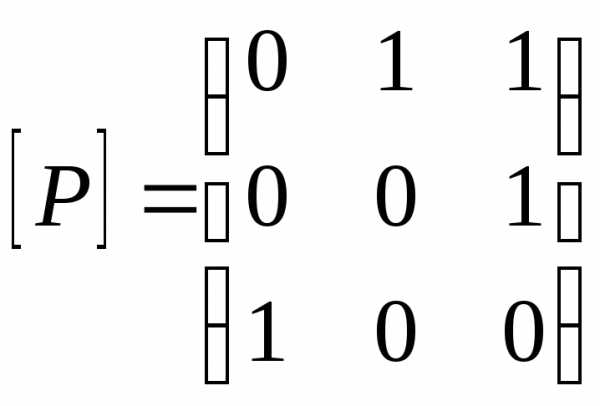
Основные свойства матриц бинарных отношений:
Если тои , где сложение осуществляется по правилам 0+0=0, 1+1=0+1=1+0=1, а умножение – обычным способом.
Итак,
Матрица
 получается перемножением соответствующих
элементов из
получается перемножением соответствующих
элементов из и
и :.
:.Если , то , где умножение матриц производится по обычному правилу умножения матриц, но произведение и сумма элементов – по определённым в свойстве 1 правилам.
Матрица обратного отношения Р-1 равна транспонированной матрице отношения Р: .
Если , то
 .
.Матрица тождественного отношения idA единична:
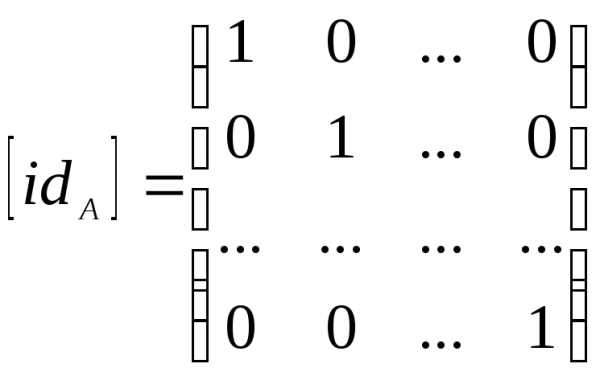
ПРИМЕР
2. Пусть 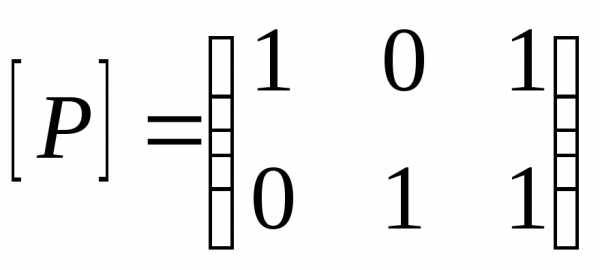
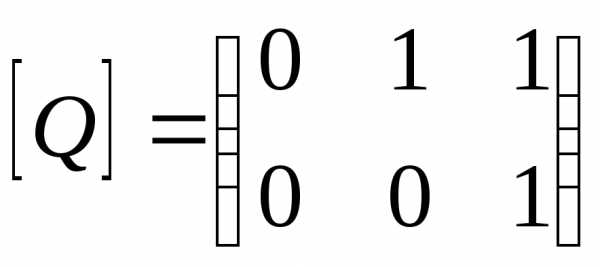 — матрицы отношений P и Q. Тогда
— матрицы отношений P и Q. Тогда
ПРИМЕР 3.
Если 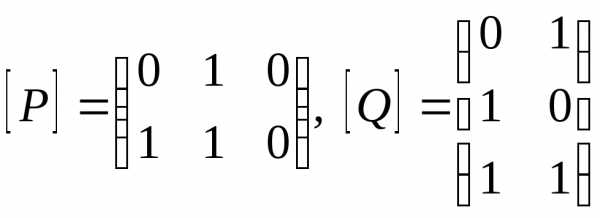 ,
то
,
то
Рассмотрим свойства отношений на языке матриц.
Пусть Р – бинарное отношение на множестве .
Отношение Р:
рефлексивно, если на главной диагонали матрицы отношения расположены только единицы;
симметрично, если матрица симметрична относительно главной диагонали;
антисимметрично, если в матрице
 все
элементы вне главной диагонали являются
нулевыми;
все
элементы вне главной диагонали являются
нулевыми;транзитивно, если выполнено соотношение .
ПРИМЕР
4. Проверим, какими свойствами обладает
отношение  ,
А={1,2,3}, изображённое на рисунке.
,
А={1,2,3}, изображённое на рисунке.
Составим
матрицу отношения Р: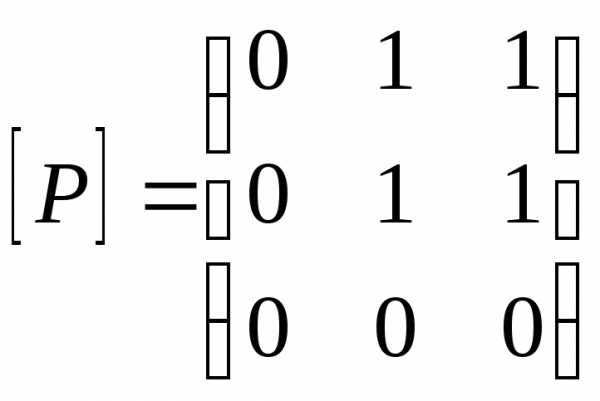
Так
как в матрице  на главной диагонали имеются нулевые
элементы, отношение Рне
рефлексивно.
на главной диагонали имеются нулевые
элементы, отношение Рне
рефлексивно.
Несимметричность
матрицы  означает, что отношение Рне
симметрично.
означает, что отношение Рне
симметрично.
Для проверки антисимметричности вычислим матрицу .
Поскольку в полученной матрице все элементы, стоящие вне главной диагонали, нулевые, отношение Р антисимметрично.
Так как (проверьте!), то есть Р являетсятранзитивным отношением.
studfiles.net
Свойства бинарных отношений
Введение
1. Рефлексивность:
2. Слабая рефлексивность:
3. Сильная рефлексивность:
4. Антирефлексивность:
5. Слабая антирефлексивность:
6. Сильная антирефлексивность:
7. Симметричность:
8. Антисимметричность:
9. Асимметричность:
10. Сильная линейность:
11. Слабая линейность:
12. Транзитивность:
Рефлексивность, свойство бинарных (двуместных, двучленных) отношений, выражающее выполнимость их для пар объектов с совпадающими членами (так сказать, между объектом и его «зеркальным отражением»): отношение R называется рефлексивным, если для любого объекта х из области его определения выполняется xRx. Типичные и наиболее важные примеры рефлексивных отношений: отношения типа равенства (тождества, эквивалентности, подобия и т.п.: любой предмет равен самому себе) и отношения нестрогого порядка (любой предмет не меньше и не больше самого себя). Интуитивные представления о «равенстве» (эквивалентности, подобии и т.п.), очевидным образом наделяющие его свойствами симметричности и транзитивности, «вынуждают» и свойство Р., поскольку последнее свойство следует из первых двух. Поэтому многие употребительные в математике отношения, по определению Р. не обладающие, оказывается естественным доопределить таким образом, чтобы они становились рефлексивными, например, считать, что каждая прямая или плоскость параллельна самой себе, и т.п.
Глава 1. Элементы теории множеств
1.1 Множества
Наиболее простая структура данных, используемая в математике, имеет место в случае, когда между отдельными изолированными данными отсутствуют какие-либо взаимосвязи. Совокупность таких данных представляет собой множество . Понятие множества является неопределяемым понятием. Множество не обладает внутренней структурой. Множество можно представить себе как совокупность элементов, обладающих некоторым общим свойством. Для того чтобы некоторую совокупность элементов можно было назвать множеством, необходимо, чтобы выполнялись следующие условия:
Должно существовать правило, позволяющее определить, принадлежит ли указанный элемент данной совокупности.
Должно существовать правило, позволяющее отличать элементы друг от друга. (Это, в частности, означает, что множество не может содержать двух одинаковых элементов).
Множества обычно обозначаются заглавными латинскими буквами. Если элемент
принадлежит множеству , то это обозначается:Если каждый элемент множества
является также и элементом множества , то говорят, что множество является подмножеством множества :Подмножество
множества называется собственным подмножеством , еслиИспользуя понятие множества можно построить более сложные и содержательные объекты.
1.2 Операции над множествами
Основными операциями над множествами являются объединение , пересечение и разность .
Определение 1 . Объединением двух множеств называется новое множество
Определение 2 . Пересечением двух множеств называется новое множество
Определение 3 . Разностью двух множеств называется новое множество
Если класс объектов, на которых определяются различные множества обозначить
(Универсум ), то дополнением множества называют разность1.3 Декартово произведение множеств
Одним из способов конструирования новых объектов из уже имеющихся множеств является декартово произведение множеств .
Пусть
и — множества. Выражение вида , где и , называется упорядоченной парой . Равенство вида означает, что и . В общем случае, можно рассматривать упорядоченную n-ку из элементов . Упорядоченные n-ки иначе называют наборы или кортежи .Определение 4 . Декартовым (прямым) произведением множеств
называется множество упорядоченных n-ок (наборов, кортежей) видаОпределение 5 . Степенью декартового произведения
называется число множеств n, входящих в это декартово произведение.Замечание. Если все множества
одинаковы, то используют обозначение .1.4 Отношение
Определение 6 . Подмножество
декартового произведения множеств называется отношением степени n (n-арным отношением ).Определение 7 . Мощность множества кортежей, входящих в отношение
, называют мощностью отношения .Замечание. Понятие отношения является очень важным не только с математической точки зрения. Понятие отношения фактически лежит в основе всей реляционной теории баз данных. Как будет показано ниже, отношения являются математическим аналогом таблиц . Сам термин «реляционное представление данных», впервые введенный Коддом [43], происходит от термина relation , понимаемом именно в смысле этого определения.
Т. к. любое множе
mirznanii.com
7 Лекция № 6. Свойства бинарных отношений
12
Продолжительность:2 часа (90 мин.)
7.1 Ключевые вопросы
7 Лекция № 6. Свойства бинарных отношений 1
7.1 Ключевые вопросы 1
7.2 Текст лекции 1
7.2.1 Свойства бинарных отношений 1
7.2.2 Отношения эквивалентности 5
7.2.3 Отношения порядка 8
7.2.4 Вопросы для контроля 12
7.2 Текст лекции
7.2.1 Свойства бинарных отношений
Отношения делятся на различные виды в зависимости от того, какими свойствами они обладают.
Пусть R – отношение на множествеМ,. Тогда:
– Отношение R рефлексивно, если ,
т.е. имеет местоaRа для любого
,
т.е. имеет местоaRа для любого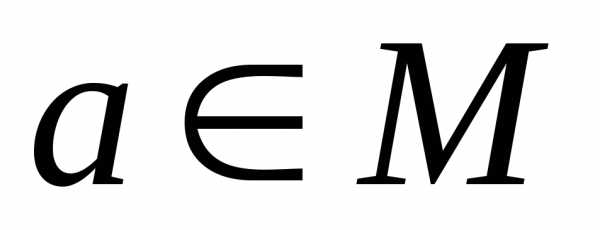 (например, отношение «жить в одном
городе» – рефлексивно).
(например, отношение «жить в одном
городе» – рефлексивно).
Рефлексивные отношения представляются матрицей, у которой на главной диагонали всегда стоят единицы. У графа, представляющего рефлексивное отношение, все вершины имеют петли.
– Отношение R антирефлексивно, если,
т.е. если ни для какого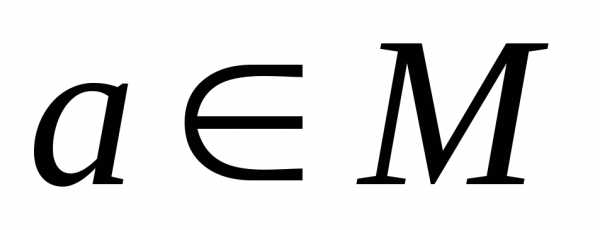 не выполняетсяaRа (например, отношение «быть сыном»
– антирефлексивно).
не выполняетсяaRа (например, отношение «быть сыном»
– антирефлексивно).
В матрице такого отношения на главной диагонали стоят нули, а в графе ни одна вершина не имеет петель.
– Отношение R симметрично, если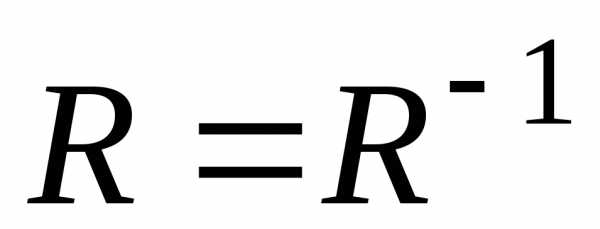 ,
т.е. если выполненоaRb,
то выполнено иbRa (например, отношение «учиться в
одной группе» – симметрично).
,
т.е. если выполненоaRb,
то выполнено иbRa (например, отношение «учиться в
одной группе» – симметрично).
В матрице этого отношения элементы,
симметрично расположенные относительно
главной диагонали, равны друг другу,
т.е. 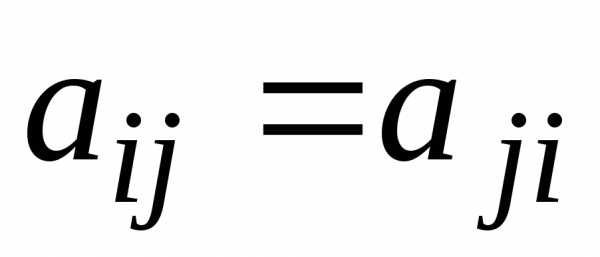 .
В графе симметричного отношения для
каждой дуги, идущей из вершиныiк вершинеj, имеется
обратная дуга. Поэтому в таком графе
можно не обозначать направление дуг и
представлять симметричное отношениенеориентированным графом.
.
В графе симметричного отношения для
каждой дуги, идущей из вершиныiк вершинеj, имеется
обратная дуга. Поэтому в таком графе
можно не обозначать направление дуг и
представлять симметричное отношениенеориентированным графом.
– Отношение R асимметрично, если. Это означает, что из двух соотношенийaRb иbRадля различных элементов по крайней мере одно не выполнено (например, отношение «быть сыном» – асимметрично).
Для элементов матрицы такого отношения выполняется , а в графе нет дуг разных направлений, соединяющих две вершины.
Если отношение асимметрично, то оно и антирефлексивно, а это значит, что диагональные элементы соответствующей матрицы равны 0 и в графе нет петель.
– Отношение R антисимметрично, если, а это означает, что выполнениеaRb иbRа возможно только приа = b (пример: отношение равенства, параллельности).
Для элементов матрицы такого отношения справедливо
В графе этого отношения могут быть петли, но встречных дуг нет ни у одной дуги.
– Отношение R транзитивно, если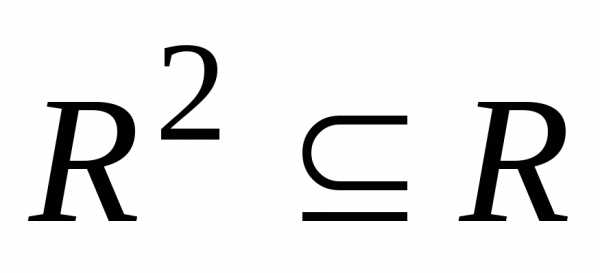 ,
а это значит, выполнениеaRb и bRc влечетaRc (например,
отношения «быть больше», «быть
моложе» – транзитивны).
,
а это значит, выполнениеaRb и bRc влечетaRc (например,
отношения «быть больше», «быть
моложе» – транзитивны).
В соответствии с определением квадрат матрицы такого отношения не должен содержать “лишних” 1, т.е. таких, которых не было в матрице отношения.
В графе этого отношения, если любые две вершины соединены путем длиной 2, то они должны быть также соединены дугой, направленной из начала пути к его концу.
Если отношение Rтранзитивно, то его транзитивное замыкание равно ему самому:R○ = R. Поэтому можно утверждать, если R = R○, то отношениеRтранзитивно.
– отношениеR антитранзитивно,
если при любыхn 2.
2.
Это означает, что наличие непосредственной связи между элементами aиbисключает обходные пути.
Если R – строгий порядок (о порядках см. п. 7.2.3), то редукция этого отношенияRr антитранзитивна (пример см. на рис. 8.15).
Любое антитранзитивное отношение асимметрично и, следовательно, антирефлексивно. В графе такого отношения нет контуров, в том числе нет петель, и нет параллельных путей.
Для отношения R(рис. 7.1), граф которого контур, получаем
,,,
и можно вроде бы считать его антитранзитивным, но , поэтому это отношение не антитранзитивно.
В общем случае для отношений Rв виде контура
Rn+1 = R, гдеn– число вершин графа.
Рисунок 7.1 – Граф не антитранзитивного отношения
Определенный интерес представляет вопрос о зависимости свойства результата операции от свойств отношений, участвующих в операции.
Ответ на этот вопрос дан в таблице 7.1. В двухместных операциях оба операнда (если не оговорено особо) должны обладать соответствующим свойством.
Таблица 7.1
Свойство | Операции | Условие |
Рефлексивность | ||
Антирефлексивность |
| |
Симметричность |
|
|
Асимметричность |
| При любом R2 |
Антисимметричность |
| |
Транзитивность |
Пример 1. Какими признаками характеризуется матрица отношенияR, если оно обладает одним из свойств: рефлексивностью, антирефлексивностью, симметричностью, асимметричностью, транзитивностью.
Пусть Rзадано наМ, .
Отношение R рефлексивно, если для любого
 имеет местоaRa, т.е. оно выполняется для всех пар (а, а),
имеет местоaRa, т.е. оно выполняется для всех пар (а, а), . В матрице этим парам соответствуют
элементысii. Такие элементы составляют главную
диагональ матрицы. Следовательно,
главная диагональ матрицы рефлексивного
отношения содержит только единицы.
. В матрице этим парам соответствуют
элементысii. Такие элементы составляют главную
диагональ матрицы. Следовательно,
главная диагональ матрицы рефлексивного
отношения содержит только единицы.Отношение R антирефлексивно, если ни для какого
 не выполняетсяaRа. Из этого следует, что главная диагональ
матрицы антирефлексивного отношения
должна содержать только нули.
не выполняетсяaRа. Из этого следует, что главная диагональ
матрицы антирефлексивного отношения
должна содержать только нули.Отношение R симметрично, если для парыизаRb следуетbRa, т.е. для любой пары отношениеR выполняется в обе стороны либо не выполняется вообще. Таким образом, если в матрице единица стоит на пересеченииi–ой строки иj–ого столбца, т.е.cij = 1, то она должна стоять и на пересеченииj–ой строки иi–ого столбца, т.е.сji= 1, и наоборот, еслиcji = 1, тоcij = 1. Таким образом, в матрице симметричного отношенияcji = cij, т.е. матрица симметрична относительно главной диагонали.
Отношение R асимметрично, если изaRb и bRа выполняется только одно. Это означает, что в соответствующей матрице ни для каких не выполняетсяcji = cij = 1. Таким образом, в матрице асимметричного отношения отсутствует симметрия относительно главной диагонали.
Отношение R транзитивно, если для любыха, b, с изaRb иbRс следуетaRc. В матрице такого отношения должно выполняться следующее условие.
если вi–ой строке стоит единица, например вj–ой координате (столбце) строки, т.е.сij = 1, то всем единицам вj–й строке (пусть этим единицам соответствуютk–е координаты такие, чтосjk= 1) должны соответствовать единицы вi–й строке в тех жеk–х координатах, т.е.сikj = 1 (и, может быть, еще и в других координатах).
Это условие иллюстрируется на рис. 7.2, где кружком выделена единица cij = 1, для которой производится проверка условия, а стрелками показана последовательность проверки данного условия.
Рисунок 7.2 – Проверка транзитивности отношенияR
В матрице транзитивного отношения это условие должно выполняться для любых таких, чтосij, = 1. И наоборот, если в матрицеR имеется хотя бы одна единицасij = 1, для которой данное условие не выполняется, тоR не транзитивно.
Пример 2.Пусть бинарное отношениеRнаМзадано в виде графа, состоящего из вершин и дуг так, что вершинам взаимно однозначно соответствуют элементы множестваМ, а дугам, соединяющим паруаиbв направлении отакb, — наличие отношенияaRb. Определить особенности графа в зависимости от характера свойств отношенияR.
Отношение рефлексивно, еслиaRa для любых
 . Соответствующий граф рефлексивного
отношения должен содержать петли у
всех вершин (т.е. дуги, начинающиеся и
заканчивающиеся в одной вершине рис.
7.3,а).
. Соответствующий граф рефлексивного
отношения должен содержать петли у
всех вершин (т.е. дуги, начинающиеся и
заканчивающиеся в одной вершине рис.
7.3,а).Отношение R антирефлексивно, если ни для каких
 не выполняетсяaRa. Граф антирефлексивного отношения
не должен содержать ни одной петли
(рис. 7.3,б,в,г).
не выполняетсяaRa. Граф антирефлексивного отношения
не должен содержать ни одной петли
(рис. 7.3,б,в,г).Отношение R симметрично, если изaRb следуетbRа. В графе симметричного отношения для каждой дуги, соединяющей две вершины, существует также дуга, соединяющая эти вершины в обратном направлении (рис. 7.3,в).
Отношение R асимметрично, если из aRb и bRa выполняется только одно. В графе асимметричного отношения не существует двух различных вершин, связанных парой (разнонаправленных) дуг, и нет петель (рис. 7.3,б,г).
Отношение R транзитивно, если изaRb и bRc следуетaRc. В графе транзитивного отношения для любых двух дуг таких, что одна направлена ота кb, а другая – отb кс, существует дуга, соединяющаяаисв направлении отакс (рис. 7.3,г).
Рисунок 7.3 – Графы отношений, обладающих свойствами
а) рефлексивности, б) антирефлексивности и асимметричности,
в) антирефлексивности и симметричности,
г) асимметричности и транзитивности
studfiles.net
Систематизация свойств. Каждое бинарное (двухместное) отношение характеризуется свойствами рефлексивности, симметричности и транзитивности. Полное или частичное отсутствие этих свойств в отношении отражается в их наименовании приставками соответственно «анти» и «не». Определённым сочетаниям этих базовых свойств даны свои специальные наименования; например, антисимметричное и антирефлексивное отношение называется асимметричным.
Свойство рефлексивности рассматривается для одного элемента множества. Отношение называется рефлексивным, если для любого предмета из области его определения имеет место это отношение предмета к самому себе. Отношение ровесник, определенное на области пар людей, рефлексивно, потому что любой человек ровесник самого себя. Если отношение имеет место не для любой такой пары, то оно называется нерефлексивным. Нерефлексивно отношение любит, определенное на области пар людей, так как не все люди любят себя. Если отношение не имеет места ни для одной такой пары, то отношение называется антирефлексивным. Отношение больше, определённое на области пар материальных предметов, антирефлексивно, поскольку ни один предмет не больше самого себя. Свойство симметричности рассматривается для двух разных элементов множества. Отношение называется симметричным, когда для любых пар предметов из области его определения верно, что, когда это отношение x и y , то оно имеет место и в паре (y,x) . Отношение ровесник симметрично, так как для любых двух людей верно, что, если первый ровесник второго, то и второй ровесник первого. Отношение называется несимметричным, если оно верно не для любых двух предметов из области определения. Несимметрично отношение любит, поскольку не для любых двух людей верно, что если первый любит второго, то второй любит первого. Отношение называется антисимметричным, если в области определения отношения не существует пар указанного вида, для которых это верно. Отношение больше антисимметрично, потому что ни для каких предметов не может быть так, что первый предмет больше второго, а второй больше первого. Свойство транзитивности рассматривается для трёх разных элементов множества. Отношение называется транзитивным, если оно обязательно имеет место для пары (x,z) при условии его наличия в парах (x,y) и (y,z) . Отношение ровесник транзитивно, так как для любых трёх людей, если один человек ровесник другого, а тот ровесник третьего, первый непременно является ровесником третьего. Отношение называется нетранзитивным, если это верно не для любых предметов из области определения отношения. Нетранзитивно отношение любит, потому что неверно, что оно имеет место в паре (x,z) всегда, когда оно наличествует в парах (x,y) и (y,z), т. е. не обязательно, чтобы первый человек любил третьего, когда первый любит второго, а второй любит третьего. Отношение называется антитранзитивным, если в области определения отношения не существует таких предметов, для которых это было бы верно. Антитранзитивно отношение отец, потому что не найдется таких трёх пар указанного вида, чтобы это отношение имело место во всех трёх. Никогда не может быть так, что первый человек — отец второго, второй — отец третьего, и при этом первый — отец третьего.
Определения.
|
www.reshim.su
1.2. Свойства бинарных отношений. Специальные бинарные отношения
Определение 12. Бинарное отношениена множестве Х называетсярефлексивным, если для любого элемента хХ выполняется хх.
Определение 13. Бинарное отношениена множествеX, заданное матрицей смежности, в которой все элементы главной диагонали − единицы, а на остальных местах стоят нули, называетсядиагональным.
Определение 14.Бинарное отношениена множестве Х называетсясимметричным, если для любых х, уХ из ху следует ух.
Матрица смежности симметричного
отношения симметрична относительно
главной диагонали: 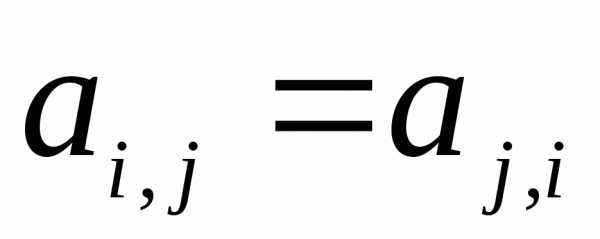 .
.
Определение 15. Отношение называетсяантирефлексивным, если
ни для одного элемента аXне выполняется а
называетсяантирефлексивным, если
ни для одного элемента аXне выполняется а а.
а.
Главная диагональ его матрицы смежности содержит только нули.
Определение 16. Бинарное отношениена множестве Х называетсятранзитивным, если для любых х, у,zХ из ху и уzследует хz.
Пример 6.
Отношения: “равенство”, , “жить в одном городе” являются транзитивными, а отношение “быть сыном” не транзитивно.
Определение 17.Бинарное отношение, которое одновременно рефлексивно, симметрично и транзитивно отношение на множестве Х называется отношениемэквивалентностина множестве Х.
Пример 7.
1. Отношение равенства на множестве целых чисел есть отношение эквивалентности.
2. Отношение подобия на множестве треугольников есть отношение эквивалентности.
3. Отношение «строго меньше» на множестве действительных чисел не рефлексивно, не симметрично и транзитивно на этом множестве.
4. Отношение перпендикулярности прямых не рефлексивно, симметрично, не транзитивно.
Пусть - отношение эквивалентности на множестве Х.
Определение 18.Классом эквивалентности, порожденным элементом х, называется подмножество множества Х, состоящее из тех элементовyY, для которых ху. Класс эквивалентности, порожденный элементом х, обозначается через [x]:
Определение 19. Бинарное отношениена множестве Х называетсяантисимметричным, если для любых х, уХ из ху и ух следует, что х=у.
 Определение
20. Бинарное отношение, которое
одновременно рефлексивно, антисимметрично
и транзитивно называетсяотношением
частичного порядка.
Определение
20. Бинарное отношение, которое
одновременно рефлексивно, антисимметрично
и транзитивно называетсяотношением
частичного порядка.
Пример 7.
1. Отношение «х у» на множестве действительных чисел − отношение частичного порядка.
2. Схема организации подчинения в учреждении −это отношение частичного порядка на множестве должностей.
Определение 21. Множество с заданным на нем отношением частичного порядка называетсячастично упорядоченным. Если при этом любые два элемента находятся в отношении, то такое множество называетсялинейно упорядоченным.
Элементы, находящиеся в отношении частичного порядка называются сравнимыми.
Определение 22. Бинарное отношение называется отношениемстрогого порядка, если оно одновременно антирефлексивно, антисимметрично и транзитивно.
Пример 8.
Приведем некоторые примеры.
1. Множество действительных чисел линейно
упорядочено относительно отношений 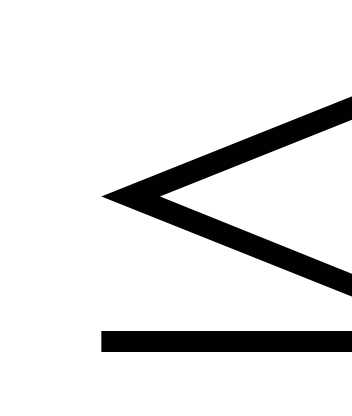 ,
,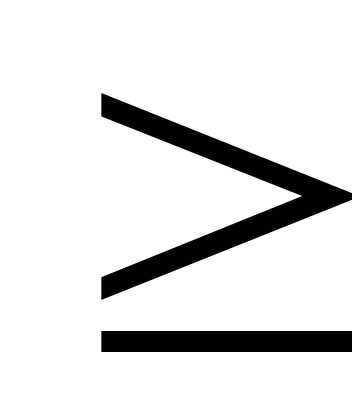 .
.
2. Отношения ина множестве действительных чисел являются отношениями строгого порядка.
3. Отношение включения на системе подмножеств множества М задает частичный порядок, причем все подмножества множества М линейно упорядочено относительно отношения.
4. Отношение включения на системе подмножеств множества М задает строгий порядок.
5. Множества {1, 2}, {1, 2, 3} сравнимы относительно отношения −{1, 2}{1, 2, 3}, a множества {1, 2} и {1, 3, 4} не сравнимы.
6. Отношения подчиненности на предприятии задает строгий частичный порядок. В нем несравнимыми будут сотрудники разных отделов.
7. Пусть порядок букв конечного алфавита
А зафиксирован, т. е. всегда один и тот
же. Тогда этот порядок определяет
линейное упорядочение букв, которое
назовем отношением предшествования и
обозначим через .
Если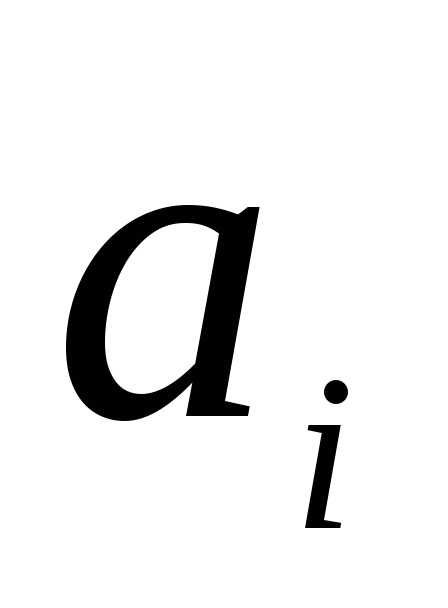 предшествует
предшествует в алфавите, то это записывается следующим
образом:
в алфавите, то это записывается следующим
образом: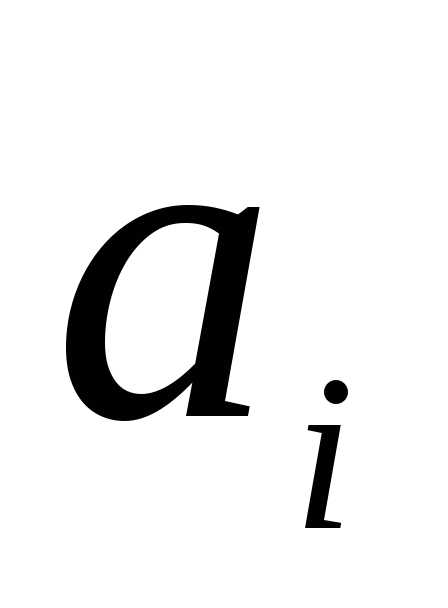
 .
На основе отношения предшествования
букв строится отношение предшествования
слов. Это отношение задает линейное
упорядочение множества всех конечных
слов в алфавите А, которое называетсялексикографическимупорядочением
слов. Примером такого упорядочения
является расположение слов в словаре.
.
На основе отношения предшествования
букв строится отношение предшествования
слов. Это отношение задает линейное
упорядочение множества всех конечных
слов в алфавите А, которое называетсялексикографическимупорядочением
слов. Примером такого упорядочения
является расположение слов в словаре.
8. Если рассматривать числа в позиционных системах счисления (например десятичной), как слова в алфавите цифр, то их лексикографическое упорядочение совпадает с обычным упорядочением чисел, при этом предполагается, что все сравниваемые числа имеют одинаковое число разрядов (такое дополнение разрядами можно провести искусственно):
20 < 1073;
0020  1073.
1073.
studfiles.net

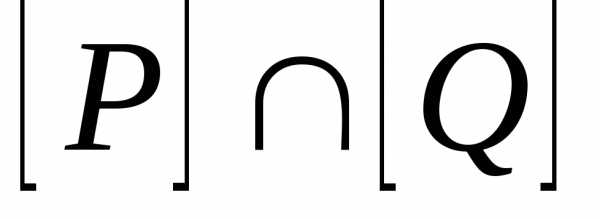 получается перемножением соответствующих
элементов из
получается перемножением соответствующих
элементов из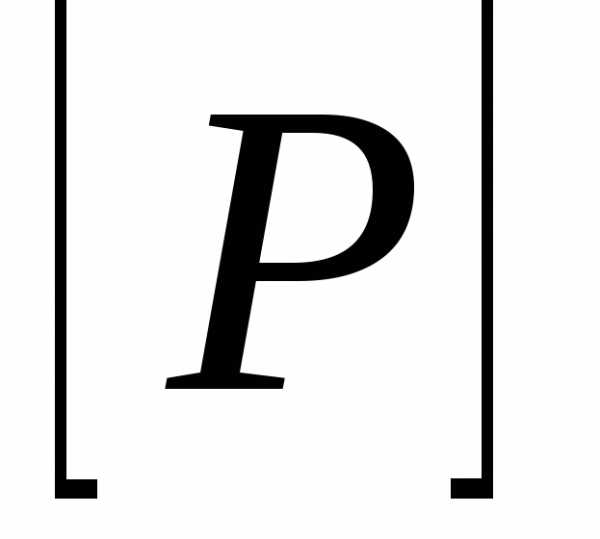 и
и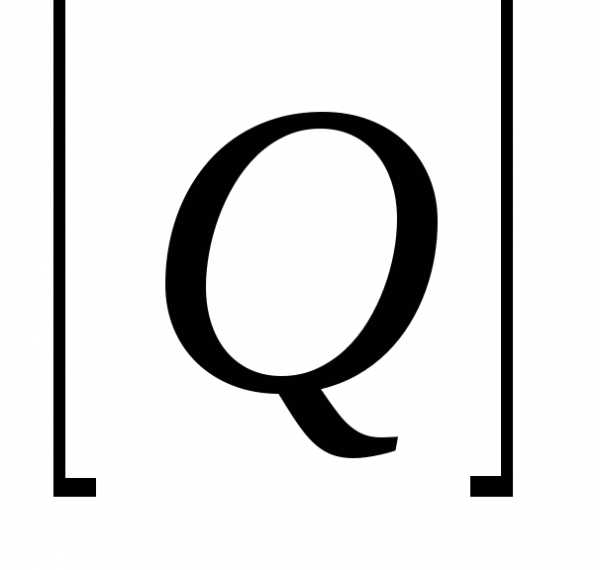 :.
:.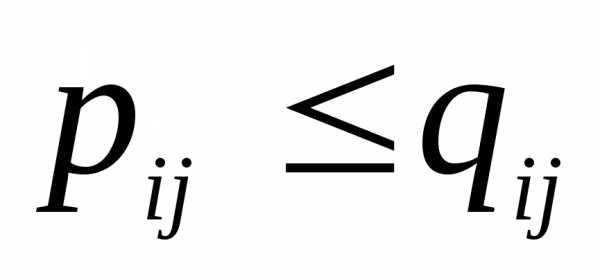 .
. все
элементы вне главной диагонали являются
нулевыми;
все
элементы вне главной диагонали являются
нулевыми;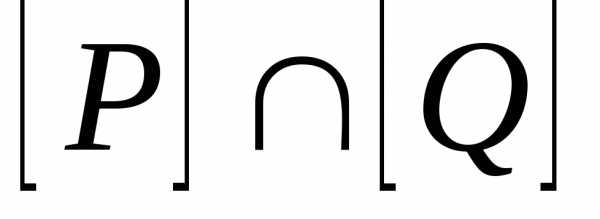 получается перемножением соответствующих
элементов из
получается перемножением соответствующих
элементов из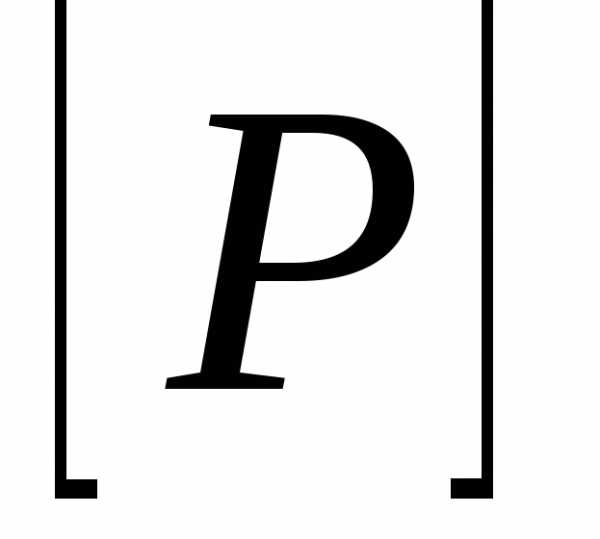 и
и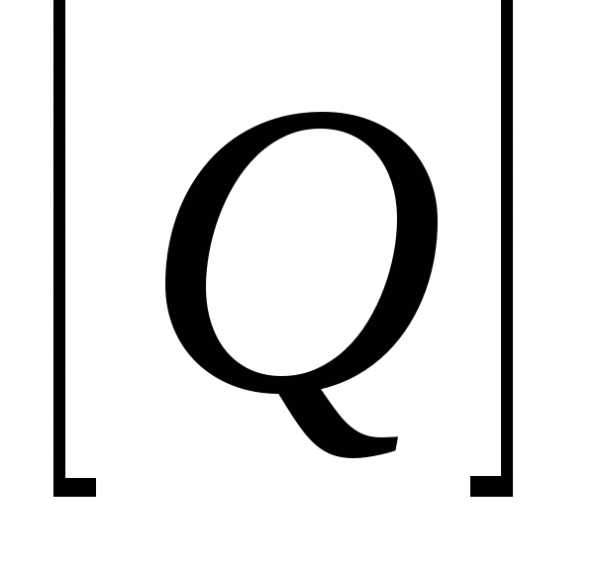 :.
:.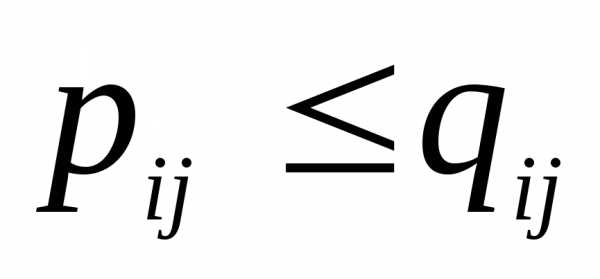 .
. все
элементы вне главной диагонали являются
нулевыми;
все
элементы вне главной диагонали являются
нулевыми;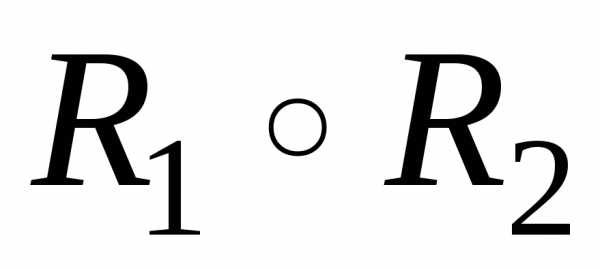
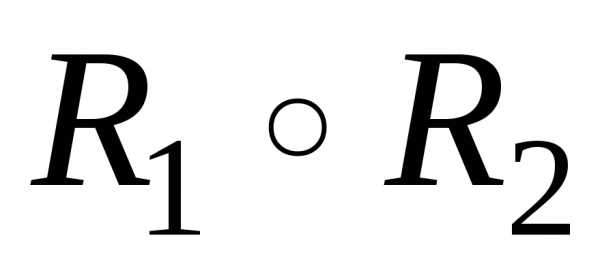
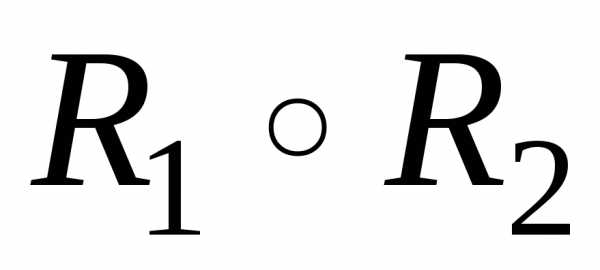 =
=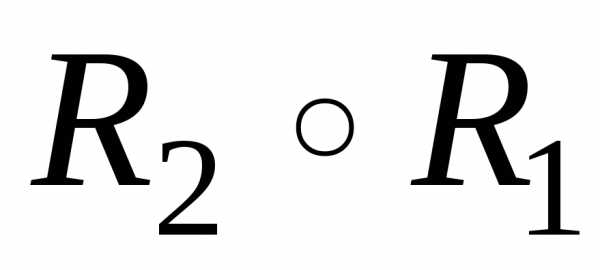
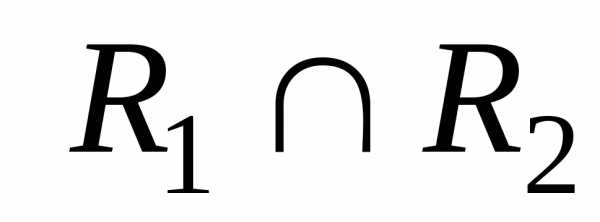
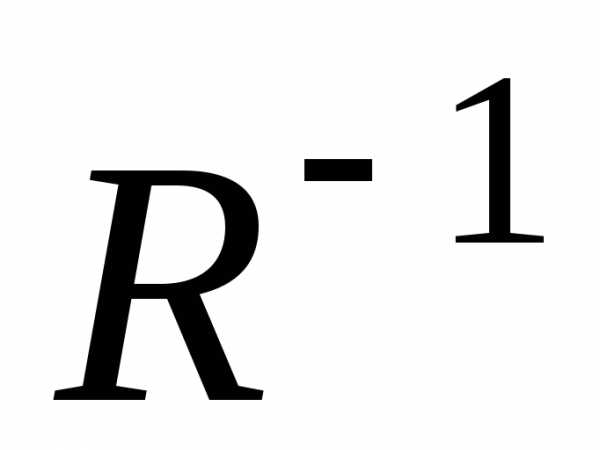
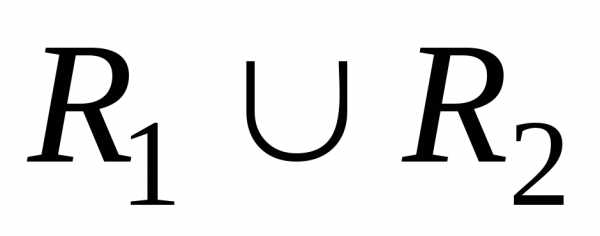
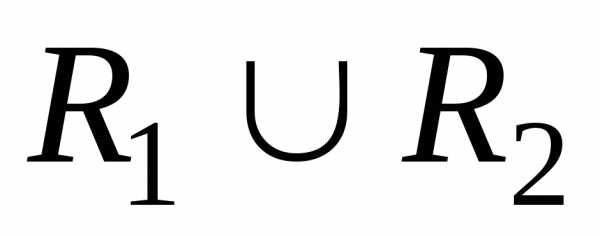
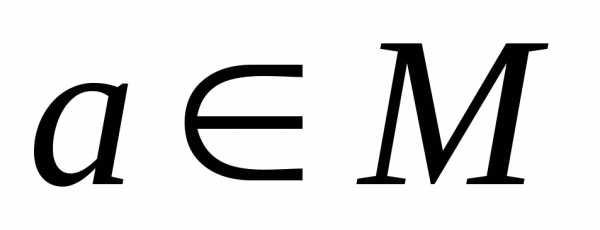 имеет местоaRa, т.е. оно выполняется для всех пар (а, а),
имеет местоaRa, т.е. оно выполняется для всех пар (а, а),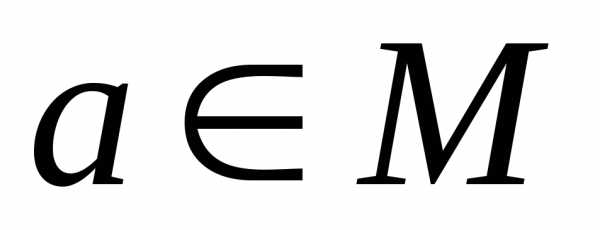 . В матрице этим парам соответствуют
элементысii. Такие элементы составляют главную
диагональ матрицы. Следовательно,
главная диагональ матрицы рефлексивного
отношения содержит только единицы.
. В матрице этим парам соответствуют
элементысii. Такие элементы составляют главную
диагональ матрицы. Следовательно,
главная диагональ матрицы рефлексивного
отношения содержит только единицы.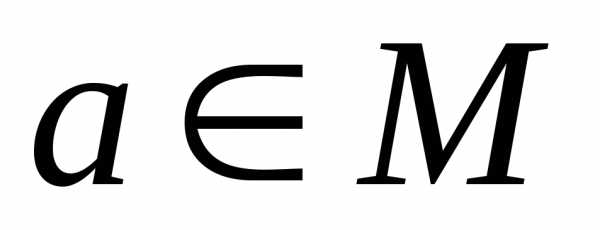 не выполняетсяaRа. Из этого следует, что главная диагональ
матрицы антирефлексивного отношения
должна содержать только нули.
не выполняетсяaRа. Из этого следует, что главная диагональ
матрицы антирефлексивного отношения
должна содержать только нули.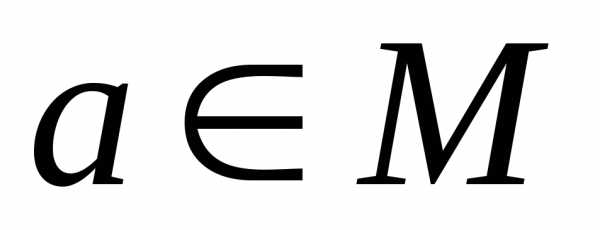 . Соответствующий граф рефлексивного
отношения должен содержать петли у
всех вершин (т.е. дуги, начинающиеся и
заканчивающиеся в одной вершине рис.
7.3,а).
. Соответствующий граф рефлексивного
отношения должен содержать петли у
всех вершин (т.е. дуги, начинающиеся и
заканчивающиеся в одной вершине рис.
7.3,а).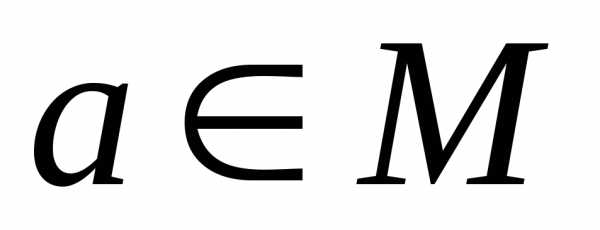 не выполняетсяaRa. Граф антирефлексивного отношения
не должен содержать ни одной петли
(рис. 7.3,б,в,г).
не выполняетсяaRa. Граф антирефлексивного отношения
не должен содержать ни одной петли
(рис. 7.3,б,в,г).