Схема горнера математика – Схема Горнера. Примеры с пояснениями.

Схема Горнера. Примеры с пояснениями.

Схема Горнера – способ деления многочлена

$$P_n(x)=\sum\limits_{i=0}^{n}a_{i}x^{n-i}=a_{0}x^{n}+a_{1}x^{n-1}+a_{2}x^{n-2}+\ldots+a_{n-1}x+a_n$$

на бином $x-a$. Работать придётся с таблицей, первая строка которой содержит коэффициенты заданного многочлена. Первым элементом второй строки будет число $a$, взятое из бинома $x-a$:

После деления многочлена n-ой степени на бином $x-a$, получим многочлен, степень которого на единицу меньше исходного, т.е. равна $n-1$. Непосредственное применение схемы Горнера проще всего показать на примерах.

Пример №1

Разделить $5x^4+5x^3+x^2-11$ на $x-1$, используя схему Горнера.

Решение

Составим таблицу из двух строк: в первой строке запишем коэффициенты многочлена $5x^4+5x^3+x^2-11$, расположенные по убыванию степеней переменной $x$. Заметьте, что данный многочлен не содержит $x$ в первой степени, т.е. коэффициент перед $x$ в первой степени равен 0. Так как мы делим на $x-1$, то во второй строке запишем единицу:

Начнем заполнять пустые ячейки во второй строке. Во вторую ячейку второй строки запишем число $5$, просто перенеся его из соответствующей ячейки первой строки:

Следующую ячейку заполним по такому принципу: $1\cdot 5+5=10$:

Аналогично заполним и четвертую ячейку второй строки: $1\cdot 10+1=11$:

Для пятой ячейки получим: $1\cdot 11+0=11$:

И, наконец, для последней, шестой ячейки, имеем: $1\cdot 11+(-11)=0$:

Задача решена, осталось только записать ответ:

Как видите, числа, расположенные во второй строке (между единицей и нулём), есть коэффициенты многочлена, полученного после деления $5x^4+5x^3+x^2-11$ на $x-1$. Естественно, что так как степень исходного многочлена $5x^4+5x^3+x^2-11$ равнялась четырём, то степень полученного многочлена $5x^3+10x^2+11x+11$ на единицу меньше, т.е. равна трём. Последнее число во второй строке (ноль) означает остаток от деления многочлена $5x^4+5x^3+x^2-11$ на $x-1$. В нашем случае остаток равен нулю, т.е. многочлены делятся нацело. Этот результат ещё можно охарактеризовать так: значение многочлена $5x^4+5x^3+x^2-11$ при $x=1$ равно нулю.

Можно сформулировать вывод и в такой форме: так как значение многочлена $5x^4+5x^3+x^2-11$ при $x=1$ равно нулю, то единица является корнем многочлена $5x^4+5x^3+x^2-11$.

Пример №2

Разделить многочлен $x^4+3x^3+4x^2-5x-47$ на $x+3$ по схеме Горнера.

Решение

Сразу оговорим, что выражение $x+3$ нужно представить в форме $x-(-3)$. В схеме Горнера будет учавствовать именно $-3$. Так как степень исходного многочлена $x^4+3x^3+4x^2-5x-47$ равна четырём, то в результате деления получим многочлен третьей степени:

Полученный результат означает, что

$$x^4+3x^3+4x^2-5x-47=(x+3)(x^3+0\cdot x^2 +4x-17)+4=(x+3)(x^3+4x-17)+4$$

В этой ситуации остаток от деления $x^4+3x^3+4x^2-5x-47$ на $x+3$ равна $4$. Или, что то самое, значение многочлена $x^4+3x^3+4x^2-5x-47$ при $x=-3$ равно $4$. Кстати, это несложно перепроверить непосредственной подстановкой $x=-3$ в заданный многочлен:

$$x^4+3x^3+4x^2-5x-47=(-3)^4+3 \cdot (-3)^3-5 \cdot (-3)-47=4.$$

Т.е. схему Горнера можно использовать, если необходимо найти значение многочлена при заданном значении переменной. Если наша цель – найти все корни многочлена, то схему Горнера можно применять несколько раз подряд, – до тех пор, пока мы не исчерпаем все корни, как рассмотрено в примере №3.

Пример №3

Найти все целочисленные корни многочлена $x^6+2x^5-21x^4-20x^3+71x^2+114x+45$, используя схему Горнера.

Решение

Коэффициенты рассматриваемого многочлена есть целые числа, а коэффициент перед старшей степенью переменной (т.е. перед $x^6$) равен единице. В этом случае целочисленные корни многочлена нужно искать среди делителей свободного члена, т.е. среди делителей числа 45. Для заданного многочлена такими корнями могут быть числа $45; \; 15; \; 9; \; 5; \; 3; \; 1$ и $-45; \; -15; \; -9; \; -5; \; -3; \; -1$. Проверим, к примеру, число $1$:

Табл. №1

Как видите, значение многочлена $x^6+2x^5-21x^4-20x^3+71x^2+114x+45$ при $x=1$ равно $192$ (последнее число в второй строке), а не $0$, посему единица не является корнем данного многочлена. Так как проверка для единицы окончилась неудачей, проверим значение $x=-1$. Новую таблицу для этого составлять не будем, а продолжим использование табл. №1, дописав в нее новую (третью) строку. Вторую строку, в которой проверялось значение $1$, выделим красным цветом и в дальнейших рассуждениях использовать её не будем.

Можно, конечно, просто переписать таблицу заново, но при заполнении вручную это займет немало времени. Тем более, что чисел, проверка которых окончится неудачей, может быть несколько, и каждый раз записывать новую таблицу затруднительно. При вычислении «на бумаге» красные строки можно просто вычёркивать.

Табл. №2

Итак, значение многочлена $x^6+2x^5-21x^4-20x^3+71x^2+114x+45$ при $x=-1$ равно нулю, т.е. число $-1$ есть корень этого многочлена. После деления многочлена $x^6+2x^5-21x^4-20x^3+71x^2+114x+45$ на бином $x-(-1)=x+1$ получим многочлен $x^5+x^4-22x^3+2x^2+69x+45$, коэффициенты которого взяты из третьей строки табл. №2 (см. пример №1). Результат вычислений можно также представить в такой форме:

\begin{equation}x^6+2x^5-21x^4-20x^3+71x^2+114x+45=(x+1)(x^5+x^4-22x^3+2x^2+69x+45) \end{equation}

Продолжим поиск целочисленных корней. Теперь уже нужно искать корни многочлена $x^5+x^4-22x^3+2x^2+69x+45$. Опять-таки, целочисленные корни этого многочлена ищут среди делителей его свободного члена, – числа $45$. Попробуем ещё раз проверить число $-1$. Новую таблицу составлять не будем, а продолжим использование предыдущей табл. №2, т.е. допишем в нее еще одну строку:

Итак, число $-1$ является корнем многочлена $x^5+x^4-22x^3+2x^2+69x+45$. Этот результат можно записать так:

\begin{equation}x^5+x^4-22x^3+2x^2+69x+45=(x+1)(x^4-22x^2+24x+45) \end{equation}

Учитывая равенство (2), равенство (1) можно переписать в такой форме:

\begin{equation}\begin{aligned} & x^6+2x^5-21x^4-20x^3+71x^2+114x+45=(x+1)(x^5+x^4-22x^2+2x^2+69x+45)=\\ & =(x+1)(x+1)(x^4-22x^2+24x+45)=(x+1)^2(x^4-22x^2+24x+45)\end{aligned}\end{equation}

Теперь уже нужно искать корни многочлена $x^4-22x^2+24x+45$, – естественно, среди делителей его свободного члена (числа $45$). Проверим еще раз число $-1$:

Число $-1$ является корнем многочлена $x^4-22x^2+24x+45$. Этот результат можно записать так:

\begin{equation}x^4-22x^2+24x+45=(x+1)(x^3-x^2-21x+45) \end{equation}

С учетом равенства (4), равенство (3) перепишем в такой форме:

\begin{equation}\begin{aligned} & x^6+2x^5-21x^4-20x^3+71x^2+114x+45=(x+1)^2(x^4-22x^3+24x+45)= \\ & =(x+1)^2(x+1)(x^3-x^2-21x+45)=(x+1)^3(x^3-x^2-21x+45)\end{aligned}\end{equation}

Теперь ищем корни многочлена $x^3-x^2-21x+45$. Проверим еще раз число $-1$:

Проверка окончилась неудачей. Выделим шестую строку красным цветом и попробуем проверить иное число, например, число $3$:

В остатке ноль, посему число $3$ – корень рассматриваемого многочлена. Итак, $x^3-x^2-21x+45=(x-3)(x^2+2x-15)$. Теперь равенство (5) можно переписать так:

\begin{equation}\begin{aligned} & x^6+2x^5-21x^4-20x^3+71x^2+114x+45= \\ & =(x+1)^3(x^3-x^2-21x+45)=(x+1)^3(x-3)(x^2+2x-15)\end{aligned}\end{equation}

Проверим ещё раз число $3$:

Полученный результат можно записать так (это продолжение равенства (6)):

\begin{equation} \begin{aligned} & x^6+2x^5-21x^4-20x^3+71x^2+114x+45=(x+1)^3(x-3)(x^2+2x-15)= \\ & =(x+1)^3(x-3)(x-3)(x+5)=(x+1)^3(x-3)^2(x+5) \end{aligned} \end{equation}

Из последней скобки видно, что число $-5$ также является корнем данного многочлена. Можно, конечно, формально продолжить схему Горнера, проверив значение $x=-5$, но необходимости в этом нет. Итак,

$$ x^6+2x^5-21x^4-20x^3+71x^2+114x+45=(x+1)^3(x-3)(x^2+2x-15)=(x+1)^3(x-3)^2(x+5)$$

Числа $-1; \; 3; \; 5$ – корни данного многочлена. Причем, так как скобка $(x+1)$ в третьей степени, то $-1$ – корень третьего порядка; так как скобка $(x-3)$ во второй степени, то $3$ – корень второго порядка; так как скобка $(x+5)$ в первой степени, то $x=-5$ – корень первого порядка (простой корень).

Вообще, обычно оформление таких примеров состоит из таблицы, в которой перебираются возможные варианты корней, и ответа:

Из таблицы следует вывод, полученный нами ранее с подробным решением:

$$ x^6+2x^5-21x^4-20x^3+71x^2+114x+45=(x+1)^3(x-3)(x^2+2x-15)=(x+1)^3(x-3)^2(x+5)$$

Пример №4

Убедиться, что числа $2$ и $-5$ являются корнями многочлена $3x^6+9x^5-28x^4+6x^3-30x^2-30x+100$. Разделить заданный многочлен на биномы $x-2$ и $x+5$.

Решение

Степень многочлена $3x^6+9x^5-28x^4+6x^3-30x^2-30x+100$ равна $6$. После деления на два заданных бинома степень заданного многочлена уменьшится на $2$, т.е. станет равна $4$.

Конечно, данный метод подбора малоэффективен в общем случае, когда корни не являются целыми числами, но для целочисленных корней метод довольно-таки неплох.

math1.ru

Схема Горнера

Всем доброго времени суток! В этой статье мы научимся делить многочлены по схеме Горнера. Это простой и мощный механизм, которым совершенно необходимо владеть, чтобы решать некоторые рациональные уравнения задания 15 профильного ЕГЭ.

При решении таких уравнений корни заранее неизвестны, да и при разложении многочлена на множители мы также не знаем заранее, на какой бином поделится наш многочлен. Как же узнать, на какой бином разделить многочлен?

Если многочлен имеет целые корни, то они являются делителями свободного члена – правило вытекает из теоремы Безу

Пример 1.

Определим, какие числа являются, например, корнями многочлена . Если этот многочлен имеет целые корни, то они являются делителями числа (-2): это могут быть . Проверим подстановкой – если при подстановке этих чисел в исходный многочлен получим ноль, то данное число – корень:

 

 

Кроме 1, ни одно число не подошло, значит, бином  поделит этот многочлен нацело (без остатка). Деление теперь можно выполнить как в столбик (уголком), так и по схеме Горнера – сейчас мы до нее дойдем, только еще раз потренируемся в определении корней.

 

Пример 2. 

Определим корни многочлена . Целые делители свободного члена – только 1 и (-1):

 

Корнем многочлена является 1, поэтому многочлен без остатка поделится на бином .

Пример 3. 

Определим корни многочлена . Целые делители свободного члена – . Проверим их:

 

Корнями многочлена являются как 1, так и (-1),  поэтому многочлен без остатка поделится на биномы и – а в итоге на .

Теперь, когда мы научились определять, есть ли у многочлена целые корни, можем перейти собственно к схеме Горнера. Чтобы ею воспользоваться, нужно составить таблицу, в верхней строке которой будут расположены коэффициенты нашего многочлена. Поучимся заполнять эту строку. Определим коэффициенты многочлена  и запишем их в таблицу. Этот многочлен пятой степени, поэтому коэффициентов будет 6: при каждой из степеней , включая нулевую (свободный член). Если какой-то степени нет в записи многочлена, то это означает, что коэффициент при ней нулевой:

Получили эдакую зашифрованную запись многочлена.

Еще пример, многочлен , его коэффициенты:

Полдела сделано: верхнюю строку научились заполнять, а нижняя – это уже решение, то есть результат деления в таком же, “зашифрованном”, виде. Каков же порядок заполнения нижней строки? Во-первых, у нее будет дополнительная ячейка слева, куда мы впишем корень многочлена, образующий бином, на который мы собираемся делить. Например, если делим на , то корнем многочлена является число 2, если делим на , то в эту ячейку впишем (-9). Пример: хотим разделить  на , таблица изначально будет выглядеть так:

Как уже было сказано, ответ будет “зашифрован” в пустых пока ячейках. Наверное, вы догадались, что там окажутся коэффициенты нового, полученного при делении, многочлена. Только внимание! Степень полученного многочлена уменьшится на 1: ведь мы делим на бином, куда  входит в первой степени. Например, если сейчас мы начнем заполнять эту табличку, то под двойкой, которая была в делимом коэффициентом при пятой степени, окажется коэффициент при четвертой степени искомого частного, под 4 – коэффициент при кубе частного и т.д.

Так же просто заполнить вторую ячейку нижней строки: в нее просто вписывается число, стоящее в первой строчке:

 

Рассмотрим дальнейшее заполнение таблицы на конкретном примере: разделим  на бином  (так как (-1) – это корень данного многочлена). Заполняем таблицу, пока только ту часть, которую умеем:вписываем коэффициенты в верхнюю строку, в дополнительную ячейку слева – корень (-1), в следующую переносим 1 из верхней строки:

 

Чтобы заполнить следующую ячейку, берем корень, умножаем его на имеющийся коэффициент и прибавляем к полученному числу то, которое стоит над пустой ячейкой:

 

Чтобы заполнить следующую, все повторяем:

 

И опять:

 

И вот так закончится заполнение таблицы:

“Расшифровываем” ответ, при этом помним, что степень понизилась на 1::

Ответ: 

Ноль в последней графе – это нулевой остаток от деления – то есть один многочлен поделился на другой “нацело”.

Решим еще пример. Разделим  на . Составим таблицу:

 

Начинаем рассчитывать коэффициенты и заполнять таблицу. Первое число из верхней строки переписываем вниз, умножаем на него корень, к результату добавляем число из верхней строки:

 

Также вычисляем следующий коэффициент:

 

И далее:

 

Получили ответ: . Здесь остаток от деления также равен нулю.

Этот способ хорош своей быстротой и простотой. Им можно пользоваться и при делении с остатком: тогда в последней графе таблицы будет стоять не ноль, а этот самый остаток. Недостаток способа – неудобство деления в случае, если корень не целый, а представляет собой дробь.

Попробуем выполнить деление по схеме Горнера, если корень не целый, да еще и остаток есть. Поделим многочлен на бином . Заполняем таблицу:

 

Расшифруем ответ:

 

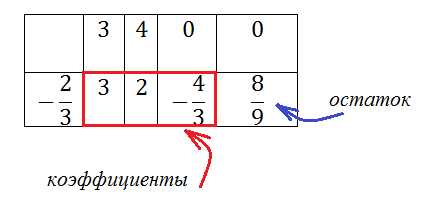
Итак, получилось следующее. При делении получился многочлен  и остаток . Запишем это иначе: . Если есть желание проверить – раскройте скобки в этой формуле.

Наконец, об уравнениях высоких степеней. Иногда однократное деление не приводит к окончанию  решения, потому что корней несколько и многочлен можно продолжать делить. В этом случае, выполнив деление и получив новый многочлен степенью ниже, снова пытаются найти целые корни среди делителей его свободного члена. При этом подстановка предполагаемых корней в многочлен может занимать даже больше времени, чем заполнение таблицы по Горнеру. Тогда таблицу продолжают вниз, дополняя ее просто новыми строками, а в случае появления остатка (деление не выполнено) эту строчку зачеркивают и пробуют новый корень в следующей строке. Пример:

Решить уравнение:  . Делителями свободного члена являются:  и так далее. Пробуем сначала подставить 1 и (-1) в сам многочлен – такая подстановка дает нам один корень, это 1.  Выполняем деление по схеме Горнера:

 

Запишем, что получилось:   – получили тот же свободный член, и можем снова использовать те же делители, чтобы проверить, не являются ли они корнями. Однако теперь подстановка 1 и (-1) показывает, что эти два числа не являются корнями. Проверяем тогда 2 и (-2) – только не будем подставлять их в многочлен, а сразу попытаемся делить по Горнеру. А таблица у нас уже готова, и в ней все коэффициенты! Поэтому продолжаем ее заполнять, добавляя строки:

 

Так как остаток ненулевой, то 2 – не корень. Строку вычеркнем и попробуем (-2):

 

Та же картина, опять получили ненулевой остаток. Далее пробуем 3 и (-3):

 

Получилось! Теперь имеем: . Делителями нового свободного члена являются  . Пробовать   не будем: очевидно, что они не могут быть корнями – это выяснилось на предыдущих этапах. Поэтому пробуем  .

 

Получили: . Дальше деление по Горнеру можно и не выполнять: корни с очевидностью можно найти по теореме Виета – это 5 и 6. Тогда . Разложение выполнено, корни уравнения найдены.

Надеюсь, статья вам помогла, до следующих исследований!

easy-physic.ru

Схема Горнера. Корни многочлена

Разделы: Математика

---

Цели урока:

• научить учащихся решать уравнения высших степеней используя схему Горнера;
• воспитывать умение работать в парах;
• создать в совокупности с основными разделами курса базу для развития способностей учащихся;
• помочь ученику оценить свой потенциал, развивать интерес к математике, умение мыслить, высказываться по теме.

Оборудование: карточки для работы в группах, плакат со схемой Горнера.

Метод обучения: лекция, рассказ, объяснение, выполнение тренировочных упражнений.

Форма контроля: проверка задач самостоятельного решения, самостоятельная работа.

Ход урока

1. Организационный момент

2. Актуализация знаний учащихся

— Какая теорема позволяет определить, является ли число корнем данного уравнения  (сформулировать теорему)? 

Теорема Безу. Остаток от деления многочлена Р(х) на двучлен х-с равен Р(с), число с называют корнем многочлена Р(х), если Р(с)=0. Теорема позволяет, не выполняя операцию деления, определить, является ли данное число корнем многочлена.

— Какие утверждения облегчают поиск корней?

а) Если старший коэффициент многочлена равен единице, то корни многочлена следует искать среди делителей свободного члена.

б) Если сумма коэффициентов многочлена равна 0, то один из корней равен 1.

в)Если сумма коэффициентов стоящих на четных местах, равна сумме коэффициентов, стоящих на нечетных местах, то один из корней равен -1.

г) Если все коэффициенты положительны, то корнями многочлена являются отрицательные числа.

д) Многочлен нечетной степени имеет хотя бы один действительный корень.

3. Изучение нового материала

При решении  целых алгебраических уравнений приходиться находить значения корней многочленов. Эту операцию можно существенно упростить, если проводить вычисления по специальному алгоритму, называемому схемой Горнера. Эта схема названа в честь английского ученого Уильяма Джорджа Горнера. Схема Горнера  это алгоритм для вычисления частного и остатка от деления многочлена Р(х) на х-с. Кратко, как он устроен.

Пусть дан произвольный многочлен Р(х)=а₀хⁿ+ а₁х^n-1+ …+ а_n-1х+ а_n. Деление этого многочлена на х-с – это представление его в виде Р(х)=(х-с)g(х) + r(х).  Частное  g(х)=в

0х^n-1+ в_nх^n-2 +…+в_n-2х + в_n-1, где в₀=а₀, в_n=св_n-1 +а_n,  n=1,2,3,…n-1. Остаток r(х)= св_n-1 +а_n . Этот метод вычисления и называется схемой Горнера. Слово « схема» в названии алгоритма связана с тем, что обычно его выполнение оформляют следующим образом. Сначала рисуют таблицу 2(n+2). В левой нижней клетке записывают число с, а в верхней строке коэффициенты  многочлена Р(х). При этом левую верхнюю клетку оставляют пустой.

	а0	а1	а2	…	аn-1	аn
с	в0=а0	в1=св1 +а1	в2=св1+а2	…	вn-1=свn-2+аn-1	r(х)=f(с)=свn-1 +аn

Число, которое после выполнения алгоритма оказывается записанным в правой нижней клетке, и есть остаток от деления многочлена Р(х) на х-с. Другие числа в₀, в₁, в₂,… нижней строки являются коэффициентами частного.

Например : Разделить многочлен Р(х)= х³-2х+3 на х-2.

1.

2.

	1	0	-2	3
2	1	1*2+0=2

3.

	1	0	-2	3
2	1	2	2*2-2 =2

4.

	1	0	-2	3
2	1	2	2	2*2+3=7

 Получаем, что х³-2х+3=(х-2) (х²+2х+2) + 7.

4. Закрепление изученного материала

Пример 1:  Разложите на множители с целыми коэффициентами многочлен Р(х)=2х4-7х³-3х²+5х-1.

Решение: 

Ищем целые корни среди делителей свободного члена -1:  1; -1. Составим таблицу:

	2	-7	-3	5	-1
-1	2	-9	6	-1	0

X = -1 – корень                                        

Р(х)= (х+1) (2х³ -9х² +6х -1)

Проверим 1/2.

	2	-9	6	-1
1/2	2	-8	2	0	Х=1/2 — корень

Следовательно, многочлен Р(х) можно представить в виде                                                  

Р(х)= (х+1) (х-1/2) (х² -8х +2) = (х+1) (2х -1) (х² — 4х +1)

Пример 2: Решить уравнение 2х⁴ — 5х³ + 5х² — 2 = 0

Решение:

Так как сумма коэффициентов многочлена , записанного в левой части уравнения, равна нулю, то один из корней 1. Воспользуемся схемой Горнера:

	2	-5	5	0	-2
1	2	-3	2	2	0	Х=1 — корень

Получаем  Р(х)=(х-1) (2х³ -3х² =2х +2). Будем искать корни среди делителей свободного члена 2.

	2	-3	2	2
1	2	-1	1	3
-1	2	-5	7	-5
2	2	1	4	10
-2	2	-7	16	-30

Выяснили, что целых корней больше нет. Проверим 1/2; -1/2.

	2	-3	2	2
1/2	2	-2	1	2,5
-1/2	2	-4	4	0	Х= -1/2 — корень

Итак (х-1) (х+1/2) (2х² – 4х +4)=0.  Далее решаем квадратное уравнение 2х²-4х +4 = 0.  Д/4=1-2= -1. Значит это уравнение корней не имеет.

Ответ: 1; -1/2.                                                                                                                                  

Пример 3: Решить уравнение 5х⁴ – 3х³ – 4х² -3х+ 5 = 0.

Решение:

Корни данного уравнения будем искать среди делителей свободного члена 5: 1;-1;5;-5. х=1 — корень уравнения, так как сумма коэффициентов равна нулю. Воспользуемся схемой Горнера:

	5	-3	-4	-3	5
1	5	2	-2	-5	0

Можно записать (х-1) (5х³ +2х² -2х-5)=0.   Для 5х³ +2х² -2х-5=0  х=1 также является корнем и

уравнение представим в виде произведения трех множителей: (х-1) (х-1) (5х² -7х + 5)=0. Решая квадратное уравнение 5х² -7х+5=0, получили Д=49-100=-51, корней нет.

Ответ: 1.

Далее работа в парах по карточкам.

Карточка 1

1. Разложите на множители многочлен: х⁴+3х³-5х²-6х-8
2. Решите уравнение: 27х³-15х²+5х-1=0

Карточка 2

1. Разложите на множители многочлен: х⁴-х³-7х²+13х-6
2. Решите уравнение: х⁴+2х³-13х²-38х-24=0

Карточка 3

1. Разложите на множители: 2х³-21х²+37х+24
2. Решите уравнение: х³-2х²+4х-8=0

Карточка 4

1. Разложите на множители: 5х³-46х²+79х-14
2. Решите уравнение: х⁴+5х³+5х²-5х-6=0

5. Подведение итогов 

Проверка знаний при решении в парах осуществляется на уроке путем узнавания способа действия и названия ответа.

Домашнее задание: 

Решите уравнения:

а) х⁴-3х³+4х²-3х+1=0

б) 5х⁴-36х³+62х²-36х+5=0

в) х⁴+х³+х+1=4х²

г) х⁴+2х³-х-2=0

 

Литература

1. Н.Я. Виленкин и др., Алгебра и начала анализа 10 класс (углубленное изучение математики): Просвещение, 2005.
2. У.И. Сахарчук, Л.С. Сагателова, Решение уравнений высших степеней: Волгоград, 2007.
3. С.Б. Гашков, Системы счисления и их применение.

10.06.2010

xn--i1abbnckbmcl9fb.xn--p1ai

Схема (метод) Горнера. Примеры. Решение кубических уравнений

РЕШЕНИЕ КУБИЧЕСКИХ УРАВНЕНИЙ ПО СХЕМЕ ГОРНЕРА

4x³ — 19x² + 19x + 6 = 0

Для начала нужно методом подбора найти один корень. Обычно он является делителем свободного члена. В данном случае делителями числа 6 являются ±1, ±2, ±3, ±6.

1: 4 — 19 + 19 + 6 = 10 ⇒ число 1 не является корнем многочлена

-1: -4 — 19 — 19 + 6 = -36 ⇒ число -1 не является корнем многочлена

2: 4 ∙ 8 — 19 ∙ 4 + 19 ∙ 2 + 6 = 0 ⇒ число 2 является корнем многочлена

Мы нашли 1 из корней многочлена. Корнем многочлена является 2, а значит исходный многочлен должен делиться на x — 2. Для того, чтобы выполнить деление многочленов, воспользуемся схемой Горнера:

В верхней строке выставляются коэффициенты исходного многочлена. В первой ячейке второй строки ставится найденный нами корень 2. Во второй строке пишутся коэффициенты многочлена, который получится в результате деления. Они считаются так:

	Во вторую ячейку второй строки запишем число 1, просто перенеся его из соответствующей ячейки первой строки.
	2 ∙ 4 — 19 = -11
	2 ∙ (-11) + 19 = -3
	2 ∙ (-3) + 6 = 0

Последнее число — это остаток от деления. Если он равен 0, значит мы все верно посчитали.

Таким образом мы исходный многочлен разложили на множители:

4x³ — 19x² + 19x + 6 = (x — 2)(4x² — 11x — 3)

И теперь, всего лишь, осталось найти корни квадратного уравнения

4x² — 11x — 3 = 0
D = b² — 4ac = (-11)² — 4 ∙ 4 ∙ (-3) = 169
D > 0 ⇒ уравнение имеет 2 корня

x1,2 =	-b ± √ D	=	11 ± 13	= -0.25; 3
	2a		2∙4

Мы нашли все корни уравнения:

x = 2; 3; -0.25

tutata.ru

Схема Горнера

Обычно многочлен представлен в виде:

$f(x)=\sum\limits_{k=0}^{n} a_k x^k$

или

f(x) = a₀ + a₁x + a₂x² + … + a_kx^k

Где a_k это действительные числа, представляющие коэффициенты многочлена и
x^k это переменные многочлена.

Вышеупомянутый многочлен называют многочленом n^-ой степени, то есть deg(f(x)) = n, где n представляет наивысшую степень переменной.

Схема Горнера для деления многочлена — это алгоритм упрощения вычисления значения многочлена f(x) при определённой величине x = x₀ методом деления многочлена на одночлены (многочлены 1^ой степени). Каждый одночлен включает в себя максимум один процесс умножения и один процесс сложения. Результат, полученный из одного одночлена, прибавляют к результату полученному от следующего одночлена и так далее в аккумулятивной манере. Такой процесс деления также называют синтетическим делением.

Чтобы объяснить вышесказанное, давайте перепишем многочлен в развёрнутой форме;

f(x₀) = a₀ + a₁x₀ + a₂x₀² + … + a_nx₀ⁿ

Это также может быть записано как:

f(x₀) = a₀ + x₀(a₁ + x₀(a₂ + x₀(a₃ + … + (a_n-1 + a_nx₀)….)

Алгоритм, предложенный данной схемой, основан на нахождении значений одночленов образованных выше, начиная с тех которые заключены в больше скобок и двигаясь наружу, для нахождения значения одночленов во внешних скобках.

Алгоритм приводится в действие, следуя нижеизложенным шагам:

1. Дано k = n
2. Пусть b_k = a_k
3. Пусть b_{k — 1} = a_{k — 1} + b_kx₀
4. Пусть k = k — 1
5. Если k ≥ 0, то вернуться на шаг 3
иначе Конец

Этот алгоритм может быть также графически визуализирован, принимая во внимание данный многочлен 5^ой степени:

f(x) = a₀ + a₁x + a₂x² + a₃x³ + a₄x⁴ + a₅x⁵

значение которого находится как x = x₀, путём перестановки его следующим образом:

f(x₀) = a₀ + x₀(a₁ + x₀(a₂ + x₀(a₃ + x₀(a₄ + a₅x₀))))

Другим способом представить результаты используя этот алгоритм можно в виде данной ниже таблицы:

K	5	4	3	2	1	0
	b5 = a5	b4 = a4 + x0b5	b3 = a3 + x0b4	b2 = a2 + x0b3	b1 = a1 + x0b2	b0 = a0 + x0b1

Пример: Найти значение многочлена f(x) = x⁴ + 3x³ + 5x² + 7x + 9 at x = 2

Решение:

Так как многочлен 4^ой степени, то n = 4

K	4	3	2	1	0
Шаг	b4 = 1	b3 = 3 + 2 * 1	b2 = 5 + 2 * 5	b1 = 7 + 2 * 15	b0 = 9 + 2 * 37
Результат	1	5	15	37	83

Таким образом, f(2) = 83.

Почему нам это необходимо делать?

Обычно, находя значения многочлена при определённом значении переменной, мы привыкли подставлять это значение в многочлен и производить вычисления. Мы также можем разработать копьютерную программу для математического вычисления, которая является необходимостью, когда мы имеем дело со сложными многочленами высоких степеней.

Метод, с помощью которого компьютер обрабатывает проблему, зависит, в основном, от того как Вы, как программист, описываете это компьютеру. Вы можете разработать Вашу программу для нахождения значения многочлена методом прямой подстановки значения переменной или использовать синтетическое деление, данное в схеме Горнера. Единственное отличие между этими двумя подходами это скорость, с которой компьютер будет находить решение том или ином случае

www.math10.com

Урок на тему «Корни многочлена. Схема Горнера»

Пример 2. Найти корни многочлена f (x) = x ⁴ + 2 x ³ – 6 x ² – 22 x + 55.

Решение. Делители 55: – 1, 1, – 5, 5, – 11, 11, – 55, 55. Заметим, что – 1 и 1 не являются корнями многочлена. Следует проверить остальные делители.

Замечание. Очень важно учащимся овладеть “длинной” схемой Горнера. В данном примере как раз удобна “длинная” схема.

x ² + 57 x + 3 129 = 0, корней нет.

Ответ: корней нет. [2]

VI. Самостоятельная работа

На доске три человека решают для последующей проверки.

Найти корни многочлена по схеме Горнера:

а) f (x) =  x ³ + 2 x ² – 5 x – 6;

Ответ: – 1; 2; – 3.

б) f (x) =  x ⁵ – 5 x ⁴ + 6 x ³ – x ² + 5 x – 6;

Ответ: 1; 2; 3.

в) f (x) =  x ⁴ + 12 x ³ + 32 x ² – 8 x – 4.

Ответ:

(Проверка осуществляется в парах, выставляются оценки).

VII. Исследовательская работа учащихся

– Ребята, вы не заметили, какие многочлены в основном мы разбирали на уроках?

(Ответы учащихся).

– Да, это многочлены с целыми коэффициентами и со старшим членом k = 1.

– В каких числах получались ответы?

(Ответы учащихся).

– Правильно, корни многочлена с целыми коэффициентами и со старшим членом k = 1 либо целое, либо иррациональное, либо целые и иррациональные, либо не имеют корней. Запишите вывод в своих тетрадях.

VIII. Задание на дом

1. № 129 (1, 3, 5, 6) – Н. Я. Виленкин – 10, стр. 78. [3]
2. Выучить теорию данного урока.

IX. Подведение итогов урока и выставление отметок

Литература

1. М.Л. Галицкий. Углубленное изучение алгебры и математического анализа. // Просвещение, 1997 г.

2. Г.В. Дорофеев. Многочлены с одной переменной. // Санкт-Петербург. Специальная литература, 1997 г.

Н.Я. Виленкин. Алгебра и математический анализ. 10 класс // Просвещение

Пояснительная записка.

Курс разработан для учащихся 10 класса физико-математического профиля, имеющих хороший уровень математической подготовки, и призван помочь им подготовиться к разным конкурсам и олимпиадам по математике, способствовать продолжению серьёзного математического образования. Он расширяет базовый курс по математике, является предметно-ориентированным и даёт учащимся возможность познакомиться с интересными, нестандартными вопросами математики, и методами решения уравнений высших степеней. В курсе заложена возможность дифференцированного обучения.

Ориентируя школьников на поиски красивых, изящных решений решения уравнений высших степеней, учитель тем самым способствует эстетическому воспитанию учащихся и повышению их математической культуры. Курс является продолжением учебника, где предусматривается обучение школьников способам самостоятельной работы, приёмам решения уравнений высших степеней. Осуществляя целенаправленное обучение школьников решению уравнений высших степеней, следует учить их наблюдать, пользоваться аналогией, индукцией, сравнениями и делать соответствующие выводы. Необходимо через уравнения высших степеней прививать учащимся не только навыки логического рассуждения, но и прочные навыки эвристического мышления.

2

Цели и задачи курса.

1. Развитие интереса к математике, эвристического мышления.

2. Способствовать продолжению серьёзного математического образования.

3. Научить осуществлять выбор рационального метода решения задач и обосновывать сделанный выбор.

4. Способствовать формированию научного стиля мышления.

5. Подготовиться к ЕГЭ.

3

Содержание курса и распределение часов курса по темам.

Данный элективный курс рассчитан 34 тематических занятий.

4

Общие методические рекомендации.

Учащимся сообщается цель и назначение элективного курса. Занятия включают в себя теоретическую и практическую части – лекции, консультации практикумы, самостоятельную и исследовательскую работу.

Изучение основных положений теории многочленов позволяет обобщить терему Виета для урвнений любой степени. Умение выполнять действия делений многочленов облегчит в дальнейшем решение задач из математического анализа.

Изучение схемы Горнера и теоремы о рациональных корнях многочлена даёт общий метод разложения на множители любого алгебраического выражения. В свою очередь умение решать уравнения высших степеней позволит знаительно расширить круг показательных, логарифмических, тригонометрических и иррациональных уравнений и неравенств.

Литература

1. Галицкий М.Л., Гольдман А.М., Звавич Л.И. Сборник задач по алгебре для 8-9 классов.

2Вавилов В.В., Мельников И.И., Олехник С.Н., ПасиченкоП.И Задачи по математике. Алгебра.

3 Олехник С.Н., ПасиченкоП.И. Нестандартные методы решения уравнений и неревенств.

4..Вавилов В.В., Мельников И.И., Олехник С.Н., ПасиченкоП.И. Уравнения и неравенства.

5. Шарыгин И.Ф. Факультативный курс по математике.

5

Оглавление

Цели и задачи курса 1

Содержание курса и распределение часов курса по темам 2

Общие методические рекомендации 3

Литература 4

Приложение 6

1

infourok.ru

Методика преподавания темы «Схема Горнера, теорема Безу и деление уголком». Из копилки приемов репетитора по математике

Сайт «профессиональный репетитор по математике» продолжает цикл методических статей о преподавании. Я публикую описания методик своей работы с наиболее сложными и проблемным темами школьной программы. Данный материал будет полезен преподавателям и репетиторам по математике, работающим с учениками 8-11 классов как по обычной программе, так и по программе математических классов.

Репетитор по математике не всегда может объяснить материал, который неудачно изложен в учебнике. К сожалению, таких тем становится все больше и больше, и ошибки изложения вслед за авторами пособий совершаются в массовом порядке. Это относится не только к начинающим репетиторам по математики и репетиторам по совместительству (репетиторы — студенты и репетиторы ВУЗов), но и к опытным преподавателям, репетиторам — профессионалам, репетиторам со стажем и квалификацией. Талант грамотного корректора шероховатостей школьных учебников имеют далеко не все репетиторы математики. Не все также понимают, что эти коррекции (или дополнении) необходимы. Адаптацией материала для его качественного восприятия детьми занимаются единицы. К сожалению, ушло то время, когда преподаватели математики вместе методистами и авторами изданий в массовом порядке обсуждали каждую букву учебника. Раньше, прежде чем пустить учебник в школы, проводили серьезные анализы и исследования результатов обучения. Пришло время дилетантов, стремящихся сделать пособия универсальными, подгоняя их под стандарты сильных математических классов.

Гонка за увеличение количества информации приводит только к снижению качества ее усвоения и, как следствие снижению уровня реальных знаний по математике. Но на это никто не обращает внимание. И наши дети вынуждены уже в 8 классе изучать то, что мы с вами проходили в институте: теорию вероятности, решение уравнений высоких степеней и кое-что еще. Адаптация материала в книжках для его полноценного восприятия ребенком оставляет желать лучшего и репетитор по математике вынужден как-то с этим бороться.

Поговорим о методике преподавания такой специфической темы, как «деление уголком многочлена на многочлен», более известной во взрослой математике как «теорема Безу и схема Горнера». Еще каких-нибудь пару лет назад вопрос не стоял перед репетитором по математике так остро, ибо он не входил в основную школьную программу. Теперь уважаемые авторы учебника под редакцией Теляковского внесли изменения в последнее издание лучшего, на мой взгляд, учебника, и, окончательно испортив его, только добавили репетитору лишних забот. Преподаватели школ и классов, не имеющих статус математических, ориентируясь на нововведения авторов, стали чаще включать дополнительные параграфы в свои уроки, а любознательные дети, рассматривая красивые странички их учебника математики, все чаще спрашивают репетитора: «Что это за деление уголком? Мы будем это проходить? Как делить уголком?» От таких прямых вопросов уже не спрятаться. Репетитору придется что-то рассказывать ребенку.

А как? Наверное, я бы не стал описывать метод работы с темой, если бы в учебниках она грамотно преподносилась. У нас ведь как все происходит? Учебники нужно печатать и продавать. А для этого их надо регулярно обновлять. Преподаватели Вузов жалуются, что дети приходят к ним с пустыми головами, без знаний и навыков? Требования к математическим знаниям растут? Отлично! Давайте мы уберем некоторые упражнения, а вместо них вставим темы, которые изучаются по другим программам. Чем наш учебник хуже? Включим какие-нибудь дополнительные главы. Школьники не знают правило деления уголком? Это же элементарная математика. Надо сделать такой параграф необязательным, озаглавив его «для тех, кто хочет знать больше». Репетиторы против? А какое нам дело до репетиторов вообще? Методисты и преподаватели школ тоже против? Мы не будем усложнять материал и рассмотрим наиболее простую его часть.

И вот тут начинается. Простота темы и качество ее усвоения заключатся, прежде всего, в понимании ее логики, а не в том, чтобы согласно предписанию авторов учебника выполнить некий набор не понятно как связанных друг с другом операций. Иначе туман в голове школьника будет обеспечен. Если расчет авторов идет на относительно сильных учеников (но обучающихся по обычной программе), то не стоит подавать тему в командной форме. А что мы видим в учебнике? Дети, надо делить по такому правилу. Получите многочлен под уголком. Таким образом, первоначальный многочлен разложится на множители. Однако, понять, почему именно так подбираются слагаемые под уголком, почему их надо умножать на многочлен над уголком, а затем вычитать из текущего остатка — непонятно. И самое главное не понятно, почему подобранные одночлены надо в итоге сложить и почему получившиеся скобки будут разложением первоначального многочлена. Любой грамотный математик поставит жирный знак вопроса над теми объяснениями, которые даются в учебнике.

Я предлагаю вниманию репетиторов и преподавателей математики свое решение проблемы, которое практически делает для ученика очевидным все то, что изложено в учебнике. Фактически мы докажем теорему Безу: если число а — корень многочлена, то этот многочлен можно разложить на множитлей, один из который x-a, а второй получается из первоначального одним из трех способов: выделением линейного множителя через преобразования, делением уголком или по схеме Горнера. Именно с такой форомулировкой репетитору по математике будет легче работать.

Что такое методика преподавания? Прежде всего это четкий порядок в последовательности объяснений и примеров, на основе которых делаются математические выводы. Данная тема не исключение. Репетитору по математике очень важно познакомить ребенка с теоремой Безу до того, как будет выполняться деление уголком. Это очень важно! Добиться понимания лучше всего на конкретном примере. Возьмем какой-нибдуь многочлен с подобранным корнем и показажем технику его разложения на множители при помощи знакомого школьнику еще с 7 класса метода тождественных преобразований. При соответствующих сопроводительных пояснениях, акцентах и подсказках репетитора по математике вполне реально донести материал без каких-либо общих математических выкладок, произвольных коэффициентов и степеней.

Важный совет репетитору по математике — следовать инструкциям от начала и до конца и не менять эту последовательнотсь.

Итак, допустим, что перед нами многочлен . Если мы подставим вместо его икса число 1, то значение многочлена будет равно нулю. Следовательно х=1 — его корень. Попробуем разложить на два слагаемых так, чтобы одно из них было произведением линейного выражения и некоторого одночлена, а второе имело бы степень на единицу меньше, чем . То есть представим его в виде

Одночлен для красного поля подберем так, чтобы при при умножении его на старший член полностью совпадал со старшим членом первоначального многочлена. Если ученик не самый слабый, то он вполне способен будет назвать репетитору по математике искомое выражение: . Репетитору следует тут же предложить вставить его в красное поле и показать что будет получаться при их раскрытии. Лучше всего этот виртуальный временный многочлен подписать под стрелочками (под фотанчиком), выделяя его каким-нибудь цветом, например, синим. Это поможет подоборать слагаемое для красного поля, называемое остатком от выделения. Я бы советовал репетиторам именно здесь указывать на то, что этот остаток можно находить вычитанием. Выполняя такую операцию получим:

Репетитор по математике должен обратить внимание ученика на то, что подставляя единицу в данное равенство, мы гарантировано получим нуль в его левой части (так как 1 — корень первоначального многочлена), а в правой, очевидно, тоже обнулим первое слагаемое. Значит без всякой проверки можно сказать, что единица — корень «зеленого остатка».

Поступим с ним так же, как мы это сделали с первоначальным многочленом, выделяя из него такой же линейный множитель . Репетитор по математике рисует перед учеником две рамки и просит заполнить слева направо.

Ученик подбирает репетитору одночлен для красного поля так, чтобы он при умножении на старшее слагаемое линейного выражения давал старшее слагаемое раскладывающегося многочлена. Вписываем в касную рамку, тут же раскрываем скобку и выделяем синим цветом то выражение, которое надо вычесть их раскладывающегося. Выполняя эту операцию получаем

И, наконец, проделывая тоже самое с последним остатком

получим окончательно

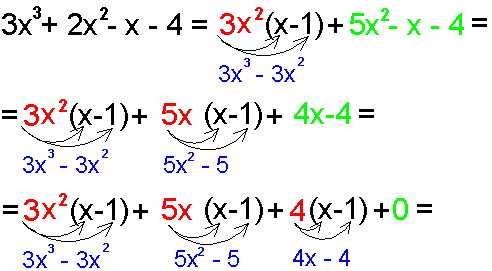
Теперь вынесем выражение за скобку и перед нами окажется разложение первоначального многочлена на множители один из которых «икс минус подобранный корень».

Для того, чтобы ученику не казалось, что последний «зеленый остаток» случайно разложился на нужные множители, репетитор по математкие должен указать на важное свойство всех зеленых остатков — каждый из них имеет корень 1. Поскольку степени этих остатков убывают, то какая бы степень начального многочлена ни была нам дана, рано или поздно, мы получим линейный «зеленый остаток» с корнем 1, а следовательно он обязательно разложиться на произведение некоторого числа и выражения .

После такой подготовительной работы репетитору по математкие не составит труда объяснить ученику, что происходит при делении уголком. Это тот же самый процесс, только в более краткой и компактной форме, без знаков равно и без переписываний одних и тех же выделенных слагаемых. Многочлен из которого выделяется линейный множитель записываем слева от уголка, подбираемые красные одночлены собираем под уголом (теперь становится понятно, почему они должны складываться), для получения «синих многочленов» надо «красные» умножать на x-1, а затем вычитать из текущего выделяемого как это делается при обычном делении чисел в столбик (вот она аналогия с раннее изученным). Получаемые «зеленые остатки» подвергаются новому выделению и подбору «красных одночленов» . И так до получения нулевого «зеленого остатка». Самое главное, что ученику становится понятна дальнейшая судьба записанных многочленов над и под уголком. Очевидно, это скобки, произведение которых равно первоначальному многочлену.

Следующий этап работы репетитора по математике — формулирование теоремы Безу. Cобственно ее формулировка при таком подходе репетитора становится очевидной: если число а — корень многочлена, то его можно разложить на множители, один из которых , а другой получается из первоначального одним из трех способов:

• непосредственным разложением (аналогом метода группировки)
• делением уголком (в столбик)
• через схему Горнера

Надо сказать, что схему горнера показывают ученикам далеко не все репетиторы математики и не все школьные преподаватели (к счастью для самих репетиторов) заходят на уроках так глубоко в тему. Однако, для учащегося математического класса я не вижу никаких оснований для остановки на делении в столбик. Более того, самый удобный и быстрый прием разложения основан именно на схеме Горнера. Для того, чтобы объяснить ребенку откуда она берется достаточно проследить на примере деления уголком появление старших коэффициентов у зеленых остатках. Становится ясно, что старший коэффициент начального многочлена сносится в коэффициент первого «красного одночлена», а дальше от второго коэффициента текущего верхнего многочлена вычитается результат умножения текущего коэффициента «красного одночлена» на . Поэтому можно прибавлять результат умножения на . После акцентирования внимания ученика на специфике действий с коэффициентами репетитор по математике может показать как обычно эти действия выполняют без записи самих переменных. Для этого удобно корень и коэффициенты первоначального многочлена по старшинству занести в такую таблицу:

Если в многочлене пропущена какая-нибудь степень, то в таблицу принудительно вносится ее нулевой коэффициент. В нижнюю строчку поочередно вписываются коэффициенты «красных многочленов» по правилу «крючка»:

Корень умножается на последний снесенный «красный коэффициент», прибавляется к следующему коэффициенту верхней строки и результат сносится в нижнюю строчку . В последней колонке гарантированно получим старший коэффициент последнего «зеленого остатка», то есть нуль. После завершения процесса, числа, зажатые между подобранным корнем и нулевым остатком оказываются коээффициентами второго (нелинейного) множителя.

Поскольку корень а дает в конце нижней строки нуль, то схему Горнера можно использовать для проверки чисел на звание корень многочлена. Если специальная теорема о подборе рационального корня. Все кандидаты на это звание, полученные с ее помощью, просто вставляются по очереди слева в схему Горнера. Как только мы получим нуль, тестируемое число будет корнем, и одновременно его строчке получим коэффициенты разложения первоначального многочлена на множители. Очень удобно.

В завершение хотелось бы отметить, что для аккуратного ввдения схемы Горнера , а также для практического закрепления темы, репетитор по математике должен иметь в своем распоряжении достаточное количество часов. Репетитору, работающему с режимом «раз в неделю» не стоит заниматься делением уголком. На Егэ по математике и на ГИА по математике вряд ли в первой части когда-нибудь встретится уравнение третьей степени, решаемое такими средствами. Если репетитор готовит ребенка экзамену по математике в МГУ — изучение темы становится обязательным. Очень уж любят преподаватели ВУЗов, не в пример составителям ЕГЭ, проверить глубину знаний абитуриента.

Колпаков Александр Николаевич, репетитор по математике Москва, Строгино

Метки: Примеры объяснений, Репетиторам по математике

ankolpakov.ru

No related posts.