Характеристика и мантисса десятичного логарифма.
2015-06-14 Десятичный логарифм
Характеристика и мантисса
Десятичным логарифмом числа называется его логарифм по основанию 10. Кроме общего обозначения $log_{10} N$ для десятичных логарифмов обычно применяют сокращенное обозначение $lg N$.
Десятичные логарифмы широко применяются в приближенных вычислениях; в связи с этим имеются подробные и весьма точные таблицы десятичных логарифмов.Для применения к приближенным вычислениям нам потребуются некоторые свойства и понятия, относящиеся к десятичным логарифмам.
Рассмотрим все числа вида $10^{n}$, где $n$ — целое число:
$\cdots; 10^{-3} = 0,001; 10^{-2} = 0,01; 10^{-1} = 0,1; 10^{0} = 1; 10^{1}=10; 10^{2}=100; 10^{3} = 1000; \cdots$
Будем говорить, что эти числа представляются единицей с нулями (с последующими нулями, если $n > 0$, и с предшествующими нулями, если $n
Десятичный логарифм числа, представляемого единицей с нулями, равен числу нулей в этом числе, если оно есть единица с последующими нулями, и числу нулей с противоположным знаком, если оно есть единица с предшествующими нулями.
Например:
$lg 0,0001=-4, lg 0,01=-2, lg 1000 = 3, lg 1000000 = 6$.
Десятичный логарифм любого числа, не равного целой степени десяти, является числом дробным (вообще говоря, иррациональным).
Напомним, что всякое число (рациональное или иррациональное) однозначно разлагается на сумму своей целой части и дробней части. При этом целой частью данного числа называется наибольшее целое число, не превосходящее данного; дробная часть любого числа заключена между нулем и единицей:
$3,176 = 3 + 0,176; — 2,143 = — 3 + 0,857 = \overline{3},857$.
Введем теперь следующее.
Определение. Для любого положительного числа целая часть десятичного логарифма называется характеристикой, а дробная часть—мантиссой этого логарифма.
Характеристику логарифма любого положительного числа можно найти точно, и делается это с помощью простого правила. Действительно, пусть дано число $N > 0$; тогда можно указать такие две степени числа 10 с последовательными целыми показателями $n$ и $n + 1$, между которыми находится данное число $N$:$10^{n}
Прологарифмируем эти неравенства по основанию 10:
$n \leq lg N
в соответствии со свойством 5 логарифмов (Определение и свойства логарифмов). Отсюда следует, что целая часть, т. е. характеристика $lg N$, равна $n: lg N = n, \cdots$ Многоточием обозначены неизвестные десятичные знаки мантиссы, т. е. дробной части $lg N$. При этом в случае $n
Для формулировки соответствующего правила рассмотрим два случая: $N > 1$ и $N
Пусть $N > 1$ (десятичный логарифм $lg N$ в этом случае положителен). Обозначим через $k$ число цифр в записи целой части $N$. Ясно, что в этом случае
$10^{k-1} \leq N
Например, для $N = 378,6$ (трехзначная целая часть)
$10^{2} \leq 378,6
Логарифмируя неравенства (1), получаем
$k – 1 \leq lg N
и видим, что характеристика $lg N$ равна $k – 1$ (например, характеристика логарифма 378,6 равна 2).
Итак, характеристика десятичного логарифма числа, большего единицы, на единицу меньше количества цифр его целой части.
Например:
$lg 3,524 = 0, \cdots; lg 47,01 = 1; \cdots, lg 936,3 = 2, \cdots$
Пусть теперь положительное число $N$ меньше единицы: $0
Запись числа $N$ начинается в этом случае с нуля целых; за этим нулем может следовать еще несколько нулей перед первой отличной от нуля цифрой числа. Если число нулей перед первой ненулевой цифрой (включая и нуль целых) равно $l$, то
$1^{-l} \leq N
Например:
$10^{-1} \leq 0,32 $10^{-2} \leq 0,032 $10^{-3} \leq 0,0032 $\cdots \cdots$
Неравенства (3) показывают, что
$- l \leq lg N
т. е. характеристика логарифма $lg N$ равна $-l$.
Итак, характеристика десятичного логарифма положительного числа, меньшего единицы, равна взятому со знаком минус числу нулей в данном числе, предшествующих первой значащей цифре, включая и нуль целых.
Например:
$lg 0,3052 = \overline{1}, \cdots; lg 0,0587 = \overline{2} \cdots; lg 0,0096 = \overline{3}, \cdots$
Мы выяснили, что характеристика десятичного логарифма числа определяется непосредственно по виду самого числа, если оно целое или представлено в виде десятичной дроби. Для определения характеристики, таким образом, не нужны никакие вычисления (и таблицы). Что же касается мантиссы, то она, как правило, берется из таблиц (например, из таблиц Брадиса). При этом следует пользоваться одним замечательным свойством мантиссы: если в логарифмируемом числе перенести запятую на любое количество знаков влево или вправо, то мантисса десятичного логарифма от этого не изменится (изменится только характеристика логарифма). В самом деле, перенести в числе запятую — это значит умножить его на некоторую целую (положительную или отрицательную) степень числа 10. Например, при переносе запятой на 2 знака вправо число умножится на $10^{2} = 100$, а при переносе запятой на 2 знака влево оно умножится на $10^{-2} = 1/100$. Пусть
$lg N = n + m$,
где $n$ — характеристика, а $m$ — мантисса этого логарифма. После переноса запятой в числе $N$ на $k$ знаков получится число $N \cdot 10^{ \pm k}$t (верхний знак относится к случаю переноса запятой вправо, а нижний — к случаю переноса запятой влево). На основании правил логарифмирования имеем
$lg (N \cdot 1^{\pm k}) = lg N \pm k lg 10 = lg N \pm k$.
Но $k$ — целое число, так что прибавление $\pm k$ к $lg N$ может отразиться лишь на его характеристике:
$lg (N \cdot 10^{\pm k}) = n + m \pm k = (n \pm k) + m$.
Из рассмотренного можно заключить, что если числа записаны с помощью одних и тех же и одинаково расположенных цифр и отличаются одно от другого только местоположением в них запятой, то десятичные логарифмы таких чисел имеют одну и ту же мантиссу (но, конечно, разные характеристики!). Таковы, например, числа $42,59, 4,259, 0,4259, 0,04259$ и т. д.
В качестве примера найдем без таблиц разность $lg 28,76 — lg 0,002876$.
Логарифмы, из которых составлена данная разность, отличаются лишь характеристиками, а мантиссы у них одинаковы и при вычитании взаимно уничтожаются. Поэтому искомая разность логарифмов равна разности их характеристик: $lg 28,76 – lg 0,002876 = 1 — ( — 3) = 1 + 3 = 4$. Этот пример можно решить и так:
$lg 28,76 — lg 0,002876 = lg \frac{28,76}{0,002876} = lg 10000 = lg 10^{4} = 4$.
earthz.ru
Таблица и формула для перехода от десятичных логарифмов к натуральным. Если Вам известен десятичный логарифм какого-то числа Х (равный lg(X)), то натуральный логарифм этого числа (равный ln(X)) будет равен, согласно основным свойствам логарифмов : ln(X)=In10*lg(X)=(1/Ig(e))*lg(X)=(1/M)*lg(X), т.е. натуральный логарифм числа, равен десятичному логарифму этого числа умноженному на «число 1/М»=1/Ig(e). Для быстрых оценок приводим табличку: Таблица для перехода от десятичных логарифмов к натуральным (таблица умножения на «число 1/М» (у англосаксов это «число 1/A») = In 10 = 2,3025851).
|
tehtab.ru
Таблица Брадиса — натуральные логарифмы.
| ||||||||||
tehtab.ru
ТерминологияОтыскание логарифма данного числа
Отыскание числа по данному логарифму
Логарифмы применяются для замены сложных математических действий более простыми, например возвышение в степень приводится при помощи логарифмов к умножению, извлечение корня — к делению и т. д.
Терминология. Если Ab = N, то b = log a N; логарифм числа N при основании «a» есть степень, в которую нужно возвести число «а», чтобы получить число N; «а» называется основанием логарифма. Логарифмы, употребляемые обычно в вычислениях, называются десятичными (обыкновенными, Бригговыми) и имеют основание а = 10.
Логарифмы при основании е = 2,7182818284… называются натуральными или неперовыми и вместо lg е N принято обозначение ln N.
Между натуральными и десятичными логарифмами существуют следующие зависимости:
Логарифм состоит из целой части, называемой характеристикой, и дробной части, называемой мантиссой, например, lg 25 = 1,39794, здесь 1 — характеристика, 39794 — мантисса.
Мантисса находится по таблицам логарифмов, а характеристика определяется в зависимости от количества цифр целой части числа N > 1, логарифм которого отыскивается, или в зависимости от положения запятой в случае, если N
Логарифмы целых чисел не выше трехзначных находятся непосредственно в таблице имеющейся на этом сайте; для того же, чтобы отыскать логарифм числа N 1, имеющего не более трех значащих цифр и на конце несколько нулей, отбрасывают запятую и нули справа и слева, затем ищут в таблице для полученного таким образом числа логарифм, из которого берут только мантиссу, характеристику же определяют по правилу, поясненному ниже:

Мантисса логарифмов всех этих чисел одна и та же, так как, если отбросить запятую и нули справа и слева у этих чисел, то получится одно и то же трехзначное число 758. Мантисса равна 87967. Характеристика логарифма каждого числа равна его значности минус единица.
Если после отбрасывания запятой и нулей останется число, содержащее больше трех значащих цифр, то логарифм его можно найти приближенно, отбрасывая при отыскании мантиссы все цифры, кроме первых трех.
Пример. Найти приближенно lg 40,536. Находим мантиссу логарифма числа 405, она равняется 60746 это приблизительно равно 6075; характеристика равняется 1, следовательно, lg 40,536, что приблизительно равно 1,6075.
По мантиссе логарифма отыскивается число. Количество цифр и положение запятой определяются по правилу, указанному выше.
Пример, lg N =3,2380. По мантиссе 2380 находим число 173. Так как характеристика равна 3, то число должно быть четырехзначным, следовательно, N приблизительно равняется 1730.
Из определения логарифма числа следует:
Натуральные и десятичные логарифмы отрицательных чисел мнимы.
Действия с логарифмами:
Эти зависимости сохраняют силу при любом основании логарифмов.
cnc.im
ШВЕЦОВ К.И., БЕВЗ Г.П. 
СОДЕРЖАНИЕ ДАННОЙ СТАТЬИ Решения. а) б) в) 36. Десятичные логарифмы 1. Свойства десятичных логарифмов а) Логарифм целого числа, изображенного единицей с последующими нулями, есть целое положительное число, содержащее столько единиц, сколько нулей в данном числе. Примеры, lg 100 = 2; lg 10000 = 4. б) Логарифм десятичной дроби, изображаемой единицей с предшествующими нулями, есть целое отрицательное число, содержащее столько отрицательных единиц, сколько нулей в изображении дроби, считая и 0 целых. Примеры. lg 0,00001 = -5; lg 0,001 = -3. в) Логарифм рационального числа, которое не является степенью 10 с целым показателем (положительным, отрицательным или нулевым), есть иррациональное число. Логарифм иррационального числа может быть как рациональным, так и иррациональным числом. Например, (рациональное число), (иррациональное число). Целая часть логарифма называется его характеристикой, а дробная — мантиссой. г) Характеристика логарифма числа, большего единицы, на единицу меньше числа цифр его целой части. Примеры. lg 3,15 = 0,…; lg 375 = 2,…; lg 2000 = 3,… д) Характеристика логарифма числа, меньшего единицы, содержит столько отрицательных единиц, сколько нулей в этом числе предшествует первой значащей цифре, считая и нуль целых. При этом мантисса логарифма положительна. Примеры. е) От умножения числа на 10, 100, 1000,…, вообще на единицу с последующими нулями, мантисса логарифма не меняется, а характеристика увеличивается на столько единиц, сколько нулей в множителе. От деления числа на единицу с нулями мантисса логарифма не изменяется, а характеристика уменьшается на столько единиц, сколько нулей в делителе. Поэтому перенесение запятой в десятичной дроби на несколько знаков вправо или влево не изменяет мантиссы логарифма этой дроби, а только характеристику. Таким образом, логарифмы чисел 0,00423; 0,0423; 4,23; 423 отличаются только характеристиками, но не мантиссами (при условии, что все мантиссы положительны). Мантиссы логарифмов чисел, имеющих одну и ту же значащую часть, одинаковы. 2. Преобразование отрицательного логарифма. Известно, что десятичные логарифмы чисел, меньших 1, отрицательны. Такие логарифмы всегда можно преобразовать так, что мантисса у них будет положительная, а характеристика — отрицательной. Это выполняется по следующему правилу. Чтобы преобразовать логарифм с отрицательной мантиссой в логарифм с положительной мантиссой, надо к характеристике прибавить минус единицу, а к мантиссе прибавить плюс единицу. Так, например, если мы имеем логарифм -2,3781, то можно его преобразовать так: -2,3781 = -2 — 0,3781 = (-2 — 1) + (1 — 0,3781) = -3 + 0,6219 = . Кратко эти действия записывают так: Примеры. 3. Таблицы десятичных логарифмов. Существуют таблицы, в которых даются десятичные логарифмы всех чисел с точностью до трех, четырех, пяти и т.д. десятичных знаков. Соответственно этому их называют трехзначными, четырехзначными, пятизначными и т.д. Чаще всего пользуются четырехзначными таблицами десятичных логарифмов. Эти таблицы содержат мантиссы логарифмов всех целых чисел от 1 до 9999 включительно, вычисленные с четырьмя десятичными знаками. Этими таблицами пользуются так. Пример 1. Найдем десятичный логарифм трехзначного числа 73,3. Его характеристика 1, так как в числе 73 две цифры. Чтобы найти мантиссу, отбрасываем запятую и ищем мантиссу числа 733. В столбце, обозначенном буквой N, находим число 73. Двигаясь по строке, в которой находится число 73, до пересечения ее со столбцом, обозначенным цифрой 3, находим 8651. Число 0,8651 и будет искомой мантиссой. Итак, lg 73,3 = 1,8651. ⇦ Ctrl предыдущая страница / страница 132 из 168 / следующая страница Ctrl ⇨мобильная версия страницы Смотрите также на этом сайте: ГАДАНИЯ, СОННИКИ, ЗАГОВОРЫ, НУМЕРОЛОГИЯ, ХИРОМАНТИЯ, ВУДУ, МАЯТНИК, ДЕНЕЖНАЯ МАГИЯ ВЯЗАНИЕ НА СПИЦАХ, КРЮЧКОМ, ТУНИССКОЕ ВЯЗАНИЕ, МОДЕЛИ ВЯЗАНОЙ ОДЕЖДЫ; ШИТЬЕ; МАШИННОЕ ВЯЗАНИЕ РАЗНООБРАЗНЫЕ КУЛИНАРНЫЕ РЕЦЕПТЫ; ГОРШОЧКИ, МИКРОВОЛНОВКА; КОНСЕРВИРОВАНИЕ СПРАВОЧНИКИ ПО ФИЗИКЕ, МАТЕМАТИКЕ, АНГЛИЙСКОМУ ЯЗЫКУ; ПОХУДЕНИЕ, АКУПУНКТУРА; НЕИСПРАВНОСТИ АВТОМОБИЛЯ МНОЖЕСТВО ИСТОРИЧЕСКИХ ФАКТОВ О СОБЫТИЯХ, ОРУЖИИ И ОБМУНДИРОВАНИИ ВТОРОЙ МИРОВОЙ ВОЙНЫ; АРМЕЙСКИЕ БОТИНКИ ВСЕХ ВРЕМЕН ПОПУЛЯРНЫЕ ПЕСЕННИКИ 1963-1987 гг.; ТОСТЫ, РОЗЫГРЫШИ, КОНКУРСЫ Пользуйтесь поиском вверху страницы! Все, что будет найдено со значком Ł — относится к данному сайту | 
|
cartalana.org
Мантиссы десятичных логарифмов, таблицы — Энциклопедия по машиностроению XXL
| Таблица V. МАНТИССЫ ДЕСЯТИЧНЫХ ЛОГАРИФМОВ | 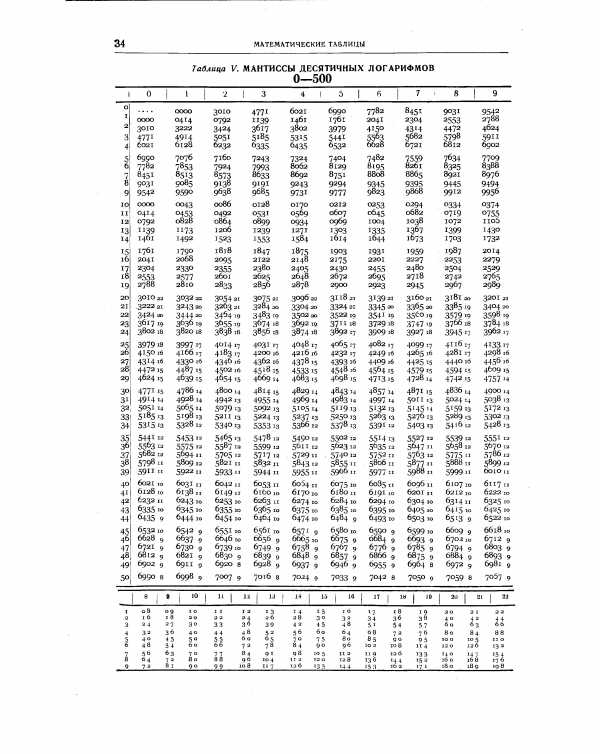 |
Отыскание чисел по их десятичным логарифмам. Для отыскания числа по его логарифму может быть использована та же таблица мантисс (табл. V, стр. 34). Если мантисса меньше 0,3030, то соответ- [c.107]
Мантисса находится по таблицам логарифмов, а характеристика определяется в зависимости от количества цифр целой части числа, логарифм которого разыскивается, или в зависимости от положения запятой в случае десятичной дроби, как указано в табл. 1. [c.85]
Логарифмы целых чисел не выше трехзначных находятся непосредственно в этой таблице для того же, чтобы отыскать логарифм числа N десятичной дроби) или числа 1, имеющего не более трех значащих цифр и на конце несколько нулей, отбрасывают запятую и нули справа и слева, затем ищут в таблице для полученного таким образом числа логарифм, из которого берут только мантиссу, характеристику же определяют по правилу, поясненному ниже [c.67]
Нахождение логарифма (десятичного) трехзначного числа производится непосредственно по таблице, а для числа с тремя значащими цифрами из таблицы берется мантисса, характеристика же устанавливается по правилам алгебры. Например, [c.34]
Математические таблицы даны, соответственно обычной практике технических справочников, в нижеследующем объёме степени, корни, натуральные логарифмы, длины окружностей, площади кругов и обратные величины (табл. I), мантиссы десятичных логарифмов (таблица 2), натуральные значения тригонометрических функций (табл. 3), характеристики дуг (табл. 4—6), специальные фужции (табл. 7 и 8), важнейщие постоянные (табл. 9) и сводка расчётных характеристик плоских фигур и тел (табл. 10 и 11). [c.9]
Мантиссы десятичных логарифмов (табл. 2) и натуральные значения тригонометрических функций (табл. 3) даны в расширенном объёме шестизначные мантиссы десятичных логарифмов для аргументов от 1 до 10000, шести-и семизначные таблицы тригонометрических функций через Г. Столь подробные таблицы исключают необходимость применения специальных математических справочников и позволяют осуществлять с необходимой точностью даже наиболее строгие вычисления по геодезии, механике, электротехнике и т. п. [c.9]
Десятичные, или бригговы, логарифмы имеют основанием число 10 и обозначаются символом Ig. Правила вычислений с десятичными логарифмами см. стр. 107. Таблица мантисс, т. е. дробной части числа, представляющего логарифм, приведена на стр. 34. [c.113]
В шестой графе таблицы, помещённой на стр. 14, указаны десятичные логарифмы целых чисел от 1 до 1000. Таким образом логарифмы целых чисел не выше трёхзначных отыскиваются непосредственно по таблицам. Для того же, чтобы разыскать логарифм десятичной дроби или числа, имеющего на конце несколько нулей, отбрасывают запятую и нули справа и слева и, обратив его в целое трехзначное число, ищут по таблицам (стр. 14) его логарифм, из которого берут только мантиссу, характеристику же опреде- ляют по правилу, пояснённому в табл. 1. [c.85]
Для определения десятичных логарифмов чисел сначала для данного числа находят характеристику его логарифма, а затем — мантиссу по таблице. Для трехзначных чисел мантиссу находят на пересечении строки, в начале которой (графа Щ стоят две первые цифры данного числа, и столбца-, озаглавленного третьей цифрой. Если заданное число имеет больше трех значапщх цифр, необходимо применить линейную интерполяцию. [c.442]
Для нахождения числа по его десятичному логарифму служит таблица вдагаржфмов. Аргументом в этой таблице является мантисса заданного логарифма. На пересечении строки, определяемой двумя Первыми [c.449]
Десятичные логарифмы записываются в виде десятичной дроби с точностью до определённого десятичного знака её целая часть называется характеристикой логарифма, а дробная —мант и сс ой например, Ig 285 = 2,454845, здесь 2 —характеристика, а 454845 — мантисса. Если число больше единицы, то характеристика положительна и на единицу меньше числа его цифр, стоящих перед запятой если число меньше единицы, то характеристика отрицательна и по абсолютной величине равна числу нулей слева, включая и нуль целых. Мантисса отыскивается по таблицам логарифмов, причём на положение запятой и на нули слева и справа не обращают внимания, так как числа, получающиеся из данного путём умножения или деления на 10 имеют одинаковые мантиссы. Мантисса всегда берётся положительной, поэтому если логарифм отрицательный, то знак минус ставится над характеристикой (3,820714= —3+0,820714= — 2,179286). [c.107]
mash-xxl.info
Мантиссы логарифмов — Справочник химика 21
Четырехзначные мантиссы логарифмов приведены в таблице п. 76. Пользование таблицей иллюстрируется примерами [c.524]
ЧЕТЫРЕХЗНАЧНЫЕ МАНТИССЫ ЛОГАРИФМОВ [c.220]
Четырехзначные мантиссы логарифмов [c.791]
Нахождение логарифмов чисел. Пусть требуется найти логарифм числа 456,78. Так как это число содержит пять значащих цифр, а четырехзначные таблицы логарифмов дают точность только до четвертой цифры, округляем это число до 456,8. Пишем характеристику логарифма, равную числу целых цифр без одной 2. Далее, не обращая внимания на запятую, находим мантиссу логарифма числа 4568. Для этого отыскиваем в таблице логарифмов точку пересечения горизонтального ряда, отвечающего перным двум цифрам этого [c.237]
Правила пользования таблицей 14. В таблице приведены трехзначные мантиссы логарифмов. Для вычисления [Н» ] по известному pH находят в первом вертикальном столбце первый знак мантиссы величины pH и в первой горизонтальной строке — второй знак этой мантиссы. Затем в точке пересечения линий, идущих от найденных цифр, получают значение [Н ], которое надо еще умножить на 10 в степени, равной характеристике pH, взятой в отрицательным знаком. Например, [c.260]
Следует учитывать, что при пользовании таблицами десятичных логарифмов числа будут определяться с относительной погрешностью, равной —где п — число знаков мантиссы логарифмов, [c.774]Представления о значащих цифрах применимы и в том случае, когда для вычислений используются логарифмы. Используя правила, аналогичные изложенным выше, следует сохранять в мантиссе логарифма такое же число значащих цифр, какое содержится в исходной численной величине, или еще одну значащую цифру, если исходная величина ближе к следующей степени 10, чем к предыдущей степени 10. Например, логарифм числа 2,472 должен быть записан с мантиссой, содержащей три цифры, а логарифм числа 9,236 — с мантиссой, содержащей четыре цифры. Обычно для подобных вычислений используют таблицы четырехзначных логарифмов. Логарифмическая линейка дает одинаковую точность во всех частях шкалы. [c.519]
В графе определяют указана формула вещества, процентное содержание которого определяют в графе получено — состав весовой формы в графе множитель — число, представляющее собой величину отношения атомного или молекулярного веса определяемого соединения к молекулярному весу весовой формы или к ее кратному значению в гра([ое логарифм приводится значение мантиссы логарифма множителя (фактора) в вычислениях, требующих перемножения нли деления многозначных чисел, необходимо пользоваться логари( )мами или логарифмической линейкой. [c.151]
По таблице пропорциональных частей при табличной разности, равной 7, на 3 единицы числа нужно прибавить 2,1 к мантиссе (см. пятизначные мантиссы логарифмов, таблицу). [c.247]
Определено Ищут Фактор Мантисса логарифма Определено Ищут Фактор Мантисса логарифма [c.357]
Логарифм числа состоит из характеристики (цифра перед запятой) и мантиссы (цифры после запятой). Логарифмы чисел с рядом одинаковых цифр различаются только характеристикой, мантисса же числа остается одной и той же. Например, числа 6265,3 62,653 0,0062653 0,000062653 будут иметь мантиссу 79 694. Ее берут из таблицы мантисс логарифмов. Характеристику определяют по числу цифр, стоящих перед запятой. Если число начинается не с нуля, то характеристика будет на единицу меньше числа цифр, стоящих до запятой, например 6265,3=3,79694 1 62,653== = 1,79694. [c.246]
Взамен обычной таблицы пятизначных логарифмов в конце книги приведена упрощенная таблица пятизначных логарифмов и антилогарифмов. Она занимает такой же объем, какой имеют таблицы четырехзначных логарифмов. Это достигнуто тем, что взамен действительных значений разностей между мантиссами даны средние их значения для каждой строки таблицы. Ошибки, возникающие при работе с этой таблицей, не превышают 0,00002. В других таблицах справочника приведены точные значения пятизначных мантисс логарифмов. [c.8]
Если данные, предназначенные для хранения, выражены обычно в их натуральной форме, то для построения стебля с листьями можно (а иногда и необходимо) использовать преобразованные числа, в наиболее простом случае — логарифмы исходных данных. Шкала логарифмов как бы расширяет диапазон распределений последних цифр разрядов (фактически — мантисс логарифмов). [c.149]
Для нахожд
www.chem21.info
