Таблица степени брадиса – Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса

Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса

Техническая информация тут Перевод единиц измерения величин Таблицы числовых значений Алфавиты, номиналы, единицы Математический справочник тут Физический справочник Химический справочник Материалы Рабочие среды Оборудование Инженерное ремесло Инженерные системы Технологии и чертежи Личная жизнь инженеров Калькуляторы Поиск на сайте DPVAПоставщики оборудованияПолезные ссылкиО проектеОбратная связьОтветы на вопросы.Оглавление

Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Математический справочник  / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса Таблица умножения — традиционная 10×10, 12х12 и 20х20Таблица деления — традиционная 10×10 и 12х12Таблицы квадратов чисел от 1. Таблица квадратов от 1 до 100. Таблица квадратных корней. Натуральных чисел от 1 до 30 и от 1 до 100. Таблица квадратов больших чисел. Квадраты чисел. Удобная расчетная таблица 1,00 — 9,99.Таблица квадратов — таблица квадратных корней натуральных чисел от 1 до 99 (от 1 до 9, от 10 до 99 ). Таблица квадратных корней. Квадраты чисел. Корни чисел.Таблица квадратов натуральных (целых) чисел от 1 до 999. Таблица квадратных корней.Таблицы кубов. Таблица кубических корней. Кубы натуральных чисел от 1 до 20 и от 1 до 100. Удобная расчетная таблица 1,00 — 9,99. Таблица кубических корней.Степени — квадрат и куб, корни — квадратный и кубический и обратные величины чисел от 1 до 100. Таблица степеней от 1 до 100. Таблица корней от 1 до 1000000Таблица степеней степеней. Степени натуральных чисел от 2 до 25 (включая от «2 до 10» и от «2 до 20»). Степени от 2 до 10. Таблица степеней.Таблица 4-ой и 5-ой степени чисел от 1 до 100.Точная и приблизительная таблицы факториалов (1!-255!)Таблицы логарифмов и основные формулы Таблица. Длина окружности диаметра D. Длина окружности через радиус (радиус=полдиаметра). Диаметр через длину окружности. Диаметр (радиус) через охват. Окружность трубы. Окружность столба.Таблица соотношений между длинами дуг, стрелками, длинами хорд, площадями сегментов при радиусе, равном единице.

dpva.ru

Таблицы Брадиса. Значения тригонометрических, логарифмических функций. Прочее

Техническая информация тут Перевод единиц измерения величин Таблицы числовых значений Алфавиты, номиналы, единицы Математический справочник тут Физический справочник Химический справочник Материалы Рабочие среды Оборудование Инженерное ремесло Инженерные системы Технологии и чертежи Личная жизнь инженеров Калькуляторы Поиск на сайте DPVAПоставщики оборудованияПолезные ссылкиО проектеОбратная связьОтветы на вопросы.Оглавление

Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса  / / Таблицы Брадиса. Значения тригонометрических, логарифмических функций. Прочее Таблица Брадиса тригонометрические функции sin x, cos x, tg x от аргумента в радианах. Значения тригонометрических функций.Таблица Брадиса тригонометрические функции sin x, cos x от аргумента в угловых градусах. Таблица Брадиса синусы-косинусы. Значения тригонометрических функций.Таблица Брадиса тригонометрические функции tg x, ctg x от аргумента в угловых градусах. Таблица Брадиса тангенсы-котангенсы. Значения тригонометрических функций.Таблица Брадиса — тангенсы углов, близких к 90°, котангенсы малых углов. Значения тригонометрических функций.Таблица Брадиса — десятичные логарифмы синусов малых углов, десятичные логарифмы косинусов углов, близких к 90° Значения тригонометрических функций.Таблица Брадиса — десятичные логарифмы синусов углов от 14° до 90° и косинусов углов от 0° до 76°Таблица Брадиса — десятичные логарифмы тангенсов малых углов, логарифмы котангенсов углов, близких к 90°

dpva.ru

Таблица Брадиса — энциклопедический справочник и словарь для студента от А до Я

ОПРЕДЕЛЕНИЕ

Таблицы Bradis представляют собой наиболее полную коллекцию всех синусоидальных, косинусных, касательных, кокасательных и других значений. Эти таблицы очень точны, достигая четырех знаков после запятой, что позволяет использовать их как для решения школьных задач в алгебре, геометрии, физике, так и для расчета сложных технических расчетов.

Правила использования таблиц: таблицы дают значения синусов (косинусов) любого острого угла, содержащие целое число и десятые доли градуса, на пересечении линии, имеющей соответствующее количество градусов в заголовке слева и столбец в заголовке выше количества минут.

ВНИМАНИЕ, в данной статье таблица приведена в виде изображения, и годится для вычислений, если вам необходимо скопировать таблицу в текстовом виде, перейдите по ссылке.

Тригонометрические функции sin x и cos x аргумента в градусах

Тригонометрические функции Брадиса tg x, ctg x аргумента в градусах

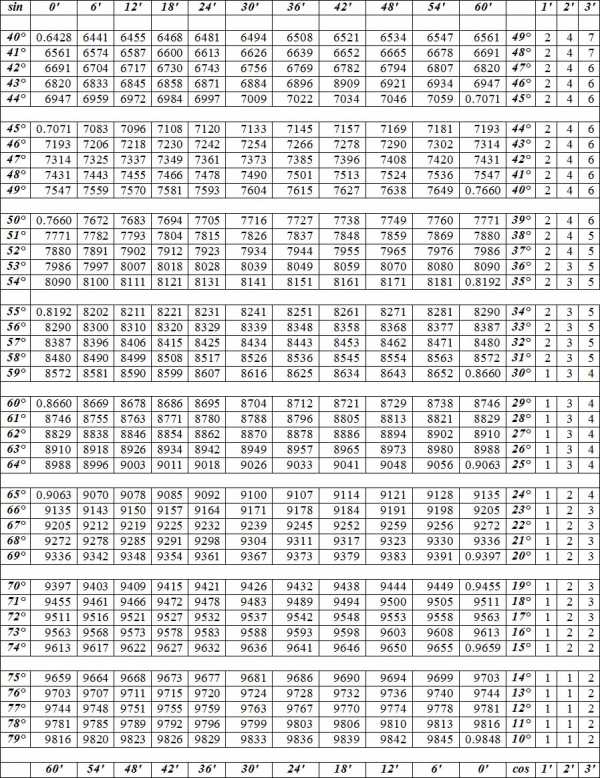
Таблица Брадиса — касательные углов, близкие к 90 °, котангенсы малых углов

Тригонометрические функции аргумента в радианах

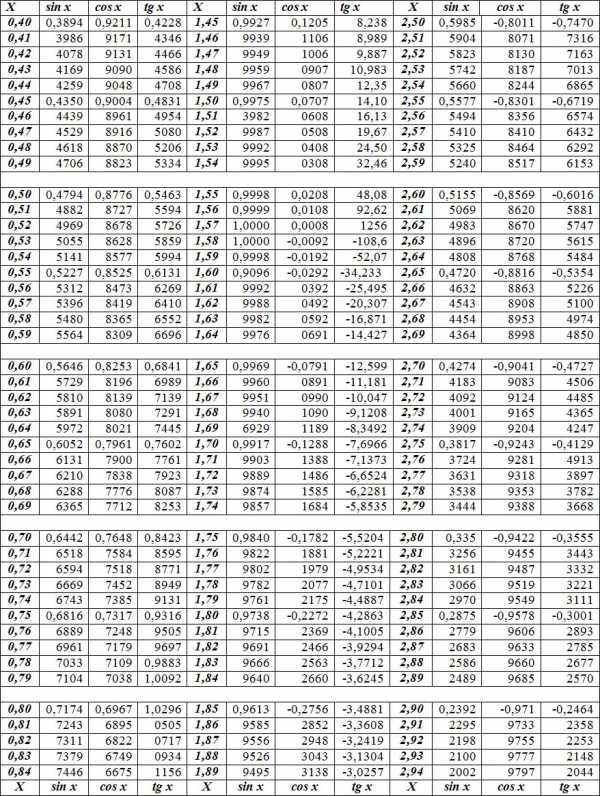
Примеры решения проблем

ПРИМЕР 1

Задача

Значение поиска

Решение.

В таблице значений синуса и косинуса в первом столбце находим и в первой строке . На пересечении соответствующей строки и столбца находится желаемое значение, равное 0,7254.

Ответ

ПРИМЕР 2

Задача

Найти значение

Решение.

В таблице значений синуса и косинуса в столбце углов с заголовком находим и в нижней строке . На пересечении соответствующей строки и столбца находится желаемое значение 0.2284.

Ответ

Если вам нужно найти значение угла, которого нет в таблице, то выбирается самое близкое к нему значение, а значение коррекции берется из колонки коррекции справа (возможная разница равна 1 ‘, 2’ , 3 ‘).

ПРИМЕР 3

Задача

Найти значение

Решение.

Чтобы вычислить значение в таблице, мы найдем значение синуса угла, ближайшего к искомому. Это . Так как , то в столбце поправок выберем и видим, что на пересечении с строкой равен 0,0006,

Ответ

ПРИМЕР 4

Задача

Значение поиска

Решение.

Чтобы вычислить значение в таблице, мы найдем значение синуса угла, ближайшего к искомому. Это . Начиная с , мы выбираем в столбце исправлений и видим, что на пересечении с строкой равен 0,0005,

Ответ

Комментарий. Для косинусов коррекция отрицательна.

ПРИМЕР 5

Задача

Найти значение

Решение.

Чтобы вычислить значение в таблице, мы найдем значение косинуса угла, ближайшего к искомому. Это . Так как , то в столбце поправок выберите и посмотрите, что на пересечении с строкой равен 0,0007,

Ответ

Эти правила справедливы и для нахождения значений касательных и котангенсов углов.

ПРИМЕР 6

Задача

Найти значение

Решение.

В таблице касательных и котангенциальных значений в первом столбце находим и в первой строке . На пересечении находим искомое значение 0.7028

Ответ

ПРИМЕР 7

Задача

Найти значение

Решение.

В таблице кокасательных значений малых углов в последнем столбце находим строку , а в последней строке . На пересечении находится желаемое значение 4,102

Ответ

Пример 8.

Задача

Найти значение и

Решение.

Поскольку в радианах указаны углы, мы используем таблицу значений тригонометрических функций аргумента в радианах. Найти в нем необходимые значения и

Ответ

и

sciterm.ru

Таблица Брадиса. Таблицы Брадиса.

Общие правила вычисления

Значения, приводимые в математических таблицах, иногда бывают точными, но чаще приближенными, представляя собой результаты округления точных значений, и содержат погрешности, не превосходящие половины единиц разряда последней цифры. Если значение взято не прямо из таблицы, а найдено посредством интерполяции, погрешность может быть больше, но в подавляющем большинстве случаев не превосходит единицы разряда последней цифры. При вычислении посредством таблиц, как и при всяком вычислении, необходимо соблюдать следующие правила:

• Надо различать, какие данные точны, какие приближенны. Приближенные данные надо округлять, сохраняя в них только надежные цифры и не более одной не вполне надежной.
• При записи целых приближенных чисел следует избегать нулей, помещаемых взамен неизвестных цифр.
• При сложении и вычитании приближенных чисел в результате следует сохранять столько десятичных знаков, сколько из в приближенном данном с наименьшим числом десятичных знаков.
Примечание. «Десятичными знаками» числа называются те цифры, которые расположены справа от знака дробности.
• При умножении и делении в результате следует сохранять столько значащих цифр, сколько их имеет приближенное с наименьшим числом значащих цифр.
Примечание. «Значащими цифрами» числа называются все его цифры, кроме нулей, расположенных левее первой, отличной от нуля, его цифры.
• При возведении в квадрат и куб в результате следует сохранять столько значащих цифр, сколько их имеет возводимое в степень приближенное число.
Примечание. Последняя цифра квадрата и особенно куба при этом менее надежна, чем последняя цифра основания.
• При извлечении квадратного и кубического корней в результате следует брать столько значащих цифр, сколь их имеет подкоренное (приближенное) число.
Примечание. Последняя цифра квадратного и особенно кубического корня при этом более надежна, чем последняя цифра подкоренного.
• При вычислении промежуточных результатов следует брать одной цифрой более, чем рекомендуют предыдущие правила.
Примечание. В окончательном результате эта «запасная цифра» отбрасывается. Рекомендуется ее подчеркивать.
• Если некоторые данные имеют больше десятичных знаков (при действиях I ступени) или больше значащих цифр (при действиях II и III ступеней), чем другие, то их предварительно следует округлить, сохраняя лишь одну лишнюю цифру.
• Если данные можно брать с произвольной точностью, то для получения результата с k цифрами данные следует брать с таким числом цифр, какое дает, согласно правилам 3 — 6, k + 1 цифру в результате.
• При вычислении посредством логарифмов значения выражения, не содержащего действий сложения и вычитания, следует подсчитать число значащих цифр в приближенном данном, имеющем наименьшее число значащих цифр, и взять таблицу логарифмов с числом десятичных знаков, на 1 большим. В окончательном результате последняя значащая цифра отбрасывается.
Применяя эти правила, следует помнить, что они отнюдь не дают гарантии точной последней цифры результата. Эта последняя цифра может иметь погрешность, достигающую в отдельных случаях даже несколько единиц, но малые значения этой погрешности более вероятны, чем большие.

---

Другие заметки по алгебре и геометрии

edu.glavsprav.ru

Таблицы Брадиса — kakras

Общие правила вычислений с помощью таблиц Брадиса:

1. Надо различать, какие данные точны, а какие приближённы. Приближённые данные надо правильно округлять, сохраняя в них только надёжные числа и не более одной, крайней, не вполне надёжной (так называемой, «лишней»).
2. При записи целых приближённых чисел, следует избегать лишних нулей, помещаемых взамен неизвестных цифр.
3 . При сложении и вычитании приближённых чисел, в результате следует оставлять столько десятичных разрядов, сколько их имеется в данном с наименьшим числом знаков после запятой (это правило не касается вычислений промежуточных результатов, а только конечных).

Пример перевода числовых значений из десятых долей градусов в минуты:
10.8° (десять целых и восемь десятых градуса)
8 / 10 = X / 60
X = (8 * 60) / 10 = 48
Итог конвертации: 10.8° = 10° 48' (десять градусов и сорок восемь минут).

Высокоточные вычисления тригонометрических функций для углов, заданных с точностью до минут и секунд — проводятся на специальных инженерных калькуляторах (в виде компьютерных программ, считающих до 32 разрядов или отдельного счётного прибора) и в электронных таблицах Excel по формуле, записанной в определённом формате. Пример строки с формулой в табличной ячейке для расчёта синуса угла, заданного с минутами и секундами:
E1 = sin (((A1 + B1/60 + C1/3600) * pi()) / 180)
где A1 — число градусов аргумента, заданное в первой строке колонки A.
     B1 — минуты;
     C1 — секунды.

При отсутствии таблиц Брадиса, инженерного калькулятора и компьютера, значения тригонометрических функций можно посчитать, с произвольно высокой точностью, и на простейшем арифмометре, с помощью аналитических операций сложения, вычитания, умножения и деления по формулам рядов:

sin x = x - x^3/1*2*3 + x^5/1*2*3*4*5 - x^7/1*2*3*4*5*6*7 + x^9/1*2*3*4*5*6*7*8*9 -...

cos x = 1 — x^2/1*2 + x^4/1*2*3*4 — x^6/1*2*3*4*5*6 + x^8/1*2*3*4*5*6*7*8 -…

tg x = x + (1/3 * x^3) + (2/15 * x^5) + (17/315 * x^7) + …

Точность, при таких вычислениях с применением знакочередующейся нескончаемой суммы ряда — определяется абсолютной величиной каждого очередного слагаемого.

В степень — число возводится с помощью многократного перемножения.
Например, аргумент в кубе:  x^3 = x*x*x   На калькуляторе, после набора числа, последовательно нажимаются кнопки: * = =

Если не нужна высокая точность и требуется быстрое вычисление, используются различные номограммы (нарисованные или напечатанные на бумаге и других материалах), логарифмические линейки и прочие приспособления и инструменты.

Список использованной литературы и ссылки на Интернет-ресурсы

Таблицы Брадиса. Москва: Просвещение, 1968 г.

https:// ru.wikipedia.org/wiki/Тригонометрические_функции

kakras.livejournal.com

Таблицы Брадиса

Таблицы Брадиса

SIN 01=0.0175	SIN 02=0.0349	SIN 03=0.0523	SIN 04=0.0698
SIN 05=0.0872	SIN 06=0.1045	SIN 07=0.1219	SIN 08=0.1392
SIN 09=0.1564	SIN 10=0.1736	SIN 11=0.1908	SIN 12=0.2079
SIN 13=0.2250	SIN 14=0.2419	SIN 15=0.2588	SIN 16=0.2756
SIN 17=0.2924	SIN 18=0.3090	SIN 19=0.3256	SIN 20=0.3420
SIN 21=0.3584	SIN 22=0.3746	SIN 23=0.3907	SIN 24=0.4067
SIN 25=0.4226	SIN 26=0.4384	SIN 27=0.4540	SIN 28=0.4695
SIN 29=0.4848	SIN 30=0.5000	SIN 31=0.5150	SIN 32=0.5299
SIN 33=0.5446	SIN 34=0.5592	SIN 35=0.5736	SIN 36=0.5878
SIN 37=0.6018	SIN 38=0.6157	SIN 39=0.6293	SIN 40=0.6428
SIN 41=0.6561	SIN 42=0.6691	SIN 43=0.6820	SIN 44=0.6947
SIN 45=0.7071	SIN 46=0.7193	SIN 47=0.7314	SIN 48=0.7431
SIN 49=0.7547	SIN 50=0.7660	SIN 51=0.7771	SIN 52=0.7880
SIN 53=0.7986	SIN 54=0.8090	SIN 55=0.8192	SIN 56=0.8290
SIN 57=0.8387	SIN 58=0.8480	SIN 59=0.8572	SIN 60=0.8660
SIN 61=0.8746	SIN 62=0.8829	SIN 63=0.8910	SIN 64=0.8988
SIN 65=0.9063	SIN 66=0.9135	SIN 67=0.9205	SIN 68=0.9272
SIN 69=0.9336	SIN 70=0.9397	SIN 71=0.9455	SIN 72=0.9511
SIN 73=0.9563	SIN 74=0.9613	SIN 75=0.9659	SIN 76=0.9703
SIN 77=0.9744	SIN 78=0.9781	SIN 79=0.9816	SIN 80=0.9848
SIN 81=0.9877	SIN 82=0.9903	SIN 83=0.9925	SIN 84=0.9945
SIN 85=0.9962	SIN 86=0.9976	SIN 87=0.9986	SIN 88=0.9994
SIN 89=0.9998	SIN 90=1.0000

cos 0= 1.0000	cos 1= 0.9998	cos 2= 0.9994	cos 3= 0.9986
cos 4= 0.9976	cos 5= 0.9962	cos 6= 0.9945	cos 7= 0.9925
cos 8= 0.9903	cos 9= 0.9877	cos 10= 0.9848	cos 11= 0.9816
cos 12= 0.9781	cos 13= 0.9744	cos 14= 0.9703	cos 15= 0.9659
cos 16= 0.9613	cos 17= 0.9563	cos 18= 0.9511	cos 19= 0.9455
cos 20= 0.9397	cos 21= 0.9336	cos 22= 0.9272	cos 23= 0.9205
cos 24= 0.9135	cos 25= 0.9063	cos 26= 0.8988	cos 27= 0.8910
cos 28= 0.8829	cos 29= 0.8746	cos 30= 0.8660	cos 31= 0.8572
cos 32= 0.8480	cos 33= 0.8387	cos 34= 0.8290	cos 35= 0.8192
cos 36= 0.8090	cos 37= 0.7986	cos 38= 0.7880	cos 39= 0.7771
cos 40= 0.7660	cos 41= 0.7547	cos 42= 0.7431	cos 43= 0.7314
cos 44= 0.7193	cos 45= 0.7071	cos 46= 0.6947	cos 47= 0.6820
cos 48= 0.6691	cos 49= 0.6561	cos 50= 0.6428	cos 51= 0.6293
cos 52= 0.6157	cos 53= 0.6018	cos 54= 0.5878	cos 55= 0.5736
cos 56= 0.5592	cos 57= 0.5446	cos 58= 0.5299	cos 59= 0.5150
cos 60= 0.5000	cos 61= 0.4848	cos 62= 0.4695	cos 63= 0.4540
cos 64= 0.4384	cos 65= 0.4226	cos 66= 0.4067	cos 67= 0.3907
cos 68= 0.3746	cos 69= 0.3584	cos 70= 0.3420	cos 71= 0.3256
cos 72= 0.3090	cos 73= 0.2924	cos 74= 0.2756	cos 75= 0.2588
cos 76= 0.2419	cos 77= 0.2250	cos 78= 0.2079	cos 79= 0.1908
cos 80= 0.1736	cos 81= 0.1564	cos 82= 0.1392	cos 83= 0.1219
cos 84= 0.1045	cos 85= 0.0872	cos 86= 0.0698	cos 87= 0.0523
cos 88= 0.0349	cos 89= 0.0175
tg 1=0.0175	tg 2=0.0349	tg 3=0.0524	tg 4=0.0699
tg 5=0.0875	tg 6=0.1051	tg 7=0.1228	tg 8=0.1405
tg 9=0.1584	tg 10=0.1763	tg 11=0.1944	tg 12=0.2126
tg 13=0.2309	tg 14=0.2493	tg 15=0.2679	tg 16=0.2867
tg 17=0.3057	tg 18=0.3249	tg 19=0.3443	tg 20=0.3640
tg 21=0.3839	tg 22=0.4040	tg 23=0.4245	tg 24=0.4452
tg 25=0.4663	tg 26=0.4877	tg 27=0.5095	tg 28=0.5317
tg 29=0.5543	tg 30=0.5774	tg 31=0.6009	tg 32=0.6249
tg 33=0.6494	tg 34=0.6745	tg 35=0.7002	tg 36=0.7265
tg 37=0.7536	tg 38=0.7813	tg 39=0.8098	tg 40=0.8391
tg 41=0.8693	tg 42=0.9004	tg 43=0.9325	tg 44=0.9657
tg 45=1.0000	tg 46=1.0355	tg 47=1.0724	tg 48=1.1106
tg 49=1.1504	tg 50=1.1918	tg 51=1.2349	tg 52=1.2799
tg 53=1.3270	tg 54=1.3764	tg 55=1.4281	tg 56=1.4826
tg 57=1.5399	tg 58=1.6003	tg 59=1.6643	tg 60=1.7321
tg 61=1.8040	tg 62=1.8807	tg 63=1.9626	tg 64=2.0503
tg 65=2.1445	tg 66=2.2460	tg 67=2.3559	tg 68=2.4751
tg 69=2.6051	tg 70=2.7475	tg 71=2.9042	tg 72=3.0777
tg 73=3.2709	tg 74=3.4874	tg 75=3.7321	tg 76=4.0108
tg 77=4.3315	tg 78=4.7046	tg 79=5.1446	tg 80=5.6713
tg 81=6.3138	tg 82=7.1154	tg 83=8.1443	tg 84=9.5144
tg 85=11.4301	tg 86=14.3007	tg 87=19.0811	tg 88=28.6363
tg 89=57.2900
tg 1=57.2900	ctg 2=28.6363	ctg 3=19.0811	ctg 4=14.3007
ctg 5=11.4301	ctg 6=9.5144	ctg 7=8.1443	ctg 8=7.1154
ctg 9=6.3138	ctg 10=5.6713	ctg 11=5.1446	ctg 12=4.7046
ctg 13=4.3315	ctg 14=4.0108	ctg 15=3.7321	ctg 16=3.4874
ctg 17=3.2709	ctg 18=3.0777	ctg 19=2.9042	ctg 20=2.7475
ctg 21=2.6051	ctg 22=2.4751	ctg 23=2.3559	ctg 24=2.2460
ctg 25=2.1445	ctg 26=2.0503	ctg 27=1.9626	ctg 28=1.8807
ctg 29=1.8040	ctg 30=1.7321	ctg 31=1.6643	ctg 32=1.6003
ctg 33=1.5399	ctg 34=1.4826	ctg 35=1.4281	ctg 36=1.3764
ctg 37=1.3270	ctg 38=1.2799	ctg 39=1.2349	ctg 40=1.1918
ctg 41=1.1504	ctg 42=1.1106	ctg 43=1.0724	ctg 44=1.0355
ctg 45=1.0000	ctg 46=0.9657	ctg 47=0.9325	ctg 48=0.9004
ctg 49=0.8693	ctg 50=0.8391	ctg 51=0.8098	ctg 52=0.7813
ctg 53=0.7536	ctg 54=0.7265	ctg 55=0.7002	ctg 56=0.6745
ctg 57=0.6494	ctg 58=0.6249	ctg 59=0.6009	ctg 60=0.5774
ctg 61=0.5543	ctg 62=0.5317	ctg 63=0.5095	ctg 64=0.4877
ctg 65=0.4663	ctg 66=0.4452	ctg 67=0.4245	ctg 68=0.4040
ctg 69=0.3839	ctg 70=0.3640	ctg 71=0.3443	ctg 72=0.3249
ctg 73=0.3057	ctg 74=0.2867	ctg 75=0.2679	ctg 76=0.2493
ctg 77=0.2309	ctg 78=0.2126	ctg 79=0.1944	ctg 80=0.1763
ctg 81=0.1584	ctg 82=0.1405	ctg 83=0.1228	ctg 84=0.1051
ctg 85=0.0875	ctg 86=0.0699	ctg 87=0.0524	ctg 88=0.0349
ctg 89=0.0175	ctg 90=0.0000\

Список литературы

Для подготовки данной работы были использованы материалы с сайта http://www.shpori4all.narod.ru/

essay.ua-referat.com