Основные элементарные функции, их свойства и графики.
Основными элементарными функциями являются: постоянная функция (константа), корень n-ой степени, степенная функция, показательная, логарифмическая функция, тригонометрические и обратные тригонометрические функции.
Постоянная функция.
Постоянная функция задается на множестве всех действительных чисел формулой , гдеC – некоторое действительное число. Постоянная функция ставит в соответствие каждому действительному значению независимой переменной x одно и то же значение зависимой переменной y – значение С. Постоянную функцию также называют константой.
Графиком постоянной функции является прямая, параллельная оси абсцисс и проходящая через точку с координатами (0,C). Для примера покажем графики постоянных функций y=5,y=-2 и , которым на рисунке, приведенном ниже, отвечают черная, красная и синяя прямые соответственно.

Свойства постоянной функции.
Область определения: все множество действительных чисел.
Постоянная функция является четной.
Область значений: множество, состоящее из единственного числа С.
Постоянная функция невозрастающая и неубывающая (на то она и постоянная).
Говорить о выпуклости и вогнутости постоянной не имеет смысла.
Асимптот нет.
Функция проходит через точку (0,C) координатной плоскости.
Корень n-ой степени.
Рассмотрим основную элементарную функцию, которая задается формулой , где n – натуральное число, большее единицы.
Корень n-ой степени, n — четное число.
Начнем с функции корень n-ой степени при четных значениях показателя корня n.
Для примера приведем рисунок с изображениями графиков функций и , им соответствуют черная, красная и синяя линии.
Аналогичный вид имеют графики функций корень четной степени при других значениях показателя.
Свойства функции корень n-ой степени при четных n.
Область определения: множество всех неотрицательных действительных чисел .
При x=0 функция принимает значение, равное нулю.
Эта функция общего вида (не является четной или нечетной).
Область значений функции: .
Функция при четных показателях корня возрастает на всей области определения.
Эта функция имеет выпуклость, направленную вверх, на всей области определения, точек перегиба нет.
Асимптот нет.
График функции корень n-ой степени при четных n проходит через точки (0,0) и(1,1).
Корень n-ой степени, n — нечетное число.
Функция корень
При других нечетных значениях показателя корня графики функции будут иметь схожий вид.
Свойства функции корень n-ой степени при нечетных n.
Область определения: множество всех действительных чисел.
Эта функция нечетная.
Область значений функции: множество всех действительных чисел.
Функция при нечетных показателях корня возрастает на всей области определения.
Эта функция вогнутая на промежутке и выпуклая на промежутке , точка с координатами (0,0) – точка перегиба.
Асимптот нет.
График функции корень n-ой степени при нечетных n проходит через точки (-1,-1),(0,0) и (1,1).
studfiles.net
Виды функций
БГЭУ 2006 | лекции по высшей математике для студентов I курса |
| ст. преподавателя, к. физ.-мат.н. Поддубной О.H. |
бесконечно много корней y , то в общем случае неявная функция является
многозначной.
Разрешая уравнение x2 + y2 −1= 0 из примера 1 относительноy получаем
две явных однозначных функции: y = 1− x2 иy = − 1− x2 , графики которых
представляют собой верхнюю и нижнюю полуокружности.
Уравнение Кеплера элементарными средствами не может быть разрешено относительно y . В таком случае функциюy приходится изучать, пользуясь
непосредственно уравнением (9.3), определяющим эту функцию.
Функция называется параметрически заданной, если она описывается множеством точек (x,y ), где
x = x(t)
t [a,b] ,t называется параметром. (9.4)
y = y(t)
x = cost
Пример 4.t [0,2π]–параметрическоезадание окружности с центом
y = sint
в начале координат и единичным радиусом. Действительно, возводя обе части каждого уравнения совокупности в квадрат и складывая полученные
результаты, получаем x2 + y2 =1.
Пусть f : X →Y , g :Y → Z . Композицией функций | f ,g называется |
функция, обозначаемая g D f :X → Z и определяемая как |
|
def | (9.5) |
(g D f )(x)= g(f (x)) |
Правая часть в (9.5) показывает, что значение композиции в точке x вычисляется в результате последовательного действия сначалаf , а затем на
полученный результат функции g .
Пример 5. Пустьf :\ → \ иf (x)= sinx ,g :\ → \ иg(x)= x2 , тогда
(g D f )(x)= (sinx)2 , а (f D g)(x)= sinx2 .
Попутно доказано, что композиция функций не является операцией
коммутативной. |
|
| y = xα , |
|
| y = ax (a> 0) , |
Функции: | степенная | показательная | ||||
логарифмическая |
| y = loga x (a > 0,a ≠1) , | тригонометрические | |||
y = sinx,y = cosx, | y = tgx, | y = ctgx | и | обратные | тригонометрические | |
y = arcsin x, y= arccos x, | y = arctgx, | y = arcctgx , постоянные | y = c называются | |||
основными элементарными функциями.
Всякая функция, которая может быть явным образом задана с помощью формулы, содержащей лишь конечное число арифметических операций и
В литературе термин «композиция функций» часто встречается под названием «суперпозиция функций» или «сложная функция»
studfiles.net
2. Способы задания функций. Виды элементарных функций.
Задать функцию — это значит задать правило или закон, согласно которому по данному значению аргумента х определяется соответствующее значение функции у.
Рассмотрим способы задания функции.
Аналитический способ — задание функции с помощью формул. Например, растворение лекарственных веществ из таблеток при приготовлении растворов подчиняется уравнению m = m0е–k t, где m0 и m – соответственно, исходное и оставшееся ко времени растворения t количество лекарственного вещества в таблетке, k —положительная постоянная, е – число примерно равное 2,718…
Графический способ — это задание функции в виде графика. Например, с помощью электрокардиографа на бумаге или на экране монитора компьютера фиксируется возникающая при работе сердца величина разности биопотенциалов U как функция времени t: U = f(t).
Табличный способ — это задание функции с помощью таблицы. Такой способ задания функции используется в экспериментах и наблюдениях. Например, измеряя температуру тела больного через определенные промежутки времени, можно составить таблицу значений температуры тела
В математике различают элементарные и сложные функции. Последние рассмотрим ниже, а здесь приведем основные виды элементарных функций:
Степенная функция – y = f(x) = xn, где х — аргумент, n – любое действительное число (1, 2, — 2,
 и т.д.).
и т.д.).Показательная функция – y = f(x) = ax, где а — постоянное положительное число, отличное от единицы (а > 0, а ≠ 0), например:
y = 10 x (a = 10), y = ex, y = e-x (a = e ≈ 2,718…)
Выделим две последние функции, они называются экспоненциальными функциями или экспонентами и описывают множество физических, биофизических, химических и социальных процессов. Причем y = ex – возрастающая экспонента, , y = e—x – убывающая экспонента.
3. Логарифмическая функция с любым основанием а: y = logax, иначе у — степень, в которую нужно возвести основание функции а, чтобы получить данное число x, т. е. a y = x
Если основание а = 10, то y называется десятичным логарифмом числа x и обозначается y = lg
Напомним некоторые правила логарифмирования:
Пусть даны два числа а и b, тогда:
lg (a·b) = lg a + lg b;
lg
 = lg a — lg b;
= lg a — lg b;lg ab = b lg a;
Ничего не изменится при замене символа lg на ln.
Полезно также помнить, что lg 10 = 1, ln е = 1, lg 1 = ln 1 = 0.
4. Тригонометрические функции: y = sin x, y = cos x, y = tg x и др.
П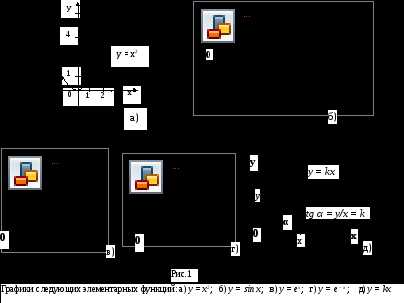 риведем
графики некоторых элементарных функций
(см. рис.1):
риведем
графики некоторых элементарных функций
(см. рис.1):
3.Понятие предела переменной. Производная функции. Таблица производных. Правила дифференцирования.
Переменная величина может изменяться так, что в процессе возрастания или убывания она приближается к некоторой конечной постоянной величине, которая является ее пределом.
По определению пределом переменной величины х называется постоянная величина А, к которой х в процессе своего изменения приближается так, что модуль разности между x и А, т.е. | х — А |, стремиться к нулю.
Обозначения предела: x→ А или lim x = A (здесь → — знак предельного перехода, lim от лат. limited, в переводе на русский – предел). Рассмотрим элементарный пример:
x : 0,9; 0,99; 0,999; 0,9999…→ 1, A = 1(lim x = 1), т.к.
| х — А |: 0,1; 0,01; 0,001; 0,0001…→ 0.
Введем понятияприращение аргумента и приращение функции.
Если переменная величина х изменяет свое значение от x1 до х2, то разность x2 – x1 = Δx называется приращением аргумента, причем Δx (читается дельта х) – единый символ приращения. Соответствующее изменение функции y2 – y1 = Δy называется приращением функции. Покажем это на графике функции y = f(x) (рис.2). Геометрически приращение аргумента изображается приращением абсциссы точки кривой, а приращение функции — приращением ординаты этой точки.
Производной заданной функции y = f(x) по аргументу х называется предел отношения приращения функции Δу к приращению аргумента Δх, вычисленный при условии, что Δх → 0 .
Она
обозначается  (читается «у штрих») или
(читается «у штрих») или 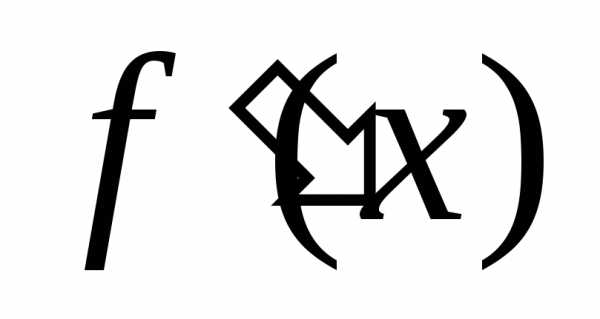 ,
илиdy/dx (читается «дэ y по дэ x»).
Таким образом, производная функции y = f(x) равна:
,
илиdy/dx (читается «дэ y по дэ x»).
Таким образом, производная функции y = f(x) равна:
(5)
Правило
для отыскания производной функции у
= f(х) по аргументу х содержится в определении этой величины:
нужно задать приращение
аргумента Δх,
найти приращение функции Δy,
составить отношение 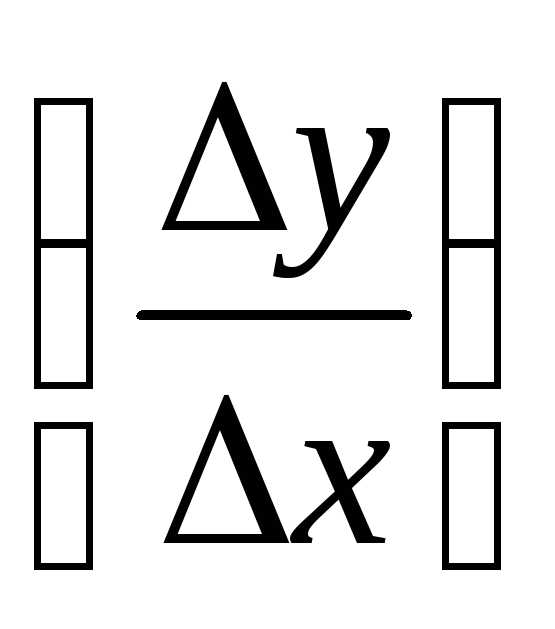 и
найти предел этого отношения при Δх→
0.
и
найти предел этого отношения при Δх→
0.
Процесс нахождения производной называется дифференцированием функции. Этим занимается раздел высшей математики называемый «Дифференциальное исчисление».
Таблица производных основных элементарных функций, полученных по указанному выше правилу, приведена ниже (табл.1)
Таблица 1.
№ п/п | Виды функции | Производная функции |
1 | Постоянная величина y = c | y’ = 0 |
2 | Степенная функция y = xn (n может быть положительным, отрицательным, целым, дробным) | y’ = nxn-1 |
3 | Показательная функция y = ax (a > 0; a ≠ 1) y = ex y = e—x | y’ = axln a y’ = ex y’ = — e-x |
4 | Логарифмическая функция y = logax (a > 0; a ≠ 1) y = ln x | y’ = y’
= |
5 | Тригонометрические функции: y = sin x y = cos x y = tg x y = ctg x | y’ = cos x y’ = — sin x y’ = y’
= |
Если выражение, производную которого надо найти, представляет собой сумму, разность, произведение или частное нескольких функций, например, u, v, z, то используются нижеследующие правила дифференцирования (табл. 2).
Таблица 2.
1. y = u + v – z | 1) y’ = u’ + v‘ — z’ |
2. y = u · v | 2) y = u’ · v + v ‘· u |
3. y = | 3) y’ = |
4. y = a · u, где a = const | 4) y’ = a · u’ |
Приведем несколько примеров вычисления производных, используя табл. 1 и табл.2.
(x + sin x )’ = (x)’ + (sin x)’ = 1 + cos x;
(x · sin x )’ = (x)’ · sin x + x · (sin x)’ = sin x + x cos x;
;
(5 tgx)’ = 5 (tg x)’ =
 .
.
studfiles.net
Виды функций государства — схема, таблица — Схемо.РФ
- Войти
- Регистрация
- Схемы
- Биология
- География
- История
- Математика и алгебра
- Медицина
- Обществознание
- Педагогика
- Политология
- Право
- Психология
- Русский язык
- Социология
- Физика
- Философия
- Химия
- Экономика
- Прочее
- Книги
- Биология
- География
- История
- Математика и алгебра
- Медицина
- Обществознание
- Педагогика
- Политология
- Право
- Психология
- Русский язык
- Социология
- Физика
- Философия
- Химия
- Экономика
- Прочее
- Комментарии
xn--e1aogju.xn--p1ai
| 5.4. Основные элементарные функции В таблице приводятся наиболее важные свойства и графики основных элементарных функций. 1. Степенная функция
5. Обратные тригонометрические функции у = arcsin х, у = arccos х, у = arctg х, у = arcctg x 4. Периодичность. Функция у = f (х) называется периодической с периодом Т 0, если для любых х из области определения функции f(x+T)=f(x). Например, функция у = sin х имеет период Т = 2, так как для любых х sin (х +2л) = sin х. Функция у аргумента х называется неявной, если она задана уравнением F(х, у) = 0, не разрешенным относительно зависимой переменной. Например, функция у (у > 0), заданная уравнением х3 + у2 — х = 0. (Заметим, что последнее уравнение задает две функции ^ Пусть у = f (х) есть функция от независимой переменной х, определенной на множестве Х с областью значений Y. Поставим в соответствие каждому у Y единственное значение х X, при котором f(х) = у. Тогда полученная функция х = (у), определенная на множестве Г с областью значений X, называется обратной. Так как традиционно независимую переменную обозначают через х, а функцию через у, то функция, обратная к функции у =f(x), примет вид у = (х). Обратную функцию у = (х) обозначают также в виде у = f–1(х) (аналогично с обозначением обратной величины). Например, для функции у = aх обратной будет функция х = logaу или (в обычных обозначениях зависимой и независимой переменных) у= logax. Можно доказать, что для любой строго монотонной функции у = (х) существует обратная функция. Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов (на рис. 5.17 показаны графики взаимно обратных функций у =ax и у = logaх при a > 1). Сложная функция. Пусть функция у =f(u) есть функция от переменной и, определенной на множестве U с областью значений Y, а переменная и в свою очередь является функцией и = (х) от переменной х, определенной на множестве Х с областью значений U. Тогда заданная на множестве Х функция y = f[(x)] называется сложной функцией (или композицией функций, суперпозицией функций, функцией от функции). Например, у = lg sin х – сложная функция, так как ее можно представить в виде у = lg и, где и = sin х. Понятие элементарной функции. Из основных функций новые функции могут быть получены двумя способами при помощи: а) алгебраических действий; б) операций образования сложной функции. Определение. Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными. Например, функция является элементарной, так как здесь число операций сложения, вычитания, умножения, деления и образования сложной функции конечно. Примерами неэлементарных функций являются функция у = [х] – целая часть х (см. рис. 6.9), функция Дирихле (с. 127). Классификация функций. Элементарные функции делятся на алгебраические и неалгебраические (трансцендентные). Алгебраической называется функция, в которой над аргументом проводится конечное число алгебраических действий. К числу алгебраических функций относятся: • целая рациональная функция (многочлен или полином): • дробно-рациональная функция – отношение двух многочленов; • иррациональная функция (если в составе операций над аргументом имеется извлечение корня). Всякая неалгебраическая функция называется трансцендентной. К числу трансцендентных функций относятся функции: показательная, логарифмическая, тригонометрические, обратные тригонометрические. ^ разделе III «Дифференциальное исчисление» будет показано, как проводить исследование функций и построение их графиков с помощью производной. Вместе с тем актуальными остаются приемы построения графиков функций с помощью преобразования графиков основных элементарных функций. Пусть задан график функции у =f(x). Тогда справедливы следующие утверждения. 1. График функции у =f(x + а) есть график у = f(х), сдвинутый (при а > 0 влево, при а вправо) на a единиц параллельно оси Ох (рис. 5.18). 2. График функции у =f(x) + b есть график у =f(x), сдвинутый (при b > 0 вверх, при b 0 – вниз) на b единиц параллельно оси Оу (см. рис. 5.18). 3. График функции у = mf(x) (т 0) есть график у =f(x), растянутый (при т>1) в т раз или сжатый (при 0 т 1) вдоль оси Оу (см. рис. 5.19). При т график функции у = mf(x) есть зеркальное отображение графика у = –тf(х) от оси Ох. 4. График функции у =f(kx) (k 0) есть график у =f(x), сжатый (при k>1) в k раз или растянутый (при 0 k 1) вдоль оси Ох (см. рис. 5.20). При -оо k график функции у =f(kx) есть зеркальное отображение графика у =f(–kx) от оси Оу.
Решение. Строим график функции у = –3cos 2х следующим образом (рис. 5.21). 1. Строим график у = cos х. 2. у = cos x -> сжатие графика в 2 раза вдоль оси Ох -> у = = cos 2х. 3. у = cos 2x -> зеркальное отражение графика от оси Ох -> у = –cos 2х. 4. у = -cos 2x-> растяжение графика в 3 раза вдоль оси Оу -> у = –3cos 2х.
При вычислениях с помощью таблиц мы часто сталкиваемся с ситуацией, когда аргумент функции задан с большей точностью, чем позволяет таблица. В этом случае мы должны прибегнуть к интерполированию (интерполяции) – приближенному нахождению неизвестных значений функций по известным ее значениям в заданных точках. Наиболее простым является линейное интерполирование, при котором допускается, что приращение функции пропорционально приращению аргумента. Если заданное значение х лежит между приведенными в таблице значениями x0 и x1 = x0 + h, которым соответствуют значения функции считают, что (рис. 5.26) Величины называются интерполяционными поправками. Эти величины вычисляются с помощью таблицы или приводятся в дополнении к таблице. Если по заданным значениям функции необходимо найти приближенное значение аргумента, то необходимо произвести обратное интерполирование.
а) Используя линейное интерполирование, найти f(2,008). б) Чему равен х, если f(x) =3,1? Теперь по интерполяционной формуле (5.1) получим б) Обратное интерполирование можно провести по той же формуле, в которой поменять местами переменные х и у. где х = (у) – неизвестное значение обратной функции. Теперь по интерполяционной формуле (5.2) получим В ряде случаев точность нахождения неизвестных значений с помощью линейного интерполирования оказывается недостаточной и используются другие методы интерполирования, например квадратичное интерполирование.
а) Область определения функции -Y найдем из системы неравенств б) Имеем систему Решая первое неравенство, получим 2n п; решая второе, найдем х2x| 2 и –2 х 2.С помощью числовой оси (рис. 5.27) находим решение системы неравенств: 0 х 2, т.е. область определения функции Х= (0; 2]. |
mir.zavantag.com
Основные элементарные функции, их свойства и графики
Национальный научно-исследовательский университет
-ИрГТУ-
Кафедра прикладной геологии
Реферат по высшей математике
На тему: «Основные элементарные функции,
их свойства и графики»
Выполнил:
.
Проверил:
преподаватель
Коваленко Е.В.
Иркутск 2010
Содержание:
Показательные функции:- 3 —
Степенные функции:- 3 —
Логарифмические функции:- 3 —
Тригонометрические функции:- 3 —
Обратные тригонометрические функции:- 3 —
Список использованной литературы:- 3 —
Список рисунков:- 3 —
Показательные функции:
Определение. Функция, заданная формулой у=ах (где а>0, а≠1), называется показательной функцией с основанием а.
Сформулируем основные свойства показательной функции :
1. Область определения — множество (R) всех действительных чисел.
2. Область значений — множество (R+) всех положительных действительных чисел.
3. При а > 1 функция возрастает на всей числовой прямой; при 0<а<1 функция убывает.
4. Является функцией общего вида.
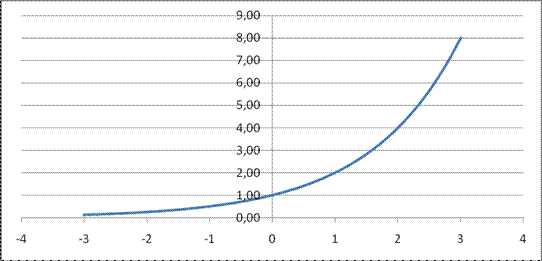
Рис. 1 График функции
, на интервале xÎ [-3;3]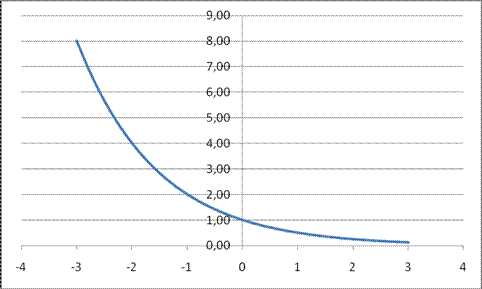
Рис. 2 График функции
, на интервале xÎ [-3;3]Степенные функции:
Функция вида у(х)=хn , где n – число ÎR, называется степенной функцией. Число n может принимать раличные значения: как целые, так и дробные, как четные, так и нечетные. В зависимости от этого, степенная функция будет иметь разный вид. Рассмотрим частные случаи, которые являются степенными функциями и отражают основные свойства данного вида кривых в следующем порядке: степенная функция у=х² (функция с четным показателем степени – парабола), степенная функция у=х³ (функция с нечетным показателем степени – кубическая парабола) и функция у=√х (х в степени ½) (функция с дробным показателем степени), функция с отрицательным целым показателем (гипербола).
Степенная функция у=х²
1. D(x)=R – функция определена на все числовой оси;
2. E(y)=[0;∞) — функция принимает положительные значения на всей области определения;
3. При х=0 у=0 — функция проходит через начало координат O(0;0).
4. Функция убывает на промежутке (-∞;0] и возрастает на промежутке [0;∞).
5. Функция является четной (симметрична относительно оси Оу).
В зависимости от числового множителя, стоящего перед х², функция может быть уже/шире и направлена вверх/вниз.
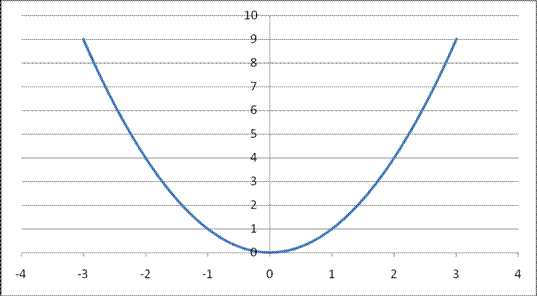
Рис. 3 График функции
, на интервале xÎ [-3;3]Степенная функция у=х³
1. График функции у=х³ называется кубической параболой. Степенная функция у=х³ обладает следующими свойствами:
2. D(x)=R – функция определена на все числовой оси;
3. E(y)=(-∞;∞) – функция принимает все значения на своей области определения;
4. При х=0 у=0 – функция проходит через начало координат O(0;0).
5. Функция возрастает на всей области определения.
6. Функция является нечетной (симметрична относительно начала координат).
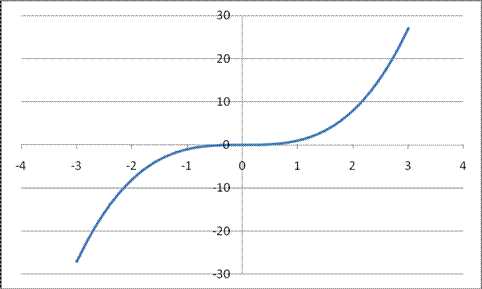
Рис. 4 График функции
, на интервале xÎ [-3;3]В зависимости от числового множителя, стоящего перед х³, функция может быть крутой/пологой и возрастать/убывать.
Степенная функция с целым отрицательным показателем:
Если показатель степени n является нечетным, то график такой степенной функции называется гиперболой. Степенная функция с целым отрицательным показателем степени обладает следующими свойствами:
1. D(x)=(-∞;0)U(0;∞) для любого n;
2. E(y)=(-∞;0)U(0;∞), если n – нечетное число; E(y)=(0;∞), если n – четное число;
3. Функция убывает на всей области определения, если n – нечетное число; функция возрастает на промежутке (-∞;0) и убывает на промежутке (0;∞), если n – четное число.
4. Функция является нечетной (симметрична относительно начала координат), если n – нечетное число; функция является четной, если n – четное число.
5. Функция проходит через точки (1;1) и (-1;-1), если n – нечетное число и через точки (1;1) и (-1;1), если n – четное число.
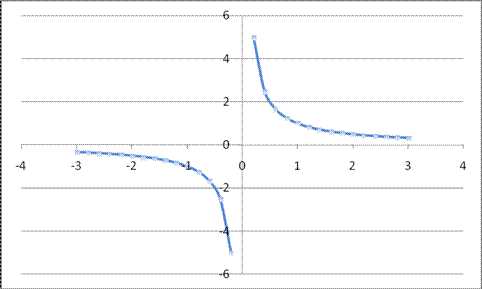
Рис. 5 График функции
, на интервале xÎ [-3;3]Степенная функция с дробным показателем
Степенная функция с дробным показателем вида (картинка) имеет график функции, изображенный на рисунке. Степенная функция с дробным показателем степени обладает следующими свойствами: (картинка)
1. D(x) ÎR, если n – нечетное число и D(x)=[0;∞), если n – четное число ;
2. E(y) Î (-∞;0)U(0;∞), если n – нечетное число; E(y)=[0;∞), если n – четное число;
3. Функция возрастает на всей области определения для любого числа n.
4. Функция проходит через начало координат в любом случае.
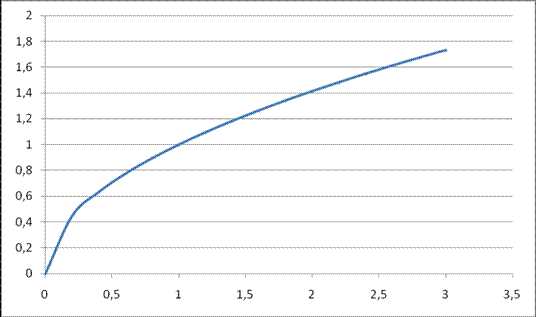
Рис. 6 График функции
, на интервале xÎ [0;3]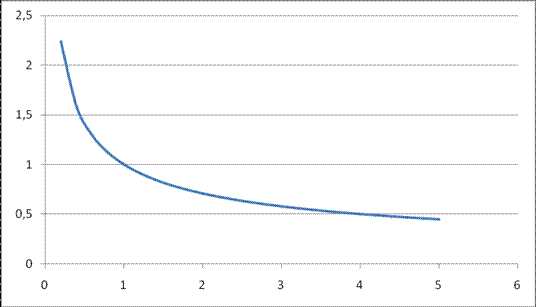
Рис. 7 График функции
, на интервале xÎ [0;5]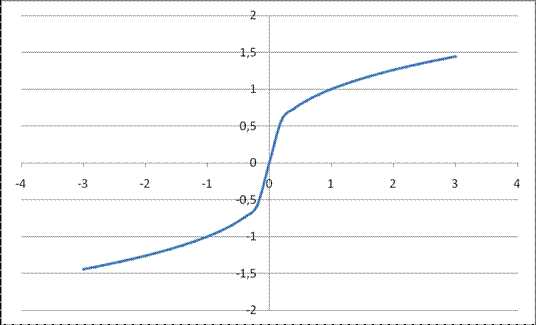
Рис. 8 График функции
, на интервале xÎ [-3;3]Логарифмические функции:
Логарифмическая функция у = loga x обладает следующими свойствами :
1. Область определения D(x)Î (0; + ∞).
2. Область значений E(y) Î ( — ∞; + ∞)
3. Функция ни четная, ни нечетная (общего вида).
4. Функция возрастает на промежутке (0; + ∞) при a > 1, убывает на (0; + ∞) при 0 < а < 1.
График функции у = loga x может быть получен из графика функции у = ах с помощью преобразования симметрии относительно прямой у = х. На рисунке 9 построен график логарифмической функции для а > 1, а на рисунке 10 — для 0 < a < 1.
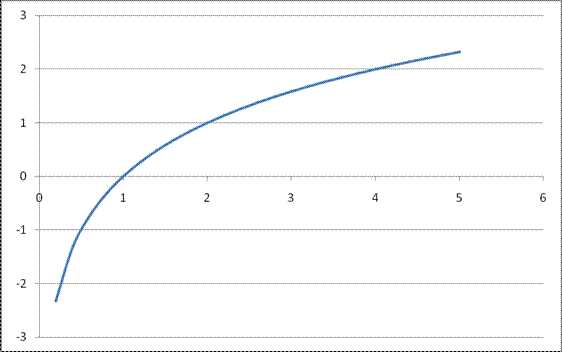
Рис. 9 График функции
; на интервале xÎ [0;5]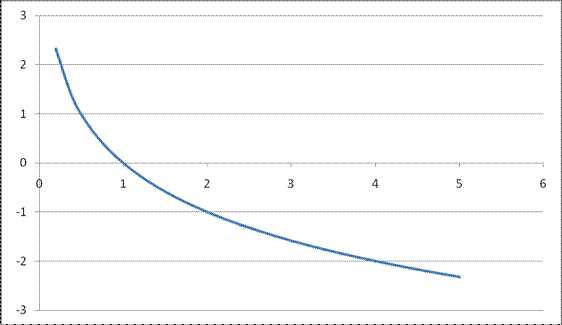
Рис. 10 График функции
; на интервале xÎ [0;5]Тригонометрические функции:
Функции y = sin х, у = cos х, у = tg х, у = ctg х называют тригонометрическими функциями.
Функции у = sin х, у = tg х, у = ctg х нечетные, а функция у = соs х четная.
Функция y = sin (х).
1. Область определения D(x) ÎR.
2. Область значений E(y) Î [ — 1; 1].
3. Функция периодическая; основной период равен 2π.
4. Функция нечетная .
5. Функция возрастает на промежутках [ -π/2 + 2πn; π/2 + 2πn] и убывает на промежутках [ π/2 + 2πn; 3π/2 + 2πn], n Î Z.
График функции у = sin (х) изображен на рисунке 11.
Рис. 11 График функции
; на интервале xÎ [-2;2]Функция y = cos(х).
1. Область определения D(x) ÎR.
2. Область значений E(y) Î [ — 1; 1].
3. Функция периодическая с основным периодом 2π.
4. Функция четная.
5. Функция убывает на промежутках [2πn; π+ 2πn] и возрастает на промежутках [-π+ 2πn; 2πn], nπZ.
График функции у = соs (х) изображен на рисунке 12.
Рис. 12 График функции
; на интервале xÎ [-2;2]Функция y = tg х.
1. Область определения: D(x) Ï π/2 + πk, kÎZ.
2. Область значений E(y) Î (- ∞; + ∞)
3. π- основной период функции.
4. Функция нечетная.
5. Функция возрастает на промежутках ( -π/2 +πn;π/2 +πn).
График функции у = tg х изображен на рисунке 13.
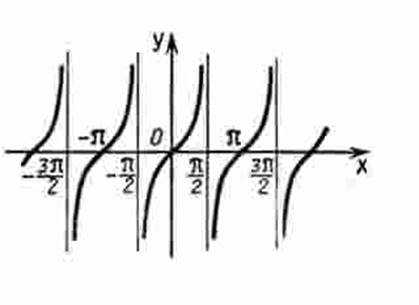
Рис. 13 График функции
; на интервале xÎ (- 😉mirznanii.com
Функция и её свойства. Способы задания функции. Виды функций и их свойства
Русская гимназия
КОНСПЕКТ
на тему:
Функция
Выполнил
ученик 10«Ф» класса Бурмистров Сергей
Руководитель
учитель Математики
Нижний Новгород
1997 год
Функция и её свойства
Функция- зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у.
Переменная х- независимая переменная или аргумент.
Переменная у- зависимая переменная
Значение функции- значение у, соответствующее заданному значению х.
Область определения функции- все значения, которые принимает независимая переменная.
Область значений функции (множество значений)- все значения, которые принимает функция.
Функция является четной- если для любого х из области определения функции выполняется равенство f(x)=f(-x)
Функция является нечетной- если для любого х из области определения функции выполняется равенство f(-x)=-f(x)
Возрастающая функция- если для любых х1и х2, таких, что х1< х2, выполняется неравенство f(х1)<f(х2)
Убывающая функция- если для любых х1и х2, таких, что х1< х2, выполняется неравенство f(х1)>f(х2)
Способы задания функции
Ё Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее употребительным является способ задания функции с помощью формулы у=f(x), где f(x)-некоторое выражение с переменной х. В таком случае говорят, что функция задана формулой или что функция задана аналитически.
Ё На практике часто используется табличный способ задания функции. При этом способе приводится таблица, указывающая значения функции для имеющихся в таблице значений аргумента. Примерами табличного задания функции являются таблица квадратов, таблица кубов.
Виды функций и их свойства
1) Постоянная функция- функция, заданная формулой у=b, где b-некоторое число. Графиком постоянной функции у=b является прямая, параллельная оси абсцисс и проходящая через точку (0;b) на оси ординат
2) Прямая пропорциональность- функция, заданная формулой у=kx, где к¹0. Число k называется коэффициентом пропорциональности.
Cвойства функции y=kx:
1. Область определения функции- множество всех действительных чисел
2. y=kx — нечетная функция
3. При k>0 функция возрастает, а при k<0 убывает на всей числовой прямой
3)Линейная функция- функция, которая задана формулой y=kx+b, где k иb—действительные числа. Если в частности, k=0, то получаем постоянную функцию y=b; если b=0, то получаем прямую пропорциональность y=kx.
Свойства функции y=kx+b:
1. Область определения- множество всех действительных чисел
2. Функция y=kx+b общего вида, т.е. ни чётна, ни нечётна.
3. При k>0функция возрастает, а при k<0 убывает на всей числовой прямой
Графиком функции является прямая.
4)Обратная пропорциональность- функция, заданная формулой y=k/х, где k¹0 Число k называют коэффициентом обратной пропорциональности.
Свойства функции y=k/x:
1. Область определения- множество всех действительных чисел кроме нуля
2. y=k/x— нечетная функция
3. Если k>0, то функция убывает на промежутке (0;+¥) и на промежутке (-¥;0). Если k<0, то функция возрастает на промежутке (-¥;0) и на промежутке
vunivere.ru

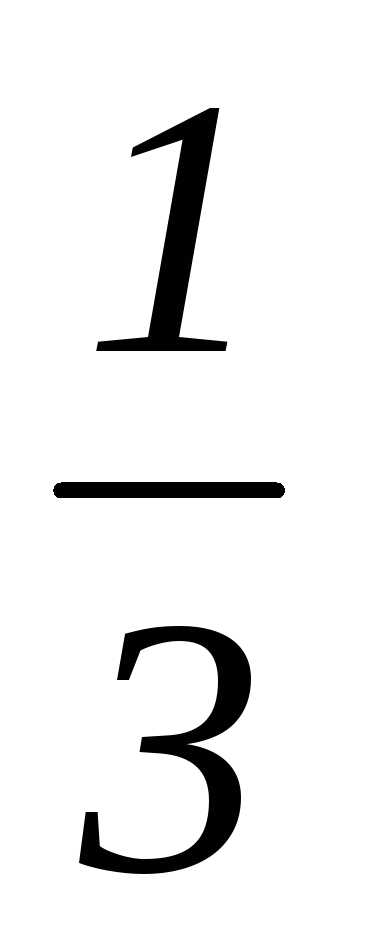 и т.д.).
и т.д.). = lg a — lg b;
= lg a — lg b;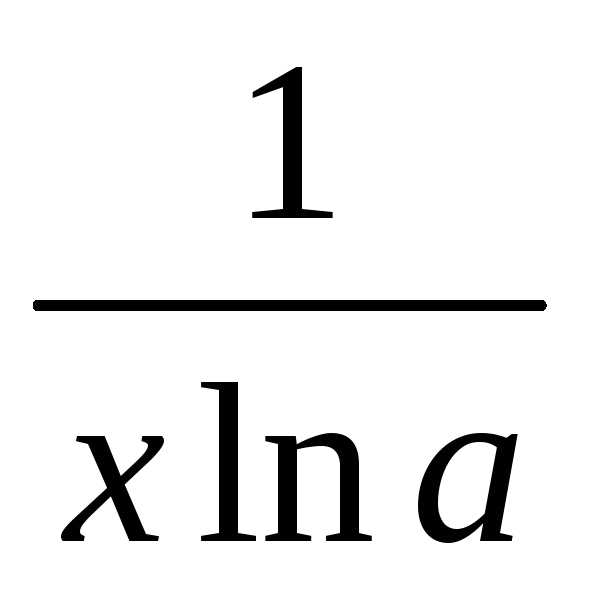

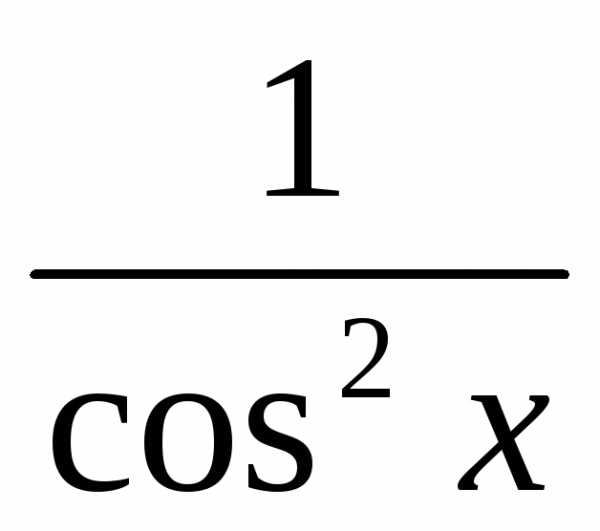


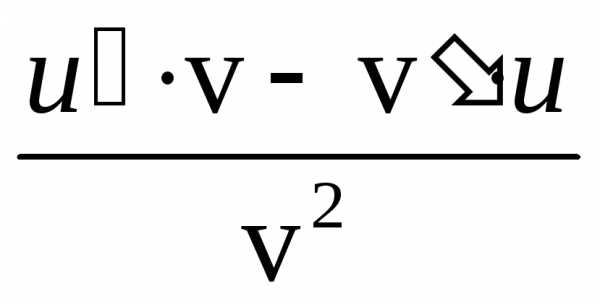
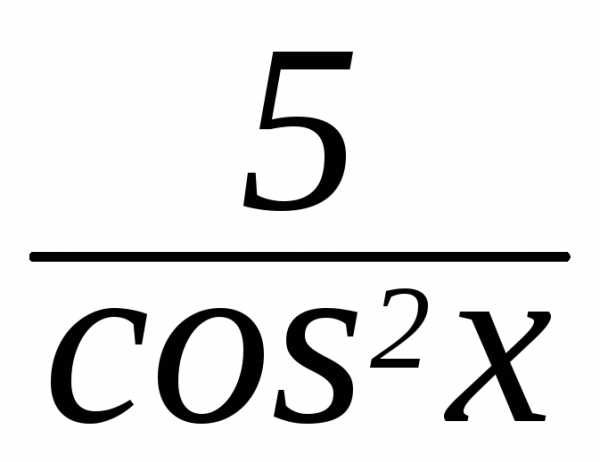 .
.