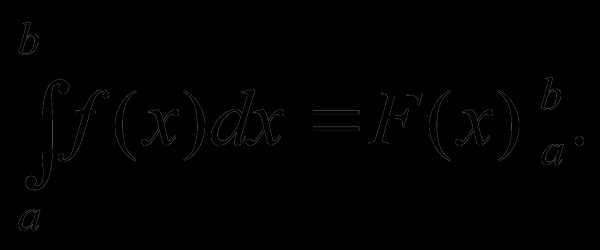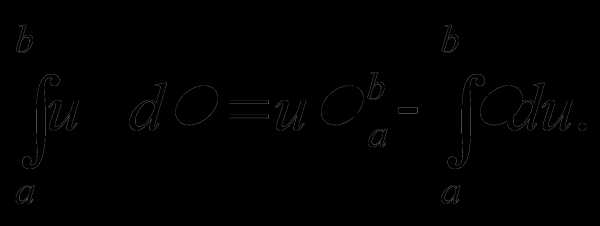Таблиця інтегралів
Інтеграл є одним з найважливіших понять в математиці.
У перекладі з латині – integer – недоторканий, цілий; integratio – відновлення.
За допомогою інтеграла можна знайти функцію по її похідної, а також вимірювати обсяги, довжини дуг, виконану роботу за певний часовий проміжок і т.д.
«Навіть у математиці вона потрібна, навіть відкриття диференціального й інтегрального числень неможливо було б без фантазії. Фантазія є якість найбільшої цінності ».
Володимир Ілліч Ленін.
Основним завданням диференціального обчислення є визначення первинної f ‘(x) або диференціала f’ (x) dx заданої функції f (x). Функцію F (х) називають первинною (або примітивної) на заданому проміжку Х для функції F (х), якщо для всіх х на цьому проміжку F ‘(х) = f (x).
Існує поняття невизначений інтеграл і певний. Безліч всіх первинних функцій f (x) на проміжку Х називають невизначеним інтегралом функції f (x) на цьому проміжку і позначають ? f (x) dx. Якщо межа інтегральної суми існує і не залежить від способу розділення відрізка [a; b] на частини і від вибору точок на цих частинах, то її називають визначеним інтегралом функції f (x) на відрізку [a; b] і позначають.
Якщо функція f (x) інтегрована на відрізку [a; b], то вона обмежена на цьому відрізку. Будь безперервна функція має первинний (і невизначений інтеграл). Основними методами інтегрування є метод підстановки (заміна змінної), метод розкладання та інтегрування частинами.
 Таблиця інтегралів
Таблиця інтегралівІнтегральна функція – це кілька пов’язаних між собою спеціальних функцій, які визначаються за допомогою інтегралів, а також елементарних функцій. Нею називають функцію f (x), яка визначає кожне значення випадкової величини Х ймовірність, що Х прийме значення менше:
х (F (x) = P (X <x))
Функція R (x) називається раціональною функцією (дробом). Для інтегрування даної функції використовується така послідовність:
Перетворити неправильну дріб в правильну, за допомогою виділення цілого виразу.
Знаменник Q (x) розкласти на нескоротні квадратні вирази або твір одночленів.
Раціональну дріб розкласти на прості.
Від найпростіших дробів обчислити інтеграл
Такі поняття як інтеграл та інтегрування виникли в ті часи, коли людині знадобилося обчислювати площі або квадратуру всіх фігур, а також обсяги або кубатуру довільних тел. Інтегрування було відзначено ще в Давньому Єгипті. Найпершим з методів є метод вичерпання Евдокса. Він знаходив обсяг і площі, ділячи їх на нескінченну кількість частин.
Таблица интегралов — это… Что такое Таблица интегралов?
- Таблица интегралов
Wikimedia Foundation. 2010.
- Таблица изотопов
- Таблица логарифмов
Смотреть что такое «Таблица интегралов» в других словарях:
Таблица неопределённых интегралов — … Википедия
Список интегралов элементарных функций — Интегрирование это одна из двух основных операций в математическом анализе, но в отличие от операции дифференцирования она выводит из множества элементарных функций. Из теоремы Лиувилля следует, например, что интеграл от не является… … Википедия
Неопределённый интеграл — для функции это совокупность всех первообразных данной функции. Если функция определена и непрерывна на промежутке и её первообразная, то есть при , то … Википедия
Определенный интеграл — Определённый интеграл как площадь фигуры В математическом анализе интегралом функции называют расширение понятия суммы. Процесс нахождения интеграла называется интегрированием. Этот процесс обычно используется при нахождений таких величин как… … Википедия
Методы интегрирования — Точное нахождение первообразной (или интеграла) произвольных функций дело гораздо более сложное, чем дифференцирование, то есть нахождение производной. Зачастую выразить интеграл в элементарных функциях невозможно. Содержание 1… … Википедия
Формулы Фруллани — относятся к нахождению несобственных интегралов Римана вида: к которым с помощью элементарных преобразовании, дифференцирования и интегрирования по параметру можно свести много других несобственных интегралов. Содержание 1 Формулы Фруллани … Википедия
Агокас, Сергей Викторович — В Википедии есть статьи о других людях с такой фамилией, см. Агокас. Агокас Сергей Викторович … Википедия
Обратные гиперболические функции — Обратные гиперболические функции определяются как обратные функции к гиперболическим функциям. Эти функции определяют площадь сектора единичной гиперболы x2 − y2 = 1 аналогично тому, как обратные тригонометрические функции определяют длину… … Википедия
Интегральное исчисление — раздел математики, в котором изучаются свойства и способы вычисления интегралов и их приложения. И. и. тесно связано с дифференциальным исчислением (См. Дифференциальное исчисление) и составляет вместе с ним одну из основных частей… … Большая советская энциклопедия
dic.academic.ru
3. Таблиця основних інтегралів
Кожна формула з таблиці похідних має відповідну формулу в таблиці інтегралів.
 .
7.
.
7.  .
. .
8.
.
.
8.
.. 9. .
 . 10. .
. 10. .. 11. .
. 12.
 .
.
Додатково варто знати формули
13. . 14..
15. . 16..
Правильність усіх формул перевіряється диференціюванням їх правих частин.
Є три основні методи інтегрування функцій: метод розкладу, метод заміни змінної та метод інтегрування за частинами.
Метод розкладу.
Справедливі наступні твердження.
Теорема 1. Якщо функції мають первісні на проміжку(a,b), то на цьому проміжку мають первісну і функції і справедлива рівність:
(1)
Теорема
2. Якщо функція 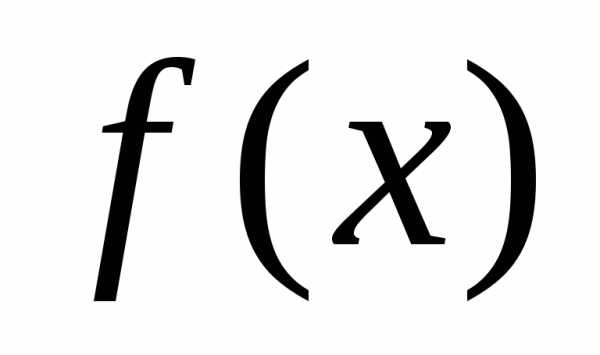 має
первісну на проміжку(a,b), то на цьому проміжку має первісну і
функція
має
первісну на проміжку(a,b), то на цьому проміжку має первісну і
функція 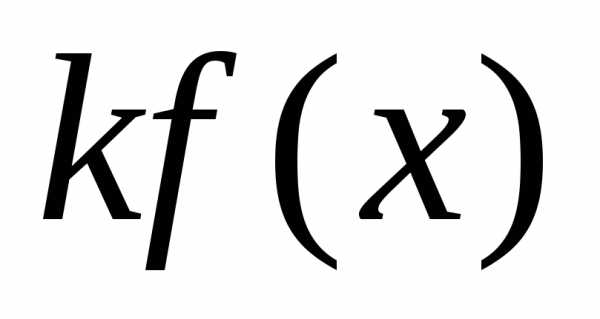 і
справедлива рівність:
і
справедлива рівність:
, k0 (2)
Наслідок. Якщо функції мають первісні на проміжку(a,b), то на цьому проміжку мають первісну і функції і справедлива рівність:
(3)
Метод інтегрування з використанням теорем 1,2 та наслідку називають методом розкладу.
Метод заміни змінної.
Теорема 3. Якщо F(x) – первісна для функції f(x) на проміжку
. (4)
Метод інтегрування за допомогою теореми 3 називається методом інтегрування способом заміни змінної.
Приклад.
Метод інтегрування частинами.
Теорема 4. Якщо функції диференційовні на проміжку (a,b) і на цьому проміжку існує первісна для функції , то на проміжку (a, b) існує первісна і для функції і має місце рівність
. (5)
До
правої частини ми не додали довільної
сталої С,
оскільки така стала міститься в іннтегралі 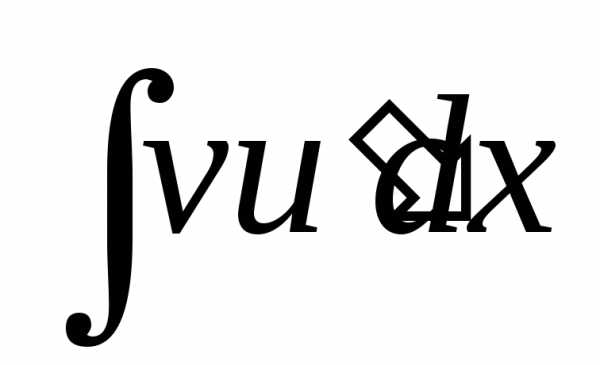 .
.
Формула (5) називається формулою інтегрування частинами, а метод інтегрування, що грунтується нга ній – методом інтегрування частинами.
Розглянемо приклад.
,
позначивши , отримаємо
.
Деколи цю формулу птрібно застосовувати декілька разів.
.
Попутно зауважимо, що для обчислення більшості інтегралів потрібно, як правило, застосовувати різні методи.
Контрольні запитання
Які функції мають первісні?
Скільки первісних має функція?
Як знайти всі первісні?
Що називається невизначеним інтегралом?
Сформулюйте і доведіть його властивості.
Чому рівні інтеграли від основних функцій?
У чому полягає інтегрування методом розкладу ?
У чому полягає інтегрування методом заміни змінної ?
У чому полягає метод інтегрування частинами ?
studfiles.net
Таблиця основних невизначених інтегралів
Користуючись тим, що інтеграція – це дія, зворотна диференціюванню, можна отримати таблицю основних інтегралів шляхом обігу відповідних формул диференціального числення (таблиця диференціалів) і використовування властивостей невизначеного інтеграла.
Наприклад, оскільки
,
то
.
Вивід ряду формул таблиці буде даний при розгляді основних методів інтегрування.
Інтеграли, що приводяться нижче в таблиці називаються табличними. Їх слід знати напам’ять. В інтегральному численні немає простих і універсальних правил пошуку первісних від елементарних функцій, як в диференціальному численні. Методи знаходження первісних (тобто інтеграції функції) зводяться до вказівки прийомів, що приводять даний (шуканий) інтеграл до табличного. Отже, необхідно знати табличні інтеграли і уміти їх розпізнавати.
Відзначимо, що в таблиці основних інтегралів змінна інтеграції може позначати як незалежну змінну, так і функцію від незалежної змінної (згідно властивості інваріантності формули інтеграції).
В справедливості приведених нижче формул можна переконатися, узявши диференціал правої частини, який буде рівний підінтегральному виразу в лівій частині формули.
Доведемо, наприклад, справедливість формули 2. Функція визначена і неперервна для всіх значень, відмінних від нуля.
Якщо , то, тоді .
Тому при.
Якщо , то. Але. Значитьпри.
Отже, формула 2 вірна.
Аналогічно, перевіримо формулу 15:
.
Таблиця основних інтегралів
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
studfiles.net
Таблиця інтегралів гіперболічних функцій
Це список інтегралів первісних функцій гіперболічних функцій Для повішого списку інтегралів дивись Таблиця інтегралів
У всіх цих формурах під a мається на увазі ненульова константа, C означає константу інтегрування
∫ sh a x d x = ch a x a + C \;ax\;dx=\;ax+C\, ∫ ch a x d x = sh a x a + C \;ax\;dx=\;ax+C\, ∫ sh 2 a x d x = sh 2 a x 4 a − x 2 + C ^ax\,dx=\;2ax-+C\, ∫ ch 2 a x d x = sh 2 a x 4 a + x 2 + C ^ax\,dx=\;2ax++C\, ∫ th 2 a x d x = x − th a x a + C ^ax\,dx=x-\;ax+C\, ∫ sh n a x d x = sh n − 1 a x ch a x a n − n − 1 n ∫ sh n − 2 a x d x ^ax\,dx=^ax\;\;ax-\int ^ax\,dx\qquad для n > 0 також: ∫ sh n a x d x = sh n + 1 a x ch a x a n + 1 − n + 2 n + 1 ∫ sh n + 2 a x d x ^ax\,dx=^ax\;\;ax-\int ^ax\,dx\qquad для n 0 також: ∫ ch n a x d x = − sh a x ch n + 1 a x a n + 1 − n + 2 n + 1 ∫ ch n + 2 a x d x ^ax\,dx=-\;ax\;^ax-\int ^ax\,dx\qquad для nДжереларед
- Двайт Г Б Гиперболичесике функции — интегралы // Таблицы интегралов и другие математические формулы / пер с англ Н В Леви ; под ред К А Семендяева — М : Наука, 1978 — С 134-140 рос
| |||||
Таблиця інтегралів гіперболічних функцій Інформацію Про
Таблиця інтегралів гіперболічних функцій Коментарі
Таблиця інтегралів гіперболічних функцій
Таблиця інтегралів гіперболічних функцій
Таблиця інтегралів гіперболічних функцій Ви переглядаєте суб єкт.
Таблиця інтегралів гіперболічних функцій що, Таблиця інтегралів гіперболічних функцій хто, Таблиця інтегралів гіперболічних функцій опис
There are excerpts from wikipedia on this article and video
www.turkaramamotoru.com
^ Основні методи інтегрування: | |||
Метод підстановки: формула заміни змінної у невизначеному інтегралі. | Метод інтегрування частинами: формула інтегрування частинами в невизначеному інтегралі. | ||
Формула Ньют-Лейбіца (для певного інтеграла): тоді | Заміна змінної у визначеному інтегралі: | ||
^ Інтегрування по частинах в певному інтегралі:
| |||
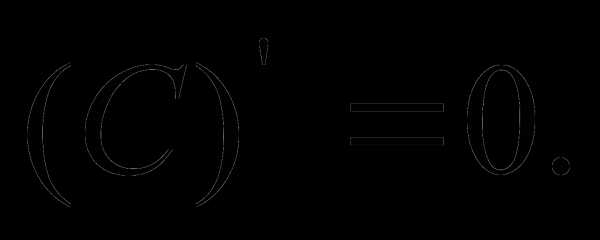
^ Найпростіші похідні: | Основні св-ва певного інтеграла: | ||
 |  |
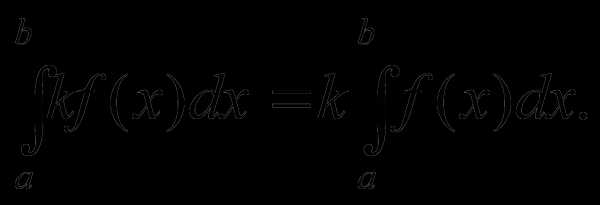
| |
 | |||
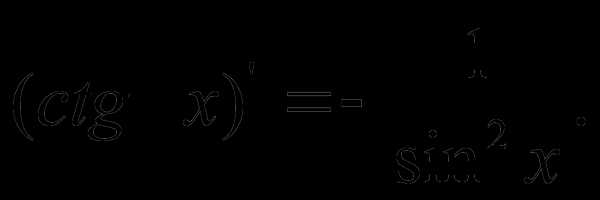 | |||
uadoc.zavantag.com
Таблиця інтегралів раціональних функцій
Цей список інтегралів первісних функцій раціональних функцій Для повнішого списку інтегралів дивись Таблиця інтегралів ∫ a x + b n d x = a x + b n + 1 a n + 1 for n ≠ − 1 dx=\qquad n\neq -1\,\! ∫ c a x + b d x = c a ln | a x + b | dx=\ln \left|ax+b\right| ∫ x a x + b n d x = a n + 1 x − b a 2 n + 1 n + 2 a x + b n + 1 for n ∉ dx=n+1n+2ax+b^\qquad n\not \in \ ∫ x a x + b d x = x a − b a 2 ln | a x + b | dx=-\ln \left|ax+b\right| ∫ x a x + b 2 d x = b a 2 a x + b + 1 a 2 ln | a x + b | dx=ax+b+\ln \left|ax+b\right| ∫ x a x + b n d x = a 1 − n x − b a 2 n − 1 n − 2 a x + b n − 1 for n ∉ dx=n-1n-2ax+b^\qquad n\not \in \ ∫ x 2 a x + b d x = b 2 ln | a x + b | a 3 + a x 2 − 2 b x 2 a 2 dx=\ln\left|ax+b\right|+-2bx ∫ x 2 a x + b 2 d x = 1 a 3 a x − 2 b ln | a x + b | − b 2 a x + b dx=\leftax-2b\ln \left|ax+b\right|-\right ∫ x 2 a x + b 3 d x = 1 a 3 ln | a x + b | + 2 b a x + b − b 2 2 a x + b 2 dx=\left\ln \left|ax+b\right|+-\right ∫ x 2 a x + b n d x = 1 a 3 − a x + b 3 − n n − 3 + 2 b a + b 2 − n n − 2 − b 2 a x + b 1 − n n − 1 for n ∉ dx=\left-+-ax+b^\right\qquad n\not \in \ ∫ 1 x a x + b d x = − 1 b ln | a x + b x | dx=-\ln \left|\right| ∫ 1 x 2 a x + b d x = − 1 b x + a b 2 ln | a x + b x | ax+bdx=-+\ln \left|\right| ∫ 1 x 2 a x + b 2 d x = − a 1 b 2 a x + b + 1 a b 2 x − 2 b 3 ln | a x + b x | ax+b^dx=-a\leftax+b+x-\ln \left|\right|\right ∫ 1 x 2 + a 2 d x = 1 a arctan x a +a^dx=\arctan \,\! ∫ 1 x 2 − a 2 d x = -a^dx=-\,\mathrm =\ln &|x||a|\end
for
a
≠
0
:
Будь-яка раціональна функція може бути проінтегрована з використанням вищенаведених рівнянь і методу розкладу на прості дроби, тобто декомпозицією раціональної функції в суму функцій вигляду:
e x + f a x 2 + b x + c n +bx+c\right^Див такожред
- Диференційний біном — інтегрування виразів x m a + b x n p d x , a+bx^^\;dx, де a, b — дійсні числа, a m, n, p — раціональні числа
Джереларед
- Двайт Г Б Рациональные алгебраические функции — интегралы // Таблицы интегралов и другие математические формулы / пер с англ Н В Леви ; под ред К А Семендяева — М : Наука, 1978 — С 22-40 рос
| |||||
| Це незавершена стаття з математики Ви можете допомогти проекту, виправивши або дописавши її |
Таблиця інтегралів раціональних функцій Інформацію Про
Таблиця інтегралів раціональних функцій Коментарі
Таблиця інтегралів раціональних функцій
Таблиця інтегралів раціональних функцій
Таблиця інтегралів раціональних функцій Ви переглядаєте суб єкт.
Таблиця інтегралів раціональних функцій що, Таблиця інтегралів раціональних функцій хто, Таблиця інтегралів раціональних функцій опис
There are excerpts from wikipedia on this article and video
www.turkaramamotoru.com

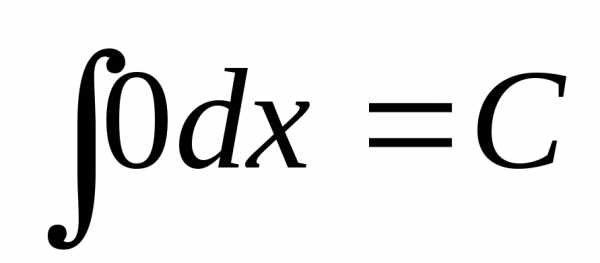 .
7.
.
7. 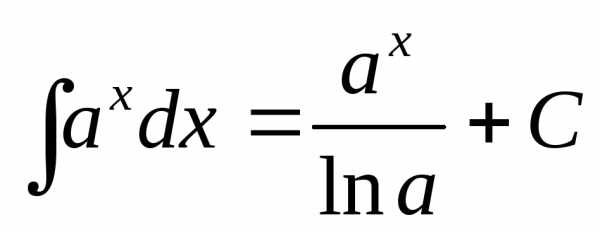 .
.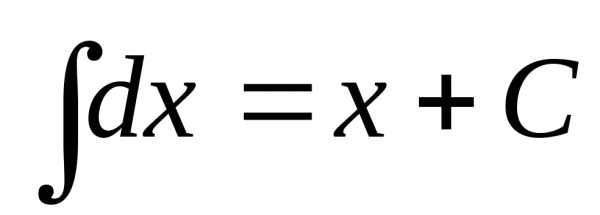 .
8.
.
.
8.
.
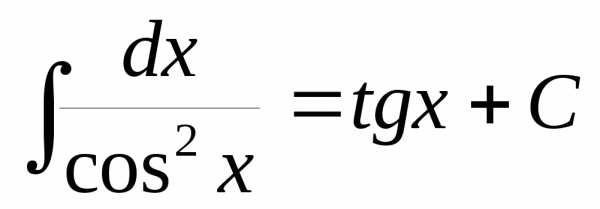 .
.