Тангенс косинус и синус угла – Синус, косинус и тангенс острого угла прямоугольного треугольника

Содержание

Синус, косинус, тангенс в прямоугольном треугольнике

Эти знания точно необходимы всем, кто планирует стать инженером или иметь дело с пространством его измерением и изменением (см. список профессий). Для остальных эта информация необходима для сдачи экзаменов и просто общего знания о мире!

Итак, в прямоугольном треугольнике:

Синус (острого угла) в прямоугольном треугольнике — отношение противолежащего катета к гипотенузе. Записывается: sin A = BC / AB

Косинус (острого угла) в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе. Записывается: cos A = AC / AB

Тангенс (острого угла) в прямоугольном треугольнике — отношение противолежащего катета к прилежащему. Или аналогично — отношение синуса к косинусу

. Записывается: tg A = BC / AC = sin A / cos A

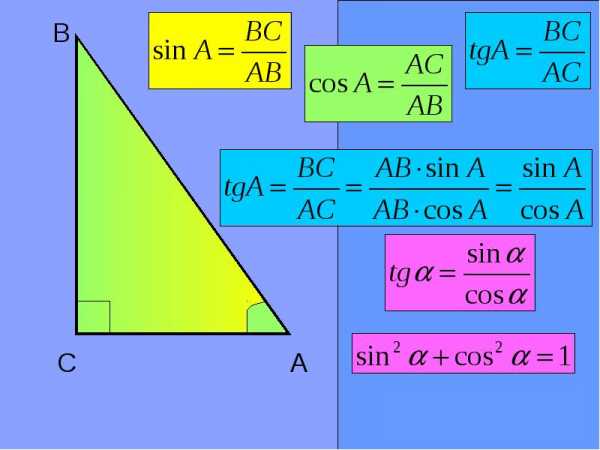
Основное тригонометрическое тождество составлено на основе квадратов синуса и косинуса:

sin² A + cos² A = 1

Естественно, при равенстве острых углов в различных прямоугольных треугольниках, значения их синусов, косинусов и тангенсов совпадают.

Редактировать этот урок и/или добавить задание и получать деньги постоянно* Добавить свой урок и/или задания и получать деньги постоянно

Добавить новость и получить деньги

Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников

uchilegko.info

Тригонометрия — ЕГЭ 2013 — Онлайн.Помощь

Определение 1. Синусом угла α называется ордина точки, полученной поворотом точки (1; 0) вокруг начала координат на угол. Обозначается sin α.

Определение 2. Косинусом угла α называется ордина точки, полученной поворотом точки (1; 0) вокруг начала координат на угол. Обозначается cos α.

Определение 3. Тангенсом угла α называется отношение синуса угла α к его косинусу. Обозначается tg α.
tg α = (sin α) / (cos α)
Определение 4. Котангенсом угла α называется отношение косинуса угла α к его синусу. Обозначается ctg α.
ctg α = (cos α) / (sin α)

α	sin α	cos α	tg α	ctg α
0 0°	0	1	0	Не существует
π/6 30°	1/2	√3/2	√3/3	√3
π/4 45°	√2/2	√2/2	1	1
π/3 60°	√3/2	1/2	√3	√3/3
π/2 90°	1	0	Не существует	0
π 180°	0	-1	0	Не существует
3π/2 270°	-1	0	Не существует	0
2π 360°	0	1	0	Не существует

Знаки синуса, косинуса и тангенса
Знаки синуса:

Знаки косинуса:

Знаки тангенса:

Зависимость между синусом, косинусом и тангенсом одного и того же угла
Основное тригонометрическое тождество:
sin² α + cos² α = 1 sin α = ± √(1 — cos² α)
cos α = ± √(1 — sin² α)
tg α · ctg α = 1
tg α = 1 / ctg α
ctg α = 1 / tg α
1 + tg² α = 1 / cos² α

1 + ctg² α = 1 / sin² α

Синус, косинус и тангенс углов α и -α

sin (α) = — sin α
cos (-α) = cos α
tg (α) = — tg α

Формулы сложения

cos (α + β) = cos α cos β — sin α sin β
cos (α — β) = cos α sin β + sin α cos β
sin (α + β) = sin α cos β + cos α sin β
sin (α — β) = sin α cos β — cos α sin β
tg (α + β) = (tg α + tg β) / (1 — tg α · tg β))

Синус, косинус и тангенс двойного угла

sin 2α = 2 sin α cos α
cos 2α = cos² α — sin² α
tg 2α = 2tg α/ (1 — tg² α)

Синус, косинус и тангенс половинного угла
sin² (α/2) = (1 — cos α) / 2
cos² (α/2) = (1 + cos α) / 2
tg² (α/2) = (1 — cos α) / (1 + cos α) sin α = 2tg (α/2) / (1 + tg² (α/2))
cos α = (1 — tg² (α/2)) / (1 + tg² (α/2))
tg α = 2tg (α/2) / (1 — tg² (α/2))

Сумма и разность синусов. Сумма и разность косинусов

sin α + sin β = 2 sin ( (α + β) / 2) cos ( (α — β) / 2)
sin α — sin β = 2 sin ( (α — β) / 2) cos ( (α + β) / 2)
cos α + cos β = 2 cos ( (α + β) / 2) cos ( (α — β) / 2)
cos α — cos β = — 2 cos ( (α + β) / 2) cos ( (α — β) / 2)

Формулы преобразования произведения в сумму

cos α cos β = 1/2 (sin (α + β) + sin (α — β) )
sin α sin β = 1/2 (cos (α — β) — cos (α + β) )
cos α cos β = 1/2 (cos (α + β) + cos (α — β) )

Формулы приведения
sin (α + 2πk) = sin α
cos (α + 2πk) = cos α, k ∈ Z
sin (π/2 — α) = cos α
sin (π — α) = sin α
sin (3π/2 — α) = — cos α

sin (π/2 + α) = cos α
sin (π + α) = — sin α
sin (3π/2 + α) = — cos α

cos (π/2 — α) = sin α
cos (π — α) = — cos α
cos (3π/2 — α) = — sin α
cos (π/2 + α) = — sin α
cos (π + α) = — cos α
cos (3π/2 + α) = sin α

tg (α + πk) = tg α, k ∈ Z
ctg (α + πk) = crg α, k ∈ Z
tg (π/2 — α) = ctg α
tg (π/2 + α) = — ctg α
ctg (π/2 — α) = tg α
ctg (π/2 + α) = — tg α

Формулы приведения запоминать необязательно. Для того чтобы записать любую из них, можно руководстоваться следующими правилами:
1) В правой части ставится тот знак, который левая часть имеет при условии 0 2) Если в левой части угол равен π/2 ± α или 3π/2 ± α, то синус заменяется на косинус, косинус — на синус, тангенс — на котангенс, котангенс — на гангенс. Если угол равен π ± α, то замены не происходит.

ege-mobile.ru

Тригонометрия — ЕГЭ 2014 — Онлайн.Помощь

α	sin α	cos α	tg α	ctg α
0 0°	0	1	0	Не существует
π/6 30°	1/2	√3/2	√3/3	√3
π/4 45°	√2/2	√2/2	1	1
π/3 60°	√3/2	1/2	√3	√3/3
π/2 90°	1	0	Не существует	0
π 180°	0	-1	0	Не существует
3π/2 270°	-1	0	Не существует	0
2π 360°	0	1	0	Не существует

Знаки синуса, косинуса и тангенса
Знаки синуса:

Знаки косинуса:

Знаки тангенса:

Зависимость между синусом, косинусом и тангенсом одного и того же угла
Основное тригонометрическое тождество:
sin² α + cos² α = 1 sin α = ± √(1 — cos² α)
cos α = ± √(1 — sin² α)
tg α · ctg α = 1
tg α = 1 / ctg α
ctg α = 1 / tg α
1 + tg² α = 1 / cos² α
1 + ctg² α = 1 / sin² α

Синус, косинус и тангенс углов α и -α

sin (α) = — sin α
cos (-α) = cos α
tg (α) = — tg α

Формулы сложения

Синус, косинус и тангенс двойного угла

sin 2α = 2 sin α cos α
cos 2α = cos² α — sin² α
tg 2α = 2tg α/ (1 — tg² α)

Формулы преобразования произведения в сумму

cos α cos β = 1/2 (sin (α + β) + sin (α — β) )
sin α sin β = 1/2 (cos (α — β) — cos (α + β) )
cos α cos β = 1/2 (cos (α + β) + cos (α — β) )

Формулы приведения
sin (α + 2πk) = sin α
cos (α + 2πk) = cos α, k ∈ Z
sin (π/2 — α) = cos α
sin (π — α) = sin α
sin (3π/2 — α) = — cos α
sin (π/2 + α) = cos α
sin (π + α) = — sin α
sin (3π/2 + α) = — cos α

cos (π/2 — α) = sin α
cos (π — α) = — cos α
cos (3π/2 — α) = — sin α
cos (π/2 + α) = — sin α
cos (π + α) = — cos α
cos (3π/2 + α) = sin α

tg (α + πk) = tg α, k ∈ Z
ctg (α + πk) = crg α, k ∈ Z
tg (π/2 — α) = ctg α
tg (π/2 + α) = — ctg α
ctg (π/2 — α) = tg α
ctg (π/2 + α) = — tg α

ege-mobile.ru

Определение синуса, косинуса, тангенса и котангенса и примеры

Для начала рассмотрим круг с радиусом 1 и с центром в (0;0). Для любого αЄR можно провести радиус 0A так, что радианная мера угла между 0A и осью 0x равна α. Направление против часовой стрелки считается положительным. Пусть конец радиуса А имеет координаты (a,b).

Определение синуса

Определение: Число b, равное ординате единичного радиуса, построенного описанным способом, обозначается sinα и называется синусом угла α.

Пример: sin 3π cos3π/2 = 0 0 = 0

Определение косинуса

Определение: Число a, равное абсциссе конца единичного радиуса, построенного описанным способом, обозначается cosα и называется косинусом угла α.

Пример: cos0 cos3π + cos3,5π = 1 (-1) + 0 = 2

Эти примеры используют определение синуса и косинуса угла через координаты конца единичного радиуса и единичной окружности. Для более наглядного представления необходимо нарисовать единичную окружность и отложить на ней соответствующие точки, а затем посчитать их абсциссы для вычисления косинуса и ординаты для вычисления синуса.

Определение тангенса

Определение: Функция tgx=sinx/cosx при x≠π/2+πk, kЄZ, называется котангенсом угла x. Область определения функции tgx это все действительные числа, кроме x=π/2+πn, nЄZ.

Пример: tg0 tgπ = 0 0 = 0

Этот пример аналогичен предыдущему. Для вычисления тангенса угла нужно поделить ординату точки на её абсциссу.

Определение котангенса

Определение: Функция ctgx=cosx/sinx при x≠πk, kЄZ называется котангенсом угла x. Область определения функции ctgx = -все действительные числа кроме точек x=πk, kЄZ.

Рассмотрим пример на обычном прямоугольном треугольнике

Чтобы было понятнее, что же такое косинус, синус, тангенс и котангенс. Рассмотрим пример на обычном прямоугольном треугольнике с углом y и сторонами a,b,c . Гипотенуза с, катеты соответственно a и b. Угол между гипотенузой c и катетом b y.

Определение: Синус угла y — это отношение противолежащего катета к гипотенузе: siny = а/с

Определение: Косинус угла y это отношение прилежащего катета к гипотенузе: сosy= в/с

Определение: Тангенс угла у — это отношение противолежащего катета к прилежащему: tgy = а/в

Определение: Котангенс угла y -это отношение прилежащего катета к противолежащему: ctgy= в/а

Cинус, косинус, тангенс и котангенс называют ещё тригонометрическими функциями. У каждого угла есть свой синус и косинус. И практически у каждого есть свой тангенс и котангенс.

Считается, что если нам дан угол, то его синус, косинус, тангенс и котангенс нам известны! И наоборот. Дан синус, или любая другая тригонометрическая функция соответственно, мы знаем угол. Созданы даже специальные таблицы, где расписаны тригонометрические функции для каждого угла.

Нужна помощь в учебе?

Предыдущая тема: Преобразования выражений, содержащих степень с дробным показателем
Следующая тема:&nbsp&nbsp&nbspСвойства синуса, косинуса, тангенса и котангенса

Все неприличные комментарии будут удаляться.