Lim предел функции – как понять, вычислить, подробное объяснение с решением

Предел функции — Электронный учебник K-tree

Предел скалярной функции от одной переменной

Обозначим открытое множество D ⊂ R и функцию f : D → R от одной переменной. Точка x₀ является предельной точкой множества D: x₀ ∈ D. Пределом функции f при x стремящемся к x₀ является h если для любого ε > 0 существует такая δ > 0, что

x ∈ D, x ≠ x₀, |x-x₀| < δ ∴ |f(x)-h| < ε
(∴ обозначает «следовательно»)

Односторонний предел

Правосторонний предел f когда x стремится к x₀ справа равен h₁, если для любого ε > 0 существует δ > 0 такая, что

x ∈ D, x > x₀, |x-x₀| < δ ∴ |f(x)-h₁| < ε

Левосторонний предел f когда x стремится к x₀ слева равен h₂, если для любого ε > 0 существует δ > 0 такая, что

x ∈ D, x < x ₀, |x-x₀| < δ ∴ |f(x)-h₂| < ε

Если существует предел f в точке x₀ и его значение равно h, то существуют односторонние пределы и они совпадают со значением h. Если односторонние пределы не совпадают, то предел не существует

Свойства пределов

Если существуют пределы функций f и g в точке a, то

• lim_x→a(c⋅f(x)) = c⋅lim_x→a(f(x))
• lim_x→a(f(x)+g(x)) = lim_x→a(f(x)) + lim_x→a(g(x))
• lim_x→a(f(x)⋅g(x)) = lim_x→a(f(x)) ⋅ lim_x→a(g(x))
• lim_x→a(f(x)/g(x)) = lim_x→a(f(x)) / lim_x→a(g(x)) (если lim_x→a(g(x))≠0)
• lim_x→a(f(x)^g(x)) = lim_x→a(f(x)) ^{lim_x→a(g(x))}

Предел функции с двумя переменными

Пусть D⊂R²

— открытое множество и функция f: D→R — функция с двумя переменными. Точка a является предельной точкой. Предел функции f, когда x стремится к a равен h, если для любого ε > 0 существует такое значение δ > 0, что

x ∈ D, x ≠ a, ||x-a|| < δ ∴ |f(x)-h| < ε

Определение предела

Пусть D — это открытое подмножество Rⁿ и функция f : D → R^m. Точка a ∈ D и h ∈ R^m. Предел функции f, когда x стремится к a, равен h если для любого ε > 0 существует δ > 0 такая, что

x ∈ D, x ≠ a, ||x-a|| < δ ∴ |f(x)-h| < ε
и записывается в виде:
lim_x→af(x) = h

Свойства предела

Точка a∈D не обязательно принадлежит множеству D, поэтому может не существовать, т.е. для существования предела в точке а нет необходимости, что бы функция была определена в данной точке.

f(x) приближается к h тогда, когда x приближается к a, другими словами, функция стремится к h, когда x стремится к a: f(x) → h.

Если существует предел lim_x→af(x), то он единственный, то есть не может существовать два различных предела в одной точке.

Предел по фильтру

Пусть дана функция f: D ⊂ Rⁿ → R^m и подмножество S ⊂ D такое, что a ∈ S. Предел по фильтру S в точке a равен h, если для любого ε > 0 существует такое значение σ > 0, что:

x ∈ S, x ≠ a, ||x-a|| < δ ∴ ||f(x)-h|| < ε

Если предел функции в какой либо точке равен h, то значение предла для любого фильтра S будет также равно h. Таким образом, если не существует предел хотя бы по одному фильтру, то, следовательно, предел не существует. Также, если пределы по двум фильтрам не совпадают, то предел не существует.

Пример

Пусть дана функция f: R²\{(0,0)} → R
f(x,y) = xy/(x²+y²)
Обозначим два фильтра S₁ = {(x,y)∈R² / x = y} и S₂ = {(x,y)∈R² / x = -y} и найдём пределы в точке 0:
x∈S₁: lim_{[(x,y)→(0,0)]}f(x,y)=lim _[x→0]x²/2x²=1/2
x∈S₂: lim_{[(x,y)→(0,0)]}f(x,y)=lim _[x→0]-x²/2x²=-1/2
Пределы не совпадают, поэтому предел не существует.

Непрерывность функции

Дана функция f: D ⊂ Rⁿ → R^m с областью определения D и точкой a ∈ D. Функция f является непрерывной в точке a если lim _x→af(x)=f(a). Функция называется непрерывной если она непрерывна в любой точке из области определения D.

Свойства непрерывных функций

Для функций f: D ⊂ R

n → R^m и g: D ⊂ Rⁿ → R^m и числа c ∈ R справедливо:

• Если f непрерывна в точке a, то функция c⋅f тоже непрерывна
• Если f и g непрерывны в точке a, то функция g+f тоже непрерывна
• Если f и g непрерывны в точке a и m=1, то функция f⋅g тоже непрерывна в точке a
• Если f ⊂ Rⁿ → R непрерывна в точке a и не равна нулю во всей области определения, то функция 1/f тоже непрерывна в точке a
• Если f ⊂ Rⁿ → R^m и f(x) = (f₁(x),…,f_m(x)), то функция f непрерывна в точке x тогда и только тогда, когда непрерывны все функции f_i(x) для 1 ≤ i ≤ m

Непрерывность сложных функций

Даны функции f:D⊂Rⁿ→R^m и g:V⊂R^m→R^p. При соблюдении условий f(D)⊂V и g(f(x)), если f непрерывна в точке a, и g непрерывна в точке b = f(a), то g(f(x)) также непрерывна в точке a.

Теорема Кантора — Гейне

Пусть дана функция f : D ⊂ Rⁿ → R ^m и такая область D, что D является компактным множеством. Если функция непрерывна, то у функции обязательно есть минимальное и максимальное значение.

k-tree.ru

Предел функции

	Главная > Учебные материалы > Математика:  Предел функции
	1.Предел функции.
	6 7 8 9 10 11 12 13 14
	1.Предел функции.
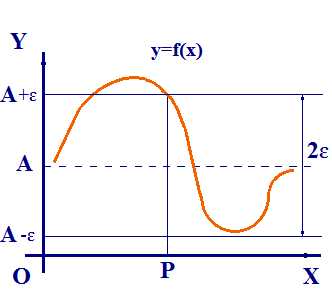
	Пусть задана некая функция f(x). Тогда число А будет называться пределом функции y = f(x) при х стремящимся к бесконечности, если при всех х больше определенного числа р, разность между значением функции и числом А по модулю будет меньше любого, сколь угодно малого положительного числа ɛ>0. Т.е. верно неравенство:    | f(x)– А | < ɛ Иными словами, при подставлении любого числа х>р данное неравенство всегда будет выполняться. Предел функции при x→∞ обозначается:        lim f(x) = А     x→∞		Рис.1
	Геометрический смысл предела функции y=f(x) в бесконечности заключается в том, что при стремлении х к бесконечности, значение функции f(x) стремится к числу А. Таким образом, неравенство | f(x) – А | < ɛ равносильно двойному неравенству:    А — ɛ < f(x) < А + ɛ и функция принимает значения в диапазоне шириной 2ɛ (рис.1).
	Примеры.
	6 7 8 9 10 11 12 13 14

www.mathtask.ru

7.2. Предел функции

7.1.3. Некоторые функциональные зависимости, используемые в экономике.

Посредством функциональной зависимости могут быть описаны многие соотношения в области экономики. Например:

1)	Функция спроса – зависимость спроса D (demand ) на
некоторый товар в зависимости от его цены p(price) :						D = f( p) ;
2)	Функция предложения – зависимость предложения S (supply)
на некоторый товар в зависимости от его цены p :						S = g(p) ;
3)	Функция полезности – субъективная числовая оценка
полезности		u (utility)	количества	f (x)	некоторого товара для
данного индивида: u = g(x) ;
4)	Однофакторная производственная функция – зависимость
объема y		продукции	от объема	b]	используемого ресурса:

y= f (x) ;

5)Функция издержек – зависимость издержек I на производствоx единиц продукции;

6)Налоговая ставка – зависимость налоговой ставки N , выраженной в процентах, от величины годового доходаf (x) .

Конкретный вид функциональной зависимости определяется с учетом обстоятельств и имеющейся информации.

Перейдем теперь к изучению более сложной формы операции предельного перехода, основанного на понятии предела (или предельного значения) функции. Ниже это понятие дается в двух эквивалентных формах – вначале, опираясь на ранее изученное понятие предела последовательности, а затем вовсе не использующее его.

7.2.1. Понятие предела функции в точке.

Пусть	функция	y = f (x) определена на некотором числовом
множестве	X ={x}	и точка	x0 является предельной точкой этого
множества	( x0 называется		предельной точкой множества x X ,

если в любой ε -окрестностиэтой точки есть точки множестваX , отличные отx0 ).

Определение 7.1. ЧислоA называется пределом функцииf (x) в точкеx0 , если для любой последовательности значений аргументаx1,x2 ,x3,…,xn ,…, сходящейся кx0 , причемxn ≠ x0 , соответствующая

последовательность	значений функции	f (x1),	f (x2 ), …,f (xn ) ,…
сходится к числу A :	f (x)= A илиf (x)→ A приx → x0 .
lim
x→x0
Данное определение предела функции в			точке называется

определением на языке последовательностей или определением предела по Гейне.

Определение 7.2. ЧислоA называется пределом функцииf (x) в

точке x0 ,				если для	любого,	сколь угодно			малого числа ε >0
существует				число	δ >0, такое,		что	для	всех	x X ( x≠ x0 ),
удовлетворяющих неравенству						[a,b]<δ ,		выполняется неравенство
	f (x) − A		<ε .							x = x0 называют
	Данное определение предела функции							в точке
определением на языке « (A ≠ B), »							или	определением предела по

Коши. Можно доказать теорему, что оба определения предела эквивалентны.

Определение 7.3. ЧислоA называется правым (левым) пределом

функции f (x) в точке		c [a,b], если для любой сходящейся кx0
последовательности	f (c)= C ,…,		для которой xn >x0			( xn <x0 ),
соответствующая	последовательность				значений	функции
f (x1),f (x2 ),f (x3 ), …,f (xn ) ,… сходится к числуA .
Правый предел (предел справа) обозначается
lim		f (x) = lim		f (x) = f(x0 +0) = A,
x→x0	, x<x0	x→x0	+0
а левый предел (предел слева)
lim		f (x) = lim		f (x)= f (x0 −0)= A.
x→x0	, x<x0	x→x0	−0
Правый и левый пределы называют односторонними пределами
функции в точке.
Теорема 7.1. Функцияf (x) имеет предел в точкеx0						тогда и
только тогда, когда в этой точке существуют					предел справа и предел

слева и они равны: f (x0 −0)= f (x +0)= A .

Определение 7.4. ЧислоA называют пределом функцииf (x) приx → ∞, если для любой бесконечно большой последовательности (xn ) значений аргумента соответствующая последовательность

( f (xn )) значений функции сходится кA : limf (x)= A.

x→∞

7.2.2. Теоремы о пределах функций.

Ниже приведены основные свойства предела функции и арифметических операций над функциями, имеющими предел, с помощью которых во многих случаях упрощается вычисление пределов.

Теорема 7.2.

Если функции

f (x)

и g(x)

имеют в точке x0

пределы A иB ,

т.е.

lim f (x)= A,

lim

g(x)= B , то:

x→x0

x→x0

1. Предел суммы (разности) функций равен сумме (разности)

пределов:

lim ( f (x)± g(x) )= limf (x)± limg(x)= A ± B ;

x→x0

x→x0

x→x0

2.

Постоянный множитель можно выносить за знак предела:

lim c f (x)= c lim

f (x) = cA;

x→x0

x→x0

3.

Предел произведения равен произведению пределов:

lim ( f (x)g(x)) )= limf (x) limg(x) =AB ;

x→x0

x→x0

x→x0

4.

Предел частного равен частному пределов:

f

(x)

lim f (x)

A

lim

=

x→x0

=

, если

B ≠ 0 .

g

(x)

lim g

(x)

B

x→x0

x→x0

Пример 7.1.

Найти lim

2×5− x3

.

x

2

− x

+2

x→1

Решение. Найдем предел знаменателя:

lim(x2 − x +2)= limx2 − limx + lim 2=12

−1+ 2= 2≠ 0 .

x→1

x→1

x→1

x→1

Значит, можно применить теорему о пределе частного:

	2x	5	− x	3		lim (2×5 − x3 )		2	5	3
lim					=	x→1	=		1	−1	=	1 .
	x2 − x+2					lim (x2 − x +2)			2
x→1												2
						x→1

7.2.3. Замечательные пределы.

Здесь приведены два важных предельных соотношения, широко

используемых в математике и ее приложениях:

lim sin x =1

(первый замечательный предел)

(7.1)

x→0

x

x

1

( 7.2)

lim 1+

x

= e (второй замечательный предел)

x→∞

Приведенные замечательные пределы часто используются при

вычислении других пределов.

3x +1 2x

Пример 7.2.

Найти lim

3x

.

Решение. Имеем

x→∞

2x

2

3x +1 2x

1 2x

1 3x 3x

lim

= lim1+

= lim

1+

= e3 =3 e2 .

x→∞3x

x→∞

3x

x→∞

3x

1

Пример 7.3.

Найти

lim(1+ x)x .

x→0

Решение.

Сделаем замену 1 = y . Тогда при

x → 0 имеем, что

x

y

1

1

y → ∞ . Следовательно,

lim(1+ x)x = lim

1+

= e .

y

x→0

y→∞

7.2.4. Бесконечно малые и бесконечно большие функции.

Для изучения асимптотического поведения функций и для

установления их эквивалентности используются				понятия бесконечно
малых и бесконечно больших функций.
Определение 7.5. Функция			f (x) называется бесконечно малой в
точке x = x0 ,	если	ее предел	в этой точке	равен нулю, т.е.
lim f (x)= 0 .	Аналогично определяются бесконечно малые функции
x→x0
при x → ∞,x → +∞,		x → −∞, x →x0 +0, x →x0 −0 .

Например, функция y = x4 −1 является бесконечно малой при

x =1 и при	x = −1; функцияy = x−3 является бесконечно малой при
x → ∞, функцияy = ex является бесконечно малой приx → −∞.
Теорема 7.3. Алгебраическая сумма и произведение любого
конечного	числа бесконечно малых функций при x → x0 ,

произведение бесконечно малой функции на ограниченную функцию являются бесконечно малыми функциями при x → x0 .

Теорема 7.4. Для того, чтобы числоA было пределом функцииf (x) в точкеx0 , необходимо и достаточно, чтобы выполнялось

равенство f (x)= A +α(x),

где α(x) ― бесконечно малая функция при

x → x0 .

Определение

7.6.

Функция

y = f (x) называется

бесконечно

большой в то чке x = x0 , если для любого

M >0 существует число

δ >0, такое,

что для любых

x X , для которых 0<

x − x0

<δ ,

выполняется

неравенство

f (x)

> M . В этом случае пишут:

lim f (x)= ∞ .

Если

же

выполняется

неравенство

f (x)> M

x→x0

( f (x) <−M ), то пишут:

lim

f (x) = +∞

( lim f (x)= −∞).

x→x0

x→x0

Теорема

7.5.

Если

f (x)

бесконечно

большая функция

при

x → x0 , то

1

бесконечно малая функция при x → x0 ; если

g(x)

f

(x)

― бесконечно

малая

функция

при

x → x0 , причем

g(x0 )≠ 0 в

некоторой окрестности

точки

x0

, то

1

бесконечно большая

g(x)

функция при

x → x0 . Например,

f (x)= x −2 бесконечно малая при

x → 2 , тогда

1

=

1

бесконечно большая при x → 2 .

f (x)

x −2

studfiles.net

Предел функции — ПриМат

Определение. Пусть функция $f$ определена на интервале $(a, b)$ и точка $x_0 \in (a, b)$. Говорят, что функция $f$ непрерывна в точке $x_0$, если
$$\lim_{x \to x_0} f(x) = f (x_0).$$

Используя определение предела функции в смысле Коши, определение непрерывности функции $f$ в точке $x_0$ в кванторах можно записать следующим образом:
$$\forall \varepsilon > 0 \space \exists \delta = \delta (\varepsilon) > 0 : \forall x \in (a, b) : |x−x_0| < \delta \Rightarrow \\ \Rightarrow |f(x)−f(x_0)| < \varepsilon.$$
В этом определении можно не требовать выполнения условия $|x−x_0| > 0$, т. к. при $|x−x_0| = 0$ неравенство $|f(x)−f(x_0)| < \varepsilon$, очевидно, выполнено.

Так как величина $\displaystyle \lim_{x \to x_0} f(x)$ зависит лишь от тех значений, которые функция $f$ принимает в сколь угодно малой окрестности точки $x_0$, то непрерывность — это локальное свойство функции.

В терминах окрестностей определение непрерывности выглядит следующим образом.

Определение. Функция $f$ называется непрерывной в точке $x_0$, если для любой окрестности $V$ точки $f(x_0)$ найдется такая окрестность $U$ точки $x_0$, что для всех $x \in U$ значение $f(x) \in V$ , т. е. $f(U \cap (a, b)) \subset V$.

Применяя определение предела функции в смысле Гейне, определение непрерывности можно сформулировать так.

Определение. Функция $f$, определенная на интервале $(a, b)$, называется непрерывной в точке $x_0 \in (a, b)$, если любая последовательность аргументов $\{x_n\} \space (x_n \in (a, b), x_n \to x_0)$ порождает последовательность значений функции $\{f(x_n)\}$, стремящуюся к $f(x_0)$.

Применяя понятие одностороннего предела (т. е. предела слева и справа) в точке $x_0$, можно дать определения непрерывности слева (справа) в точке $x_0$. Именно, функция $f$ называется непрерывной слева (справа) в точке $x_0$, если $\displaystyle \lim_{x \to x_0−0} f(x) = f(x_0) (\lim_{x \to x_0+0} f(x) = f(x_0))$. При этом в определении непрерывности слева достаточно считать, что функция $f$ определена лишь в левой полуокрестности точки $x_0$, т. е. на $(a, x_0]$, а для непрерывности справа — на $[x_0, b)$.

Легко видеть, что справедливо следующее

Утверждение. Для того, чтобы функция $f$ была непрерывной в точке $x_0$, необходимо и достаточно, чтобы $f$ была непрерывной слева и справа в точке $x_0$.

Определение. Функция $f$, определенная на интервале $(a, b)$, называется разрывной в точке $x_0 \in (a, b)$, если $f$ не является непрерывной в этой точке.

Итак, функция $f$ является разрывной в точке $x_0$, если выполнено одно из двух следующих условий.

1. Либо не существует $\displaystyle \lim_{x \to x_0} f(x)$.

2. Либо предел $\displaystyle \lim_{x \to x_0} f(x)$ существует, но он не равен $f(x_0)$.

Пример 1. $f(x) \equiv C = Const$. Эта функция непрерывна в каждой точке $x_0 \in \mathbb{R}$, т. к. для любого $x \in \mathbb{R} \space |f(x)−f(x_0)| = 0$.

Пример 2. $f(x) = x^2, −\infty < x < +\infty, x_0 \in \mathbb{R}$. Зададим $\varepsilon > 0$. Тогда из неравенства
$$|x^2-x_0^2| \leq (|x|+|x_0|)|x-x_0|$$
следует, что при $|x−x_0| < \delta = \min{\Bigr(1, \frac{\varepsilon}{2|x_0|+1}\Bigl)}$ справедливо неравенство $|x^2-x_0^2| < \varepsilon$, т. е. $\displaystyle \lim_{x \to x_0} x^2 = x_0^2$, а значит, функция $f(x) = x^2$ непрерывна в любой точке $x_0 \in \mathbb{R}$.

Пример 3. $f(x) = \sqrt{x}, \space 0 \leq x < +\infty$. Если $x_0 \in (0, +\infty)$, то
$$|\sqrt{x}-\sqrt{x_0}| = \frac{|x-x_0|}{\sqrt{x}+\sqrt{x_0}} \leq \frac{1}{\sqrt{x_0}} |x-x_0| < \varepsilon,$$
если только $|x-x_0| < \delta \equiv \sqrt{x_0} \cdot \varepsilon$. Таким образом, функция $f(x) = \sqrt{x}$ непрерывна в каждой точке $x_0 > 0$. В точке $x_0 = 0$ можно ставить вопрос о непрерывности справа. Имеем $|\sqrt{x}-\sqrt{0}| = \sqrt{x} < \varepsilon \space$, если только $0 \leq x < \delta \equiv \varepsilon^2$. Итак, $\displaystyle \lim_{x \to 0+} \sqrt{x} = 0 = \sqrt{0}$, т. е. функция $f(x) = \sqrt{x}$ непрерывна справа в точке $0$.

Пример 4. $f(x)=\sin{x}, -\infty < x < +\infty$. Пусть $x_0 \in \mathbb{R}$. Тогда
$$|\sin{x}−\sin{x_0}| = \Bigg|2\cos{\frac{x+x_0}{2}}\sin{\frac{x-x_0}{2}}\Bigg| \leq \\ \leq 2\Bigg|\sin{\frac{x-x_0}{2}}\Bigg| \leq |x−x_0|,$$
где последнее неравенство в этой цепочке следует из доказанного выше неравенства $|\sin{t}| \leq |t| \space (0 < |t| < \pi/2)$. Можем считать, что $|x−x_0| < \pi$. Тогда при $|x−x_0| < \delta \equiv \min{(\pi, \varepsilon)}$ справедливо $|\sin{x}−\sin{x_0}| < \varepsilon$, т. е. функция $f(x) = \sin{x}$ непрерывна в каждой точке $x_0 \in \mathbb{R}$.

Аналогично доказываем, что функция $f(x) = \cos{x}$ непрерывна в каждой точке $x_0 \in \mathbb{R}$.

Пример 5. $f(x) = x \cdot \sin{\frac{1}{x}}$ при $x \neq 0$ и $f(0) = 0$. Покажем, что функция $f$ непрерывна в точке $x_0= 0$. Имеем $f(0) = 0$ и
$$\lim_{x \to 0} f(x) = \lim_{x \to 0} x \sin{\frac{1}{x}} = 0$$
(т. к. $|f(x)−0| = |x \sin{\frac{1}{x}}| \leq |x| < \varepsilon$, если только $|x−0| = |x| < \delta \equiv \varepsilon$). Итак, $\displaystyle \lim_{x \to 0} f(x) = f(0)$, так что $f$ непрерывна в точке $0$.

Пример 6. $f(x) = \operatorname{sign} x, x \in R$. Если $x_0 \neq 0$, то функция $f$ постоянна в некоторой окрестности точки $x_0$ и, следовательно, непрерывна в этой точке. Если же $x_0 = 0$, то не существует предела функции $f$ при $x \to 0$. Значит, функция $f$ разрывна в точке $0$. Более того, $\displaystyle \lim_{x \to 0+} \operatorname{sign} x = 1, \lim_{x \to 0−} \operatorname{sign} x = −1, \operatorname{sign} 0 = 0$, так что функция $\operatorname{sign} x$ разрывна в точке $0$ как слева, так и справа.

Пример 7. Рассмотрим функцию Дирихле
$$\begin{equation*}D(x) = \begin{cases} 1, \quad x \in \mathbb{Q}, \\ 0, \quad x \in \mathbb{R \setminus Q}. \end{cases} \end{equation*}$$
Пусть $x_0 \in \mathbb{R}$. Покажем, что не существует предела функции $D$ при $x \to x_0$. Для этого выберем последовательность $\{x^\prime_n\}$ отличных от $x_0$ рациональных чисел, стремящуюся к $x_0$. Тогда $D(x^\prime_n) = 1$ и, значит, $\displaystyle \lim_{n \to \infty} D(x^\prime_n) = 1$. Если же взять последовательность $\{x^{\prime\prime}_n\}$, отличных от $x_0$ иррациональных чисел, стремящуюся к $x_0$, то получим, что $D(x^{\prime\prime}_n) = 0$ и $\displaystyle \lim_{n \to \infty} D(x^{\prime\prime}_n) = 0$. В силу определения предела функции по Гейне получаем, что функция $D$ не имеет предела в точке $x_0$. Так как $x_0 \in \mathbb{R}$ — произвольная точка, то это означает, что функция Дирихле разрывна в каждой точке.

Пример 8. $f(x) = x \cdot D(x), \space x \in \mathbb{R}$. Функция $f$ разрывна в каждой точке $x_0 \neq 0$. В самом деле, если $\{x^\prime_n\}$ и $\{x^{\prime\prime}_n\}$ соответственно последовательности рациональных и иррациональных отличных от $x_0$ чисел, стремящиеся к $x_0$, то $\displaystyle \lim_{n \to \infty} f(x^\prime_n) = 0$ и $\displaystyle \lim_{n \to \infty} f(x^{\prime\prime}_n) = 0$, так что, в силу определения предела функции по Гейне, функция $f$ не имеет предела в точке $x_0$. Если же $x_0 = 0$, то $\displaystyle \lim_{x \to 0} f(x) = 0 = f(0)$. Действительно, $|f(x)| = |x \cdot D(x)| \leq |x| < \varepsilon$, если только $|x−0| = |x| < \delta \equiv \varepsilon$. Это означает, что данная функция непрерывна в единственной точке $x_0 = 0$.

Примеры решения задач

Пусть функция $f$ определена в окрестности точки $x_0$, кроме самой точки $x_0$. Доопределить функцию $f$, задав $f(x_0)$ так, чтобы получившаяся функция была непрерывна в точке $x_0$, если:

1. $\displaystyle f(x) = \frac{x^2-1}{x+1}, \space x_0 = -1$. Решение

   $$\lim_{x \to x_0} f(x) = \lim_{x \to x_0} \frac{(x-1)(x+1)}{x+1} = \lim_{x \to -1} (x-1) = -2$$
   Таким обр

ib.mazurok.com

Внеклассный урок — Предел функции

Предел функции

 

Предел функции в заданной точке, предельной для области определения функции, – это такая величина,  к которой стремится функция при стремлении ее аргумента к данной точке.

Предел функции — это обобщение понятия предела последовательности.

 

Любой предел функции состоит из трех частей: — значка предела lim; — записи под lim предельной точки, к которой стремится х; — самой функции.

 

Пример 1: Возьмем выражение lim  (x + 5)
                                                    ^x→1

Читается оно так: предел функции х + 5 при стремлении х к единице.

Что значит «стремление х к единице»?
Это значит, что х последовательно принимает значения, которые бесконечно приближаются к единице, но не совпадают с ней.

Вопрос: чему равен предел такой функции?

Решение:

Чтобы найти предел функции в нашем примере, надо просто подставить 1 в функцию (так как x→1):

lim  (x + 5) = 1 + 5 = 6.
^x→1

Ответ: пределом функции x + 5 при стремлении х к единице является 6:

lim  (x + 5) =  6.
^x→1

 

Пример 2 (с бесконечностью):

Возьмем наш первый пример, но при стремлении х к бесконечности:

lim  (x + 5).
^x→∞

x→∞ — это случай, когда х не стремится к какому-то числу, а неограниченно возрастает.
К примеру, сначала х = 10, потом х = 20, потом х = 30 и т.д. до бесконечности.
В этом случае функция тоже неограниченно возрастает, стремясь к бесконечности:

10 + 5 = 15
20 + 5 = 25
30 + 5 = 35 и т.д.

Таким образом, получаем ответ:

lim  (x + 5) = ∞
^x→∞

Пример 3 (с минус бесконечностью):

Найдем предел функции 5 – х:

lim   (5 – х) = ?
^x→∞

Решение:

Допустим, х имеет следующие значения: 2, 4, 6, 8, 10, 12 и т.д. до бесконечности.
Тогда наша функция будет иметь следующие значения: 3, 1, –1, –3, –5, –7 и так до минус бесконечности.
Мы видим, что функция неограниченно убывает, стремясь к минус бесконечности.

Ответ: lim   (5 – х) = –∞
           ^x→∞

Пример 4 (с дробью):

Не всегда при x→∞^{функция неограниченно возрастает.}

Возьмем функцию с дробью и найдем ее предел при стремлении х к бесконечности:

lim  3/х = ?
^x→∞

Решение:

Допустим, х имеет следующие значения: 1, 2, 3, 4, 5 и т.д. до бесконечности.
Тогда мы получим следующие значения функции: 3, 3/2, 1, 3/4, 3/5 и т.д.
Если мы продолжим этот ряд до бесконечности, то увидим, что каждое последующее значение функции меньше предыдущего, но ни одно из них не опускается ниже нуля. То есть функция стремится к нулю, но не пересекает его. А говоря иначе, ноль является пределом нашей функции.

Таким образом:

lim  3/х = 0.
^x→∞

 
 

 

raal100.narod.ru

Предел и непрерывность функции / math5school.ru

 

Предел функции y = f(x) при х → ∞

Вычисление пределов функции при х → ∞

Непрерывные функции

Теоремы про непрерывность функции

Замечательные пределы

Вычисление пределов функции в точке

  

Предел функции y = f(x) при х → ∞

Определение.

Число b называется пределом функции y = f(x) при х→+∞, если для любого числа ε > 0 найдётся такое число М > 0, что для всех х > М выполняется неравенство |f(x) – b|< ε.

Записывают так:

lim _х→+∞f(x) = b.

Геометрически это означает, что график функции y = f(x) при выборе достаточно больших значений х безгранично приближается к прямой у = b. Это означает, что расстояние от точки графика до прямой у = b по мере удаления точки в бесконечность может быть сделано меньше любого числа ε > 0. Прямая  называется в этом случае горизонтальной асимптотой графика функции y = f(x).  

Например: lim _х→+∞ 1/х = 0 и функция y = 1/х имеет горизонтальную асимптоту у = 0.

 

Определение.

Число b называется пределом функции y = f(x) при х→–∞, если для любого числа ε > 0 найдётся такое число М > 0, что для всех х < –М выполняется неравенство |f(x) – b|< ε.

Записывают так:

lim _х→–∞f(x) = b.

В этом случае прямая y = b также является горизонтальной асимптотой функции  y = f(x), график которой бесконечно близко приближается к ней при достаточно больших по модулю, но отрицательных значениях х.

Например: lim _х→–∞ (3 + 2^х) = 3 и функция y = (3 + 2^х) имеет горизонтальную асимптоту у = 3.

 

Наконец, прямая у = b  может быть горизонтальной асимптотой графика функции  и при х→+∞, и при х→–∞. Пишут так: х→∞.

Определение.

Число b называется пределом функции y = f(x) при х → ∞, если для любого числа ε > 0 найдётся такое число М > 0, что для всех x таких, что |х| > М, выполняется неравенство |f(x) – b|< ε.

Записывают так:

lim _х→∞f(x) = b.

Например: lim _х→∞х²/(х²+1) = 1 и функция y = х²/(х²+1) имеет горизонтальную асимптоту у = 1.

 

Вычисление пределов функции при х → ∞

Для вычисления пределов функций при х→∞ используются следующие теоремы об операциях над пределами:

 

Теорема о вынесении постоянного множителя за знак предела:

Если lim _х→∞f(x) = a, то lim _х→∞k · f(x) = k · а.

 

Теорема о пределе суммы:

Если lim _х→∞ f(x) = a, lim _х→∞ g(x) = b, то lim _х→∞ (f(x) + g(x)) = а + b.

 

Теорема о пределе произведения:

Если lim _х→∞ f(x) = a, lim _х→∞ g(x) = b, то lim _х→∞ f(x) · g(x) = а · b.

 

Теорема о пределе частного:

Если lim _х→∞ f(x) = a, lim _х→∞ g(x) = b и b ≠ 0, то lim _х→∞ f(x) / g(x) = а / b.

  

Непрерывные функции 

Определение.

Функция y = f(x) называется непрерывной в точке х = а, если существует предел функции в этой точке, т.е.

lim _х→а f(x) = f(a).

Функция y = f(x) будет непрерывной в точке х = а тогда и только тогда, когда выполняются условия:

• функция y = f(x) определена в точке х = а, т.е. существует f(a);
• существует предел lim _х→а f(x) функции в точке х = а;
• предел функции в точке х = а равен значению функции в этой точке, т.е.

lim _х→а f(x) = f(a). 

Другими словами верно и такое

Определение.

Функция y = f(x) непрерывна в точке х = а, если для любого числа ε > 0 существует такое число δ > 0, что для всех х, удовлетворяющих условию |x – a| < δ, выполняется неравенство |f(x) – f(a)| < ε.

Определение.

Если функция y = f(x) непрерывна в каждой точке некоторого промежутка, то её называют непрерывной на данном промежутке.

 

Теоремы про непрерывность функции

Теорема 1:

Если функции f(x) и g(x) непрерывны в точке х = а, то в этой точке непрерывны и функции  f(x) + g(x), f(x) – g(x), f(x) · g(x).

 

Теорема 2:

Если функции f(x) и g(x) непрерывны в точке х = а и g(а) ≠ 0, то в точке х = а  будет непрерывной также функция f(x) / g(x).

 

Исходя из двух последних теорем можно утверждать:

• многочлен y = a₀ + a₁x + . . . + a_nxⁿ – непрерывная функция в любой точке а ∈ R;
• дробно-рациональная функция

y =	a0 + a1x + a2x2 + . . . + anxn
	b0 + b1x + b2x2 + . . . + bmxm

        непрерывна во всех точках числовой оси, кроме нулей знаменателя;

• функции у = sin x, y = cos x, y = tg x, y = ctg x, y = a^x, y = log_ax, y = ⁿ√х, y = |x|, у = arcsin x, y = arccos x, y = arctg x, y = arcctg x также непрерывны во всех точках области определения.

 

Замечательные пределы

Замечательные пределы – термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известных математических тождеств со взятием предела. Особенно известны:

 

Первый замечательный предел:

lim х→ 0	sin x	= 1.
	x

Следствия из первого замечательного предела: 

lim х→ 0	tg x	= 1,
	x

lim х→ 0	arcsin x	= 1,
	x

lim х→ 0	arctg x	= 1,
	x

lim х→ 0	2 · (1 – cos x)	= 1.
	x2

 

Второй замечательный предел:

lim _х→∞ (1 + 1/x)^x = e  или  lim _х→0 (1 + x)^1/x = e.

 

Следствия из второго замечательного предела:

lim х→ 0

(1 + u)1/u = e,

lim х→ ∞

(1 + k/x)x = ek,

lim х→ 0	ln(1 + x)	= 1,
	x

lim х→ 0	ex – 1	= 1,
	x

lim х→ 0	ax – 1	= 1,
	x · ln a

lim х→ 0	(1 + x)α – 1	= 1.
	αx

 

Вычисление пределов функции в точке 

Если y = f(x) непрерывна в точке х = а, то lim _х→а f(x) = f(a).

Если в результате подстановки х = а при вычислении предела получаем выражение типа 0 / 0, то имеет смысл попытаться воспользоваться одним из следующих приёмов:

• попробовать разложить числитель и знаменатель дроби на множители, выполнить сокращение, а затем найти предел;
• избавиться от иррациональности в знаменателе, а затем находить предел:
• преобразовать функцию так, чтобы можно было воспользоваться первым замечательным пределом или его следствием.

 

     Смотрите также: 

Таблицы чисел 

Алгебраические тождества

Степени

Арифметический корень n-й степени

Логарифмы 

Графики элементарных функций

Построение графиков функций геометрическими методами

Тригонометрия

Таблицы значений тригонометрических функций

Треугольники

Четырёхугольники

Многоугольники

Окружность 

Площади геометрических фигур

Прямые и плоскости

Многогранники 

Тела вращения 

 

math4school.ru

Предел (математика) — Википедия. Что такое Предел (математика)

Преде́л — одно из основных понятий математического анализа. Различают предел последовательности и предел функции.

Понятие предела на интуитивном уровне использовалось ещё во второй половине XVII века Ньютоном, а также математиками XVIII века, такими как Эйлер и Лагранж. Первые строгие определения предела последовательности дали Больцано в 1816 году и Коши в 1821 году.

История

Основной источник: ^[1]

Интуитивное понятие о предельном переходе использовалось еще учеными Древней Греции при вычислении площадей и объемов различных геометрических фигур. Методы решения таких задач в основном были развиты Архимедом.

При создании дифференциального и интегрального исчислений математики XVII века (и, прежде всего, Ньютон) также явно или неявно использовали понятие предельного перехода. Впервые определение понятия предела было введено в работе Валлиса «Арифметика бесконечных величин» (XVII век), однако исторически это понятие не лежало в основе дифференциального и интегрального исчислений.

Лишь в XIX веке в работах Коши теория пределов была использована для строгого обоснования математического анализа. Дальнейшей разработкой теории пределов занимались Вейерштрасс и Больцано.

С помощью теории пределов во второй половине XIX века было, в частности, обосновано использование в анализе бесконечных рядов, которые явились удобным аппаратом для построения новых функций.

Предел последовательности

Пределом последовательности называют объект, к которому члены последовательности в некотором смысле стремятся или приближаются с ростом номера.

Число a{\displaystyle a} называется пределом последовательности x1,x2,…,xn,…{\displaystyle x_{1},x_{2},…,x_{n},…} , если

∀{\displaystyle \forall } ϵ>0{\displaystyle \epsilon >0} , ∃{\displaystyle \exists } N(ϵ){\displaystyle N(\epsilon )} , ∀{\displaystyle \forall } n>N(ϵ){\displaystyle n>N(\epsilon )}: |xn−a|<ϵ{\displaystyle |x_{n}-a|<\epsilon }.

Предел последовательности обозначается limn→+∞xn{\displaystyle \lim _{n\to +\infty }x_{n}}. Куда именно стремится n{\displaystyle n}, можно не указывать, поскольку n{\displaystyle n} ∈N{\displaystyle \in \mathbb {N} }, оно может стремиться только к +∞{\displaystyle +\infty }.

Свойства:

Предел функции

График функции, предел которой при аргументе, стремящемся к бесконечности, равен L{\displaystyle L}.

Функция f(x){\displaystyle f(x)} имеет предел A{\displaystyle A} в точке x0{\displaystyle x_{0}}, если для всех значений x{\displaystyle x}, достаточно близких к x0{\displaystyle x_{0}}, значение f(x){\displaystyle f(x)} близко к A{\displaystyle A}.

Число b называется пределом функции f(x) в точке a, если ∀ϵ>0{\displaystyle \forall \epsilon >0} существует δ>0{\displaystyle \delta >0}, такое что ∀x,0<|x−a|<δ{\displaystyle \forall x,0<|x-a|<\delta } выполняется |f(x)−b|<ϵ{\displaystyle |f(x)-b|<\epsilon }.

Для пределов функций справедливы аналогичные свойства, как и для пределов последовательностей, например, limx→x0(f(x)+g(x))=limx→x0f(x)+limx→x0g(x){\displaystyle \lim _{x\to x_{0}}(f(x)+g(x))=\lim _{x\to x_{0}}f(x)+\lim _{x\to x_{0}}g(x)}, если все члены существуют.

Обобщенное понятие предела последовательности

Пусть X{\displaystyle X} — некоторое множество, в котором определено понятие окрестности U{\displaystyle U} (например, метрическое пространство). Пусть xi∈X{\displaystyle x_{i}\in X} — последовательность точек (элементов) этого пространства. Говорят, что x∈X{\displaystyle x\in X} есть предел этой последовательности, если в любой окрестности точки x{\displaystyle x} лежат почти все члены последовательности то есть ∀U(x)∃n∀i>nxi∈U(x){\displaystyle \forall U(x)\exists n\forall i>nx_{i}\in U(x)}

См. также

Примечания

1. ↑ А.Г. Цыпкин. Справочник по математике, 1983, Москва «Наука».

wiki.sc