Теория графов. Решение задач
©кабинет 21, 2006-2017
Теория графов. Решение задач
Класс: 8-9 класс.
Цели урока.
Образовательные: формирование понятия «граф» и его основных элементов; формирование умения составлять граф по таблице.
Развивающие: развивать логическое мышление, внимание, памяти, умение планировать свою деятельность.
Воспитательные: воспитывать усидчивость, трудолюбие.
Ход урока:
1. Введение. Для того, чтобы представить информацию о составе и структуре системы графически, необходимо в виде чертежа изобразить компоненты системы и соединить их между собой какими-либо линиями. Например: Структура молекулы воды: компоненты системы (атомы) соединены между собой линиями.
Граф — это средство для наглядного представления состава и структуры системы.
Элементы графа: Вершины графа — это компоненты системы изображаемые кругами, овалами, прямоугольниками. Ребра — это линии, связывающие компоненты между собой определенным образом.
2. История происхождения. Издавна среди жителей Кёнигсберга (Калининград) была распространена загадка: как пройти по всем мостам (через реку Преголь), не проходя ни по одному из них дважды. Многие люди пытались решить эту задачу как теоретически, так и практически, во время прогулок. Но доказать или опровергнуть возможность существования такого маршрута никто не мог.
В 1736 году задача заинтересовала выдающегося математика Леонарда Эйлера и вскоре он смог найти правило, пользуясь которым, легко определить, можно ли пройти по всем мостам, не проходя дважды ни по одному из них.
На упрощённой схеме части города (графе) мостам соответствуют линии (дуги графа), а частям города — точки соединения линий (вершины графа). В ходе рассуждений Эйлер пришёл к следующим выводам:
Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа должно быть чётно. Не может существовать граф, который имел бы нечётное число нечётных вершин.
Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.
Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.
Созданная Эйлером теория графов нашла широкое применение (в транспортных системах – составление оптимальных маршрутов доставки грузов, экономике и т.д.).
3. Решение задач. Нахождение кратчайшего маршрута по таблице.
Задача, разбор и решение ее – находится в Презентации:
https://www.emaze.com/@AOORWLRII/breaking-news?hidebuttons
xn--j1ahfl.xn--p1ai
Применение теории графов к решению задач

«Применение теории графов к решению задач»


Свойства графов
Решая задачу про Кенигсбергские мосты, Эйлер установил, в частности, следующие СВОЙСТВА графа:
- Если в фигуре только четные вершины , то ее можно нарисовать одним росчерком, независимо от того, с какого места начинается черчение.
2) Если в фигуре имеется только одна пара нечетных вершин, то такую фигуру можно нарисовать одним росчерком, начав черчение в одной из нечетных вершин.
3) Если фигура имеет более одной пары нечетных вершин, то она вовсе не может быть нарисована одним росчерком.
В задаче о семи Кенигсбергских мостах все четыре вершины соответствующего графа — нечетные, т.е. нельзя пройти по всем мостам ровно один раз и закончить путь там, где он был начат.

Свойства графов
Кроме трех свойств графа, которые установил Эйлер, решая задачу про Кенигсбергские мосты, он вывел еще два СВОЙСТВА :
4) Число нечетных вершин графа всегда четно.
5) Если в графе имеются нечетные вершины, то наименьшее число росчерков, которыми можно нарисовать граф, равно половине числа нечетных вершин этого графа.
Например, если фигура имеет четыре нечетные вершины, то ее можно начертить самое меньшее двумя росчерками.

Этот вопрос положил начало циклу новых увлекательных задач:
если дана геометрическая фигура, как начертить ее на бумаге одним росчерком пера , не проводя дважды ни одну линию?
Например: как проложить дорожки в дендропарке, чтобы посетители увидели все растения не проходя дважды по одной.
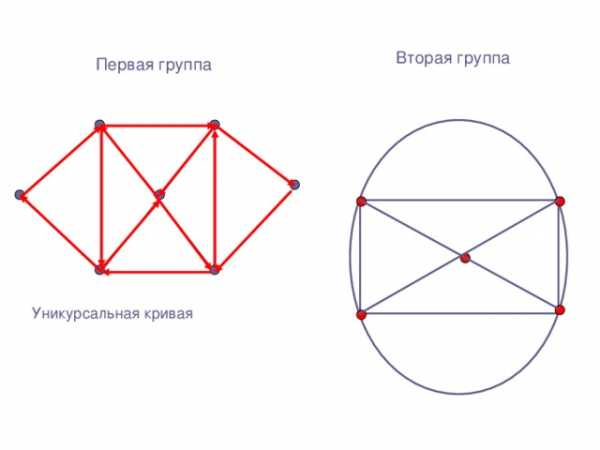
Вторая группа
Первая группа
Уникурсальная кривая
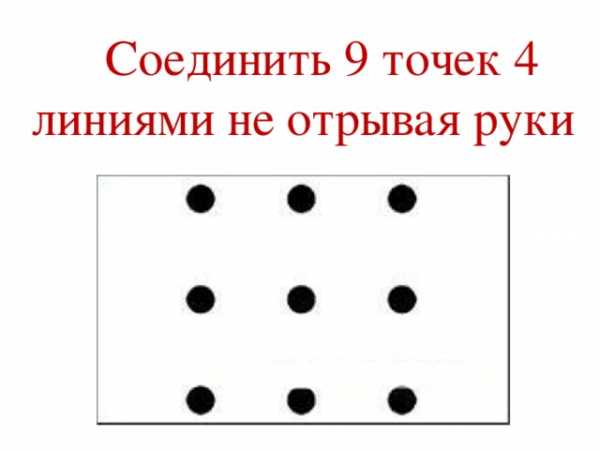
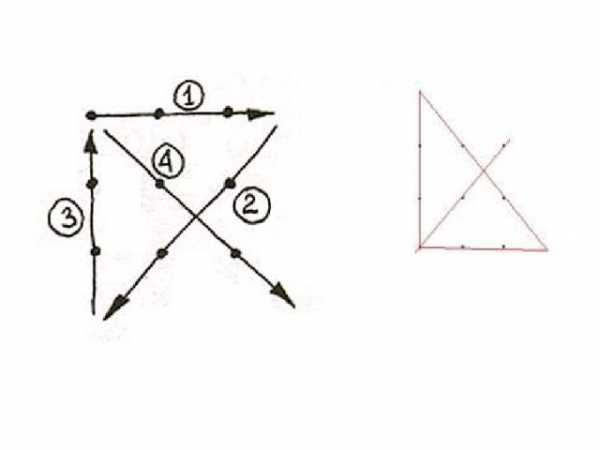
Соединить 9 точек 4 линиями не отрывая руки
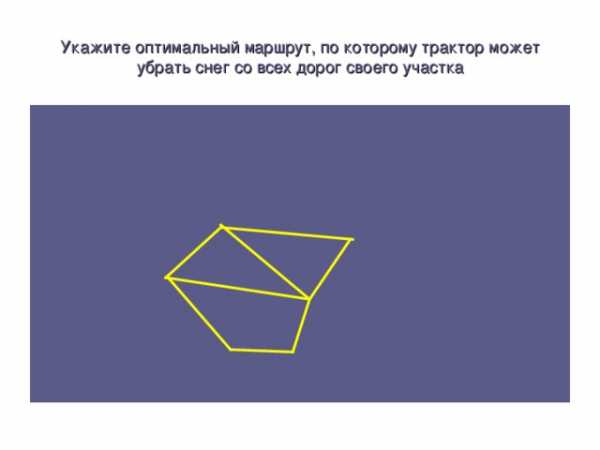
Укажите оптимальный маршрут, по которому трактор может убрать снег со всех дорог своего участка
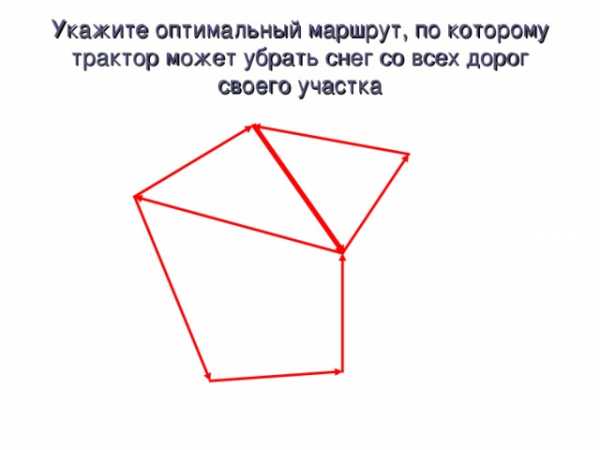
Укажите оптимальный маршрут, по которому трактор может убрать снег со всех дорог своего участка
Примеры графов
- Изображение железных дорог на географических картах;
- Схемы авиалиний
- Схемы метро
- Иерархия объектов (например структура школы)
- Файлы системы компьютера
Схема железнодорожных станций
Схема метро
Схема горнолыжных трасс
Географическая карта
Блок – схемы программ для ЭВМ
Схема авиалиний

Графы используются :
В строительстве
для составления чертежей;
для расчета материала;
для расчета количества рабочих;
для расчетов устойчивости откоса
В физике
Анализ электрических цепей распознаётся методом графов, также применяется в классической электродинамике СТО, энергетике, радиоэлектронике и др.
В химии
Используется для составления формул
Для исследования стационарной кинетически ферментативных реакций

Финансы и кредит
«Теория графов в управлении организационными системами»
Экология (геоботаника)
Метод графов при составлении дихотомических ключей для определения растений.
Транспорт
Для расчета пассажиропотока
Медицина
Исследование биоритмов
Биология
Для анализа биологических структур и генных систем
Спорт
Разработка стратегии игры

С помощью построения графа решается ряд задач входящих в ЕГЭ и ОГЭ:
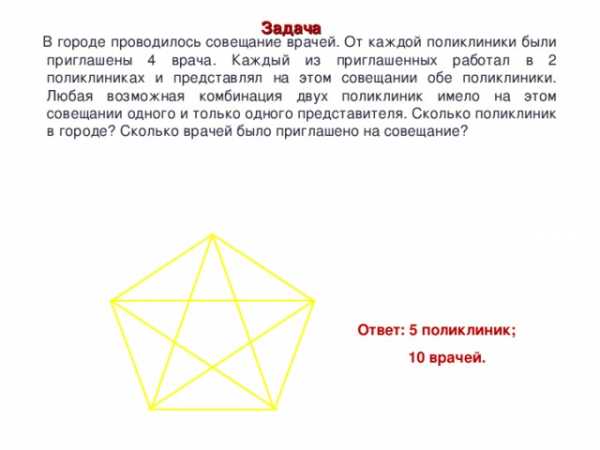
Задача
В городе проводилось совещание врачей. От каждой поликлиники были приглашены 4 врача. Каждый из приглашенных работал в 2 поликлиниках и представлял на этом совещании обе поликлиники. Любая возможная комбинация двух поликлиник имело на этом совещании одного и только одного представителя. Сколько поликлиник в городе? Сколько врачей было приглашено на совещание?
Ответ: 5 поликлиник;
10 врачей.
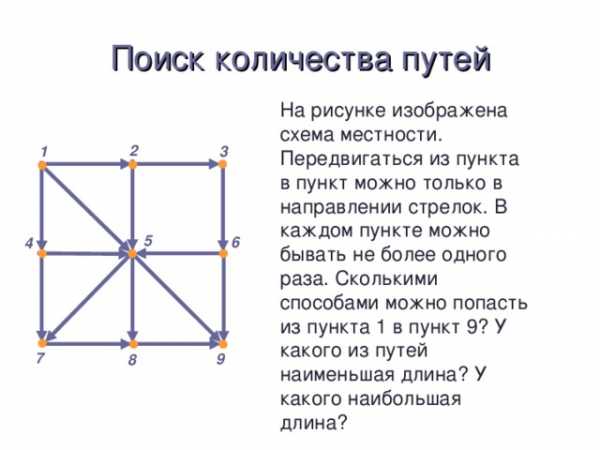
Поиск количества путей
На рисунке изображена схема местности. Передвигаться из пункта в пункт можно только в направлении стрелок. В каждом пункте можно бывать не более одного раза. Сколькими способами можно попасть из пункта 1 в пункт 9? У какого из путей наименьшая длина? У какого наибольшая длина?
2
3
1
5
6
4
7
9
8
2
1
3
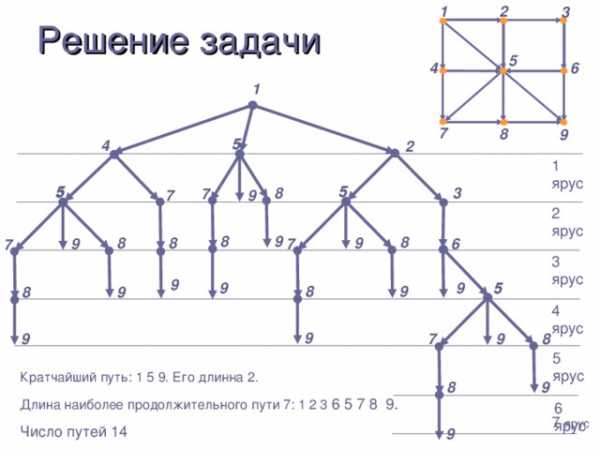
Решение задачи
5
6
4
1
7
8
9
5
5
4
2
1 ярус
5
5
5
5
8
7
7
9
2 ярус
8
9
8
9
8
8
6
9
7
7
3 ярус
9
9
5
9
5
9
8
9
8
4 ярус
9
8
9
9
7
5 ярус
Кратчайший путь: 1 5 9. Его длинна 2.
Длина наиболее продолжительного пути 7: 1 2 3 6 5 7 8 9.
Число путей 14
9
8
6 ярус
7 ярус
9
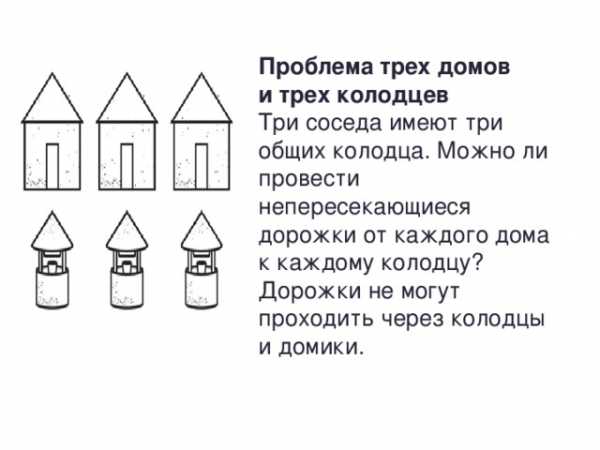
Проблема трех домов и трех колодцев
Три соседа имеют три общих колодца. Можно ли провести непересекающиеся дорожки от каждого дома к каждому колодцу? Дорожки не могут проходить через колодцы и домики.
Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 3, а во второй – 2 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 3 раза число камней в какой-то куче, или добавляет 1 камень в какую-то кучу. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 16 камней. Кто выигрывает при безошибочной игре – игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.
3,2, ∑ 5
1 ход
1 игрок
3,6, ∑ 9
9,2, ∑ 11
3,3, ∑ 6
3,3, ∑ 6
4,2, ∑ 6
2 ход
2 игрок
3,4, ∑ 7
3,9, ∑ 12
12,2 , ∑ 14
3,18, ∑ 21
5,2, ∑ 7
4,3, ∑ 7
27,2, ∑ 29
4,6, ∑ 10
Правильное указание выигрывающего игрока и его ходов со строгим доказательством правильности (с помощью дерева игры)
Оценивается максимальным кол-вом баллов.
Выигрывает второй игрок.
Для доказательства рассмотрим неполное дерево игры
Числа соответствуют количеству камней на каждом этапе игры, в первой и второй кучах соответственно и их сумма.
Второй игрок выигрывает на четвертом ходу, после любого ответа первого игрока.
Дерево содержит все возможные варианты ходов первого игрока. Из него видно,
что при любом ходе первого игрока у второго имеется ход, приводящий к победе.
3 ход
1 игрок
12,3, ∑ 15
4,9, ∑ 13
5,3, ∑ 8
4,4, ∑ 8
4 ход
2 игрок
36,3, ∑ 39
15,3, ∑ 18
4,27, ∑ 31
12,9, ∑ 21
13,3, ∑ 16
12,9, ∑21
12,4, ∑ 16
12,4, ∑ 16
24
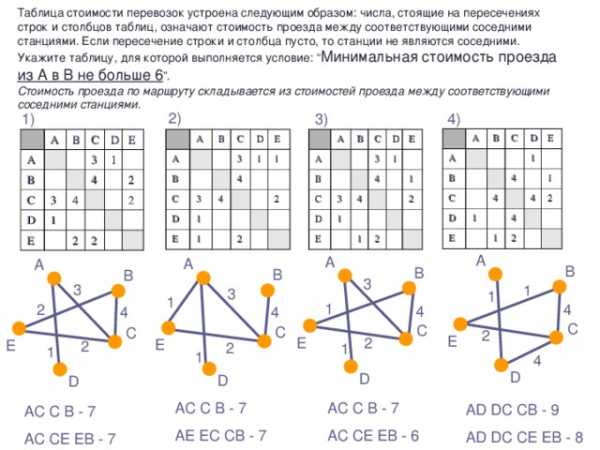
Таблица стоимости перевозок устроена следующим образом: числа, стоящие на пересечениях строк и столбцов таблиц, означают стоимость проезда между соответствующими соседними станциями. Если пересечение строки и столбца пусто, то станции не являются соседними.
Укажите таблицу, для которой выполняется условие: “ Минимальная стоимость проезда
из А в B не больше 6 ”.
Стоимость проезда по маршруту складывается из стоимостей проезда между соответствующими соседними станциями.
2)
1)
3)
4)
A
A
B
B
C
C
D
D
4
4
1
1
Е
Е
4
1
4
1
2
2
A
A
A
A
A
A
B
B
B
B
B
B
C
C
C
C
C
C
3
3
3
3
3
3
D
D
D
D
D
D
1
Е
1
4
4
Е
Е
1
4
Е
1
4
4
Е
4
Е
1
1
1
1
1
2
2
1
2
2
2
2
2
2
A
A
A
A
B
B
B
B
3
3
1
3
1
1
1
2
4
4
4
4
C
C
C
C
2
E
E
2
E
E
2
2
1
1
1
4
D
D
D
D
AC C B — 7
AC CE EB — 6
AC C B — 7
AE EC CB — 7
AD DC CB — 9
AD DC CE EB — 8
AC C B — 7
AC CE EB — 7

Рефлексия
Выберите ответ:
1. На занятии я узнал что-то новое да нет
2. На занятии мне понравилось:
история графов практические задания
3. Я применю это в своей практике да нет
kopilkaurokov.ru
Задача по теории графов с решением Характеристики графа
Основы теории графов. V-множество вершин, E- множество ребер Граф — G(V, Е). Л. Эйлер 1736 г.
V-множество вершин, E- множество ребер Граф — G(V, Е). Л. Эйлер 1736 г. G(V, Е, f) V,E множества, отображение инциденции f: Е V&V множества Е в V&V V={A,В,С,D,F,Н,P} множество точек, E={a,b,с,d,e,f,g,h,p,l}
Подробнее} пространства R и множества E = { e i
3 Задание: Дан неориентированный граф G, где V(G) — множество вершин; Е(G) — множество ребер Изобразить его графически Определить степени его вершин Указать висячие/изолированные вершины Является ли граф
ПодробнееСОДЕРЖАНИЕ ЛАБОРАТОРНОЙ РАБОТЫ
СОДЕРЖАНИЕ ЛАБОРАТОРНОЙ РАБОТЫ 1. Цели работы Изучение основ теории графов, базовых понятий и определений; ознакомление с задачами, возникающими в теории графов и методами их решения; освоение компьютерных
ПодробнееКонтрольная работа Вариант 2
Контрольная работа Вариант 2 Задача 1 Заданы множества A, B и C Считать, что элементы этих множеств образуют универсальное множество U Найти A + B + C, P( A B C), проверить равенство ( A B) C = ( A C)
ПодробнееТема 2.2. Маршруты, связность, расстояния. Задачи об обходах. Тема Маршруты, циклы, связность, расстояния, диаметр и центр графа
Тема 2.2. Маршруты, связность, расстояния. Задачи об обходах Тема 2.2.1. Маршруты, циклы, связность, расстояния, диаметр и центр графа Маршрутом в графе называется чередующаяся последовательность вершин
ПодробнееПРИКЛАДНАЯ ТЕОРИЯ ГРАФОВ
ПРИКЛАДНАЯ ДИСКРЕТНАЯ МАТЕМАТИКА 2013 Прикладная теория графов 3(21) ПРИКЛАДНАЯ ТЕОРИЯ ГРАФОВ УДК 519.17 ХАРАКТЕРИЗАЦИЯ ОРГРАФОВ С ТРЕМЯ ДОПОЛНИТЕЛЬНЫМИ ДУГАМИ В МИНИМАЛЬНОМ ВЕРШИННОМ 1-РАСШИРЕНИИ М. Б.
Подробнеесайты:
Федеральное агентство по образованию Уральский государственный экономический университет Ю. Б. Мельников Элементы теории графов Раздел электронного учебника для сопровождения лекции Изд. 3-е, испр. и доп.
ПодробнееЛекция 14: Орграфы. Б.М.Верников, А.М.Шур
Уральский федеральный университет, Институт математики и компьютерных наук, кафедра алгебры и дискретной математики Вступительные замечания Если мы захотим изобразить схему дорожного движения в городе
ПодробнееГлава II. Теория графов.
Глава II. Теория графов.. Из истории теории графов Родоначальником теории графов является Леонард Эйлер (707 782). В 736 году Эйлер решил задачу о Кенигсбергских мостах. Задача состояла в следующем: «Найти
ПодробнееЗадание для курсовой работы
Задание для курсовой работы Цель курсовой работы: освоение математического аппарата задания, анализа графовых моделей дискретных систем и решения ряда основных задач на графах. Индивидуальный вариант графов
ПодробнееДискретная математика. Теория графов
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования Ухтинский государственный технический университет Дискретная математика. Теория графов
ПодробнееУчебный центр «Резольвента» МАТЕМАТИКА
Учебный центр «Резольвента» Доктор физико-математических наук профессор К. Л. САМАРОВ МАТЕМАТИКА Учебно-методическое пособие по разделу ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. СЕТЕВОЕ ПЛАНИРОВАНИЕ
ПодробнееY 1 X 1. Рис Рис Рис Рис. 4.32
7 Алгоритмы Глава Рис Рис 0 Рис Рис З а м е ч а н и е Паросочетание на рис 8 не единственное Имеется еще одно наибольшее ( ребра) паросочетание (рис ) Множества вершин, не входящие в паросочетание, это
ПодробнееЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ
Федеральное агентство связи Государственное образовательное учереждение высшего профессионального образования «Сибирский государственный университет телекоммуникаций и информатики» ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ
ПодробнееТР по дискретной математике для ЗРП.
ТР по дискретной математике для ЗРП. ОМГТУ 2009г. 1 Содержание Задача 1. Операции над множествами 3 Задача 2. Эквивалентные множества. Мощность 4 Задача 3. Группы, подгруппы 5 Задача 4. Кольца, поля 7
ПодробнееВведение в теорию графов
Министерство образования и науки Российской Федерации Костромской государственный технологический университет Кафедра высшей математики А.В. Чередникова, И.В. Землякова Введение в теорию графов Рекомендовано
ПодробнееЗадача о доминирующем множестве:
Задача о доминирующем множестве: Ds = { G, k G неориентированный граф (V, E). Существует множество C V, такое что С = k и каждая вершина в V\C связана ребром из E с некоторой вершиной из C }. Задача о
ПодробнееЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ 4325 РЯЗАНСКИЙ ГОСУДАРСТВЕННЫЙ РАДИОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ Методические указания Рязань 2010 УДК 519.17 Элементы теории графов: методические
ПодробнееМЕТОДИЧЕСКИЕ УКАЗАНИЯ
Учреждение образования «Полоцкий государственный университет» МЕТОДИЧЕСКИЕ УКАЗАНИЯ к практической подготовке по дисциплине «Дискретная математика» для студентов заочного отделения машиностроительного
ПодробнееЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ
ПодробнееФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования «Уральский государственный университет им. А.М. Горького» ИОНЦ «Информационная безопасность»
ПодробнееОсновные понятия теории графов
Министерство образования и науки Российской Федерации Федеральное агенство по образованию Елецкий государственный университет им. И. А. Бунина О. Б. Гладких, О. Н. Белых Основные понятия теории графов
ПодробнееТЕОРИЯ ГРАФОВ. ЧАСТЬ 1
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ
Подробнее4.3. Топологическая сортировка сети
Алгоритмы Глава Поток в насыщенной сети можно посчитать по потоку, выходящему из истока или входящему в сток. Очевидно, эти числа должны быть равны. Кроме того, для проверки решения следует проверить условие
ПодробнееПРАКТИЧЕСКИЕ ЗАДАНИЯ ПО ГРАФАМ
Саратовский государственный университет им. Н.Г.Чернышевского М.Б.Абросимов, А.А.Долгов ПРАКТИЧЕСКИЕ ЗАДАНИЯ ПО ГРАФАМ Учебное пособие Издание второе ИЗДАТЕЛЬСТВО «НАУЧНАЯ КНИГА» САРАТОВ 2009 УДК 519.17
ПодробнееГРАФЫ. МОДЕЛИ ВЫЧИСЛЕНИЙ. СТРУКТУРЫ ДАННЫХ
Министерство образования и науки Российской Федерации Федеральное агентство по образованию Нижегородский государственный университет им. Н.И. Лобачевского В.Е. АЛЕКСЕЕВ, В.А. ТАЛАНОВ ГРАФЫ. МОДЕЛИ ВЫЧИСЛЕНИЙ.
Подробнее54 Махнев А. А., Чуксина Н. В. (x 1, y 1 ), (x 2, y 2 ) смежны тогда и только тогда, когда x 1 = x 2 или y 1 = y 2. Граф Клебша (граф Шлефли) это един
Владикавказский математический журнал 2008, Том 10, Выпуск 1, С. 53 67 УДК 519.17 О РЕБЕРНО РЕГУЛЯРНЫХ ГРАФАХ, В КОТОРЫХ КАЖДАЯ ВЕРШИНА ЛЕЖИТ НЕ БОЛЕЕ ЧЕМ В ОДНОЙ ХОРОШЕЙ ПАРЕ 1 А. А. Махнев, Н. В. Чуксина
ПодробнееТема: Графическое изображение графов.
Практическая работа Тема: Графическое изображение графов. Цель: изучить основы теоретико-множественного и графического представлений графов, простейших свойств графов, получить практический навык задания
ПодробнееМАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ СИСТЕМ
Министерство образования Республики Беларусь Учреждение образования «Белорусский государственный университет информатики и радиоэлектроники» Кафедра систем управления А. В. Павлова МАТЕМАТИЧЕСКИЕ ОСНОВЫ
ПодробнееЗадача A. Остовное дерево (1 балл)
Задача A. Остовное дерево (1 балл) spantree.in spantree.out Даны точки на плоскости, являющиеся вершинами полного графа. Вес ребра равен расстоянию между точками, соответствующими концам этого ребра. Требуется
ПодробнееО.А. Воронина, В.Т. Еременко, В.А. Лобанова
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ — УЧЕБНО-НАУЧНО- ПРОИЗВОДСТВЕННЫЙ КОМПЛЕКС» УЧЕБНО-НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ
ПодробнееЛекция 4: Эйлеров и гамильтонов цикл
Уральский федеральный университет, Институт математики и компьютерных наук, кафедра алгебры и дискретной математики Эйлеров цикл Определение Цикл, содержащий все ребра графа, называется эйлеровым. Граф
Подробнее4. Метод ветвей и границ
4. Метод ветвей и границ Задачи дискретной оптимизации имеют конечное множество допустимых решений, которые теоретически можно перебрать и выбрать наилучшее (дающее минимум или максимум целевой функции).
ПодробнееТема 8. Гамильтоновы графы
Тема 8. Гамильтоновы графы 8.1. Определение гамильтонова графа и достаточные условия гамильтоновости Определение. Если граф имеет простой цикл, содержащий все вершины графа по одному разу, то такой цикл
ПодробнееДискретная математика
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ УХТИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Дискретная математика Методические указания для выполнения контрольных работ Ухта, 7 УДК 68..6(76) Г Семериков, А.В.
ПодробнееПРИКЛАДНАЯ ТЕОРИЯ ГРАФОВ
ПРИКЛАДНАЯ ДИСКРЕТНАЯ МАТЕМАТИКА 015 Прикладная теория графов 4(30) ПРИКЛАДНАЯ ТЕОРИЯ ГРАФОВ УДК 519.1 О НЕКОТОРЫХ КЛАССАХ ЭКСТРЕМАЛЬНЫХ ОРИЕНТИРОВАННЫХ ГРАФОВ А. Ю. Зубов Московский государственный университет
Подробнееоглавление 158 ОГЛАВЛеНИе ВВеДеНИе… 5
оглавление ВВеДеНИе… 5 Глава 1. КОДИфИКАТОР… 7 Глава 2. СПРАВОчНЫЙ МАТеРИАЛ РАЗДеЛА «ДИСКРеТНАя МАТеМАТИКА»… 11 2.1. Элементы теории множеств…11 Множества: основные определения…11 числовые множества…11
ПодробнееЛекция 7: Двудольные графы
Уральский федеральный университет, Институт математики и компьютерных наук, кафедра алгебры и дискретной математики Определение и пример Определение Граф G = V,E называется двудольным, если существуют
ПодробнееЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ
ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ В.Н. Бурков, Д.А. Новиков Теория графов в качестве теоретической дисциплины может рассматриваться как раздел дискретной математики, исследующий свойства конечных множеств (бесконечные
ПодробнееДЕТЕРМИНИРОВАННАЯ РАСКРАСКА ГРАФОВ
Секция 7. Технологии и системы искусственного интеллекта 433 УДК 004.932.2+004.932.72’1 Е.С. Левицкая Донецкий национальный технический университет, г. Донецк Кафедра программного обеспечения интеллектуальных
ПодробнееЛекция 1: Знакомство с графами
Уральский федеральный университет, Институт математики и компьютерных наук, кафедра алгебры и дискретной математики Понятие графа Определение Графом называется геометрическая фигура, состоящая из точек
Подробнееdocplayer.ru
Примеры решения задач
Задача 1. На множестве людей L задано отношение Г – «жить на одной улице». Проверить, является ли оно отношением эквивалентности.
Решение. Для того чтобы отношение Г было отношением эквивалентности, необходимо, чтобы оно было рефлексивным, симметричным, транзитивным.
Так как каждый человек живет сам с собой на одной улице, то lГl выполняется, а значит отношение Г – рефлексивно.
Так как из того, что человек l1 живет на одной улице с человеком l2 следует, что и l2 живет на одной улице с l1, т.е. из l1Гl2 l2Гl1, то значит отношение Г – симметрично.
Очевидно, что из l1Гl2 и l2Гl3 следует l1Гl3.
Таким образом, отношение Г – отношение эквивалентности.
Задача 2. Пусть А=R – множество действительных чисел. Введем на R отношение Г: хГу, если ху. Проверить, является ли отношение Г отношением порядка.
Решение. 1. Проверим на рефлексивность. Так как хГх выполняется , т.е. хх, то Г – рефлексивно. 2. Проверим на симметричность. Так как из хГууГх только в случае, когда х=у (ху, ух х=у), то отношение Г – асимметрично. 3. Проверим на транзитивность. Так как из хГу, уГzхГz (ху, уzхz), то отношение Г – транзитивно.
Из 1.-3. следует, что Г – отношение нестрогого порядка, а значит, отношение Г является отношением порядка.
Задачи для самостоятельного решения
Задача 1. На множестве L людей задано отношение Г «быть одной группы крови» Проверить, является ли оно отношением эквивалентности. Что служит классом эквивалентности?
Задача 2. На плоскости хОу рассмотрим отношение Г: (х1, у1) Г (х2, у2), если выполнено х1+ у1= х2+ у2. Является ли оно отношением эквивалентности? Что служит классом эквивалентности?
Задача 3. На плоскости хОу рассмотрим отношение Г: (х1, у1) Г (х2, у2), если выполнено х1>x1, y2> у2. Является ли оно отношением порядка?
Задача 4. На множестве людей рассмотрим отношение «быть одной национальности». Является ли оно отношением эквивалентности?
Тема 2. Теория графов
§1. Основные понятия теории графов: графы, ориентированные и неориентированные графы, пути, маршруты, циклы
Представим на плоскости конечное множество точек V и некоторое множество линий Х, соединяющих попарно какие-то точки из V. Например, схема автодорог, соединяющих населенные пункты Брянской области.
Множество точек (населенных пунктов) назовем множеством вершин, а соединяющие линии (автодороги) – множеством ребер. Совокупность двух множеств (вершин и ребер) называют графом.
На некоторых участках допускается только одностороннее движение. Тогда соответствующее ребро называется дугой и изображается стрелкой, направленной от начальной вершины к конечной.
Граф, состоящий из дуг, называют ориентированным (или просто орграфом), а образованный ребрами – неориентированным.
Один и тот же граф можно изобразить по разному. Вершины можно располагать по своему усмотрению и произвольно выбирать форму соединяющих линий.
Ребро, концевые вершины которого совпадают, называется петлей. Ребро с одинаковыми концевыми вершинами называются кратными. Изолированная вершина не соединена с другими вершинами.
Часто на графе требуется выделить различные маршруты, обладающие определенными свойствами.
Маршрут длины m – это последовательность х1,…,хm m ребер графа (не обязательно различных) таких, что любые два соседних ребра xi, xi+1 имеют общую концевую вершину.
Замкнутый маршрут приводит в ту же вершину, из которой он начался.
Цепь – это маршрут, все ребра которого различны.
Простая цепь – это цепь без повторяющихся вершин. Замкнутая цепь называется циклом. Простой цикл – это простая замкнутая цепь.
В случае «орграфа» слово «цепь» заменяется на «путь», а «цикл» на «контур».
studfiles.net
Решение задач с применением понятия граф
скачать Муниципальное общеобразовательное учреждениесредняя общеобразовательная школа № 37
Практический проект по теме
«Графы»
Выполнила:
Брель Юлия Вениаминовна
обучающаяся 6 А класса
МОУСОШ № 37
Руководитель:
Баталова Е.А.
Учитель математики
МОУСОШ № 37
ТОМСК — 2008
Содержание
-
Введение
-
Математическое понятие граф и его элементы
-
Решение задач с применением понятия граф
-
Заключение
-
Список литературы
Введении.
Слово «граф» в математике означает картинку, где нарисовано несколько точек, некоторые из которых соединены линиями. Графами являются блок – схемы программ для ЭВМ, сетевые графики строительства, где вершины – события, означающие окончания работ на некотором участке, а ребра, связывающие эти вершины, — работы, которые возможно начать по совершении одного события и необходимо выполнить для совершения следующего.
Теория графов является частью как топологии, так и комбинаторики. То, что это топологическая теория, следует из независимости свойств графа. А удобство формулировок комбинаторных задач в терминах графов привела к тому, что теория графов стала одним из мощнейших аппаратов комбинаторики. С 2006 года раздел математики комбинаторику ввели в школьный курс. Многие задачи по комбинаторики можно просто решить используя понятие граф.
Теория графов позволяет решать наиболее легким способом, наглядно многие логические задачи, которые способствуют развитию мышления и интеллекта. Поэтому тема выбранная мною актуальна и интересна.
Целью работы является: Изучить понятие граф и его элементы, продемонстрировать решение задач с помощью графов.
На основании поставленной цели, сформулируем задачи:
-
Проанализировать литературу по теме
исследования, рассмотреть основные понятия.
2. Подобрать и решить задачи с использованием понятия графа.
3. Доказать и показать обучающимся 6 А класса, что используя понятие граф можно упростить и рационально решать многие логические задачи.
Математическое понятие граф и его элементы
Математические графы с дворянским титулом «граф» связывает общее происхождение от латинского слова «графио» — пишу. Типичными графами являются схемы авиалиний, которые часто вывешивается в аэропортах, схемы метро, а на географических картах – изображение железных дорог. Выбранные точки графа называются его вершинами, а соединяющие их линии – ребрами.
Графы — это замечательные математические объекты, с помощью, которых можно решать математические, экономические и логические задачи. Также можно решать различные головоломки и упрощать условия задач по физике, химии, электронике, автоматике. Графы используют при составлении карт и генеалогических древ.
В математике даже есть специальный раздел, который так и называется: «Теория графов».
Слово «граф» в математике означает картинку, где нарисовано несколько точек, некоторые из которых соединены линиями. С дворянским титулом «граф» их связывает общее происхождение от латинского слова «графио» — пишу.
В математике графом называется конечное множество точек, некоторые из которых соединены линиями. Точки называются вершинами графа, а соединяющие линии – рёбрами.
Примерами графов могут служить схемы авиалиний, дорог, электросхемы, чертежи многоугольников. Одними из самых распространённых графов являются схемы линий метрополитена. Используют графы и при построении генеалогических деревьев (рис.1).
На рисунке приведена часть генеалогического дерева знаменитого дворянского рода. Его вершины – члены этого рода, а связывающие их отрезки – отношения родственности, ведущие от родителей к детям.
Схема графа, состоящая из «изолированных» вершин, называется нулевым графом. (рис.2)
Графы, в которых не построены все возможные ребра, называются неполными графами. (рис.3)
Графы, в которых построены все возможные ребра, называются полными графами. (рис.4)
рис. 1
Граф, который можно нарисовать, не отрывая карандаша от бумаги, называется эйлеровым.
Такими графы названы в честь учёного Леонарда Эйлера.
Граф называется связным, если любые две его вершины могут быть соединены путем, т. е. последовательностью ребер, каждое следующее из которых начинается в конце предыдущего.
Граф называется несвязным, если это условие не выполняется.
Висячей вершиной называется вершина, из которой выходит ровно одно ребро.
Граф, на рёбрах которого расставлены стрелки, называется ориентированным или направленным.
Использует графы и дворянство. На рисунке 2 приведена часть генеалогического дерева знаменитого дворянского рода. Здесь его вершины – члены этого рода, а связывающие их отрезки – отношения родственности, ведущие от родителей к детям.
Слово «дерево» в теории графов означает граф, в котором нет циклов, то есть в котором нельзя из некоторой вершины пройти по нескольким различным ребрам и вернуться в ту же вершину. Генеалогическое дерево будет деревом и в смысле теории графов, если в этом семействе не было браков между родственниками.
Не трудно понять, что граф – дерево всегда можно изобразить так, чтобы его ребра не пересекались. Тем же свойством обладают графы, образованные вершинами и ребрами выпуклых многогранников. На рисунке 3 приведены графы, соответствующие пяти правильным многогранникам. В графе соответствующем тетраэдру, все четыре вершины попарно соединены ребрами.
Рассмотрим граф с пятью вершинами, попарно соединенными друг с другом (рис. 4). Здесь ребра графа пересекаются. Невозможно его изобразить так, чтобы пересечений не было, как невозможно выполнить намерения трех человек, описанных Льюсом Кэрроллом.
Они жили в трех домиках, неподалеку от них находились три колодца: один с водой, другой с маслом, а третий с повидлом, и ходили к ним по тропинкам, изображенным на рисунке 5. Однажды эти люди перессорились и решили провести тропинки от своих домов к колодцам так, чтобы эти тропинки не пересекались. На рисунке 6 изображена очередная попытка проложить такие тропы.
Графы, изображенные на рисунках 4 и 5, как оказалось, играют решающую роль при определение для каждого графа – является ли он плоским, то есть может ли он быть изображен на плоскости без пересечения его ребер. Польский математик Г. Куратовский и академик Л. С. Понтрягин независимо доказали, что если граф не является плоским, то в нем «сидит» хотя бы один из графов, изображенных на рисунках 4 и 5, то есть «полный пятивершинник» или граф «домики – колодцы».
Графами являются блок – схемы программ для ЭВМ, сетевые графики строительства, где вершины – события, означающие окончания работ на некотором участке, а ребра, связывающие эти вершины, — работы, которые возможно начать по совершении одного события и необходимо выполнить для совершения следующего.
Если на ребрах графа нанесены стрелочки, указывающие направление ребер, то такой граф называют направленным.
Свойство графов не зависят от того, соединены вершины отрезками или кривыми линиями, что дает возможность изучения их свойств с помощью одной из молодых наук – топологии.
Впервые основы теории графов появились в работе Л. Эйлера, где он описывал решение головоломок и математических развлекательных задач. Широкое развитие теория графов получила с 50-х гг. 20 в. в связи со становлением кибернетики и развитием вычислительной техники.
Решение задач с применением понятия граф.
В терминах графов легко формулируется и решается задача о назначении на должности. А именно: если имеется несколько вакантных должностей и группа лиц, желающих их занять, причем каждый из претендентов имеет квалификацию для нескольких должностей, то при каких условиях каждый из претендентов сможет получить работу по одной из своих специальностей?
Свойства графов не зависят от того, соединены вершины отрезками или кривыми линиями. Это дает возможность изучения их свойств с помощью одной из молодых наук – топологии, хотя сами задачи теории графов являются типичными задачами комбинаторики.
Вот несколько задач теории графов. Задача об эйлеровом пути: найти путь по ребрам графа, проходящий по каждому ребру ровно один раз. Такой путь существует лишь в том случае, если граф – связный, т. е. от каждой его вершины к каждой другой можно пройти по ребрам графа, и из каждой вершины, кроме, может быть, двух, выходит четное число ребер. На графе, изображенном на рис. 3,а, он есть, а на рис. 3,б его нет.
Хроматическим числом графа называется наименьшее количество красок, с помощью которых можно так раскрасить вершины графа, что любые две вершины, соединенные ребром, окрашиваются при этом в разные цвета. Долгое время математики не могли решить эту проблему: достаточно ли четырех красок, для того чтобы раскрасить произвольную графическую карту так, чтобы любые две стороны, имеющие общую границу, были окрашены разными красками? Если изобразить страны точками – вершинами графа, соединив ребрами те вершины, для которых соответствующие им страны граничат , то задача сведется к следующей: верно ли, что хроматическое число любого графа, расположенного на плоскости, не больше четырех? Положительный ответ на этот вопрос был лишь недавно получен с помощью ЭВМ.
Используя графы можно решать задачи. Вот, например, как выглядит последняя американская версия известной задачи Дьюдени:
1. Смит, Джонс и Робинсон работают в одной поездной бригаде машинистом, кондуктором и кочегаром. Профессии их названы не обязательно в том же порядке, что и фамилии. В поезде, который обслуживает бригада, едут трое пассажиров с теми же фамилиями. В дальнейшем каждого пассажира мы будем почтительно называть «мистер» (м-р)
2. М-р Робинсон живет в Лос-Анджелесе.
3. Кондуктор живет в Омахе.
4. М-р Джонс давно позабыл всю алгебру, которой его учили в колледже.
5. Пассажир – однофамилец кондуктора живет в Чикаго.
6. Кондуктор и один из пассажиров, известный специалист по математической физике, хотя в одну церковь.
7. Смит всегда выигрывает у кочегара, когда им случается встречаться за партией в бильярд.
Как фамилия машиниста?
Здесь 1-5 – номера ходов, в скобках – номера пунктов задачи, на основании которых сделаны ходы (выводы).
Далее следует из п.7, что кочегар не Смит, следовательно, Смит-машинист.
Графы часто используют для решения логических проблем, связанных с перебором вариантов. Для примера рассмотрим такую задачу. В ведре 8 л воды, и имеется две кастрюли емкостью 5 и 3 л. требуется отлить в пятилитровую кастрюлю 4 л воды и оставить в ведре 4 л, т. е. разлить воду поровну в ведро и большую кастрюлю.
Ситуацию в каждый момент можно описать тремя числами, где А-количество литров воды в ведре, Б- в большой кастрюле, В — в меньшей. В начальный момент ситуация описывалась тройкой чисел ( 8, 0, 0), от нее мы можем перейти в одну из двух ситуаций: ( 3, 5, 0),если наполним водой большую кастрюлю, или ( 5, 0, 3), если наполним меньшую кастрюлю.
В результате получаем два решения: одно в 7 ходов, другое в 8 ходов.
Подобным образом можно ставить граф любой позиционной игры: шахмат, шашек, «крестиков – ноликов», где позиции станут вершинами, а направленные отрезки между ними будут означать, что одним ходом можно перейти от одной позиции к другой, по направлению стрелки.
Однако для шахмат и шашек такой граф будит очень большим, поскольку различные позиции в этих играх исчисляются миллионами. А вот для игры «крестики – нолики» на доске 3 * 3 соответствующий граф нарисовать не так уж трудно, хотя и он будет содержать несколько десятков (но не миллионов) вершин.
Рассмотрим еще некоторые задачи:
Между планетами введено космическое сообщение по следующим маршрутам: З-К, П-В, З-П, П-К, К-В, У-М, М-С, С-Ю, Ю-М, М-У. Можно ли добраться с З до М?
Решение:
Составим схему-граф маршрутов:
Мы видим, что от З до М добраться нельзя.
Вашему вниманию предложена еще одна задача
Мальчики 10 б класса Андрей, Витя, Сережа, Валера, Дима при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному разу). Сколько всего рукопожатий было сделано?
Решение:
Пусть каждому из пяти молодых людей соответствует определенная точка на плоскости, названная первой буквой его имени, а производимому рукопожатию — отрезок или часть кривой, соединяющая конкретные точки — имена.
Если подсчитать число ребер графа, изображенного на рисунке справа, то это число и будет равно количеству совершенных рукопожатий между пятью молодыми людьми. Их 10.
В спортивном зале собрались Витя, Коля, Петя, Сережа и Максим. Каждый из мальчиков знаком только с двумя другими. Кто с кем знаком.
Решение: Построим граф
Ответ: Витя знаком с Колей и Сережей, Сережа с Витей и и Петей, Петя с Сережей и Максимом, Максим с Петей и Колей, Коля с Петей и Максимом.
Заключение
В настоящей работе рассмотрены математические графы, области их применения, решено несколько задач с помощью графов. Графы достаточно широко применяются в математике, технике, экономике, управлении. Знание основ теории графов необходимо в различных областях, связанных с управлением производством, бизнесом (например, сетевой график строительства, графики доставки почты). Кроме того, данная работа представлена обучающимся 6 –ых классов МОУСОШ № 37, проведены практические занятия с одноклассниками, что повысило их кругозор, а некоторые способ решение задач с помощью графов будут использовать при решении различных задач.
Список литературы
-
Энциклопедический словарь юного математика \Сост. А.П.Савин.- М.: Педагогика, 1989 -
Квант №6 1994г. -
М. Гарднер «Математические досуги» М.: Мир, 1972
-
Берж К. Теория графов и ее применение. ИЛ, 1962.
-
Абрахамс Дж., Каверли Дж. Анализ электрических цепей методом графов. Изд-во «Мир», 1967.
скачать
nenuda.ru
