Теория вероятности формула байеса – .

alexxlab / / Школьная жизнь

Формула Байеса

При выводе формулы полной вероятности предполагалось, что вероятности гипотез известны до опыта. Формула Байеса позволяет производить переоценку первоначальных гипотез в свете новой информации, состоящей в том, что событие произошло. Поэтому формулу Байеса называют формулой уточнения гипотез.

Теорема (Формула Байеса). Если событие может происходить только с одной из гипотез , которые образуют полную группу событий, то вероятность гипотез при условии, что событие произошло, вычисляется по формуле

, .

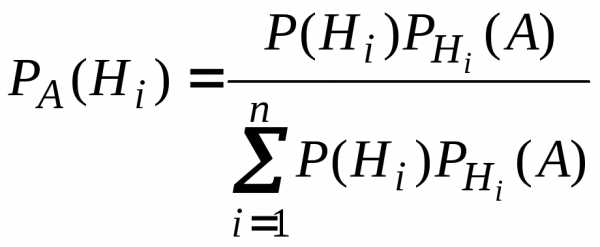
Доказательство.

Формула Байеса или байесовский подход к оценке гипотез играет важную роль в экономике, т.к. дает возможность корректировать управленческие решения, оценки неизвестных параметров распределения изучаемых признаков в статистическом анализе и.т.п.

Пример. Электролампы изготовляются на двух заводах. Первый завод производит 60% общего количества электроламп, второй – 40%. Продукция первого завода содержит 70% стандартных ламп, второго – 80%. В магазин поступает продукция обоих заводов. Лампочка купленная в магазине оказалась стандартной. Найти вероятность того, что лампа изготовлена на первом заводе.

Запишем условие задачи, вводя соответствующие обозначения.

Дано: событие состоит в том, что лампа стандартная.

Гипотеза состоит в том, что лампа изготовлена на первом заводе

.

Гипотеза состоит в том, что лампа изготовлена на втором заводе

.

Найти .

Решение.

5. Повторные независимые испытания. Формула Бернулли

Рассмотрим схему независимых испытаний или схему Бернулли, которая имеет важное научное значение и разнообразные практические применения.

Пусть производится независимых испытаний, в каждом из которых может произойти некоторое событие

.

Определение. Испытания называются независимыми, если в каждом из них событие наступает с одной и той же вероятностью, не зависящей от того появилось или не появилось событиев других испытаниях.

Пример. На испытательный стенд поставлены 20 ламп накаливания, которые испытываются под нагрузкой в течении 1000 часов. Вероятность того, что лампа выдержит испытание, равна 0,8 и не зависит от того, что случилось с другими лампами.

В этом примере под испытанием понимается проверка лампы на ее способность выдержать нагрузку в течении 1000 часов. Поэтому число испытаний равно

. В каждом отдельном испытании возможны только два исхода:

  1. событие , состоящее в том, что лампа выдержала испытание, произошло. Вероятность этого события и не зависит от исходов остальных испытаний.

  2. событие не произошло, т.е. наступило событие , состоящее в том, что лампа не выдержала испытания. Вероятность этого события.

Определение. Серия повторных независимых испытаний, в каждом из которых событие наступает с одной и той же вероятностью

, не зависящей от номере испытания, называетсясхемой Бернулли.

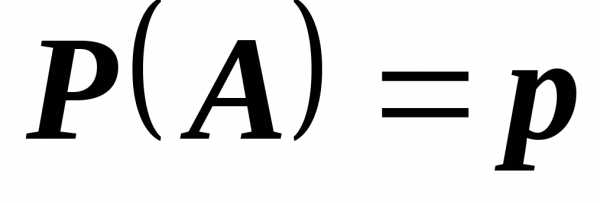
Вероятность противоположного события обозначают , причем, как было доказано выше,

.

Теорема. В условиях схемы Бернулли вероятность того, что при независимых испытаниях событиепоявитсяраз, определяется по формуле

, (1)

где число проведенных независимых испытаний;

число появлений события ;

вероятность наступления события в отдельном испытании;

вероятность не наступления события в отдельном испытании;

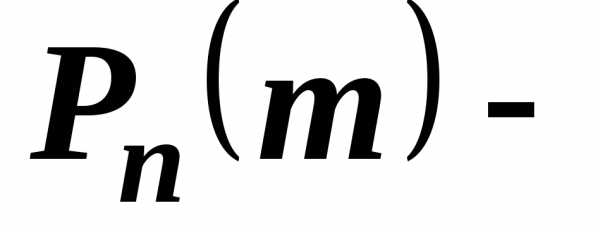вероятность того, что в независимых испытаниях событияпроизойдет

раз.

Формула (1) называется формулой Бернулли или биномиальной формулой, т.к. ее правая часть является членом бинома Ньютона

.

Теорему примем без доказательства.

Пример. Производится 6 выстрелов по цели. Вероятность попадания в цель при каждом выстреле равна 0,7. найти вероятность того, что произойдет 2 попадания.

Запишем, прежде всего, условие задачи, вводя соответствующие обозначения.

Дано: событие попадание при отдельном выстреле;

.

Найти

Решение.

34

studfiles.net

Формулы полной вероятности и Байеса (с доказательством). Примеры.

Формула полной вероятности. Теорема.

Теорема. Если событие F может произойти только при условии появления одного из событий (гипотез) A1,А2,…,Аn образующих полную группу, то вероятность события F равна сумме произведений вероятностей каждого из этих событий (гипотез) на соответствующие условные вероятности события F:

□ По условию гипотезы А1,А2,…,Аn образуют полную группу, следовательно, они единственно возможные и несовместные. Т.к гипотезы А

1,А2,…,Аn — единственно возможные, а событие F может произойти только вместе с 1 из гипотез, то

.

В силу того что гипотезы А1,А2,…,Аn несовместны, можно применить теорему сложения вероятностей:

По теореме умножения вероятностей .■

Следствием теоремы умножения и формулы полной вероятности является формула Байеса.

Она применяется, когда событие F, которое может появиться только с одной из гипотез А1,А2,…,Аn образующих полную группу событий, произошло и необходимо произвести количественную переоценку априорных вероятностей этих гипотез P(A1), Р(А2),…, Р(Аn), известных о испытания, Т.е. надо найти апостериорные (получаемые после проведения испытания) условные вероятности гипотез PF(A1

),PF(А2),…,РF(Аn).

□ Для получения искомой формулы запишем теорему умножения вероятностей событий F и Аi в двух формах:

, откуда

или с учетом формулы полной вероятности: . ■

Значение формулы Байеса состоит в том, что при наступлении события Р, т.е. по мере получения новой информации, мы можем проверять и корректировать выдвинутые до испытания гипотезы. Такой подход, называемый байесовским, дает возможность корректировать управленческие решения в эк-ке, оценки неизвестных параметров распределения изучаемых признаков в статистическом анализе и т.п.

Пример: Два стрелка независимо друг от друга стреляют по мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка равна 0,8; для второго — 0,4. После стрельбы в мишени обнаружена одна пробоина. Какова вероятность того, что она принадлежит: а) l-му стрелку; б) 2-му стрелку?

Решение. Обозначим события:

А1 — оба стрелка не попали в мишень; А2 — оба стрелка попали в мишень; А3 — 1-й стрелок попал в мишень, 2-й нет; А4 — 1-й стрелок не попал в мишень, 2-й попал; F — в мишени одна пробоина (одно попадание).

Найдем вероятности гипотез и условные вероятности события F для этих гипотез:

Р(A1) = 0,2 · 0,6 = 0,12, РА1(F) = 0;

Р(А2) = 0,8 · 0,4 = 0,32, РА2(F) = 0;

Р(А3) = 0,8 · 0,6 = 0,48, РА3(F) = l;

Р(А4) = 0,2 · 0,4 = 0,08, РА4(F) = l.

Теперь по формуле Байеса:

, ,

Т.е. вероятность того, что попал в цель l-й стрелок при наличии одной пробоины, в 6 раз выше, чем для второго стрелка.

  1. Повторные независимые испытания. Формула Бернулли (с выводом). Примеры.

Если вероятность наступления события А в каждом испытании не меняется в зависимости от исходов других, то такие испытания называются независимыми относительно события А. Если независимые повторные испытания проводятся при одном и том же комплексе условий, то вероятность наступления события А в каждом испытании одна и та же. Эта последовательность независимых испытаний получила название схемы Бернулли.

Формула Бернулли

Теорема. Если вероятность р наступления события А в каждом испытании постоянна, то вероятность Рm,nтого, что событие А наступит m раз в n независимых испытаниях, равна

Где .

□ Пусть и— соответственно появление и непоявление событияА в i-ом испытании (i = 1,2,…,n), а — событие, состоящее в том, что вn независимых испытаниях событие А появилось m раз.

Представим событие 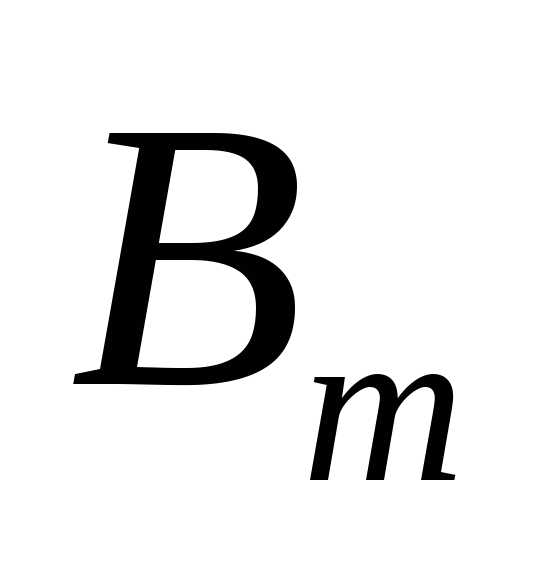через элементарные события.

Например, при n = 3, m = 2 событие ,

т.е. событие А произойдет 2 раза в 3 испытаниях, если оно произойдет в l-м и 2-м испытаниях (и не произойдет в 3-м), или в l-м и 3-м (и не произойдет во 2-м), или произойдет во 2-м и 3-м (и не произойдет в l-м).

В общем виде

,

Т.е. каждый вариант появления события Вm (каждый член суммы) состоит из m появлений события А и n-m непоявлений, т.е. из m событий А и из n-m событий с различными индексами.

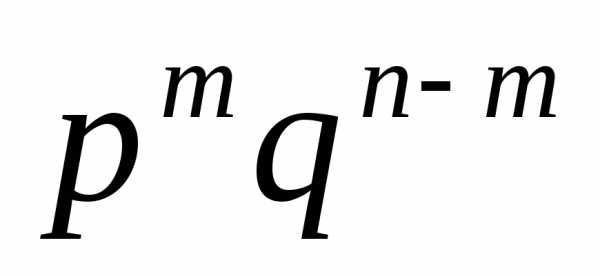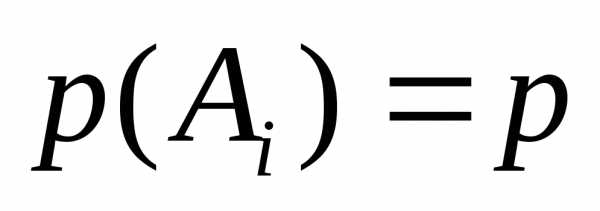Число всех комбинаций (слагаемых суммы) равно числу способов выбора из n испытаний m, в которых событие А произошло, т.е. числу сочетаний . Вероятность каждой такой комбинации (каждого варианта появления события Вm) по теореме умножения для независимых событий равна , т.к., а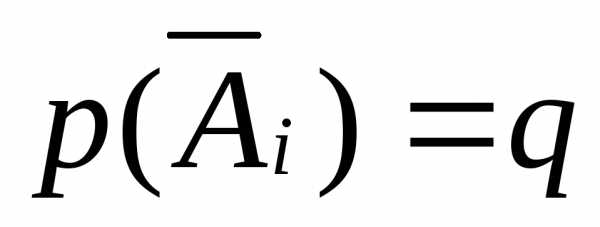,i = 1,2,…,n. В связи с тем, что комбинации между собой несовместны, по теореме сложения вероятностей получим

.■

studfiles.net

Формула полной вероятности и формула Бейеса Байеса и их применение

Сибирский государственный университет телекоммуникаций и информатики

Кафедра высшей математики

РЕФЕРАТ

по дисциплине : «Теория вероятностей и математическая статистика»

на тему:

«Формула полной вероятности и формула Бейеса(Байеса) и их применение»

Выполнил:

Руководитель: профессор Б.П.Зеленцов

Новосибирск, 2010

Содержание

Введение 3

1. Формула полной вероятности 4-5

2. Формула Байеса(Бейеса) 5-6

3. Задачи с решениями 7-11

4. Основные сферы применения формулы Байеса(Бейеса) 11

Заключение 12

Литература 13

Введение

Теория вероятностей является одним из классических разделов математики. Она имеет длительную историю. Основы этого раздела науки были заложены великими математиками. Назову, например, Ферма, Бернулли, Паскаля.
Позднее развитие теории вероятностей определились в работах многих ученых.
Большой вклад в теорию вероятностей внесли ученые нашей страны:
П.Л.Чебышев, А.М.Ляпунов, А.А.Марков, А.Н.Колмогоров. Вероятностные и статистические методы в настоящее время глубоко проникли в приложения. Они используются в физике, технике, экономке, биологии и медицине. Особенно возросла их роль в связи с развитием вычислительной техники.

Например, для изучения физических явлений производят наблюдения или опыты. Их результаты обычно регистрируют в виде значений некоторых наблюдаемых величин. При повторении опытов мы обнаруживаем разброс их результатов. Например, повторяя измерения одной и той же величины одним и тем же прибором при сохранении определенных условий (температура, влажность и т.п.), мы получаем результаты, которые хоть немного, но все же отличаются друг от друга. Даже многократные измерения не дают возможности точно предсказать результат следующего измерения. В этом смысле говорят, что результат измерения есть величина случайная. Еще более наглядным примером случайной величины может служить номер выигрышного билета в лотерее. Можно привести много других примеров случайных величин. Все же и в мире случайностей обнаруживаются определенные закономерности. Математический аппарат для изучения таких закономерностей и дает теория вероятностей.
Таким образом, теория вероятностей занимается математическим анализом случайных событий и связанных с ними случайных величин.

Пусть имеется группа событий H 1 , H 2 ,…, Hn , обладающая следую­щими свойствами:

1) все события попарно несовместны: Hi

Hj =Æ; i , j =1,2,…,n ; i ¹ j ;

2) их объединение образует пространство элементарных исходов W:

W =

.

В этом случае будем говорить, что H 1 , H 2 ,…,Hn образуют полную группу событий . Такие события иногда называют гипотезами .

Пусть А – некоторое событие: А ÌW (диаграмма Венна представлена на рисунке 8). Тогда имеет место формула полной вероятности:

P (A ) = P (A /H 1 )P (H 1 ) + P (A /H 2 )P (H 2 ) + …+P (A /Hn )P (Hn ) =

Доказательство. Очевидно: A =

, причем все события (i = 1,2,…,n ) попарно несовместны. Отсюда по теореме сложения вероятностей получаем

P (A ) = P (

) + P () +…+ P (

Если учесть, что по теореме умножения P (

) = P (A/H i )P (H i ) (i = 1,2,…,n ), то из последней формулы легко получить приведенную выше формулу полной вероятности.

Пример . В магазине продаются электролампы производства трех заводов, причем доля первого завода — 30%, второго — 50%, третьего — 20%. Брак в их продукции составляет соответственно 5%, 3% и 2%. Какова вероятность того, что случайно выбранная в магазине лампа оказалась бракованной.

Пусть событие H 1 состоит в том, что выбранная лампа произведена на первом заводе, H 2 на втором, H 3 — на третьем заводе. Очевидно:

P (H 1 ) = 3/10, P (H 2 ) = 5/10, P (H 3 ) = 2/10.

Пусть событие А состоит в том, что выбранная лампа оказалась бракованной; A/Hi означает событие, состоящее в том, что выбрана бракованная лампа из ламп, произведенных на i -ом заводе. Из условия задачи следует:

P (A / H 1 ) = 5/10; P (A / H 2 ) = 3/10; P (A / H 3 ) = 2/10

По формуле полной вероятности получаем

Пусть H 1 ,H 2 ,…,Hn — полная группа событий и А Ì W – некоторое событие. Тогда по формуле для условной вероятности

(1)

Здесь P (Hk /A ) – условная вероятность события (гипотезы) Hk или вероятность того, что Hk реализуется при условии, что событие А произошло.

По теореме умножения вероятностей числитель формулы (1) можно представить в виде

P = P = P (A /Hk )P (Hk )

Для представления знаменателя формулы (1) можно использовать формулу полной вероятности

P (A )

Теперь из (1) можно получить формулу, называемую формулой Байеса :

По формуле Байеса исчисляется вероятность реализации гипотезы Hk при условии, что событие А произошло. Формулу Байеса еще называют формулой вероятности гипотез. Вероятность P (Hk ) называют априорной вероятностью гипотезы Hk , а вероятность P (Hk /A ) – апостериорной вероятностью.

Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленному на полную вероятность этого события.

Пример. Рассмотрим приведенную выше задачу об электролампах, только изменим вопрос задачи. Пусть покупатель купил электролампу в этом магазине, и она оказалась бракованной. Найти вероятность того, что эта лампа изготовлена на втором заводе. Величина P (H 2 ) = 0,5 в данном случае это априорная вероятность события, состоящего в том, что купленная лампа изготовлена на втором заводе. Получив информацию о том, что купленная лампа бракованная, мы можем поправить нашу оценку возможности изготовления этой лампы на втором заводе, вычислив апостериорную вероятность этого события.

Выпишем формулу Байеса для этого случая

Из этой формулы получаем: P (H 2 /A ) = 15/34. Как видно, полученная информация привела к тому, что вероятность интересующего нас события оказывается ниже априорной вероятности.

3. Задачи с решениями.

Задача 1. В магазин поступила новая продукция с трех предприятий. Процентный состав этой продукции следующий: 20% — продукция первого предприятия, 30% — продукция второго предприятия, 50% — продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии — 5% и на третьем — 20% продукции высшего сорта. Найти вероятность того, что случайно купленная новая продукция окажется высшего сорта.

Решение. Обозначим через В событие, заключающееся в том, что будет куплена продукция высшего сорта, через

обозначим события, заключающиеся в покупке продукции, принадлежащей соответственно первому, второму и третьему предприятиям.

Можно применить формулу полной вероятности, причем в наших обозначениях:

Подставляя эти значения в формулу полной вероятности, получим искомую вероятность:

Задача 2. Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго — 0,5; для третьего — 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.

Решение. Возможны три гипотезы:

— на линию огня вызван первый стрелок, — на линию огня вызван второй стрелок, — на линию огня вызван третий стрелок.

mirznanii.com

§9. Формула полной вероятности. Формулы Байеса.

Одним из эффективных методов подсчёта вероятностей является формула полной вероятности, с помощью которой решается широкий круг задач.

Пусть событие Aможет наступить с одним и только одним из нескольких попарно несовместных событийН1,Н2,…,Нn, называемых гипотезами, т.е.

.

Так как Н1,Н2,…Нn попарно несовместны, то несовместны и событияАН1,АН2,…АНn. Отсюда получаем, применяя формулы сложения и умножения вероятностей

Полученная формула

(1)

называется формулой полной вероятности.

Пример 1.(см. пример 1 §8). Из урны, в которой находятсяmбелых и n—m чёрных шаров, без возвращения выбираются два шара. Найдём вероятность событияB={второй вынутый шар – белый},

Рассмотрим гипотезы: H1= {первый вынутый шар – белый) ипервый вынутый шар – чёрный}. ТогдаПо формуле полной вероятности получаем

Таким образом, мы получим

.

Аналогично можно установить, что вынимая последовательно без возвращения шары, мы получим одну и ту же вероятность вынуть белый шар на любом месте. Таким образом, при правильно организованной жеребьёвке, шансы всех участников одинаковы, независимо от того, в какой очерёдности они тянут жребий.

Замечание.Эту же задачу можно интерпретировать, как вычисление вероятности вытащить белый шар из урны, из которой был случайно утерян один или несколько шаров.

В тесной связи с формулой полной вероятности находятся так называемые формулы Байеса. Они относятся к той же ситуации, что и формула полной вероятности.

Поскольку событие Аможет наступить только вместе с одним изnпопарно несовместных событийН1,…Нn , то найдём вероятностьР(Нк |А) – вероятность того, что событиеАнаступит вместе с гипотезойНк.

По формуле умножения получаем

Откуда имеем

(2)

Или, если воспользоваться формулой полной вероятности (1) получим:

(3)

Это и есть формулы Байеса.

Запомнить эти формулы нетрудно: в знаменателе стоит выражение для полной вероятности, а в числителе – одно из слагаемых (к-ое) в этом выражении.

Формулы Байеса можно интерпретировать следующим образом.

Пусть A– результат некоторого эксперимента,

Нк– гипотезы. ВероятностиР(Нк)– этоаприорные вероятности гипотез, вычисленные до проведения опыта, а условные вероятностиР(Нк|А)– этоапостериорныевероятности гипотез, вычисляемые после того, как стал известен исход экспериментаА. Формулы Байеса позволяют по априорным вероятностям гипотез и по условным вероятностям событияАпри гипотезахвычислять апостериорные вероятностиР(Нк|А).

Пример 2. При обследовании больного имеется подозрение на одно из двух заболеванийН1иН2. Их вероятности в данных условияхР(Н1)=0,6,Р(Н2)=0,4. Для уточнения диагноза назначается анализ, результатом которого является положительная или отрицательная реакция. В случае болезниН1вероятность положительной реакции равна 0,9, отрицательной – 0,1. В случаеН2положительная и отрицательная реакции равновероятны. Анализ провели дважды, и оба раза реакция оказалась отрицательной (событиеА). Требуется найти вероятности каждого заболевания после проделанных анализов.

Решение.В случае заболеванияН1событиеАпроисходит с вероятностью, а в случае заболеванияН2– с вероятностью. Следовательно по формуле Байеса имеем.

.

Отсюда видно, что полученные результаты анализов дают веские основания предполагать болезнь Н2.

studfiles.net

1.3.4. Формула полной вероятности и формула Байеса

Теорема. Пусть A — некоторое событие, и события H1, H2, , Hn , , попарно несовместные, т.е. Hi Hj= , ij, образующие полную группу, и появление одного из них и только одного есть событие достоверное.

Допустим, что событие A может произойти вместе с одним из событий Hi Тогда имеет место формула полной вероятности

p(A) = p( A Hi) (1.10)

и формула Байеса p(Hi A)=. (1.11)

Замечание. События Hi называют гипотезами, вероятности p(Hi) — априорными вероятностями гипотез Hi, а вероятности p(HiA) — апостериорными вероятностями гипотез Hi.

Пример 1.19. В первой урне находится 4 белых и 6 черных шаров, а во второй – 2 белых и 7 черных шаров. Из первой урны во вторую наудачу перекладывают один шар. После этого из второй урны наудачу извлекают один шар.

1) Найти вероятность, что шар, извлеченный из второй урны, белый.

2) Известно, что из второй урны извлечен белый шар. Найти вероятность того, что из первой урны во вторую был переложен черный шар.

Решение. Обозначим события

H1 = {из первой урны во вторую был переложен белый шар},

H2 = {из первой урны во вторую был переложен черный шар},

A = {шар, извлеченный из второй урны, белый}.

а) По классическому определению вероятности находим вероятности гипотез H1 и H2 :

p(H1) — вероятность того, что из всех находящихся в первой урне шаров во вторую был переложен белый шар — p(H1) = 4 / 10 = 0,4,

p(H 2) — — вероятность того, что из всех находящихся в первой урне шаров во вторую был переложен черный шар — p(H2) = 6/ 10 = 0,6,

и условные вероятности:

p(A/H1) – вероятность того, что из второй урны будет вынут белый шар, при условии, что в нее был переложен белый шар — p(A/H1) = 3/10 = 0,3.

p(A/H2) — вероятность того, что из второй урны будет вынут белый шар, при условии, что в нее был переложен черный шар — p(A/H2) = 2/10 = 0,2.

Тогда по формуле полной вероятности находим вероятность искомого события A

p(A) = p(H1) p(A/H1)+p(A/H2)p(H2) = 0,40,3 +0,60,2 = 0,24.

б) Во второй части задачи требуется найти условную вероятность p(H2/A). Для этого можно использовать формулу Байеса (1.11):

p(H2/A) = .

Вопросы для самопроверки

  1. Какие условия должны быть выполнены для проведения опытов по схеме Бернулли?

  2. По какой формуле вычисляется условная вероятность?

  3. Как вычисляется вероятность произведения:

а) для независимых событий?

б) для несовместных событий?

в) для любых других типов событий?

  1. В чем смысл формулы полной вероятности?

В результате изучения материала раздела 1 студент может выполнить задание № 1 из методических указаний по выполнению контрольной работы по вычислительной математике, основам теории вероятностей и элементам математической статистики ( [ 8 ] ).

Раздел 2. Случайные величины

В этом разделе содержится материал о случайных величинах: дискретных и непрерывных. Приводятся определения и описываются способы задания случайных величин с помощью ряда распределения и функции распределения. Способы определения плотности вероятности зависят от того, какое распределение имеет случайная величина. Рассматривается решение задач, в которых необходимо вычислить числовые характеристики случайных величин, а также написать выражение для плотности вероятности случайной величины, если она имеет биномиальное распределение, равномерное распределение или нормальное распределение.

Изучение материала раздела заканчивается ответами на вопросы для самопроверки и рассмотрением репетиционного теста №2, приведенного в Блоке контроля и освоения дисциплины. После того, как эта часть работы проделана, студент может приступить к выполнению задачи № 2 из Методических указаний по выполнению контрольной работы по вычислительной математике, основам теории вероятностей и элементам математической статистики [ 8 ].

studfiles.net

Условная вероятность. Независимые события. Формула полной вероятности и Байеса.

1. Условная вероятность. Независимые события.

Пусть ислучайные события из алгебры событий.

Определение. Вероятностью события при условии, что событиенаступило, или просто условной вероятностью событияназывают выражение

(1)

Проиллюстрируем это понятие в случае, когда пространство элементарных событий конечно. Пусть, то естьесть число всевозможных исходов опыта. Пустьk, m есть количество исходов опыта при которых наступают события исоответственно (очевидно, что). Тогдаи по определениюЭто соответствует классическому определению вероятности для нового опыта, в котором общее количество исходов равно(в стольких случаях наступает событие), а число случаев, когда еще наступает событие(то естьинаступают одновременно) равно.

Замечание. Условная вероятность обладает всеми свойствами обычной вероятности. Из формулы (1) следует также, что

(2)

Пример. Какова вероятность того, что вытащенная кость домино окажется «дуплем», если известно, что сумма очков на этой кости является четным числом?

Решение.

Пусть событие состоит в том, что вытащенная кость есть дупль, а событиесостоит в том, что сумма очков на ней четна. Из 28 костей домино 16 имеют четную сумму и на 7 дублях сумма очков четна. Поэтому

Заметим, что безусловная вероятность

Определение. Случайные события инезависимы, если наступление событияне изменит вероятности наступления события:

(3)

Замечание. Если случайные события инезависимы, то из формул (1), (2) следует следующее правило умножения вероятностей:

(4)

В дальнейшем независимость случайных событий ибудет пониматься, как выполнение равенства (4).

Задача. Доказать, что если инезависимы, то независимы также событияи,и,и.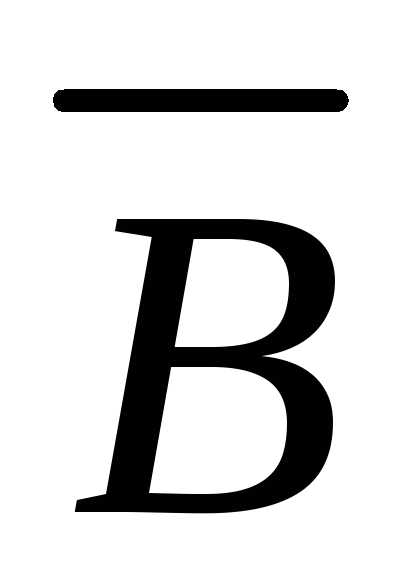

Пример. Брошены монета и игральная кость. Найти вероятность того, что выпадет «герб» или «6».

Решение.

Пусть иесть случайные события, состоящие в падении герба и шестерки соответственно. Пустьесть искомое случайное событие. Очевидно, что

Появление герба не влияет на появление шестерки. Поэтому события инезависимы и

По формуле вероятности суммы событий

Замечание. При решении многих задач на вероятность мы будем следовать по такому же плану, как в последнем примере.

Приведем этот план:

  1. Обозначить буквами события, рассматриваемые в задаче.

  2. С помощью введенных обозначений выразить случайное событие, вероятность которого требуется найти.

  3. Выбрать необходимую для решения формулу и выполнить необходимые вычисления.

2. Формула полной вероятности и Байеса.

Пусть — пространство элементарных событий с алгеброй случайных событий.

Определение. Говорят, что случайные события образуют полную группу событий, если они попарно несовместны (то естьи

Такие случайные события называют также гипотезами. Заметим, что для полной группы событий из аксиом 2, 3 следует, что

Теорема. Пусть полная группа событий. Тогда

(5)

Доказательство.

Так как полная группа событий, то не трудно доказать, что

При этом события как и событияпопарно несовместны. Из последнего равенства, аксиомы 3 и формулы (2) следует (5). Теорема доказана.

Формула (5) называется формулой полной вероятности.

Пример. В первой урне находится три белых и четыре черных шара, а во второй – пять белых и два черных. Из первой урны во вторую перекладывается один шар. Какова вероятность того, что шар, вынутый наугад из второй урны, окажется белым?

Решение.

Обозначим искомое событие через . Состав второй урны зависит от того, какой шар переложили из первой урны.

Обозначим через случайные события, состоящие в том, что из первой урны переложен белый и черный шары соответственно. Очевидно, чтоисоставляют полную группу событий. Найдем

Если переложили белый шар (то есть верна гипотеза ), то во второй урне окажется 6 белых и 2 черных шара. Поэтому

Аналогично,

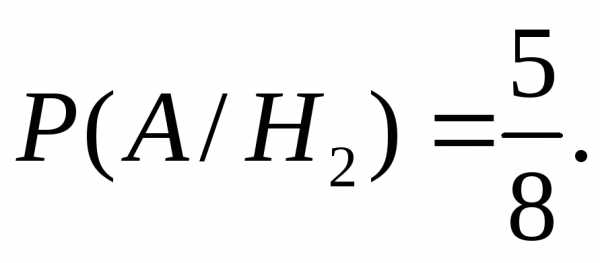
По формуле полной вероятности

В качестве следствия из формулы полной вероятности выведем формулу Байеса, которая в некотором смысле решает обратную задачу. Пусть полная группа событий. Допустим, что в результате некоторого опыта наступило случайное событие. Требуется найти вероятности выполнения гипотезто есть вычислить

Найдем вероятность , гдеИз формулы (2) следуют равенства

; ;

Приравнивая правые части, получим

; .

Выразив P(A) по формуле полной вероятности, выведем формулу

,

которая называется формулой Байеса.

studfiles.net

Лекция 1.5. Формула полной вероятности. Формула Байеса

Тема 1.5. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ, ФОРМУЛА БАЙЕСА

План лекции:

  1. Независимость событий.

  2. Формула полной вероятности.

  3. Формула Байеса.

Список литературы:

  1. Вентцель, Е.С. Теория вероятностей [Текст] / Е.С. Вентцель. – М.: Высшая школа, 2006. – 575 с.

  2. Гмурман, В.Е. Теория вероятностей и математическая статистика [Текст] / В.Е. Гмурман. — М.: Высшая школа, 2007. — 480 с.

  3. Кремер, Н.Ш. Теория вероятностей и математическая статистика [Текст] / Н.Ш. Кремер — М: ЮНИТИ, 2002. – 543 с.

п.1. Независимость событий

Если при наступлении события вероятность событияне меняется, то событияиназываютсянезависимыми.

Теорема: Вероятность совместного появления двух независимых событий и(произведенияи) равна произведению вероятностей этих событий.

Доказательство: События инезависимы, следовательно. В этом случае формула произведения событийиможно записать как.

События называютсяпопарно независимыми, если независимы любые два из них.

События называютсянезависимыми в совокупности, если каждое из этих событий и событие равное произведению любого числа остальных событий, независимы.

Теорема: Вероятность произведения конечного числа независимых в совокупности событий равна произведению вероятностей этих событий.

.

Простейшие свойства вероятностей:

  1. ;

  2. ;

  3. ;

  4. ;

  5. ;

Свойства условных вероятностей

  1. ;

  2. ;

  3. ;

  4. если , то;

  5. ;

  6. ;

  7. ;

  8. .

п.2. Формула полной вероятности

Теорема 1 (формула полной вероятности). Пусть события образуют полную группу несовместных событий. Будем эти события называть гипотезами. Тогда вероятность любого событиятого же поля событий равна:

Доказательство. Так как события образуют полную группу событий, то событиеможно представить в виде:(это означает, что событие может произойти А только вместе с одним из событий). Так как событиянесовместны то:

Пример 1. Детали поступают на конвейер с трех станков. Первый станок производит 25% всех деталей, второй 35% и третий 40% деталей. Первый станок выпускает 1% бракованных деталей, второй 3% , третий 5%. Определить вероятность того, что случайно выбранная с конвейера деталь окажется бракованной.

Решение. Введем обозначения событий: — деталь окажется бракованной; события— деталь изготовлена соответственно первым, вторым или третьим производителем. По условию задачи:

, ,;

, ,.

По формуле полной вероятности находим:

п.3. Формула Байеса

Теорема 2 (формула Байеса). Пусть событие , которое могло произойти вместе с одним из событий, образующих полную группу несовместных событий, наступило. Тогда условная вероятность того, что осуществилась гипотезаравна:

Поскольку данная формула позволяет вычислить апостериорные вероятности по априорным, то ее также называют формулой переоценки гипотез.

Доказательство. По определению условной вероятности:

.

Пример 3. В условиях примера 1 определить вероятность того, что взятая деталь была изготовлена на первом станке, если она оказалась бракованной.

Решение. Требуется переоценить вероятность гипотезы . По формуле Байеса имеем:

.

Вероятность стала меньше, поскольку если деталь оказалась бракованной, то более вероятно, что она произведена вторым, либо третьим станком.

Пример 4. В корзине находится один шар — с равной вероятностью белый или черный. В корзину опускается белый шар, и после перемешивания извлекается один шар. Он оказался белым. Какова вероятность, что в корзине остался белый шар.

Решение. Пусть гипотеза — в корзине исходно находится белый шар, гипотеза- в корзине находится черный шар. Так как с равной вероятностью в корзине может находиться как белый, так и черный шар, то:. После того, как в корзину был опущен белый шар, вероятность вынуть белый шар (событие) в предположении гипотезыесть:. Аналогично, вероятность вынуть белый шар в предположении гипотезы:. Следовательно по формуле полной вероятности:

.

Тогда вероятность, что в корзине остался белый шар (то есть верна гипотеза ):

.

Пример 5. Два стрелка стреляют по мишени, делая по одному выстрелу. Вероятность попадания для первого стрелка 0,8, для второго – 0,4. После стрельбы в мишени обнаружена только одна пробоина. Найти вероятность того, что попал первый стрелок.

Решение. Некоторая сложность в данной задаче состоит в том, что мы уже решали аналогичную прямую задачу, не привлекая при этом формулу полной вероятности.

Введем обозначения: — попал в цель только один стрелок,первый стрелок попал в цель,-второй стрелок попал в цель. Тогда:. То есть, можно считать, что событиеможет наступить в результате осуществления двух гипотез:- попал в цель только первый стрелок,- попал в цель только второй стрелок. Имеем:,,,.

..

studfiles.net

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *