Тождество параллелограмма
Тождество параллелограмма — одно из равеств в векторной алгебре и векторном анализе.
Содержание
- 1 В Евклидовой геометрии
- 2 В пространствах со скалярным произведением
- 3 В нормированных пространствах (поляризационное тождество)
- 4 Примечания
- 5 Ссылки
В Евклидовой геометрии
Сумма квадратов длин сторон параллелограмма равна сумме квадратов длин его диагоналей.
( A B ) 2 + ( B C ) 2 + ( C D ) 2 + ( D A ) 2 = ( A C ) 2 + ( B D ) 2 . {\displaystyle \ (AB)^{2}+(BC)^{2}+(CD)^{2}+(DA)^{2}=(AC)^{2}+(BD)^{2}.}В пространствах со скалярным произведением
Иллюстрация к тождеству параллелограммаВ векторных пространствах со скалярным произведением это тождество выглядит так:
2 ∥ x ∥ 2 + 2 ∥ y ∥ 2 = ∥ x + y ∥ 2 + ∥ x − y ∥ 2 {\displaystyle \ 2\|x\|^{2}+2\|y\|^{2}=\|x+y\|^{2}+\|x-y\|^{2}}где
∥ x ∥ 2 = ⟨ x , x ⟩ . {\displaystyle \ \|x\|^{2}=\langle x,x\rangle .}В нормированных пространствах (поляризационное тождество)
В нормированном пространстве (V, ∥ ⋅ ∥ {\displaystyle \|\cdot \|} ), для которого справедливо тождество параллелограмма, можно ввести скалярное произведение ⟨ x , y ⟩ {\displaystyle \langle x,\ y\rangle } , поражающее эту норму, то есть такое что ∥ x ∥ 2 = ⟨ x , x ⟩ {\displaystyle \|x\|^{2}=\langle x,\ x\rangle } всех векторов x {\displaystyle x} пространства V {\displaystyle V} . Эта теорема приписывается Фреше, фон Нейману и Йордану. Это можно сделать следующем способом:
- для действительного пространства ⟨ x , y ⟩ = ∥ x + y ∥ 2 − ∥ x − y ∥ 2 4 , {\displaystyle \langle x,y\rangle ={\|x+y\|^{2}-\|x-y\|^{2} \over 4},} или ∥ x + y ∥ 2 − ∥ x ∥ 2 − ∥ y ∥ 2 2 , {\displaystyle {\|x+y\|^{2}-\|x\|^{2}-\|y\|^{2} \over 2},} или ∥ x ∥ 2 + ∥ y ∥ 2 − ∥ x − y ∥ 2 2 . {\displaystyle {\|x\|^{2}+\|y\|^{2}-\|x-y\|^{2} \over 2}.}
- для комплексного пространства ⟨ x , y ⟩ = ∥ x + y ∥ 2 − ∥ x − y ∥ 2 4 + i ∥ i x − y ∥ 2 − ∥ i x + y ∥ 2 4 . {\displaystyle \langle x,y\rangle ={\|x+y\|^{2}-\|x-y\|^{2} \over 4}+i{\|ix-y\|^{2}-\|ix+y\|^{2} \over 4}.}
Вышеуказанные формулы, выражающие скалярное произведение двух векторов в терминах нормы, называются поляризационным тождеством.
Очевидно, что норма, выраженная через любое скалярное произведение следующим образом ∥ x ∥ 2 = ⟨ x , x ⟩ {\displaystyle \ \|x\|^{2}=\langle x,x\rangle } , будет удовлетворять этому тождеству.
Поляризационное тождество часто используется для превращения банаховых пространств в гильбертовы.
Обобщение
Если B — симметричная билинейная форма в векторном пространстве, а квадратичная форма Q выражена как
Q ( v ) = B ( v , v ) {\displaystyle \ Q(v)=B(v,v)} ,тогда
4 B ( u , v ) = Q ( u + v ) − Q ( u − v ) , 2 B ( u , v ) = Q ( u + v ) − Q ( u ) − Q ( v ) , 2 B ( u , v ) = Q ( u ) + Q ( v ) − Q ( u − v ) . {\displaystyle {\begin{array}{l}4B(u,v)=Q(u+v)-Q(u-v),\\2B(u,v)=Q(u+v)-Q(u)-Q(v),\\2B(u,v)=Q(u)+Q(v)-Q(u-v).\end{array}}}Примечания
- ↑ Philippe Blanchard, Erwin Brüning. Proposition 14.1.2 (Fréchet–von Neumann–Jordan) // Mathematical methods in physics: distributions, Hilbert space operators, and variational methods. — Birkhäuser, 2003. — P. 192. — ISBN 0817642285.
- ↑ Gerald Teschl. Theorem 0.19 (Jordan–von Neumann) // Mathematical methods in quantum mechanics: with applications to Schrödinger operators. — American Mathematical Society Bookstore, 2009. — P. 19. — ISBN 0-8218-4660-4.
Ссылки
- Аналитическая геометрия на плоскости и в пространстве / Векторная алгебра (рус.)
Тождество параллелограмма Информацию О

Тождество параллелограмма Комментарии
Тождество параллелограмма
Тождество параллелограмма
Тождество параллелограмма Вы просматриваете субъект
Тождество параллелограмма что, Тождество параллелограмма кто, Тождество параллелограмма описание
There are excerpts from wikipedia on this article and video
www.turkaramamotoru.com
Тождество параллелограмма — Howling Pixel
Тождество параллелограмма — одно из равенств в векторной алгебре и векторном анализе.
В Евклидовой геометрии
Сумма квадратов длин сторон параллелограмма равна сумме квадратов длин его диагоналей.
- (AB)2+(BC)2+(CD)2+(DA)2=(AC)2+(BD)2.{\displaystyle \ (AB)^{2}+(BC)^{2}+(CD)^{2}+(DA)^{2}=(AC)^{2}+(BD)^{2}.}
В пространствах со скалярным произведением
В векторных пространствах со скалярным произведением это тождество выглядит так[1]:
- 2‖x‖2+2‖y‖2=‖x+y‖2+‖x−y‖2{\displaystyle \ 2\|x\|^{2}+2\|y\|^{2}=\|x+y\|^{2}+\|x-y\|^{2}}
где
- ‖x‖2=⟨x,x⟩.{\displaystyle \ \|x\|^{2}=\langle x,x\rangle .}
В нормированных пространствах (поляризационное тождество)
В нормированном пространстве (V, ‖⋅‖{\displaystyle \|\cdot \|}), для которого справедливо тождество параллелограмма, можно ввести скалярное произведение ⟨x, y⟩{\displaystyle \langle x,\ y\rangle }, порождающее эту норму, то есть такое что ‖x‖2=⟨x, x⟩{\displaystyle \|x\|^{2}=\langle x,\ x\rangle } всех векторов x{\displaystyle x} пространства V{\displaystyle V}. Эта теорема приписывается Фреше, фон Нейману и Йордану[2][3]. Это можно сделать следующем способом:
- для действительного пространства
- ⟨x,y⟩=‖x+y‖2−‖x−y‖24,{\displaystyle \langle x,y\rangle ={\|x+y\|^{2}-\|x-y\|^{2} \over 4},} или ‖x+y‖2−‖x‖2−‖y‖22,{\displaystyle {\|x+y\|^{2}-\|x\|^{2}-\|y\|^{2} \over 2},} или ‖x‖2+‖y‖2−‖x−y‖22.{\displaystyle {\|x\|^{2}+\|y\|^{2}-\|x-y\|^{2} \over 2}.}
- для комплексного пространства
- ⟨x,y⟩=‖x+y‖2−‖x−y‖24+i‖ix−y‖2−‖ix+y‖24.{\displaystyle \langle x,y\rangle ={\|x+y\|^{2}-\|x-y\|^{2} \over 4}+i{\|ix-y\|^{2}-\|ix+y\|^{2} \over 4}.}
Вышеуказанные формулы, выражающие скалярное произведение двух векторов в терминах нормы, называются поляризационным тождеством.
Очевидно, что норма, выраженная через любое скалярное произведение следующим образом ‖x‖2=⟨x,x⟩{\displaystyle \ \|x\|^{2}=\langle x,x\rangle }, будет удовлетворять этому тождеству.
Поляризационное тождество часто используется для превращения банаховых пространств в гильбертовы.
Обобщение
Если B — симметричная билинейная форма в векторном пространстве, а квадратичная форма Q выражена как
- Q(v)=B(v,v){\displaystyle \ Q(v)=B(v,v)},
тогда
- 4B(u,v)=Q(u+v)−Q(u−v),2B(u,v)=Q(u+v)−Q(u)−Q(v),2B(u,v)=Q(u)+Q(v)−Q(u−v).{\displaystyle {\begin{array}{l}4B(u,v)=Q(u+v)-Q(u-v),\\2B(u,v)=Q(u+v)-Q(u)-Q(v),\\2B(u,v)=Q(u)+Q(v)-Q(u-v).\end{array}}}
Примечания
- ↑ Шилов, 1961, с. 185.
- ↑ Philippe Blanchard, Erwin Brüning. Proposition 14.1.2 (Fréchet–von Neumann–Jordan) // Mathematical methods in physics: distributions, Hilbert space operators, and variational methods. — Birkhäuser, 2003. — P. 192. — ISBN 0817642285.
- ↑ Gerald Teschl. Theorem 0.19 (Jordan–von Neumann) // Mathematical methods in quantum mechanics: with applications to Schrödinger operators. — American Mathematical Society Bookstore, 2009. — P. 19. — ISBN 0-8218-4660-4.
Ссылки
Литература
- Шилов Г.Е. Математический анализ. Специальный курс. — М.: Наука, 1961. — 436 с.
Ги́льбертово простра́нство — обобщение евклидова пространства, допускающее бесконечную размерность.
Названо в честь Давида Гильберта.
Важнейшим объектом исследования в гильбертовом пространстве являются линейные операторы. Само понятие гильбертова пространства сформировалось в работах Гильберта и Шмидта по теории интегральных уравнений, а абстрактное определение было дано в работах фон Неймана, Риса и Стоуна по теории эрмитовых операторов.
ПараллелограммПараллелогра́мм (др.-греч. παραλληλόγραμμον от παράλληλος — параллельный и γραμμή — линия) — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
Пространство непрерывных функцийПространство непрерывных функций — линейное нормированное пространство, элементами которого являются непрерывные на отрезке [a,b]{\displaystyle [a,b]} функции (обычно обозначается C[a,b]{\displaystyle {\mathrm {C} }[a,b]}, иногда C0[a,b]{\displaystyle C^{0}[a,b]} или C(0)[a,b]{\displaystyle C^{(0)}[a,b]}) . Норма в этом пространстве определяется следующим образом:
- ||x||C[a,b]=maxt∈[a,b]|x(t)|{\displaystyle ||x||_{{\mathbf {C} }[a,b]}=\max _{t\in [a,b]}|x(t)|}
Эту норму также называют нормой Чебышёва или равномерной нормой, так как сходимость по этой норме эквивалентна равномерной сходимости.
Теорема АполлонияВ планиметрии теорема Аполлония является формулой, выражающей длину медианы треугольника через его стороны. В частности, если в каком-либо треугольнике ABC медиана AD, то
- AB2+AC2=2(AD2+BD2).{\displaystyle AB^{2}+AC^{2}=2(AD^{2}+BD^{2}).}
Это частный случай теоремы Стюарта. Для равнобедренного треугольника теорема сводится к теореме Пифагора. Из факта, что диагонали параллелограмма делят друг друга пополам, можно доказать, что теорема эквивалентна тождеству параллелограмма.
Теорема называется в честь Аполлония Пергского.
Теорема косинусовТеорема косинусов — теорема евклидовой геометрии, обобщающая теорему Пифагора на произвольные плоские треугольники.
Функциональное уравнениеФункциональное уравнение — уравнение, выражающее связь между значением функции в одной точке с её значениями в других точках. Многие свойства функций можно определить, исследуя функциональные уравнения, которым эти функции удовлетворяют. Термин «функциональное уравнение» обычно используется для уравнений, несводимых простыми способами к алгебраическим уравнениям. Эта несводимость чаще всего обусловлена тем, что аргументами неизвестной функции в уравнении являются не сами независимые переменные, а некоторые данные функции от них.
This page is based on a Wikipedia article written by authors
(here).
Text is available under the CC BY-SA 3.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.
howlingpixel.com
3. Скалярное произведение. Гильбертово пространство. Аксиомы и свойства. Ортонормированные системы. Ортогонализация по Шмидту. Тождество параллелограмма.
Определение 2.
Линейное пространство Н называется предгильбертовым
пространством, если указано правило, которое позволяет
сопоставить каждой паре элементов x и y пространства Н вещественное
(или комплексное) число, называемое
скалярным произведением векторов x и y и обозначенное 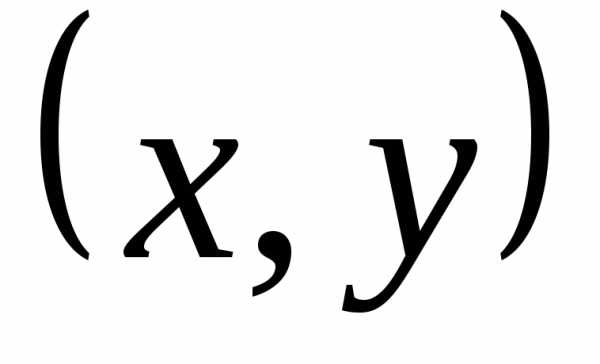 ,
удовлетворяющее следующим условиям:
,
удовлетворяющее следующим условиям:
а) (в случае комплексного значения)
б)
в) для любого вещественного числа;
г) 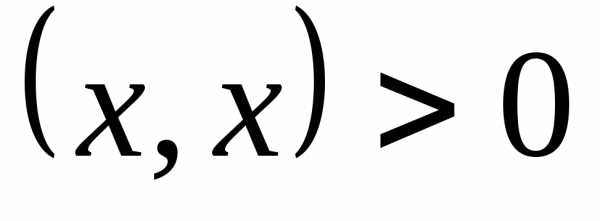 при
при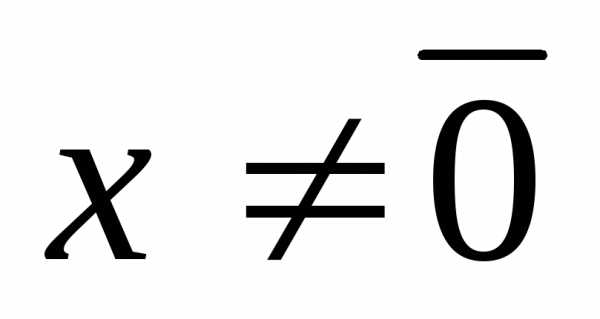 и
и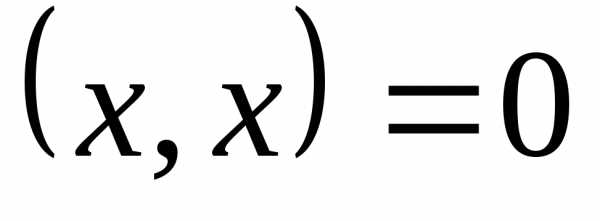 при
при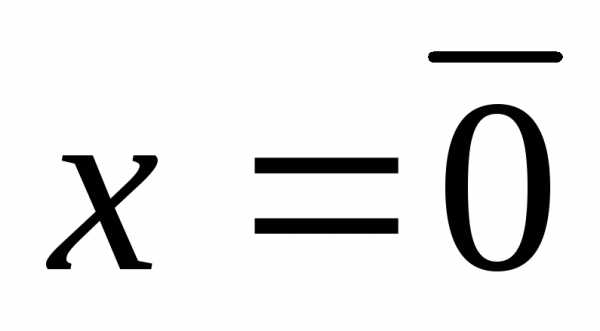 ;
;
Число 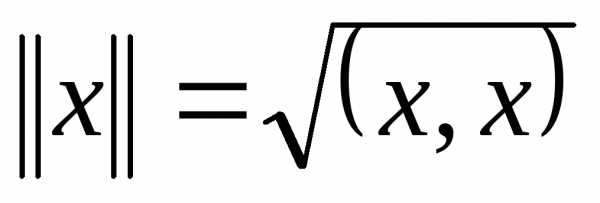 назовём нормой элементах.
Ниже мы покажем, что эта величина
удовлетворяет всем требованиям нормы.
В случае, если Н полное
пространство по этой норме, его называют гильбертовым.
Таким образом, гильбертово пространство
есть частный случай банахова пространства.
Далее,если не оговорено противное, мы
будем рассматривать гильбертовы
пространства над полем вещественных
чисел.
назовём нормой элементах.
Ниже мы покажем, что эта величина
удовлетворяет всем требованиям нормы.
В случае, если Н полное
пространство по этой норме, его называют гильбертовым.
Таким образом, гильбертово пространство
есть частный случай банахова пространства.
Далее,если не оговорено противное, мы
будем рассматривать гильбертовы
пространства над полем вещественных
чисел.
Пример 9. Пространство l2 становится гильбертовым, если для любых двух его элементов иположить
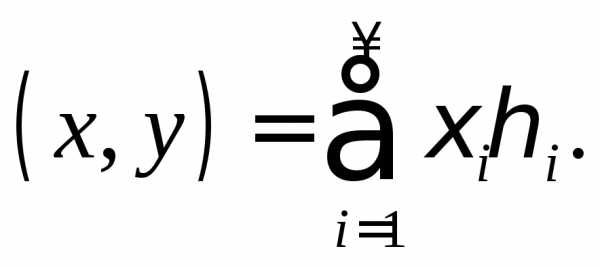
Сходимость этого ряда для любых x и y из l2 вытекает из неравенства Буняковского для рядов.
Пример 10. Пространство 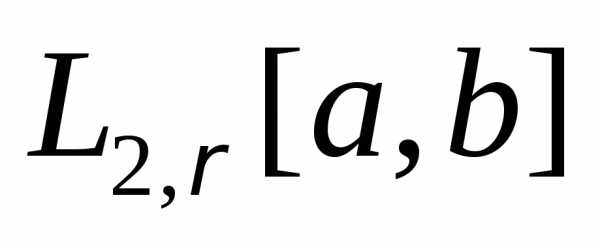
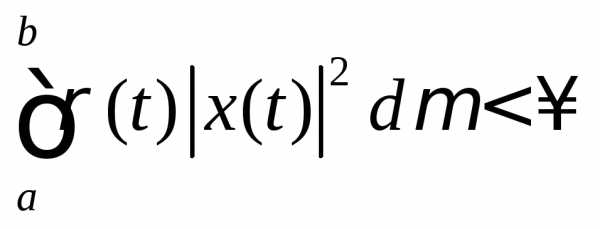 ,
,
где 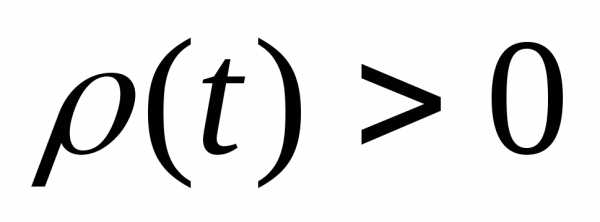 почти всюду на [a, b].
почти всюду на [a, b].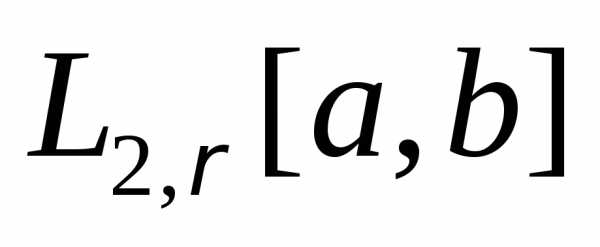 будет гильбертовым пространством, если
положить для
будет гильбертовым пространством, если
положить для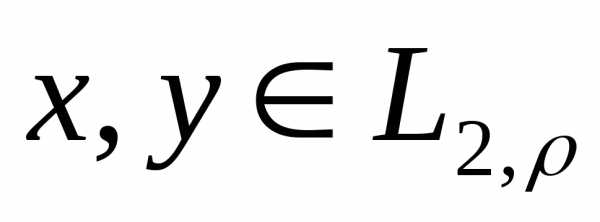
Существование
этого интеграла при любом 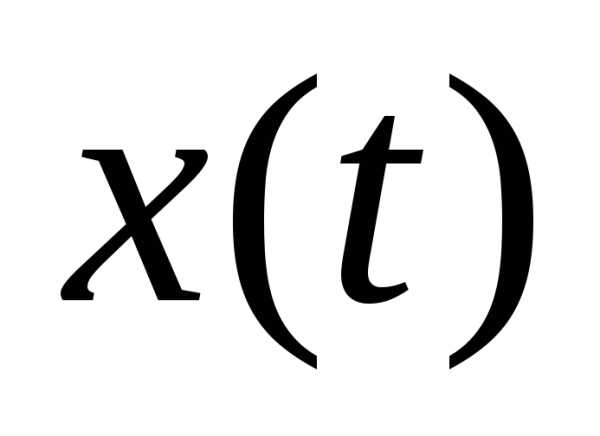 и
и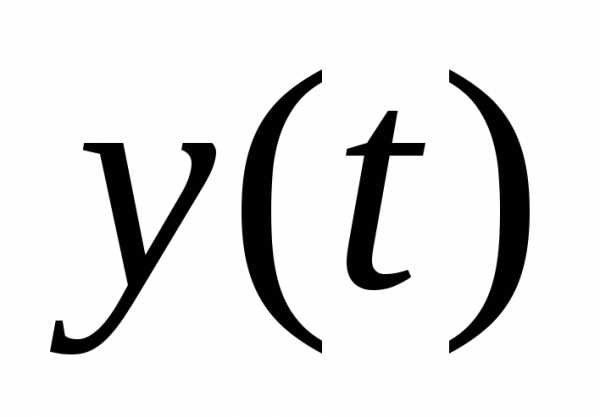 из
из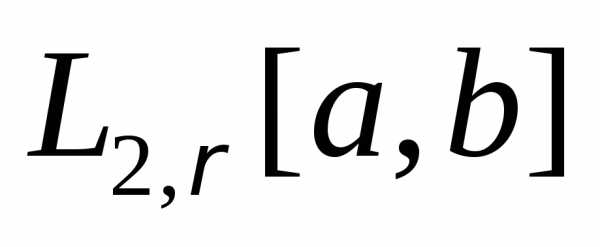 вытекает из неравенства Гельдера для
интегралов.
вытекает из неравенства Гельдера для
интегралов.
Рассмотрим простейшие свойства гильбертовых пространств.
Из аксиом б) и в) легко получается общая формула
справедливая для произвольных векторов и произвольных вещественных чисел
Установим теперь для скалярного произведения неравенство Коши — Буняковского. Для любых и любогоR, имеем илиРассматривая это выражение как квадратный трехчлен относительно, получаем, что условием его неотрицательности является неположительность его дискриминанта, т.е.(х, у)2 – (у, у)(х, х) 0 или |(x, y)| – это и есть неравенство Коши – Буняковского.
Теорема 6. Величина 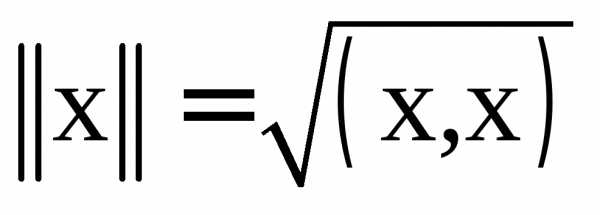 является нормой в пространстве со
скалярным произведением.
является нормой в пространстве со
скалярным произведением.
Доказательство. 1. Неотрицательность следует из неотрицательности скалярного произведения.
2.
3. . По неравенству Коши-Буняковского,
.
Извлекая из обеих частей квадратный корень, получим неравенство .
Легко доказывается непрерывность скалярного произведения.
Теорема 7. Скалярное произведение есть непрерывная функция относительно сходимости по норме.
Доказательство. Пусть 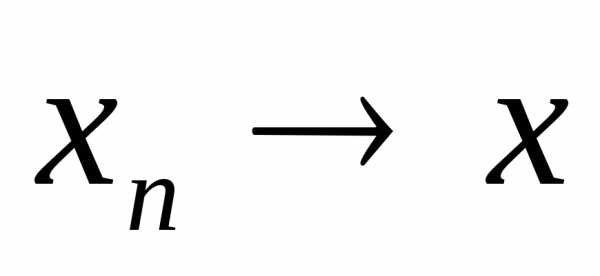 и
и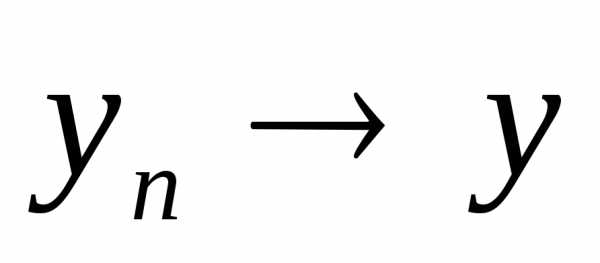 .
Тогда числа
.
Тогда числа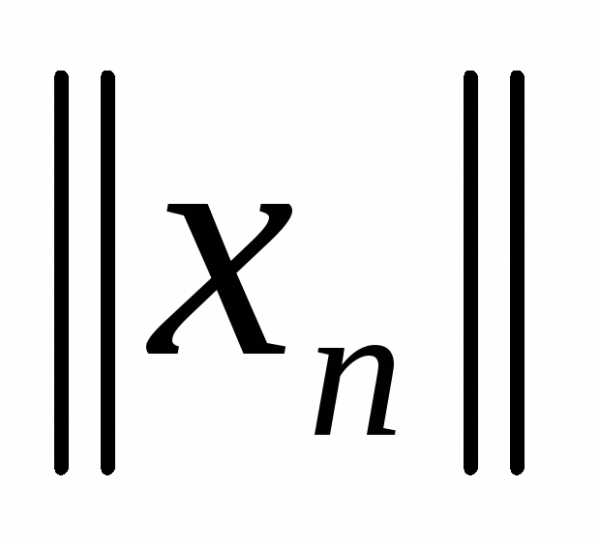 и
и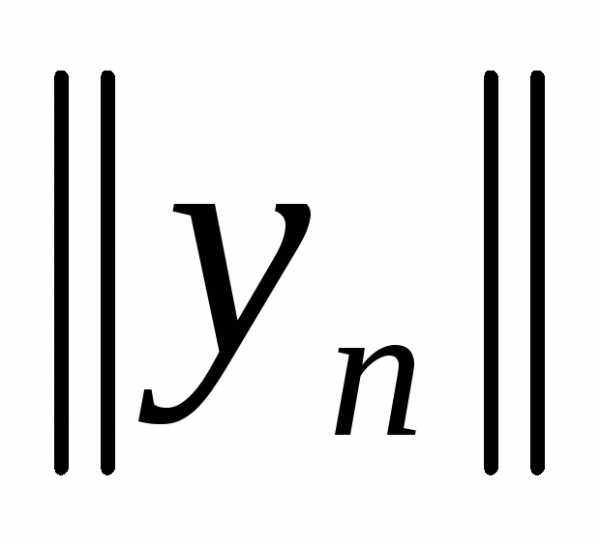 ограничены; пустьМ
– их верхняя
граница.
ограничены; пустьМ
– их верхняя
граница.
Имеем
Так как ипри,то ипри, что и требовалось доказать.
Наличие скалярного произведения позволяет ввести в гильбертовом пространстве понятие длины (нормы) вектора и угла между векторами по формулам
Из неравенства Коши – Буняковского следует корректность этих формул. Эти определения согласуются с обычными формулами аналитической геометрии.
Два вектора х и y Н называются ортогональными (в этом случае записывают 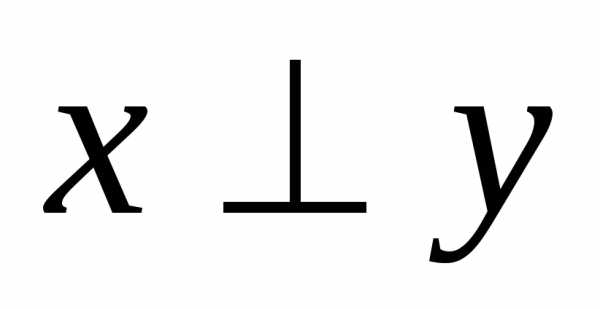 ),
если.
Если
),
если.
Если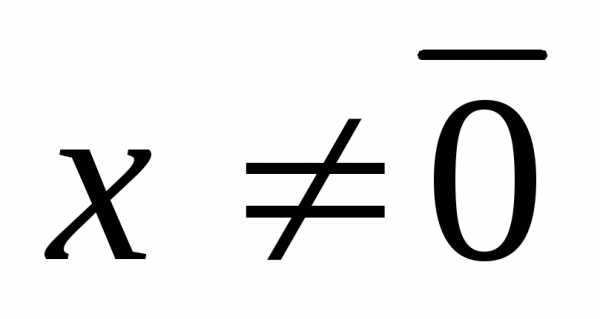 и
и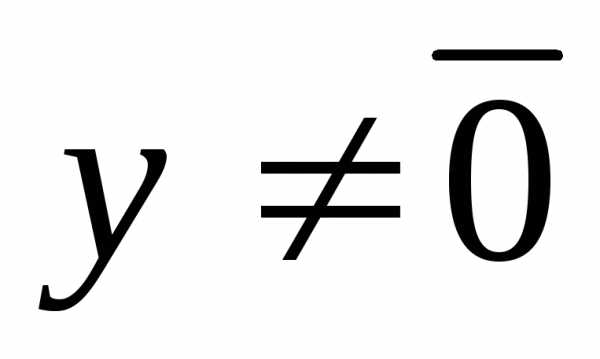 ,
то это определение, в соответствии с
общим определением угла между векторами,
означает, чтоx и y образуют
угол в
,
то это определение, в соответствии с
общим определением угла между векторами,
означает, чтоx и y образуют
угол в 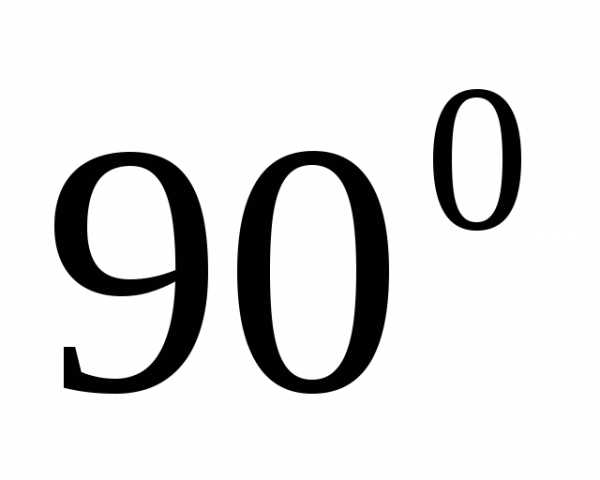 .
Нулевой вектор оказывается ортогональным
любому векторух Н.
.
Нулевой вектор оказывается ортогональным
любому векторух Н.
В пространстве 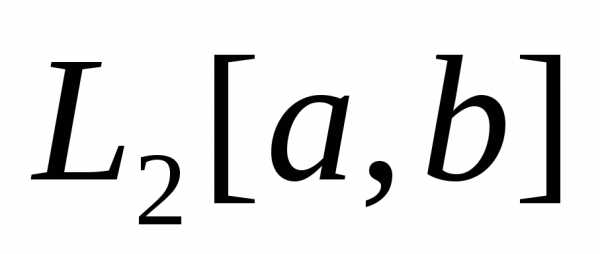 условие ортогональности векторов
условие ортогональности векторов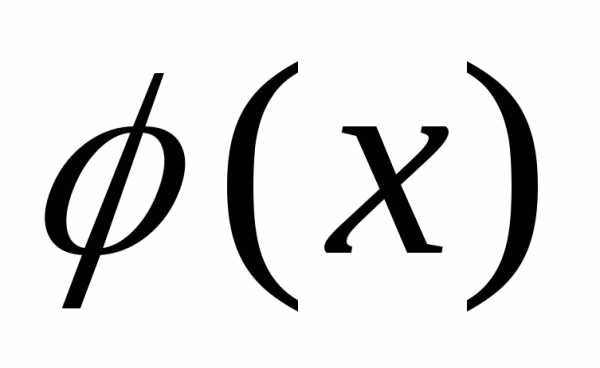 и
и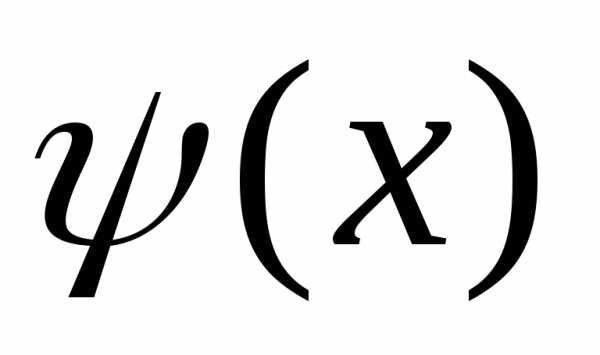
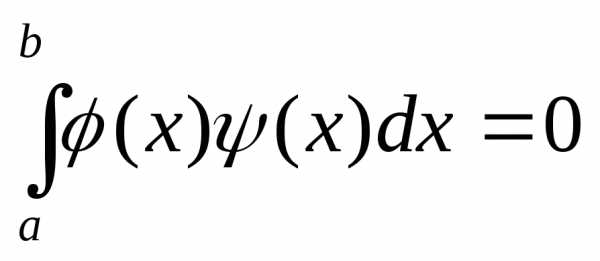 .
.
Легко проверить,
вычислив соответствующие интегралы,
что в пространстве 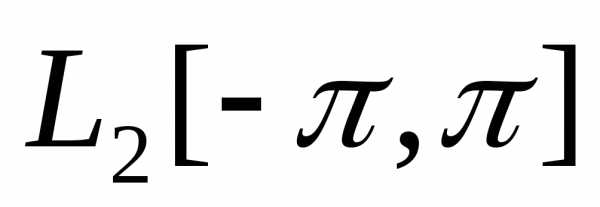 любые два вектора тригонометрической
системы
любые два вектора тригонометрической
системы
взаимно ортогональны.
Отметим несколько простых свойств, связанных с понятием ортогональности.
1) Если вектор х ортогонален векторам  то
он ортогонален и любой линейной комбинации
этих векторов.
то
он ортогонален и любой линейной комбинации
этих векторов.
2) Если векторы
ортогональны
векторух и 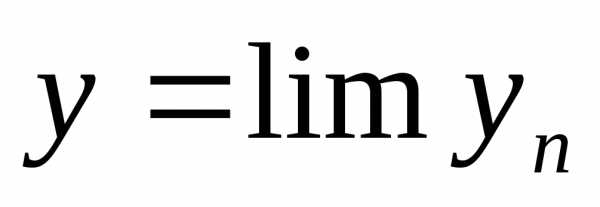 ,
то вектору
,
то вектору также ортогонален векторух.
также ортогонален векторух.
Из свойств 1) и 2) следует, что совокупность всех векторов ортогональных вектору х (или произвольному фиксированному множеству Х векторов в Н), образует замкнутое подпространство – ортогональное дополнение к вектору х (к множеству Х).
Система 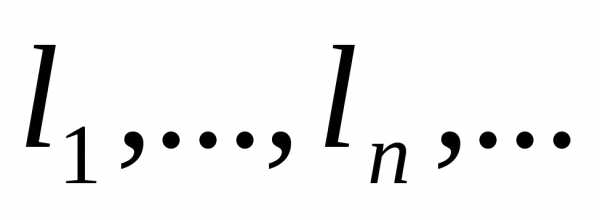 векторов пространстваН называется ортонормальной
системой,
если
векторов пространстваН называется ортонормальной
системой,
если
.
Бесконечная система элементов линейного пространства называется линейно независимой, если любая конечная подсистема этой системы линейно независима.
Любую систему  линейно независимых элементов можно
превратить в ортонормальную с помощью
следующегопроцесса
ортогонализации Шмидта.
линейно независимых элементов можно
превратить в ортонормальную с помощью
следующегопроцесса
ортогонализации Шмидта.
Полагаем 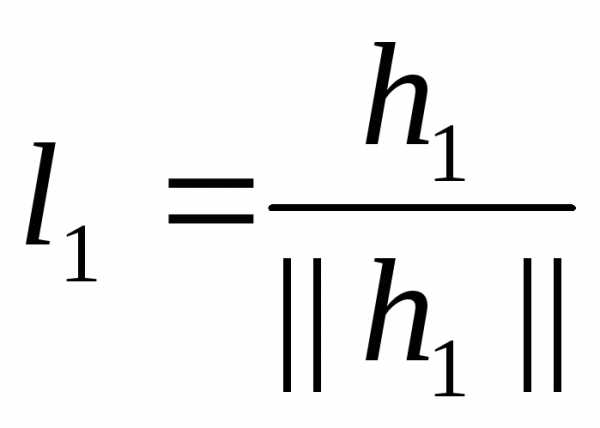 .
Пусть.
Подберем число
.
Пусть.
Подберем число так, чтобы
так, чтобы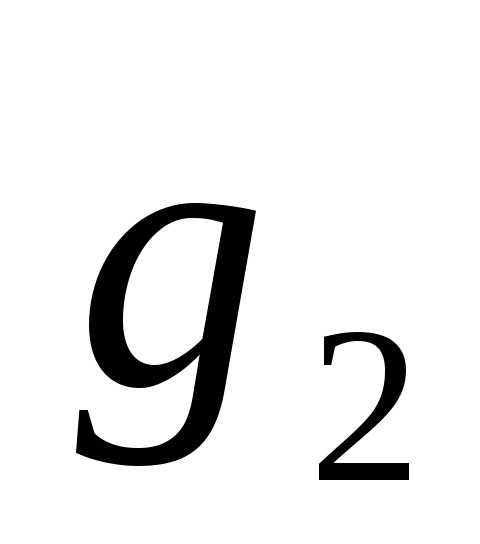 было ортогональным
было ортогональным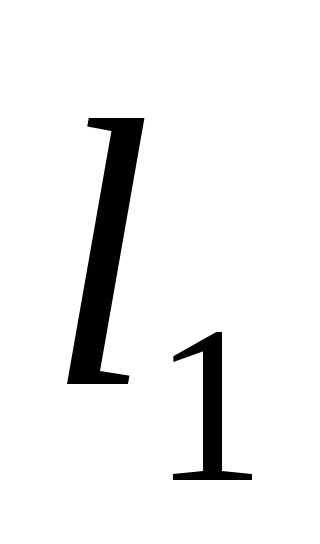 .
Имеем.
Отсюда следует, что для этого следует
взять.
Полагаем
.
Имеем.
Отсюда следует, что для этого следует
взять.
Полагаем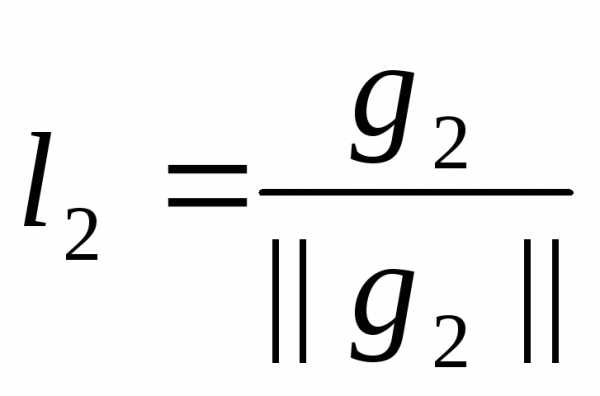 ;
при этом
;
при этом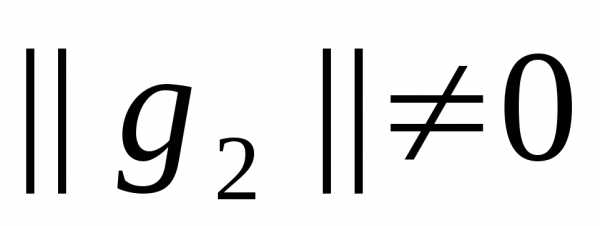 ,
так как в противном случае
,
так как в противном случае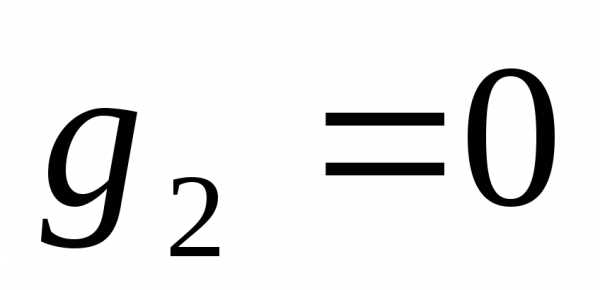 и вектора
и вектора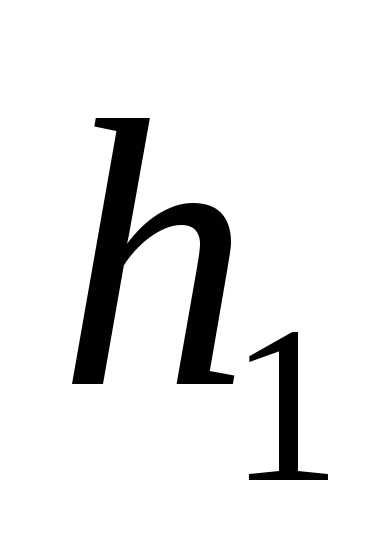 и
и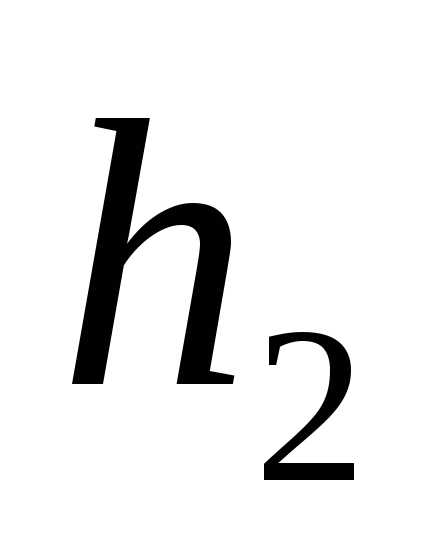 будут линейно зависимы, что противоречит
условию. Пусть
будут линейно зависимы, что противоречит
условию. Пусть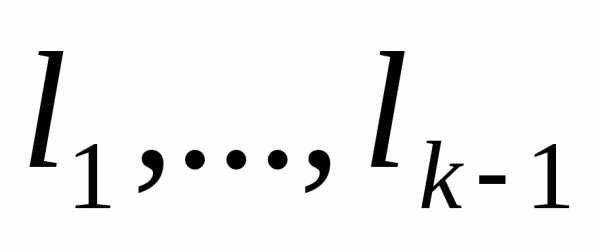 уже построены. Возьмем
уже построены. Возьмем
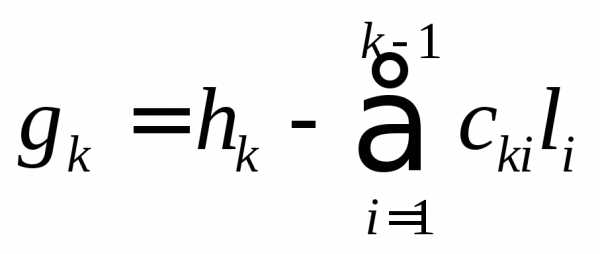
и подберем числа 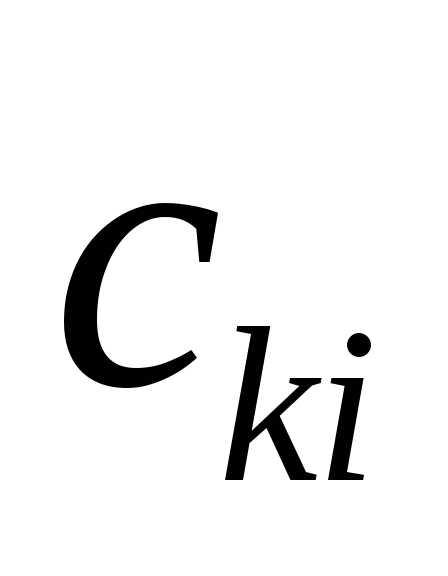 так, чтобы
так, чтобы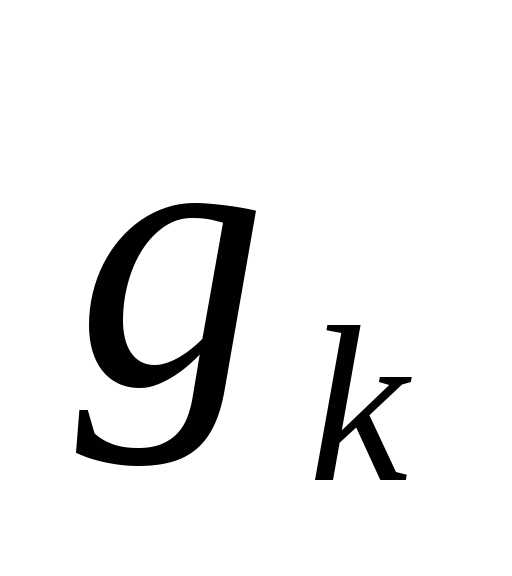 было ортогонально
было ортогонально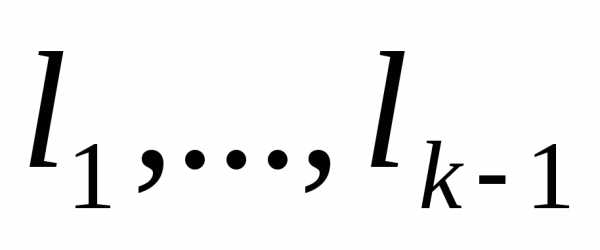 ;
для этого следует взять.
Полагаем
;
для этого следует взять.
Полагаем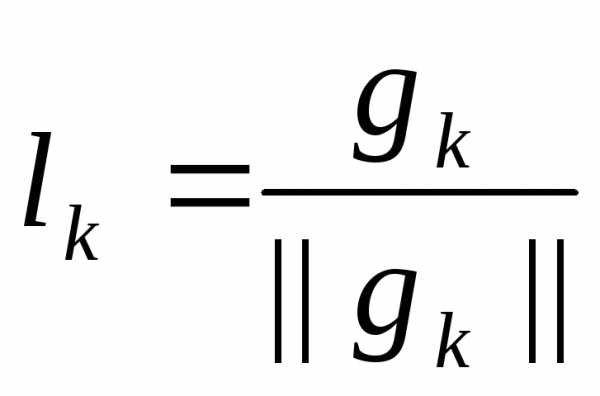 ,
причем снова
,
причем снова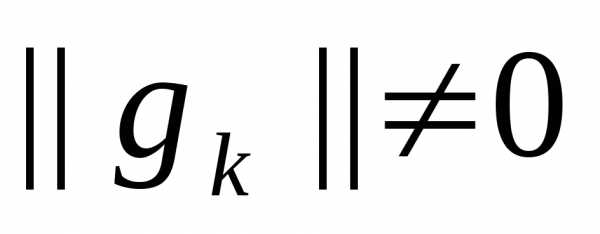 и т.д.
и т.д.
Пример 11.
Если совокупность степеней
ортогонализовать
в пространстве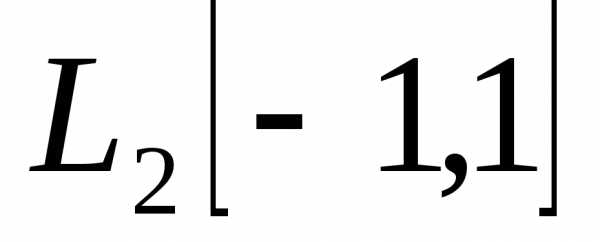 то мы придём к системе многочленовназываемых многочленами Лежандра. Можно
показать, что n-ый многочлен Лежандра
имеет вид.
то мы придём к системе многочленовназываемых многочленами Лежандра. Можно
показать, что n-ый многочлен Лежандра
имеет вид.
Пример 12. Функции, получающиеся при ортогонализации выражений в пространстве, называются функциями Эрмита. Можно показать, что n-ая функция Эрмита имеет вид.
Пример 13. Функции, получающиеся при ортогонализации
выражений
в пространстве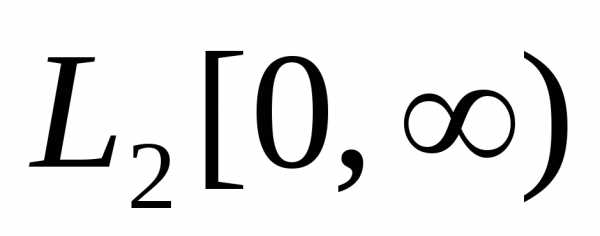 называется функциями Лагерра. Можно
показать, что n-ая функция Лагерра имеет
вид.
называется функциями Лагерра. Можно
показать, что n-ая функция Лагерра имеет
вид.
Теорема 8. (равенство параллелограмма) В пространстве со скалярным произведением выполняется следующее тождество:
||x + y||2 + ||x y||2 = 2||x||2 + 2||y||2.
Доказательство. В пространстве со скалярным произведением выполняются равенства
||x + y||2 = (x + y, x + y) = (x, x) + 2(x, y) + (y, y) = ||x||2 + 2(x, y) + ||y||2,
||x y||2 = (x y, x y) = (x, x) 2(x, y) + (y, y) = ||x||2 2(x, y) + ||y||2.
Складывая, получим нужное тождество.
studfiles.net
Тождество параллелограмма — Википедия. Что такое Тождество параллелограмма
Материал из Википедии — свободной энциклопедии ПараллелограммТождество параллелограмма — одно из равенств в векторной алгебре и векторном анализе.
В Евклидовой геометрии
Сумма квадратов длин сторон параллелограмма равна сумме квадратов длин его диагоналей.
- (AB)2+(BC)2+(CD)2+(DA)2=(AC)2+(BD)2.{\displaystyle \ (AB)^{2}+(BC)^{2}+(CD)^{2}+(DA)^{2}=(AC)^{2}+(BD)^{2}.}
В пространствах со скалярным произведением
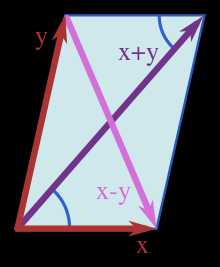 Иллюстрация к тождеству параллелограмма
Иллюстрация к тождеству параллелограммаВ векторных пространствах со скалярным произведением это тождество выглядит так[1]:
- 2‖x‖2+2‖y‖2=‖x+y‖2+‖x−y‖2{\displaystyle \ 2\|x\|^{2}+2\|y\|^{2}=\|x+y\|^{2}+\|x-y\|^{2}}
где
- ‖x‖2=⟨x,x⟩.{\displaystyle \ \|x\|^{2}=\langle x,x\rangle .}
В нормированных пространствах (поляризационное тождество)
В нормированном пространстве (V, ‖⋅‖{\displaystyle \|\cdot \|}), для которого справедливо тождество параллелограмма, можно ввести скалярное произведение ⟨x, y⟩{\displaystyle \langle x,\ y\rangle }, порождающее эту норму, то есть такое что ‖x‖2=⟨x, x⟩{\displaystyle \|x\|^{2}=\langle x,\ x\rangle } всех векторов x{\displaystyle x} пространства V{\displaystyle V}. Эта теорема приписывается Фреше, фон Нейману и Йордану[2][3]. Это можно сделать следующем способом:
- для действительного пространства
- ⟨x,y⟩=‖x+y‖2−‖x−y‖24,{\displaystyle \langle x,y\rangle ={\|x+y\|^{2}-\|x-y\|^{2} \over 4},} или ‖x+y‖2−‖x‖2−‖y‖22,{\displaystyle {\|x+y\|^{2}-\|x\|^{2}-\|y\|^{2} \over 2},} или ‖x‖2+‖y‖2−‖x−y‖22.{\displaystyle {\|x\|^{2}+\|y\|^{2}-\|x-y\|^{2} \over 2}.}
- для комплексного пространства
- ⟨x,y⟩=‖x+y‖2−‖x−y‖24+i‖ix−y‖2−‖ix+y‖24.{\displaystyle \langle x,y\rangle ={\|x+y\|^{2}-\|x-y\|^{2} \over 4}+i{\|ix-y\|^{2}-\|ix+y\|^{2} \over 4}.}
Вышеуказанные формулы, выражающие скалярное произведение двух векторов в терминах нормы, называются поляризационным тождеством.
Очевидно, что норма, выраженная через любое скалярное произведение следующим образом ‖x‖2=⟨x,x⟩{\displaystyle \ \|x\|^{2}=\langle x,x\rangle }, будет удовлетворять этому тождеству.
Поляризационное тождество часто используется для превращения банаховых пространств в гильбертовы.
Обобщение
Если B — симметричная билинейная форма в векторном пространстве, а квадратичная форма Q выражена как
- Q(v)=B(v,v){\displaystyle \ Q(v)=B(v,v)},
тогда
- 4B(u,v)=Q(u+v)−Q(u−v),2B(u,v)=Q(u+v)−Q(u)−Q(v),2B(u,v)=Q(u)+Q(v)−Q(u−v).{\displaystyle {\begin{array}{l}4B(u,v)=Q(u+v)-Q(u-v),\\2B(u,v)=Q(u+v)-Q(u)-Q(v),\\2B(u,v)=Q(u)+Q(v)-Q(u-v).\end{array}}}
Примечания
Ссылки
Литература
- Шилов Г.Е. Математический анализ. Специальный курс. — М.: Наука, 1961. — 436 с.
wiki.sc
WikiZero — Тождество параллелограмма
open wikipedia design.
ПараллелограммТождество параллелограмма — одно из равенств в векторной алгебре и векторном анализе.
Содержание
- 1 В Евклидовой геометрии
- 2 В пространствах со скалярным произведением
- 3 В нормированных пространствах (поляризационное тождество)
- 3.1 Обобщение
- 4 Примечания
- 5 Ссылки
- 6 Литература
Сумма квадратов длин сторон параллелограмма равна сумме квадратов длин его диагоналей.
- (AB)2+(BC)2+(CD)2+(DA)2=(AC)2+(BD)2.{\displaystyle \ (AB)^{2}+(BC)^{2}+(CD)^{2}+(DA)^{2}=(AC)^{2}+(BD)^{2}.}
В пространствах со скалярным произведением[править | править код]
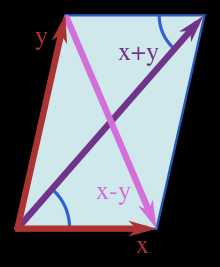 Иллюстрация к тождеству параллелограмма
Иллюстрация к тождеству параллелограммаВ векторных пространствах со скалярным произведением это тождество выглядит так[1]:
- 2‖x‖2+2‖y‖2=‖x+y‖2+‖x−y‖2{\displaystyle \ 2\|x\|^{2}+2\|y\|^{2}=\|x+y\|^{2}+\|x-y\|^{2}}
где
- ‖x‖2=⟨x,x⟩.{\displaystyle \ \|x\|^{2}=\langle x,x\rangle .}
В нормированных пространствах (поляризационное тождество)[править | править код]
В нормированном пространстве (V, ‖⋅‖{\displaystyle \|\cdot \|}), для которого справедливо
www.wikizero.com
Тождество параллелограмма Википедия
ПараллелограммТождество параллелограмма — одно из равенств в векторной алгебре и векторном анализе.
В Евклидовой геометрии[ | ]
Сумма квадратов длин сторон параллелограмма равна сумме квадратов длин его диагоналей.
- (AB)2+(BC)2+(CD)2+(DA)2=(AC)2+(BD)2.{\displaystyle \ (AB)^{2}+(BC)^{2}+(CD)^{2}+(DA)^{2}=(AC)^{2}+(BD)^{2}.}
В пространствах со скалярным произведением[ | ]
 Иллюстрация к тождеству параллелограмма
Иллюстрация к тождеству параллелограммаВ векторных пространствах со скалярным произведением это тождество выглядит так[1]:
- 2‖x‖2+2‖y‖2=‖x+y‖2+‖x−y‖2{\displaystyle \ 2\|x\|^{2}+2\|y\|^{2}=\|x+y\|^{2}+\|x-y\|^{2}}
где
- ‖x‖2=⟨x,x⟩.{\displaystyle \ \|x\|^{2}=\langle x,x\rangle .}
В нормированных пространствах (поляризационное тождество)[ |
ru-wiki.ru
Тождество параллелограмма — ВиКи
В нормированном пространстве (V, ‖⋅‖{\displaystyle \|\cdot \|} ), для которого справедливо тождество параллелограмма, можно ввести скалярное произведение ⟨x, y⟩{\displaystyle \langle x,\ y\rangle } , порождающее эту норму, то есть такое что ‖x‖2=⟨x, x⟩{\displaystyle \|x\|^{2}=\langle x,\ x\rangle } всех векторов x{\displaystyle x} пространства V{\displaystyle V} . Эта теорема приписывается Фреше, фон Нейману и Йордану[2][3]. Это можно сделать следующем способом:
- для действительного пространства
- ⟨x,y⟩=‖x+y‖2−‖x−y‖24,{\displaystyle \langle x,y\rangle ={\|x+y\|^{2}-\|x-y\|^{2} \over 4},} или ‖x+y‖2−‖x‖2−‖y‖22,{\displaystyle {\|x+y\|^{2}-\|x\|^{2}-\|y\|^{2} \over 2},} или ‖x‖2+‖y‖2−‖x−y‖22.{\displaystyle {\|x\|^{2}+\|y\|^{2}-\|x-y\|^{2} \over 2}.}
- для комплексного пространства
- ⟨x,y⟩=‖x+y‖2−‖x−y‖24+i‖ix−y‖2−‖ix+y‖24.{\displaystyle \langle x,y\rangle ={\|x+y\|^{2}-\|x-y\|^{2} \over 4}+i{\|ix-y\|^{2}-\|ix+y\|^{2} \over 4}.}
Вышеуказанные формулы, выражающие скалярное произведение двух векторов в терминах нормы, называются поляризационным тождеством.
Очевидно, что норма, выраженная через любое скалярное произведение следующим образом ‖x‖2=⟨x,x⟩{\displaystyle \ \|x\|^{2}=\langle x,x\rangle } , будет удовлетворять этому тождеству.
Поляризационное тождество часто используется для превращения банаховых пространств в гильбертовы.
Обобщение
Если B — симметричная билинейная форма в векторном пространстве, а квадратичная форма Q выражена как
- Q(v)=B(v,v){\displaystyle \ Q(v)=B(v,v)} ,
тогда
- 4B(u,v)=Q(u+v)−Q(u−v),2B(u,v)=Q(u+v)−Q(u)−Q(v),2B(u,v)=Q(u)+Q(v)−Q(u−v).{\displaystyle {\begin{array}{l}4B(u,v)=Q(u+v)-Q(u-v),\\2B(u,v)=Q(u+v)-Q(u)-Q(v),\\2B(u,v)=Q(u)+Q(v)-Q(u-v).\end{array}}}
xn--b1aeclack5b4j.xn--j1aef.xn--p1ai
