Транспонована матриця — Howling Pixel
Транспонована матриця — матриця AT{\displaystyle A^{T}}, що виникає з матриці A{\displaystyle A} в результаті унарної операції транспонування: заміни її рядків на стовпчики.
Формально, транспонована матриця AT=(bij){\displaystyle \ A^{T}=(b_{ij})} для матриці A=(aij){\displaystyle \ A=(a_{ij})} визначається як
- bij=aji,i=1,n¯,j=1,m¯.{\displaystyle \ b_{ij}=a_{ji},\quad i={\overline {1,n}},\quad j={\overline {1,m}}.}
Наприклад:
- [1234]T=[1324]{\displaystyle {\begin{bmatrix}1&2\\3&4\end{bmatrix}}^{\mathrm {T} }={\begin{bmatrix}1&3\\2&4\end{bmatrix}}} та [123456]T=[135246]{\displaystyle {\begin{bmatrix}1&2\\3&4\\5&6\end{bmatrix}}^{\mathrm {T} }={\begin{bmatrix}1&3&5\\2&4&6\end{bmatrix}}}
Властивості
Пов’язані означення
- AT=A{\displaystyle \ A^{\mathrm {T} }=A}
- AT=−A{\displaystyle \ A^{\mathrm {T} }=-A}
- A∗=(A¯)T=AT¯{\displaystyle A^{*}=({\overline {A}})^{T}={\overline {A^{T}}}}
Див. також
Джерела
Алгоритм Лукаса — КанадеАлгоритм Лукаса — Канаде — широко використовуваний у комп’ютерному зорі диференційний локальний метод обчислення оптичного потоку.
Основне рівняння оптичного потоку містить дві незалежні змінні і не може бути однозначно розв’язаною. Алгоритм Лукаса — Канаде вирішує неоднозначність за рахунок використання інформації про сусідні пікселі в кожній точці. Метод ґрунтується на припущенні, що в локальному околі кожного пікселя значення оптичного потоку однакове, таким чином можна записати рівняння оптичного потоку для всіх пікселів в околі і розв’язати систему рівнянь методом найменших квадратів.
Лінійне програмуванняЛінійне програмування або лінійна оптимізація (LP, англ. Linear Programming) — метод досягнення найліпшого виходу (такого як найбільший прибуток або найменша вартість) у математичній моделі чиї вимоги представлені через лінійні відношення. Лінійне програмування є особливим випадком математичного програмування (математичної оптимізації).
Більш формально, лінійне програмування є технікою для оптимізації лінійної цільової функції, що обмежена лінійними рівняннями і лінійними нерівностями. Її допустима множина є опуклим політопом, який є множиною визначеною як перетин скінченної кількості півпростірів, кожен з яких визначає лінійна нерівність. Її цільова функція є дійсно-значима афінна функція визначена на цьому багатограннику. Алгоритм лінійного програмування знаходить точку на багатограннику де ця функція набуває найбільшого чи найменшого значення якщо така точка існує.
Матриця (математика)Ма́триця — математичний об’єкт, записаний у вигляді прямокутної таблиці чисел (чи елементів кільця), він допускає операції (додавання, віднімання, множення та множення на скаляр). Зазвичай матриці представляються двовимірними (прямокутними) таблицями. Іноді розглядають багатовимірні матриці або матриці непрямокутної форми. В цій статті вони розглядатися не будуть.
Матриці є корисними для запису даних, що залежать від двох категорій, наприклад: для коефіцієнтів систем лінійних рівнянь та лінійних перетворень.
Ортогональна матрицяОртогональна матриця — невироджена квадратна матриця A{\displaystyle \ A} (зазвичай з дійсними елементами) така, що
- AAT=ATA=I{\displaystyle \ AA^{T}=A^{T}A=I},
де
- AT{\displaystyle \ A^{T}} — транспонована матриця до матриці A{\displaystyle \ A},
- I{\displaystyle \ I} — одинична матриця,
Еквівалентне твердження:, її обернена матриця дорівнює транспонованій матриці:
- A−1=AT.{\displaystyle \!A^{-1}=A^{T}.}
Ортогональна матриця є частковим випадком унітарної матриці.
Перелік матрицьТут зібрані найважливіші класи матриць, що використовуються в математиці, науці (в цілому) і прикладній науці (зокрема).
Під матрицею розуміється прямокутний масив чисел, що називаються елементами. Матриці мають довгу історію досліджень та застосувань, що призводить до різних способів їх класифікації. Перша група матриць задовольняє конкретним умовам і обмеженням на їх елементи, включаючи постійні матриці — матриці, що складаються з певних чисел. Важливим прикладом матриць такого виду є одинична матриця:
In=[10⋯001⋯0⋮⋮⋱⋮00⋯1].{\displaystyle I_{n}={\begin{bmatrix}1&0&\cdots &0\\0&1&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &1\end{bmatrix}}.}
Інші способи класифікації матриць пов’язані або з їх власними значеннями, або з умовами, які представляються у вигляді матричних рівнянь (співвідношень). Нарешті, в багатьох областях науки, зокрема у фізиці і в хімії, зустрічаються матриці спеціального виду, які застосовуються виключно в цих областях.
This page is based on a Wikipedia article written by authors
(here).
Text is available under the CC BY-SA 3.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.
howlingpixel.com
Властивості транспонування матриці
| ► A2 = A× |
| æ1 2ö | æ1 2ö | æ | 1×1+ 2× 0 1× 2+ 2× 3ö | æ1 | 8ö | ||||||||||
| A = ç |
|
| ÷ ×ç | ÷ = ç |
| ÷ = ç |
|
| ÷, | ||||||||
|
|
|
| ç |
|
| ÷ | ç | ÷ | ç |
| ÷ | ç |
| 9 | ÷ | ||
|
|
| è0 3 | ø | è0 3ø | è | 0 ×1+ 3× 0 0× 2+ 3×3ø | è0 | ø | |||||||||
A3 | = A2 | æ | 1 | 8ö | æ | 1 |
| 2ö | æ1 | ×1 | + | 8 × 0 1× 2+ 8× 3ö | æ1 | 26 | ö |
| ||
× A = ç |
| ÷ ×ç |
|
| ÷ = ç |
|
| ÷ = ç |
|
| ÷. < | |||||||
|
| ç | 0 | ÷ | ç | 0 |
| ÷ | ç | ×1 | + | ÷ | ç | 27 | ÷ |
| ||
|
| è | 9ø | è |
| 3ø | è0 | 9 × 0 0× 2+ 9×3ø | è0 | ø |
| |||||||
6.Транспонування матриці – перехід від матриціАm´n до матриціАTn´m, в якій рядки й стовпці помінялися місцями зі збереженням порядку їх слідування, наприклад, якщо
æ0 | -12 | 5 | ö | æ | 0 | 4ö | ||
ç |
|
| ÷ | |||||
A = ç |
|
|
| ÷, тоAT = | ç | -123 . | ||
ç | 4 | 3 | 1 | ÷ |
|
| ÷ | |
è | ø | ç | 5 | 1 | ÷ | |||
|
|
|
|
| è | ø | ||
|
|
|
|
|
|
| ||||||||||||
|
| 1) (A + B)T = AT + BT; |
| 3) (AB)T = BTAT; |
|
|
| |||||||||||
|
| 2) ( | l | A) | T | l |
| T |
|
|
| 4) (AT)T = A. |
|
|
| |||
|
|
| = |
| A ; |
|
|
|
|
|
|
|
|
|
| |||
| Приклад 1.6. Перевірити властивість (AB)T = BTAT, якщо |
|
|
| ||||||||||||||
|
|
|
|
|
|
|
| æ1 |
| 0 | 2ö |
| æ2 | 0 ö |
|
|
| |
|
|
|
|
|
|
|
|
| B = | ç | 6 | ÷ |
|
|
| |||
|
|
|
|
|
|
|
| A =ç |
|
| ÷, | ç | -3 . |
|
|
| ||
|
|
|
|
|
|
|
| ç |
| 5 | ÷ |
|
| ÷ |
|
|
| |
|
|
|
|
|
|
|
| è3 |
| 4ø |
| ç | 1 | ÷ |
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| è | 8 ø |
|
|
| |
|
|
|
|
|
|
|
| æ 4 |
| 16ö |
|
|
|
| æ 4 | 40ö | ||
| ► Оскільки A× B = ç |
|
| ÷ (приклад 1.3), то (A× B)T | = ç |
| ÷. | |||||||||||
|
|
|
|
|
|
|
| ç |
|
| ÷ |
|
|
|
| ç | 17 | ÷ |
|
|
|
|
|
|
|
| è40 | 17ø |
|
|
|
| è16 | ø | |||
|
|
|
|
|
| æ | 1 | 3ö | æ | 2 ×1+ 6×0 | +1× 2 2 | ×3+ 6×5+1×4ö | æ 4 40ö | |||||
B | T T | æ2 6 1öç |
| ÷ | ||||||||||||||
A | = ç |
|
|
| ÷ç | 0 5÷ = ç |
|
|
|
|
| ÷ | = ç |
| ÷. | |||
|
| ç |
|
|
| ÷ |
|
| ç | 0 ×1- 3×0 |
|
|
| ÷ | ç |
| ÷ | |
|
| è0 | — 3 8øç | 2 | ÷ è | +8× 2 0×3-3×5+ 8× 4ø | è16 17 | ø | ||||||||||
|
|
|
|
|
| è | 4ø |
|
|
|
|
|
|
|
|
|
| |
Рівність (AB)T = BTAT виконується.<
1.3. ВИЗНАЧНИКИ
Квадратній матриціАn´n можна поставити у відповідністьчисло-
ву характеристику – визначник (детермінант) n-го порядку. Визнач-
ник позначають так: | A |, ∆(А), ∆, ∆n, det(A) і записують у вигляді
| a11 | a12 | … | a | 1 n |
|
|
D (A )= | a 21 | a 22 | … | a | 2 n | . | (1.3) |
| … | … | … | … |
|
| |
| a n 1 | a n 2 | … | a nn |
|
| |
ДВНЗ “Українська академія банківської справи НБУ”

Мінором Мik елемента aik називається визначник(n- 1)-го поряд-
ку, отриманий із визначника n-гопорядку викреслюваннямi-горядка
та k-гостовпця. ВеличинаАik = (-1)i + kМik | називається алгебраїчним | |||||||||||||||||||
доповненням елемента aik. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
| æ1 | 0 | 3ö |
|
|
|
| 1 |
| 0 | 3 |
|
| ||
|
|
|
|
|
|
|
|
|
|
| ||||||||||
Приклад 1.7. Для матриці | ç | 5 | ÷ | маємо: D( A) = |
| 4 |
| 5 | 6 |
| , | |||||||||
A = ç4 | 6÷ |
|
|
| ||||||||||||||||
|
|
|
|
|
| ç | 8 | ÷ |
|
|
|
| 2 |
| 8 | 9 |
|
| ||
|
|
|
|
|
| è2 | 9ø |
|
|
|
|
|
|
| ||||||
M 11= |
| 5 6 |
| , M 23= |
| 1 0 |
| , | A11= (-1)1+1 M 11= M 11, |
|
|
|
| |||||||
|
|
|
|
|
|
|
| |||||||||||||
| 8 9 |
|
| 2 8 |
| A = (-1)2 +3 M | 23 | = -M | 23 | . |
|
|
| |||||||
|
|
|
|
|
|
|
|
|
| 23 |
|
|
|
|
|
|
|
| ||
Теорема Лапласа: визначник дорівнює сумі добутків елементівбудь-якогорядка чи стовпця на їх алгебраїчні доповнення
n
· ∆(А) =åaij Aij – розклад визначника за елементамиi-горядка;
j=1n
· ∆(А)= åaij Aij – розклад визначника за елементамиj-гостовпця.
i =1
Визначник першого порядку: ∆1(А) =│a11│=a11. Визначник другого порядку:
|
| ∆2(А) = |
| a11 | a12 | = a | a | 22 | — a | 21 | a . | (1.4) | ||
|
|
|
|
| a21 | a22 | 11 |
|
| 12 |
| |||
Визначник третього порядку: |
|
|
|
|
|
| ||||||||
| a11 | a12 | a13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
3 (A)= | a21 | a22 | a23 | = | a11a22a33+ a12a23a31+ a21a32a13- | (1.5) | ||||||||
| a31 | a32 | a33 |
|
| — (a31a22a13+ a21a12a33+ a32a23a11). |
| |||||||
Формулу (1.5) можна записати символічно у вигляді правила трикутника (правила Саррюса):
ДВНЗ “Українська академія банківської справи НБУ”

Властивості визначників
1. При транспонуванні визначник не змінюється:
D(A)= D(AT ).
Приклад 1.8. Обчислимо визначники:
D(A)= | 1 | — 2 | = 1×5- 3× (-2)= 11, | D(AT )= | 1 | 3 | = 1×5- (-2)×3= 11. |
| 3 | 5 |
|
| — 2 | 5 |
|
2.Якщо всі елементи деякого рядка(стовпця) визначника дорівню-
ють 0, то det(A)= 0.
3.Якщо всі елементи деякого рядка (стовпця) визначника помножити на число λ, то і визначник помножиться на це число.
Наслідок: спільний множник усіх елементів рядка (стовпця) можна винести за знак визначника.
Приклад 1.9. Обчислимо визначник:D = 2 8 = 2×15- 3×8= 6. 3 15
Винесемо за знак визначника спільні множники для елементів першого та другого рядків (2 і 3 відповідно) і обчислимо визначник:
D= 2×31 4 = 6(1×5-1× 4)= 6.
15
4.При перестановці двох рядків (стовпців) визначник змінює знак.
Приклад 1.10. Обчислимо визначники:
D = | 3 | 1 | = 3×5- 2×1= 13, | D1 | = | 2 | 5 | = 2×1- 3×5= -13. |
| 2 | 5 |
|
|
| 3 | 1 |
|
5.Визначник, що має однакові рядки (стовпці), дорівнює 0.
6.Визначник, що має пропорційні рядки (стовпці), дорівнює 0.
Приклад 1.11. Обчислимо визначник із пропорційними рядками:
D = 1 3 =1×6 -2 ×3 =0.
26
7.Сума добутків елементів будь-якогорядка (стовпця) визначника на алгебраїчні доповнення елементів іншого рядка(стовпця) дорівнює 0:
n
åaikAjk= 0 (i ¹ j).
k = 1
ДВНЗ “Українська академія банківської справи НБУ”

Приклад 1.12. Обчислимо суму добутків елементів1-горядка визна-
| 1 | 2 | 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чника D = | -1 | 4 | 5 | на алгебраїчні доповнення елементів 3-горядка: | ||||||||||||||
| 0 | 6 | 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a11A31+a12A32 | +a13A33 | 3+1 |
| 2 | 3 |
| 3+2 |
| 1 3 |
| 3+3 |
| 1 2 |
| = | |||
|
|
|
|
|
| |||||||||||||
=1×(-1) |
| 4 | 5 |
| +2×(-1) |
| -15 |
| +3×(-1) |
| -14 |
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
=(2 ×5- 4×3)- 2(1×5- (-1)×3)+ 3(1× 4- (-1)× 2)= -2-16+18= 0.
8.Визначник не зміниться, якщо до елементів будь-якогорядка (стовпця) додати відповідні елементи іншого рядка(стовпця), помножені на одне і те саме число.
Приклад 1.13. За формулою трикутника обчислимо визначник:
1 2 3
D = -14 5=1×4×1+ 2×5×0+ (-1)×1×3- (0×4×3+ 2×(-1)×1+1×5×1)=1- 3= -2.
0 1 1
Додамо до елементів першого рядка відповідні елементи третього рядка, помножені на 2 і обчислимо цей визначник:
1 4 5
D1 = -14 5=1×4×1+ 4×5×0+ (-1)×1×5- (0×4×5+ 4×(-1)×1+1×5×1)= -1-1= -2.0 1 1
Визначники співпадають: D = D1.
9.Визначник добутку двох квадратних матриць дорівнює добутку їх визначників: C =A × B Þ │C│=│A│×│B│.
Приклад 1.14. Обчислити визначник матриціC =A × B, якщо
|
|
|
| æ1 | 2 | ö | æ -1 | 5 | ö |
|
|
|
|
| |
|
|
|
| ç |
|
| ÷ | ç |
| ÷ |
|
|
|
|
|
|
|
| A = ç | 3 | 4 | ÷, | B = ç | 7 | ÷. |
|
|
|
|
| |
|
|
|
| è | ø | è-2 | ø |
|
|
|
|
| |||
► Обчислимо матрицю C і її визначник: |
|
|
|
|
|
| |||||||||
æ1 | 2ö æ-1 | 5ö æ | 1×(-1)+ 2×(-2)1×5 | + 2 | ×7 ö æ | — 5 19ö | |||||||||
C =A ×B = ç | ÷ | ×ç |
| ÷ | = ç |
|
|
|
|
|
|
| ÷ | = ç | ÷, |
ç | ÷ | ç | 7 | ÷ | ç | 3×(-1)+ 4×(-2)3×5+ 4×7 | ÷ | ç | ÷ | ||||||
è3 | 4ø è- 2 | ø è | ø è | -1143ø | |||||||||||
C= — 5 19 = -5×43- (-11)×19= -215+ 209= -6.
-11 43
ДВНЗ “Українська академія банківської справи НБУ”

Обчислимо визначники матриць A,B і застосуємо властивість 9:
A |
| = | 1 | 2 | = 4 -6 =-2, |
| B |
| = | -1 | 5 | = -7+10=3, |
| C |
| = |
| A |
| × |
| B |
| = -2×3 =-6. | < |
|
|
|
|
|
|
|
|
| |||||||||||||||||
|
|
| 3 | 4 |
|
|
|
|
| -2 | 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10.Визначник діагональної чи трикутної матриці дорівнює добутку елементів головної діагоналі.
Приклад 1.15. За формулою трикутника обчислимо визначник:
| 1 | 2 | 3 |
|
|
|
|
|
|
|
D = | 0 | 4 | 5 | = 1× 4×1+ 2×5×0+ 0×0×3- (0× 4×3+ 2×0×1+ 0×5×1)= 4. | ||||||
| 0 | 0 | 1 |
|
|
|
|
|
|
|
|
|
|
|
| 1 | 2 | 3 |
|
| |
|
|
|
|
| ||||||
За властивістю 10 маємо: D = |
| 0 | 4 | 5 |
| =1×4×1= 4. | ||||
|
|
|
|
| 0 | 0 | 1 |
|
| |
Зауваження 1. При обчисленні визначника доцільно одержати в рядку (стовпці) значну кількість нулів, а потім розкласти його за елементами цього рядка (стовпця) або перетворити визначник до трикутного вигляду і застосувати властивість (10).
Зауваження 2. Для наочності виду перетворень визначника позначимоi-йрядок- ei. Тоді записe2/2 означає ділення кожного елемен-
та 2-горядка на2 (при цьому за знак визначника виноситься множник 2), записe2 — 2e1 означає, що з кожного елемента2-горяд-
ка необхідно відняти відповідні елементи 1-горядка, помножені на 2.
1 2 3
|
|
| Приклад 1.16. Обчислити визначник3-гопорядку:2 | 2 | 6 . | |||
|
|
|
| 2 | 0 | 4 | ||
|
|
| ► Обчислимо визначник чотирма способами: |
|
| |||
1) за формулою (1.5) (за правилом трикутника): |
|
| ||||||
|
| 1 | 2 | 3 |
| =1× 2× 4+ 2× 6× 2+ 2× 0×3- (3× 2× 2+ 2× 2× 4+ 6× 0×1)= 32- 28= 4; | ||
|
| |||||||
|
| 2 | 2 | 6 |
| |||
|
| 2 | 0 | 4 |
|
|
|
|
2) розкладом за елементами 2-гостовпця, що містить 0:
1 | 2 | 3 | 1+2 |
| 2 | 6 |
| 2+2 |
| 1 | 3 |
| 3+2 |
| 1 | 3 |
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
2 | 2 | 6 |
|
|
|
|
| = -2(8 | -12) | +2(4-6) | = 4; | |||||||||
=2×(-1) |
| 2 | 4 |
| +2×(-1) |
| 2 | 4 |
| +0×(-1) |
| 2 | 6 | |||||||
2 | 0 | 4 |
|
|
|
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ДВНЗ “Українська академія банківської справи НБУ”

3) розкладом за елементами 1-гостовпця з одержанням у ньому нулів:
| 1 | 2 | 3 |
| ì | ü |
| 1 | 2 | 3 |
| ì | ü |
| 1 | 2 | 3 |
|
| -1 | 0 |
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||
| 2 | 2 | 6 |
| ï | ï | =2×21 | 1 | 3 |
| ï | ï | =4 | 0 | -1 | 0 | =4×1×(-1 | 1+1 | =4(1-0) | =4; | |||
|
| =íe2 | / 2ý |
| =íe2 | -e1ý | ) | -2 | -1 | ||||||||||||||
| 2 | 0 | 4 |
| ï | ï | 1 | 0 | 2 |
| ï | ï |
| 0 | -2 | -1 |
|
|
|
| |||
|
| îe3 | / 2þ |
| îe3 | -e1þ |
|
|
|
|
|
|
| ||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4) зведенням визначника до трикутного вигляду:
1 | 2 | 3 |
| 1 | 2 | 3 | = {e3 -2e2 }=4 | 1 | 2 | 3 |
|
2 | 2 | 6 | ={див. спосіб 3}= 4 | 0 | -1 | 0 | 0 | -1 | 0 | = 4.< | |
2 | 0 | 4 |
| 0 | — 2 | -1 |
| 0 | 0 | -1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Зауваження. Правило трикутника (1.5) застосовується лише для обчислення визначниківтретього порядку, а способи2-4- для обчислення визначниківбудь-якого порядку. Спосіб 2 дозволяє звести обчисленняодного визначникаn-гопорядку до обчисленняn визначників (n –1)-гопорядку, а спосіб 3 – до обчисленняодного визначника (n –1)-гопорядку. Найбільш економічним для обчислення визначників порядкуn > 3 є спосіб 4.
Приклад 1.17. Обчислити визначник4-гопорядку:
2 1 1 8
1 — 3- 6 9.
0 2 2 — 5
1 4 6 0
►Обчислимо визначник трьома способами:
1)розкладом за елементами 1-гостовпця, що містить 0:
| 2 | 1 | 1 | 8 |
|
|
|
|
| — 3 | — 6 | 9 |
| 1 | 1 | 8 |
| |||
|
|
|
|
|
|
|
| |||||||||||||
| 1 | — 3 | — 6 | 9 | = 2×(-1)1+1 | +1×(-1)2+1 |
| |||||||||||||
D = | 2 | 2 | — 5 | 2 | 2 | — 5 | + 0 + | |||||||||||||
0 | 2 | 2 | — 5 | |||||||||||||||||
| 1 | 4 | 6 | 0 |
|
|
|
|
| 4 | 6 | 0 |
| 4 | 6 | 0 |
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
|
| +1×(-1)4+1 |
| 1 | 1 | 8 |
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
|
|
| — 3 | — 6 | 9 |
|
| = 2[0+120+108- (72+ 90- 0)]- |
| |||||||||||
|
|
|
|
|
| 2 | 2 | — 5 |
|
|
|
|
|
|
|
|
|
| ||
-[0- 20+96-(64-30+0)]-[30+18- 48-(-96+18+15)]= 27;
ДВНЗ “Українська академія банківської справи НБУ”
studfiles.net
WikiZero — Транспонована матриця
Wikipedia open wikipedia design.Транспонована матриця — матриця AT{\displaystyle A^{T}}, що виникає з матриці A{\displaystyle A} в результаті унарної операції транспонування: заміни її рядків на стовпчики.
Формально, транспонована матриця AT=(bij){\displaystyle \ A^{T}=(b_{ij})} для матриці A=(aij){\displaystyle \ A=(a_{ij})} визначається як
- bij=aji,i=1,n¯,j=1,m¯.{\displaystyle \ b_{ij}=a_{ji},\quad i={\overline {1,n}},\quad j={\overline {1,m}}.}
Наприклад:
- [1234]T=[1324]{\displaystyle {\begin{bmatrix}1&2\\3&4\end{bmatrix}}^{\mathrm {T} }={\begin{bmatrix}1&3\\2&4\end{bmatrix}}} та [123456]T=[135246]{\displaystyle {\begin{bmatrix}1&2\\3&4\\5&6\end{bmatrix}}^{\mathrm {T} }={\begin{bmatrix}1&3&5\\2&4&6\end{bmatrix}}}
- (AT)T=A{\displaystyle \ (A^{\mathrm {T} })^{\mathrm {T} }=A} — операція транспонування є інволюцією.
- (rA)T=rAT
www.wikizero.com
Властивості транспонування матриці
| ► A2 = A× |
| æ1 2ö | æ1 2ö | æ | 1×1+ 2× 0 1× 2+ 2× 3ö | æ1 | 8ö | ||||||||||
| A = ç |
|
| ÷ ×ç | ÷ = ç |
| ÷ = ç |
|
| ÷, | ||||||||
|
|
|
| ç |
|
| ÷ | ç | ÷ | ç |
| ÷ | ç |
| 9 | ÷ | ||
|
|
|
| è0 3 | ø | è0 3ø | è | 0 ×1+ 3× 0 0× 2+ 3×3ø | è0 | ø | ||||||||
A3 | = A2 | æ | 1 | 8ö | æ | 1 |
| 2ö | æ1 | ×1 | + | 8 × 0 1× 2+ 8× 3ö | æ1 | 26 | ö |
| ||
× A = ç |
| ÷ ×ç |
|
| ÷ = ç |
|
| ÷ = ç |
|
| ÷. < | |||||||
|
| ç | 0 | ÷ | ç | 0 |
| ÷ | ç | ×1 | + | ÷ | ç | 27 | ÷ |
| ||
|
| è | 9ø | è |
| 3ø | è0 | 9 × 0 0× 2+ 9×3ø | è0 | ø |
| |||||||
6.Транспонування матриці – перехід від матриціАm´n до матриціАTn´m, в якій рядки й стовпці помінялися місцями зі збереженням порядку їх слідування, наприклад, якщо
æ0 | -12 | 5 | ö | æ | 0 | 4ö | ||
ç |
|
| ÷ | |||||
A = ç |
|
|
| ÷, тоAT = | ç | -123 . | ||
ç | 4 | 3 | 1 | ÷ |
|
| ÷ | |
è | ø | ç | 5 | 1 | ÷ | |||
|
|
|
|
| è | ø | ||
|
|
|
|
|
|
| ||||||||||||
|
| 1) (A + B)T = AT + BT; |
| 3) (AB)T = BTAT; |
|
|
| |||||||||||
|
| 2) ( | l | A) | T | l |
| T |
|
|
| 4) (AT)T = A. |
|
|
| |||
|
|
| = |
| A ; |
|
|
|
|
|
|
|
|
|
| |||
| Приклад 1.6. Перевірити властивість (AB)T = BTAT, якщо |
|
|
| ||||||||||||||
|
|
|
|
|
|
|
| æ1 |
| 0 | 2ö |
| æ2 | 0 ö |
|
|
| |
|
|
|
|
|
|
|
|
| B = | ç | 6 | ÷ |
|
|
| |||
|
|
|
|
|
|
|
| A =ç |
|
| ÷, | ç | -3 . |
|
|
| ||
|
|
|
|
|
|
|
| ç |
| 5 | ÷ |
|
| ÷ |
|
|
| |
|
|
|
|
|
|
|
| è3 |
| 4ø |
| ç | 1 | ÷ |
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| è | 8 ø |
|
|
| |
|
|
|
|
|
|
|
| æ 4 |
| 16ö |
|
|
|
| æ 4 | 40ö | ||
| ► Оскільки A× B = ç |
|
| ÷ (приклад 1.3), то (A× B)T | = ç |
| ÷. | |||||||||||
|
|
|
|
|
|
|
| ç |
|
| ÷ |
|
|
|
| ç | 17 | ÷ |
|
|
|
|
|
|
|
| è40 | 17ø |
|
|
|
| è16 | ø | |||
|
|
|
|
|
| æ | 1 | 3ö | æ | 2 ×1+ 6×0 | +1× 2 2 | ×3+ 6×5+1×4ö | æ 4 40ö | |||||
B | T T | æ2 6 1öç |
| ÷ | ||||||||||||||
A | = ç |
|
|
| ÷ç | 0 5÷ = ç |
|
|
|
|
| ÷ | = ç |
| ÷. | |||
|
| ç |
|
|
| ÷ |
|
| ç | 0 ×1- 3×0 |
|
|
| ÷ | ç |
| ÷ | |
|
| è0 | — 3 8øç | 2 | ÷ è | +8× 2 0×3-3×5+ 8× 4ø | è16 17 | ø | ||||||||||
|
|
|
|
|
| è | 4ø |
|
|
|
|
|
|
|
|
|
| |
Рівність (AB)T = BTAT виконується.<
1.3. ВИЗНАЧНИКИ
Квадратній матриціАn´n можна поставити у відповідністьчисло-
ву характеристику – визначник (детермінант) n-го порядку. Визнач-
ник позначають так: | A |, ∆(А), ∆, ∆n, det(A) і записують у вигляді
| a11 | a12 | … | a | 1 n |
|
|
D (A )= | a 21 | a 22 | … | a | 2 n | . | (1.3) |
| … | … | … | … |
|
| |
| a n 1 | a n 2 | … | a nn |
|
| |
ДВНЗ “Українська академія банківської справи НБУ”

Мінором Мik елемента aik називається визначник(n- 1)-го поряд-
ку, отриманий із визначника n-гопорядку викреслюваннямi-горядка
та k-гостовпця. ВеличинаАik = (-1)i + kМik | називається алгебраїчним | |||||||||||||||||||
доповненням елемента aik. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
| æ1 | 0 | 3ö |
|
|
|
| 1 |
| 0 | 3 |
|
| ||
|
|
|
|
|
|
|
|
|
|
| ||||||||||
Приклад 1.7. Для матриці | ç | 5 | ÷ | маємо: D( A) = |
| 4 |
| 5 | 6 |
| , | |||||||||
A = ç4 | 6÷ |
|
|
| ||||||||||||||||
|
|
|
|
|
| ç | 8 | ÷ |
|
|
|
| 2 |
| 8 | 9 |
|
| ||
|
|
|
|
|
| è2 | 9ø |
|
|
|
|
|
|
| ||||||
M 11= |
| 5 6 |
| , M 23= |
| 1 0 |
| , | A11= (-1)1+1 M 11= M 11, |
|
|
|
| |||||||
|
|
|
|
|
|
|
| |||||||||||||
| 8 9 |
|
| 2 8 |
| A = (-1)2 +3 M | 23 | = -M | 23 | . |
|
|
| |||||||
|
|
|
|
|
|
|
|
|
| 23 |
|
|
|
|
|
|
|
| ||
Теорема Лапласа: визначник дорівнює сумі добутків елементівбудь-якогорядка чи стовпця на їх алгебраїчні доповнення
n
· ∆(А) =åaij Aij – розклад визначника за елементамиi-горядка;
j=1n
· ∆(А)= åaij Aij – розклад визначника за елементамиj-гостовпця.
i =1
Визначник першого порядку: ∆1(А) =│a11│=a11. Визначник другого порядку:
|
| ∆2(А) = |
| a11 | a12 | = a | a | 22 | — a | 21 | a . | (1.4) | ||
|
|
|
|
| a21 | a22 | 11 |
|
| 12 |
| |||
Визначник третього порядку: |
|
|
|
|
|
| ||||||||
| a11 | a12 | a13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
3 (A)= | a21 | a22 | a23 | = | a11a22a33+ a12a23a31+ a21a32a13- | (1.5) | ||||||||
| a31 | a32 | a33 |
|
| — (a31a22a13+ a21a12a33+ a32a23a11). |
| |||||||
Формулу (1.5) можна записати символічно у вигляді правила трикутника (правила Саррюса):
ДВНЗ “Українська академія банківської справи НБУ”

Властивості визначників
1. При транспонуванні визначник не змінюється:
D(A)= D(AT ).
Приклад 1.8. Обчислимо визначники:
D(A)= | 1 | — 2 | = 1×5- 3× (-2)= 11, | D(AT )= | 1 | 3 | = 1×5- (-2)×3= 11. |
| 3 | 5 |
|
| — 2 | 5 |
|
2.Якщо всі елементи деякого рядка(стовпця) визначника дорівню-
ють 0, то det(A)= 0.
3.Якщо всі елементи деякого рядка (стовпця) визначника помножити на число λ, то і визначник помножиться на це число.
Наслідок: спільний множник усіх елементів рядка (стовпця) можна винести за знак визначника.
Приклад 1.9. Обчислимо визначник:D = 2 8 = 2×15- 3×8= 6. 3 15
Винесемо за знак визначника спільні множники для елементів першого та другого рядків (2 і 3 відповідно) і обчислимо визначник:
D= 2×31 4 = 6(1×5-1× 4)= 6.
15
4.При перестановці двох рядків (стовпців) визначник змінює знак.
Приклад 1.10. Обчислимо визначники:
D = | 3 | 1 | = 3×5- 2×1= 13, | D1 | = | 2 | 5 | = 2×1- 3×5= -13. |
| 2 | 5 |
|
|
| 3 | 1 |
|
5.Визначник, що має однакові рядки (стовпці), дорівнює 0.
6.Визначник, що має пропорційні рядки (стовпці), дорівнює 0.
Приклад 1.11. Обчислимо визначник із пропорційними рядками:
D = 1 3 =1×6 -2 ×3 =0.
26
7.Сума добутків елементів будь-якогорядка (стовпця) визначника на алгебраїчні доповнення елементів іншого рядка(стовпця) дорівнює 0:
n
åaikAjk= 0 (i ¹ j).
k = 1
ДВНЗ “Українська академія банківської справи НБУ”

Приклад 1.12. Обчислимо суму добутків елементів1-горядка визна-
| 1 | 2 | 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чника D = | -1 | 4 | 5 | на алгебраїчні доповнення елементів 3-горядка: | ||||||||||||||
| 0 | 6 | 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a11A31+a12A32 | +a13A33 | 3+1 |
| 2 | 3 |
| 3+2 |
| 1 3 |
| 3+3 |
| 1 2 |
| = | |||
|
|
|
|
|
| |||||||||||||
=1×(-1) |
| 4 | 5 |
| +2×(-1) |
| -15 |
| +3×(-1) |
| -14 |
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
=(2 ×5- 4×3)- 2(1×5- (-1)×3)+ 3(1× 4- (-1)× 2)= -2-16+18= 0.
8.Визначник не зміниться, якщо до елементів будь-якогорядка (стовпця) додати відповідні елементи іншого рядка(стовпця), помножені на одне і те саме число.
Приклад 1.13. За формулою трикутника обчислимо визначник:
1 2 3
D = -14 5=1×4×1+ 2×5×0+ (-1)×1×3- (0×4×3+ 2×(-1)×1+1×5×1)=1- 3= -2.
0 1 1
Додамо до елементів першого рядка відповідні елементи третього рядка, помножені на 2 і обчислимо цей визначник:
1 4 5
D1 = -14 5=1×4×1+ 4×5×0+ (-1)×1×5- (0×4×5+ 4×(-1)×1+1×5×1)= -1-1= -2.0 1 1
Визначники співпадають: D = D1.
9.Визначник добутку двох квадратних матриць дорівнює добутку їх визначників: C =A × B Þ │C│=│A│×│B│.
Приклад 1.14. Обчислити визначник матриціC =A × B, якщо
|
|
|
| æ1 | 2 | ö | æ -1 | 5 | ö |
|
|
|
|
| |
|
|
|
| ç |
|
| ÷ | ç |
| ÷ |
|
|
|
|
|
|
|
| A = ç | 3 | 4 | ÷, | B = ç | 7 | ÷. |
|
|
|
|
| |
|
|
|
| è | ø | è-2 | ø |
|
|
|
|
| |||
► Обчислимо матрицю C і її визначник: |
|
|
|
|
|
| |||||||||
æ1 | 2ö æ-1 | 5ö æ | 1×(-1)+ 2×(-2)1×5 | + 2 | ×7 ö æ | — 5 19ö | |||||||||
C =A ×B = ç | ÷ | ×ç |
| ÷ | = ç |
|
|
|
|
|
|
| ÷ | = ç | ÷, |
ç | ÷ | ç | 7 | ÷ | ç | 3×(-1)+ 4×(-2)3×5+ 4×7 | ÷ | ç | ÷ | ||||||
è3 | 4ø è- 2 | ø è | ø è | -1143ø | |||||||||||
C= — 5 19 = -5×43- (-11)×19= -215+ 209= -6.
-11 43
ДВНЗ “Українська академія банківської справи НБУ”

Обчислимо визначники матриць A,B і застосуємо властивість 9:
A |
| = | 1 | 2 | = 4 -6 =-2, |
| B |
| = | -1 | 5 | = -7+10=3, |
| C |
| = |
| A |
| × |
| B |
| = -2×3 =-6. | < |
|
|
|
|
|
|
|
|
| |||||||||||||||||
|
|
| 3 | 4 |
|
|
|
|
| -2 | 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10.Визначник діагональної чи трикутної матриці дорівнює добутку елементів головної діагоналі.
Приклад 1.15. За формулою трикутника обчислимо визначник:
| 1 | 2 | 3 |
|
|
|
|
|
|
|
D = | 0 | 4 | 5 | = 1× 4×1+ 2×5×0+ 0×0×3- (0× 4×3+ 2×0×1+ 0×5×1)= 4. | ||||||
| 0 | 0 | 1 |
|
|
|
|
|
|
|
|
|
|
|
| 1 | 2 | 3 |
|
| |
|
|
|
|
| ||||||
За властивістю 10 маємо: D = |
| 0 | 4 | 5 |
| =1×4×1= 4. | ||||
|
|
|
|
| 0 | 0 | 1 |
|
| |
Зауваження 1. При обчисленні визначника доцільно одержати в рядку (стовпці) значну кількість нулів, а потім розкласти його за елементами цього рядка (стовпця) або перетворити визначник до трикутного вигляду і застосувати властивість (10).
Зауваження 2. Для наочності виду перетворень визначника позначимоi-йрядок- ei. Тоді записe2/2 означає ділення кожного елемен-
та 2-горядка на2 (при цьому за знак визначника виноситься множник 2), записe2 — 2e1 означає, що з кожного елемента2-горяд-
ка необхідно відняти відповідні елементи 1-горядка, помножені на 2.
1 2 3
|
|
| Приклад 1.16. Обчислити визначник3-гопорядку:2 | 2 | 6 . | |||
|
|
|
| 2 | 0 | 4 | ||
|
|
| ► Обчислимо визначник чотирма способами: |
|
| |||
1) за формулою (1.5) (за правилом трикутника): |
|
| ||||||
|
| 1 | 2 | 3 |
| =1× 2× 4+ 2× 6× 2+ 2× 0×3- (3× 2× 2+ 2× 2× 4+ 6× 0×1)= 32- 28= 4; | ||
|
| |||||||
|
| 2 | 2 | 6 |
| |||
|
| 2 | 0 | 4 |
|
|
|
|
2) розкладом за елементами 2-гостовпця, що містить 0:
1 | 2 | 3 | 1+2 |
| 2 | 6 |
| 2+2 |
| 1 | 3 |
| 3+2 |
| 1 | 3 |
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
2 | 2 | 6 |
|
|
|
|
| = -2(8 | -12) | +2(4-6) | = 4; | |||||||||
=2×(-1) |
| 2 | 4 |
| +2×(-1) |
| 2 | 4 |
| +0×(-1) |
| 2 | 6 | |||||||
2 | 0 | 4 |
|
|
|
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ДВНЗ “Українська академія банківської справи НБУ”

3) розкладом за елементами 1-гостовпця з одержанням у ньому нулів:
| 1 | 2 | 3 |
| ì | ü |
| 1 | 2 | 3 |
| ì | ü |
| 1 | 2 | 3 |
|
| -1 | 0 |
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||
| 2 | 2 | 6 |
| ï | ï | =2×21 | 1 | 3 |
| ï | ï | =4 | 0 | -1 | 0 | =4×1×(-1 | 1+1 | =4(1-0) | =4; | |||
|
| =íe2 | / 2ý |
| =íe2 | -e1ý | ) | -2 | -1 | ||||||||||||||
| 2 | 0 | 4 |
| ï | ï | 1 | 0 | 2 |
| ï | ï |
| 0 | -2 | -1 |
|
|
|
| |||
|
| îe3 | / 2þ |
| îe3 | -e1þ |
|
|
|
|
|
|
| ||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4) зведенням визначника до трикутного вигляду:
1 | 2 | 3 |
| 1 | 2 | 3 | = {e3 -2e2 }=4 | 1 | 2 | 3 |
|
2 | 2 | 6 | ={див. спосіб 3}= 4 | 0 | -1 | 0 | 0 | -1 | 0 | = 4.< | |
2 | 0 | 4 |
| 0 | — 2 | -1 |
| 0 | 0 | -1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Зауваження. Правило трикутника (1.5) застосовується лише для обчислення визначниківтретього порядку, а способи2-4- для обчислення визначниківбудь-якого порядку. Спосіб 2 дозволяє звести обчисленняодного визначникаn-гопорядку до обчисленняn визначників (n –1)-гопорядку, а спосіб 3 – до обчисленняодного визначника (n –1)-гопорядку. Найбільш економічним для обчислення визначників порядкуn > 3 є спосіб 4.
Приклад 1.17. Обчислити визначник4-гопорядку:
2 1 1 8
1 — 3- 6 9.
0 2 2 — 5
1 4 6 0
►Обчислимо визначник трьома способами:
1)розкладом за елементами 1-гостовпця, що містить 0:
| 2 | 1 | 1 | 8 |
|
|
|
|
| — 3 | — 6 | 9 |
| 1 | 1 | 8 |
| |||
|
|
|
|
|
|
|
| |||||||||||||
| 1 | — 3 | — 6 | 9 | = 2×(-1)1+1 | +1×(-1)2+1 |
| |||||||||||||
D = | 2 | 2 | — 5 | 2 | 2 | — 5 | + 0 + | |||||||||||||
0 | 2 | 2 | — 5 | |||||||||||||||||
| 1 | 4 | 6 | 0 |
|
|
|
|
| 4 | 6 | 0 |
| 4 | 6 | 0 |
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
|
| +1×(-1)4+1 |
| 1 | 1 | 8 |
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
|
|
| — 3 | — 6 | 9 |
|
| = 2[0+120+108- (72+ 90- 0)]- |
| |||||||||||
|
|
|
|
|
| 2 | 2 | — 5 |
|
|
|
|
|
|
|
|
|
| ||
-[0- 20+96-(64-30+0)]-[30+18- 48-(-96+18+15)]= 27;
ДВНЗ “Українська академія банківської справи НБУ”
studfiles.net
Основні властивості транспонування матриці
1) | |
2) | |
3) | ; |
4) | . |
Наприклад,
якщо  ,
то
,
то .
.
Приклад 1.3. | Для
матриць |
Розв’язання. Запишемо
транспоновану матрицю 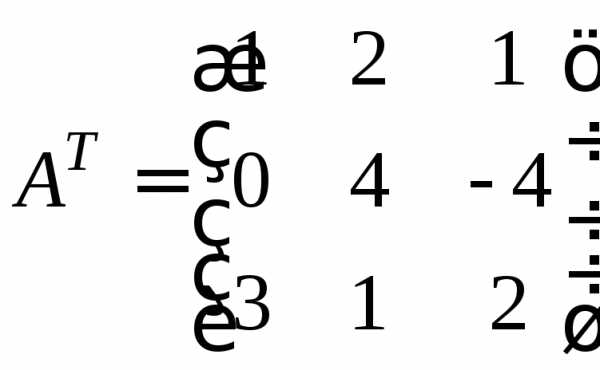 .
Тоді
.
Тоді
.
5. | Знаходження оберненої матриці |
Матрицю , , (1.1) називають оберненою
матрицею до матриці |
Зауваження. | Зрозуміло,
що матриця |
1.2. Визначники та способи їх обчислення
Квадратній
матриці можна поставити у відповідність
число, яке називають
її визначником (або детермінантом)
і позначають:  або
або  .
.
Правило обчислення визначника залежить від його порядку.
Визначником другого порядку називають число, яке обчислюють за правилом: |
Згідно формули (1.2) визначник другого порядку дорівнює різниці добутку елементів головної діагоналі і добутку елементів допоміжної діагоналі.
Рисунок 1.1 – Обчислення визначника другого порядку
Наприклад,
Визначником третього порядку називають число, яке обчислюють за правилом: . (1.3) |
Визначник третього порядку можна обчислювати різними способами. Наведемо три з них.
1. | Метод трикутників (правило Саррюса) |
Якщо елементи визначника позначити точками, то три доданки зі знаком «+» складають з елементів, що лежать на головній діагоналі та у вершинах трикутників, одна з сторін яких паралельна головній діагоналі. Аналогічно співмножники трьох доданків із знаком «» лежать на допоміжній діагоналі і у вершинах трикутників, одна з сторін яких паралельна їй.
Рисунок 1.2 – Метод трикутників
Наприклад, .
2. | Метод дописування стовпців |
Праворуч від визначника дописують перші два стовпці. Із знаком «+» записують доданки, співмножники яких містяться на головній діагоналі та на діагоналях, паралельних їй. Доданки із знаком «» утворюють з елементів, що розташовані на допоміжній діагоналі і на діагоналях паралельних їй.
Рисунок 1.3 – Метод дописування стовпців.
Наприклад, .
3. | Метод розкладання (універсальний) |
Значення визначника обчислюють як суму добутків всіх елементів рядка (або стовпця) на (-1) в ступені суми індексів елемент4у на визначник, меншого на одиницю порядку, який залишається після викреслювання рядку та стовпця, на перетині яких стоїть елемент.
Для обчислення визначника третього порядку розкладення за першим рядком має вигляд:
Одержані визначники другого порядку знаходять за відомим правилом.
Наприклад,
розкладаючи за другим рядком, маємо: 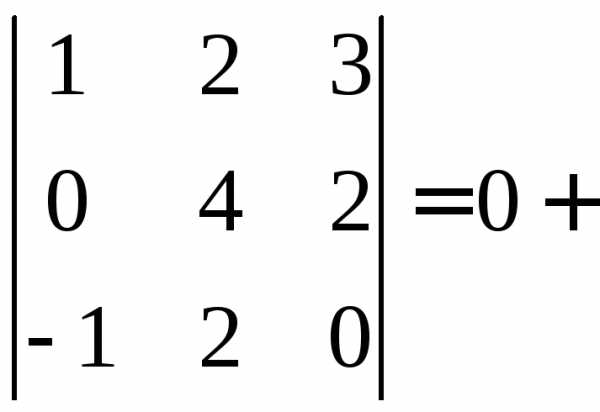 4.
4.
Зауваження. Для розкладання зручно вибирати рядок чи стовпець, в якому є найбільша кількість нульових елементів.
Метод розкладення є універсальним методом обчислення визначників, його можна застосовувати до обчислення визначників будь-якого порядку.
З
елементів будь-якої матриці  можна скласти різні визначники, зберігаючи
порядок елементів матриці
можна скласти різні визначники, зберігаючи
порядок елементів матриці .
.
Мінором порядку |
Вважають, що
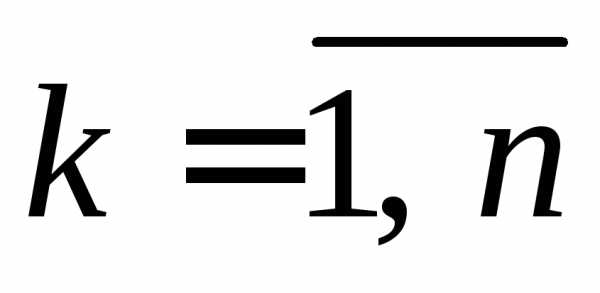 ,
якщо
,
якщо 
квадратна матриця порядку
квадратна матриця порядку  ;
;
,
якщо 
прямокутна матриця порядку
прямокутна матриця порядку 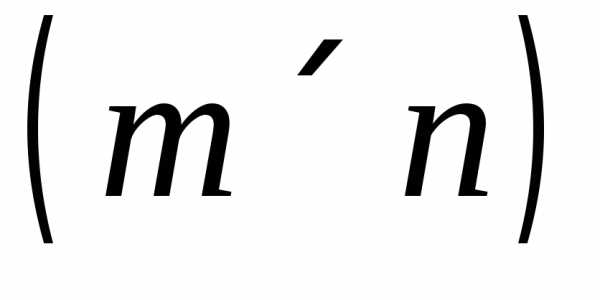 .
.
Визначники
високих порядків 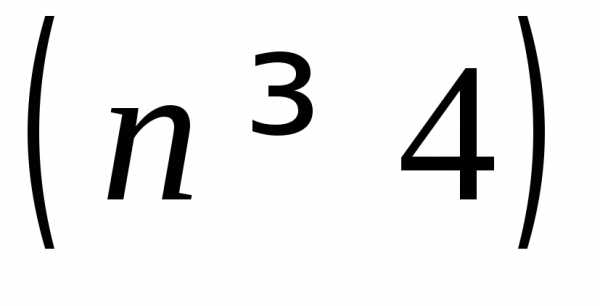 обчислюють, знижуючи їх порядок за
теоремою Лапласа.
обчислюють, знижуючи їх порядок за
теоремою Лапласа.
Теорема 1.1. (Лапласа) | Визначник дорівнює сумі добутків елементів будь-якого рядка (стовпця) на їх алгебраїчні доповнення: , (1.4) . (1.5) |
Метод розкладання є застосуванням теореми Лапласа до обчислення визначника третього порядку.
studfiles.net
Транспонування матриць
Матриця, отримана з даної заміною кожного її рядка (стовпчика) стовпчиком (рядком) з тим же номером, називається транспонованою до даної.
Матрицю, транспоновану до матриці , позначають .
Операція знаходження матриці, транспонованої до даної, називається транспонуванням матриці.
Якщо – матриця розмірів , то має розміри .
Справедливі наступні властивості:
1. ;
2. ;
3. , де і – матриці однакових розмірів;
4. , де матриця узгоджена з матрицею .
Приклад 1.4.Знайти матрицю, транспоновану до матриці
.
Розв’язок.
. t
Теоретичні питання
1.1. Що називається матрицею розмірів ?
1.2. Які матриці називаються рівними?
1.3. Яка матриця називається квадратною?
1.4. Яка матриця називається діагональною?
1.5. Яка матриця називається одиничною?
1.6. Яка матриця називається трикутною?
1.7. Яка матриця називається трапецієвидною?
1.8. Яка матриця називається нульовою?
1.9. Які дії над матрицями називаються лінійними?
1.10. Які властивості лінійних операцій над матрицями?
1.11. Які матриці називаються узгодженими?
1.12. Що називається добутком матриці А на матрицю В?
1.13. Які властивості добутку матриць?
1.14. Які перетворення матриць називають елементарними?
1.15. Яка матриця називається транспонованою до даної?
1.16. Які властивості має операція транспонування матриці?
Задачі та вправи
1.1. Вказати розміри матриць:
а) ; б) ; в) ; г) .
1.2. Чому рівні в матриці А елементи , якщо
?
1.3. Вказати, які з матриць
;
є: а) діагональними; б) одиничними; в) трикутними; г) трапецієвидними?
1.4. Знайти матрицю Х, якщо
а) ; б) .
1.5. Знайти:
,
де .
Розв’язок. Обчислення розіб’ємо на окремі дії:
1)
;
2) ;
3) ;
4) ;
5) ;
6) ;
7) .t
1.6. Знайти добуток матриць:
а) ; б) ; в) .
5rik.ru
Практичне заняття № 1 Тема: Матриці. Дії з матрицями
Матрицею розміру (розмірності) 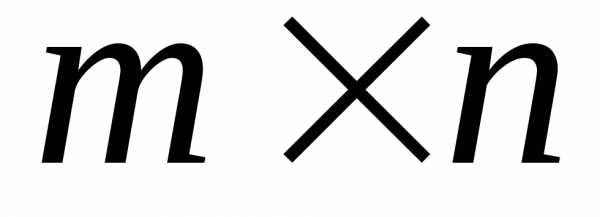 ,
де
,
де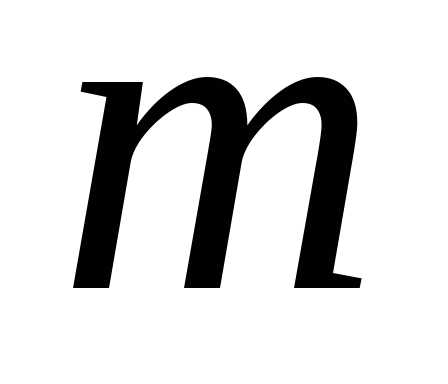 – число рядків,
– число рядків,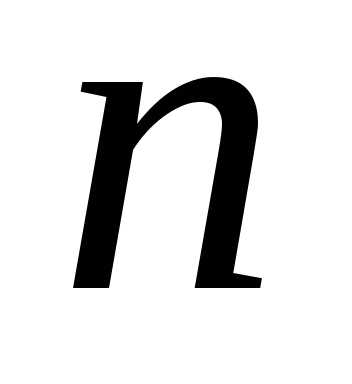 – число стовпців, називається прямокутна
таблиця з
– число стовпців, називається прямокутна
таблиця з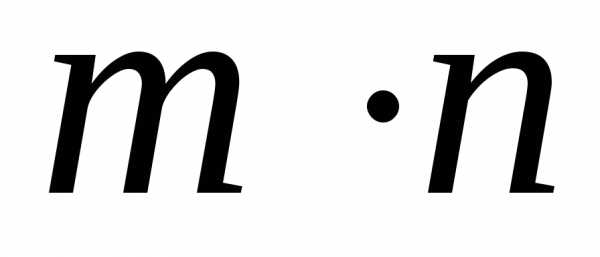 елементів деякої множини. Якщо елементами
матриці є числа, то матриця називається
числовою, якщо вектори, то – векторною,
якщо функції, то – функціональною.
Розглянемо числову матрицю. Місце
кожного елемента
елементів деякої множини. Якщо елементами
матриці є числа, то матриця називається
числовою, якщо вектори, то – векторною,
якщо функції, то – функціональною.
Розглянемо числову матрицю. Місце
кожного елемента матриці однозначно визначається номером
рядка
матриці однозначно визначається номером
рядка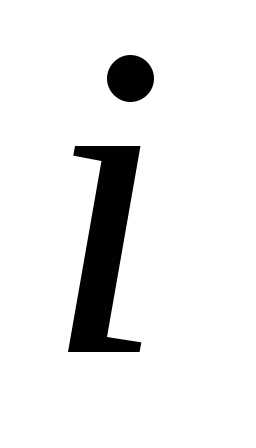 й стовпця
й стовпця ,
на перетині яких він знаходиться.
Позначають:
,
на перетині яких він знаходиться.
Позначають:
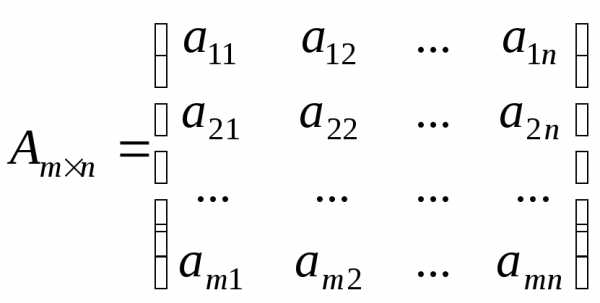 або
або 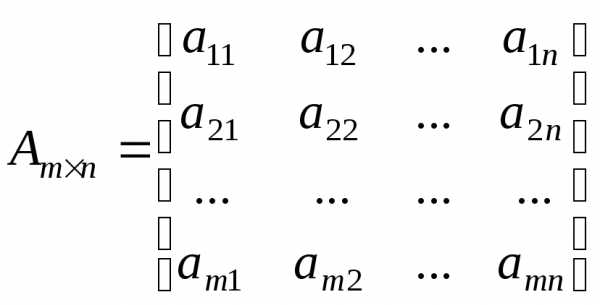 ,
,
або .
Матриця,
у якої число рядків дорівнює числу
стовпців, називається квадратною (квадратну матрицю розмірності  називають матрицею
називають матрицею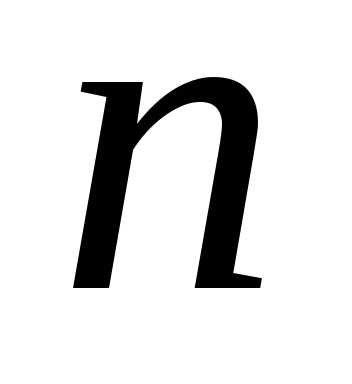 -го
порядку і позначають
-го
порядку і позначають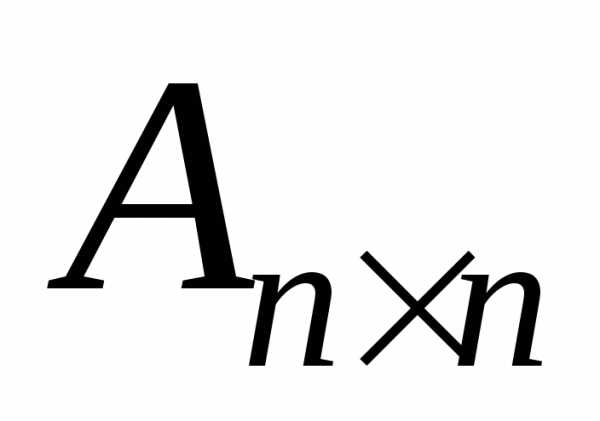 або
або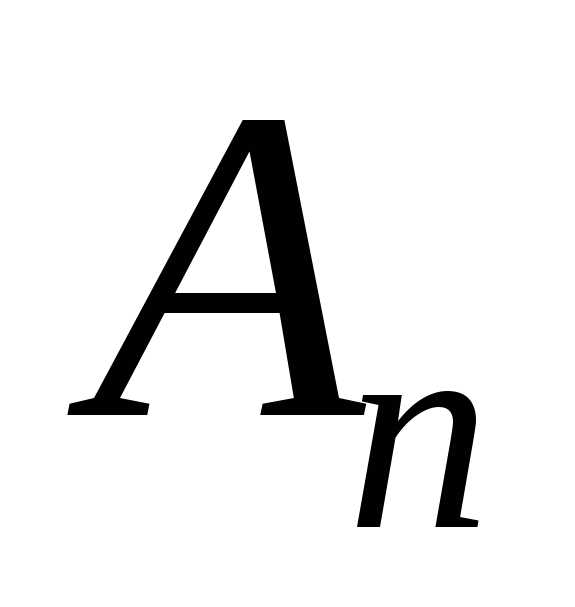 ).
).
Елементи  ,
,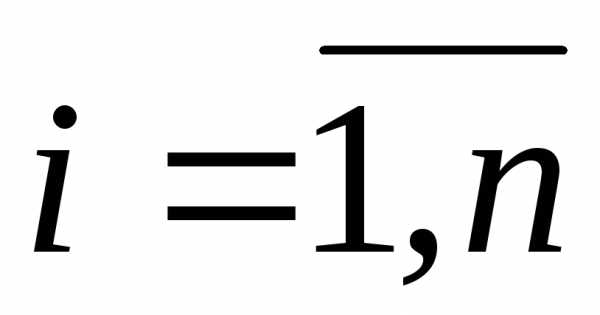 ,
у яких номери рядка й стовпця, на перетині
яких вони знаходяться, співпадають,
утворюютьголовну
діагональ.
,
у яких номери рядка й стовпця, на перетині
яких вони знаходяться, співпадають,
утворюютьголовну
діагональ.
Квадратна матриця, у якої всі елементи, окрім головної діагоналі, дорівнюють нулю, називається діагональною.
Діагональна матриця, у якої всі елементи головної діагоналі дорівнюють одиниці, називається одиничною. Позначають:
.
Квадратна матриця називається верхньотрикутною (нижньотрикутною), якщо всі елементи, розташовані нижче (вище) головної діагоналі, дорівнюють нулю.
Приклад. Верхньотрикутна 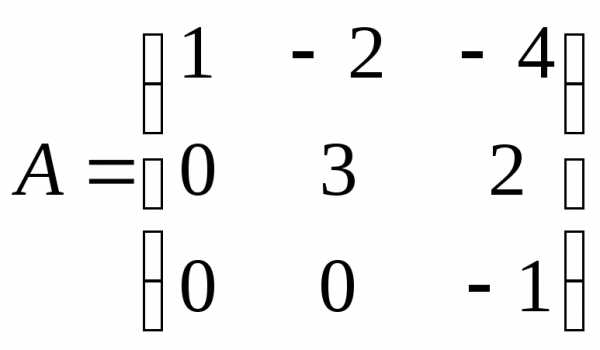 та нижньотрикутна
та нижньотрикутна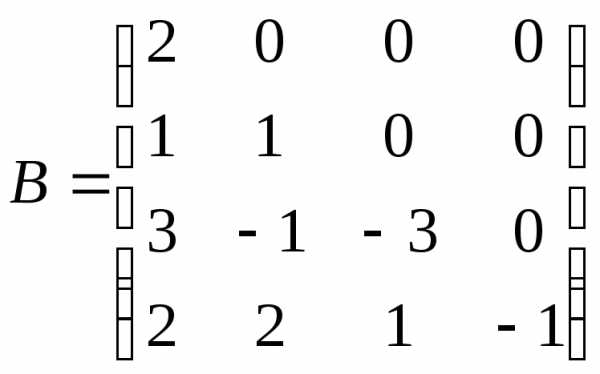 матриці.
матриці.
Квадратна матриця, всі елементи якої дорівнюють нулю, називається нульовою і позначається:
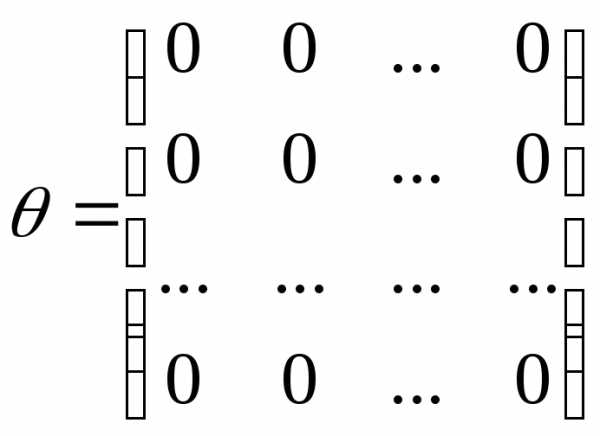 .
.
Матриці 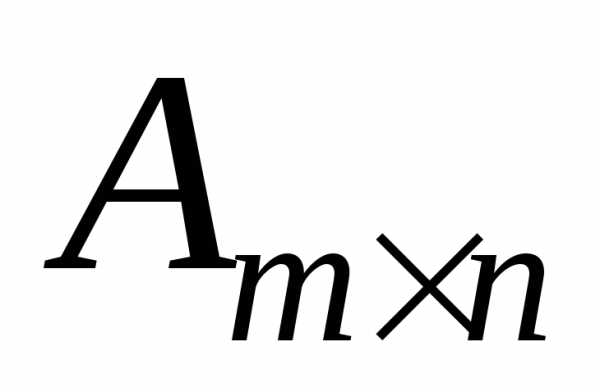 і
і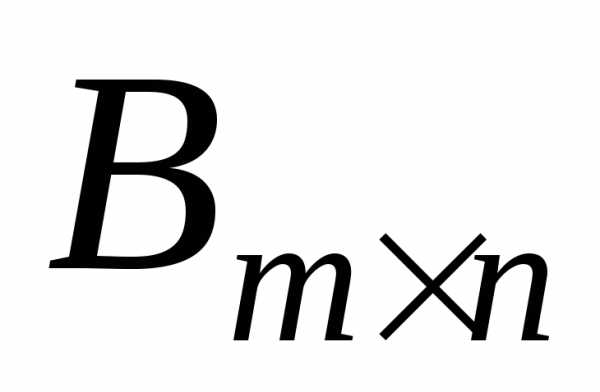 називаютьсярівними,
якщо вони мають однакові розміри й рівні
відповідні елементи, тобто
називаютьсярівними,
якщо вони мають однакові розміри й рівні
відповідні елементи, тобто
 ,
якщо
,
якщо 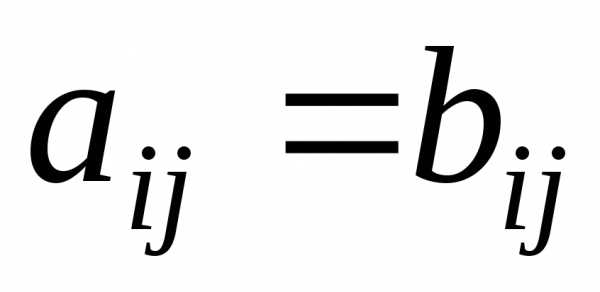 ,
де
,
де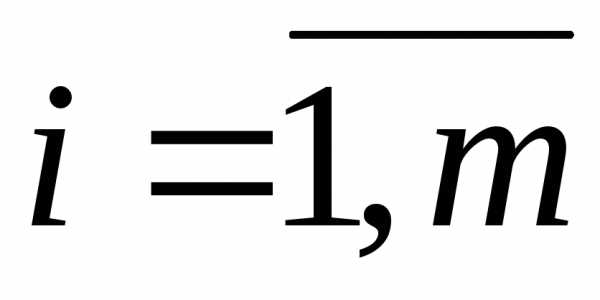 ,
,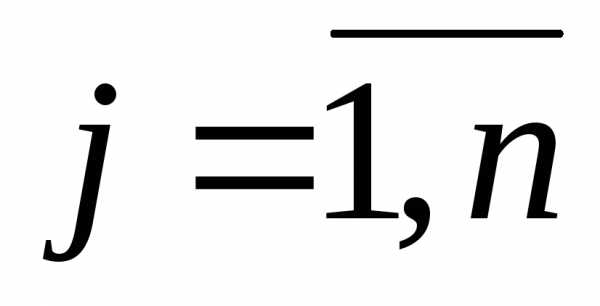 .
.
Якщо
для всіх елементів матриці виконується
умова 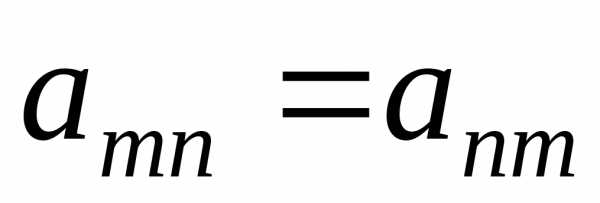 (симетрія відносно головної діагоналі),
то матриця називаєтьсясиметричною.
(симетрія відносно головної діагоналі),
то матриця називаєтьсясиметричною.
Приклад.
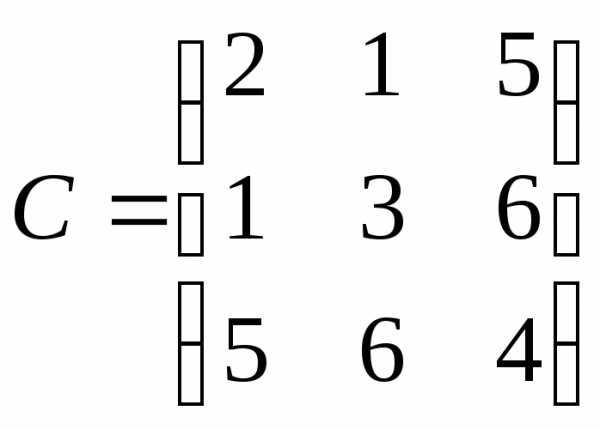 .
.
Матриця, що містить один рядок, називається вектором або матрицею-рядком, а матриця, що містить один стовпець, також називається вектором або матрицею-стовпцем. Їх вид:
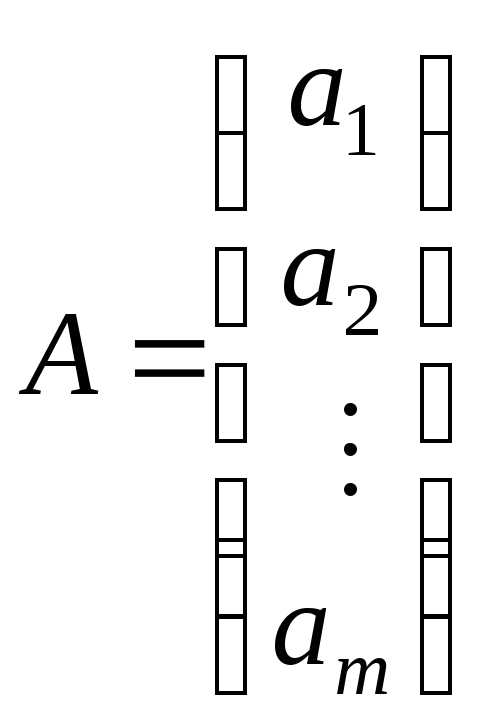 –матриця-стовпець, – матриця-рядок.
–матриця-стовпець, – матриця-рядок.
Матриця
розміру 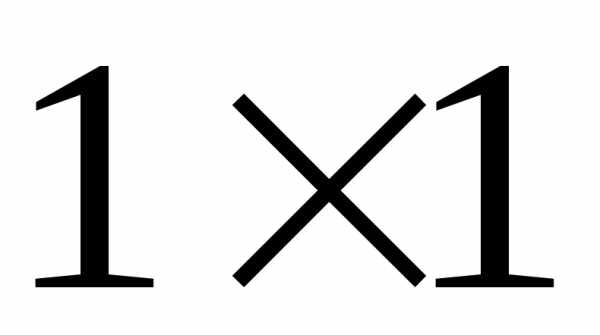 ,
що складається з одного числа, ототожнюється
з цим числом, тобто
,
що складається з одного числа, ототожнюється
з цим числом, тобто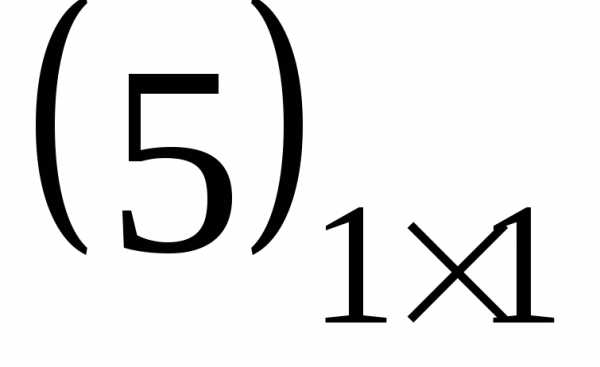 є число 5.
є число 5.
Транспонування матриць
Матриця,
отримана з даної заміною кожного її
рядка стовпцем з тим же номером,
називається матрицею, транспонованою до
даної. Позначають:  або
або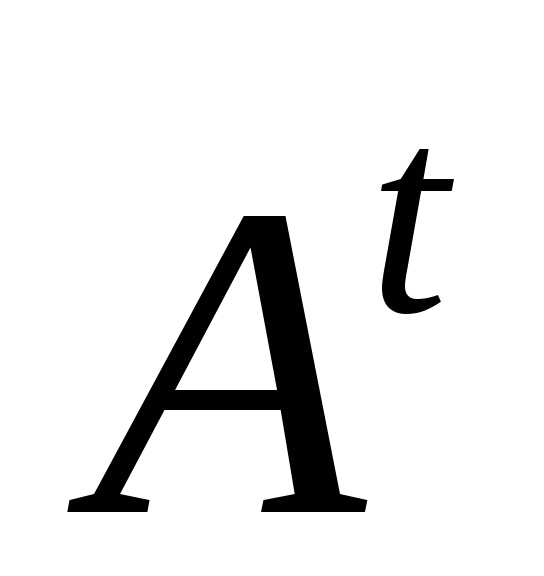 .
.
Приклад.
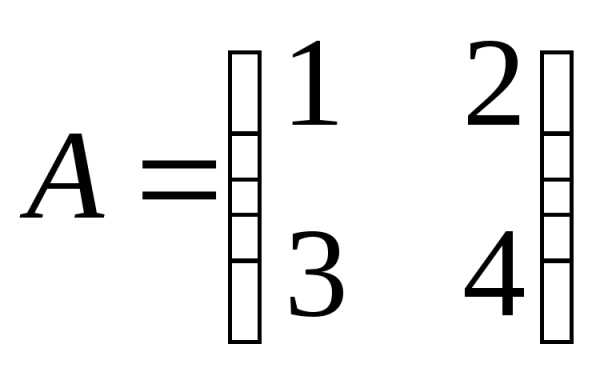 ,
, 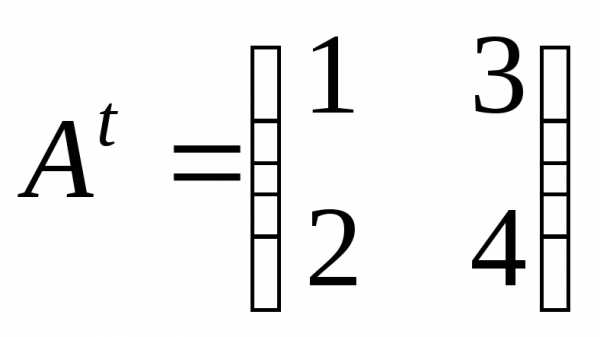 ;
;
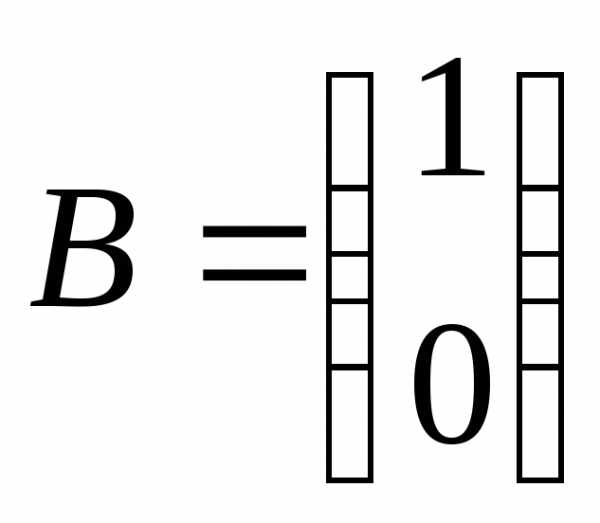 ,
, 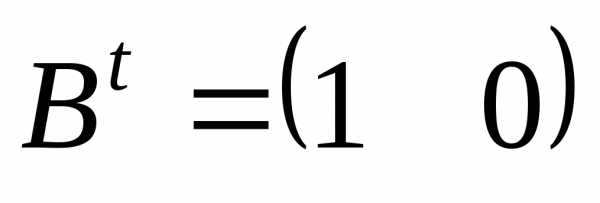 .
.
Транспонування
матриць має таку властивість: 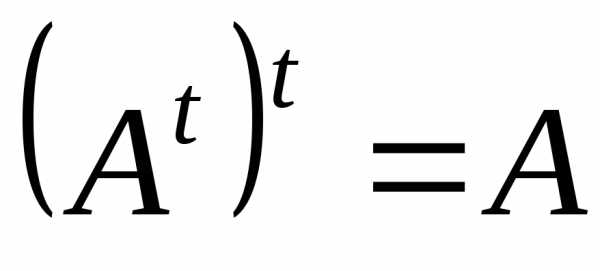 .
.
Додавання матриць
Сумою
двох матриць  і
і однакового
розміру називається матриця
однакового
розміру називається матриця того ж розміру, кожний елемент якої є
сумою відповідних елементів
матриць-доданків, тобто якщой,
то,
де
того ж розміру, кожний елемент якої є
сумою відповідних елементів
матриць-доданків, тобто якщой,
то,
де ,
,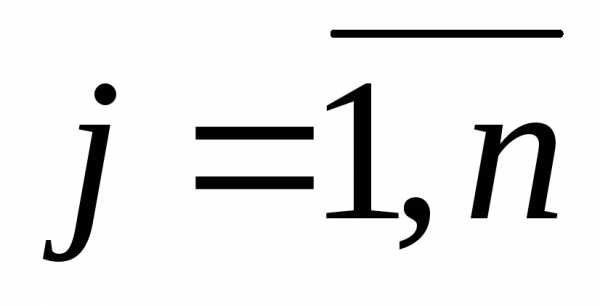 .
.
Приклад.
.
Аналогічно
визначається різниця
матриць:
,
де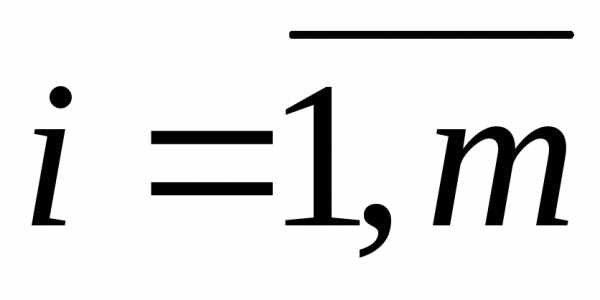 ,
,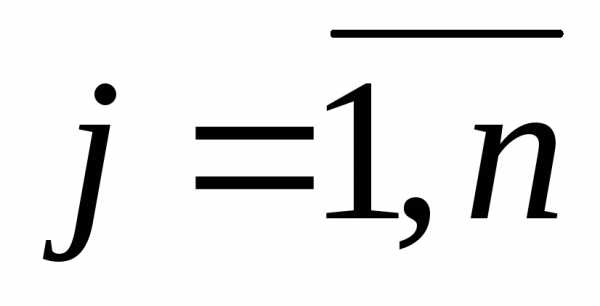 .
.
Множення матриці на число
Добутком матриці на
дійсне число  називається матриця,
кожний елемент якої є добутком відповідного
елемента матриці
називається матриця,
кожний елемент якої є добутком відповідного
елемента матриці та числа
та числа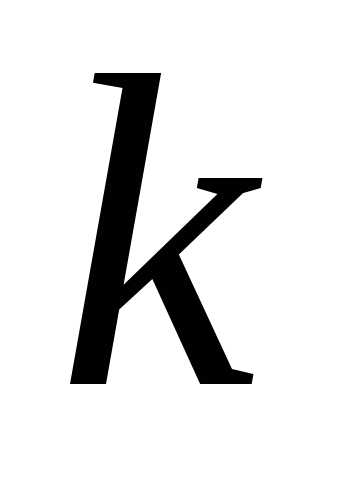 ,
тобто,
де
,
тобто,
де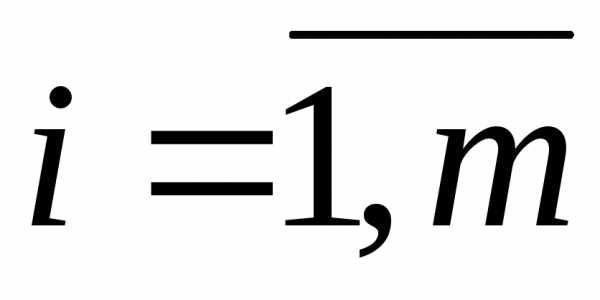 ,
,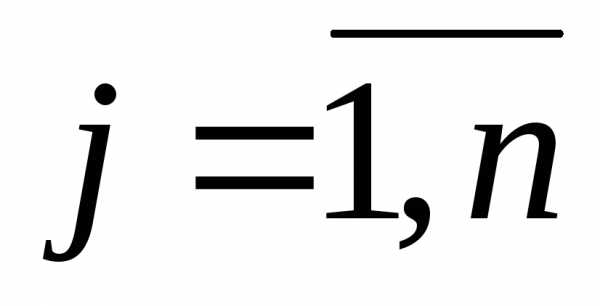 .
.
Приклад.
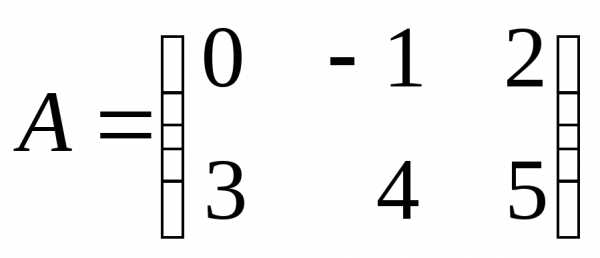 , .
, .
Матриця 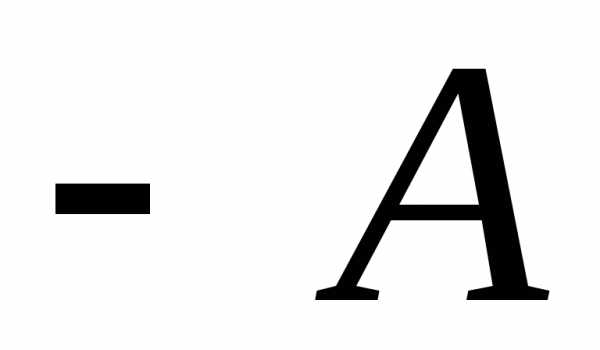 такого ж розміру, що і матриця
такого ж розміру, що і матриця ,
називаєтьсяпротилежною до матриці
,
називаєтьсяпротилежною до матриці  ,
якщо.
Наслідком з цього є рівність
,
якщо.
Наслідком з цього є рівність
Різницю
матриць 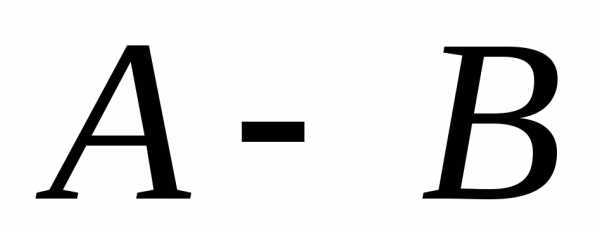 можна визначити й так:.
можна визначити й так:.
Властивості операцій додавання матриць і
множення матриці на число
(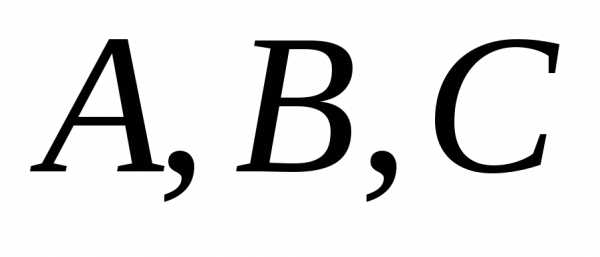 – матриці,
– матриці,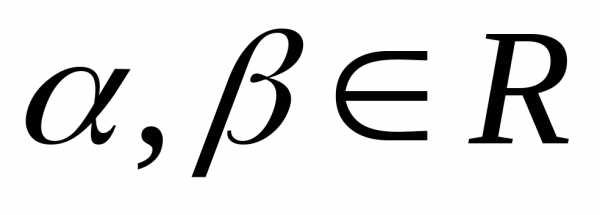 ):
):
–комутативність додавання;
–асоціативність додавання;
;
;
;
–дистрибутивність;
–дистрибутивність;
–асоціативність.
Добуток матриць
Добутком матриці
на матрицюназивається матриця,
кожний елемент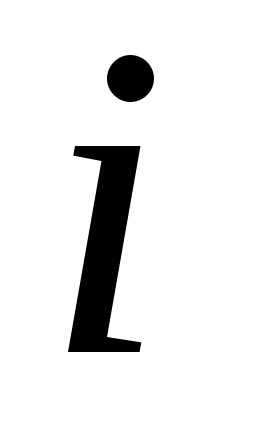 -ого
рядка й
-ого
рядка й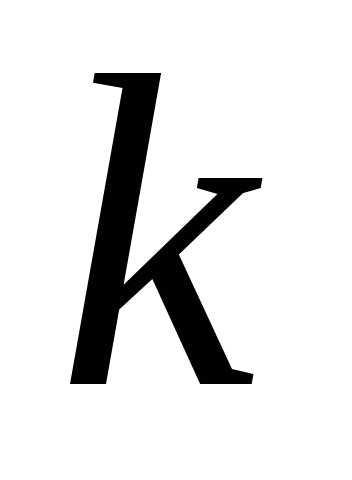 -ого
стовпця якої дорівнює сумі добутків
відповідних елементів
-ого
стовпця якої дорівнює сумі добутків
відповідних елементів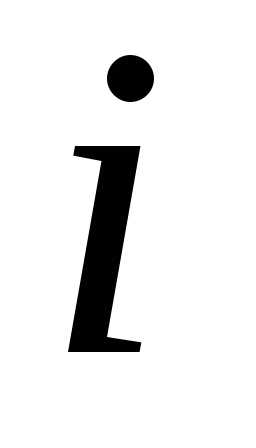 -ого
рядка матриці
-ого
рядка матриці та
та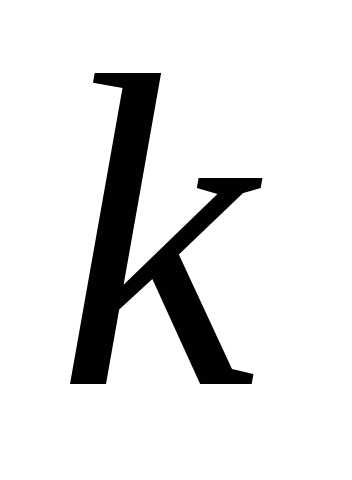 -ого
стовпця матриці
-ого
стовпця матриці ,
тобто
,
тобто
,
де 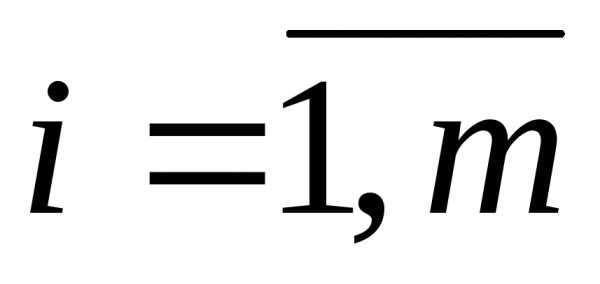 ,
, .
.
Зауваження 1. Добуток матриць можливий у випадку, коли кількість стовпців першої матриці дорівнює кількості рядків другої.
Зауваження
2. Якщо квадратні матриці  й
й одного порядку, то добутки
одного порядку, то добутки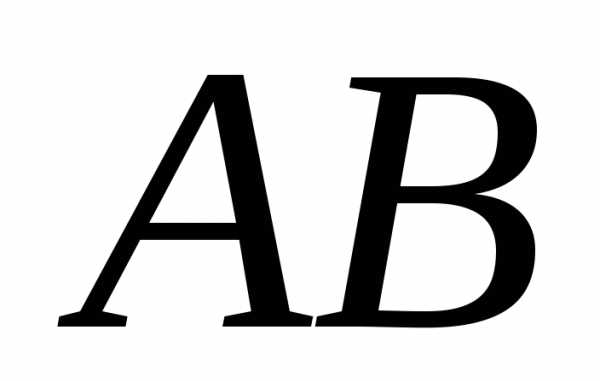 й
й завжди існують.
завжди існують.
Приклад. Знайти добутки 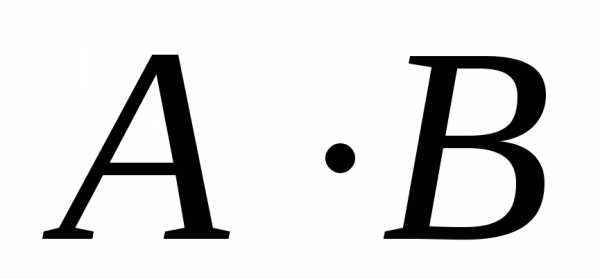 та
та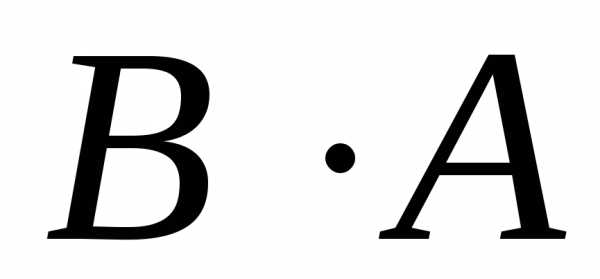 матриць: а)
матриць: а) і
і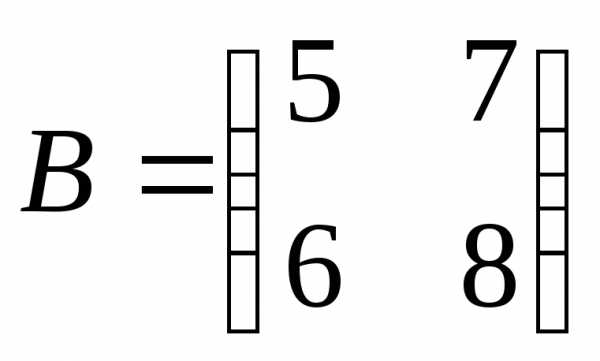 ;
б)
;
б) і.
і.
Розв’язання:
а) ,
;
,
.
б) ,
;
,
.
Зауваження
3. У загальному випадку добутки 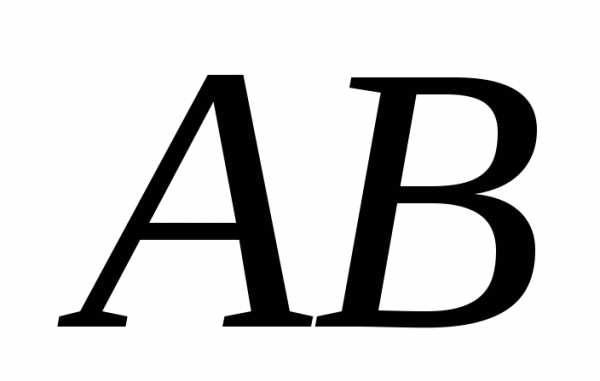 й
й не дорівнюють один одному:.
не дорівнюють один одному:.
Матриці  та
та називаютьсяпереставними,
якщо
.
називаютьсяпереставними,
якщо
.
Добуток 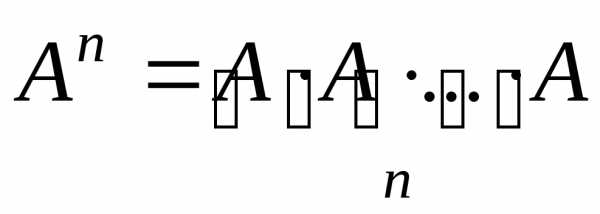 називається
називається -им степенем матриці
-им степенем матриці .
.
Властивості операцій транспонування, множення,
додавання матриць і множення матриці на число
(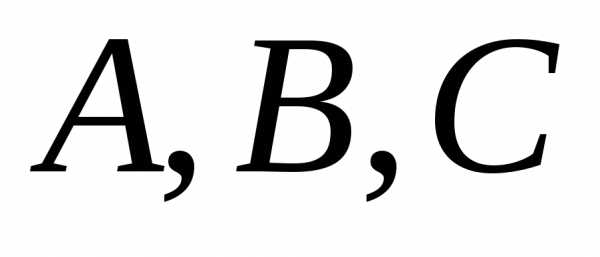 – матриці,
– матриці,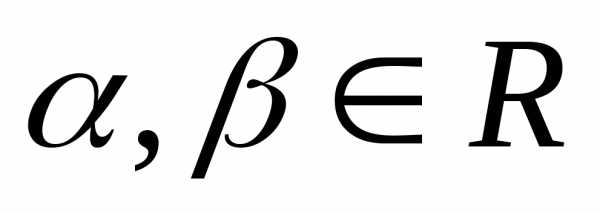 ),
якщо записані операції мають сенс:
),
якщо записані операції мають сенс:
; 5. ;
; 6. ;
; 7. ;
; 8. .
studfiles.net

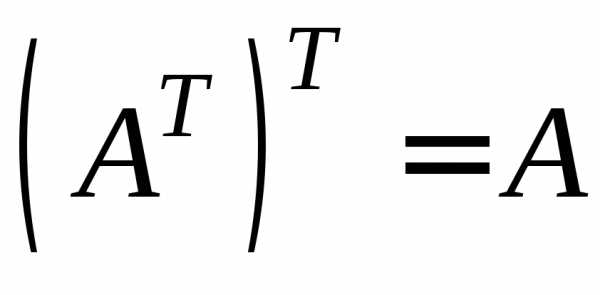 ;
;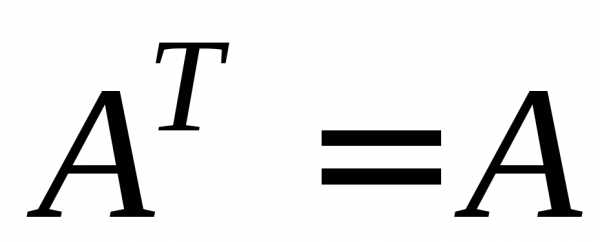 ,
якщо
,
якщо  − діагональна;
− діагональна;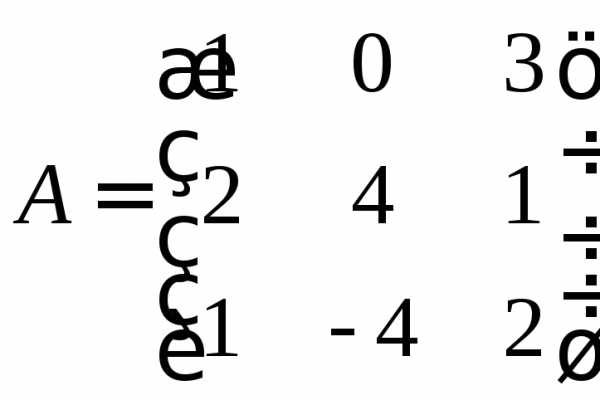 ,
,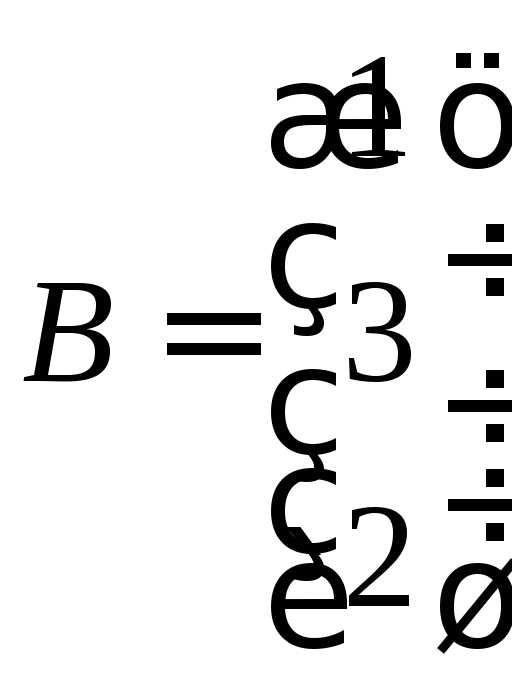 ,
,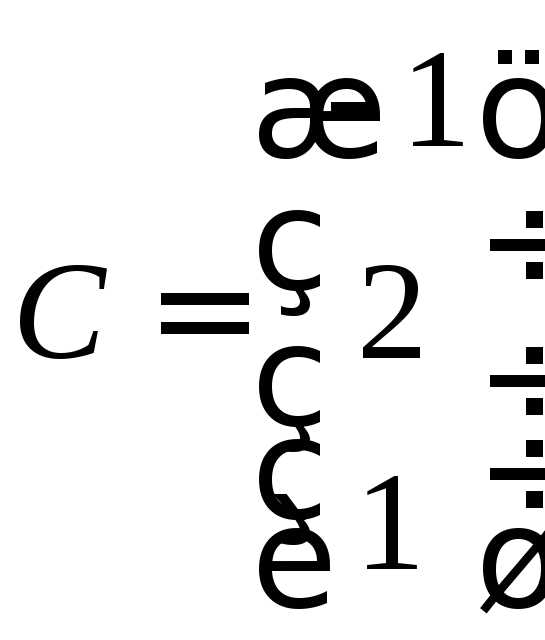 знайти.
знайти. ,
яка задовольняє співвідношенням:
,
яка задовольняє співвідношенням: .
. повинна бути квадратною, щоб її можна
було зліва та справа помножити на
повинна бути квадратною, щоб її можна
було зліва та справа помножити на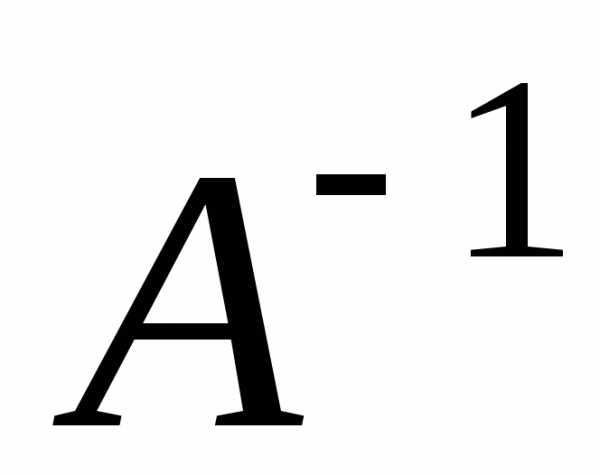 .
.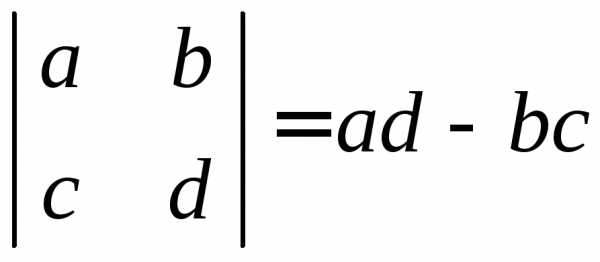 .
(1.2)
.
(1.2)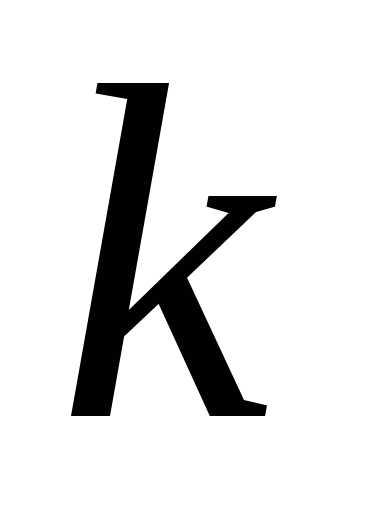 називають визначник
називають визначник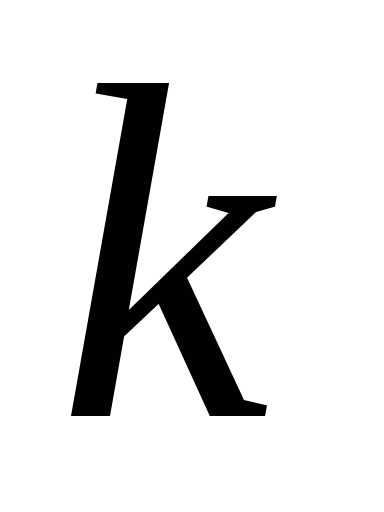 -го
порядку, який утворено з елементів
матриці
-го
порядку, який утворено з елементів
матриці ,
зберігаючи їх порядок.
,
зберігаючи їх порядок.