Признаки равенства треугольников [wiki.eduVdom.com]
Рис.1
Два треугольника называются равными, если их можно совместить наложением. На рисунке 1 изображены равные треугольники ABC и А1В1С1. Каждый из этих треугольников можно наложить на другой так, что они полностью совместятся, т. е. попарно совместятся их вершины и стороны. Ясно, что при этом совместятся попарно и углы этих треугольников.
Таким образом, если два треугольника равны, то элементы (т. е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника. Отметим, что в равных треугольниках против соответственно равных сторон (т. е. совмещающихся при наложении) лежат равные углы, и обратно: против соответственно равных углов лежат равные стороны.
Так, например, в равных треугольниках ABC и A1B1C1, изображенных на рисунке 1, против соответственно равных сторон АВ и А
Рис.2
Теорема 1. Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны (рис.2).
Доказательство. Рассмотрим треугольники ABC и A1B1C1, у которых АВ = A1B1, АС = A1C1 ∠ А = ∠ А1 (см. рис.2). Докажем, что Δ ABC = Δ A1B1C1.
Так как ∠ А = ∠ А 1, то треугольник ABC можно наложить на треугольник А1В1С1 так, что вершина А совместится с вершиной А1, а стороны АВ и АС наложатся соответственно на лучи А1В1 и A1C1. Поскольку АВ = A1B1, АС = А1С1, то сторона АВ совместится со стороной А1В1 а сторона АС — со стороной А1C1; в частности, совместятся точки В и В1, С и C1. Следовательно, совместятся стороны ВС и В1С1. Итак, треугольники ABC и А1В1С1 полностью совместятся, значит, они равны.
Аналогично методом наложения доказывается теорема 2.
Рис.3
Теорема 2. Второй признак равенства треугольников. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны
Замечание. На основе теоремы 2 устанавливается теорема 3.
Теорема 3. Сумма любых двух внутренних углов треугольника меньше 180°.
Из последней теоремы вытекает теорема 4.
Теорема 4. Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
Теорема 5. Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого
треугольника, то такие треугольники равны (подробнее).
Пример 1. В треугольниках ABC и DEF (рис. 4)
Рис.4
∠ А = ∠ Е, АВ = 20 см, АС = 18 см, DE = 18 см, EF = 20 см. Сравнить треугольники ABC и DEF. Какой угол в треугольнике DEF равен углу В?
Решение. Данные треугольники равны по первому признаку. Угол F треугольника DEF равен углу В треугольника ABC, так как эти углы лежат против соответственно равных сторон DE и АС.
Пример 2. Отрезки АВ и CD (рис. 5) пересекаются в точке О, которая является серединой каждого из них. Чему равен отрезок BD, если отрезок АС равен 6 м?
Рис.5
Решение. Треугольники АОС и BOD равны (по первому признаку): ∠ АОС = ∠ BOD (вертикальные), АО = ОВ, СО = OD (по условию).
Из равенства этих треугольников следует равенство их сторон, т. е. АС = BD. Но так как по условию АС = 6 м, то и BD = 6 м.
Пример 3. В треугольниках ABC и DEF (см. рис. 4) АВ = EF, ∠A = ∠E, ∠B = ∠F.
Рис.4
Сравнить эти треугольники. Какие стороны в треугольнике DEF равны соответственно сторонам ВС и СА?
Решение. Треугольники ABC и DEF равны по второму признаку. Стороны DF и DE треугольника DEF равны соответственно сторонам ВС и СА треугольника ABC, так как стороны DF и ВС (DE и СА) лежат против равных углов Е и A (F и В).
Пример 4. На рисунке 6 углы DAB и СВА, CAB и DBA равны, СА = 13 м. Найти DB.
Решение. Треугольники АСВ и ADB имеют одну общую сторону АВ и по два равных угла, которые прилежат к этой стороне. Следовательно, треугольники АСВ и ADB равны (по второму признаку). Из равенства этих треугольников следует равенство сторон BD и АС, т. е. BD = 13 м.
www.wiki.eduvdom.com
Построение треугольников. Признаки равенства треугольников.
Построение треугольников по одному или двум элементам
Пусть требуется построить треугольник по данной стороне а. Так как об углах треугольника и о других его сторонах ничего не сказано, то можем построить сколько угодно различных треугольников, у которых одна сторона будет равна отрезку а
Пусть требуется построить треугольник по данному углу α. В этом случае также можно построить сколько угодно различных треугольников, имеющих данный угол,
Точно так же можно построить сколько угодно различных треугольников по двум сторонам, или по двум углам, или по углу и стороне (см. рис.).
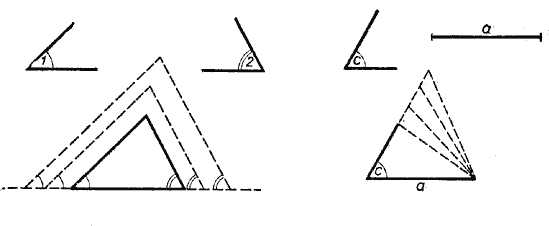
Таким образом, если будут заданы только один или два элемента треугольника, то по этим элементам можно построить сколько угодно различных треугольников.
Далее о построении треугольников не по одному и не по двум, а по трём элементам:
1. Построение треугольника по двум данным его сторонам и углу между ними.
Первый признак равенства треугольников
Пусть требуется построить треугольник, одна сторона которого равна, например,
35 мм, другая сторона равна 32 мм и угол, заключённый между этими сторонами, равен 46°.
Построим с помощью транспортира ∠A, равный 46°, и на его сторонах отложим отрезки АВ и АС, соответственно равные 35 мм и 32 мм. Соединив точки В и С, получим искомый треугольник ABC.
По тем же данным построим другой треугольник — Δ А’В’С’.
Докажем, что эти треугольники равны между собой.
Для этого наложим Δ А’В’С на Δ AВС так, чтобы вершины А’ и А совместились. Сторону А’С’ направим по стороне АС. Тогда точка С совместится с точкой С’, потому что А’С’ = АС.
Сторона А’В’ пойдёт по стороне АВ, так как ∠A’ = ∠A. Точка В’ совместится с точкой В, так как А’В’ = АВ. Если точки С и С’, В и В’ совместились, то совместятся и стороны В’С’ и ВС.Треугольники ABC и А’В’С’ совпали, значит, они равны.
Мы можем по этим же данным построить сколько угодно треугольников, и все они будут равны между собой.
Таким образом, если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны между собой.
Назовём это первым признаком равенства треугольников.
Построение треугольника по стороне и двум прилежащим к ней углам.
Второй признак равенства треугольников
Пусть требуется построить треугольник, одна сторона которого равна, например, 40 мм, а углы, прилежащие к ней, равны 50° и 48°.
На произвольной прямой построим отрезок АС, равный 40 мм. Затем на этом отрезке при точке А построим угол, равный 50°, а при точке С — угол, равный 48°.
Если мы достаточно продолжим стороны этих углов, то они пересекутся в некоторой точке В. Получим треугольник ABC.
По тем же данным построим другой треугольник — Δ А’В’С’ и докажем, что эти треугольники будут равны между собой.
Для этого наложим Δ А’В’С’ на Δ ABC так, чтобы совместились равные стороны АС и А’С’. Тогда сторона А’В’ пойдёт по стороне АВ, так как ∠A’ = ∠A, и сторона С’В’ пойдёт по стороне СВ, так как ∠C’ = ∠C. Точка В’ одновременно должна быть и на стороне АВ, и на стороне СВ, следовательно, она совместится с точкой В, так как две прямые могут пересечься только в одной точке.
Треугольники ABC и А’В’С’ совпали, значит, они равные. По этим же данным можно построить сколько угодно треугольников, и все они будут равны между собой.
Таким образом, если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны между собой.
Назовём это вторым признаком равенства треугольников.
Построение треугольника по трём данным его сторонам.
Третий признак равенства треугольников
Пусть требуется построить треугольник по трём его сторонам, например, сторона а = 30 мм, сторона с = 40 мм и сторона b = 42 мм. (Заданные размеры должны удовлетворять условию: сумма двух любых сторон треугольника больше третьей стороны.)
Сначала на произвольной прямой построим отрезок АС, равный данному отрезку b, т. е. 42 мм; мы сразу получим две вершины искомого треугольника — А и С.
Так как длина второй и третьей сторон соответственно равна отрезкам с и а (в данном случае 40 мм и 30 мм), то третья вершина треугольника должна находиться как на дуге, описанной из центра А радиусом, равным 40 мм, так и на дуге, описанной из центра С радиусом, равным 30 мм. Следовательно, третьей вершиной треугольника будет точка пересечения этих дуг. Обозначив эту точку буквой В и соединив её отрезками с точками А и С, получим искомый треугольник ABC.
По тем же данным построим второй треугольник — Δ А’В’С’ и докажем,
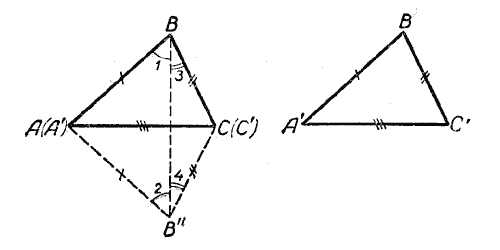
что Δ АВС = Δ А’В’С’. Для этого приложим треугольник А’В’С’ к треугольнику ABC так, чтобы их равные стороны А’С’ и AС совместились, причём точка А’ совпала бы с точкой А, точка С — с точкой С. Тогда треугольник А’В’С’ примет положение АВ»С. Сторона АВ будет равна стороне АВ» и сторона ВС — стороне В»С.
Соединив отрезком прямой точки В и В», получим два равнобедренных треугольника ВАВ» и ВСВ», у которых ∠1 = ∠2, а ∠3 = ∠4, откуда ∠B = ∠B».
Следовательно, Δ АВС = Δ АВ»С, но тогда и Δ АВС = Δ А’В’С’.
По этим же данным можно построить сколько угодно треугольников, и все они будут равны между собой.
Мы доказали, что если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны между собой.
Назовём это третьим признаком равенства треугольников.
Замечания. 1. Во всех трёх признаках равенства треугольников в число трёх данных элементов входит хотя бы одна сторона треугольника.
2. В равных треугольниках против равных сторон лежат равные углы и, обратно, против равных углов лежат равные стороны.
Итак, три признака равенства треугольников:
1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны между собой2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны между собой
3. Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны между собой
razdupli.ru
формулировка и доказательство (7 класс)
В этой статье мы расскажем, как можно сформулировать и доказать первый признак равенства треугольников, который проходят в 7 классе.
Формулировка первого признака равенства треугольников
«Если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.»
Сокращенно его называют равенство «по двум сторонам и углу между ними».
Прежде чем перейти к доказательству теоремы необходимо вспомнить, что называют треугольником и в каком случае можно утверждать, что два треугольника равны.
Что такое треугольник и когда они считаются равными?
Треугольник – это геометрическая фигура из трёх отрезков, соединяющих три точки (при условии, что они не лежат на одной прямой. Эти точки считаются вершинами треугольника. А соединяющие их отрезки – сторонами).
На рисунке 1 представлен треугольник ABС. Который имеет три вершины (А, В и С). И стороны – АВ, АС и ВС.
Рисунок 1
Треугольники считаются равными, когда все их стороны и углы соответственно равны друг другу (в случае, когда равны лишь углы, а стороны пропорциональны, треугольники называются подобными). Таким образом очевидно, что равные треугольники можно наложить друг на друга – и они полностью совпадут.
Доказательство первого признака равенства треугольников
Дано:
Два треугольника: ABC и DEF (рисунок 2).
Рисунок 2
По условию теоремы две пары отрезков этих треугольников равны между собой (АС = FD и СВ = EF). Углы между отрезками также равны (т.е. ∠АСВ = ∠EFD).
Доказать, что треугольник ABC равен треугольнику DEF.
Доказательство:
- Поскольку имеется равенство углов (∠АСВ = ∠EFD), треугольники можно наложить друг на друга, так чтобы вершина С совпадала с вершиной F.
- При этом отрезки СА и СВ наложатся на отрезки FE и FD.
- А поскольку отрезки двух треугольников равны между собой (АС = FD и СВ = EF по условию), то отрезок АВ также совпадёт со стороной ED.
- Это в свою очередь даст совмещение вершин А и D, В и Е.
- Следовательно, треугольники полностью совместятся, а значит, они равны.
Теорема доказана.
Понравилась статья, расскажите о ней друзьям:
Скорее всего, Вам будет интересно:
people-ask.ru
геометрия. 3 признака равенства треугольников?? ? помогите пожалуйста
По двум сторонам и углу между ними, по стороне и прилегающим к ней углам, по трем сторонам
Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Второй признак равенства треугольников. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны. Теорема 3 (третий признак равенства треугольников — по трем сторонам) Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
<img src=»//otvet.imgsmail.ru/download/213248691_956510158a744e26feccfd17679f0a17_800.jpg» data-lsrc=»//otvet.imgsmail.ru/download/213248691_956510158a744e26feccfd17679f0a17_120x120.jpg» data-big=»1″>
Там есть теоремы в учебнике
3) признак- если у одного треуг. 3 стороны равны 3-м сотронам другого треугольника то такие треугольники равны. 1) признак- если у одного треуг. 2 стороны и угол между ними равны 2-м сторонам и углу между ними другого треуга. то такие трег. равны 2)если у одного треугольника 2 угла и сторона между ними равны 2-м углам и стороне между ними другого треуга то такие треугольники равны!
3) признак- если у одного треуг. 3 стороны равны 3-м сотронам другого треугольника то такие треугольники равны. 1) признак- если у одного треуг. 2 стороны и угол между ними равны 2-м сторонам и углу между ними другого треуга. то такие трег. равны 2)если у одного треугольника 2 угла и сторона между ними равны 2-м углам и стороне между ними другого треуга то такие треугольники равны!
3) признак- если у одного треуг. 3 стороны равны 3-м сотронам другого треугольника то такие треугольники равны. 1) признак- если у одного треуг. 2 стороны и угол между ними равны 2-м сторонам и углу между ними другого треуга. то такие трег. равны 2)если у одного треугольника 2 угла и сторона между ними равны 2-м углам и стороне между ними другого треуга то такие треугольники равны!
1) признак- если у одного треуг. 2 стороны и угол между ними равны 2-м сторонам и углу между ними другого треуга. то такие трег. равны 2)если у одного треугольника 2 угла и сторона между ними равны 2-м углам и стороне между ними другого треуга то такие треугольники равны! 3) признак- если у одного треуг. 3 стороны равны 3-м сотронам другого треугольника то такие треугольники равны.
Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Второй признак равенства треугольников. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны. Теорема 3 (третий признак равенства треугольников — по трем сторонам) Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
ну и нафига вы по 100 раз копируете и отвечаете?
1 признак- если 2 стороны и угол между ними одного треугольника равны 2-м сторонам и углу между ними другого треугольника то они равны 2 признак — если 2 угла и сторона между ними одного треугольника равны 2-м углам и стороне между ними другого треугольника то такие треугольники равны 3 признак- если 3 стороны одного треугольника равны 3-м стронам другого треугольника то такие треугольники равны
1) признак- если у одного треугольника. 2 стороны и угол между ними равны 2-м сторонам и углу между ними другого треугольника то такие треугольники равны. 2)если у одного треугольника 2 угла и сторона между ними равны 2-м углам и стороне между ними другого треугольника то такие треугольники равны! 3) признак- если у одного треугольника 3 стороны равны 3-м сотронам другого треугольника то такие треугольники равны.
1) признак- если у одного треугольника. 2 стороны и угол между ними равны 2-м сторонам и углу между ними другого треугольника то такие треугольники равны. 2)если у одного треугольника 2 угла и сторона между ними равны 2-м углам и стороне между ними другого треугольника то такие треугольники равны! 3)
Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Второй признак равенства треугольников. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны. Теорема 3 (третий признак равенства треугольников — по трем сторонам) Если три стороны одного треугольника соответственно рав
Спасибки за ОтВеТиК!!!
touch.otvet.mail.ru
Признак равенства треугольников по двум сторонам и углу между ними

Признак равенства
треугольников по
двум сторонам и
углу между ними
В 1
В
С 1
С
А
А 1
Первый признак равенства треугольников
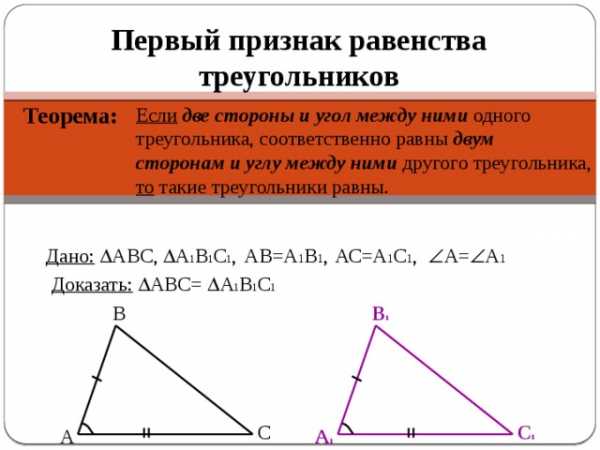
Теорема:
Если две стороны и угол между ними одного
треугольника, соответственно равны двум
сторонам и углу между ними другого треугольника,
то такие треугольники равны.
Дано: АВС, А 1 В 1 С 1 ,
А= А 1
АС=А 1 С 1 ,
АВ=А 1 В 1 ,
Доказать: АВС= А 1 В 1 С 1
В
В 1
С
С 1
А 1
А
В
В 1
С
С 1
А 1
А
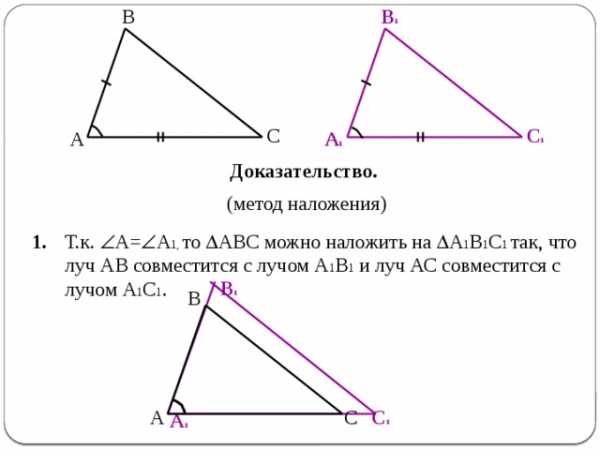
Доказательство.
(метод наложения)
Т.к. А= А 1, то АВС можно наложить на А 1 В 1 С 1 так, что луч АВ совместится с лучом А 1 В 1 и луч АС совместится с лучом А 1 С 1 .
1.
В 1
В
С 1
А
С
А 1

2.
Т.к. АВ=А 1 В 1 , то
сторона АВ совместится со стороной А 1 В 1
(точка В совместится с точкой В 1 ).
В 1
В
А 1
А
С 1
С
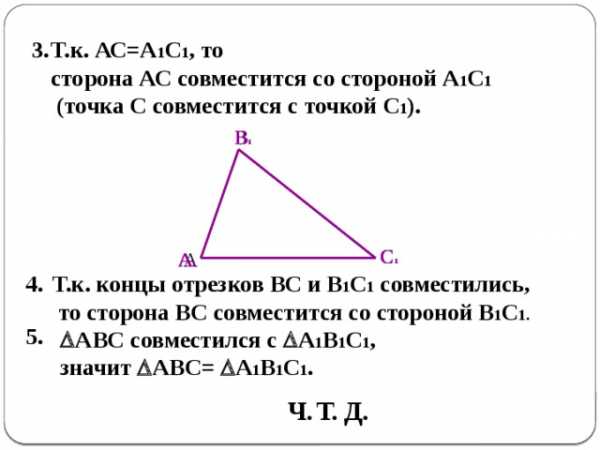
3.
Т.к. АС=А 1 С 1 , то
сторона АС совместится со стороной А 1 С 1
(точка С совместится с точкой С 1 ).
В 1
В 1
В
С 1
С 1
С
А 1
А
А 1
Т.к. концы отрезков ВС и В 1 С 1 совместились,
4.
то сторона ВС совместится со стороной В 1 С 1.
5.
АВС совместился с А 1 В 1 С 1 ,
значит АВС= А 1 В 1 С 1 .
Ч.
Т.
Д.

В 1
В
В
А
С 1
С
А 1
С
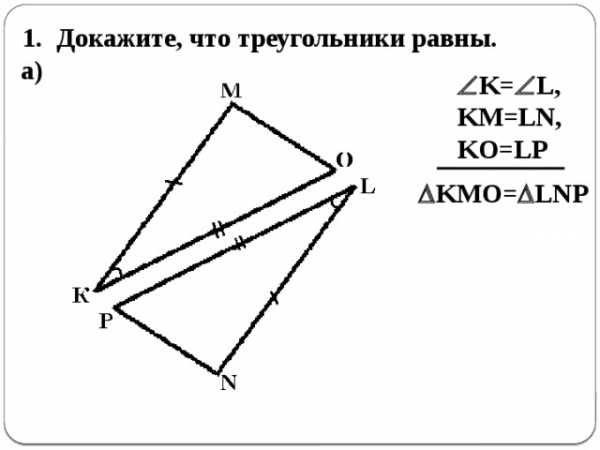
Докажите, что треугольники равны.
1.
а)
K= L,
KM=LN,
KO=LP
KMO= LNP
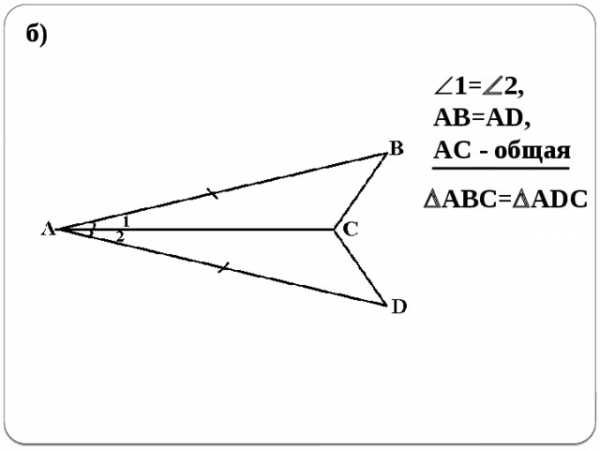
б)
1= 2,
AB=AD,
AC — общая
ABC= ADC
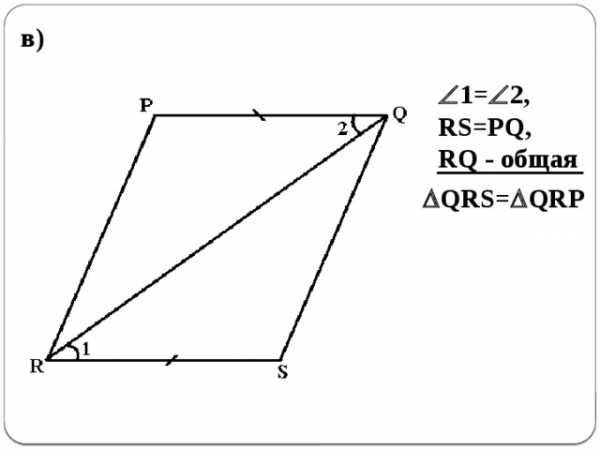
в)
1= 2,
RS=PQ,
RQ — общая
QRS= QRP

2. Дополните условия так, чтобы
треугольники были равны по первому
признаку равенства треугольников.
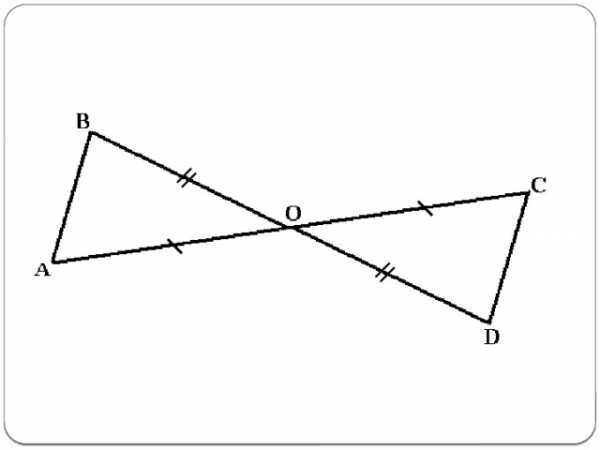
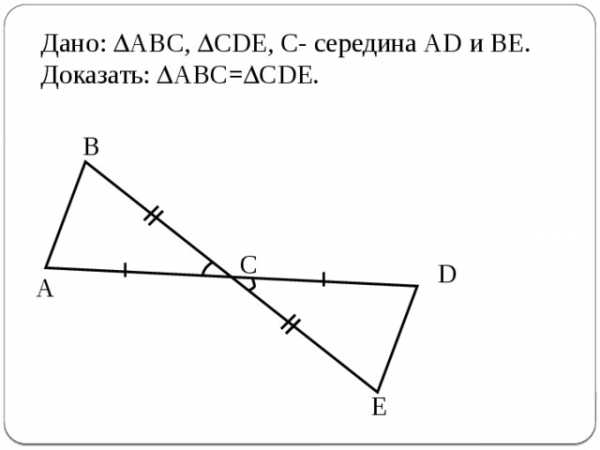
Дано: ABC, CDE, С- середина АD и BE.
Доказать: ABC= CDE.
B
C
D
A
E

Домашнее задание:
Глава II, §1, п. 14-15 читать,
выучить записи в тетради.
Спасибо за внимание!!!
videouroki.net
Ответы@Mail.Ru: определение равных треугольников
Два треугольника называются равными ( Δ ABC = Δ A1B1C1), если у них соответствующие стороны равны и соответствующие углы равны Признаки равенства треугольников: 1 признак равенства треугольников. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны. 2 признак равенства треугольников. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны. 3 признак равенства треугольников. Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.
Определения: 1. Два треугольника называются равными ( Δ ABC = Δ A1B1C1), если у них соответствующие стороны равны и соответствующие углы равны 2. Равные треугольники совпадают при наложении Признаки равенства: Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Второй признак равенства треугольников. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны. Третий признак равенства треугольников. Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.
1. Два треугольника называются равными ( Δ ABC = Δ A1B1C1), если у них соответствующие стороны равны и соответствующие углы равны 2. Равные треугольники совпадают при наложении Признаки равенства: Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Второй признак равенства треугольников. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны. Третий признак равенства треугольников. Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.
Два треугольника называются равными, если у них соответствующие стороны равны и соответствующие углы равны
.Два треугольника называются равными ( Δ ABC = Δ A1B1C1), если у них соответствующие стороны равны и соответствующие углы равны
Два треугольника называются равными, если у них соответствующие стороны и соответствующие углы равны
Два треугольника называются равными ( Δ ABC = Δ A1B1C1), если у них соответствующие стороны равны и соответствующие углы равны Признаки равенства треугольников: 1 признак равенства треугольников. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны. 2 признак равенства треугольников. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны. 3 признак равенства треугольников. Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.
Два треугольника называются равными, если у них соответствующие стороны равны и соответствующие углы равны
Треугольника считаются равными — если равны : 1) соотвествующие стороны этих треугольников 2) соотвествующие углы этих треугольников. Существуют признаки равенства треугольников. А именно: 1-ый признак. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны. 2-ой признак. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны. 3-ий признак. Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны. Подробнее — на Znanija.com — <a rel=»nofollow» href=»https://znanija.com/task/2139990#readmore» target=»_blank»>https://znanija.com/task/2139990#readmore</a>
За чем вы копируйте друг за другом дибилы.
touch.otvet.mail.ru
| Действия учителя | Действия учащихся |
|---|---|
І. Мотивационно-ориентировочный этап.
|
|
| — Какая фигура называется треугольником? | — Геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой, соединенных отрезками, называется треугольником. |
| — Какие треугольники называются равными? | — Два треугольника называются равными, если их можно совместить наложением. |
| — Как установить равенство двух треугольников? | — Наложить один треугольник на другой, если они совместятся, то треугольники равны. Можно сравнить все стороны и углы одного треугольника со сторонами и углами другого. |
| — Все эти способы возможны, но они не всегда удобны, громоздки. А нет ли другого способа доказательства равенства двух треугольников? | — ??? |
| — Оказывается, равенство двух треугольников можно установить, не накладывая один треугольник на другой, а лишь сравнивая некоторые элементы этих фигур. | |
|
|
| — Попробуем решить практическую задачу. Пусть надо измерить расстояние на местности от пункта А до пункта В, между которыми расположено озеро, поэтому с мерной лентой по прямой пройти нельзя. — На практике, для решения этой задачи поступают так:<br> Выбирают некоторую точку С так, чтобы расстояние от точки С до точек А и В можно было измерить мерной лентой. Затем, на прямой АС отмечают точку К так, чтобы отрезок АС = СК, а на прямой ВС отмечают точку М так, чтобы отрезок ВС = СМ. Тогда на местности можно измерить расстояние МК, при этом утверждают, что оно равно искомому расстоянию между пунктами А и В. | |
| — Почему можно утверждать, что МК = АВ? Когда можно найти другие равные элементы в треугольниках? |
— Когда треугольники равны. |
| — Вероятно, ∆ АВС = ∆ МКС? | |
| — А каким свойством обладают равные треугольники? | — В равных треугольниках против соответственно равных сторон лежат равные углы, и наоборот, против равных углов, лежат равные стороны. |
| — Мы пока не знаем, равны наши треугольники или нет, ∆ АВС = ∆ МКС? Перечислите все равные элементы в этих треугольниках. | — АС = СК, ВС = СМ – по построению, ∠ АСВ = ∠ МСК как вертикальные. |
| — Итак, нам нужно установить равенство сторон АВ и МК, а равенство сторон следует из равенства треугольников. То есть, если мы докажем равенство треугольников, то равенство сторон будет доказано. Какова же цель урока? | — Доказать равенство треугольников. |
| — Используя равенства каких элементов? | — Двух сторон и угла между ними. |
| — Сформулируйте цель урока. | |
| — Попробуем сформулировать утверждение, почему треугольники равны, по каким элементам? | — Если две стороны и угол между ними одного треугольника, соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. |
| — Данное утверждение называется теоремой. Теорема – утверждение, которое необходимо доказать, а сами рассуждения называют доказательством. Сформулированную теорему называют первым признаком равенства треугольников или признаком равенства треугольников по двум сторонам и углу между ними. (С этого этапа каждое обоснование сопровождается слайдом с презентации (приложение 1)) — Запишем в тетрадях тему. Признак равенства треугольников по двум сторонам и углу между ними. — Запишем формулировку теоремы. Теорема: Если две стороны и угол между ними одного треугольника, соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.— Теорему можно назвать задачей, в которой есть условие, (то, что дано) и заключение, то, что необходимо доказать. |
|
| — В теореме, начиная со слова если до слова то является условием теоремы. Прочитайте условие теоремы. | — Если две стороны и угол между ними одного треугольника, соответственно равны двум сторонам и углу между ними другого треугольника. |
| — Все, что записано после слова то, называют заключением. Прочитайте заключение. | — Такие треугольники равны. |
| — Запишем в тетрадях: Дано: |
|
| — О каких фигурах идет речь? — Запишем в дано: ∆ АВС и ∆ А1В1С1. |
— О треугольниках. |
| — О равенстве каких элементов говорится в условии? | — О равенстве двух сторон и угла между этими сторонами. |
| — Выберем эти стороны и найдем угол между этими сторонами. АВ = А1В1, АС = А1С1, ∠ А = ∠ А1 |
|
| — Что нужно доказать? | — Что ∆ АВС = ∆ А1В1С1. |
| — Запишем: Доказать: ∆ АВС =∆ А1В1С1 |
|
ІІ Исполнительский этап.
|
|
| — Каким способом будем доказывать равенство треугольников? | — Методом наложения. |
| — Запишем: Доказательство (метод наложения)
— С чего начнем проводить доказательство? С наложения каких элементов? |
|
|
|
| — Запишем: 1. Т.к. ∠ А = ∠ А1, то ∆ АВС можно наложить на ∆ А1В1С1 так, что луч АВ совместится с лучом А1В1 и луч АС совместится с лучом А1С1. |
|
| — Какие элементы треугольника будем потом сравнивать? Что еще дано в условии? | — АВ = А1В1 |
| — Что произойдет с точками В и В1? | — Эти точки совпадут. |
| — Посмотрим на экран, запишем: 2. Т.к. АВ = А1В1, то сторона АВ совместится со стороной А1В1 (точка В совместится с точкой В1). |
|
| — О какой стороне еще говорится в условии? | — АC = А1C1 |
| — Сделайте вывод о точках С и С1. — Посмотрим на экран, действительно ли совпадут эти точки? |
— Эти точки совпадут. |
| — Ваше утверждение верно, запишем: 3. Т.к. АC = А1C1, то сторона АС совместится со стороной А1C1 (точка С совместится с точкой С1). |
|
| — Что произошло с концами отрезков ВС и В1С1? | — Концы отрезков ВС и В1С1 совпали. |
| — Что теперь можно сказать про отрезки ВС и В1С1? | — ВС = В1С1 |
| — Правильно, запишем: 4. Т.к. концы отрезков ВС и В1С1 совместились, то сторона ВС совместится со стороной В1С1. |
|
| — Что произошло с ∆ АВС и ∆ А1В1С1? | — Треугольники совпали, значит они равны. |
| — Молодцы, запишем: 5. ∆ АВС совместился с ∆ А1В1С1, значит ∆ АВС = ∆ А1В1С1. |
|
ІІІ Рефлексивно – оценочный этап. |
|
| — Достигли мы цели урока? | — Достигли. |
| — Сформулируйте доказанную теорему. | — Если две стороны и угол между ними одного треугольника, соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. |
| — Сверим доказанную теорему с теоремой в учебнике п.15, стр. 30 (Учебник по геометрии для 7 класса, автор Л.С. Атанасян). Прочитайте её, эту теорему мы только что доказали? Выделите условие и заключение теоремы. | — «Если две стороны и угол между ними одного треугольника, соответственно равны двум сторонам и углу между ними другого треугольника» — это условие, то что дано. — «такие треугольники равны» — заключение, что требуется доказать. |
| — Каким методом мы проводили доказательство? | — Методом наложения. |
| — С наложения каких элементов мы начали проводить доказательство? | — С наложения углов. |
| (Можно использовать для помощи приложение 1 слайд №6 ) — Равенство каких элементов еще использовали? |
— Равенство сторон: АВ = А1В1, то сторона АВ совместится со стороной А1В1, точка В совместится с точкой В1; — АС = А1C1, то сторона АС совместится со стороной А1C1 точка С совместится с точкой C1. |
| — Что можно сказать про стороны ВС и B1C1? | — Они совпадут, значит эти стороны равны. |
| — Для чего необходима доказанная теорема? | — Можно лишь сравнивать элементы треугольника, а не накладывать треугольники, не всегда возможно наложить треугольники практически. — Для решения задач. |
|
|
| — Сколько пар соответственно равных элементов надо отыскать, чтобы доказать равенство треугольников по первому признаку? | — Три пары, две стороны и угол. |
| — Где должен лежать угол? | — Между сторонами. |
Далее учащиеся устно решают задачи на отработку изученного признака.
|
|
|
|
| Домашнее задание: Глава II, §1, п. 14-15 читать, выучить записи в тетради. | |
|
|
| — С помощью сигнальных карточек покажите, каким стало ваше настроение к концу урока. | |
xn--i1abbnckbmcl9fb.xn--p1ai
