Тригонометрический круг. Текст к рисунку
Нарисована единичная окружность то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями OX и OY , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси OX против часовой стрелки. Полный круг 360 градусов.
Точка с координатами (1; 0) соответствует углу в 0 градусов. Точка с координатами ( 1; 0) отвечает углу в , точка с координатами (0; 1) углу в . Каждому углу от нуля до 360 градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси OX) точки на единичной окружности, соответствующей данному углу .
Синусом угла называется ордината (то есть координата по оси OY ) точки на единичной окружности, соответствующей данному углу .
Например:
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус координаты точки на единичной окружности, соответствующей данному углу. Косинус абсцисса (x), синус ордината (y). Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от 1 до 1:
.
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать от-дельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по x (это косинус угла ) и по y (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: 360 градусов, то есть полный круг, соответствует 2 радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки он положительный. Если отсчитывать по часовой стрелке угол будет отрицательным. Например, угол это угол величиной в , который отложили от положительного направления оси x по часовой стрелке. Легко заметить, что
Углы могут быть и больше 360 градусов. Например, угол это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по x и по y, значения синуса и косинуса повторяются через . То есть:
где n целое число. То же самое можно записать в радианах:
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. Ведь
В результате получим следующую таблицу.
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Тригонометрия. Единичная окружность
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (322,7 кБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цель: научить использовать единичную окружность при решении различных тригонометрических заданий.
В школьном курсе математики возможны различные варианты введения тригонометрических функций. Наиболее удобной и часто используемой является «числовая единичная окружность». Её применение в теме «Тригонометрия» весьма обширно.
Единичная окружность используется для:
– определения синуса, косинуса, тангенса и котангенса угла;
– нахождения значений тригонометрических функций для некоторых значений числового и углового аргумента;
– выведение основных формул тригонометрии;
– выведения формул приведения;
– нахождения области определения и области значений тригонометрических функций;
– определения периодичности тригонометрических функций;
– определения четности и нечетности тригонометрических функций;
– определения промежутков возрастания и убывания тригонометрических функций;
– определения промежутков знакопостоянства тригонометрических функций;
– радианного измерения углов;
– нахождения значений обратных тригонометрических функций;
– решение простейших неравенств и др.
Таким образом, активное осознанное владение учащимися данным видом наглядности дает неоспоримые преимущества для овладения разделом математики «Тригонометрия».
Использование ИКТ на уроках преподавания математики позволяет облегчить овладение числовой единичной окружностью. Конечно, интерактивная доска имеет широчайший диапазон применения, однако не во всех классах она есть. Если же говорить о применении презентаций, то на просторах Интернета и их выбор велик, и каждый педагог может найти наиболее приемлемый вариант для своих уроков.
В чем особенность представляемой мною презентации?
Данная презентация предполагает различные варианты использования и не является наглядностью к конкретному уроку в теме «Тригонометрия». Каждый слайд данной презентации можно использовать обособлено, как на этапе объяснения материала, формирования навыков, так и для рефлексии. При создании данной презентации особое внимание уделялось «читаемости» её с дальнего расстояния, поскольку количество учеников со сниженным зрением постоянно растет. Продумано цветовое решение, логически связанные объекты объединены единым цветом. Презентация анимирована таким образом, чтобы учитель имел возможность комментировать фрагмент слайда, а ученик задать вопрос. Таким образом, данная презентация – это своего рода «подвижные» таблицы. Последние слайды не анимированы и используются для проверки усвоения материала, в ходе решения тригонометрических заданий. Окружность на слайдах максимально упрощена внешне и максимально приближена к изображаемой на тетрадном листе учениками. Это условие я считаю принципиальным. У учащихся важно сформировать мнение о единичной окружности, как о доступном и мобильном (хотя и не единственном) виде наглядности при решении тригонометрических заданий.
Данная презентация поможет педагогам познакомить учеников с единичной окружностью в 9 классе на уроках геометрии при изучении темы «Соотношения между сторонами и углами треугольника». И, конечно, она поможет расширить и углубить навык работы с единичной окружностью при решении тригонометрических заданий у учащихся старшего звена обучения на уроках алгебры.
Слайды 3, 4 поясняют построение единичной окружности; принцип определения местоположения точки на единичной окружности в I и II координатных четвертях; переход от геометрических определений функций синус и косинус (в прямоугольном треугольнике) к алгебраическим на единичной окружности.
Слайды 5-8 поясняют, как найти значения тригонометрических функций для основных углов I координатной четверти.
Слайды 9-11 поясняет знаки функций в координатных четвертях; определение промежутков знакопостоянства тригонометрических функций.
Слайд 12 используется для формирования представлений о положительных и отрицательных значениях углов; знакомством с понятием периодичности тригонометрических функций.
Слайды 13, 14 используются при переходе на радианную меру угла.
Слайды 15-18 не анимированы и используются при решении различных тригонометрических заданий, закрепления и проверки результатов усвоения материала.
Содержание:
- Титульный лист.
- Целеполагание.
- Построение единичной окружности. Основные значения углов в градусной мере.
- Определение синуса и косинуса угла на единичной окружности.
- Табличные значения для синуса в порядке возрастания.
- Табличные значения для косинуса в порядке возрастания.
- Табличные значения для тангенса в порядке возрастания.
- Табличные значения для котангенса в порядке возрастания.
- Знаки функции sin α.
- Знаки функции cos α.
- Знаки функций tg α и ctg α.
- Положительные и отрицательные значения углов на единичной окружности.
- Радианная мера угла.
- Положительные и отрицательные значения углов в радианах на единичной окружности.
- Различные варианты единичной окружности для закрепления и проверки результатов усвоения материала.
12.04.2013
Поделиться страницей:urok.1sept.ru
Симметрия корней и оптимизация ответов в тригонометрии
Внимание! Еще одна часть видеоурока находится ниже!
Когда вы решаете квадратное уравнение относительно синуса или косинуса, то в ответе получается много отдельных множеств, работать с которыми крайне неудобно. Поэтому сегодня мы научимся объединять их, научимся искать симметрию в наборах корней и упрощать себе ответы, а, следовательно, и работу с множествами.
На самом деле существует два способа упростить решение квадратных тождеств. Назовем их условно геометрическим и алгебраическим. Алгебраический подход рассказывается в школе, но большинство учеников пропускают этот способ мимо ушей. Поэтому сегодняшний видео урок будет состоять из двух частей: второй — целиком посвященной геометрическому подходу, когда мы отмечаем корни на тригонометрическом круге, и первой части — в ней рассказывается о формулах понижения степеней. Итак, начнем.
Алгебраический подход
Сейчас мы будем использовать только алгебраический подход. Все, что нам потребуется для решения — это формула косинуса двойного угла:
\[\cos 2x=2{{\cos }^{2}}x-1\]
Давайте немного преобразуем ее:
\[\cos 2x+1=2{{\cos }^{2}}x\]
\[{{\cos }^{2}}x=\frac{\cos 2x+1}{2}\]
\[{{\cos }^{2}}x=\frac{1+\cos 2x}{2}\]
Но как мы знаем, формулу косинуса двойного угла можно переписать и по-другому, а именно:
\[\cos 2x=1-2{{\sin }^{2}}x\]
Давайте выразим отсюда $2{{\sin }^{2}}x$:
\[2{{\sin }^{2}}x=1-\cos 2x\]
\[{{\sin }^{2}}x=\frac{1-\cos 2x}{2}\]
Вот эти две конструкции сейчас мы и будем использовать.
Решаем реальные задачи
Задача №1
\[{{\cos }^{2}}x=\frac{3}{4}\]
Заменяем ${{\cos }^{2}}x$:
\[\frac{1+\cos 2x}{2}=\frac{3}{4}\]
Воспользуемся основным свойством пропорции:
\[\left( 1+\cos 2x \right)\cdot 4=6\]
\[4+4\cos 2x=6\]
\[4\cos 2x=2\]
\[\cos 2x=\frac{1}{2}\]
Решаем обычное тригонометрическое тождество:
\[2=\pm \frac{\text{ }\!\!\pi\!\!\text{ }}{3}+2\text{ }\!\!\pi\!\!\text{ }n,n\in Z\]
Это обычная формула, с помощью которой решаются подобные конструкции. Но у нас известно $2x$, а не $x$, поэтому разделим обе стороны на 2:
\[2=\pm \frac{\text{ }\!\!\pi\!\!\text{ }}{6}+\text{ }\!\!\pi\!\!\text{ }n,n\in Z\]
Мы нашли корни тригонометрического уравнения.
Задача №2
\[{{\sin }^{2}}x=1\]
Применяем нашу вторую конструкцию:
\[\frac{1-\cos 2x}{2}=\frac{1}{1}\]
Снова получили пропорцию, перемножаем крест-накрест:
\[1-\cos 2x=2\]
\[-\cos 2x=1\]
\[\cos 2x=1\]
\[2=\text{ }\!\!\pi\!\!\text{ }+2\text{ }\!\!\pi\!\!\text{ }n,n\in Z\]
\[=\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}+\text{ }\!\!\pi\!\!\text{ }n,n\in Z\]
Мы снова получили корни уравнения.
Задача №3
\[{{\sin }^{2}}x=\frac{1}{2}\]
Снова применяем наши выкладки:
\[\frac{1-\cos 2x}{2}=\frac{1}{2}\]
\[1-\cos 2x=1\]
\[-\cos 2x=0\]
\[\cos 2x=0\]
\[2=\frac{\text{ }\!\!\pi\!\!\text{ }}{2}+\text{ }\!\!\pi\!\!\text{ }n,n\in Z\]
\[=\frac{\text{ }\!\!\pi\!\!\text{ }}{4}+\frac{\text{ }\!\!\pi\!\!\text{ }n}{2},n\in Z\]
Если вы сравните эти ответы с тем, что мы получили в предыдущей части этого урока, то обнаружите, что ответы абсолютно одинаковые. Мы получили один и тот же результат, используя разные подходы — геометрический с помощью тригонометрического круга и алгебраический с помощью формул понижения степеней.
Кстати, почему формулы называются формулами понижения степеней? Смотрите, был ${{\cos }^{2}}x$, а стал просто $\cos 2x$. То же самое и здесь: был ${{\sin }^{2}}x$, а стал просто $\sin 2x$, опять же без квадрата. Эти выкладки сокращают объем вычислений, но чтобы воспользоваться ними, их нужно знать. Кроме того, на последнем шаге везде выполняется деление на 2. Здесь тоже очень часто допускают ошибку. Нужно делить оба слагаемых на два. Каждое из слагаемых нужно разделить на два, и тогда уравнение относительно синуса и косинуса становится элементарным.
Геометрический подход
Реальные задачи
Пример №1
\[{{\cos }^{2}}=\frac{3}{4}\]
Сначала избавляемся от квадрата. Как всегда, если функция в квадрате равна какому-либо числу, то сама функция равна либо корню из этого числа, либо «минус» корню из этого числа:
\[{{f}^{2}}=a\]
\[\left[ \begin{align}& f=\sqrt{a} \\& f=-\sqrt{a} \\\end{align} \right.\]
\[a\ge 0\]
Решаем уравнение, чтобы найти корни тригонометрического выражения:
\[\cos x=\sqrt{\frac{3}{4}}\]
\[\cos x=\frac{\sqrt{3}}{2}\]
\[x=\pm \frac{\text{ }\!\!\pi\!\!\text{ }}{6}+2\pi n\]
В контексте нашего сегодняшнего урока все числа принадлежат множеству целых чисел.
\[\cos x=-\sqrt{\frac{3}{4}}\]
\[\cos x=-\frac{\sqrt{3}}{2}\]
\[x=\pm \arccos \left( -\frac{\sqrt{3}}{2} \right)+2\text{ }\!\!\pi\!\!\text{ }k\]
\[x=\pm \left( \text{ }\!\!\pi\!\!\text{ }-\frac{\pi }{6} \right)+2\text{ }\!\!\pi\!\!\text{ }k\]
\[x=\pm \frac{5\text{ }\!\!\pi\!\!\text{ }}{6}+2\text{ }\!\!\pi\!\!\text{ }k\]
Вот мы и получили два множества. Давайте отметим эти числа на тригонометрической окружности и найдем корни:
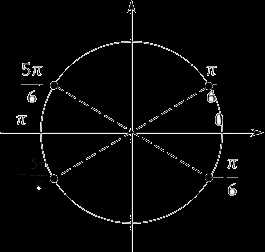
Все наше множество сводится к четырем точкам. А теперь заметим, что $\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$ и $-\frac{5\text{ }\!\!\pi\!\!\text{ }}{6}$ симметричны относительно начала координат. В этом легко убедиться, если вычесть из одного числа другое. Например:
\[\frac{\text{ }\!\!\pi\!\!\text{ }}{6}-\left( -\frac{5\text{ }\!\!\pi\!\!\text{ }}{6} \right)=\text{ }\!\!\pi\!\!\text{ }\]
Другими словами, расстояние между этими числами по окружности равно $\text{ }\!\!\pi\!\!\text{ }$.
То же самое можно сказать про $-\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$ и $\frac{5\text{ }\!\!\pi\!\!\text{ }}{6}$ — они симметричны друг другу относительно начала координат или, другими словами, можно сказать, что они лежат на одном диаметре. Если идти по нашей окружности, то расстояние между ними будет равно $\text{ }\!\!\pi\!\!\text{ }$, а это значит, что если мы возьмем точку $\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$, а потом шагнем от нее на $\text{ }\!\!\pi\!\!\text{ }$, то получим точку $-\frac{5\text{ }\!\!\pi\!\!\text{ }}{6}$. Потом еще шагнем на $\text{ }\!\!\pi\!\!\text{ }$ — снова попадем в точку $\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$, но уже $+2\text{ }\!\!\pi\!\!\text{ }$. И так постоянно прибавляя $\text{ }\!\!\pi\!\!\text{ }$, мы охватим все точки вида $\frac{\text{ }\!\!\pi\!\!\text{ }}{6}+2\text{ }\!\!\pi\!\!\text{ }$ и $-\frac{\text{ }\!\!\pi\!\!\text{ }}{6}+2\text{ }\!\!\pi\!\!\text{ k}$. Таким образом, мы можем записать эти корни уравнения в виде одного множества:
\[\frac{\text{ }\!\!\pi\!\!\text{ }}{6}+\pi k\]
Теперь разберемся со вторым набором. Тут все то же самое:\[-\frac{\text{ }\!\!\pi\!\!\text{ }}{6}+\text{ }\!\!\pi\!\!\text{ }k\]. Таким образом, мы можем просто спереди поставить ±, и это будет наш окончательный ответ:
\[x=\pm \frac{\text{ }\!\!\pi\!\!\text{ }}{6}+\text{ }\!\!\pi\!\!\text{ }k\]
Вместо четырех множеств (или двух) мы получили всего одно множество. В этом и состоит смысл симметрии корней. В дальнейшем, когда нам нужно будет что-то сделать с этими корнями, мы уже будем работать не с 4 наборами, а всего лишь с двумя.
Пример №2
\[{{\sin }^{2}}x=1\]
Опять же используем наши выкладки и избавляемся от квадрата:
\[\sin x=1\]
\[x=\frac{\text{ }\!\!\pi\!\!\text{ }}{2}+2\text{ }\!\!\pi\!\!\text{ }n\]
И второе уравнение:
\[\sin x=-1\]
\[x=-\frac{\text{ }\!\!\pi\!\!\text{ }}{2}\text{+}2\text{ }\!\!\pi\!\!\text{ }k\]
Отмечаем эти числа на тригонометрической окружности:
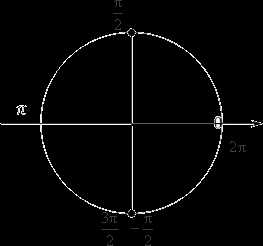
Из рисунка становится очевидно, что эти точки лежат на одном диаметре — он является осью $Oy$, осью синусов. Это значит, чтобы получить из\[\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}+2\text{ }\!\!\pi\!\!\text{ }n\]\[-\frac{\text{ }\!\!\pi\!\!\text{ }}{2}+2\text{ }\!\!\pi\!\!\text{ }k\], достаточно шагнуть из точки $\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}$ до $-\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}$ на $\text{ }\!\!\pi\!\!\text{ }$. Таким образом мы объединяем два множества корней и получаем:
\[x=\frac{\text{ }\!\!\pi\!\!\text{ }}{2}+\text{ }\!\!\pi\!\!\text{ }n˜˜˜˜˜˜\]
Пример №3
\[{{\sin }^{2}}x=\frac{1}{2}\]
Снова считаем по нашим выкладкам:
\[\sin x=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}\]
\[\sin x=\frac{\sqrt{2}}{2}\]
\[x=\frac{\text{ }\!\!\pi\!\!\text{ }}{4}+2\text{ }\!\!\pi\!\!\text{ }n\]
\[x=\text{ }\!\!\pi\!\!\text{ }-\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}+2\text{ }\!\!\pi\!\!\text{ }n\]
\[x=\frac{3\text{ }\!\!\pi\!\!\text{ }}{4}+2\text{ }\!\!\pi\!\!\text{ }n\]
Переходим ко второму выражению:
\[\sin x=-\frac{\sqrt{2}}{2}\]
\[x=-\frac{\text{ }\!\!\pi\!\!\text{ }}{4}+2\text{ }\!\!\pi\!\!\text{ }l\]
\[x=\text{ }\!\!\pi\!\!\text{ }-\left( -\frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)+2\text{ }\!\!\pi\!\!\text{ }m\]
\[x=\text{ }\!\!\pi\!\!\text{ }+\frac{\text{ }\!\!\pi\!\!\text{ }}{4}+2\text{ }\!\!\pi\!\!\text{ }m\]
\[x=\frac{5\text{ }\!\!\pi\!\!\text{ }}{4}+2\text{ }\!\!\pi\!\!\text{ }m\]
Вот мы и получили четыре набора корней. Давайте отметим их:

Еще очень важно, что между $\frac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}$ и $\frac{\text{ }\!\!\pi\!\!\text{ }}{4}$ угол равен 90°. Также и между $\frac{5\text{ }\!\!\pi\!\!\text{ }}{4}$ и $-\frac{\text{ }\!\!\pi\!\!\text{ }}{4}$ угол равен 90°. Наконец, и между $\frac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}$и $\frac{5\text{ }\!\!\pi\!\!\text{ }}{4}$ угол тоже равен 90°. Это значит, что все четыре точки мы можем свести к одной точке вида\[\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}+\frac{\text{ }\!\!\pi\!\!\text{ }n}{2}\].
На первый взгляд эта конструкция, все эти вычисления могут показаться очень сложными. Геометрический подход, действительно, понимают не все ученики. Однако стоит немного потренироваться, и вы будете щелкать квадратные уравнения как орешки.
Ключевые моменты
Решая уравнения, квадратные относительно синуса или косинуса, вы постоянно будете натыкаться на громоздкие ответы, работать с которыми (например, для отбора корней) совершенно невозможно. Однако при желании можно значительно упростить эти конструкции. И сегодня мы поговорим о двух методах упрощения:
- Графический — отмечаем ответы на тригонометрическом круге и пытаемся найти закономерности.
- Алгебраический — переходим от квадратного уравнения к линейному с помощью формул понижения степеней.
Вы можете использовать любой прием — ответ получится один и тот же. Кому-то (например, мне) удобнее отмечать точки на тригонометрическом круге, а кому-то проще раз и навсегда запомнить формулы понижения степени (которые, кстати, совсем несложные).
Симметрия корней на тригонометрическом круге
Тут все банально. Решаем равенство, отмечаем полученные корни на круге, а затем ищем какую-нибудь закономерность в их расположении. Например, корни могут отстоять друг от друга на половину исходного периода, либо располагаться симметрично относительно начала координат.
Формулы понижения степеней
Это уникальная фишка, которая работает только в тригонометрических уравнениях. Уравнения, квадратные относительно синуса или косинуса, легком сводятся к равносильным линейным. Все, что для этого потребуется — формулы косинуса двойного угла:
\[\cos 2x=2\cos 2\text{ }x-1;\]
\[\cos 2x=1-2\sin 2x.\]
Смотрите также:
- Однородные тригонометрические уравнения: общая схема решения
- Учимся расщеплять ответы в тригонометрических уравнениях
- Решение задач B6: №362—377
- Геометрическая вероятность
- Пробный ЕГЭ по математике 2015: 2 вариант
- Задача B2 на проценты: вычисление полной стоимости покупки
www.berdov.com
Тригонометрический круг — это… Что такое Тригонометрический круг?
Тригонометрический круг — построенная на плоскости с прямоугольными декартовыми координатами окружность, имеющая центр в точке начала координат и единичный радиус, т.е. единичная окружность, которая используется для геометрического определения тригонометрических функций. Название «тригонометрический круг» не совсем удачно, поскольку речь идёт об окружности, а не о круге; тем не менее, часто используется именно это название.
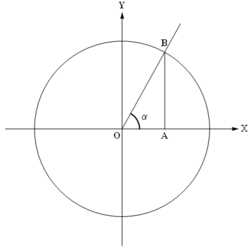 Единичная окружность и угол , отложенный от оси абсцисс в верхнюю полуплоскость
Единичная окружность и угол , отложенный от оси абсцисс в верхнюю полуплоскостьОпределение тригонометрических функций произвольного угла строится с помощью тригонометрического круга следующим образом. Угол (назовём его ) откладывается от положительной полупрямой оси абсцисс в верхнюю полуплоскость («против часовой стрелки») и рассматривается точка пересечения полученного луча (составляющего угол с положительной полупрямой оси абсцисс) с единичной окружностью. Абсцисса этой точки принимается за , ордината — за . Для введения других тригонометрических функций используются дополнительные построения, такие, например, как линия тангенсов (прямая ) и линия котангенсов (прямая ).
 Численные значения тригонометрических функций угла на тригонометрическом круге (радиус равен единице)
Численные значения тригонометрических функций угла на тригонометрическом круге (радиус равен единице)muller.academic.ru
Тригонометрический круг — это… Что такое Тригонометрический круг?
Тригонометрический круг — построенная на плоскости с прямоугольными декартовыми координатами окружность, имеющая центр в точке начала координат и единичный радиус, т.е. единичная окружность, которая используется для геометрического определения тригонометрических функций. Название «тригонометрический круг» не совсем удачно, поскольку речь идёт об окружности, а не о круге; тем не менее, часто используется именно это название.
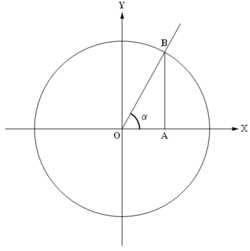 Единичная окружность и угол , отложенный от оси абсцисс в верхнюю полуплоскость
Единичная окружность и угол , отложенный от оси абсцисс в верхнюю полуплоскостьОпределение тригонометрических функций произвольного угла строится с помощью тригонометрического круга следующим образом. Угол (назовём его ) откладывается от положительной полупрямой оси абсцисс в верхнюю полуплоскость («против часовой стрелки») и рассматривается точка пересечения полученного луча (составляющего угол с положительной полупрямой оси абсцисс) с единичной окружностью. Абсцисса этой точки принимается за , ордината — за . Для введения других тригонометрических функций используются дополнительные построения, такие, например, как линия тангенсов (прямая ) и линия котангенсов (прямая ).
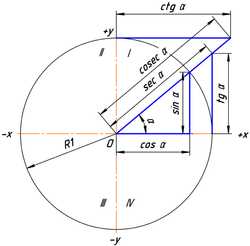 Численные значения тригонометрических функций угла на тригонометрическом круге (радиус равен единице)
Численные значения тригонометрических функций угла на тригонометрическом круге (радиус равен единице)ushakov.academic.ru
