Геометрия. Урок 1. Тригонометрия — ЁП
Содержание страницы:
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.
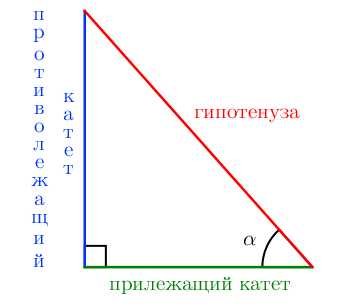
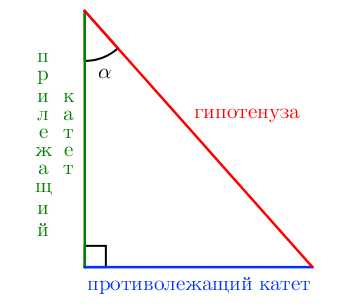
Синус угла – отношение противолежащего катета к гипотенузе.
sinα=Противолежащий катетгипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cosα=Прилежащий катетгипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tgα=Противолежащий катетПрилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctgα=Прилежащий катетПротиволежащий катет
Рассмотрим прямоугольный треугольник ABC, угол C равен 90°:
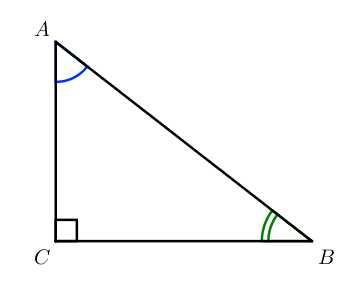
sin∠A=CBAB
cos∠A=ACAB
tg∠A=sin∠Acos∠A=CBAC
ctg∠A=cos∠Asin∠A=ACCB
sin∠B=ACAB
cos∠B=BCAB
tg∠B=sin∠Bcos∠B=ACCB
ctg∠B=cos∠Bsin∠B=CBAC
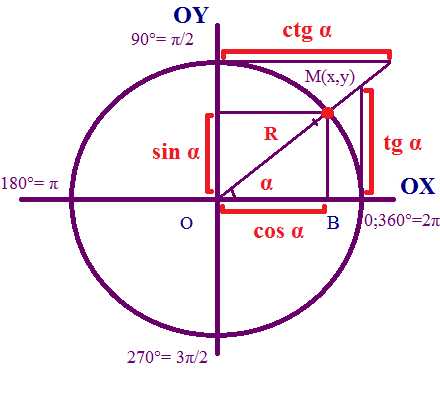
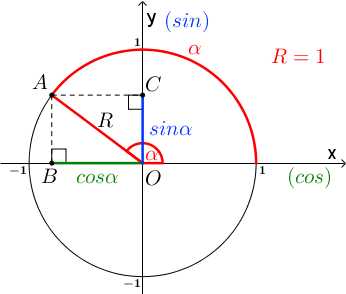
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Такая окружность пересекает ось х в точках (−1;0) и (1;0), ось y в точках (0;−1) и (0;1)
На данной окружности будет три шкалы отсчета – ось x, ось y и сама окружность, на которой мы будем откладывать углы.
Углы на тригонометрической окружности откладываются от точки с координатами (1;0), – то есть от положительного направления оси x, против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A. Рассмотрим ∠SOA, обозначим его за α. Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠SOA=α=∪SA.

Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B) и на ось игрек (точка C).

Отрезок OB является проекцией отрезка OA на ось x, отрезок OC является проекцией отрезка OA на ось y.
Рассмотрим прямоугольный треугольник AOB:
cosα=OBOA=OB1=OB
sinα=ABOA=AB1=AB
Поскольку OCAB – прямоугольник, AB=CO.
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α — тупой, то есть больше 90°:
Опускаем из точки A перпендикуляры к осям x и y. Точка B в этом случае будет иметь отрицательную координату по оси x.
Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0° до 180°. Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x. Отметим на этой окружности углы 0°,30°,45°,60°,90°,120°,135°,150°,180°. Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y.
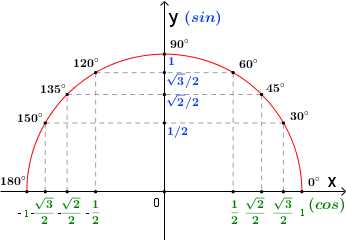
Координата по оси x – косинус угла, координата по оси y – синус угла.
Пример:
cos150°=−32
sin150°=12
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный.
Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный.
sin2α+cos2α=1
Данное тождество – теорема Пифагора в прямоугольном треугольнике OAB:

AB2+OB2=OA2
sin2α+cos2α=R2
sin2α+cos2α=1
|
|
0° | 30° | 45° | 60° | 90° |
| sinα | 0 | 12 | 22 | 32 | 1 |
| cosα | 1 | 32 | 22 | 12 | 0 |
| tgα | 0 | 33 | 1 | 3 | нет |
| ctgα | нет | 3 | 1 | 33 | 0 |
Если внимательно рассмотреть данный рисунок,

можно заметить, что:
sin180°=sin(180°−0°)=sin0°
sin150°=sin(180°−30°)=sin30°
sin135°=sin(180°−45°)=sin45°
sin120°=sin(180°−60°)=sin60°
cos180°=cos(180°−0°)=−cos0°
cos150°=cos(180°−30°)=−cos30°
cos135°=cos(180°−45°)=−cos45°
cos120°=cos(180°−60°)=−cos60°
Рассмотрим тупой угол β:
Для произвольного тупого угла β=180°−α всегда будут справедливы следующие равенства:
sin(180°−α)=sinα
cos(180°−α)=−cosα
tg(180°−α)=−tgα
ctg(180°−α)=−ctgα
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.

asin∠A=bsin∠B=csin∠C
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.

asin∠A=bsin∠B=csin∠C=2R
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

a2=b2+c2−2bc⋅cos∠A
b2=a2+c2−2ac⋅cos∠B
Модуль геометрия: задания, связанные с тригонометрией.
Скачать домашнее задание к уроку 1.
epmat.ru
| Главная > Учебные материалы > Математика: Тригонометрия | ||||
|
1.Тригонометрия. 2.Тригонометрические функции.
|
||||
| 1 2 3 4 5 6 7 8 9 | ||||
1. Тригонометрия – раздел математики, изучающий зависимости между углами и сторонами в треугольниках и тригонометрические функции. Основная задача тригонометрии — вычисление неизвестных величин треугольника, если известны значения других его величин. В тригонометрии также решают задачу о вычислении углов треугольника, если известны его стороны, задачу о вычислении сторон треугольника и т.д. |
||||
Для измерения углов между сторонами треугольника используется такая единица измерения, как градус. Вся окружность с центром в точке О составляет 360°. Помимо градусной меры углов, также используется радианная мера. 1 рад ≈ 57,295779513° ≈ 57°17′44,806″ ≈ 206265″. Радианная и градусная меры связаны зависимостью 180°=π радиан. Угол в n° равен πn/ 180 радиан. Для того, чтобы рассчитать длину дуги угла α, используется следующая формула: l= αr Площадь S сектора круга радиуса r, дуга которого содержит α радиан, рассчитывается так: S = αr² / 2 |
 Площадь сектора круга. |
|||
2. Тригонометрические функции. Тригонометрические функции — математические функции от величины угла. Они используются при изучении геометрии, а также при исследовании переодических процессов в разных областях науки. Тригонометрические функции определяют отношения сторон прямоугольного треугольника в единичной окружности. Пусть на плоскости задана прямоугольная система координат с началом в точке O и с осями OX и OY . Возьмем в этой системе координат окружность с центром в точке O и радиусом, равным единице. Пусть отрезок OМ поворачивается на произвольный угол α вокруг центра O. Так как треугольник ОМВ прямоугольный, то тригонометрические функции угла α определяется из соотношений в прямоугольном треугольнике. Тогда: |
||||
| Синусом угла α называется отношение противолежащего катета к гипотенузе или отношение координаты y точки М к длине отрезка OМ=R, где R — радиус окружности. Синус угла α обозначают sinα. Так как длина отрезка OМ=1, следовательно sinα = y. Косинусом угла α называется отношение прилежащего катета к гипотенузе или отношение координаты х точки М к длине отрезка OМ. Косинус угла α обозначают cosα. Так как ОМ=1, то cosα = х. Тангенсом угла α называется отношение противолежащего катета к прилежащему или координаты y точки М к x. Тангенс угла α обозначают tgα. Так как y = sin α и x = cos α, то tgα= sin α / cos α. Котангенсом угла α называется отношение прилежащего катета к противолежащему или отношение координаты х точки М к y. Котангенс угла α обозначают ctgα. Так как y = sin α и x = cos α, то ctgα= cosα / sinα. Из последних двух соотношений следует: ctg α= 1 / tg α |
sin, cos, tg, ctg на тригонометрическом круге. |
|||
y = sin x
|
График функции sin. |
|||
y = cos x
|
График функции cos. |
|||
y = tg x
|
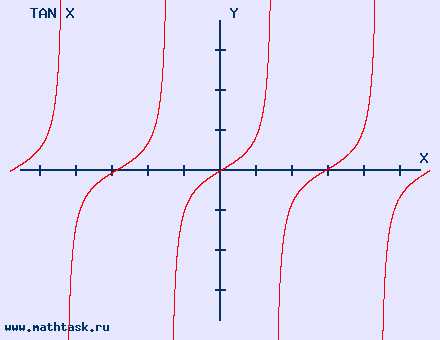 График функции tg. |
|||
y = ctg x
|
График функции сtg. |
|||
 |
||||
Значения синуса и косинуса для некоторых углов. |
||||
 |
||||
 |
||||
| Значения тангенса и котангенса для углов 30, 45 и 60 находятся аналогично. | ||||
Пример 1 |
||||
 |
||||
| Пример 2 | ||||
| 1 2 3 4 5 6 7 8 9 | ||||
www.mathtask.ru
Отсчёт углов на тригонометрическом круге. Положительные и отрицательные углы. Распределение углов по четвертям.
В прошлом уроке мы с вами успешно освоили (или повторили – кому как) ключевые понятия всей тригонометрии. Это тригонометрический круг, угол на круге, синус и косинус этого угла, а также освоили знаки тригонометрических функций по четвертям. Освоили подробно. На пальцах, можно сказать.
Но этого пока мало. Для успешного практического применения всех этих простых понятий нам необходим ещё один полезный навык. А именно – правильная работа с углами в тригонометрии. Без этого умения в тригонометрии – никак. Даже в самых примитивных примерах. Почему? Да потому, что угол – ключевая действующая фигура во всей тригонометрии! Нет, не тригонометрические функции, не синус с косинусом, не тангенс с котангенсом а именно сам угол. Нет угла – нету и тригонометрических функций, да…
Как правильно работать с углами на круге? Для этого нам надо железно усвоить два пункта.
1) Как отсчитываются углы на круге?
2) В чём они считаются (измеряются)?
Ответ на первый вопрос – и есть тема сегодняшнего урока. С первым вопросом мы детально разберёмся прямо здесь и сейчас. Ответ на второй вопрос здесь не дам. Ибо достаточно развёрнутый он. Как и сам второй вопрос очень скользкий, да.) Вдаваться в подробности пока не буду. Это – тема следующего отдельного урока.
Приступим?
Как отсчитываются углы на круге? Положительные и отрицательные углы.
У прочитавших название параграфа, возможно, уже волосы встали дыбом. Как так?! Отрицательные углы? Разве такое вообще возможно?
К отрицательным числам мы с вами уже попривыкли. На числовой оси их изображать умеем: справа от нуля положительные, слева от нуля отрицательные. Да и на градусник за окном поглядываем периодически. Особенно зимой, в мороз.) И денежки на телефоне в «минус» (т.е. долг) иногда уходят. Это всё знакомо.
А что же с углами? Оказывается, отрицательные углы в математике тоже бывают! Всё зависит от того, как отсчитывать этот самый угол… нет, не на числовой прямой, а на числовой окружности! То бишь, на круге. Круг – вот он, аналог числовой прямой в тригонометрии!
Итак, как же отсчитываются углы на круге? Ничего не поделать, придётся нам для начала этот самый круг нарисовать.
Я нарисую вот такую красивую картинку:
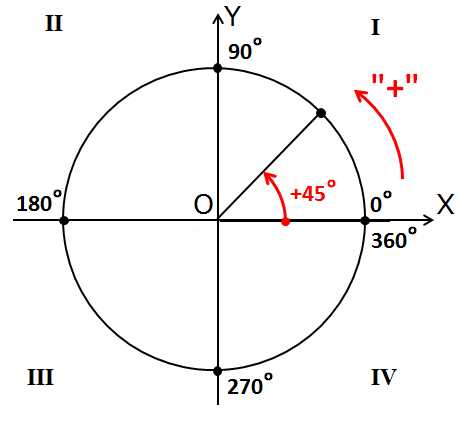
Она очень похожа на картинки из прошлого урока. Есть оси, есть окружность, есть угол. Но есть и новая информация.
Во-первых, я добавил номера четвертей (или квадрантов). Напоминаю, что четверти всегда нумеруются против часовой стрелки.
Также я добавил циферки 0°, 90°, 180°, 270° и 360° на осях. Вот это уже поинтереснее.) Что это за циферки? Правильно! Это значения углов, отсчитанные от нашей неподвижной стороны, которые попадают на координатные оси. Вспоминаем, что неподвижная сторона угла у нас всегда крепко-накрепко привязана к положительной полуоси ОХ. И любой угол в тригонометрии отсчитывается именно от этой полуоси. Это базовое начало отсчёта углов надо держать в голове железно. А оси – они же под прямым углом пересекаются, верно? Вот и прибавляем по 90° в каждой четверти.
И ещё добавлена красная стрелочка. С плюсом. Красная – это специально, чтобы в глаза бросалась. И в память хорошенько врезалась. Ибо это надо запомнить надёжно.) Что же означает эта стрелочка?
Так вот оказывается, если наш угол мы будем крутить по стрелочке с плюсом (против часовой стрелки, по ходу нумерации четвертей), то угол будет считаться положительным! В качестве примера на рисунке показан угол +45°. Кстати, обратите внимание, что осевые углы 0°, 90°, 180°, 270° и 360° также отмотаны именно в плюс! По красной стрелочке.
А теперь посмотрим на другую картинку:
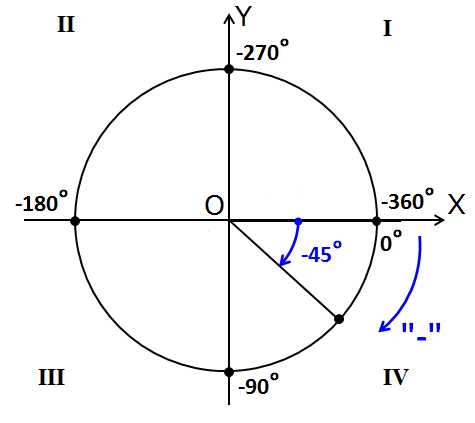
Здесь почти всё то же самое. Только углы на осях пронумерованы в обратную сторону. По часовой стрелке. И имеют знак «минус».) Ещё нарисована синяя стрелочка. Также с минусом. Эта стрелочка – направление отрицательного отсчёта углов на круге. Она нам показывает, что, если мы будем откладывать наш угол по ходу часовой стрелки, то угол будет считаться отрицательным. Для примера я показал угол -45°.
Кстати, прошу заметить, что нумерация четвертей никогда не меняется! Неважно, в плюс или в минус мы мотаем углы. Всегда строго против часовой стрелки.)
Запоминаем:
1. Начало отсчёта углов – от положительной полуоси ОХ. По часам – «минус», против часов – «плюс».
2. Нумерация четвертей всегда против часовой стрелки вне зависимости от направления исчисления углов.
Кстати говоря, подписывать углы на осях 0°, 90°, 180°, 270°, 360°, каждый раз рисуя круг – вовсе не обязаловка. Это чисто для понимания сути сделано. Но эти циферки обязательно должны присутствовать в вашей голове при решении любой задачи по тригонометрии. Почему? Да потому, что эти элементарные знания дают ответы на очень многие другие вопросы во всей тригонометрии! Самый главный вопрос – в какую четверть попадает интересующий нас угол? Хотите верьте, хотите нет, но правильный ответ на этот вопрос решает львиную долю всех остальных проблем с тригонометрией. Этим важным занятием (распределением углов по четвертям) мы займёмся в этом же уроке, но чуть позже.
Величины углов, лежащих на осях координат (0°, 90°, 180°, 270° и 360°), надо запомнить! Запомнить накрепко, до автоматизма. Причём как в плюс, так и в минус.
А вот с этого момента начинаются первые сюрпризы. И вместе с ними и каверзные вопросы в мой адрес, да…) А что будет, если отрицательный угол на круге совпадёт с положительным? Выходит, что одну и ту же точку на круге можно обозначить как положительным углом, так и отрицательным???
Совершенно верно! Так и есть.) Например, положительный угол +270° занимает на круге то же самое положение, что и отрицательный угол -90°. Или, например, положительный угол +45° на круге займёт то же самое положение, что и отрицательный угол -315°.
Смотрим на очередной рисунок и всё видим:
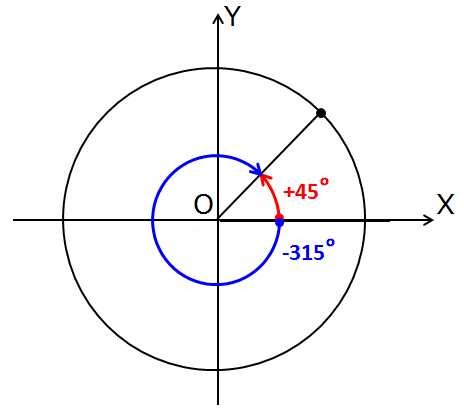
Точно так же положительный угол +150° попадёт туда же, куда и отрицательный угол -210°, положительный угол +230° – туда же, куда и отрицательный угол -130°. И так далее…
И что теперь делать? Как именно считать углы, если можно и так и сяк? Как правильно?
Ответ: по-всякому правильно! Ни одно из двух направлений отсчёта углов математика не запрещает. А выбор конкретного направления зависит исключительно от задания. Если в задании ничего не сказано прямым текстом про знак угла (типа «определите наибольший отрицательный угол» и т.п.), то работаем с наиболее удобными нам углами.
Конечно, например, в таких крутых темах, как тригонометрические уравнения и неравенства направление исчисления углов может колоссально влиять на ответ. И в соответствующих темах мы эти подводные камни рассмотрим.
Запоминаем:
Любую точку на круге можно обозначить как положительным, так и отрицательным углом. Любым! Каким хотим.
А теперь призадумаемся вот над чем. Мы выяснили, что угол 45° в точности совпадает с углом -315°? Как же я узнал про эти самые 315°? Не догадываетесь? Да! Через полный оборот.) В 360°. У нас есть угол 45°. Сколько не хватает до полного оборота? Отнимаем 45° от 360° – вот и получаем 315°. Мотаем в отрицательную сторону – и получаем угол -315°. Всё равно непонятно? Тогда смотрим на картинку выше ещё раз.
И так надо поступать всегда при переводе положительных углов в отрицательные (и наоборот) – рисуем круг, отмечаем примерно заданный угол, считаем, сколько градусов не хватает до полного оборота, и мотаем получившуюся разность в противоположную сторону. И всё.)
Чем ещё интересны углы, занимающие на круге одно и то же положение, как вы думаете? А тем, что у таких углов совершенно одинаковые синус, косинус, тангенс и котангенс! Всегда!
Например:
sin45° = sin(-315°)
cos120° = cos(-240°)
tg249° = tg(-111°)
ctg333° = ctg(-27°)
И так далее и тому подобное. В общем, вы поняли… Кстати, прошу заметить, что углы в этих парочках различны. Зато тригонометрические функции у них – одинаковы! Идея ясна?
А вот это уже крайне важно! Зачем? Да всё за тем же!) Для упрощения выражений. Ибо упрощение выражений – ключевая процедура успешного решения любых заданий по математике. И по тригонометрии в том числе.
Итак, с общим правилом отсчёта углов на круге разобрались. Ну а коли мы тут заикнулись про полные обороты, про четверти, то пора бы уже покрутить и порисовать эти самые углы. Порисуем?)
Начнём пока с положительных углов. Они попроще в рисовании будут.
Рисуем углы в пределах одного оборота (между 0° и 360°).
Нарисуем, например, угол 60°. Тут всё просто, никаких заморочек. Рисуем координатные оси, круг. Можно прямо от руки, безо всякого циркуля и линейки. Рисуем схематично: у нас не черчение с вами. Никаких ГОСТов соблюдать не надо, не накажут.)
Можно (для себя) отметить значения углов на осях и указать стрелочку в направлении против часов. Ведь мы же в плюс откладывать собираемся?) Можно этого и не делать, но в голове держать всяко надо.
И теперь проводим вторую (подвижную) сторону угла. В какой четверти? В первой, разумеется! Ибо 60 градусов – это строго между 0° и 90°. Вот и рисуем в первой четверти. Под углом примерно 60 градусов к неподвижной стороне. Как отсчитать примерно 60 градусов без транспортира? Легко! 60° – это две трети от прямого угла! Делим мысленно первую чертвертинку круга на три части, забираем себе две трети. И рисуем… Сколько у нас там по факту получится (если приложить транспортир и померить) – 55 градусов или же 64 – неважно! Важно, что всё равно где-то около 60°.
Получаем картинку:
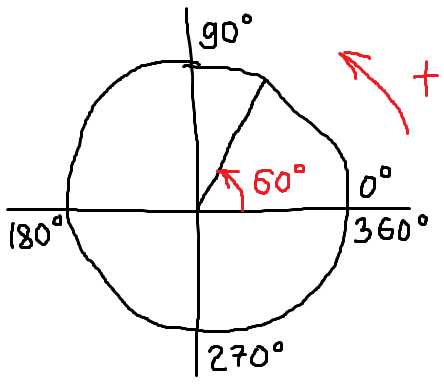
Вот и всё. И инструментов не понадобилось. Развиваем глазомер! В задачах по геометрии пригодится.) Этот неказистый рисунок бывает незаменим, когда надо нацарапать круг и угол на скорую руку, не особо задумываясь о красоте. Но при этом нацарапать правильно, без ошибок, со всей необходимой информацией. Например, как вспомогательное средство при решении тригонометрических уравнений и неравенств.
Нарисуем теперь угол, например, 265°. Прикидываем, где он может располагаться? Ну, ясное дело, что не в первой четверти и даже не во второй: они на 90 и на 180 градусов оканчиваются. Можно сообразить, что 265° — это 180° плюс ещё 85°. То есть, к отрицательной полуоси ОХ (там, где 180°) надо добавить примерно 85°. Или, что ещё проще, догадаться, что 265° не дотягивает до отрицательной полуоси OY (там, где 270°) каких-то несчастных 5°. Одним словом, в третьей четверти будет этот угол. Очень близко к отрицательной полуоси OY, к 270 градусам, но всё-таки в третьей!
Рисуем:
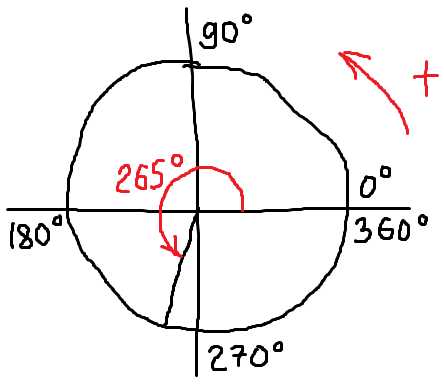
Повторюсь, абсолютная точность здесь не требуется. Пускай в реальности этот угол получился, скажем 263 градуса. Но на самый главный вопрос (какая четверть?) мы ответили безошибочно. Почему этот вопрос самый главный? Да потому, что любая работа с углом в тригонометрии (неважно, будем мы рисовать этот угол или не будем) начинается с ответа именно на этот вопрос! Всегда. Если этот вопрос проигнорировать или пробовать на него ответить мысленно, то ошибки почти неизбежны, да… Оно вам надо?
Запоминаем:
Любая работа с углом (в том числе и рисование этого самого угла на круге) всегда начинается с определения четверти, в которую попадает этот угол.
Теперь, я надеюсь, вы уже безошибочно изобразите углы, например, 182°, 88°, 280°. В правильных четвертях. В третьей, первой и четвёртой, если что…)
Четвёртая четверть заканчивается углом 360°. Это один полный оборот. Ясен перец, что этот угол занимает на круге то же самое положение, что и 0° (т.е. начало отсчёта). Но углы на этом не заканчиваются, да…
Что делать с углами, большими 360°?
«А такие разве бывают?» – спросите вы. Бывают, ещё как! Бывает, например, угол 444°. А бывает, скажем, угол 1000°. Всякие углы бывают.) Просто визуально такие экзотические углы воспринимаются чуть сложнее, чем привычные нам углы в пределах одного оборота. Но рисовать и просчитывать такие углы тоже надо уметь, да.
Для правильного рисования таких углов на круге необходимо всё то же самое – выяснить, в какую четверть попадает интересующий нас угол. Здесь умение безошибочно определять четверть куда более важно, чем для углов от 0° до 360°! Сама процедура определения четверти усложняется всего одним шагом. Каким, скоро увидите.
Итак, например, нам надо выяснить, в какую четверть попадает угол 444°. Начинаем крутить. Куда? В плюс, разумеется! Угол-то нам дали положительный! +444°. Крутим, крутим… Крутанули на один оборот – дошли до 360°.
Ну и крутим себе дальше!
Сколько там осталось до 444°? Считаем оставшийся хвостик:
444°-360° = 84°.
Итак, 444° — это один полный оборот (360°) плюс ещё 84°. Очевидно, это первая четверть. Итак, угол 444° попадает в первую четверть. Полдела сделано.
Осталось теперь изобразить этот угол. Как? Очень просто! Делаем один полный оборот по красной (плюсовой) стрелке и добавляем ещё 84°.
Вот так:
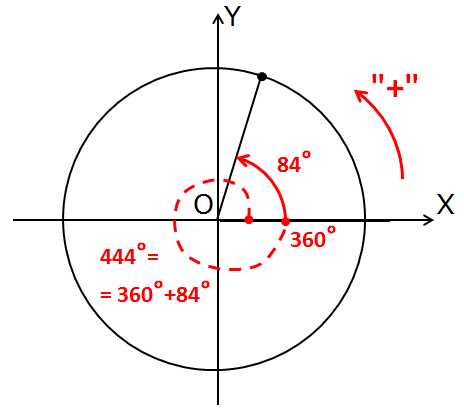
Здесь я уж не стал загромождать рисунок – подписывать четверти, рисовать углы на осях. Это всё добро уже давно в голове быть должно.)
Зато я «улиткой» или спиралькой показал, как именно складывается угол 444° из углов 360° и 84°. Пунктирная красная линия – это один полный оборот. К которому дополнительно прикручиваются 84° (сплошная линия). Кстати, обратите внимание, что, если этот самый полный оборот отбросить, то это никак не повлияет на положение нашего угла!
А вот это важно! Положение угла 444° полностью совпадает с положением угла 84°. Никаких чудес нет, так уж получается.)
А можно ли отбросить не один полный оборот, а два или больше?
А почему – нет? Если угол здоровенный, то не просто можно, а даже нужно! Угол-то не изменится! Точнее, сам-то угол по величине, конечно же, изменится. А вот его положение на круге – никак нет!) На то они и полные обороты, что сколько экземпляров ни добавляй, сколько ни убавляй, всё равно будешь в одну и ту же точку попадать. Приятно, правда?
Запоминаем:
Если к углу прибавить (отнять) любое целое число полных оборотов, положение исходного угла на круге НЕ изменится!
Например:
В какую четверть попадает угол 1000°?
Никаких проблем! Считаем, сколько полных оборотов сидит в тысяче градусов. Один оборот — это 360°, ещё один – уже 720°, третий — 1080°… Стоп! Перебор! Значит, в угле 1000° сидит два полных оборота. Выбрасываем их из 1000° и считаем остаток:
1000° — 2·360° = 280°
Значит, положение угла 1000° на круге то же самое, что и у угла 280°. С которым работать уже гораздо приятнее.) И куда же попадает этот угол? В четвёртую четверть он попадает: 270° (отрицательная полуось OY) плюс ещё десяточка.
Рисуем:
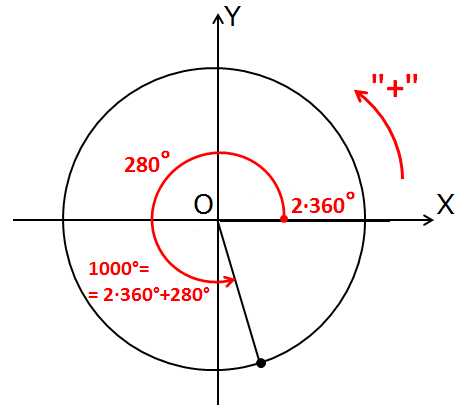
Здесь я уже не рисовал пунктирной спиралькой два полных оборота: уж больно длинная она получается. Просто нарисовал оставшийся хвостик от нуля, отбросив все лишние обороты. Как будто бы их и не было вовсе.)
И ещё раз. По-хорошему, углы 444° и 84°, а также 1000° и 280° – разные. Но для синуса, косинуса, тангенса и котангенса эти углы – одинаковые!
Как вы видите, для того чтобы работать с углами, большими 360°, надо определить, сколько полных оборотов сидит в заданном большом угле. Это и есть тот самый дополнительный шаг, который обязательно надо предварительно проделывать при работе с такими углами. Ничего сложного, правда?
Отбрасывание полных оборотов, конечно, занятие приятное.) Но на практике при работе с совсем уж кошмарными углами случаются и затруднения.
Например:
В какую четверть попадает угол 31240° ?
И что же, будем много-много раз прибавлять по 360 градусов? Можно, если не горит особо. Но мы же не только складывать можем.) Ещё и делить умеем!
Вот и поделим наш большущий угол на 360 градусов!
Этим действием мы как раз и узнаем, сколько полных оборотов запрятано в наших 31240 градусах. Можно уголком поделить, можно (шепну на ушко :)) на калькуляторе.)
Получим 31240:360 = 86,777777….
То, что число получилось дробным – не страшно. Нас же только целые обороты интересуют! Стало быть, до конца делить и не надо.)
Итак, в нашем лохматом угле сидит аж 86 полных оборотов. Ужас…
В градусах это будет 86·360° = 30960°
Вот так. Именно столько градусов можно безболезненно выкинуть из заданного угла 31240°. Останется:
31240° — 30960° = 280°
Всё! Положение угла 31240° полностью идентифицировано! Там же, где и 280°. Т.е. четвёртая четверть.) Кажется, мы уже изображали этот угол ранее? Когда угол 1000° рисовали?) Там мы тоже на 280 градусов вышли. Совпадение.)
Итак, мораль сей басни такова:
Если нам задан страшный здоровенный угол, то:
1. Определяем, сколько полных оборотов сидит в этом угле. Для этого делим исходный угол на 360 и отбрасываем дробную часть.
2. Считаем, сколько градусов в полученном количестве оборотов. Для этого умножаем число оборотов на 360.
3. Отнимаем эти обороты от исходного угла и работаем с привычным углом в пределах от 0° до 360°.
Как работать с отрицательными углами?
Не вопрос! Точно так же, как и с положительными, только с одним единственным отличием. Каким? Да! Крутить углы надо в обратную сторону, в минус! По ходу часовой стрелки.)
Нарисуем, например, угол -200°. Сначала всё как обычно для положительных углов – оси, круг. Ещё синюю стрелочку с минусом изобразим да углы на осях по-другому подпишем. Их, естественно, также придётся отсчитывать в отрицательном направлении. Это будут всё те же самые углы, шагающие через 90°, но отсчитанные в обратную сторону, в минус: 0°, -90°, -180°, -270°, -360°.
Картинка станет вот такой:
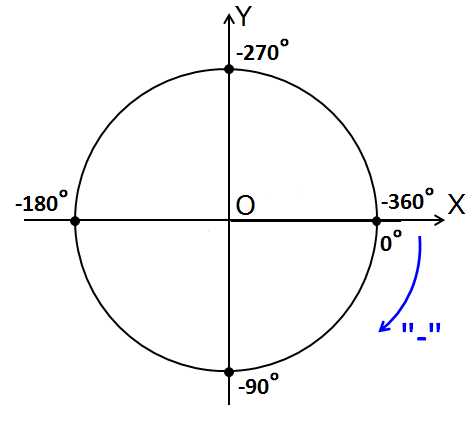
При работе с отрицательными углами часто возникает чувство лёгкого недоумения. Как так?! Получается, что одна и та же ось – это одновременно, скажем, и +90° и -270°? Неее, что-то тут нечисто…
Да всё чисто и прозрачно! Мы ведь же уже в курсе, что любую точку на круге можно обозвать как положительным углом, так и отрицательным! Совершенно любую. В том числе и на какой-то из координатных осей. В нашем случае нам нужно отрицательное исчисление углов. Вот и отщёлкиваем в минус все углы.)
Теперь нарисовать правильно угол -200° никакого труда не составляет. Это -180° и минус ещё 20°. Начинаем мотать от нуля в минус: четвёртую четверть пролетаем, третью тоже мимо, доходим до -180°. Куда мотать оставшуюся двадцатку? Да всё туда же! По часам.) Итого угол -200° попадает во вторую четверть.
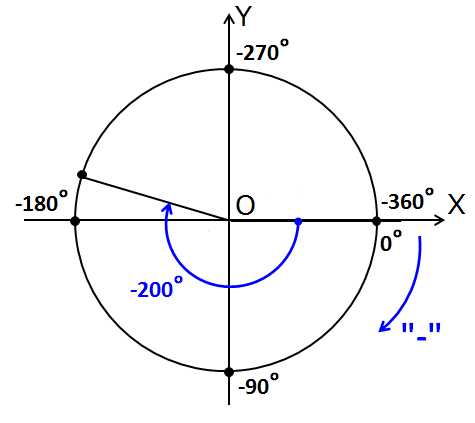
Теперь вы понимаете, насколько важно железно помнить углы на осях координат?
Углы на осях координат (0°, 90°, 180°, 270°, 360°) надо помнить именно для того, чтобы безошибочно определять четверть, куда попадает угол!
А если угол большой, с несколькими полными оборотами? Ничего страшного! Какая разница, куда эти самые полные обороты крутить – в плюс или в минус? Точка-то на круге не изменит своего положения!
Например:
В какую четверть попадает угол -2000°?
Всё то же самое! Для начала считаем, сколько полных оборотов сидит в этом злом угле. Чтобы не косячить в знаках, оставим минус пока в покое и просто поделим 2000 на 360. Получим 5 с хвостиком. Хвостик нас пока не волнует, его чуть позже сосчитаем, когда рисовать угол будем. Считаем пять полных оборотов в градусах:
5·360° = 1800°
Воот. Именно столько лишних градусов можно смело выкинуть из нашего угла без ущерба для здоровья.
Считаем оставшийся хвостик:
2000° – 1800° = 200°
А вот теперь можно и про минус вспомнить.) Куда будем мотать хвостик 200°? В минус, конечно же! Нам же отрицательный угол задан.)
-2000° = -1800° — 200°
Вот и рисуем угол -200°, только уже без лишних оборотов. Только что его рисовали, но, так уж и быть, накалякаю ещё разок. От руки.

Ясен перец, что и заданный угол -2000°, так же как и -200°, попадает во вторую четверть.
Итак, мотаем себе на кру… пардон… на ус:
Если задан очень большой отрицательный угол, то первая часть работы с ним (поиск числа полных оборотов и их отбрасывание) та же самая, что и при работе с положительным углом. Знак «минус» на данном этапе решения не играет никакой роли. Учитывается знак лишь в самом конце, при работе с углом, оставшимся после удаления полных оборотов.
Как видите, рисовать отрицательные углы на круге ничуть не сложнее, чем положительные.
Всё то же самое, только в другую сторону! По часам!
А вот теперь — самое интересное! Мы рассмотрели положительные углы, отрицательные углы, большие углы, маленькие — полный ассортимент. Также мы выяснили, что любую точку на круге можно обозвать положительным и отрицательным углом, отбрасывали полные обороты… Нету никаких мыслей? Должно отложиться…
Да! Какую точку на круге ни возьми, ей будет соответствовать бесконечное множество углов! Больших и не очень, положительных и отрицательных — всяких! И разница между этими углами будет составлять целое число полных оборотов. Всегда! Так уж тригонометрический круг устроен, да…) Именно поэтому обратная задача — найти угол по известным синусу/косинусу/тангенсу/котангенсу — решается неоднозначно. И куда сложнее. В отличие от прямой задачи — по заданному углу найти весь набор его тригонометрических функций. И в более серьёзных темах тригонометрии (арки, тригонометрические уравнения и неравенства) мы с этой фишкой будем сталкиваться постоянно. Привыкаем.)
Итак, будем считать, что самые-самые азы работы с углами на круге мы с вами освоили. Можно и на вопросы поотвечать. Самостоятельно.)
1. В какую четверть попадает угол -345°?
2. В какую четверть попадает угол 666°?
3. В какую четверть попадает угол 5555°?
4. В какую четверть попадает угол -3700°?
Всё хорошо? Поехали дальше.
5. Какой знак имеет cos999°?
6. Какой знак имеет ctg999°?
И это получилось? Прекрасно! Есть проблемы? Тогда вам сюда.
Ответы:
1. 1
2. 4
3. 2
4. 3
5. «+»
6. «-«
В этот раз ответы выданы по порядку в нарушение традиций. Ибо четвертей всего четыре, а знаков так и вовсе два. Особо не разбежишься…)
В следующем уроке мы с вами поговорим про радианы, про загадочное число «пи», научимся легко и просто переводить радианы в градусы и обратно. И с удивлением обнаружим, что даже этих простых знаний и навыков нам будет уже вполне достаточно для успешного решения многих нетривиальных задачек по тригонометрии!
abudnikov.ru
Тригонометрия: синус, косинус, тангенс, котангенс
История тригонометрии
Тригонометрия, как наука, зародилась на Древнем Востоке. Первые тригонометрические соотношения были выведены астрономами для создания точного календаря и ориентированию по звездам. Данные вычисления относились к сферической тригонометрии, в то время как в школьном курсе изучают соотношения сторон и угла плоского треугольника.
Тригонометрия – это раздел математики, занимающийся свойствами тригонометрических функций и зависимостью между сторонами и углами треугольников.
В период расцвета культуры и науки I тысячелетия нашей эры знания распространились с Древнего Востока в Грецию. Но основные открытия тригонометрии – это заслуга мужей арабского халифата. В частности, туркменский ученый аль-Маразви ввел такие функции, как тангенс и котангенс, составил первые таблицы значений для синусов, тангенсов и котангенсов. Понятие синуса и косинуса введены индийскими учеными. Тригонометрии посвящено немало внимания в трудах таких великих деятелей древности, как Евклида, Архимеда и Эратосфена.
Основные величины тригонометрии
Основные тригонометрические функции числового аргумента – это синус, косинус, тангенс и котангенс. Каждая из них имеет свой график: синусоида, косинусоида, тангенсоида и котангенсоида.
В основе формул для расчета значений указанных величин лежит теорема Пифагора. Школьникам она больше известна в формулировке: «Пифагоровы штаны, во все стороны равны», так как доказательство приводится на примере равнобедренного прямоугольного треугольника.

Синус, косинус и другие зависимости устанавливают связь между острыми углами и сторонами любого прямоугольного треугольника. Приведем формулы для расчета этих величин для угла A и проследим взаимосвязи тригонометрических функций:
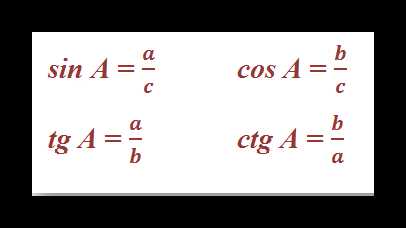
Как видно, tg и ctg являются обратными функциями. Если представить катет a как произведение sin A и гипотенузы с, а катет b в виде cos A * c, то получим следующие формулы для тангенса и котангенса:
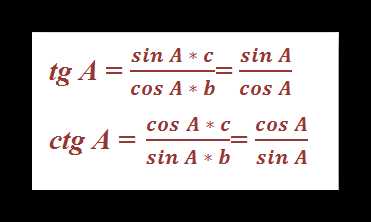
Тригонометрический круг
Графически соотношение упомянутых величин можно представить следующим образом:

Окружность, в данном случае, представляет собой все возможные значения угла α — от 0° до 360°. Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от величины угла. Например, sin α будет со знаком «+», если α принадлежит I и II четверти окружности, то есть, находится в промежутке от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.
Попробуем построить тригонометрические таблицы для конкретных углов и узнать значение величин.
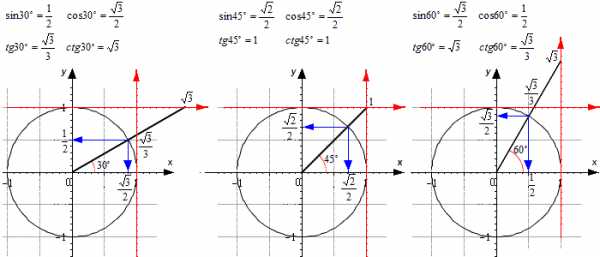
Значения α равные 30°, 45°, 60°, 90°, 180° и так далее – называют частными случаями. Значения тригонометрических функций для них просчитаны и представлены в виде специальных таблиц.

Данные углы выбраны отнюдь не случайно. Обозначение π в таблицах стоит для радиан. Рад — это угол, при котором длина дуги окружности соответствует ее радиусу. Данная величина была введена для того, чтобы установить универсальную зависимость, при расчетах в радианах не имеет значение действительная длина радиуса в см.

Углы в таблицах для тригонометрических функций соответствуют значениям радиан:
Итак, не трудно догадаться, что 2π – это полная окружность или 360°.
Свойства тригонометрических функций: синус и косинус
Для того, чтобы рассмотреть и сравнить основные свойства синуса и косинуса, тангенса и котангенса, необходимо начертить их функции. Сделать это можно в виде кривой, расположенной в двумерной системе координат.
Рассмотри сравнительную таблицу свойств для синусоиды и косинусоиды:
| Синусоида | Косинусоида |
|---|---|
| y = sin x | y = cos x |
| ОДЗ [-1; 1] | ОДЗ [-1; 1] |
| sin x = 0, при x = πk, где k ϵ Z | cos x = 0, при x = π/2 + πk, где k ϵ Z |
| sin x = 1, при x = π/2 + 2πk, где k ϵ Z | cos x = 1, при x = 2πk, где k ϵ Z |
| sin x = — 1, при x = 3π/2 + 2πk, где k ϵ Z | cos x = — 1, при x = π + 2πk, где k ϵ Z |
| sin (-x) = — sin x, т. е. функция нечетная | cos (-x) = cos x, т. е. функция четная |
| функция периодическая, наименьший период — 2π | функция периодическая, наименьший период — 2π |
| sin x › 0, при x принадлежащем I и II четвертям или от 0° до 180° (2πk, π + 2πk) | cos x › 0, при x принадлежащем I и IV четвертям или от 270° до 90° (- π/2 + 2πk, π/2 + 2πk) |
| sin x ‹ 0, при x принадлежащем III и IV четвертям или от 180° до 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, при x принадлежащем II и III четвертям или от 90° до 270° (π/2 + 2πk, 3π/2 + 2πk) |
| возрастает на промежутке [- π/2 + 2πk, π/2 + 2πk] | возрастает на промежутке [-π + 2πk, 2πk] |
| убывает на промежутках [ π/2 + 2πk, 3π/2 + 2πk] | убывает на промежутках [2πk, π + 2πk] |
| производная (sin x)’ = cos x | производная (cos x)’ = — sin x |
Определить является ли функция четной или нет очень просто. Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Введение радиан и перечисление основных свойств синусоиды и косинусоиды позволяют привести следующую закономерность:
Убедиться в верности формулы очень просто. Например, для x = π/2 синус равен 1, как и косинус x = 0. Проверку можно осуществить обративших к таблицам или проследив кривые функций для заданных значений.
Свойства тангенсоиды и котангенсоиды
Графики функций тангенса и котангенса значительно отличаются от синусоиды и косинусоиды. Величины tg и ctg являются обратными друг другу.
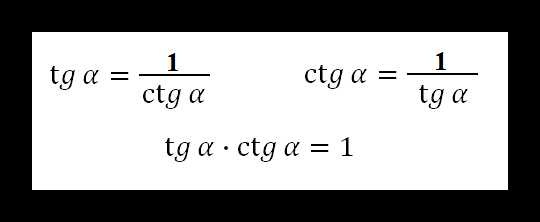
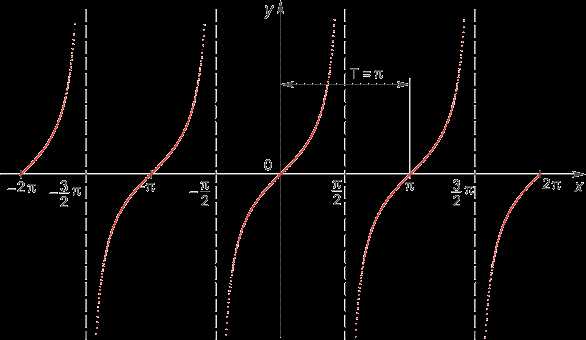
Основные свойства котангенсоиды:
- Y = tg x.
- В отличие от функций синуса и косинуса, в тангенсоиде Y может принимать значения множества всех действительных чисел.
- Тангенсоида стремится к значениям y при x = π/2 + πk, но никогда не достигает их.
- Наименьший положительный период тангенсоиды равен π.
- Tg (- x) = — tg x, т. е. функция нечетная.
- Tg x = 0, при x = πk.
- Функция является возрастающей.
- Tg x › 0, при x ϵ (πk, π/2 + πk).
- Tg x ‹ 0, при x ϵ ( — π/2 + πk, πk).
- Производная (tg x)’ = 1/cos2x .
Рассмотрим графическое изображение котангенсоиды ниже по тексту.

Основные свойства котангенсоиды:
- Y = ctg x.
- В отличие от функций синуса и косинуса, в тангенсоиде Y может принимать значения множества всех действительных чисел.
- Котангенсоида стремится к значениям y при x = πk, но никогда не достигает их.
- Наименьший положительный период котангенсоиды равен π.
- Ctg (- x) = — ctg x, т. е. функция нечетная.
- Ctg x = 0, при x = π/2 + πk.
- Функция является убывающей.
- Ctg x › 0, при x ϵ (πk, π/2 + πk).
- Ctg x ‹ 0, при x ϵ (π/2 + πk, πk).
- Производная (ctg x)’ = — 1/sin2x Исправить
Похожие статьи
Рекомендуем почитать:
karate-ege.ru
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Тригонометрия
| Справочник по математике | Тригонометрия |
| Связи между тригонометрическими функциями одного угла |
| Тригонометрические функции суммы и разности двух углов |
| Тригонометрические функции двойного угла |
| Формулы понижения степени для квадратов тригонометрических функций |
| Формулы понижения степени для кубов синуса и косинуса |
| Выражение тангенса угла через синус и косинус двойного угла |
| Преобразование суммы тригонометрических функций в произведение |
| Преобразование произведения тригонометрических функций в сумму |
| Выражение тригонометрических функций через тангенс половинного угла |
| Тригонометрические функции тройного угла |
Связи между тригонометрическими функциями одного угла
| sin2α + cos2α = 1 |
Тригонометрические функции суммы и разности двух углов
| Формула | Название формулы |
| sin (α + β) = sin α cos β + cos α sin β | Синус суммы |
| sin (α – β) = sin α cos β – cos α sin β | Синус разности |
| cos (α + β) = cos α cos β – sin α sin β | Косинус суммы |
| cos (α – β) = cos α cos β + sin α sin β | Косинус разности |
| Тангенс суммы | |
| Тангенс разности |
| Синус суммы |
| sin (α + β) = sin α cos β + + cos α sin β |
| Синус разности |
| sin (α – β) = sin α cos β – – cos α sin β |
| Косинус суммы |
| cos (α + β) = cos α cos β – – sin α sin β |
| Косинус разности |
| cos (α – β) = cos α cos β + + sin α sin β |
| Тангенс суммы |
| Тангенс разности |
Тригонометрические функции двойного угла
| Формула | Название формулы |
| sin 2α = 2 sin α cos α | Синус двойного угла |
cos 2α = cos 2α – sin2α cos 2α = 2cos 2α – 1 cos 2α = 1 – 2sin 2α | Косинус двойного угла |
| Тангенс двойного угла |
| Синус двойного угла |
| sin 2α = 2 sin α cos α |
| Косинус двойного угла |
cos 2α = cos 2α – sin2α cos 2α = 2cos 2α – 1 cos 2α = 1 – 2sin 2α |
| Тангенс двойного угла |
Формулы понижения степени для квадратов тригонометрических функций
| Формула | Название формулы |
| Выражение квадрата синуса через косинус двойного угла | |
| Выражение квадрата косинуса через косинус двойного угла | |
| Выражение квадрата тангенса через косинус двойного угла |
| Выражение квадрата синуса через косинус двойного угла |
| Выражение квадрата косинуса через косинус двойного угла |
| Выражение квадрата тангенса через косинус двойного угла |
Формулы понижения степени для кубов синуса и косинуса
| Формула | Название формулы |
| Выражение куба синуса через синус угла и синус тройного угла | |
| Выражение куба косинуса через косинус угла и косинус тройного угла |
| Выражение куба синуса через синус угла и синус тройного угла |
| Выражение куба косинуса через косинус угла и косинус тройного угла |
Выражение тангенса через синус и косинус двойного угла
Преобразование суммы тригонометрических функций в произведение
| Формула | Название формулы |
| Сумма синусов | |
| Разность синусов | |
| Сумма косинусов | |
| Разность косинусов | |
| Сумма тангенсов | |
| Разность тангенсов |
| Сумма синусов |
| Разность синусов |
| Сумма косинусов |
| Разность косинусов |
| Сумма тангенсов |
| Разность тангенсов |
Преобразование произведения тригонометрических функций в сумму
| Формула | Название формулы |
| Произведение синусов | |
| Произведение косинусов | |
| Произведение синуса и косинуса |
| Произведение синусов |
| Произведение косинусов |
| Произведение синуса и косинуса |
Выражение тригонометрических функций через тангенс половинного угла
| Формула | Название формулы |
| Выражение синуса угла через тангенс половинного угла | |
| Выражение косинуса угла через тангенс половинного угла | |
| Выражение тангенса угла через тангенс половинного угла |
| Выражение синуса угла через тангенс половинного угла |
| Выражение косинуса угла через тангенс половинного угла |
| Выражение тангенса угла через тангенс половинного угла |
Тригонометрические функции тройного угла
| Формула | Название формулы |
| sin 3α = 3sin α – 4sin3α | Синус тройного угла |
| cos 3α = 4cos3α –3cos α | Косинус тройного угла |
| Тангенс тройного угла |
| Синус тройного угла |
| sin 3α = 3sin α – 4sin3α |
| Косинус тройного угла |
| cos 3α = 4cos3α –3cos α |
| Тангенс тройного угла |
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
| подготовительные курсы для школьников 10 и 11 классов |
У нас также для школьников организованы
| индивидуальные занятия с репетиторами по математике и русскому языку |
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Тригонометрия
Рассмотрим тригонометрические круги, изображенные на рисунке 1 и рисунке 2.

Рис.1

Рис.2
На тригонометрическом круге, изображенном на рисунке 1, центральные углы измерены в градусах, а на тригонометрическом круге, изображенном на рисунке 2, те же центральные углы измерены в радианах.
Углом в 1 градус называют угол, составляющий полного угла. Углом в k° называют угол в k раз больший угла в 1° .
Углом в 1 радиан называют центральный угол тригонометрического круга, которому соответствует дуга окружности тригонометрического круга длиной 1 . Углом в k радиан называют центральный угол тригонометрического круга в k раз больший угла в 1 радиан.
Следствие 1. Углом в k радиан является центральный угол тригонометрического круга, которому соответствует дуга окружности тригонометрического круга длиной k .
Следствие 2. Полный угол является углом в 2π радиан.
Для того, чтобы найти формулы, связывающие градусную и радианную меры угла, рассмотрим рисунки 3 и 4
| Рис.3 | Рис.4 |
| Рис.3 |
| Рис.4 |
На этих рисунках изображены прямые углы, причем на рисунке 3 прямой угол измерен в градусах и равен 90° , а на рисунке 4 прямой угол измерен в радианах и равен радиан. Следовательно,
Таким образом, формулы, связывающие градусную и радианную меры угла, имеют вид

Поскольку , то
По этой причине углы, составляющие целое число радиан, изображаются на тригонометрическом круге так, как это показано на рисунке 5.
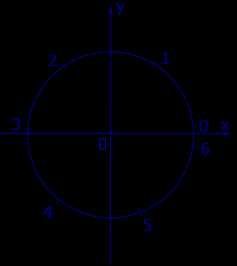
Рис.5
Замечание. Тригонометрическая формула sin α означает, что рассматривается синус угла в α радиан, а тригонометрическая формула sin α° означает, что рассматривается синус угла в α градусов. По такому же правилу определяются значения косинуса, тангенса и котангенса.
Пример. Найти наименьшее из чисел:
Решение. Поскольку
то наименьшим числом является число cos 3 .
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Тригонометрические функции
|
Величины углов (аргументы функций): α, x |
Радиус круга: r |
1. Тригонометрические функции представляют собой элементарные функции, аргументом которых является угол. С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике. Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решении дифференциальных и функциональных уравнений.
2. К тригонометрическим функциям относятся следующие 6 функций: синус, косинус, тангенс,котангенс, секанс и косеканс. Для каждой из указанных функций существует обратная тригонометрическая функция.
3. Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга. На приведенном ниже рисунке изображен круг радиусом r=1. На окружности обозначена точка M(x,y). Угол между радиус-вектором OM и положительным направлением оси Ox равен α.
4. Синусом угла α называется отношение ординаты y точки M(x,y) к радиусу r:
sinα=y/r.
Поскольку r=1, то синус равен ординате точки M(x,y).
5. Косинусом угла α называется отношение абсциссы x точки M(x,y) к радиусу r:
cosα=x/r
6. Тангенсом угла α называется отношение ординаты y точки M(x,y) к ee абсциссе x:
tanα=y/x,x≠0
7. Котангенсом угла α называется отношение абсциссы x точки M(x,y) к ее ординате y:
cotα=x/y,y≠0
8. Секанс угла α − это отношение радиуса r к абсциссе x точки M(x,y):
secα=r/x=1/x,x≠0
9. Косеканс угла α − это отношение радиуса r к ординате y точки M(x,y):
cscα=r/y=1/y,y≠0
10. В единичном круге проекции x, y точки M(x,y) и радиус r образуют прямоугольный треугольник, в котором x,y являются катетами, а r − гипотенузой. Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом:
Синусом угла α называется отношение противолежащего катета к гипотенузе.
Косинусом угла α называется отношение прилежащего катета к гипотенузе.
Тангенсом угла α называется противолежащего катета к прилежащему.
Котангенсом угла α называется прилежащего катета к противолежащему.
Секанс угла α представляет собой отношение гипотенузы к прилежащему катету.
Косеканс угла α представляет собой отношение гипотенузы к противолежащему катету.
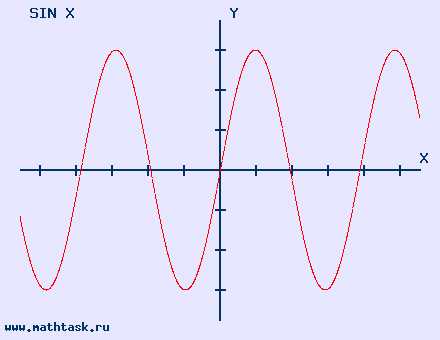
11. График функции синус
y=sinx, область определения: x∈R, область значений: −1≤sinx≤1
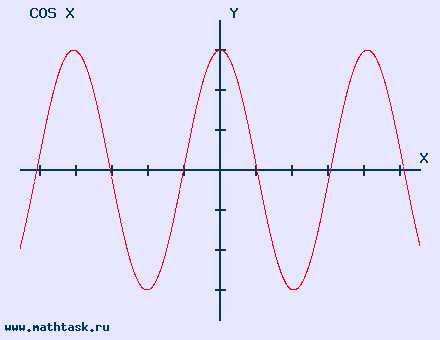
12. График функции косинус
y=cosx, область определения: x∈R, область значений: −1≤cosx≤1
13. График функции тангенс
y=tanx, область определения: x∈R,x≠(2k+1)π/2, область значений: −∞<tanx<∞
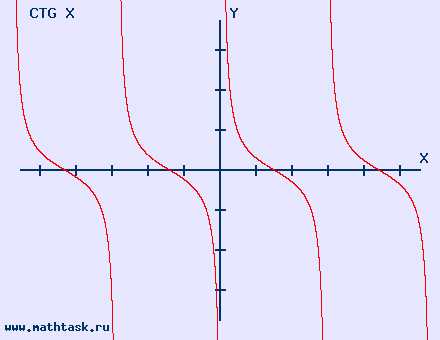
14. График функции котангенс
y=cotx, область определения: x∈R,x≠kπ, область значений: −∞<cotx<∞
15. График функции секанс
y=secx, область определения: x∈R,x≠(2k+1)π/2, область значений:secx∈(−∞,−1]∪[1,∞)
16. График функции косеканс
y=cscx, область определения: x∈R,x≠kπ, область значений: cscx∈(−∞,−1]∪[1,∞)
Где применяется тригонометрия
Тригонометрические вычисления применяются практически во всех сферах жизнедеятельности людей. Следует отметить применение в таких областях как: астрономия, физика, природа, биология, музыка, медицина и многие другие.
Тригонометрия в астрономии:
Потребность в решении треугольников раньше всего обнаружилась в астрономии; поэтому, в течение долгого времени тригонометрия развивалась и изучалась как один из разделов астрономии.
Потребность в решении треугольников раньше всего обнаружилась в астрономии; поэтому, в течение долгого времени тригонометрия развивалась и изучалась как один из разделов астрономии.
Составленные Гиппархом таблицы положений Солнца и Луны позволили предвычислять моменты наступления затмений (с ошибкой 1—2 ч). Гиппарх впервые стал использовать в астрономии методы сферической тригонометрии. Он повысил точность наблюдений, применив для наведения на светило крест нитей в угломерных инструментах — секстантах и квадрантах. Ученый составил огромный по тем временам каталог положений 850 звезд, разделив их по блеску на 6 степеней (звездных величин). Гиппарх ввел географические координаты — широту и долготу, и его можно считать основателем математической географии. (ок. 190 до н. э. — ок. 120 до н. э.)
Достижения Виета в тригонометрии
Полное решение задачи об определении всех элементов плоского или сферического треугольников по трем данным элементам, важные разложения sin пх и cos пх по степеням cos х и sinx. Знание формулы синусов и косинусов кратных дуг дало возможность Виету решить уравнение 45-й степени, предложенное математиком А. Рооменом; Виет показал, что решение этого уравнения сводится к разделению угла на 45 равных частей и что существуют 23 положительных корня этого уравнения. Виет решил задачу Аполлония с помощью линейки и циркуля.
Решение сферических треугольников- одна из задач астрономии Вычислять стороны и углы любого сферического треугольника по трем подходящим образом заданным сторонам или углам позволяют следующие теоремы: (теорема синусов) (теорема косинусов для углов) (теорема косинусов для сторон).
Тригонометрия в физике:
В окружающем нас мире приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Эти процессы называются колебательными. Колебательные явления различной физической природы подчиняются общим закономерностям и описываются одинаковыми уравнениями. Существуют разные виды колебательных явлений.
Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом:
Где х — значение изменяющейся величины, t — время, А — амплитуда колебаний, ω — циклическая частота колебаний, — полная фаза колебаний, r — начальная фаза колебаний.
Обобщенное гармоническое колебание в дифференциальном виде x’’ + ω²x = 0.
Механические колебания . Механическими колебаниями называют движения тел, повторяющиеся точно через одинаковые промежутки времени. Графическое изображение этой функции дает наглядное представление о протекании колебательного процесса во времени. Примерами простых механических колебательных систем могут служить груз на пружине или математический маятник.
Тригонометрия в природе.
Мы часто задаем вопрос «Почему мы иногда видим то, чего нет на самом деле?». Для исследования предложены следующие вопросы: «Как возникает радуга? Северное сияние?», «Что такое оптические иллюзии?» ,«Как тригонометрия может помочь найти ответы на эти вопросы?».
Впервые теория радуги была дана в 1637 году Рене Декартом. Он объяснил радугу, как явление, связанное с отражением и преломлением света в дождевых каплях.
Северное сияние Проникновение в верхние слои атмосферы планет заряженных частиц солнечного ветра определяется взаимодействием магнитного поля планеты с солнечным ветром.
Сила, действующая на движущуюся в магнитном поле заряженную частицу называется силой Лоренца. Она пропорциональна заряду частицы и векторному произведению поля и скорости движения частицы.
Многофункциональная тригонометрия
· Американские ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения.
· К тому же в биологии используется такое понятие как синус сонный, синус каротидный и венозный или пещеристый синус.
· Тригонометрия играет важную роль в медицине. С ее помощью иранские ученые открыли формулу сердца — комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии.
Тригонометрия и тригонометрические функции в медицине и биологии.
· Одно из фундаментальных свойств живой природы — это цикличность большинства происходящих в ней процессов.
· Биологические ритмы, биоритмы – это более или менее регулярные изменения характера и интенсивности биологических процессов.
· Основной земной ритм – суточный.
· Модель биоритмов можно построить с помощью тригонометрических функций.
Тригонометрия в биологии
Какие биологические процессы связаны с тригонометрией?
· Тригонометрия играет важную роль в медицине. С ее помощью иранские ученые открыли формулу сердца — комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии.
· Биологические ритмы, биоритмы связаны с тригонометрией
Связь биоритмов с тригонометрией
· Модель биоритмов можно построить с помощью графиков тригонометрических функций. Для этого необходимо ввести дату рождения человека ( день, месяц, год ) и длительность прогноза
Движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения.
При полёте птицы траектория взмаха крыльев образует синусоиду.
Возникновение музыкальной гармонии
· Согласно дошедшим из древности преданиям, первыми, кто попытался сделать это, были Пифагор и его ученики.
· Частоты, соответствующие одной и той же ноте в первой, второй и т.д. октавах, относятся, как 1:2:4:8…
· диатоническая гамма 2:3:5
Тригонометрия в архитектуре
· Детская школа Гауди в Барселоне
· Страховая корпорация Swiss Re в Лондоне
· Феликс Кандела Ресторан в Лос-Манантиалесе
Значения тригонометрических функций
Ключевые слова: радиан, радианная мера угла, тригонометрическая окружность, знаки тригонометрических функций
В геометрии угол определяется как часть плоскости, ограниченная двумя лучами.
При таком определении получаются углы от 0° до 180°. Однако угол можно рассматривать и как меру поворота.
Возьмем на координатной плоскости окружность радиуса R с центром O в начале координат.
Пусть одна сторона угла с вершиной в начале координат O идет по оси абсцисс, а сам угол положительный, то есть, по определению, отложен по направлению против часовой стрелки от положительного направления оси абсцисс.
Из геометрии известно, что отношение длины дуги l , на которую опирается этот угол, к радиусу R этой окружности не зависит от самого радиуса. Поэтому это отношение может быть выбрано характеристикой и мерой данного угла: =lR.
Такая мера называется радианной мерой угла и используется наравне с угловой.
Говорят, что угол равен определенному числу радиан.
Ясно, что угол в один радиан опирается на длину дуги окружности, равную её радиусу.
В самом деле: =RR=1 радиан. Обозначение радиана – «рад».
Так как длина всей окружности радиуса R равна 2R , то всей окружности соответствует угол =R2R=2 радиан. Поскольку вся окружность содержит 360°, то один радиан соответствует 2360=180 градусов:
1рад=1805717. И наоборот, 1=180рад.
Значит, можно написать следующие формулы перехода от градусного измерения к радианному:
=180рад
и от радианного измерения к градусному:
=180 .
Обозначение «рад» при записи часто опускают и вместо, например, 180° = рад пишут просто 180° = .
Пользуясь этими формулами, легко получить следующую таблицу перевода некоторых наиболее часто встречающихся углов из градусной меры в радианную и обратно.
|
Угол, градусы |
0° |
30° |
45° |
60° |
90° |
180° |
270° |
360° |
|
Угол, радианы |
0 |
6 |
4 |
3 |
2 |
23 |
2 |
Так как, синус по определению равен ординате точки на единочной окружности, а косинус — абсциссе, то знаки тригонометрических функций по четвертям будут такими:
|
I |
II |
III |
IV |
|
|
sin |
+ |
+ |
— |
— |
|
cos |
+ |
— |
— |
+ |
|
tg |
+ |
— |
+ |
— |
|
ctg |
+ |
— |
+ |
— |
Вычисление тригонометрических функций некоторых углов.
Тригонометрические функции числового и углового аргументов
Тригонометрические функции числового аргумента.
Тригонометрические функции числового аргумента t – это функции вида y = cos t,
y = sin t, y = tg t, y = ctg t.
С помощью этих формул через известное значение одной тригонометрической функции можно найти неизвестные значения других тригонометрических функций.
Пояснения.
1) Возьмем формулу cos2 t + sin2 t = 1 и выведем с ее помощью новую формулу.
Для этого разделим обе части формулы на cos2 t (при t ≠ 0, то есть t ≠ π/2 + πk). Итак:
cos2 t sin2 t 1
——— + ——— = ———
cos2 t cos2 t cos2 t
Первое слагаемое равно 1. Мы знаем, что отношение синуса к конисусу – это тангенс, значит, второе слагаемое равно tg2 t. В результате мы получаем новую (и уже известную вам) формулу:
|
1 π |
2) Теперь разделим cos2 t + sin2 t = 1 на sin2 t (при t ≠ πk):
cos2 t sin2 t 1
——— + ——— = ———, где t ≠ πk + πk, k – целое число
sin2 t sin2 t sin2 t
Отношение косинуса к синусу – это котангенс. Значит:
|
1 |
Зная элементарные основы математики и выучив основные формулы тригонометрии, вы легко сможете самостоятельно выводить большинство остальных тригонометрических тождеств. И это даже лучше, чем просто зазубривать их: выученное наизусть быстро забывается, а понятое запоминается надолго, если не навсегда. К примеру, необязательно зазубривать, чему равна сумма единицы и квадрата тангенса. Забыли – можно легко вспомнить, если вы знаете самую простую вещь: тангенс – это отношение синуса к косинусу. Примените вдобавок простое правило сложения дробей с разными знаменателями – и получите результат:
sin2 t 1 sin2 t cos2 t + sin2 t 1
1 + tg2 t = 1 + ——— = — + ——— = —————— = ———
cos2 t 1 cos2 t cos2 t cos2 t
Точно так же легко можно найти сумму единицы и квадрата котангенса, как и многие другие тождества.
Тригонометрические функции углового аргумента.
В функциях у = cos t, у = sin t, у = tg t, у = ctg t переменная t может быть не только числовым аргументом. Ее можно считать и мерой угла – то есть угловым аргументом.
С помощью числовой окружности и системы координат можно легко найти синус, косинус, тангенс, котангенс любого угла. Для этого должны быть соблюдены два важных условия:
1) вершиной угла должен быть центр окружности, который одновременно является центром оси координат;
2) одной из сторон угла должен быть положительный луч оси x.
В этом случае ордината точки, в которой пересекаются окружность и вторая сторона угла, является синусом этого угла, а абсцисса этой точки – косинусом данного угла.
Пояснение. Нарисуем угол, одна сторона которого – положительный луч оси x, а вторая сторона выходит из начала оси координат (и из центра окружности) под углом 30º (см.рисунок). Тогда точка пересечения второй стороны с окружностью соответствует π/6. Нам известны ордината и абсцисса этой точки. Они же являются косинусом и синусом нашего угла:
√3 1
——; ——
2 2
А зная синус и косинус угла, вы уже легко сможете найти его тангенс и котангенс.
Таким образом, числовая окружность, расположенная в системе координат, является удобным способом найти синус, косинус, тангенс или котангенс угла.
Но есть более простой способ. Можно и не рисовать окружность и систему координат. Можно воспользоваться простыми и удобными формулами:
|
πα |
πα |
Пример: найти синус и косинус угла, равного 60º.
Решение:
π · 60 π √3
sin 60º = sin ——— = sin —— = ——
180 3 2
π 1
cos 60º = cos —— = —
3 2
ya-znau.ru