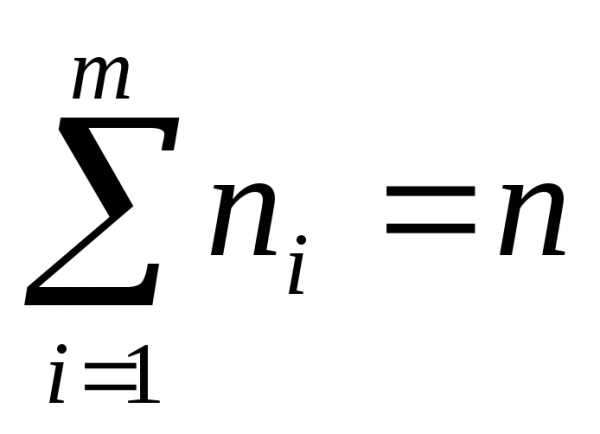7. Распределение Стьюдента с степенями свободы
(t-распределение)
В нормальном
распределении средняя арифметическая
зависит от дисперсии слагаемых величин.
Однако на практике дисперсия исследуемой
величины, как правило, неизвестна. В
этой связи возникла задача определения
закона распределения  ,
не зависящего от
,
не зависящего от ,
которую решил английский статистик В.
Госсет, публиковавшийся под псевдонимом
Стьюдент. Дадим следующее определение:
,
которую решил английский статистик В.
Госсет, публиковавшийся под псевдонимом
Стьюдент. Дадим следующее определение:
Если случайная
величина Z
имеет нормальное нормированное
распределение N(0,1),
а величина U2 имеет распределение 
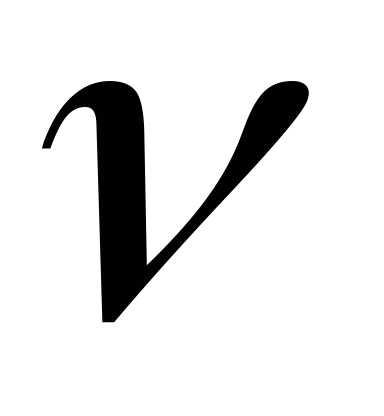 степенями
свободы, причемZ
и U
взаимно независимы, то случайная величина
степенями
свободы, причемZ
и U
взаимно независимы, то случайная величина 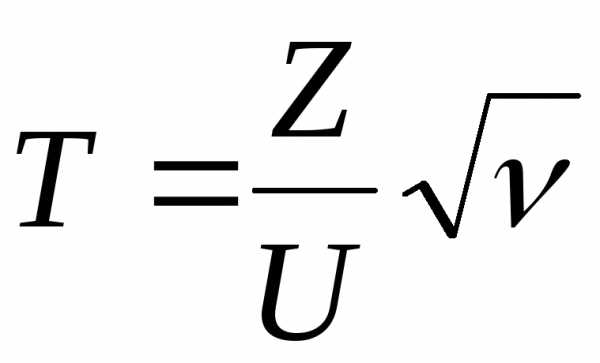
имеет t-распределение
с  степенями свободы. Плотность распределения
описывается формулой
степенями свободы. Плотность распределения
описывается формулой
 .
.
Функция плотности
является унимодальной и симметричной
относительно  .
Основные числовые характеристики:
.
Основные числовые характеристики:
среднее, мода, медиана: ;
дисперсия: ;
асимметрия:  ;
;
эксцесс: .
Ниже на рисунке
приведены сравнительные графики функции
плотности t-распределения
при  и стандартного нормального распределенияN(0,1).
и стандартного нормального распределенияN(0,1).

Рис. 9.2.График t-распределения
при 


Если из генеральной
совокупности Х с нормальным законом распределения 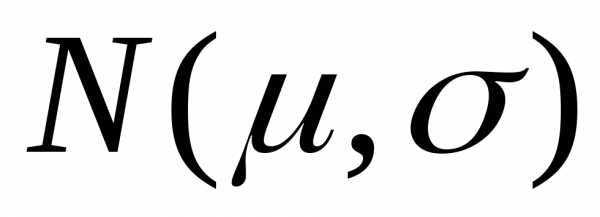 взята случайная выборка объёмаn,
то статистика
взята случайная выборка объёмаn,
то статистика

имеет распределение Стьюдента с степенями свободы. ЗдесьS-выборочное среднее квадратическое отклонение.
Распределение
Стьюдента используется при интервальной
оценке математического ожидания при
неизвестном значении среднего
квадратического отклонения 
8. Распределение Фишера-Снедекора (f-распределение).
Пусть имеются две
независимые случайные величины 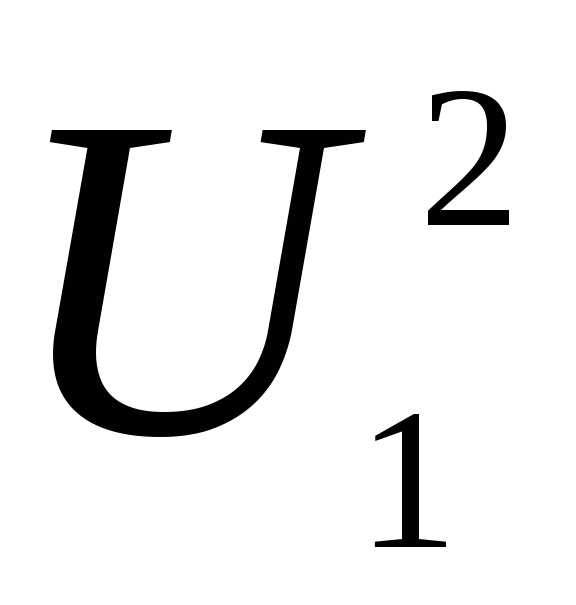 и
и имеющие
имеющие -распределение
соответственно со степенями свободы
-распределение
соответственно со степенями свободы и
и .
Тогда величина
.
Тогда величина

имеет F-распределение
с 
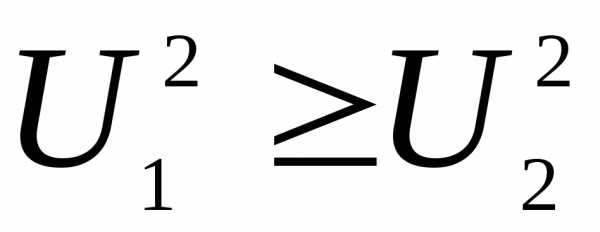 ,
так что
,
так что .
.Это распределение впервые было построено английским статистиком Р. Фишером. Американский статистик Дж. Снедекор составил таблицы для данного распределения, поэтому его часто называют распределением Фишера-Снедекора.
Используется в дисперсионном анализе при проверке статистических гипотез.
Раздел II математическая статистика Лекция 1. Генеральная совокупность. Выборка. Способы образования выборки. Статистическая оценка параметров распределения.
В математической статистике множество возможных значений случайной величины Х называют генеральной совокупностью случайной величины Х или просто генеральной совокупностью Х.
Исходным материалом для изучения свойств генеральной совокупности являются экспериментальные (статистические) данные, под которыми понимают значения случайной величины, полученные в результате независимых повторных наблюдений (имеется ввиду, что эксперимент может, хотя бы теоретически, быть повторен сколько угодно раз в одних и тех же условиях).
Совокупность
независимых случайных величин Х1,
… , Хn , имеющих
на множествах исходов 1, … , n-го
экспериментов (наблюдений) то же
распределение, что и случайная величина
Х, называется случайной
выборкой.
При этом число n называют объемом выборки. Любое возможное
значение (х1
, … , хn)
случайной выборки — эмпирическим рядом,
а числа хi его вариантами. При этом некоторые
варианты могут повторяться. Число
повторений вариант называют эмпирической
частотой и обозначают ni (или mi).
Таблица, в которой варианты записаны
по одному разу и в порядке возрастания,
а также указаны их частоты или  ,
называемыевесами, называется
вариационным дискретным рядом.
,
называемыевесами, называется
вариационным дискретным рядом.
Пример 1. В течении суток измеряют напряжение Х тока в электросети в вольтах. В результате опыта получена выборка объема n = 30:
107 108 110 109 110 111 109 110 111 107
108 109 110 108 107 110 109 111 111 110
109 112 113 110 106 110 109 110 108 112
Построим вариационный ряд этой выборки.
Наименьшее значение в выборке х1 = 106, наибольшее – х8 = 113. Подсчитываем частоту каждого хi, i = 1,…, 8 и строим таблицу 1.1.
хi
106
107
108
109
110
111
112
113
ni
1
3
4
6
9
4
2
1
При большом объеме
выборки ( свыше 50 ) исходные данные
рассматривают на интервале J = ( х1, хn).
Этот интервал разбивают на m промежутков равной длины 
Таблица 1.2.
J1
J2
. . .
Jm
n1
n2 . . .
nm

В зависимости от того, является ли генеральная случайная величина Х дискретной или непрерывной, результаты выборки записывают в виде вариационного или интервального рядов. Для интервального ряда вводят понятие эмпирической плотности распределения, как функции, определяемой формулой:
 и равна 0, если
и равна 0, если  .
.
График функции плотности называют гистограммой.
studfiles.net
О степенях свободы в статистике / Stepik.org corporate blog / Habr
В одном из предыдущих постов мы обсудили, пожалуй, центральное понятие в анализе данных и проверке гипотез — p-уровень значимости. Если мы не применяем байесовский подход, то именно значение p-value мы используем для принятия решения о том, достаточно ли у нас оснований отклонить нулевую гипотезу нашего исследования, т.е. гордо заявить миру, что у нас были получены статистически значимые различия.Однако в большинстве статистических тестов, используемых для проверки гипотез, (например, t-тест, регрессионный анализ, дисперсионный анализ) рядом с p-value всегда соседствует такой показатель как число степеней свободы, он же degrees of freedom или просто сокращенно df, о нем мы сегодня и поговорим.

Степени свободы, о чем речь?
По моему мнению, понятие степеней свободы в статистике примечательно тем, что оно одновременно является и одним из самым важных в прикладной статистике (нам необходимо знать df для расчета p-value в озвученных тестах), но вместе с тем и одним из самых сложных для понимания определений для студентов-нематематиков, изучающих статистику.
Давайте рассмотрим пример небольшого статистического исследования, чтобы понять, зачем нам нужен показатель df, и в чем же с ним такая проблема. Допустим, мы решили проверить гипотезу о том, что средний рост жителей Санкт-Петербурга равняется 170 сантиметрам. Для этих целей мы набрали выборку из 16 человек и получили следующие результаты: средний рост по выборке оказался равен 173 при стандартном отклонении равном 4. Для проверки нашей гипотезы можно использовать одновыборочный t-критерий Стьюдента, позволяющий оценить, как сильно выборочное среднее отклонилось от предполагаемого среднего в генеральной совокупности в единицах стандартной ошибки:
Проведем необходимые расчеты и получим, что значение t-критерия равняется 3, отлично, осталось рассчитать p-value и задача решена. Однако, ознакомившись с особенностями t-распределения мы выясним, что его форма различается в зависимости от числа степеней свобод, рассчитываемых по формуле n-1, где n — это число наблюдений в выборке:
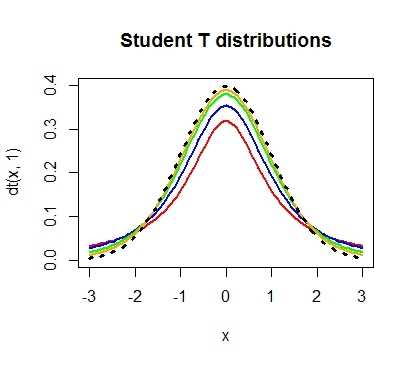
Сама по себе формула для расчета df выглядит весьма дружелюбной, подставили число наблюдений, вычли единичку и ответ готов: осталось рассчитать значение p-value, которое в нашем случае равняется 0.004.
Но почему n минус один?
Когда я впервые в жизни на лекции по статистике столкнулся с этой процедурой, у меня как и у многих студентов возник законный вопрос: а почему мы вычитаем единицу? Почему мы не вычитаем двойку, например? И почему мы вообще должны что-то вычитать из числа наблюдений в нашей выборке?
В учебнике я прочитал следующее объяснение, которое еще не раз в дальнейшем встречал в качестве ответа на данный вопрос:
“Допустим мы знаем, чему равняется выборочное среднее, тогда нам необходимо знать только n-1 элементов выборки, чтобы безошибочно определить чему равняется оставшейся n элемент”. Звучит разумно, однако такое объяснение скорее описывает некоторый математический прием, чем объясняет зачем нам понадобилось его применять при расчете t-критерия. Следующее распространенное объяснение звучит следующим образом: число степеней свободы — это разность числа наблюдений и числа оцененных параметров. При использовании одновыборочного t-критерия мы оценили один параметр — среднее значение в генеральной совокупности, используя n элементов выборки, значит df = n-1.
Однако ни первое, ни второе объяснение так и не помогает понять, зачем же именно нам потребовалось вычитать число оцененных параметров из числа наблюдений?
Причем тут распределение Хи-квадрат Пирсона?
Давайте двинемся чуть дальше в поисках ответа. Сначала обратимся к определению t-распределения, очевидно, что все ответы скрыты именно в нем. Итак случайная величина:
имеет t-распределение с df = ν, при условии, что Z – случайная величина со стандартным нормальным распределением N(0; 1), V – случайная величина с распределением Хи-квадрат, с ν числом степеней свобод, случайные величины Z и V независимы. Это уже серьезный шаг вперед, оказывается, за число степеней свободы ответственна случайная величина с распределением Хи-квадрат в знаменателе нашей формулы.
Давайте тогда изучим определение распределения Хи-квадрат. Распределение Хи-квадрат с k степенями свободы — это распределение суммы квадратов k независимых стандартных нормальных случайных величин.
Кажется, мы уже совсем у цели, по крайней мере, теперь мы точно знаем, что такое число степеней свободы у распределения Хи-квадрат — это просто число независимых случайных величин с нормальным стандартным распределением, которые мы суммируем. Но все еще остается неясным, на каком этапе и зачем нам потребовалось вычитать единицу из этого значения?
Давайте рассмотрим небольшой пример, который наглядно иллюстрирует данную необходимость. Допустим, мы очень любим принимать важные жизненные решения, основываясь на результате подбрасывания монетки. Однако, последнее время, мы заподозрили нашу монетку в том, что у нее слишком часто выпадает орел. Чтобы попытаться отклонить гипотезу о том, что наша монетка на самом деле является честной, мы зафиксировали результаты 100 бросков и получили следующий результат: 60 раз выпал орел и только 40 раз выпала решка. Достаточно ли у нас оснований отклонить гипотезу о том, что монетка честная? В этом нам и поможет распределение Хи-квадрат Пирсона. Ведь если бы монетка была по настоящему честной, то ожидаемые, теоретические частоты выпадания орла и решки были бы одинаковыми, то есть 50 и 50. Легко рассчитать насколько сильно наблюдаемые частоты отклоняются от ожидаемых. Для этого рассчитаем расстояние Хи-квадрат Пирсона по, я думаю, знакомой большинству читателей формуле:
Где O — наблюдаемые, E — ожидаемые частоты.
Дело в том, что если верна нулевая гипотеза, то при многократном повторении нашего эксперимента распределение разности наблюдаемых и ожидаемых частот, деленная на корень из наблюдаемой частоты, может быть описано при помощи нормального стандартного распределения, а сумма квадратов k таких случайных нормальных величин это и будет по определению случайная величина, имеющая распределение Хи-квадрат.
Давайте проиллюстрируем этот тезис графически, допустим у нас есть две случайные, независимые величины, имеющих стандартное нормальное распределение. Тогда их совместное распределение будет выглядеть следующим образом:
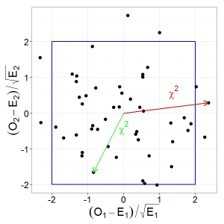
При этом квадрат расстояния от нуля до каждой точки это и будет случайная величина, имеющая распределение Хи-квадрат с двумя степенями свободы. Вспомнив теорему Пифагора, легко убедиться, что данное расстояние и есть сумма квадратов значений обеих величин.
Пришло время вычесть единичку!
Ну а теперь кульминация нашего повествования. Возвращаемся к нашей формуле расчета расстояния Хи-квадрат для проверки честности монетки, подставим имеющиеся данные в формулу и получим, что расстояние Хи-квадрат Пирсона равняется 4. Однако для определения p-value нам необходимо знать число степеней свободы, ведь форма распределения Хи-квадрат зависит от этого параметра, соответственно и критическое значение также будет различаться в зависимости от этого параметра.
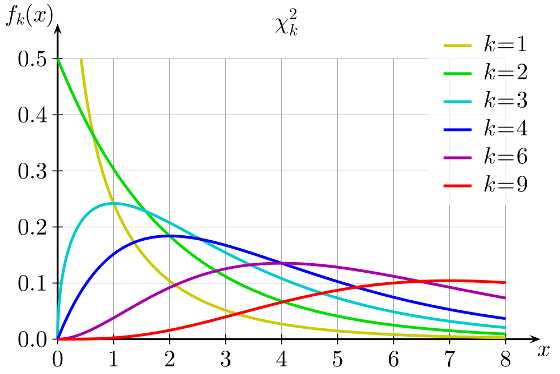
Теперь самое интересное. Предположим, что мы решили многократно повторять 100 бросков, и каждый раз мы записывали наблюдаемые частоты орлов и решек, рассчитывали требуемые показатели (разность наблюдаемых и ожидаемых частот, деленная на корень из ожидаемой частоты) и как и в предыдущем примере наносили их на график.
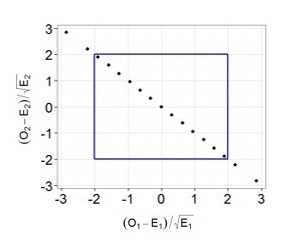
Легко заметить, что теперь все точки выстраиваются в одну линию. Все дело в том, что в случае с монеткой наши слагаемые не являются независимыми, зная общее число бросков и число решек, мы всегда можем точно определить выпавшее число орлов и наоборот, поэтому мы не можем сказать, что два наших слагаемых — это две независимые случайные величины. Также вы можете убедиться, что все точки действительно всегда будут лежать на одной прямой: если у нас выпало 30 орлов, значит решек было 70, если орлов 70, то решек 30 и т.д. Таким образом, несмотря на то, что в нашей формуле было два слагаемых, для расчета p-value мы будем использовать распределение Хи-квадрат с одной степенью свободы! Вот мы наконец-то добрались до момента, когда нам потребовалось вычесть единицу. Если бы мы проверяли гипотезу о том, что наша игральная кость с шестью гранями является честной, то мы бы использовали распределение Хи-квадрат с 5 степенями свободы. Ведь зная общее число бросков и наблюдаемые частоты выпадения любых пяти граней, мы всегда можем точно определить, чему равняется число выпадений шестой грани.
Все становится на свои места
Теперь, вооружившись этими знаниями, вернемся к t-тесту:
в знаменателе у нас находится стандартная ошибка, которая представляет собой выборочное стандартное отклонение, делённое на корень из объёма выборки. В расчет стандартного отклонения входит сумма квадратов отклонений наблюдаемых значений от их среднего значения — то есть сумма нескольких случайных положительных величин. А мы уже знаем, что сумма квадратов n случайных величин может быть описана при помощи распределения хи-квадрат. Однако, несмотря на то, что у нас n слагаемых, у данного распределения будет n-1 степень свободы, так как зная выборочное среднее и n-1 элементов выборки, мы всегда можем точно задать последний элемент (отсюда и берется это объяснение про среднее и n-1 элементов необходимых для однозначного определения n элемента)! Получается, в знаменателе t-статистики у нас спрятано распределение хи-квадрат c n-1 степенями свободы, которое используется для описания распределения выборочного стандартного отклонения! Таким образом, степени свободы в t-распределении на самом деле берутся из распределения хи-квадрат, которое спрятано в формуле t-статистики. Кстати, важно отметить, что все приведенные выше рассуждения справедливы, если исследуемый признак имеет нормальное распределение в генеральной совокупности (или размер выборки достаточно велик), и если бы у нас действительно стояла цель проверить гипотезу о среднем значении роста в популяции, возможно, было бы разумнее использовать непараметрический критерий.
Схожая логика расчета числа степеней свободы сохраняется и при работе с другими тестами, например, в регрессионном или дисперсионном анализе, все дело в случайных величинах с распределением Хи-квадрат, которые присутствуют в формулах для расчета соответствующих критериев.
Таким образом, чтобы правильно интерпретировать результаты статистических исследований и разбираться, откуда возникают все показатели, которые мы получаем при использовании даже такого простого критерия как одновыборочный t-тест, любому исследователю необходимо хорошо понимать, какие математические идеи лежат в основании статистических методов.
Онлайн курсы по статистике: объясняем сложные темы простым языком
Основываясь на опыте преподавания статистики в Институте биоинформатики , у нас возникла идея создать серию онлайн курсов, посвященных анализу данных, в которых в доступной для каждого форме будут объясняться наиболее важные темы, понимание которых необходимо для уверенного использования методов статистики при решении различного рода задача. В 2015 году мы запустили курс Основы статистики, на который к сегодняшнему дню записалось около 17 тысяч человек, три тысячи слушателей уже получили сертификат о его успешном завершении, а сам курс был награждён премией EdCrunch Awards и признан лучшим техническим курсом. В этом году на платформе stepik.org стартовало продолжение курса Основы статистики. Часть два, в котором мы продолжаем знакомство с основными методами статистики и разбираем наиболее сложные теоретические вопросы. Кстати, одной из главных тем курса является роль распределения Хи-квадрат Пирсона при проверке статистических гипотез. Так что если у вас все еще остались вопросы о том, зачем мы вычитаем единицу из общего числа наблюдений, ждем вас на курсе!
Стоит также отметить, что теоретические знания в области статистики будут определенно полезны не только тем, кто применяет статистику в академических целях, но и для тех, кто использует анализ данных в прикладных областях. Базовые знания в области статистики просто необходимы для освоения более сложных методов и подходов, которые используются в области машинного обучения и Data Mining. Таким образом, успешное прохождение наших курсов по введению в статистику — хороший старт в области анализа данных. Ну а если вы всерьез задумались о приобретении навыков работы с данными, думаем, вас может заинтересовать наша онлайн — программа по анализу данных, о которой мы подробнее писали здесь. Упомянутые курсы по статистике являются частью этой программы и позволят вам плавно погрузиться в мир статистики и машинного обучения. Однако пройти эти курсы без дедлайнов могут все желающие и вне контекста программы по анализу данных.
habr.com
Степени свободы Стьюдента распределение — Справочник химика 21
В основе статистических оценок нормально распределенных случайных величин по выборочным параметрам лежит распределение Стьюдента, связывающее три важнейших характеристики выборочной совокупности — ширину доверительного интервала, соответствующую ему доверительную вероятность и объем выборки п (или число степеней свободы выборки / = [c.833]
Распределение Стьюдента. Пусть 2 нормально распределенная случайная величина с нулевым математическим ожиданием и единичной дисперсией, а V — независимая от Г случайная величина, которая распределена по закону «хи-квадрат» с К степенями свободы. Тогда величина [c.14]
Таким образом, распределение Стьюдента зависит только от числа степеней свободы /, с которым была определена выборочная дисперсия (рис. 18). На рис. 18 приведены графики плотности t-распределения для /=1, f = 5 и нормальная кривая. Кривые рас-пре/.еления по своей форме напоминают нормальную кривую, но [c.41]Распределение величины I по = п—степеням свободы носит название распределения Стьюдента. Сравним его с распределением Лапласа. Если мера отклонения среднего результата измерений от математического ожидания в единицах генерального стандартного отклонения среднего о(л ), то коэффициент Стьюдента — аналогичная мера в единицах выборочного стандартного отклонения среднего результата и- = (Х — ц)/а (Г) = АХ- л/п/а-, 1- = (Х — ц)/5 (X) = АХ- / 3 . [c.833]
Попытка подставить выборочное д в изложенное выше решение задачи приводит к уменьшению по сравнению с истинными доверительных интервалов. Это объясняется тем, что величина (х — МУб распределена уже не нормально, а по распределению Стьюдента с N—1 степенью свободы. Плотность распределения Стьюдента имеет вид [c.175]
Распределением Стьюдента (или распределением) с п степенями свободы называется распределение, которым обладает с. в. [c.292]
Если число измерений мало п 20 для практических целей), то распределение Гаусса дает слишком оптимистичные оценки в этом случае применяют распределение Стьюдента. В этом распределении учитывается число степеней свободы V = га — 1. При V -> оо нормальное распределение и распределение Стьюдента совпадают. Кривая плотности распределения Стьюдента более размазана , чем кривая распределения Гаусса. [c.38]
Можно доказать, что при исходных нормальных совокупностях величина 1-) имеет расиределение Стьюдента с / = /п—2 степенями свободы. При проверке гипотезы нормальности по большому числу малых выборок из каждой выборки случайным образом отбирается по одному значению. Здесь возможно некоторое упрощение — можно отобрать только первые измерения, только вторые и т. д. Такой отбор также можно рассматривать как случайный. Если число элементов в выборках велико, например т>10, то мой- ет быть сделано несколько самостоятельных проверок гипотезы, например, по первым и последним элементам каждой выборки. Затем, если т==4, для каждого отобранного значения по формуле (П. 131) вычисляется т, если тфА, по формуле (П. 134) т). После перехода к величинам т и т) для проверки гипотезы равномерного распределение т илп распределения Стьюдента т] (и, следовательно, нормальности исходного распределения) может быть применен любой из ра смотренных ранее критериев согласия. [c.68]
Кроме того, необходимо отметить, что при числе степеней свободы V = N — уИнормальной кривой распределения [функция Лапласа Ф(i)], а по распределению Стьюдента [141] в зависимости от V и Р. [c.275]
Здесь /р, I — квантиль распределения Стьюдента ири числе степеней свободы I = п — 1 и двухсторонней доверительной вероятности Р (значения 1р, / см. в табл. 2.3). [c.30]
Чем меньше число
www.chem21.info
Распределение Стьюдента и малые выборки
Если среднее рассчитывается по данным малой выборки, то отклонение имеет распределение Стьюдента, называемое также t-распределением. Распределение Стьюдента близко к нормальному распределению, но отличается от него: концентрация отклонений в центральной части распределения меньше.
Если случайная величина X1 распределена по нормальному закону, а случайная величина X2 распределена по закону Хи-квадрат с v степенями свободы, тогда случайная величина, получаемая как
,
имеет распределение Стьюдента (t-распределение) с v степенями свободы.
Преимущество распределения Стьюдента заключается в его независимости от параметров генеральной совокупности: оно зависит только от объёма выборки n. В случае малых выборок (с объёмом менее 30 наблюдений) для определения доверительного интервала среднего значения нельзя использовать критические значения стандартизированного нормального распределения, так как это приводит к грубым оценкам.
Нередко проведение каждого наблюдения настолько сложно, трудоёмко и связано с высокой стоимостью, что невозможно многократное повторение эксперимента. Чтобы оценить среднее значение малой выборки, нужно учитывать, что дисперсия малой выборки рассчитывается по формуле несмещённой оценки дисперсии:
.
Функцию плотности распределения Стьюдента в рассчётах непосредственно не используют, обычно используют таблицы интегральных функций, которые есть в приложениях почти ко всем книгам по статистике, или же её значение выдаёт программа, в которой выполняются рассчёты, например, STATISTICA. В таблицах значения интегральной функции даны для тех же пределов интегрирования, что и у функции нормального распределения. Функция нормального распределения рассчитана для определённого значения аргумента z, а интегральная функция распределения Стьюдента — для аргумента t и числа степеней свободы v = n — 1. Если число степеней свободы стремится к бесконечности, то распределение Стьюдента стремится к нормальному распределению.
Числом степеней свободы в статистике называют число взаимно независимых элементов информации, используемых для вычисления стандартной ошибки. Число степеней свободы равно числу элементов выборки, из которого вычтено число условий, связывающих данные.
Если объём выборки мал и стандартное отклонение генеральной совокупности неизвестно, то доверительный интервал оценки среднего рассчитывается следующим образом:
,
где — критическое значение распределения Стьюдента для уровня значимости α = 1 — P и числа степеней свободы v
s — стандартное отклонение выборки.
Распределение Стьюдента названо в честь Уильяма Госсета, который впервые использовал свойства этого распределения и публиковал свои работы под псевдонимом Стьюдент.
Пример. Производитель кваса решил выяснить, каков доверительный интервал 95% незаполненного уровня в бутылках с квасом (в миллимитрах от пробки). Рассчитать этот доверительный интервал.
Решение.
Случайно выбраны 20 бутылок с квасом, по которым собраны значения незаполненного уровня. С помощью функций MS Excel рассчитаны сумма этих значений и сумма отклонений . Тогда среднее , а стандартное отклонение .
Так как для проверки выбраны только 20 бутылок, то для определения доверительного интервала среднего следует использовать распределение Стьюдента:
,
где 2,093 — критическое значение распределения Стьюдента для уровня значимости 0,05 и числа степеней свободы 19 (найдено по статистической таблице, которые есть в приложениях почти во всех книгах по статистике).
Таким образом, доверительный уровень 95% незаполненного уровня бутылок с квасом составил от 46,44 до 53,76 миллиметров.
Всё по теме «Математическая статистика»
function-x.ru
Распределение Стьюдента, Распределение Пирсона, Распределение Фишера-Снедекора
. Теоретические положения по оценке выборочных характеристик на основе малых выборок (п 30) впервые (1908) разработал английский математик-статистик. ВГоссет (что печатал свои работы под псевдонимом. Стьюди дент). Позже (1925). РФишер дал более строгое доказательство этого распределения, которое получило названиео назву и — распределения. Стьюдента
. Отклонение выборочных средних от генеральной средней. Стьюдент выразил в единицах стандартного отклонения
где в знаменателе используется среднее квадратическое отклонение выборки, тогда как в нормальном распределении — среднее квадратическое отклонение генеральной совокупности (сто). РФишер выразил эти отклонения в од диницях. Стандартная ошибкаки
__ 5_
где ~ — средняя ошибка в малых выборках
. Среднее квадратическое отклонение в малых выборках определяется с учетом числа степеней свободы вариации (п — 1):
. Теоретический и-распределение. Стьюдента не зависит от параметров генеральной совокупности, он связан только с величинами, которые определяются непосредственно по данным выборки
. В литературе по математической статистике доказывается, что дифференциальная функцияі — распределения. Стьюдента (плотность распределения вероятностей) имеет вид
где. А — величина, определяемая с учетом числа степеней свободы вариации (к = п — 1) с помощью гамма-функции (Г — функции):
где. Г (п) | х е сих -. Гамма-функция
0
. Как видно, величина. А зависит только от объема выборки и соответствует максимальной ординате кривой распределения при и = 0. Вероятность того, что ошибка выборки будет не больше заданной величины. Премьер = и. М. определяется интегральной функцией
. Иначе говоря, п) =. Р (и табл и факг) где и табл и и факг — табличное (теоретическое) и фактическое значение нормированного отклонения
и-распределение. Стьюдента справедлив только для выборок, взятых из генеральной совокупности с нормальным распределением случайной величины
. На рис 62 сравнивается кривая и-распределения. Стьюдента с кривой нормального распределения
. Рис 22. Сравнение и — распределения. Стьюдента и нормального распределения: 1 — нормальное распределение; второй-распределение. Стьюдента
Кривая t — распределения. Стьюдента симметрична относительно оси ординат. В отличие от нормального распределения под концами кривой t — распределения. Стьюдента при тех же значениях t размещена значительно большая часть площади. Так ким образом, на долю больших отклонений от генеральной средней приходится значительная часть площади. Это означает, что для малых выборок вероятность допущения больших ошибок существенно повышаетсяься.
При увеличении объема выборкиt — распределение. Стьюдента приближается к нормальному распределению (практически считается достаточным и 30), а при и ^ й он становится нормальным
Для определения значений функции S (t, и) распределения. Стьюдента составлен ряд специальных таблиц, в которых приводятся расчетные значения S (t, и) при соответствующем числе степеней свободы вариации. По этим и аблиц можно найти вероятность ошибки выборки при заданном значении нормированного отклонения t или значение t при заданном уровне вероятности суждения. Р
Приведем выдержку из таблицы вероятностей S (t, и) для значений nit, которые наиболее часто применяются (табл. 62)
. Таблица 62. Извлечение из таблицы значений функции S (t n) распределения. Стьюдента (вероятности умноженные на 1000)
и t | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 15 | 20 | 00 |
1 | 608 | 626 | 636 | 644 | 650 | 654 | 656 | 662 | 666 | 670 | 683 |
2 | 860 | 884 | 902 | 908 | 914 | 920 | 924 | 930 | 936 | 940 | 954 |
3 | 942 | 960 | 970 | 976 | 980 | 984 | 984 | 988 | 992 | 992 | 997 |
Как видно из данных таблицы, вероятность различия между выборочной средней малой выборки и генеральной средней зависит от двух величин: численности выборкип и нормированного отклонения и можно увидеть, что при увеличениип это распределение стремится к нормальному и при п = 20 уже мало от него отличается. При п ^ й в таблице приведены значения для функции нормального распределения
. Другой аспект применения распределения. Стьюдента приведен в приложении 3, в котором данные значения и — критерия. Стьюдента при разном уровне значимости (а) и числе степеней свободы вариации (к)
Распределение Пирсона
. Для оценки различий между эмпирическими и теоретическими частотами разработан ряд критериев согласия, среди которых наиболее широкое применение получил критерий% г — хи-квадрат. На основе сопоставления фактического в и теоретического (табличного) значения% г — критерия можно выяснить принадлежность данного эмпирического распределения некотором известном теоретическом типа распределения (например, есть или ни исследуемый распределение нор мальным, биномиальным и др..).
. Кривая, характеризующая распределение% г описывается уравнением
гдек — число степеней свободы вариации
. Учитывая, что для целых положительных чисел гамма-функция. Г (п) = п — 1, можно записать
. Из уравнения плотности вероятности видно, что распределение х 2 зависит только от числа степеней свободы вариации (к = п — 1). Распределение% г не зависит от генеральной средней и генеральной дисперсии. При большой численности выборки (прип = 30 — 40) распределение% г практически становится нормальным
. Для% г критерия составлены специальные таблицы, в которых приведены его значение при определенном числе степеней свободы вариации и заданном уровне вероятности (доп 6)
. Изложение аспектов прикладного применения% г — критерия дается в разделе, посвященном вопросам проверки статистических гипотез (раздел 7)
Распределение Фишера-Снедекора
. При решении ряда задач корреляционно-регрессионного и дисперсионного анализа используется распределение. Е, названный так по первой букве фамилии английского математика-статистика. РФишера
. Еслии иV — независимые случайные величины, распределенные по закону% г с степенями свободы к1 и к2 то величина
подчиняется распределения. Е. Фишера-Снедекора с степенями свободы к1 и к2 . Принимая, что и V, величина. Е будет иметь значение не менее единицы. Плотность распределенияЕ имеет вид
. Из формулы видно, что распределение. Е определяется двумя параметрами, то есть числами степеней свободы вариации к1 и к2. Это позволяет составить таблицы распределения случайной величины. Е, в которых различным значением уровня значимости и различным сообще нием величин к1 и к2 соответствуют определенные значения. Е-критерия (доп 4 и 55).
. Использование. Е-критерия в статистическом анализе подробно рассмотрен в разделе 8″Дисперсионный анализ»
uchebnikirus.com
18. Основные распределения в статистике. Распределение хи-квадрат. Распределение Стьюдента. Распределение Фишера.
Распределение ²
Пусть независимые случ.величины ξi где распределены по нормальному закону распределения, причемM[ξi]=0, а средн.квадратич. отклонение=1, тогда величина ξi распределена по закону ² с n степенями свободы.
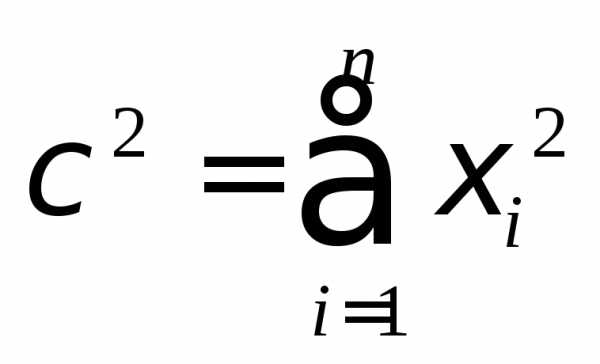
ξi распределено по норм.закону-это значит,что:
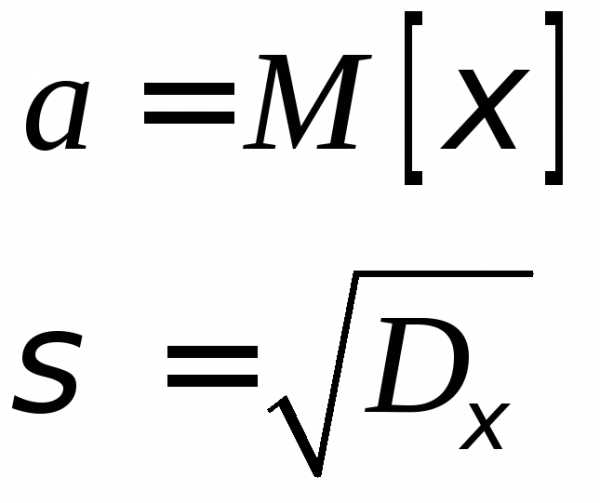


-гамма функция
m-положительна Г(m+1)=Г(m)
m-целое Г(m)=(m-1)!
Распределение ² опред.одним параметром — числом степеней свободы n
f(x) — называется графиком Пирснона
Они ассиметричны и начинаются с n>2, имею один максимум в значении x=n-2

Характериситческая ф-ция

Распределение Стьюдента:
Пусть V не зависит от Z и V распределена по закону ², и есть n степеней свободы, тогда вводим величину
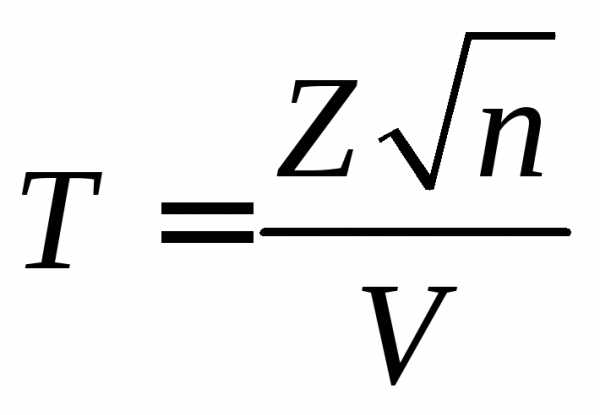 ,
тогда величина T
имеет распределение Стьюдента t
с n-степенями
свободы.
,
тогда величина T
имеет распределение Стьюдента t
с n-степенями
свободы.

Плотность распределения:

Графики fT(x) наз.кривыми Стьюдента, симметрична при всех n = 1,2,… относительно оси ординат.
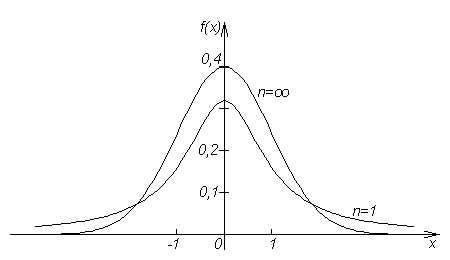
С возрастанием числа степеней свободы распр-е Стьюдента быстро приближается к нормальному.
Распределение Фишера:
 -независимые
случ.величины, распределены по нормальному
закону ²
с n и m степенями свободы,
-независимые
случ.величины, распределены по нормальному
закону ²
с n и m степенями свободы,
тогда
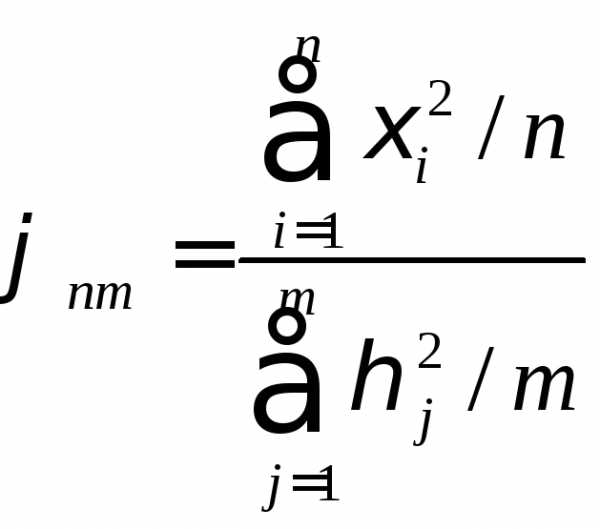
распределение Фишера с n и m степенями свободы.
Плотность этого распределения:
где

Распределение Фишера определяется 2-мя параметрами – числами степеней свободы.
19. Статистические оценки. Точечные оценки. Метод максимального правдоподобия. Метод наименьших квадратов. Интервальные оценки.
Стат.оценкой неизвестного параметра теоретического распределения нзв ф-цию от наблюдаемых случайных величин.
Несмещенной нзв стат.оценку, мат.ожид.к-рой равно оцениваемому параметру при любом объеме выборки, т.е. M[*]=.
Смещенной нзв оценку, мат.ожид.к-рой не равно оцениваемому параметру.
Эффективной нзв оценку, к-рая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию.
Состоятельной нзв оценку, к-рая при n∞ стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при n∞ стремится к 0, то такая оценка оказывается и состоятельной.
Точечные оценки
Точечной нзв оценку, к-рая опред-ся одним числом, например: генеральная средняя, выборочная средняя, групповая и общая средние, генеральная дисперсия, выборочная дисперсия и др.
xi – значения выборки
При выборке малого объема точечная оценка может знач.отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.
Несмещенной оценкой генеральной средней (мат ожидания) служит выборочная средняя
 ,где
xi–варианта
выборки, ni-частота
,где
xi–варианта
выборки, ni-частота
варианты xi,  —объем
выборки.
—объем
выборки.
Замечание1.Если первоначальные варианты xi-большие числа,то для упрощения расчета из каждой варианты одно и то же число С,т.е. перейти к условным вариантам ui=xi-C, тогда .
Смещенной оценкой генеральной дисперсии служит выборочная дисперсия
,эта оценка является
смещенной, т к 
Замечание2.Если первоначальные варианты xi-большие числа, то целесообразно вычесть из всех вариант одно и то же число C,равное выборочной средней или близкое к ней,т.е. перейти к условным вариантам ui=xi-C (дисперсия при этом не изменится).
Тогда
Замечание 3. Если первоначальные варианты являются десятичными дробями с k десятичными знаками после запятой, то, чтобы избежать действий с дробями,умножают первоначальные варианты на постоянное число C=10k,т.е. переходят к условным вариантам ui=Cxi. При этом дисперсия увеличится в C2 раз. Поэтому, найдя дисперсию условных вариант, надо разделить ее на C2:
Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия
В условных вариантах она имеет вид
Причем если
ui=xi-C,то
s2x= ;
еслиui=Cxi, то s2x=
;
еслиui=Cxi, то s2x=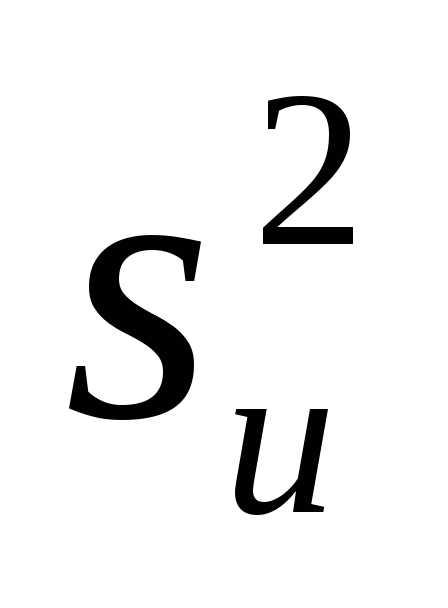 ,то
s2x=
,то
s2x=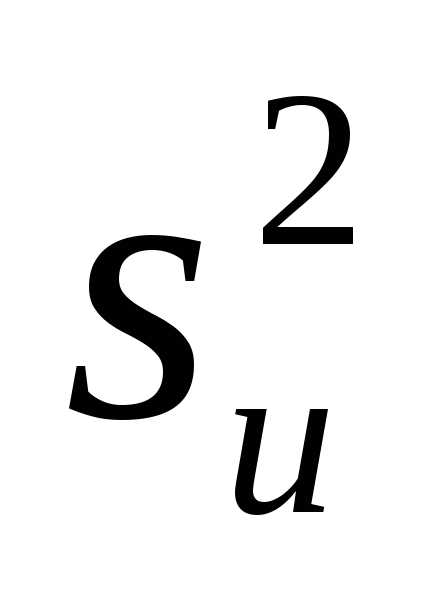 /C2.
/C2.
Примечание 4. При большом числе данных используют метод произведений или метод сумм.
Метод максимального правдоподобия.
Метод м.п. точечной оценки неизвестных параметров заданного распределения сводится к отысканию максимума ф-ции одного или нескольких оцениваемых параметров.
А) Дискретные случ величины. Пусть Х-дискретная случ величина,кот в результате n опытов приняла возможные значения х1,х2..хn.Допустим,что вид закона распределения случ велич Х задан,но неизвестен параметр ,которым определяется этот закон;требуется найти его точечную оценку *=*( х1,х2..хn).
Обозначим вероятность того,что в результате испытания величина Х примет значение хi через p(xn; ).
Функцией правдоподобия дискретной случайной величины Х назыв ф-цию аргумента :
L(х1,х2..хn; )=p(x1; )* p(x2; )… p(xn; ) .
Оценкой наибольшего правдоподобия параметра назыв такое его значение *,при кот ф-ция правдоподобия достигает максимума.Функции L и lnL достигают максимума при одном и том же значении ,поэтому вместо отыскания максимума ф-ции L ищут,что удобнее,максимум ф-ции lnL.
Логарифмической ф-цией правдоподобия назыв ф-цию lnL.Точку максимума ф-ции lnL аргумента можно искать,например,так:
1.найти производную 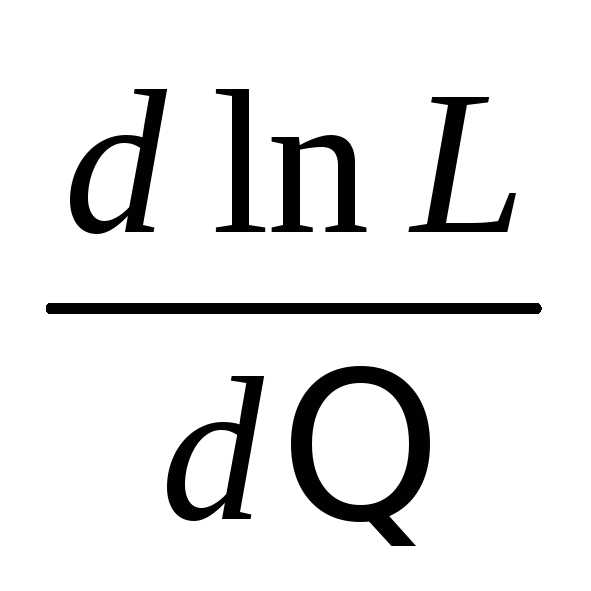
2.приравнять производную 0 и найти критич точку *-корень получ ур-ия (ур-ия правдоподобия)
3.найти вторую
производную 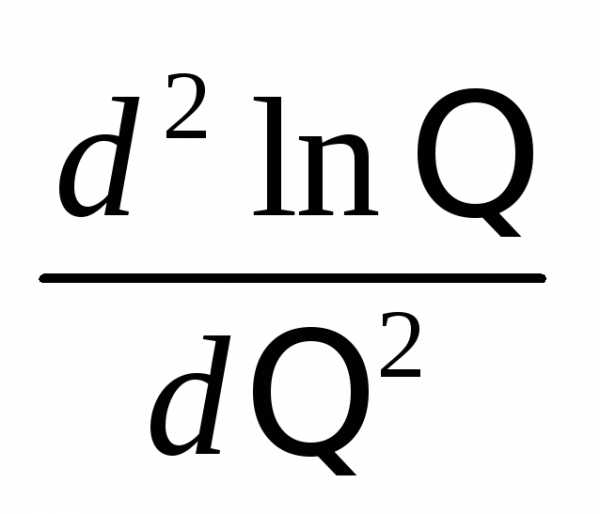 ,если вторая производная при=*
отрицательна,то *-точка
максимума. Найденную точку максимума
*
принимают в качестве оценки наибольшего
правдоподобия параметра .
,если вторая производная при=*
отрицательна,то *-точка
максимума. Найденную точку максимума
*
принимают в качестве оценки наибольшего
правдоподобия параметра .
Б) Непрерывные случайные величины. Пусть Х-непрерывн случ велич,которая в результате n испытаний приняла значения х1,х2..хn. Допустим,что вид плотности распределения-ф-ции f(x) – задан,но неизвестен параметр θ,которым определяется эта ф-ция. Ф-ией правдоподобия непрерывной случ величины Х назыв ф-цию аргумента :
L(х1,х2..хn; )=f(x1; )* f(x2; )… f(xn; ).
Оценку наибольшего правдоподобия неизвестного параметра распределения непрерывной случ величины ищут также,как в случае дискретной случ величины.
Если плотность распределения f(x) непрерывной случ величины определяется двумя неизвестными параметрами 1и 2,то ф-ция правдоподобия есть ф-ция двух независ аргументов 1и 2:
L= f(x1; 1, 2)* f(x2; 1, 2)… f(xn; 1, 2). Далее находят логарифмическую ф-цию правдоподобия и для отыскания ее максимума составл и решают систему
Метод наименьших квадратов
а0, а1,…,an

(m+1) уравнений
y=ax+b
(x1, y1), (x2, y2)…
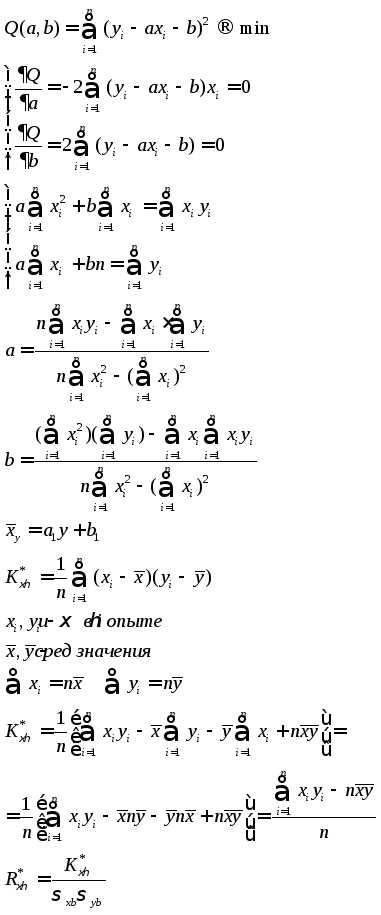
Интервальные оценки
Интервальной нзв оценку, к-рая определяется двумя числами – концами интервала. Инт.оценки позволяют установить точность и надежность оценок.
Надежностью (доверительной вероятностью) оценки по * нзв вер-ть γ, с к-рой осуществл.нерав-во | — *|<δ. Заменив нерав-во | — *|<δ равносильным ему двойным нерав-вом -δ< — *<δ или *-δ<<δ+* имеем
Доверительным нзв интервал (*-δ, *+δ), к-рый покрывает неизвестный параметр с заданной надежностью γ.
1.Интервальной
оценкой (с надежностью γ) математического
ожидания а нормально распределенного
количественного признака X
по выборочной средней  при известном среднем квадратическом
отклонении σ генеральной совокупности
служит доверительный интервал
при известном среднем квадратическом
отклонении σ генеральной совокупности
служит доверительный интервал
Где — точность оценки,n-объем выборки, t-значение аргумента ф-ции Лапласа Ф(t),при котором Ф(t)=γ/2; при неизвестном σ (и объеме выборки n<30)
где s-«исправленное» выборочное среднее квадратическое отклонение, tγ находят по таблице по заданным n и γ.
2. Интервальной оценкой (с надежностью γ) среднего квадратического отклонения σ нормально распределенного количественного признака X по «исправленному» выборочному среднему квадратическому отклонению s служит довер. инт-л
(при q<1)
(при q>1)
Где q находят по таблице по заданным n и γ
3. Интервальной оценкой (с надежностью γ) неизвестной вер-ти p биноминального распред-я по относ. частоте ω служит довер.инт-л (с приближ. концами p1 и p2)
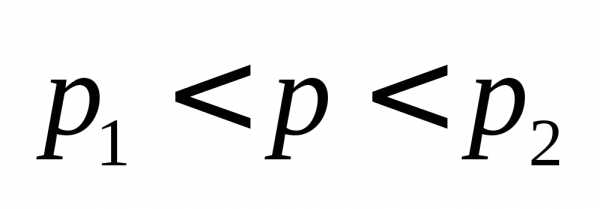
где
Где n-общее число испытаний; m-число появлений событий; ω-относ.частота, равная отношению m/n;t-значение аргумента ф-ции Лапласа, при к-ром Ф(t)=γ/2(γ-заданная надежность).
Замечание. При больших значениях n (порядка сотен) можно принять в кач-ве приближ.границ довер.инт-ла
20. Статистическая проверка гипотез. Основные понятия. Статистический критерий, ошибки 1-го и 2-го родов, уровень значимости и мощность критерия. Критерий согласия Пирсона. Проверка гипотезы о значении параметров нормального распределения. Проверка гипотезы о законе распределения случайной величины.
Статистическая проверка гипотез. Основные понятия. Уровень значимости и мощности критерия
Статистической гипотезой наз всякое непротиворечивое множество утверждений относительно закона распределения случайной величины.
С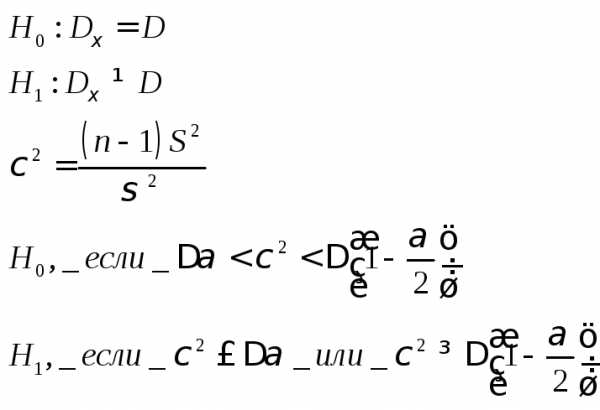 татистикой нзв произвольная функция Z = φ(Zn)
выборки Zn,
для значений к-рой известны условные
плотности
распределения f(z|H0)
и f(z|H1)
относительно проверяемой гипотезы H0 и конкурирующей с ней альтернативной
гипотезы H1.
Из опред следует, что Z есть СВ.
Практическое применение мат. статистики
состоит в проверке соответствия
результатов экспериментов предполагаемой
гипотезе. С этой целью строится процедура
(правило) проверки гипотезы. Критерием
согласия называется правило, в соответствии с
которым по реализации
статистики Z,
вычисленной на основании апостериорной
выборки zn,
гипотеза H0 принимается или отвергается. Критической
областью G называется область реализаций z статистики Z,
при которых гипотеза H0 отвергается. Доверительной
областью G называется область значений z статистики Z,
при которых гипотеза H0 принимается. Уровнем
значимости α критерия
согласия
называется вероятность события, стоящего
в том, что гипотеза H0 отвергается, когда она верна, т.е.
татистикой нзв произвольная функция Z = φ(Zn)
выборки Zn,
для значений к-рой известны условные
плотности
распределения f(z|H0)
и f(z|H1)
относительно проверяемой гипотезы H0 и конкурирующей с ней альтернативной
гипотезы H1.
Из опред следует, что Z есть СВ.
Практическое применение мат. статистики
состоит в проверке соответствия
результатов экспериментов предполагаемой
гипотезе. С этой целью строится процедура
(правило) проверки гипотезы. Критерием
согласия называется правило, в соответствии с
которым по реализации
статистики Z,
вычисленной на основании апостериорной
выборки zn,
гипотеза H0 принимается или отвергается. Критической
областью G называется область реализаций z статистики Z,
при которых гипотеза H0 отвергается. Доверительной
областью G называется область значений z статистики Z,
при которых гипотеза H0 принимается. Уровнем
значимости α критерия
согласия
называется вероятность события, стоящего
в том, что гипотеза H0 отвергается, когда она верна, т.е.
α =P{ZG|H0}
где вероятность P соответствует условной плотности распределения f(z|H0). Мощностью γ критерия согласия называется вероятность события, состоящего в том, что гипотеза H0 отвергается, когда она неверна, т.е.
γ=P{ZG|H1}
где вероятность P соответствует условной плотности f(z|H1). Критической точкой zβ называется точка на оси Oz, являющаяся квантилем уровня
β=1 – α
распределения F(z|H0), соответствующего плотности распределения f(z|H0). На рис. показана графическая интерпретация введенных понятий, где β + α = 1, δ + γ = 1.
Статистический критерий, ошибки 1-го и 2-го родов
Ошибка 1-го рода состоит в отклонении гипотезы, если она верна (пропуск цели).
Вероятность совершения ошибки 1-го рода обозначается α и наз. Уровнем значимости.
Ошибка 2-го рода – гипотеза принимается, если она неверна – β (ложное срабатывание).
Вероятность не совершить ошибку 2-го рода (1-β) наз. ложностью критерия.
Критерием (статистическим критерием) наз. случайная величина , которая позволяет принять или отклонить нулевую гипотезу.
Проверка гипотез о законе распределения случайной величины. Критерий согласия Пирсона.
Пусть имеется апостериорная выборка zn и требуется проверить гипотезу H0, состоящую в том, что непрерывная СВ X имеет определенный закон распределения f(x) (например, нормальный, равномерный и т.д.). Истинный закон распределения f(x) неизвестен. Для проверки такой гипотезы обычно используют критерий согласия хи-квадрат χ² (критерий Пирсона).
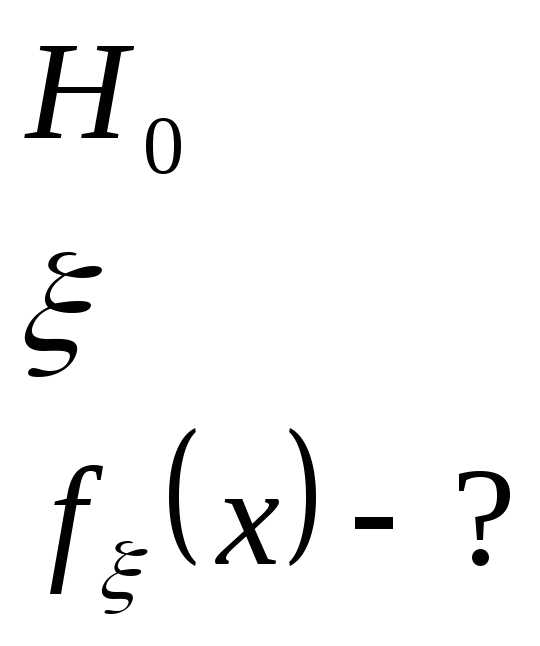
Критерием согласия называется критерий, использованный для проверки гипотез о предполагаемом законе распределения.
Проверка состоит в следующем:
1)Строится интервал — статистический ряд и гистограмма
2) По виду гистограммы
3) На основе выборки находим точечные оценки
4) Интервал возможных значений разбиваем на m непересекаемых интервалов. В каждом из них фиксируем число показаний
5) Вычисляем вероятность показаний ξ в каждом интервале
6) Строим критерий χ²

Аналитическое
выражение плотности ²-
сложное, поэтому задаем уровень значимости
α; k;
находим 
Проверка гипотезы о значении параметров нормального распределения.
Пусть известно, что СВ X имеет нормальное распределение. Требуется проверить гипотезу H0, состоящую в том, что mX = m (m — некоторое фиксированное число), используя апостериорную выборку zn. Возможны два случая: дисперсия (σX)2 известна или неизвестна.
1) Дисперсия известна

2) Дисперсия неизвестна
В качестве оценки вводим выборочную дисперсию
В качестве статистики:

Гипотезы о значении дисперсии
studfiles.net
Распределение Стьюдента
Распределение Стьюдента (t- распределение) имеет важное значение при статических вычислениях, связанных с нормальным законом, а именно тогда, когда среднеквадратичное отклонение не известно и еще подлежит определению по опытным данным.
Пусть X и X1, X2, …Xn – независимые случайные величины, имеющие нормальное распределение с параметрами:
M[X] = M[X1] = M [X2] = … = M[Xn] = 0
И
Случайная величина:
являющаяся функцией нормально распределенных случайных величин, называется безразмерной дробью Стьюдента. Распределения случайной величины T не зависит от параметров распределения независимых случайных величин X и X1, X2, …Xn, а зависит только от одного параметра – числа степеней свободы r.
Математическое ожидание и дисперсия случайной величины T соответственно равны:
M[T] = 0 D[T] = r > 2
При неограниченном увеличении числа степеней свободы распределения Стьюдента асимптотически переходит в нормальное распределение Гаусса с параметрами
M[T] = 0 и D[T] = 1.
В математической статистике часто используется квантили распределения Стьюдента в зависимости от числа степеней свободы r и заданного уровня вероятности.
С геометрической точки зрения нахождение квантилей распределения Стьюдента , заключается в таком выборе значения, при котором суммарная площадь под кривой плотностина участкахибыла бы равно.
2.2 Расчеты
Дана выборка:
41,77 | 41,81 | 41,64 | 41,54 | 41,91 | 41,67 | 41,55 | 41,84 | 41,61 | 41,80 |
42 | 62 | 86 | 65 | 70 | 85 | 60 | 69 | 95 | 62 |
71 | 50 | 76 | 73 | 66 | 43 | 68 | 52 | 70 | 46 |
58 | 89 | 56 | 32 | 53 | 99 | 83 | 35 | 61 | 37 |
95 | 57 | 87 | 75 | 82 | 50 | 41 | 78 | 42 | 98 |
64 | 80 | 65 | 58 | 72 | 80 | 60 | 72 | 70 | 62 |
70 | 92 | 53 | 60 | 74 | 69 | 61 | 55 | 38 | 51 |
82 | 44 | 97 | 78 | 80 | 34 | 70 | 49 | 60 | 63 |
75 | 63 | 70 | 48 | 52 | 73 | 69 | 71 | 78 | 47 |
58 | 74 | 55 | 65 | 78 | 54 | 51 | 68 | 56 | 64 |
Количество интервалов Nint=6
Минимальное и максимальное значение выборки:
Ширина подынтервала:
Граничные точки подынтервалов
Чтобы найти полигон частот отсортируем выборку с помощью функции sort() и запустим цикл для данной выборки.
Проверим данные частоты с помощью функции hist()
Значения верны. Построим гистограмму:
Найдем оценки для математического ожидания и дисперсии:
Для этого найдем середины отрезков данных интервалов
Доверительный интервал для мат.ожидания:
Надёжность равна 0.95
Квантили распределения Стьюдента найденные по таблице:
Левая и правая границы доверительного интервала:
Доверительный интервал для дисперсии при той же надежности:
Квантили распределения Пирсона найденные по таблице:
Левая и правая границы доверительного интервала:
Для того чтобы проверить гипотезу о том, что наша выборка извлечена из нормальной генеральной совокупности, найдем теоретические частоты.
Функция распределения Лапласа
Найденные частоты:
Проверим данную гипотезу с помощью критерия Х2 Пирсона:
По таблице найдем критическую точку для данной выборки при уровне значимости равным 0.05 и степенями свободы равным k:
Где S –количество интервалов, т.е равно 6 и r– количество параметров, для нормального распределения их 2.
Значит, гипотезу о нормальном распределении выборки отвергаем.
2.3. Выводы
В ходе работы над первой частью курсовой работы был написан теоретический обзор по точечному и интервальному оцениванию. В работе выполнены расчеты, связанные с нахождение доверительных интервалов для математического ожидания, дисперсии и вероятности. Для заданной генеральной совокупности построены гистограмма и полигон, найдены оценки математического ожидания и дисперсии, а также доверительные интервалы для математического ожидания и дисперсии. С помощью критерия согласия Пирсона проверена гипотеза о том, что выборка извлечена из нормальной генеральной совокупности. В результате анализа, гипотеза не подтвердилась, т.к. получилось, что. Отсюда следует вывод, что гипотеза о нормальном законе распределения генеральной совокупности должна быть отвергнута.
studfiles.net