Внутренние накрест лежащие углы | Треугольники
Внутренние накрест лежащие углы — один из видов углов, образованных при пересечении двух прямых секущей.
Две прямые разбивают плоскость на внутреннюю (внутри между прямыми) и внешнюю области. Углы, лежащие во внутренней части, так и называются — внутренние.
Внутренние накрест лежащие углы — это углы, которые лежат во внутренней области по разные стороны от секущей (накрест друг от друга).
При пересечении двух прямых секущей образуется две пары внутренних накрест лежащих углов.
∠1 и∠2 — внутренние накрест лежащие углы при прямых a и b и секущей c.
∠3 и∠4 — внутренние накрест лежащие углы при прямых a и b и секущей c.
Из всех внутренних накрест лежащих углов наибольший интерес представляют углы при параллельных прямых.
Свойство параллельных прямых
Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны.
Если a ∥ b, то
∠3=∠4
(как внутренние накрест лежащие углы при a ∥ b и секущей c).
Признак параллельных прямых
Если внутренние накрест лежащие углы равны, то прямые параллельны.
∠1=∠2.
А так как эти углы — внутренние накрест лежащие при прямых a и b и секущей c,
то a ∥ b (по признаку параллельных прямых).
Равенство внутренних накрест лежащих углов при параллельных прямых используется, в частности, при доказательстве равенства треугольников и подобия треугольников.
www.treugolniki.ru
Теорема о накрест лежащих углах
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Параллельные прямые
- Теорема о накрест лежащих углах
Теорема
| Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны. |
Дано: , АВ — секущая, 1 и 2 — накрест лежащие (Рис.1).
Доказать: 1 =2.
Доказательство:
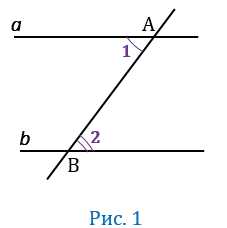
Предположим,что углы 1 и 2 не равны друг другу. Отложим от луча АВ угол РАВ, равный углу 2, так, чтобы РАВ и 2 были накрест лежащими углами при пересечении прямых
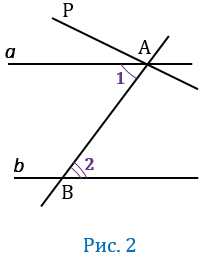
По построению накрест лежащие углы РАВ и 2 равны, значит АР (по признаку параллельности двух прямых). То есть мы получили, что через точку А проходят две прямые и АР, параллельные прямой . Но это противоречит аксиоме параллельных прямых. Значит наше предположение неверно и 1 = 2. Что и требовалось доказать.
Следствие
Дано: , (Рис.3).
Доказать: .
Доказательство:
Прямая пересекает прямую , при этом , значит пересекает и прямую (смотри следствие 20 из аксиомы параллельных прямых). При пересечении параллельных прямых и секущей образуются равные накрест лежащие углы: 1 =2 (по теореме о накрест лежащих углах). По условию , т.е. 1 = 900, значит и 2 = 900 , т.е. . Что и требовалось доказать.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Параллельные прямые
Признаки параллельности двух прямых
Практические способы построения параллельных прямых
Аксиомы геометрии
Аксиома параллельных прямых
Теорема о соответственных углах
Теорема об односторонних углах
Теорема об углах с соответственно параллельными сторонами
Параллельные прямые
Правило встречается в следующих упражнениях:
7 класс
Задание 201, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 204, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 211, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 16, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 17, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 243, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 342, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 425, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 518, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 621, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
© 2019 — budu5.com, Буду отличником!
budu5.com
Теорема о равенстве накрест лежащих углов
Например, рассмотрим один из признаков параллельности прямых:
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Здесь условие утверждения: Если при пересечении двух прямых секущей накрест лежащие углы равны. А заключение: прямые параллельны.
Теоремой, обратной данной, называется такая теорема, в которой условием является заключение данной теоремы, а заключением — условие данной теоремы.
Теорема:
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Доказательство:
Пусть прямые а и b параллельны и пересечены секущей CD. Доказать, что накрест лежащие углы 1 и 2 равны.
Предположим, что углы 1 и 2 не равны. Тогда от луча CD отложим ∠ЕCD=∠2 так, чтобы ∠ЕCD и ∠2 были накрест лежащими углами при пересечении прямых СЕ и b секущей CD.
По построению эти накрест лежащие углы равны, а поэтому прямая CD параллельна прямой b. Получили, что через точку С проходят две прямые (а и CЕ) параллельные прямой b. А это противоречит аксиоме параллельности прямых. Следовательно, предположение неверно и угол ∠1=∠2. Что и требовалось доказать.
Пример.
Прямая АВ параллельна прямой CD, АD - биссектриса угла BAC, а ∠ADC=50 градусов. Чему равна градусная мера ∠CAD?
Так как прямые АВ и CD параллельны и AD - секущая при этих параллельных прямых, то накрест лежащие углы ADC и BAD равны. Значит, ∠BAD=50 градусов.
Так как AD - биссектриса ∠BAC, то ∠CAD=∠BAD. Следовательно, градусная мера ∠CAD=50 градусов.
Пример.
Прямые АВ и CD параллельны. Отрезок АВ=СD. Доказать, что прямая АС параллельна прямой BD.
Рассмотрим треугольник ABD и треугольник ACD.
АВ=CD по условию задачи, AD - общая. А углы BAD и ADC равны как накрест лежащие углы при параллельных прямых АВ и CD и секущей АD. Следовательно, треугольники ABD и ACD равны по первому признаку равенства треугольников. А значит, у них соответственные стороны и углы равны.
То есть ∠CAD=∠BDA. А эти углы являются накрест лежащими при прямых AC и BD и секущей AD. Это означает, что прямые AC и BD параллельны. Что и требовалось доказать.
Пример.
На рисунке ∠CBD=∠ADB. Доказать, что ∠ВСА=∠CAD.
Углы CBD и ADB - накрест лежащие углы при прямых AD и BC и секущей BD. А так как эти углы равны, то прямые AD и BC параллельны.
∠ВСА и ∠CAD являются накрест лежащими при параллельных прямых AD и BC и секущей АС, а следовательно, они равны. Что и требовалось доказать.
Отметим, что если доказана какая-либо теорема, то это не означает, что обратная ей теорема верна.
Например, если углы вертикальные, то они равны. А вот если углы равны, то это ещё не означает, что они вертикальные.
videouroki.net
Накрест лежащие Википедия
Параллельные прямые (от греч. παράλληλος, буквально — идущий рядом) — в планиметрии прямые, которые не пересекаются, сколько бы их ни продолжали в обе стороны.
В евклидовой геометрии[ | ]
На чертежах параллельные линии выделяются одинаково направленными стрелками.В евклидовой геометрии параллельными прямыми называются прямые, которые лежат в одной плоскости и не пересекаются
Параллельность прямых m{\displaystyle m} и n{\displaystyle n} обычно обозначается:
- m∥n{\displaystyle m\parallel n}
Свойства[ | ]
- Через любую точку, не лежащую на прямой, можно провести прямую, параллельную данной, и притом только одну. Последняя часть этого утверждения — знаменитый пятый постулат Евклида. Отказ от пятого постулата ведёт к геометрии Лобачевского (см. ниже).
- Если прямая пересекает одну из параллельных прямых, то она пересекает и другую (такая прямая называется секущей). При этом образуется 8 углов, некоторые характерные пары которых имеют особые названия и свойства:
- Соответственные углы равны (Рис.1).
- Накрест лежащие углы равны (Рис.2).
- Внутренние односторонние углы в сумме составляют 180° (Рис.3).
| Рис.1: Соответственные углы равны, α=α1 |
ru-wiki.ru
А.В. Погорелов. Геометрия. 7 класс. §4. Контрольные вопросы, ответы
- Подробности
- Родительская категория: Математика
- Категория: Геометрия, 7 класс, контрольные вопросы, ответы
Страница 1 из 2
Вопрос 1. Докажите, что две прямые, параллельные третьей, параллельны.
Ответ. Теорема 4.1. Две прямые, параллельные третьей, параллельны.
Доказательство. Пусть прямые a и b параллельны прямой c. Допустим, что a и b не параллельны (рис. 69). Тогда они не пересекаются в некоторой точке C. Значит, через точку C проходят две прямые, параллельные прямой c. Но это невозможно, так как через точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной. Теорема доказана.

Вопрос 2. Объясните, какие углы называются внутренними односторонними. Какие углы называются внутренними накрест лежащими?
Ответ. Пары углов, которые образуются при пересечении прямых AB и CD секущей AC, имеют специальные названия.
Если точки B и D лежат в одной полуплоскости относительно прямой AC, то углы BAC и DCA называются внутренними односторонними (рис. 71, а).
Если точки B и D лежат в разных полуплоскостях относительно прямой AC, то углы BAC и DCA называются внутренними накрест лежащими (рис. 71, б).

Рис. 71
Вопрос 3. Докажите, что если внутренние накрест лежащие углы одной пары равны, то внутренние накрест лежащие углы другой пары тоже равны, а сумма внутренних односторонних углов каждой пары равна 180°.
Ответ. Секущая AC образует с прямыми AB и CD две пары внутренних односторонних и две пары внутренних накрест лежащих углов. Внутренние накрест лежащие углы одной пары, например угол 1 и угол 2, являются смежными внутренним накрест лежащим углам другой пары: угол 3 и угол 4 (рис. 72).
Рис. 72
Поэтому если внутренние накрест лежащие углы одной пары равны , то внутренние накрест лежащие углы другой пары тоже равны.
Пара внутренних накрест лежащих углов, например угол 1 и угол 2, и пара внутренних односторонних углов, например угол 2 и угол 3, имеют один угол общий – угол 2, а два других угла смежные: угол 1 и угол 3.
Поэтому если внутренние накрест лежащие углы равны, то сумма внутренних углов равна 180°. И обратно: если сумма внутренних накрест лежащих углов равна 180°, то внутренние накрест лежащие углы равны. Что и требовалось доказать.
Вопрос 4. Докажите признак параллельности прямых.
Ответ. Теорема 4.2 (признак параллельности прямых). Если внутренние накрест лежащие углы равны или сумма внутренних односторонних углов равна 180°, то прямые параллельны.
Доказательство. Пусть прямые a и b образуют с секущей AB равные внутренние накрест лежащие углы (рис. 73, а). Допустим, прямые a и b не параллельны, а значит, пересекаются в некоторой точке C (рис. 73, б).
Рис. 73
Секущая AB разбивает плоскость на две полуплоскости. В одной из них лежит точка C. Построим треугольник BAC1, равный треугольнику ABC, с вершиной C1 в другой полуплоскости. По условию внутренние накрест лежащие углы при параллельных a, b и секущей AB равны. Так как соответствующие углы треугольников ABC и BAC1 с вершинами A и B равны, то они совпадают с внутренними накрест лежащими углами. Значит, прямая AC1 совпадает с прямой a, а прямая BC1 совпадает с прямой b. Получается, что через точки C и C1 проходят две различные прямые a и b. А это невозможно. Значит, прямые a и b параллельны.
Если у прямых a и b и секущей AB сумма внутренних односторонних углов равна 180°, то, как мы знаем, внутренние накрест лежащие углы равны. Значит, по доказанному выше, прямые a и b параллельны. Теорема доказана.
Вопрос 5. Объясните, какие углы называются соответственными. Докажите, что если внутренние накрест лежащие углы равны, то соответственные углы тоже равны, и наоборот.
Ответ. Если у пары внутренних накрест лежащих углов один угол заменить вертикальным ему, то получится пара углов, которые называются соответственными углами данных прямых с секущей. Что и требовалось объяснить.
Из равенства внутренних накрест лежащих углов следует равенство соответственных углов, и наоборот. Допустим, у нас есть две параллельные прямые (так как по условию внутренние накрест лежащие углы равны) и секущая, которые образуют углы 1, 2, 3. Углы 1 и 2 равны как внутренние накрест лежащие. А углы 2 и 3 равны как вертикальные. Получаем: \(\angle\)1 = \(\angle\)2 и \(\angle\)2 = \(\angle\)3. По свойству транзитивности знака равенства следует, что \(\angle\)1 = \(\angle\)3. Аналогично доказывается и обратное утверждение.
Отсюда получается признак параллельности прямых по соответственным углам. Именно: прямые параллельны, если соответственные углы равны. Что и требовалось доказать.
Вопрос 6. Докажите, что через точку, не лежащую на данной прямой, можно провести параллельную ей прямую. Сколько прямых, параллельных данной, можно провести через точку, не лежащую на этой прямой?
Ответ. Задача (8). Даны прямая AB и точка C, не лежащая на этой прямой. Докажите, что через точку C можно провести прямую, параллельную прямой AB.
Решение. Прямая AC разбивает плоскость на две полуплоскости (рис. 75). Точка B лежит в одной из них. Отложим от полупрямой CA в другую полуплоскость угол ACD, равный углу CAB. Тогда прямые AB и CD будут параллельны. В самом деле, для этих прямых и секущей AC углы BAC и DCA внутренние накрест лежащие. А так как они равны, то прямые AB и CD параллельны. Что и требовалось доказать.
Сопоставляя утверждение задачи 8 и аксиомы IX (основного свойства параллельных прямых), приходим к важному выводу: через точку, не лежащую на данной прямой, можно провести параллельную ей прямую, и только одну.
Вопрос 7. Докажите, что если две прямые пересекаются третьей прямой, то внутренние накрест лежащие углы равны, а сумма внутренних односторонних углов равна 180°.
Ответ. Теорема 4.3 (обратная теореме 4.2). Если две параллельные прямые пересекаются третьей прямой, то внутренние накрест лежащие углы равны, а сумма внутренних односторонних углов равна 180°.
Доказательство. Пусть a и b – параллельные прямые и c – прямая, пересекающая их в точках A и B. Проведём через точку A прямую a1 так, чтобы внутренние накрест лежащие углы, образованные секущей c с прямыми a1 и b, были равны (рис. 76).
По признаку параллельности прямых прямые a1 и b параллельны. А так как через точку A проходит только одна прямая, параллельная прямой b, то прямая a совпадает с прямой a1.
Значит, внутренние накрест лежащие углы, образованные секущей с
параллельными прямыми a и b, равны. Теорема доказана.
Вопрос 8. Докажите, что две прямые, перпендикулярные третьей, параллельны. Если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
Ответ. Из теоремы 4.2 следует, что две прямые, перпендикулярные третьей, параллельны.
Предположим, что две какие-либо прямые перпендикулярны третьей прямой. Значит, эти прямые пересекаются с третьей прямой под углом, равным 90°.
Из свойства углов, образованных при пересечении параллельных прямых секущей, следует, что если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.
Вопрос 9. Докажите, что сумма углов треугольника равна 180°.
Ответ. Теорема 4.4. Сумма углов треугольника равна 180°.
Доказательство. Пусть ABC – данный треугольник. Проведём через вершину B прямую, параллельную прямой AC. Отметим на ней точку D так, чтобы точки A и D лежали по по разные стороны от прямой BC (рис. 78).
Углы DBC и ACB равны как внутренние накрест лежащие, образованные секущей BC с параллельными прямыми AC и BD. Поэтому сумма углов треугольника при вершинах B и C равна углу ABD.
А сумма всех трёх углов треугольника равна сумме углов ABD и BAC. Так как эти углы внутренние односторонние для параллельных AC и BD и секущей AB, то их сумма равна 180°. Теорема доказана.
Вопрос 10. Докажите, что у любого треугольника по крайней мере два угла острые.
Ответ. Действительно, допустим, что у треугольника только один острый угол или вообще нет острых углов. Тогда у этого треугольника есть два угла, каждый из которых не меньше 90°. Сумма этих двух углов уже не меньше 180°. А это невозможно, так как сумма всех углов треугольника равна 180°. Что и требовалось доказать.
oftob.ru
Признаки параллельности двух прямых. Свойства параллельных прямых [wiki.eduVdom.com]
Признаки параллельности двух прямых
Рис.1
Теорема 1. Если при пересечении двух прямых секущей:
накрест лежащие углы равны, или
соответственные углы равны, или
сумма односторонних углов равна 180°, то
прямые параллельны (рис.1).
Доказательство. Ограничимся доказательством случая 1.
Пусть при пересечении прямых а и b секущей АВ накрест лежащие углы равны. Например, ∠ 4 = ∠ 6. Докажем, что а || b.
Предположим, что прямые а и b не параллельны. Тогда они пересекаются в некоторой точке М и, следовательно, один из углов 4 или 6 будет внешним углом треугольника АВМ. Пусть для определенности ∠ 4 — внешний угол треугольника АВМ, а ∠ 6 — внутренний. Из теоремы о внешнем угле треугольника следует, что ∠ 4 больше ∠ 6, а это противоречит условию, значит, прямые а и 6 не могут пересекаться, поэтому они параллельны.
Следствие 1. Две различные прямые на плоскости, перпендикулярные одной и той же прямой, параллельны (рис.2).
Рис.2
Замечание. Способ, которым мы только что доказали случай 1 теоремы 1, называется методом доказательства от противного или приведением к нелепости. Первое название этот способ получил потому, что в начале рассуждения делается предположение, противное (противоположное)
тому, что требуется доказать. Приведением к нелепости он называется вследствие того, что, рассуждая на основании сделанного предположения, мы приходим к нелепому выводу (к абсурду). Получение такого вывода заставляет нас отвергнуть сделанное вначале допущение и принять то, которое требовалось доказать.
Задача 1. Построить прямую, проходящую через данную точку М и параллельную данной прямой а, не проходящей через точку М.
Решение. Проводим через точку М прямую р перпендикулярно прямой а (рис. 3).
Рис.3
Затем проводим через точку М прямую b перпендикулярно прямой р. Прямая b параллельна прямой а согласно следствию из теоремы 1.
Из рассмотренной задачи следует важный вывод:
через точку, не лежащую на данной прямой, всегда можно провести прямую, параллельную данной.
Основное свойство параллельных прямых состоит в следующем.
Аксиома параллельных прямых. Через данную точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Рассмотрим некоторые свойства параллельных прямых, которые следуют из этой аксиомы.
1) Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую (рис.4).
Рис.4
2) Если две различные прямые параллельны третьей прямой, то они параллельны (рис.5).
Рис.5
Справедлива и следующая теорема.
Теорема 2. Если две параллельные прямые пересечены секущей, то:
накрест лежащие углы равны;
соответственные углы равны;
сумма односторонних углов равна 180°.
Следствие 2. Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой (см. рис.2).
Рис.2
Замечание. Теорема 2 называется обратной теореме 1. Заключение теоремы 1 является условием теоремы 2. А условие теоремы 1 является заключением теоремы 2. Не всякая теорема имеет обратную, т. е. если данная теорема верна, то обратная теорема может быть неверна.
Поясним это на примере теоремы о вертикальных углах. Эту теорему можно сформулировать так: если два угла вертикальные, то они равны. Обратная ей теорема была бы такой: если два угла равны, то они вертикальные. А это, конечно, неверно. Два равных угла вовсе не обязаны быть вертикальными.
Пример 1. Две параллельные прямые пересечены третьей. Известно, что разность двух внутренних односторонних углов равна 30°. Найти эти углы.
Решение. Пусть условию отвечает рисунок 6.
Рис.6
Углы 1 и 2 внутренние односторонние, их сумма равна 180°, т. е.
∠ l + ∠ 2 = 180°. (1)
Обозначим градусную меру угла 1 через х. По условию ∠ 2 — х = 30°, или ∠ 2 = 30° + x.
Подставим в равенство (1) значения углов 1 и 2, получим
х + 30° + х = 180°.
Решая это уравнение, получим х = 75°, т. е.
∠ 1 = 75°, a ∠ 2 = 180° — 75° = 105°.
Пример 2. Две параллельные прямые пересечены третьей. Известно, что сумма двух внутренних накрест лежащих углов равна 150°. Чему равны эти углы и остальные шесть?
Решение. Пусть условию задачи соответствует рисунок 7.
Рис.7
Углы 1 и 2 внутренние накрест лежащие, следовательно, они равны. Сумма этих углов по условию задачи равна 150°, тогда ∠ 1 = ∠ 2 = 75°.
Найдем остальные углы (рис. 8):
Рис.8
∠ 1 = ∠ 3 = 75° и ∠ 2 = ∠ 7 = 75° (вертикальные). Углы 4 и 5, 6 и 8 равны как вертикальные, a ∠ 5 = ∠ 6 как внутренние накрест лежащие. Все перечисленные углы 4, 5, 6 и 8 равны между собой и равны по 105°, так как ∠ 4 + ∠ 3 = 180°, a ∠ 4 = 180° — ∠ 3.
Получили четыре угла по 75°, четыре угла по 105°.
www.wiki.eduvdom.com
Внутренние односторонние углы | Треугольники
Еще один вид углов, образованных при пересечении двух прямых секущей — внутренние односторонние углы.
Две прямые разбивают плоскость на части. Та часть, которая лежит между прямыми — внутренняя. Углы, которые расположены в этой части, так и называются — внутренние. Внутренние односторонние углы — это углы, которые лежат внутри между прямыми по одну сторону от секущей (поэтому они так и называются).
При пересечении двух прямых секущей образуется две пары внутренних односторонних углов.
∠1 и∠2
∠3 и∠4
— внутренние односторонние углы при прямых a и b и секущей c.
Наибольший интерес вызывают внутренние накрест лежащие углы, образованные параллельными прямыми.
Свойство параллельных прямых
Если две параллельные прямые пересечены третьей прямой, то сумма внутренних односторонних углов равна 180º.
Если a ∥ b, то
∠1 +∠2 =180º
(как внутренние односторонние при a ∥ b и секущей c).
Признак параллельных прямых
Если сумма внутренних односторонних углов равна 180º, то прямые параллельны.
∠3+∠4 =180º
А так как эти углы — внутренние односторонние при a и b и секущей c,
то a ∥ b (по признаку параллельных прямых).
Могут ли быть внутренние односторонние углы равны?
Да. Внутренние односторонние углы равны, если прямые параллельны, а секущая им перпендикулярна.
∠1 и ∠2 — внутренние односторонние углы при прямых a и b и секущей c
∠1 =∠2
тогда и только тогда, когда a ∥ b, а секущая c перпендикулярна и прямой a, и прямой b.
www.treugolniki.ru
