Ekzamen_geodezia (1) / 12.Уклон линии. Графики заложений для определения уклонов и углов наклона. Проектирование направлений с заданным уклоном
12.Уклон линии. Графики заложений для определения уклонов и углов наклона. Проектирование направлений с заданным уклоном.
Рис. 31. Определение уклона и угла наклона ската
Уклоном линии местности называют отношение превышения к горизонтальному проложению. Из формулы следует (рис. 31), что уклон безразмерная величина. Его выражают в сотых долях (%) или тысячных долях – промиллях (‰).
Если угол наклона ската до 45°, то он изображается горизонталями, если его крутизна более 45°, то рельеф обозначают специальными знаками.
Для изображения рельефа горизонталями выполняют топографическую съемку участка местности. По результатам съемки определяют координаты (две плановые и высоту) для характерных точек рельефа и наносят их на план (рис. 33). В зависимости от характера рельефа, масштаба и назначения плана выбирают высоту сечения рельефа
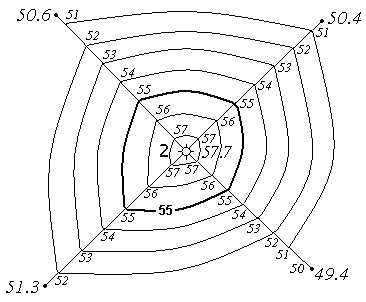
Рис. 33. Изображение рельефа горизонталями
Для инженерного проектирования обычно h = 1 м. Отметки горизонталей в этом случае будут кратны одному метру.
Положение горизонталей на плане или карте определяется с помощью интерполирования. На рис. 33 приведено построение горизонталей с отметками 51, 52, 53, 54, 55, 56, 57 м. Горизонтали кратные 5 или 10 м проводят на чертеже утолщенными и подписывают. Подписи наносят таким образом, чтобы верх цифр указывал сторону повышения рельефа. На рис. 33 подписана горизонталь с отметкой 55 м.
Там, где заложения больше, наносят штриховые линии (полугоризонтали). Иногда, чтобы сделать чертеж более наглядным, горизонтали сопровождают небольшими черточками, которые ставятся перпендикулярно горизонталям, по направлению ската (в сторону стока воды). Эти черточки называются бергштрихи
studfiles.netБилет №18. Определение уклонов и углов наклона по карте. Построение линии заданного уклона.
Определение уклонов и углов наклона. Отрезки линий на земной поверхности обычно имеют наклон, отчего начало и конец отрезка находятся на разных высотах. Разность их высот – превышение, а проекция отрезка на горизонтальную плоскость – его горизонтальное проложение.
Уклоном i линии называется отношение превышения h к горизонтальному проложению d:
i = h / d. (4.2)
Для определения по карте уклона линии на участке KL между двумя горизонталями (рис. 4.7) измеряют его горизонтальное проложение – заложение d. Поскольку концы отрезка лежат на смежных горизонталях, превышение hмежду ними равно высоте сечения рельефа, подписанному под южной рамкой карты. Воспользовавшись формулой (4.2), вычисляют уклон, который принято выражать в тысячных. Если, например, h=1 м,
| Рис. 4.7. Определение высоты точки M и уклона на отрезке KL |
С другой стороны, отношение превышения h к горизонтальному проложению d равно тангенсу угла n наклона линии. Поэтому
i =tg n,
что позволяет, вычислив уклон определить по нему угол наклона.
При пользовании картой углы наклона не вычисляют, а определяют с помощью графика заложений (рис. 4.8), расположенного под южной рамкой карты. По горизонтальной оси графика отложены углы наклона, а по вертикальной — соответствующие этим углам заложения d, выраженные в масштабе карты и рассчитанные по формуле
d = h¤(Mtg n),
гдеh — высота сечения рельефа, а M – знаменатель масштаба карты.
| Рис. 4.8. График заложений |
Для определения угла наклона отрезка KL (рис. 4.7), расположенного между горизонталями, берут его в раствор циркуля и на графике заложений (рис. 4.8) находят такой угол, над которым ордината равна раствору циркуля d. Это и есть искомый угол наклона.
При необходимости многократного определения уклонов пользуются графиком уклонов, построенным аналогично графику заложений, но с отложением по горизонтальной оси не углов наклона, а уклонов.
Проведение линии с уклоном, не превышающим заданного предельного. Необходимость решения такой задачи возникает, например, при выборе трассы для будущей дороги. Вычисляют соответствующее заданному предельному уклону iпр заложение, выраженное в масштабе карты, (здесь M – знаменатель масштаба). .
| Рис. 4.9. Построение линии с заданным уклоном |
Чтобы уклон линии не превосходил iпр, ни одно заложение на ней не должно быть меньше, чем рассчитанное d. Если расстояние между горизонталями больше рассчитанного, направление линии можно выбирать произвольно. В противном случае в раствор циркуля берут отрезок, равный d, и строят ломаную линию, умещая между горизонталями рассчитанное предельное заложение (рис. 4.9).
Билет№19. Определение площадей по картам и планам.
Аналитический способ. если участок представляет собой замкнутый многоугольник, то, сняв с плана прямоугольные координаты его вершин, площадь участка вычисляют по формуле:
Графический способ. Участок на плане разбивают на простые геометрические фигуры(обычно – треугольники), элементы которых измеряют с помощью измерителя и поперечного масштаба, а площади вычисляют по известным формулам и суммируют. Разбиение на простые фигуры выполняют также, применяя палетки.
Полярный планиметр.
cyberpedia.su
Определение уклона линии
1. Определить по карте отметки точек С и D.
2. Измерить длину линии CD по карте.
3. Вычислить уклон по формуле (1.9).
4. Составить вертикальную проекцию по линии СД.
D
Рис.1.11. Вертикальная проекция по линии CD
Пример
1. Отметки точек Cи D:HC=157.5+(159.7–157.5)/2 =158.6 м,HD=150+h/4 = 150.6 м.
2. Длина линии CD : d= 23.5 мм10000=235 м.
Контроль знака i по рельефу: по линии CD понижение ската, следовательно, уклон с минусом.
Построение профиля местности
1. На миллиметровке, 296х210 мм, построить профильную сетку (см. рис. 1.12, составленный по карте рис.1.1). В графе «расстояния» (ширина 10 мм) отметить пересечения линией AB(от точкиAк точкеB) всех горизонталей, характерных точек и линийрельефа (вершина, котловина, седловина, обрыв, хребет, лощина).

Масштабы: горизонтальный 1:10000, вертикальный 1:1000
Рис. 1.12. Профиль местности по линии АВ
2. Расстояния между точками измерить по карте и выписать в графу «расстояния» в метрах на местности. Сумма расстояний равна длине АВ.
3. В графу «отметки земли» (15 мм) выписать отметки всех намеченных точек, определенных по правилам пункта 1.5 с округлением до 0.1 м.
4. В масштабе 1:1000 подписать сантиметровые линии миллиметровки так, чтобы высота ординат была в пределах 612 см.
5. Отложить отметки земли по вертикали и полученные точки соединить прямыми линиями.
6. Подписать отметку условного горизонта (Уг.) кратной 10 м.
7. Профиль оформить по правилам черчения.
Примечание:на крутых склонах при расстояниях между горизонталями на карте меньше 4 мм, профиль можно строить через одну или две горизонтали.
ЛИТЕРАТУРА
1. Инженерная геодезия / Г. В. Багратуни, В. Н. Ганьшин [и др.]. — М.: Недра, 1984. — 344 с.
Инженерная геодезия для строителей: учеб. пособие /А.Т. Черкозьянов, А. А. Землянский — Саратов: Сарат. гос. техн. ун-т, 2003.- 96 с.
3. Инженерная геодезия. Практикум: учеб. пособие. / А. Т. Черкозьянов, А. А. Землянский. — Саратов: Сарат. гос. техн. ун-т, 2003. — 182 с.
СОДЕРЖАНИЕ
1. Решение задач по карте . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.1. Основные понятия . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.2. Порядок и методика выполнения работы . . . . . . . . . . . . . . . . . . . . . 10
Литература . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
Решение задач по карте
Задания и методические указания
к самостоятельной работе по инженерной геодезии
для студентов специальности 290300 заочной формы обучения
Составил: Черкозьянов Андрей Тимофеевич
Рецензент С. А Ращепкина
Редактор Л. В. Максимова
Корректор А. М. Рогачева
Подписано в печать Формат 6084 1/16
Бумага тип. Усл. печ. л. 1.25 Уч.-изд. л. 1.75
Тираж 100 экз. Заказ Бесплатно
Саратовский государственный технический университет
410054, г. Саратов, ул. Политехническая, 77
Копипринтер БИТТиУ, 413840, г. Балаково, ул. Чапаева, 140
studfiles.net
Уклон линии. Графики заложений
- Подробности
- Категория: Учебное пособие по инженерной геодезии
Уклон i линии – отношение превышения h к заложению линии d (рис. 5.22). Уклон – мера крутизны ската.
Например, h = 1 м, d = 20 м. i = 1/20 = 0,05.
Уклоны выражаются в процентах i = 5% или в промиллях i = 50 ‰. Чем больше d, тем меньше крутизна <.
уклон линии ; (5.1)
крутизна ската <.
Рис. 5.22. Уклон линии
График заложений по уклонам
График строится по формуле ,
где h – константа для данной карты; i – задается.
Пример: Масштаб 1:10 000, h = 1 м, i = 0,001 (табл. 5.2). Подставляя в формулу, получим = 1000 м, что на карте масштаба 1:10 000 составляет 10 см.
Таблица 5.2
h, м | 1 | 1 | 1 | 1 | 1 | 1 |
i ‰ | 0,001 | 0,002 | 0,003 | 0,004 | 0,005 | 0,006 |
d, м | 1000 | 500 | 333 | 250 | 200 | 167 |
на карте, см | 10 | 5 | 3,33 | 2,5 | 2,0 | 1,67 |
Рис. 5.23. График заложений по уклонам
График заложений по углам
График строится по формуле ,
где h – константа для данной карты;
< – задается.
Пример: Масштаб 1:10 000, h = 2,5 м (табл. 5.3). Для < = 0°30r; d = 2,5 · ctg 0°30r = 286,5 м, что на карте составляет 2,86 см и т.д. для углов 1°, 2°, 3°… 10°.
Таблица 5.3
h, м | 2,5 | 2,5 | 2,5 | 2,5 | 2,5 | 2,5 | 2,5 |
<, град. | 0°30r | 1° | 2° | 3° | 5° | … | 10° |
ctg < | 114.59 | 57.29 | 28.64 | 19.08 | 11.43 | … | 5.67 |
d, м | 286.47 | 143.22 | 71.59 | 47.70 | 28.58 | … | 14.18 |
На карте, см | 2,86 | 1,43 | 0,72 | 0,48 | 0,29 | … | 0,14 |
Рис. 5.24. График заложений по углам
cities-blago.ru
Наклон линии (крутизна)
Наклон линии (крутизна)
Предствим, что частица движется вдоль участка не вертикальной прямой из точки p1( x1,y1 ) к точке p1( x1,y1 ). Вертикальное изменение y2 – y1 называется подъемом, а горизонтальное изменение x2 – x1 — расстоянием.
ОПРЕДЕЛЕНИЕ
Если P(x1, y1) и P(x2, y2) есть точками на невертикальной прямой, тогда крутизна m прямой определяется как:
Не имеет значение, какая точка называется P1 и какая точка называется P2
Slope of P1P2
= (y2 — y1)/(x2 — x1)
= -(y1 — y2)/[-(x1 — x2)]
= (y1 — y2)/(x1 — x2) = Крутизна P1P2
Любые две различные точки на не вертикальной прямой могут быть использованы для расчета крутизны (наклона) прямой. Для измерения наклона, мы обычно двигаемся слева направо, когда измеряем дистанцию, пройденную горизонтально.
Из-за этого, иногда понятие падения подменяется подъемом!
Пример
В каждой части найдите наклон линии, проходящей через
(A) (6, 2) и (9, 8)
(B) (2, 9) и (4, 3)
(C) (-2, 7) и (5, 7)
Решение:
Мы знаем, что наклон линии, проходящей через две точкиP1(x1, y1) иp1(x1, y1) , определяется как
m= (y2 — y1)/ (x2 — x1)
Отсюда
a) m= (8 — 2)/(9 — 6) = 6/3 = 2
На координатной плоскости xy
Подобным образом
b) m= (3 — 9)/(4 — 2) = -6/2 = -3
На координатной плоскости xy
Также
c) m= (7 -7)/[5 — (-2)] = 0/7 = 0
На координатной плоскости xy
Определение (Угол наклона)
Для прямой L не параллельной к оси абсцисс, угол наклона есть наименьший углом φ, измеренный против часовой стрелки от направления положительная оси х к L.
Для прямой, параллельной оси x, мы берём φ = 0
Как показано на следующих рисунках.
Если m есть наклоном прямой, тогда
m = rise/run
= скорость изменения y относительно к x
ТЕОРЕМА
Для не вертикальной прямой наклон m и угол наклона φ связаны отношением
m = tan φ
Пример:
Найдите угол наклона для прямой с наклоном m = 1 и угол наклона для прямой с наклоном m = -1
Solution:
Если m=1 tan φ = 1, и поэтому φ = π/4 = 45°
Если m=-1 tan φ = -1, так как 0 φ = 3π/4 = 135°
Теорема
Пусть L1 и L2 есть прямыми с наклонами m1 и m2, соответственно
(a) Прямые параллельны тогда и только тогда m1 = m2
(b) Прямые параллельны тогда и только тогда m1m2 = -1
Доказательство: (a)
Если L1 и L2 не являются вертикальными прямыми, тогда их углы наклона φ1 и φ2 равны.
φ1 =φ2
Так,
m1 = tanφ1 = tanφ2 = m2
И наоборот, если два наклона линий равны, т.e.
M1 = M2
⇒ tan(φ1) = tan(φ2)
⇒ φ1 = φ2
То есть, прямые параллельны.
(b) Предположим, что φ
www.math10.com
Билет №14. Определение уклонов и углов наклона по карте. Построение линии заданного уклона
Определение уклонов и углов наклона. Отрезки линий на земной поверхности обычно имеют наклон, отчего начало и конец отрезка находятся на разных высотах. Разность их высот – превышение, а проекция отрезка на горизонтальную плоскость – его горизонтальное проложение.
Уклоном i линии называется отношение превышения h к горизонтальному проложению d:
i = h / d. (4.2)
Для определения по карте уклона линии на участке KL между двумя горизонталями (рис. 4.7) измеряют его горизонтальное проложение – заложение d. Поскольку концы отрезка лежат на смежных горизонталях, превышение hмежду ними равно высоте сечения рельефа, подписанному под южной рамкой карты. Воспользовавшись формулой (4.2), вычисляют уклон, который принято выражать в тысячных. Если, например, h=1 м, d=48 м , то уклон равен i =1 м / 48 м = 0,021=21‰.
| Рис. 4.7. Определение высоты точки M и уклона на отрезке KL |
С другой стороны, отношение превышения h к горизонтальному проложению d равно тангенсу угла n наклона линии. Поэтому
i =tg n,
что позволяет, вычислив уклон определить по нему угол наклона.
При пользовании картой углы наклона не вычисляют, а определяют с помощью графика заложений (рис. 4.8), расположенного под южной рамкой карты. По горизонтальной оси графика отложены углы наклона, а по вертикальной — соответствующие этим углам заложения d, выраженные в масштабе карты и рассчитанные по формуле
d = h¤(Mtg n),
гдеh — высота сечения рельефа, а M – знаменатель масштаба карты.
| Рис. 4.8. График заложений |
Для определения угла наклона отрезка KL (рис. 4.7), расположенного между горизонталями, берут его в раствор циркуля и на графике заложений (рис. 4.8) находят такой угол, над которым ордината равна раствору циркуля d. Это и есть искомый угол наклона.
При необходимости многократного определения уклонов пользуются графиком уклонов, построенным аналогично графику заложений, но с отложением по горизонтальной оси не углов наклона, а уклонов.
Проведение линии с уклоном, не превышающим заданного предельного. Необходимость решения такой задачи возникает, например, при выборе трассы для будущей дороги. Вычисляют соответствующее заданному предельному уклону iпр заложение, выраженное в масштабе карты, (здесь M – знаменатель масштаба). .
| Рис. 4.9. Построение линии с заданным уклоном | Рис. 4.10. Водосборная площадь |
Чтобы уклон линии не превосходил iпр, ни одно заложение на ней не должно быть меньше, чем рассчитанное d. Если расстояние между горизонталями больше рассчитанного, направление линии можно выбирать произвольно. В противном случае в раствор циркуля берут отрезок, равный d, и строят ломаную линию, умещая между горизонталями рассчитанное предельное заложение (рис. 4.9).
megaobuchalka.ru
Определение уклонов и углов наклона — Мегаобучалка
Отрезки линий на земной поверхности обычно имеют наклон, отчего начало и конец отрезка находятся на разных высотах. Разность их высот – превышение, а проекция отрезка на горизонтальную плоскость – его горизонтальное проложение.
Уклоном i линии называется отношение превышения h к горизонтальному проложению d:
i = h / d. (4.2)
Для определения по карте уклона линии на участке KL между двумя горизонталями (рис. 4.7) измеряют его горизонтальное проложение – заложение d. Поскольку концы отрезка лежат на смежных горизонталях, превышение hмежду ними равно высоте сечения рельефа, подписанному под южной рамкой карты. Воспользовавшись формулой (4.2), вычисляют уклон, который принято выражать в тысячных. Если, например, h=1 м, d=48 м , то уклон равен i =1 м / 48 м = 0,021=21‰.
| Рис. 4.7. Определение высоты точки M и уклона на отрезке KL |
С другой стороны, отношение превышения h к горизонтальному проложению d равно тангенсу угла n наклона линии. Поэтому
i = tg n,
что позволяет, вычислив уклон определить по нему угол наклона.
При пользовании картой углы наклона не вычисляют, а определяют с помощью графика заложений (рис. 4.8), расположенного под южной рамкой карты. По горизонтальной оси графика отложены углы наклона, а по вертикальной — соответствующие этим углам заложения d, выраженные в масштабе карты и рассчитанные по формуле
d = h ¤ (M tg n),
где h — высота сечения рельефа, а M – знаменатель масштаба карты.
| Рис. 4.8. График заложений |
Для определения угла наклона отрезка KL (рис. 4.7), расположенного между горизонталями, берут его в раствор циркуля и на графике заложений (рис. 4.8) находят такой угол, над которым ордината равна раствору циркуля d. Это и есть искомый угол наклона.
При необходимости многократного определения уклонов пользуются графиком уклонов, построенным аналогично графику заложений, но с отложением по горизонтальной оси не углов наклона, а уклонов.
Проведение линии с уклоном, не превышающим заданного предельного. Необходимость решения такой задачи возникает, например, при выборе трассы для будущей дороги. Вычисляют соответствующее заданному предельному уклону iпр заложение, выраженное в масштабе карты, (здесь M – знаменатель масштаба). .
| Рис. 4.9. Построение линии с заданным уклоном | Рис. 4.10. Водосборная площадь |
Чтобы уклон линии не превосходил iпр, ни одно заложение на ней не должно быть меньше, чем рассчитанное d. Если расстояние между горизонталями больше рассчитанного, направление линии можно выбирать произвольно. В противном случае в раствор циркуля берут отрезок, равный d, и строят ломаную линию, умещая между горизонталями рассчитанное предельное заложение (рис. 4.9).
12. Абсолютные, условные, относительные высоты точек.
Возьмём на поверхности земли 2 точки А и В.
Расстояние по вертикали от уровенной поверхности до заданной точки земной поверхности — абсолютная высота точки (Н). Не всегда нужно искать абсолютную высоту, можно взять условную поверхность – расстояние от условной отсчётной поверхности до заданной точки. Расстояние по вертикали между двумя смежными точками – относительная высота (превышение). Высота точки, выраженная числом – отметка. НА – 120,375 м. За уровенную поверхность принята среднее положение уровня Балтийского моря.
Балтийская система высот – принятая в России и ряде других стран СНГ система система абсолютных высот, отсчет которых ведется от нуля Кронштадтского футштока. От этой отметки отсчитаны высоты опорных геодезических пунктов, которые обозначены на местности разными геодезическими знаками и нанесены на карты.
Балтийская система высот была принята в 1977 году в СССР.
Превышение (топографическое превышение) — понятие в классификации относительных высот гор, являющееся одним из главных критериев позволяющих считать вершины независимыми горами. Превышение вершины — это высота этой вершины относительно самой низкой точки на кривой, проведенной по наиболее высокому водоразделу от этой вершины к первой более высокой вершине на этом водоразделе, называемой родительской горой.
megaobuchalka.ru
