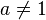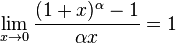Замечательные пределы, формулы и доказательства
Первый замечательный предел:
Следствия:
Подробнее про первый замечательный предел читайте в отдельной теме.
Примеры решений с первым замечательным пределом
Второй замечательный предел
здесь – постоянная Эйлера
Следствия:
Подробнее про второй замечательный предел читайте в отдельной теме.
Примеры решений со вторым замечательным пределом
| Понравился сайт? Расскажи друзьям! | |||
Замечательные пределы — Википедия с видео // WIKI 2
- Первый замечательный предел:
- lim x → 0 sin x x = 1. {\displaystyle \lim _{x\to 0}{\frac {\sin x}{x}}=1.}
- Второй замечательный предел:
- lim x → ∞ ( 1 + 1 x ) x = e . {\displaystyle \lim _{x\to \infty }\left(1+{\frac {1}{x}}\right)^{x}=e.}
Энциклопедичный YouTube
1/5
Просмотров:252 109
17 301
5 739
1 036
21 881
✪ Задачи на замечательные пределы — от bezbotvy
✪ Замечательные пределы
✪ Пределы №5 Число e. Второй замечательный предел.
✪ 15 — Мат. анализ. Замечательные пределы
✪ Математический анализ. 16. Вычисление пределов. Примеры
Содержание
Первый замечательный предел
lim x → 0 sin x x = 1 {\displaystyle \lim _{x\to 0}{\frac {\sin x}{x}}=1}
Доказательство:
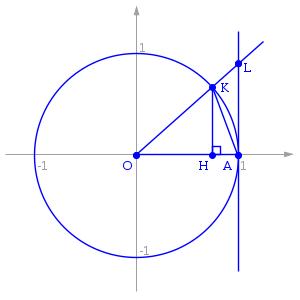
Рассмотрим односторонние пределы lim x → + 0 sin x x {\displaystyle \lim _{x\to +0}{\frac {\sin x}{x}}} и lim x → − 0 sin x x {\displaystyle \lim _{x\to -0}{\frac {\sin x}{x}}} и докажем, что они равны 1.
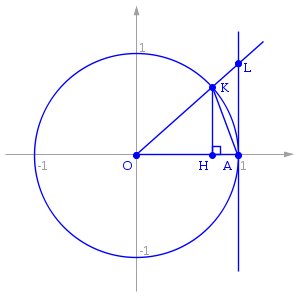
Пусть x ∈ ( 0 ; π 2 ) {\displaystyle x\in \left(0;{\frac {\pi }{2}}\right)} . Отложим этот угол на единичной окружности так, чтобы его вершина совпадала с началом координат, а одна сторона совпадала с осью O X {\displaystyle OX} . Пусть K {\displaystyle K} — точка пересечения второй стороны угла с единичной окружностью, а точка L {\displaystyle L} — с касательной к этой окружности в точке A = ( 1 ; 0 ) {\displaystyle A=\left(1;0\right)} . Точка H {\displaystyle H} — проекция точки K {\displaystyle K} на ось O X {\displaystyle OX} .
Очевидно, что:
- S △ O A K < S s e c t K O A < S △ O A L {\displaystyle S_{\triangle OAK}<S_{sectKOA}<S_{\triangle OAL}} (1)
(где S s e c t K O A {\displaystyle S_{sectKOA}} — площадь сектора K O A {\displaystyle KOA} )
Поскольку | K H | = sin x , | L A | = tg x {\displaystyle \left|KH\right|=\sin x,\,\left|LA\right|=\operatorname {tg} x} :
- S △ O A K = 1 2 ⋅ | O A | ⋅ | K H | = 1 2 ⋅ 1 ⋅ sin x = sin x 2 {\displaystyle S_{\triangle OAK}={\frac {1}{2}}\cdot \left|OA\right|\cdot \left|KH\right|={\frac {1}{2}}\cdot 1\cdot \sin x={\frac {\sin x}{2}}}
- S s e c t K O A = 1 2 ⋅ | O A | 2 ⋅ x = x 2 {\displaystyle S_{sectKOA}={\frac {1}{2}}\cdot \left|OA\right|^{2}\cdot x={\frac {x}{2}}}
- S △ O A L = 1 2 ⋅ | O A | ⋅ | L A | = tg x 2 {\displaystyle S_{\triangle OAL}={\frac {1}{2}}\cdot \left|OA\right|\cdot \left|LA\right|={\frac {\operatorname {tg} x}{2}}}
Подставляя в (1), получим:
- sin x 2 < x 2 < tg x 2 {\displaystyle {\frac {\sin x}{2}}<{\frac {x}{2}}<{\frac {\operatorname {tg} x}{2}}}
Так как при x → + 0 : sin x > 0 , x > 0 , tg x > 0 {\displaystyle x\to +0:\sin x>0,\,x>0,\,\operatorname {tg} x>0} :
- 1 tg x < 1 x < 1 sin x {\displaystyle {\frac {1}{\operatorname {tg} x}}<{\frac {1}{x}}<{\frac {1}{\sin x}}}
Умножаем на sin x {\displaystyle \sin x} :
- cos x < sin x x < 1 {\displaystyle \cos x<{\frac {\sin x}{x}}<1}
Перейдём к пределу:
- lim x → + 0 cos x ⩽ lim x → + 0 sin x x ⩽ 1 {\displaystyle \lim _{x\to +0}\cos x\leqslant \lim _{x\to +0}{\frac {\sin x}{x}}\leqslant 1}
- 1 ⩽ lim x → + 0 sin x x ⩽ 1 {\displaystyle 1\leqslant \lim _{x\to +0}{\frac {\sin x}{x}}\leqslant 1}
- lim x → + 0 sin x x = 1 {\displaystyle \lim _{x\to +0}{\frac {\sin x}{x}}=1}
Найдём левый односторонний предел (так как функция четна, в этом нет необходимости, достаточно доказать это для правого предела):
- lim x → − 0 sin x x = [ u = − x x = − u u → + 0 x → − 0 ] = lim u → + 0 sin ( − u ) − u = lim u → + 0 − sin ( u ) − u = lim u → + 0 sin ( u ) u = 1 {\displaystyle \lim _{x\to -0}{\frac {\sin x}{x}}=\left[{\begin{matrix}u=-x\\x=-u\\u\to +0\\x\to -0\end{matrix}}\right]=\lim _{u\to +0}{\frac {\sin(-u)}{-u}}=\lim _{u\to +0}{\frac {-\sin(u)}{-u}}=\lim _{u\to +0}{\frac {\sin(u)}{u}}=1}
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.
Следствия:
- lim x → 0 tg x x = 1 {\displaystyle \lim _{x\to 0}{\frac {\operatorname {tg} x}{x}}=1}
- lim x → 0 arcsin x x = 1 {\displaystyle \lim _{x\to 0}{\frac {\operatorname {arcsin} x}{x}}=1}
- lim x → 0 arctg x x = 1 {\displaystyle \lim _{x\to 0}{\frac {\operatorname {arctg} x}{x}}=1}
- lim x → 0 1 − cos x x 2 2 = 1 {\displaystyle \lim _{x\to 0}{\frac {1-\cos x}{\frac {x^{2}}{2}}}=1}
Доказательство следствий
- lim x → 0 tg x x = lim x → 0 sin x x cos x = lim x → 0 sin x x ⋅ lim x → 0 1 cos x = 1 ⋅ 1 = 1 {\displaystyle \lim _{x\to 0}{\frac {\operatorname {tg} x}{x}}=\lim _{x\to 0}{\frac {\sin x}{x\cos x}}=\lim _{x\to 0}{\frac {\sin x}{x}}\cdot \lim _{x\to 0}{\frac {1}{\cos x}}=1\cdot 1=1}
- lim x → 0 arcsin x x = [ u = arcsin x x = sin u u → 0 x → 0 ] = lim u → 0 u sin u = 1 {\displaystyle \lim _{x\to 0}{\frac {\operatorname {arcsin} x}{x}}=\left[{\begin{matrix}u=\operatorname {arcsin} x\\x=\sin u\\u\to 0\\x\to 0\end{matrix}}\right]=\lim _{u\to 0}{\frac {u}{\sin u}}=1}
- lim x → 0 arctg x x = [ u = arctg x x = tg u u → 0 x → 0 ] = lim u → 0 u tg u = 1 {\displaystyle \lim _{x\to 0}{\frac {\operatorname {arctg} x}{x}}=\left[{\begin{matrix}u=\operatorname {arctg} x\\x=\operatorname {tg} u\\u\to 0\\x\to 0\end{matrix}}\right]=\lim _{u\to 0}{\frac {u}{\operatorname {tg} u}}=1}
- lim x → 0 1 − cos x x 2 2 = lim x → 0 2 ⋅ sin 2 x 2 2 ⋅ ( x 2 ) 2 = lim x 2 → 0 ( sin x 2 x 2 ) 2 = 1 2 = 1 {\displaystyle \lim _{x\to 0}{\frac {1-\cos x}{\frac {x^{2}}{2}}}=\lim _{x\to 0}{\frac {2\cdot \sin ^{2}{\frac {x}{2}}}{2\cdot \left({\frac {x}{2}}\right)^{2}}}=\lim _{{\frac {x}{2}}\to 0}\left({\frac {\sin {\frac {x}{2}}}{\frac {x}{2}}}\right)^{2}=1^{2}=1}
Второй замечательный предел
lim x → ∞ ( 1 + 1 x ) x = e {\displaystyle \lim _{x\to \infty }\left(1+{\frac {1}{x}}\right)^{x}=e} или lim x → 0 ( 1 + x ) 1 / x = e {\displaystyle \lim _{x\to 0}\left(1+x\right)^{1/x}=e}
Доказательство существования второго замечательного предела:
Доказательство для натуральных значений x
◂ {\displaystyle \blacktriangleleft } Докажем вначале теорему для случая последовательности x n = ( 1 + 1 n ) n ; n ∈ N {\displaystyle x_{n}=\left(1+{\frac {1}{n}}\right)^{n};\ n\in \mathbb {N} }
По формуле бинома Ньютона: ( a + b ) n = a n + n 1 ⋅ a n − 1 ⋅ b + n ( n − 1 ) 1 ⋅ 2 ⋅ a n − 2 ⋅ b 2 + . . . + n ( n − 1 ) ( n − 2 ) . . . ( n − ( n − 1 ) ) 1 ⋅ 2 ⋅ 3 ⋅ . . . ⋅ n ⋅ b n ; n ∈ N {\displaystyle (a+b)^{n}=a^{n}~+~{\frac {n}{1}}\cdot a^{n-1}\cdot b~+~{\frac {n(n-1)}{1\cdot 2}}\cdot a^{n-2}\cdot b^{2}~+~…~+~{\frac {n(n-1)(n-2)…(n-(n-1))}{1\cdot 2\cdot 3\cdot …\cdot n}}\cdot b^{n};\ n\in \mathbb {N} }
Полагая a = 1 ; b = 1 n {\displaystyle a=1;~b={\frac {1}{n}}} , получим:
- ( 1 + 1 n ) n = 1 + n 1 ⋅ 1 n + n ( n − 1 ) 1 ⋅ 2 ⋅ 1 n 2 + n ( n − 1 ) ( n − 2 ) 1 ⋅ 2 ⋅ 3 ⋅ 1 n 3 + . . . + n ( n − 1 ) ( n − 2 ) . . . ( n − ( n − 1 ) ) 1 ⋅ 2 ⋅ 3 ⋅ . . . ⋅ n ⋅ 1 n n = {\displaystyle \left(1+{\frac {1}{n}}\right)^{n}=1~+~{\frac {n}{1}}\cdot {\frac {1}{n}}~+~{\frac {n(n-1)}{1\cdot 2}}\cdot {\frac {1}{n^{2}}}~+~{\frac {n(n-1)(n-2)}{1\cdot 2\cdot 3}}\cdot {\frac {1}{n^{3}}}~+~…~+~{\frac {n(n-1)(n-2)…(n-(n-1))}{1\cdot 2\cdot 3\cdot …\cdot n}}\cdot {\frac {1}{n^{n}}}=}
- = 1 + 1 + 1 1 ⋅ 2 ⋅ ( 1 − 1 n ) + 1 1 ⋅ 2 ⋅ 3 ⋅ ( 1 − 1 n ) ⋅ ( 1 − 2 n ) + . . . + 1 1 ⋅ 2 ⋅ 3 ⋅ . . . ⋅ n ⋅ ( 1 − 1 n ) ⋅ ( 1 − 2 n ) ⋅ . . . ⋅ ( 1 − n − 1 n ) {\displaystyle =1~+~1~+~{\frac {1}{1\cdot 2}}\cdot \left(1-{\frac {1}{n}}\right)~+~{\frac {1}{1\cdot 2\cdot 3}}\cdot \left(1-{\frac {1}{n}}\right)\cdot \left(1-{\frac {2}{n}}\right)~+~…~+~{\frac {1}{1\cdot 2\cdot 3\cdot …\cdot n}}\cdot \left(1-{\frac {1}{n}}\right)\cdot \left(1-{\frac {2}{n}}\right)\cdot …\cdot \left(1-{\frac {n-1}{n}}\right)} (1)
Из данного равенства (1) следует, что с увеличением n число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении n число 1 n {\displaystyle {\frac {1}{n}}} убывает, поэтому величины ( 1 − 1 n ) , ( 1 − 2 n ) , . . . {\displaystyle \left(1-{\frac {1}{n}}\right),\left(1-{\frac {2}{n}}\right),…} возрастают. Поэтому последовательность { x n } = { ( 1 + 1 n ) n } ; n ∈ N {\displaystyle \{x_{n}\}=\left\{\left(1+{\frac {1}{n}}\right)^{n}\right\};\ n\in \mathbb {N} } — возрастающая, при этом
- ( 1 + 1 n ) n ≥ 2 , n ∈ N {\displaystyle \left(1+{\frac {1}{n}}\right)^{n}\geq 2,n\in \mathbb {N} } (2).
Покажем, что она ограничена. Заменим каждую скобку в правой части равенства на единицу, правая часть увеличится, получим неравенство
- ( 1 + 1 n ) n < 1 + 1 + 1 1 ⋅ 2 + 1 1 ⋅ 2 ⋅ 3 + . . . + 1 1 ⋅ 2 ⋅ 3 ⋅ . . . ⋅ n {\displaystyle \left(1+{\frac {1}{n}}\right)^{n}<1+1+{\frac {1}{1\cdot 2}}+{\frac {1}{1\cdot 2\cdot 3}}~+~…~+~{\frac {1}{1\cdot 2\cdot 3\cdot …\cdot n}}}
Усилим полученное неравенство, заменим 3,4,5, …, стоящие в знаменателях дробей, числом 2:
- ( 1 + 1 n ) n < 1 + ( 1 + 1 2 + 1 2 2 + . . . + 1 2 n − 1 ) {\displaystyle \left(1+{\frac {1}{n}}\right)^{n}<1+\left(1+{\frac {1}{2}}+{\frac {1}{2^{2}}}+…+{\frac {1}{2^{n-1}}}\right)} .
Сумму в скобке найдём по формуле суммы членов геометрической прогрессии:
- 1 + 1 2 + 1 2 2 + . . . + 1 2 n − 1 = 1 ⋅ ( 1 − ( 1 2 ) n ) 1 − 1 2 = 2 ⋅ ( 1 − 1 2 n ) < 2 {\displaystyle 1+{\frac {1}{2}}+{\frac {1}{2^{2}}}+…+{\frac {1}{2^{n-1}}}={\frac {1\cdot \left(1-({\frac {1}{2}})^{n}\right)}{1-{\frac {1}{2}}}}=2\cdot \left(1-{\frac {1}{2^{n}}}\right)<2} .
Поэтому ( 1 + 1 n ) n < 1 + 2 = 3 {\displaystyle \left(1+{\frac {1}{n}}\right)^{n}<1+2=3} (3).
Итак, последовательность ограничена сверху, при этом ∀ n ∈ N {\displaystyle \forall n\in \mathbb {N} } выполняются неравенства (2) и (3): 2 ≤ ( 1 + 1 n ) n < 3 {\displaystyle 2\leq \left(1+{\frac {1}{n}}\right)^{n}<3} .
Следовательно, на основании теоремы Вейерштрасса (критерий сходимости последовательности) последовательность x n = ( 1 + 1 n ) n , n ∈ N {\displaystyle x_{n}=\left(1+{\frac {1}{n}}\right)^{n},\ n\in \mathbb {N} } монотонно возрастает и ограничена, значит имеет предел, обозначаемый буквой e. Т.е. lim n → ∞ ( 1 + 1 n ) n = e {\displaystyle \lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}=e} ▸ {\displaystyle \blacktriangleright }
◂ {\displaystyle \blacktriangleleft } Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что lim x → ∞ ( 1 + 1 x ) x = e ; x ∈ R {\displaystyle \lim _{x\to \infty }\left(1+{\frac {1}{x}}\right)^{x}=e;\ x\in \mathbb {R} } . Рассмотрим два случая:
1. Пусть x → + ∞ {\displaystyle x\rightarrow +\infty } . Каждое значение x заключено между двумя положительными целыми числами: n ⩽ x < n + 1 {\displaystyle n\leqslant x<n+1} , где n = [ x ] {\displaystyle n=[x]} — это целая часть x.
- Отсюда следует: 1 n + 1 < 1 x ⩽ 1 n ⟺ 1 + 1 n + 1 < 1 + 1 x ⩽ 1 + 1 n {\displaystyle {\frac {1}{n+1}}<{\frac {1}{x}}\leqslant {\frac {1}{n}}~~\Longleftrightarrow ~~1+{\frac {1}{n+1}}<1+{\frac {1}{x}}\leqslant 1+{\frac {1}{n}}} , поэтому
- ( 1 + 1 n + 1 ) n < ( 1 + 1 x ) x ⩽ ( 1 + 1 n ) n + 1 {\displaystyle \left(1+{\frac {1}{n+1}}\right)^{n}<\left(1+{\frac {1}{x}}\right)^{x}\leqslant \left(1+{\frac {1}{n}}\right)^{n+1}} .
- Если x → + ∞ {\displaystyle x\rightarrow +\infty } , то n → ∞ {\displaystyle n\rightarrow \infty } . Поэтому, согласно пределу lim n → ∞ ( 1 + 1 n ) n = e {\displaystyle \lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}=e} , имеем:
- lim n → ∞ ( 1 + 1 n + 1 ) n = lim n → ∞ ( 1 + 1 n + 1 ) n + 1 lim n → ∞ ( 1 + 1 n + 1 ) = e 1 = e {\displaystyle \lim _{n\to \infty }\left(1+{\frac {1}{n+1}}\right)^{n}={\frac {\lim \limits _{n\to \infty }(1+{\frac {1}{n+1}})^{n+1}}{\lim \limits _{n\to \infty }\left(1+{\frac {1}{n+1}}\right)}}={\frac {e}{1}}=e}
- lim n → ∞ ( 1 + 1 n ) n + 1 = lim n → ∞ ( 1 + 1 n ) n ⋅ lim n → ∞ ( 1 + 1 n ) = e ⋅ 1 = e {\displaystyle \lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n+1}=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}\cdot \lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)=e\cdot 1=e} .
- По признаку (о пределе промежуточной функции) существования пределов lim x → + ∞ ( 1 + 1 x ) x = e {\displaystyle \lim _{x\to +\infty }\left(1+{\frac {1}{x}}\right)^{x}=e} .
2. Пусть x → − ∞ {\displaystyle x\to -\infty } . Сделаем подстановку − x = t {\displaystyle -x=t} , тогда
- lim x → − ∞ ( 1 + 1 x ) x = lim t → + ∞ ( 1 − 1 t ) − t = lim t → + ∞ ( t t − 1 ) t = lim t → + ∞ ( 1 + 1 t − 1 ) t = {\displaystyle \lim _{x\to -\infty }\left(1+{\frac {1}{x}}\right)^{x}=\lim _{t\to +\infty }\left(1-{\frac {1}{t}}\right)^{-t}=\lim _{t\to +\infty }\left({\frac {t}{t-1}}\right)^{t}=\lim _{t\to +\infty }\left(1+{\frac {1}{t-1}}\right)^{t}=}
- = lim t → + ∞ ( 1 + 1 t − 1 ) t − 1 ⋅ lim t → + ∞ ( 1 + 1 t − 1 ) 1 = e ⋅ 1 = e {\displaystyle =\lim _{t\to +\infty }\left(1+{\frac {1}{t-1}}\right)^{t-1}\cdot \lim _{t\to +\infty }\left(1+{\frac {1}{t-1}}\right)^{1}=e\cdot 1=e} .
Очевидно, из двух этих случаев вытекает, что lim x → ∞ ( 1 + 1 x ) x = e {\displaystyle \lim _{x\to \infty }\left(1+{\frac {1}{x}}\right)^{x}=e} для вещественного x. ▸ {\displaystyle \blacktriangleright }
Следствия
- lim u → 0 ( 1 + u ) 1 u = e {\displaystyle \lim _{u\to 0}(1+u)^{\frac {1}{u}}=e}
- lim x → ∞ ( 1 + k x ) x = e k {\displaystyle \lim _{x\to \infty }\left(1+{\frac {k}{x}}\right)^{x}=e^{k}}
- lim x → 0 ln ( 1 + x ) x = 1 {\displaystyle \lim _{x\to 0}{\frac {\ln(1+x)}{x}}=1}
- lim x → 0 e x − 1 x = 1 {\displaystyle \lim _{x\to 0}{\frac {e^{x}-1}{x}}=1}
- lim x → 0 a x − 1 x ln a = 1 {\displaystyle \lim _{x\to 0}{\frac {a^{x}-1}{x\ln a}}=1} для a > 0 {\displaystyle a>0} , a ≠ 1 {\displaystyle a\neq 1}
- lim x → 0 ( 1 + x ) α − 1 α x = 1 {\displaystyle \lim _{x\to 0}{\frac {(1+x)^{\alpha }-1}{\alpha x}}=1}
Доказательства следствий
Применение
Замечательные пределы и их следствия используются при раскрытии неопределённостей для нахождения других пределов.
См. также
Литература
Ссылки
 Эта страница в последний раз была отредактирована 6 мая 2020 в 20:07.
Эта страница в последний раз была отредактирована 6 мая 2020 в 20:07.«Что такое замечательные пределы?» – Яндекс.Кью
Перечитал кучу ерунды от предыдущих авторов. Прежде чем отвечать на такие вопросы, нужно хорошо разобраться в СТО (специальная теория относительности) и, во всяком случае, не путать её с ОТО (общая теория относительности). Оба названия неудачные. Принцип относительности есть не только в СТО, но и в классической механике, созданой Ньютоном, причём, этот принцип был сформулирован Галилеем ещё до Ньютона. СТО фактически является новой механикой, согласующейся с электродинамикой Максвелла. Что касается ОТО, то это теория гравитации, уточняющая ньютоновский же закон всемирного тяготения и согласованная с СТО в том смысле, что при отсутствии гравитационного поля ОТО отличается от СТО только математическим аппаратом, который в ОТО гораздо более сложный.
Обычно СТО основывают на двух постулатах. Первый — это принцип относительности, а второй утверждает существование инвариантной скорости (со времён Эйнштейна эта скорость называется «скорость света») и сформулирован самим Эйнштейном так: свет распространяется в «неподвижной» системе координат с определённой скоростью V, не зависящей от движения источника (сейчас скорость света в вакууме обозначается не «V», а «c»). Под «неподвижной» системой координат Эйнштейн подразумевает то, что позже стало называться инерциальной системой отсчёта (ИСО). Кстати, в классической механике инвариантная скорость тоже есть, но она бесконечная.
Как видим, нет ни одного слова про максимальность скорости света.
Из СТО, однако, вытекают следующие ограничения:
1) если частица в какой-то момент движется со скоростью, меньшей скорости света, то она всегда в прошлом, пока существовала, двигалась со скоростью, меньшей скорости света, и всегда в будущем, пока будет существовать, будет двигаться со скоростью, меньшей скорости света;
2) если частица в какой-то момент движется со скоростью света, то она всегда в прошлом, пока существовала, двигалась со скоростью света, и всегда в будущем, пока будет существовать, будет двигаться со скоростью света;
3) если частица в какой-то момент движется со скоростью, большей скорости света, то она всегда в прошлом, пока существовала, двигалась со скоростью, большей скорости света, и всегда в будущем, пока будет существовать, будет двигаться со скоростью, большей скорости света.
Таким образом, мы не можем ничего разогнать до сверхсветовой скорости, но, в принципе, сверхсветовая частица может родиться при столкновении обычных частиц.
Гипотетические частицы, движущиеся быстрее света, были названы тахионами. Их тщательно исследовали как в рамках СТО, так и в рамках квантовой теории. Насколько мне известно, существование тахионов противоречит квантовой теории, но здесь я не специалист. СТО самой по себе существование тахионов не проиворечит. Однако принцип причинности, понимаемый как невозможность послать самому себе сигнал в прошлое, запрещает существование тахионов: в СТО, располагая источником тахионов, можно отправить сигнал самому себе в прошлое, хотя посылка такого сигнала в прошлое на сколько-нибудь значительное время требует использования ретранслятора тахионного сигнала, движущегося от Земли с околосветовой скоростью далеко в космосе (скорее всего, можно было бы придумать конструкцию, обходящую это препятствие).
Тахионы также искали в специальных экспериментах, но обнаружить их не удалось. Так что отсутствие частиц и тел, движущихся со сверхсветовой скоростью, на настоящее время можно считать экспериментальным фактом. Со словом «доказано» нужно быть осторожным: остутсвие тахионов не доказано и никогда не будет доказано. Точно так же ни одна физическая теория не доказана и никогда не будет доказана. Что касается СТО и ОТО, то они, конечно, не доказаны, но подтверждаются (проверены) очень большим количеством экспериментов. Ссылки: СТО и ОТО.
То, что обычно пишут про то, как выглядит окружающий мир при движении с околосветовой скоростью, — полная ерунда. Никакие «шарики» не сплющиваются. Тела сокращались бы, если бы мы могли их видеть с помощью сигналов, распространяющихся с бесконечной скоростью. А так как мы их видим с помощью того же света, распространяющегося с конечной скоростью, мы видим их с запаздыванием, в других цветах (эффект Доплера) и не сократившимися, а повёрнутыми. Существует забавная игра, показывающая, как это выглядит. В игре происходит уменьшение скорости света по мере накопления призов. После скачивания нужно просто распаковать архив, и сразу можно играть. Обзор игры. Правда, автор видеоролика плохо переводит с английского.
Презентация по математике на тему: «ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ»

Описание презентации по отдельным слайдам:
1 слайд Описание слайда:
Описание слайда:Замечательные пределы
2 слайд Описание слайда:
Описание слайда:Первый замечательный предел
3 слайд Описание слайда:
Описание слайда:Второй замечательный предел Первый замечательный предел раскрывает неопределенность
4 слайд Описание слайда:
Описание слайда:Первый замечательный предел При вычислении пределов тригонометрических функций часто используется предел отношения синуса дуги к самой дуге:
5 слайд
Первый замечательный предел Следствия из первого замечательного предела
6 слайд Описание слайда:
Описание слайда:Первый замечательный предел
7 слайд Описание слайда:
Описание слайда:Первый замечательный предел (Если при Пусть
8 слайд Описание слайда:
Описание слайда:Первый замечательный предел
9 слайд Описание слайда:
Описание слайда:Примеры Первый замечательный предел
10 слайд
Первый замечательный предел
11 слайд Описание слайда:
Описание слайда:Первый замечательный предел
12 слайд Описание слайда:
Описание слайда:Первый замечательный предел
13 слайд Описание слайда:
Описание слайда:Первый замечательный предел
14 слайд Описание слайда:
Описание слайда:Второй замечательный предел
15 слайд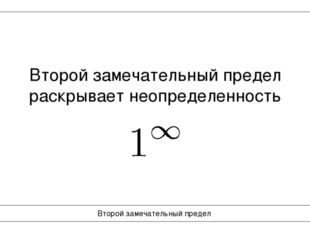
Второй замечательный предел Второй замечательный предел раскрывает неопределенность
16 слайд Описание слайда:
Описание слайда:Второй замечательный предел
17 слайд Описание слайда:
Описание слайда:Второй замечательный предел Число
18 слайд Описание слайда:
Описание слайда:Второй замечательный предел Следствия из второго замечательного предела
19 слайд Описание слайда:
Описание слайда:Второй замечательный предел
 Описание слайда:
Описание слайда:Второй замечательный предел
21 слайд Описание слайда:
Описание слайда:Второй замечательный предел
22 слайд Описание слайда:
Описание слайда:Второй замечательный предел Примеры
23 слайд Описание слайда:
Описание слайда:Второй замечательный предел
24 слайд Описание слайда:
Описание слайда:Второй замечательный предел
 Описание слайда:
Описание слайда:Второй замечательный предел

Курс повышения квалификации
Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Проверен экспертом
Общая информация
Номер материала: ДБ-1031404
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Первый и второй замечательный предел
Найти замечательные пределы трудно не только многим студентам первого, второго курса обучения которые изучают теорию пределов, но и некоторым преподавателям.
Формула первого замечательного предела
Следствия первого замечательного предела запишем формулами
1. 2. 3. 4. Но сами по себе общие формулы замечательных пределов никому на экзамене или тесте не помогают. Суть в том что реальные задания построены так что к записанным выше формулам нужно еще прийти. И большинство студентов, которые пропускают пары, заочно изучают этот курс или имеют преподавателей, которые сами не всегда понимают о чем объясняют, не могут вычислить самых элементарных примеров на замечательные пределы. Из формул первого замечательного предела видим, что с их помощью можно исследовать неопределенности типа ноль разделить на ноль для выражений с тригонометрическими функциями. Рассмотрим сначала ряд примеров на первый замечательный пределу, а потом изучим второй замечательный предел.
Пример 1. Найти предел функции sin(7*x)/(5*x)
Решение: Как видите функция под пределом близка к первому замечательному пределу, но сам предел функции точно не равен единице. В такого рода заданиях на пределы следует в знаменателе выделить переменную с таким же коэффициентом, который содержится при переменной под синусом. В данном случае следует разделить и умножить на 7
Некоторым такая детализация покажется лишней, но большинству студентов которым трудно даются пределы поможет лучше понять правила и усвоить теоретический материал.
Также, если есть обратный вид функции — это также первый замечательный предел. А все потому, что замечательный предел равен единице
Это же правило касается и следствий 1 замечательного предела. Поэтому если Вас спросят «Чему равен первый замечательный предел?» Вы без колебаний должны ответить, что это — единица.
Пример 2. Найти предел функции sin(6x)/tan(11x)
Решение: Для понимания конечного результата распишем функцию в виде
Чтобы применить правила замечательного предела умножим и разделим на множители
Далее предел произведения функций распишем через произведение пределов
Без сложных формул мы нашли предел часки тригонометрических функций. Для усвоения простых формул попробуйте придумать и найти предел на 2 и 4 формулу следствия 1 замечательного предела. Мы рассмотрим более сложные задачи.
Пример 3. Вычислить предел (1-cos(x))/x^2
Решение: При проверке подстановкой получим неопределенность 0/0. Многим неизвестно, как свести такой пример до 1 замечательного предела. Здесь следует использовать тригонометрическую формулу
При этом предел преобразится к понятному виду
Нам удалось свести функцию к квадрату замечательного предела.
Пример 4. Найти предел
Решение: При подстановке получим знакомую особенность 0/0. Однако переменная стремится к Pi, а не к нулю. Поэтому для применения первого замечательного предела выполним такую замену переменной х, чтобы новая переменная направлялась к нулю. Для этого знаменатель обозначим за новую переменную Pi-x=y
Таким образом использовав тригонометрическую формулу, которая приведена в предыдущем задании, пример сведен к 1 замечательному пределу.
Пример 5. Вычислить предел
Решение: Сначала неясно как упростить пределы. Но раз есть пример, значит должен быть и ответ. То что переменная направляется к единице дает при подстановке особенность вида ноль умножить на бесконечность, поэтому тангенс нужно заменить по формуле
После этого получим нужную неопределенность 0/0. Далее выполняем замену переменных в пределе, и используем периодичность котангенса
Последние замены позволяют использовать следствие 1 замечательного предела.
Второй замечательный предел равен экспоненте
Замечательные пределы, примеры решений
Теория по замечательным пределам
Первый замечательный предел раскрывает неопределенность и имеет вид:
Следствия из первого замечательного предела:
Второй замечательный предел раскрывает неопределенность и имеет вид:
где . Он имеет следующие основные следствия:
Примеры
| Понравился сайт? Расскажи друзьям! | |||
44. Замечательные пределы, их вывод. Эквивалентные бесконечно малые величины.
Как показывает
приведённый выше пример
2.36, пределы отношения бесконечно
малых можно упрощать, откидывая бесконечно
малые слагаемые большего порядка и
заменяя множители в числителе и
знаменателе на эквивалентные бесконечно
малые. Для того, чтобы этот способ
вычисления пределов (точнее, раскрытия
неопределённостей вида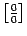 )
можно было применять к возможно большему
числу примеров, мы должны иметь достаточно
большой запас известных пар эквивалентных
бесконечно малых величин. Для наиболее
употребительной базы
)
можно было применять к возможно большему
числу примеров, мы должны иметь достаточно
большой запас известных пар эквивалентных
бесконечно малых величин. Для наиболее
употребительной базы создадим
такой запас в виде таблицы «стандартных»
эквивалентных бесконечно малых.
создадим
такой запас в виде таблицы «стандартных»
эквивалентных бесконечно малых.
Поскольку
в этой таблице мы всегда будем рассматривать
базу 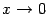 ,
для простоты записи обозначение этой
базы будем пропускать и писать знак
,
для простоты записи обозначение этой
базы будем пропускать и писать знак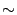 вместо
вместо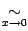 .
.
1) 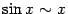 .
Эту формулу мы уже доказали и использовали
в примерах. Эквивалентность
.
Эту формулу мы уже доказали и использовали
в примерах. Эквивалентность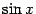 и
и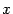 при
при означает
в точности, что первый замечательный
предел равен 1.
означает
в точности, что первый замечательный
предел равен 1.
2) 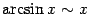 .
Эта эквивалентность тоже была доказана
выше в одном из примеров.
.
Эта эквивалентность тоже была доказана
выше в одном из примеров.
3) 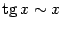 .
Докажем эту эквивалентность:
.
Докажем эту эквивалентность:
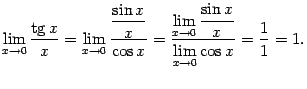
4) 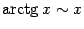 .
Докажите это в качестве упражнения,
сделав замену
.
Докажите это в качестве упражнения,
сделав замену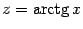 и
применив предыдущую табличную формулу.
и
применив предыдущую табличную формулу.
5)  .
Для доказательства воспользуемся
формулой
.
Для доказательства воспользуемся
формулой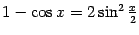 .
Далее, имеем:
.
Далее, имеем:
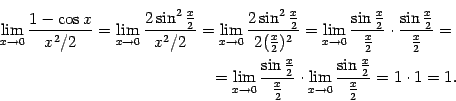
Это означает, что доказываемая эквивалентность имеет место.
6) 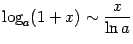 (
(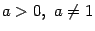 ).
Для доказательства этой эквивалентности
сделаем такое преобразование:
).
Для доказательства этой эквивалентности
сделаем такое преобразование:
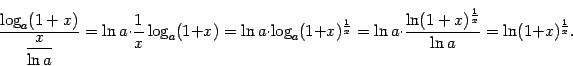
Для вычисления предела правой части воспользуемся непрерывностью логарифма и вторым замечательным пределом:

и мы доказали формулу 6.
В
частном случае, при 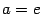 ,
получаем эквивалентность
,
получаем эквивалентность
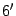 )
) 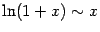 .
.
7) 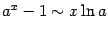 (
(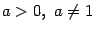 ).
Для доказательства сделаем замену
).
Для доказательства сделаем замену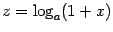 и
выразим
и
выразим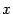 через
через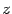 :
: .
Согласно формуле 6,
.
Согласно формуле 6,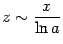 при
при ,
откуда
,
откуда .
Из непрерывности логарифма следует,
что
.
Из непрерывности логарифма следует,
что и,
значит,
и,
значит,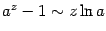 при
при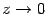 .
В этой формуле осталось лишь сменить
обозначение переменного
.
В этой формуле осталось лишь сменить
обозначение переменного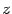 на
на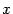 ,
чтобы получить формулу 7.
,
чтобы получить формулу 7.
В
частном случае, при 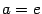 ,
получаем эквивалентность
,
получаем эквивалентность
 )
) 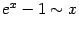 .
.
Сведём
теперь полученные формулы в итоговую
таблицу. Всюду в ней 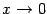 .
.
1) |
|
2) |
|
3) |
|
4) |
|
5) |
|
6) |
|
|
|
7) |
|
|
|
Приведём
примеры применения табличных формул
для раскрытия неопределённостей вида 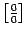 .
.
Замеча́тельные преде́лы— термин, использующийся в советских и российских учебниках поматематическому анализудля обозначения некоторых широко известныхматематических тождествсо взятиемпредела. Особенно известны:
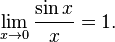
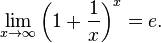
Содержание
Первый замечательный предел

Доказательство
Рассмотрим
односторонние
пределы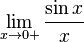 и
и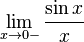 и
докажем, что они равны 1.
и
докажем, что они равны 1.
Пусть  .
Отложим этот угол на единичной окружности
(
.
Отложим этот угол на единичной окружности
( ).
).
Точка K— точка пересечения луча с
окружностью, а точкаL— с
касательной к единичной окружности в
точке .
ТочкаH— проекция точкиKна
осьOX.
.
ТочкаH— проекция точкиKна
осьOX.
Очевидно, что:
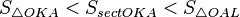 (1)
(1)
(где  —
площадь сектора
—
площадь сектора )
)
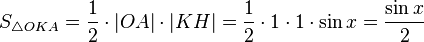
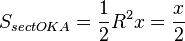

(из 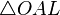 :
: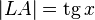 )
)
Подставляя в (1), получим:
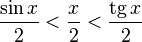
Так
как при 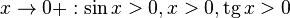 :
:
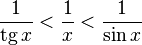
Умножаем
на  :
:
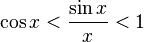
Перейдём к пределу:
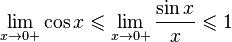
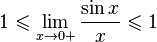
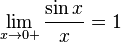
Найдём левый односторонний предел:
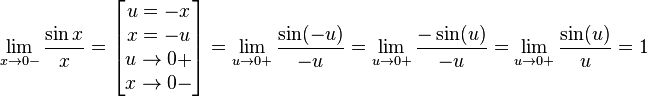
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.
Следствия
Доказательство следствий [показать]
Второй замечательный предел
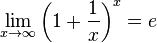 или
или 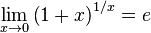
Доказательство второго замечательного предела:
Доказательство для натуральных значений x [показать]
 Зная,
что второй замечательный предел верен
для натуральных значений x, докажем
второй замечательный предел для
вещественных x, то есть докажем, что
.
Рассмотрим два случая:
Зная,
что второй замечательный предел верен
для натуральных значений x, докажем
второй замечательный предел для
вещественных x, то есть докажем, что
.
Рассмотрим два случая:
1.
Пусть  .
Каждое значение x заключено между двумя
положительными целыми числами:
.
Каждое значение x заключено между двумя
положительными целыми числами: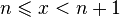 ,
где
,
где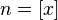 —
это целая часть x.
—
это целая часть x.
Отсюда следует: 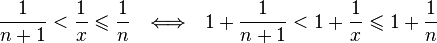 ,
поэтому
,
поэтому
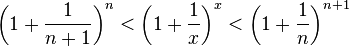 .
.
Если 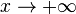 ,
то
,
то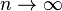 .
Поэтому, согласно пределу
.
Поэтому, согласно пределу ,
имеем:
,
имеем:
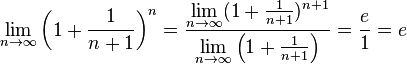
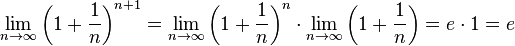 .
.
По признаку (о пределе промежуточной
функции) существования пределов 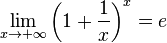 .
.
2.
Пусть  .
Сделаем подстановку
.
Сделаем подстановку ,
тогда
,
тогда
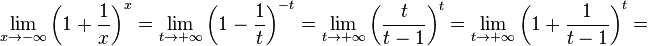
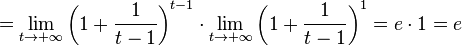 .
.
Из
двух этих случаев вытекает, что 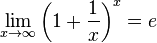 для
вещественного x.
для
вещественного x.
Следствия



 для
для ,
,

Формулы расчета пределов
Предел постоянной равен этой постоянной:
limxacc (c — постоянная)
Лимит суммы равен сумме лимитов:
limxafxgxlimxafxlimxagx
Предел разницы равен разнице лимитов:
limxafxgxlimxafxlimxagx
Предел умножения равен умножению пределов:
limxafxgxlimxafxlimxagx
Предел деления равен делению лимитов:
limxafxgxlimxafxlimxagx если условие limxagx0 удерживается
Предел функции мощности:
limxafxmlimxafxm (м — натуральное число)
Предел корневой функции:
limxamfxmlimxafx (м — натуральное число)
Основные лимиты:
Первый замечательный предел:
limx0sinxx1 (x — угол в радианах)
Второй замечательный предел:
limx∞11xxe
Другие полезные формулы пределов:
бесконечно малая
Бесконечно малый эквивалент:
Так как х → 0 , следующие функции эквивалентны:
х ~ грех (х) ~ arcsin (x) ~ tg (x) ~ arctg (x) ~ Ln (1 + х)
Чтобы найти предел деления двух бесконечно малых функций, их можно заменить их эквивалентами:
limx0ln1xxlimx0xx1
limx0sinxxlimx0xx1
limx0sinxx2x42xx3sinxx2x4 ~ x2xx3 ~ 2xlimx0x2x12
к рассчитать пределы Вы можете воспользоваться нашим онлайн-калькулятором.
,Сообщение мамы о «замечательном» водителе службы доставки Tesco, связанном со своим аутичным малышом, становится вирусным
МОЛОДАЯ мама похвалила «замечательного» водителя службы доставки Tesco после того, как он связался с ее аутичным малышом в сообщении в Facebook, которое с тех пор стало вирусным.
У 24-летней Лорен Браун в понедельник еженедельно доставляли магазин, и ее трехлетний сын Томми открыл дверь.
7
Лорен Браун была со своим трехлетним сыном Томми, когда прибыла покупка Фото: Fortitude PressМальчик не ответил работнику супермаркета, который спросил Томми: «Ты не хочешь поговорить сегодня, малыш?»
Лорен из Андовера, Хантс, затем объяснила, что у него аутизм, и он ожидал получить один из обычных ответов, который включает кивок головы или «благослови его».
Однако она была удивлена, когда «замечательный джентльмен» не стал относиться к нему иначе и начал давать ему легкие вещи из магазина, чтобы он убрал их.
После того, как все продукты были уложены и Лорен подписала заказ, мужчина попросил Томми подписать и доставку и помог ему нажать кнопку «Готово».
7
Она была рада и шокирована, когда водитель обращался с ним «нормально». Фото: Fortitude Press.7
Она поблагодарила водителя в посте на Facebook, который с тех пор стал вируснымКредит: Fortitude PressЛорен, мама двоих детей, сказала: «Я сразу поняла, что он хороший человек.Это был действительно сладкий момент.
«Он относился к Томми как к нормальному человеку и ничем не отличался от того, что было до того, как узнал, что у него аутизм.
«Его это не шокировало, что было очень приятно. Было приятно, что его включили.
«Многие люди не понимают этого [аутизма], но он был действительно прекрасен.
«Было приятно смотреть. На самом деле мы не видим много людей, взаимодействующих с Томми на таком уровне.
«Я просто надеюсь, что каждый с дополнительными потребностями может быть принят таким, какой он есть, и что больше людей узнают, как такой простой жест может действительно так много значить для кого-то.”
7
Она связалась с отцом Томми, Дэном Мэтьюзом, чтобы поделиться хорошими новостямиКредит: Fortitude Press7
Томми был диагностирован аутизм в январе этого года Фото: Fortitude PressЛорен была поражена заботой и сразу же позвонила отцу Томми, Дэну Мэтьюзу, 24 года, и они решили использовать социальные сети, чтобы передать свою благодарность этому загадочному человеку.
Она добавила: «Когда люди узнают о его аутизме, они, как правило, уклоняются от этого и вместо этого говорят со мной, но я понимаю, что людям это может быть трудно.
«Я не думаю, что многие люди имеют образование в области аутизма. На самом деле об этом не говорят ».
Позже в тот же день Лорен написала в сообщении на Facebook: «Я просто хотела поблагодарить этого прекрасного человека.
7
Он даже помог своей маме убрать часть покупокКредит: Fortitude Press7
Томми — большой футбольный фанатКредит: Fortitude Press«Вместо того, чтобы игнорировать его или стесняться новостей, которые он только что узнал, он нашел альтернативный способ общения с ним, и это действительно много значит для меня.
«Я уверен, что другие родители с детьми, у которых есть дополнительные потребности, тоже оценят это.
«К сожалению, я не узнал его имя, но мистер Доставщик, если вы это видите, мы очень вам благодарны за вашу доброту».
Пост в Facebook с тех пор получил 8,6 тысяч лайков, и Лорен говорит, что говорила с командой обслуживания клиентов Tesco, и ей сказали, что ее благодарность будет передана водителю доставки.
ФАКТИЧЕСКАЯ КОРОБКА: ЧТО ТАКОЕ АУТИЗМ?
— Аутизм — это пожизненная инвалидность в развитии и расстройство спектра, которое влияет на то, как люди воспринимают мир и взаимодействуют с другими.
— Аутичные люди видят, слышат и чувствуют мир иначе, чем другие люди.
Некоторые говорят, что мир кажется подавляющим, что может вызвать у них серьезное беспокойство.
— Хотя аутичные люди разделяют определенные трудности, это может повлиять на них по-разному. Отношение к другим людям и понимание других может быть проблемой, как и участие в повседневных социальных, семейных и школьных мероприятиях.
— Человек с аутизмом может нуждаться в различных уровнях поддержки в зависимости от того, есть ли у него проблемы с обучением, проблемы с психическим здоровьем или другие состояния.
— В Великобритании около 700 000 аутичных людей.
— Для того чтобы получить диагноз аутизма, человек обычно проявляет признаки трудностей с социальным общением, социальным взаимодействием и с раннего возраста демонстрирует ограниченные и повторяющиеся модели поведения, деятельности или интересов, которые могут «ограничивать и ухудшать повседневное функционирование». ,
KILLER PLAGUE
Мужчина в возрасте 20 лет умирает от BUBONIC PLAGUE после того, как поймал редкое заболеваниеMONSTER CAGED
Ужасающий момент зверь хватает женщину и уносит ее, чтобы изнасиловать ееIN THE MONEY
Удачливый британец получает огромные 10 фунтов стерлингов.Джекпот в 7 миллионов лото при четырехкратном переносеПРАЗДНИЧНЫЙ СПИСОК
Опасения, что Турция может попасть в карантинный список Великобритании из-за всплеска вирусных заболеванийПРЕДУПРЕЖДЕНЫ
Новорожденный ребенок умирает после того, как мама, находящаяся на грани рождения, была отвергнута из больницыЭксклюзив
ДЕНЬ В СУДЕ
Руни, готовые к сексуальной жизни, показывают на суде над «Вагатой Кристи»Томми официально диагностировали аутизм в январе этого года после того, как его родители начали замечать его медленное развитие и недостаток общения.
Им сказали, что в настоящее время он умственный возраст 18-месячного ребенка.
СС Tesco связались для получения комментариев.
Мы платим за ваши истории! У вас есть история для новостной команды The Sun Online? Напишите нам по адресу [email protected] или позвоните по телефону 0207 782 4368. Вы можете отправить нам WhatsApp по телефону 07810 791 502. Мы также платим за видео. Щелкните здесь, чтобы загрузить свой.
,
Текст обращения Стива Джобса к выпуску (2005 г.)
Стэнфордский отчет, 14 июня 2005 г.Это подготовленный текст вступительной речи Стива Джобса, генерального директора Apple Computer и Pixar Animation Studios, 12 июня 2005 г.
Видео вступительной речи.
Для меня большая честь быть с вами сегодня, когда вы поступаете в один из лучших университетов мира. я никогда не заканчивал колледж.По правде говоря, это самое близкое, что я когда-либо был к окончанию колледжа. Сегодня я хочу рассказать вам три истории из своей жизни. Вот и все. Ничего страшного. Всего три этажа.
Первый рассказ о соединении точек.
Я бросил Рид-колледж после первых 6 месяцев, но затем оставался там в качестве дроп-ин еще 18 месяцев или около того, прежде чем действительно бросил. Так почему я бросил учебу?
Это началось еще до моего рождения. Моя биологическая мать была молодой незамужней выпускницей колледжа, и она решила отдать меня на усыновление.Она очень сильно чувствовала, что меня должны усыновить выпускники колледжа, поэтому все было готово для того, чтобы я был усыновлен юристом и его женой при рождении. Вот только когда я появился, они в последнюю минуту решили, что действительно хотят девушку. Итак, моим родителям, которые были в списке ожидания, позвонили посреди ночи и спросили: «У нас родился неожиданный мальчик; вы хотите его?» Они сказали: «Конечно». Моя биологическая мать позже узнала, что моя мать никогда не заканчивала колледж, а мой отец никогда не окончил среднюю школу.Она отказалась подписать окончательные документы об усыновлении. Она уступила только несколько месяцев спустя, когда мои родители пообещали, что я когда-нибудь поступлю в институт.
И 17 лет спустя я поступил в институт. Но я наивно выбрал колледж, который был почти таким же дорогим, как Стэнфорд, и все сбережения моих родителей из рабочего класса тратились на мое обучение в колледже. Через шесть месяцев я не увидел в этом ценности. Я понятия не имел, чем хочу заниматься в жизни, и не представлял, как колледж поможет мне в этом разобраться.И здесь я тратил все деньги, которые мои родители копили за всю свою жизнь. Поэтому я решил бросить учебу и поверить, что все пойдет хорошо. В то время это было довольно страшно, но, оглядываясь назад, это было одно из лучших решений, которые я когда-либо принимал. В ту минуту, когда я бросил учебу, я мог перестать посещать требуемые классы, которые меня не интересовали, и начать посещать те, которые казались мне интересными.
Не все было романтично. У меня не было комнаты в общежитии, поэтому я спал на полу в комнатах друзей, я возвращал бутылки кока-колы за депозит в 5 центов, чтобы купить еду, и каждое воскресенье вечером я ходил пешком 7 миль по городу, чтобы получить одну хорошую питание в неделю в храме Харе Кришна.Я люблю это. И многое из того, на что я наткнулся, следуя своему любопытству и интуиции, позже оказалось бесценным. Приведу один пример:
Reed College в то время предлагал, пожалуй, лучшее обучение каллиграфии в стране. По всему кампусу каждый плакат, каждая этикетка на каждом ящике была красиво нарисована вручную. Поскольку я бросил учебу и не должен был посещать обычные уроки, я решил пойти на уроки каллиграфии, чтобы узнать, как это делать. Я узнал о шрифтах с засечками и без засечек, о том, как варьировать расстояние между различными комбинациями букв, о том, что делает отличную типографику отличной.Это было красиво, исторически, художественно тонко, что наука не может охватить, и я нашел это увлекательным.
Ничего из этого не было даже надежды на практическое применение в моей жизни. Но 10 лет спустя, когда мы проектировали первый компьютер Macintosh, все это вернулось ко мне. И мы разработали все это для Mac. Это был первый компьютер с красивой типографикой. Если бы я никогда не заглянул на этот единственный курс в колледже, на Mac никогда бы не было нескольких гарнитур или пропорциональных шрифтов.А поскольку Windows просто скопировала Mac, вполне вероятно, что ни на одном персональном компьютере их не было. Если бы я никогда не бросил учебу, я бы никогда не пошел на этот урок каллиграфии, а на персональных компьютерах могло бы не быть такой замечательной типографики, как у них. Конечно, когда я учился в колледже, было невозможно соединить точки в ожидании. Но 10 лет спустя это было очень, очень ясно.
Опять же, вы не можете соединить точки, глядя вперед; вы можете соединить их, только глядя назад.Так что вы должны верить, что точки каким-то образом соединятся в вашем будущем. Вы должны во что-то верить — в свою интуицию, судьбу, жизнь, карму, что угодно. Такой подход никогда меня не подводил и полностью изменил мою жизнь.
Моя вторая история о любви и потерях.
Мне повезло — я рано нашел то, что мне нравилось делать. Мы с Возом основали Apple в гараже моих родителей, когда мне было 20. Мы много работали, и за 10 лет Apple выросла из нас двоих в гараже в компанию стоимостью 2 миллиарда долларов, в которой работает более 4000 сотрудников.Мы только что выпустили наше лучшее творение — Macintosh — годом ранее, и мне только исполнилось 30. А потом меня уволили. Как вас могут уволить из созданной вами компании? Что ж, по мере роста Apple мы наняли кого-то, кого я считал очень талантливым, чтобы вместе со мной управлять компанией, и в течение первого года дела шли хорошо. Но затем наши представления о будущем начали расходиться, и в конце концов мы поссорились. Когда мы это сделали, наш совет директоров встал на его сторону. Так что в 30 лет меня не было. И очень публично.То, что было целью всей моей взрослой жизни, исчезло, и это было ужасно.
Я действительно не знал, что делать в течение нескольких месяцев. Я чувствовал, что подвел предыдущее поколение предпринимателей — что я уронил эстафету, когда ее передавали мне. Я встретился с Дэвидом Паккардом и Бобом Нойсом и попытался извиниться за такую ужасную ошибку. Я был публичным неудачником и даже думал о том, чтобы сбежать из долины. Но что-то постепенно начало понимать меня — я все еще любил то, что делаю.Поворот событий в Apple этого нисколько не изменил. Меня отвергли, но я все еще любил. И я решил начать все сначала.
Тогда я этого не видел, но оказалось, что увольнение из Apple — лучшее, что со мной могло случиться. Тяжесть успеха сменилась легкостью снова стать новичком, менее уверенным во всем. Это дало мне свободу вступить в один из самых творческих периодов моей жизни.
В течение следующих пяти лет я основал компанию NeXT, другую компанию под названием Pixar, и влюбился в удивительную женщину, которая стала моей женой.Pixar создала первый в мире компьютерный анимационный художественный фильм « Toy Story » и теперь является самой успешной анимационной студией в мире. При знаменательном повороте событий Apple купила NeXT, я вернулся в Apple, а технология, которую мы разработали в NeXT, лежит в основе нынешнего возрождения Apple. И у нас с Лорен прекрасная семья.
Я почти уверен, что ничего этого не произошло бы, если бы меня не уволили из Apple. Это было ужасное лекарство на вкус, но, полагаю, пациенту оно было необходимо.Иногда жизнь бьет вас кирпичом по голове. Не теряйте веры. Я убежден, что единственное, что меня поддерживало, — это то, что мне нравилось то, что я делал. Вы должны найти то, что любите. И это верно как для вашей работы, так и для ваших любовников. Ваша работа займет большую часть вашей жизни, и единственный способ быть по-настоящему удовлетворенным — это делать то, что вы считаете великой работой. И единственный способ делать отличную работу — любить то, что делаешь. Если вы еще не нашли его, продолжайте поиски. Не соглашайтесь. Как и во всем, что касается сердца, вы узнаете, когда найдете его.И, как любые отличные отношения, с годами они становятся все лучше и лучше. Так что продолжайте искать, пока не найдете. Не соглашайтесь.
Моя третья история о смерти.
Когда мне было 17, я прочитал цитату примерно такого рода: «Если вы будете жить каждый день так, как если бы он был вашим последним, когда-нибудь вы наверняка будете правы». Это произвело на меня впечатление, и с тех пор на протяжении последних 33 лет я каждое утро смотрел в зеркало и спрашивал себя: «Если бы сегодня был последний день в моей жизни, хотел бы я делать то, что собираюсь сделать? сделать сегодня? » И всякий раз, когда ответ слишком много дней подряд был отрицательным, я знаю, что мне нужно что-то изменить.
Память о том, что я скоро умру, — это самый важный инструмент, с которым я когда-либо сталкивался, чтобы помочь мне сделать важный выбор в жизни. Потому что почти все — все внешние ожидания, вся гордость, весь страх затруднений или неудач — все это просто исчезает перед лицом смерти, оставляя только то, что действительно важно. Память о том, что ты умрешь, — лучший из известных мне способов избежать ловушки мысли, что тебе есть что терять. Вы уже голые. Нет причин не следовать своему сердцу.
Около года назад у меня обнаружили рак. Мне сделали сканирование в 7:30 утра, и оно четко показало опухоль на моей поджелудочной железе. Я даже не знал, что такое поджелудочная железа. Врачи сказали мне, что это почти наверняка неизлечимый вид рака и что мне не придется жить дольше трех-шести месяцев. Мой врач посоветовал мне пойти домой и привести свои дела в порядок, что является кодексом врача для подготовки к смерти. Это означает попытаться рассказать своим детям все, что, по вашему мнению, у вас будет в ближайшие 10 лет, чтобы рассказать им всего за несколько месяцев.Это означает, что все должно быть застегнуто, чтобы вашей семье было как можно проще. Это значит попрощаться.
Я прожил с этим диагнозом весь день. Позже тем же вечером мне сделали биопсию, при которой мне воткнули эндоскоп в горло, через желудок и в кишечник, ввели иглу в поджелудочную железу и взяли несколько клеток из опухоли. Мне дали успокоительное, но моя жена, которая была там, сказала мне, что, когда они рассматривали клетки под микроскопом, врачи начали плакать, потому что это оказалась очень редкая форма рака поджелудочной железы, которую можно вылечить хирургическим путем.Мне сделали операцию, и теперь я в порядке.
Это был самый близкий мне путь к смерти, и я надеюсь, что это был самый близкий момент за несколько десятилетий. Пережив это, я теперь могу сказать вам это с большей уверенностью, чем когда смерть была полезной, но чисто интеллектуальной концепцией:
Никто не хочет умирать. Даже люди, которые хотят попасть в рай, не хотят умереть, чтобы попасть туда. И все же смерть — это наша общая цель. Никто не избежал этого. Так и должно быть, потому что Смерть, скорее всего, является лучшим изобретением Жизни.Это агент изменения жизни. Он очищает старое, чтобы уступить место новому. Прямо сейчас новое — это вы, но когда-нибудь, не так давно, вы постепенно станете старым и будете очищены. Извините за такую драматичность, но это правда.
Ваше время ограничено, поэтому не тратьте его зря на чужую жизнь. Не попадайтесь в ловушку догм, которые живут на основе мышления других людей. Не позволяйте шуму чужих мнений заглушить ваш собственный внутренний голос. И самое главное, имейте смелость следовать своему сердцу и интуиции.Они каким-то образом уже знают, кем вы действительно хотите стать. Все остальное вторично.
Когда я был молод, была замечательная публикация под названием The Whole Earth Catalog , которая была одной из библий моего поколения. Он был создан парнем по имени Стюарт Брэнд недалеко отсюда, в Менло-Парке, и воплотил его в жизнь с помощью своего поэтического подхода. Это было в конце 1960-х, до персональных компьютеров и настольных издательских систем, поэтому все это было сделано с помощью пишущих машинок, ножниц и фотоаппаратов Polaroid.Это было что-то вроде Google в мягкой обложке за 35 лет до появления Google: он был идеалистическим и был переполнен изящными инструментами и отличными идеями.
Стюарт и его команда выпустили несколько выпусков каталога The Whole Earth Catalog , а затем, когда он закончился, они выпустили последний выпуск i
.Русская дача как феномен культуры
Слово «дача» происходит от глагола «дат» — дарить и существительного «дар» — дарить. На протяжении многих лет получение земельного участка в личное пользование было большим и очень ценным подарком — будь то царское или советское правительство. Но то, как люди использовали эту землю, в разные времена сильно отличалось. Невозможно полностью понять Россию, не понимая культурного контекста русской дачи.
Дача — до революции 1917 года
За чайным столом К.Коровина, 1888
Первые дачи в России появились в начале 18 века при Петре Великом. Он хотел, чтобы подчиненные оставались рядом с ним даже в отпуске, поэтому подарил им участки под Санкт-Петербургом. Эти участки были стратегически расположены на пути к Петергофу, царской резиденции, поэтому он всегда мог остановиться и посмотреть, как его люди проводят свободное время.
В 1803 году известный русский историк Карамзин писал, что летом Москва пустеет, так как люди уезжают на дачи.А к середине 19 века дачи стали излюбленным местом отдыха и развлечений всех аристократов, которые могли себе позволить такое времяпрепровождение. Дачи часто представляли собой простые деревянные дома, но всегда имели террасу, где жители могли обедать, пить чай и развлекаться долгими летними вечерами. Не у всех были дачи, некоторые арендовали их на лето и обычно ездили на дачу всей семьей и прислугой. Если хотите узнать больше о дачных историях того времени, читайте Антона Чехова!
Дача — советское время
Первый в мире санаторий для сельскохозяйственных рабочих, Ливадия, Крым, 1931 год
Октябрьская революция 1917 года принесла с собой закон, запрещающий частную собственность на землю в России «навсегда».Идея заключалась в том, что все граждане страны смогут использовать все ресурсы страны, все люди будут равны, и никто не сможет эксплуатировать других людей или быть более богатым, чем они. Ценности новой Советской республики были в основном коллективистскими. И вместо индивидуальных дач население получило доступ к групповым объектам отдыха, таким как санатории. Популярная советская фраза гласила: «Все вокруг принадлежит народу, все вокруг принадлежит мне».
Но была и другая поговорка — «все равны, но одни равнее других».Иосиф Сталин, правивший страной с 1924 по 1953 год, сам любил хороший загородный отдых. У него было много дач в самых живописных уголках России — от Подмосковья до Черного моря. Это были огромные особняки, полностью укомплектованные персоналом и готовые приветствовать его в любое время, когда он решит появиться.
Старая дача в «писательской деревне»
Сталин полагал, что предоставление такой привилегии, как дача, ближайшим людям в правительстве и высокопоставленным лицам из культурной и научной элиты будет для них очень мотивирующим фактором.Эти дачи не принадлежали их обитателям, на мебели и светильниках были номера маршрутов, но эти дачи были большой роскошью, и получить ее считалось огромной привилегией. Для упрощения — дачи сгруппированы по роду занятий — так до сих пор остались «деревни» писателей, композиторов, художников, ученых и т. Д. В то время все дачи были местом отдыха, рыбалки, сбора ягод и грибов, занятий спортом. и развлекайся с друзьями.
Выращивание продуктов на даче
После Второй мировой войны ограниченные продовольственные ресурсы в стране вынудили правительство разрешить людям приобретать участки земли и поддерживать семьи, выращивая там овощи.Однако строительство дома на этом участке было категорически запрещено. В 60-е годы, во время правления Никиты Хрущева, простым людям наконец разрешили получить дачи. Но получить его было так непросто. Распределение было основано на заслугах, нужно было полностью соответствовать идеологии и ждать в длинной очереди, иногда по много лет.
«Дачный поселок» отличался от обычного поселка. Небольшие участки земли, высокая плотность домов
Эти дачи были не такими роскошными — обычно это были крохотные участки земли с разрешением на строительство там небольшого одноэтажного дома.Жители по-прежнему не владели им, но могли использовать его для выращивания продуктов строго для семейного потребления (не для продажи). Тем не менее, люди чувствовали себя так, как будто это их земля, поэтому получение дачи стало одной из мечтаний советских людей, так же как получение квартиры или машины. Было много манипуляций — как быстрее получить дачу. В России законы и правила всегда были партикулярными, поэтому, если бы вы знали кого-то, вы могли бы добраться до желаемой дачи намного быстрее.
Построить дом тоже было непросто.Дефицит строительных материалов. Трудно представить, что сейчас, но нельзя было просто пойти в магазин и купить дерево, кирпич или что-нибудь еще, нужно было каким-то образом «достать» нужные материалы через свою сеть контактов или заплатить втрое на черном рынке.
Консервы на зиму
Это было время, когда функция дачи начала трансформироваться — она стала местом тяжелой работы в поле, а не местом отдыха и развлечений. Эта функция дачи очень пригодилась в неспокойные 90-е годы, когда в магазинах было мало продуктов и люди реально поддерживали свои семьи, выращивая на своей земле картофель, огурцы, свежие продукты, ягоды и яблоки.Многие домашние продукты консервировали на зиму в маринованном или соленом виде или в виде домашних джемов.
«Дача» В. Губарева — шутливый способ портрета «советских дачных» феноменов
Дача — современность
В 90-х наконец разрешили владеть собственностью. Это еще одна большая и интересная история, но в результате люди стали покупать дачи, если у них были деньги. Или, если у них уже были дачи, они могли приватизировать их, официально сделав их собственностью.Также были сняты ограничения на размер земельного участка или этажность дома. Наконец, вы можете делать все, что хотите, на своей земле. Любопытно, что случилось потом?
Типичная дача богатого человека 90-х — дом из красного кирпича, скрытый за высоким забором из красного кирпича
Люди, всегда лишенные такого множества вариантов, начали экспериментировать. Богатые «новые русские» тут же начали строить огромные особняки на своих небольших участках земли. Многим из этих домов не хватало вкуса или стиля.Поколения местных жителей не видели красивых загородных домов, а коммерческая промышленность в этом районе еще не была развита. На смену традициям строительства деревянных домов пришли кирпичные или каменные. Раньше дачи были просто дачными домиками, а теперь многие стали строить дома круглый год.
Теперь, наконец, промышленность работает так же, как и в любой другой стране, и если вы хотите построить красивый дом в любом стиле — он будет построен для вас. Но это будет дорого. Как и за любые коммерческие товары и услуги в России — от одежды до маникюра, вы платите больше за хорошие вещи!
На многих типичных дачных участках все еще больше земли, отведенной под выращивание продуктов, чем под площадку для отдыха
Итак, как сейчас люди проводят время на дачах? Это действительно по-разному.Многие люди по-прежнему работают весь день, выращивая картофель, огурцы, клубнику и т. Д. Большинство из этих людей работают полный рабочий день в городе, они не сельскохозяйственные рабочие, но каждую пятницу вечером они уезжают из города, чтобы провести выходные. действительно тяжелая работа в поле. Что и говорить — им приходится преодолевать огромные пробки по дороге на дачу и обратно. Иногда добраться до дачи в 50-100 км от города можно за 3-4 часа. Дать рациональное объяснение, почему продолжают выращивать картофель, невозможно, хотя их легко можно купить в любом магазине.Экономически это не имеет смысла, но люди иррациональны. Для некоторых выращивание продуктов является привычкой, некоторые (в основном пожилые люди) любят обрабатывать землю своими руками, некоторым нравится идея органических продуктов или говорят, что картофель, выращенный в собственном саду, просто вкуснее.
Еще одно явление, которое мы, местные жители, называем «Балкон, дача, мусорный бак». Это история бережливости, вызванной дефицитом вещей в магазинах в советское время и нехваткой складских площадей в городских квартирах.Русские не любят выбрасывать вещи, даже если некоторые вещи им не нужны — они все равно хранят их. Этот хлам сначала приземляется на балкон, потом переезжает на дачу и только в том случае, если он действительно старый или совсем сломанный, попадает в мусор. В результате многие люди на даче носят старую одежду. И у большинства есть стопки старой одежды на дачах, хотя в магазинах уже нет дефицита.
Тем не менее, многие считают дачу местом, где можно развлечься. Эти люди косят газоны и сажают цветы, поэтому им еще предстоит проделать свою долю полевых работ, чтобы дачный дом выглядел презентабельно.Но вместо того, чтобы проводить все время в саду, они приглашают друзей и развлекают их, жарят мясо на гриле, едят клубнику, сидя в беседках, занимаются спортом и наслаждаются другими развлечениями. Надеюсь, это станет массовым трендом и большему количеству людей понравится отдыхать на даче, а не работать там!
Некоторые развлечения на Даче включают:
Для этого слайд-шоу необходим JavaScript.
Желаю вернуться к Чеховскому т
.
 .
.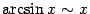 .
.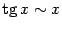 .
.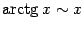 .
. .
.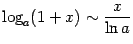 (
(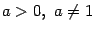 ).
).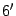 )
)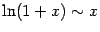 .
.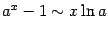 (
(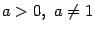 ).
).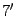 )
)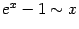 .
.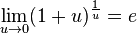
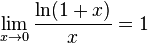
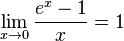
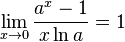 для
для ,
,