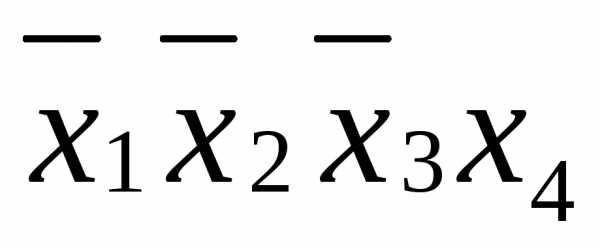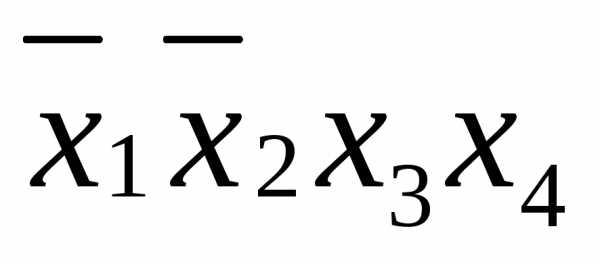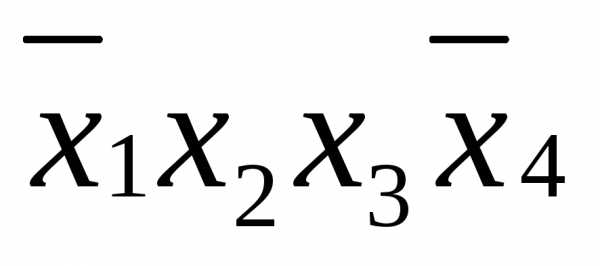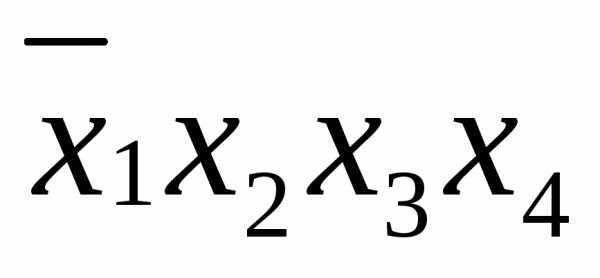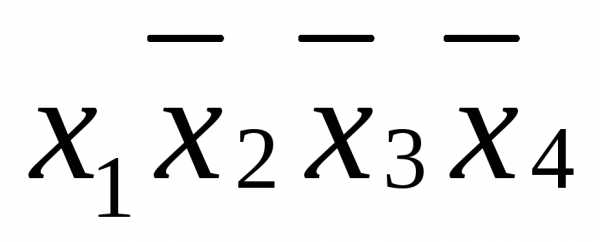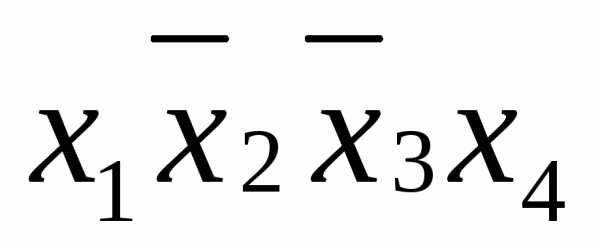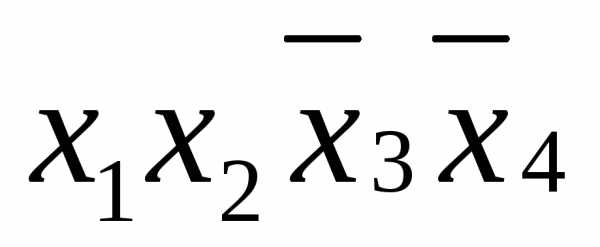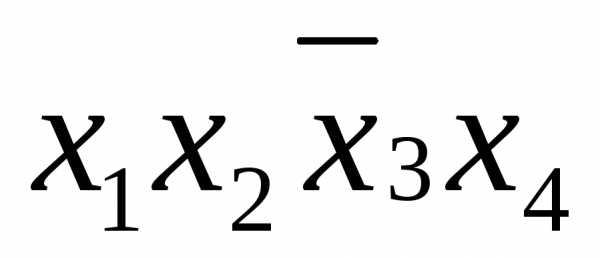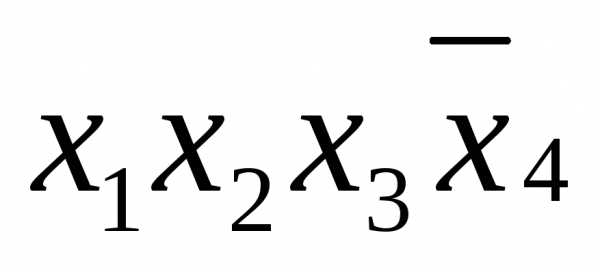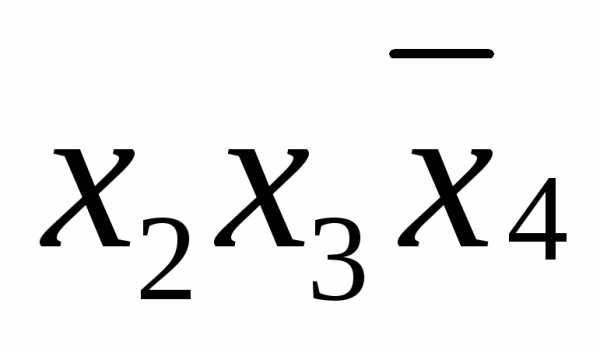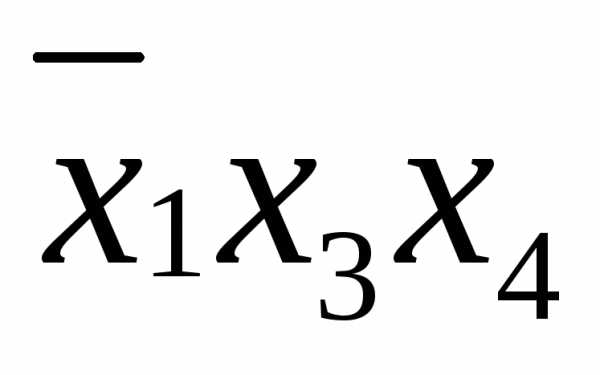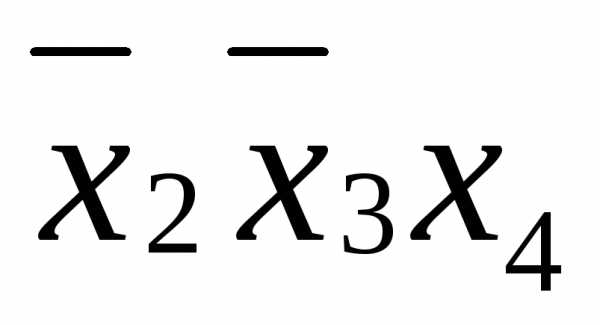4.5. Сднф булевой функции и ее упрощение
Пусть A1=– булева алгебра, носителем которой
служит множество всех булевых функций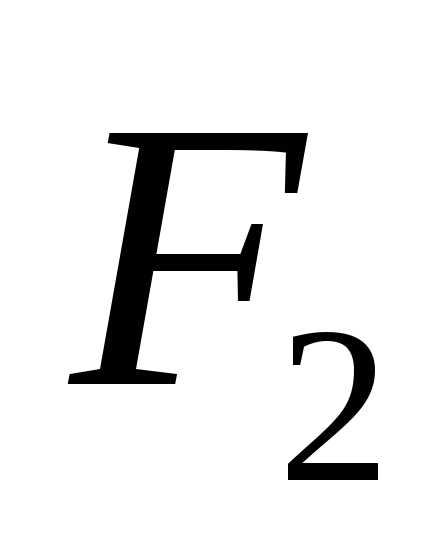 .
.
Выпишем таблицы операций сигнатуры этой алгебры.
Таблица 4.3 Таблица отрицания | Таблица 4.4 Таблица конъюнкции | Таблица 4.5 Таблица дизъюнкции | |||||||
x |
|
|
|
|
|
| |||
0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | ||
1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | ||
1 | 0 | 0 | 1 | 0 | 1 | ||||
1 | 1 | 1 | 1 | 1 | 1 | ||||
Основные свойства этих операций в любой булевой алгебре записаны в таблице 4.1. Отметим их дополнительные свойства.
1. ,
2. ,
3.  – закон противоречия,
– закон противоречия,
1′ 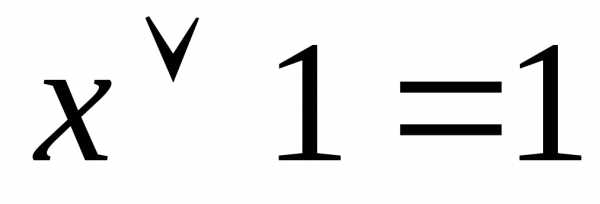 ,
,
2′ ,
3′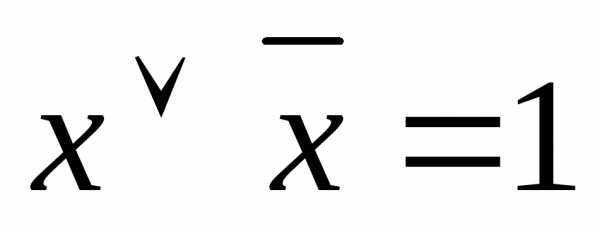 – закон исключения третьего.
– закон исключения третьего.
4. – Закон снятия двойного отрицания.
Пусть имеем булеву функцию .
Определение 4.8. Элементарной конъюнкциейназывают конъюнкцию, содержащую переменные или их отрицания.
Примеры элементарных конъюнкций: 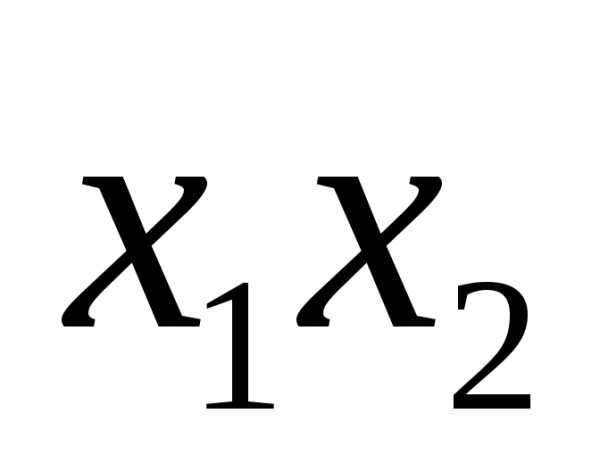 ,
,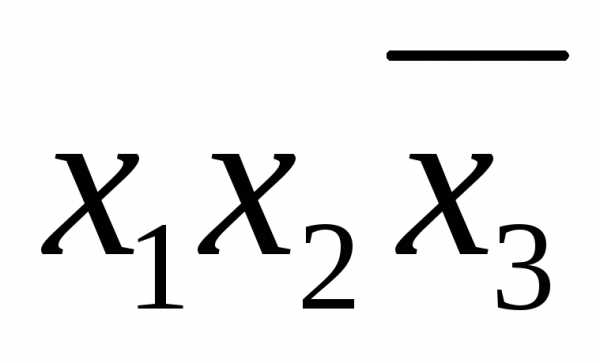 ,
,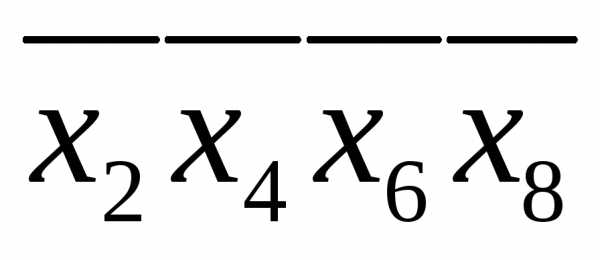 и т.п.
и т.п.
Определение 4.9. Элементарной дизъюнкциейназывают дизъюнкцию, содержащую переменные или их отрицания.
Примеры элементарных дизъюнкций: 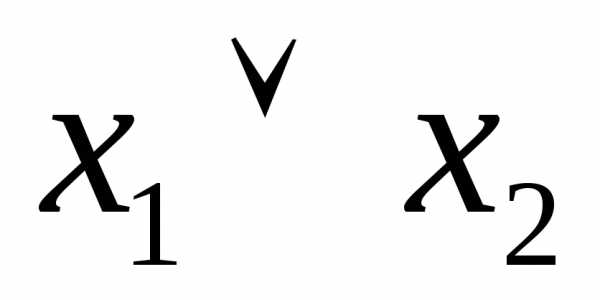 ,
,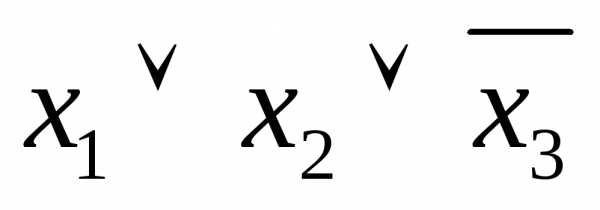 ,и т.п.
,и т.п.
Определение 4.10. Формулу булевой функции, в которой элементарные конъюнкции соединены знаками дизъюнкции, называютдизъюнктивной нормальной формой(ДНФ) этой функции. Формулу, в которой элементарные дизъюнкции соединены знаками конъюнкции, называютконъюнктивной нормальной формой(КНФ) функции.
Пример.
| | |
| Элементарные конъюнкции | Булева функция задана таблицей. Для
каждой строки единичного набора
запишем элементарные конъюнкции,
включающие все три аргумента булевой
функции, по следующему правилу: если Соединив все элементарные конъюнкции знаками дизъюнкции, получим дизъюнктивную нормальную форму: ДНФ= На любой строке единичного набора одна из элементарных конъюнкций равна 1, а следовательно, и вся ДНФ имеет значение 1. На любой строке нулевого набора ни одна из элементарных конъюнкций единице не равна, поэтому ДНФ имеет значение 0. | |
0 | 0 | 1 |
| |||
0 | 0 | 1 | 1 |
| ||
0 | 1 | 0 | 0 | |||
0 | 1 | 1 | 0 | |||
1 | 0 | 0 | 1 |
| ||
1 | 0 | 1 | 1 |
| ||
1 | 1 | 0 | 1 |
| ||
1 | 1 | 1 | 0 |
Таким образом, на всех наборах значений аргументов значения ДНФ и функции совпадают. Следовательно, ДНФ=. Построенную таким образом ДНФ называютсовершенной дизъюнктивной нормальной формой (СДНФ) функции
Если построить аналогичным образом элементарные конъюнкции на нулевом наборе, то, соединив их знаками дизъюнкции, получим СДНФ отрицания функции :
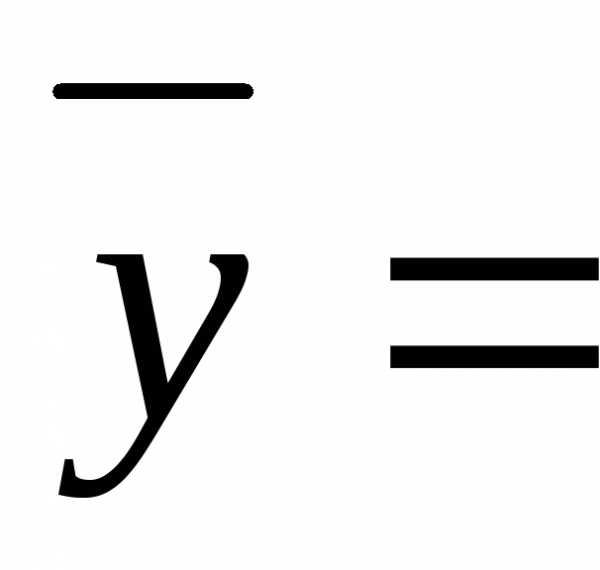
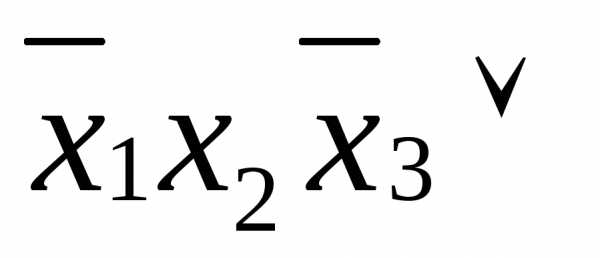
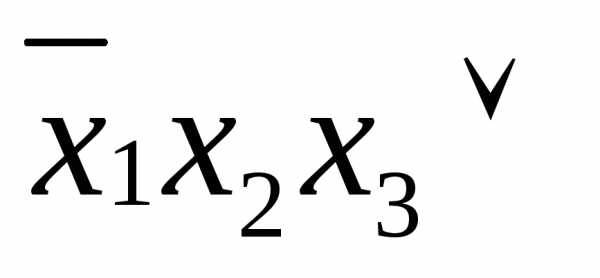
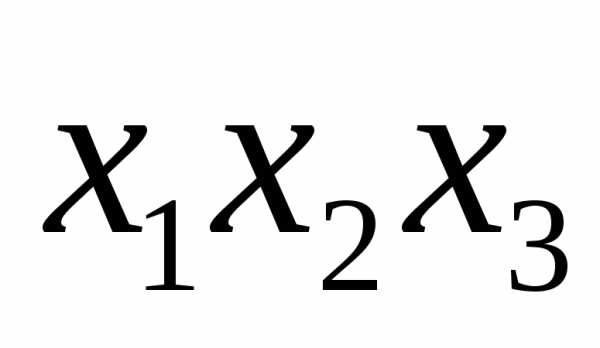 .
.
Воспользовавшись принципом двойственности для булевой алгебры, получим формулу:
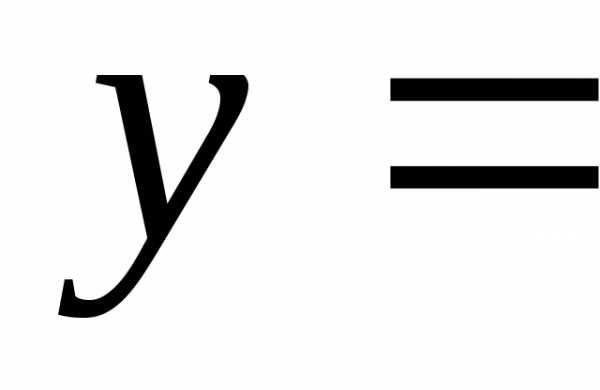 ,
,
которую называют совершенной конъюнктивной нормальной формой (СКНФ) функции .
Определение 4.11. Дизъюнктивную
(конъюнктивную) нормальную форму от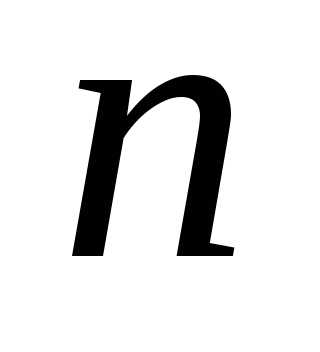 переменных называютсовершенной, если она обладает следующими
свойствами:
переменных называютсовершенной, если она обладает следующими
свойствами:
1) каждая элементарная конъюнкция
(дизъюнкция) содержит все 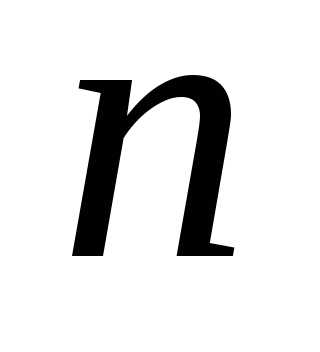 переменных,
переменных,
2) все элементарные конъюнкции различны,
3) ни одна элементарная конъюнкция (дизъюнкция) не содержит одновременно переменную и ее отрицание,
4) ни одна элементарная конъюнкция (дизъюнкция) не содержит одну и ту же переменную дважды.
Свойства 1 – 4 ДНФ (КНФ) называют свойствами совершенства.
Определение 4.12.ДНФ (КНФ), обладающая свойствами совершенства, называютсовершенной дизъюнктивной (конъюнктивной) нормальной формой.
Аббревиатура совершенных форм: СДНФ, СКНФ.
Справедливы утверждения.
Утверждение 1.Любая ненулевая булева функцияединственным образом представима в виде СДНФ от своих аргументов.
Утверждение 2.Любая ненулевая булева функцияединственным образом представима в виде СКНФ от своих аргументов.
Практическое построение СДНФ и СКНФ выполняется так, как показано в приведенном выше примере. Основная задача представления булевой функции формулой состоит в упрощении совершенных форм. Поскольку конъюнктивные формы всегда могут быть получены по принципу двойственности, достаточно рассмотреть этот вопрос для дизъюнктивных форм.
Существует довольно много методов упрощения СДНФ. Все они основаны на основных и дополнительных свойствах операций булевой алгебры. Рассмотрим два из них: карты Карно и таблицы Куайна.
Карты
Карно. Пусть булева функциязадана таблицей. Таблица содержит 2nстрок, в которых перечислены все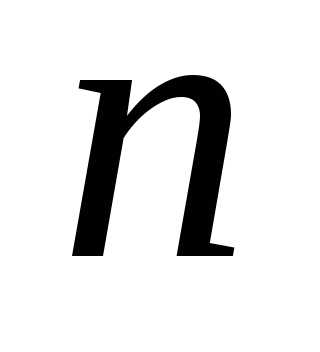 -мерные
двоичные векторы и для каждого вектора
указано значение функции – 0 или 1.
-мерные
двоичные векторы и для каждого вектора
указано значение функции – 0 или 1.
Начертим таблицу (см. рис. 4.2), содержащую 2nклеток так, чтобы две соседние клетки отличались друг от друга значением одной и только одной компоненты вектора. Полученная таблица и называется картой Карно.
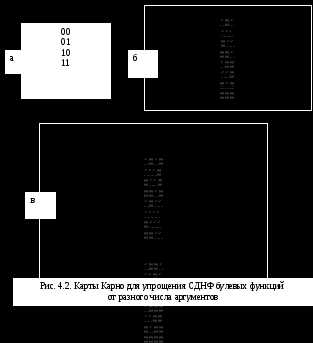
Карты Карно для функций от двух переменных (рис. 4.2а) имеют 4 клетки, для функций от трех переменных – 8 клеток (рис. 4.2б), для функций от четырех переменных 16 клеток (рис. 4.2в) и т.д. На картах отмечено расположение элементарных конъюнкций, которые могут входить в СДНФ рассматриваемой функции.
Рассмотрим примеры использования карт Карно для упрощения СДНФ некоторых функций.
Примеры.
Десятичные номера аргументов | | | |
| Элементарные конъюнкции | 1.
Функция
задана таблицей. Единичный набор
соответствует строкам: (001,010, 011, 101).
Если представить эти двоичные векторы
числами в десятичной записи, получимсписок
единичного набора:
(1,2,3,5). Такой список полностью определяет
функцию СДНФ( Заполним карту Карно, отметив в ней единицами клетки, соответствующие единичному набору. Объединим рядом стоящие отмеченные клетки попарно: 011 – 001, 011 – 010, 101 – 001. Различие в каждой паре составляет только одна координата, именно такие клетки и требуют объединения. По этому признаку клетки 101 и 001, расположенные на противоположных сторонах карты, считаются «рядом стоящими». В СДНФ объединенные клетки соответствуют следующим дизъюнкциям: (011
– 001) (011
– 010) (101
– 001) |
0 | 0 | 0 | 0 | 0 | ||
1 | 0 | 0 | 1 | 1 |
| |
2 | 0 | 1 | 0 | 1 |
| |
3 | 0 | 1 | 1 | 1 |
| |
4 | 1 | 0 | 0 | 0 | ||
5 | 1 | 0 | 1 | 1 |
| |
6 | 1 | 1 | 0 | 0 | ||
7 | 1 | 1 | 1 | 0 | ||
Пользуясь свойствами
коммутативности конъюнкции и дизъюнкции,
дистрибутивностью конъюнкции относительно
дизъюнкции (см. табл. 4.1), законом
исключения третьего: 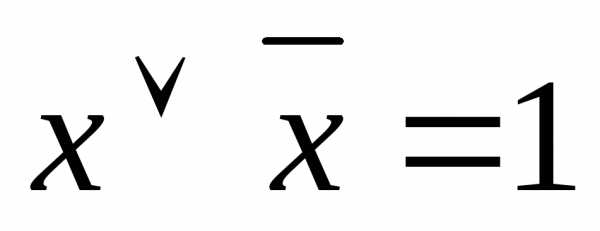 и дополнительным свойством конъюнкции:,
упрощаем выписанные формулы.
и дополнительным свойством конъюнкции:,
упрощаем выписанные формулы.
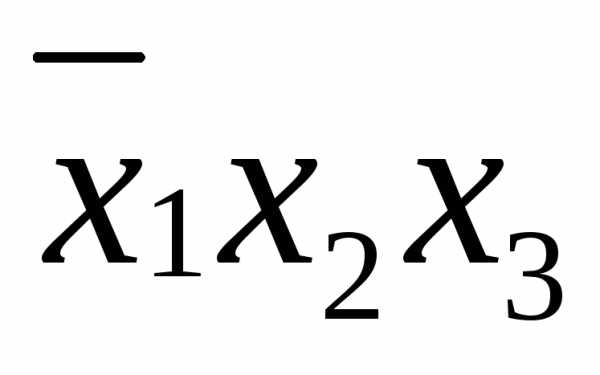
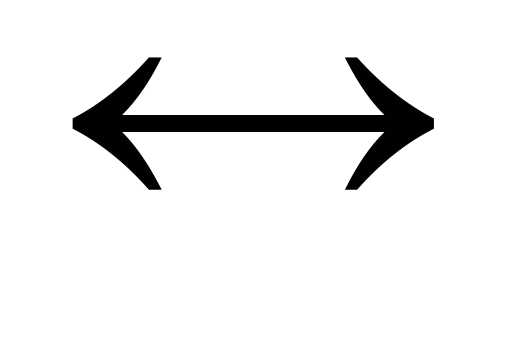
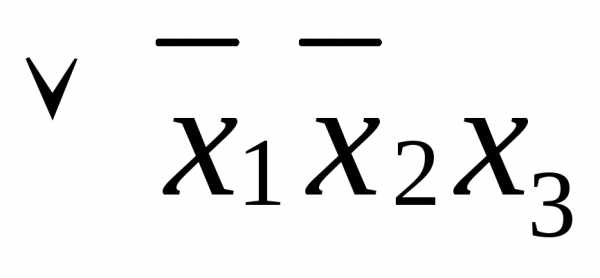 ;
;
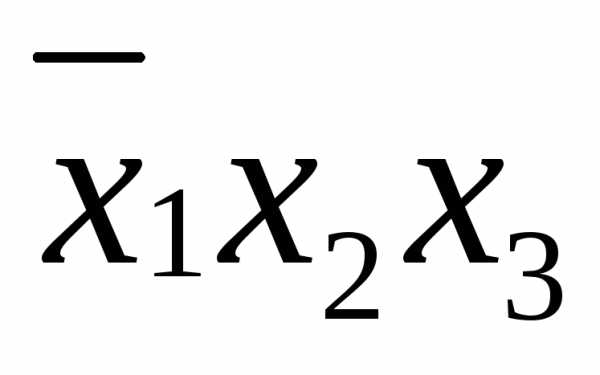
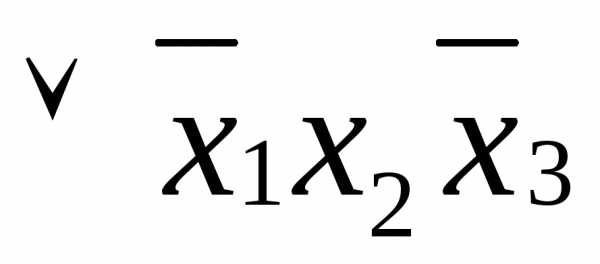 ;
;
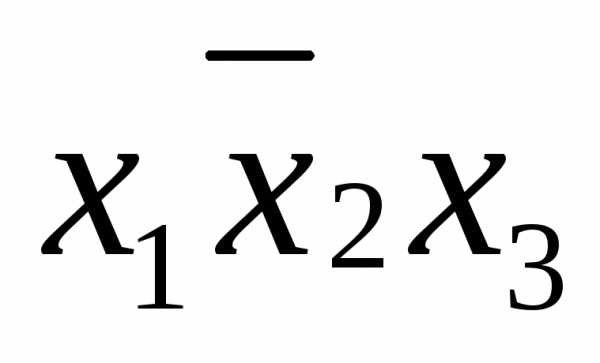
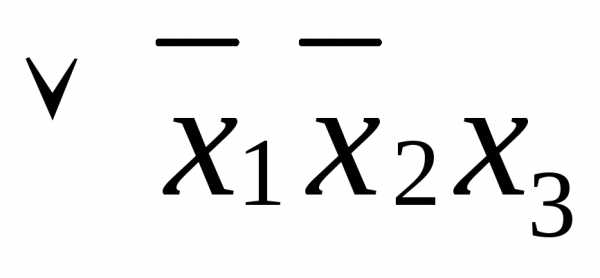 .
.
Применяя к СДНФ свойства ассоциативности и идемпотентности (табл.4.1) и заменяя в ней соответствующие дизъюнкции упрощенными формулами, получаем упрощенную КНФ функции :
СДНФ( )=
)=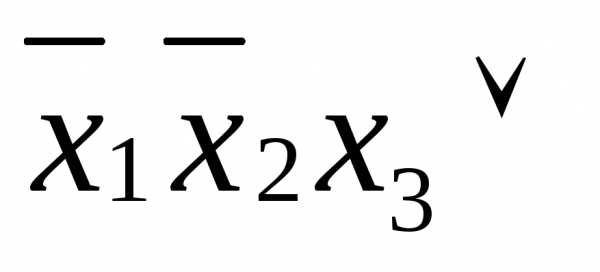
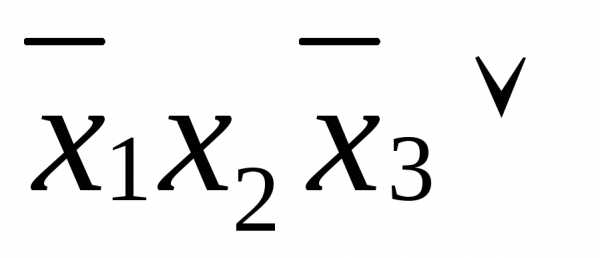
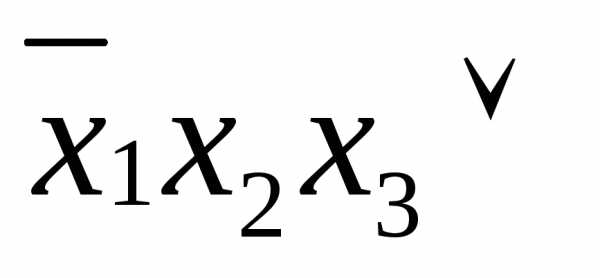
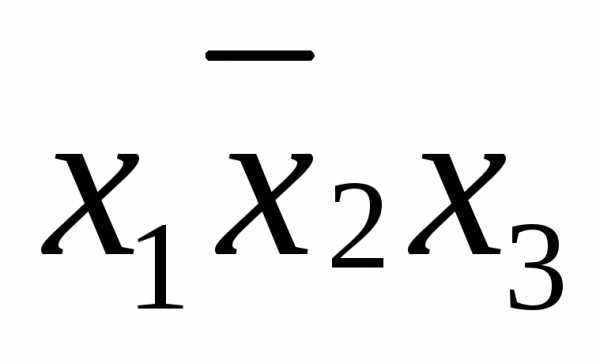 =
=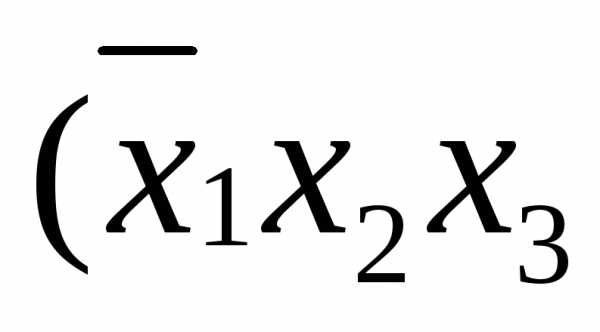
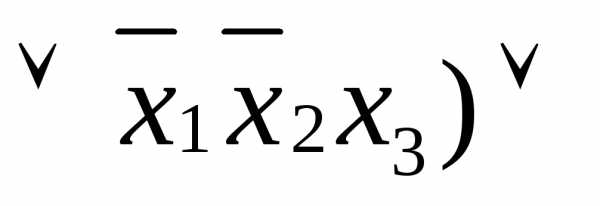
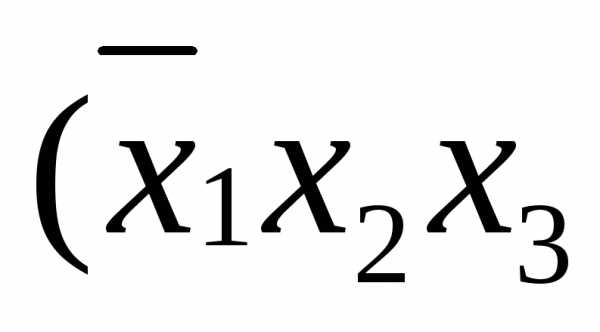
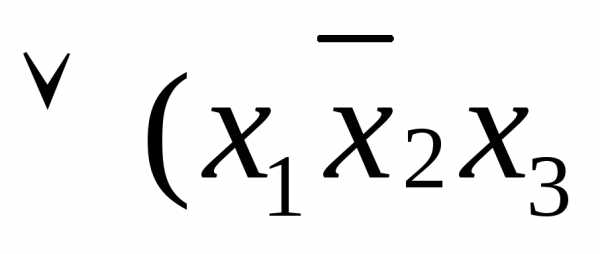
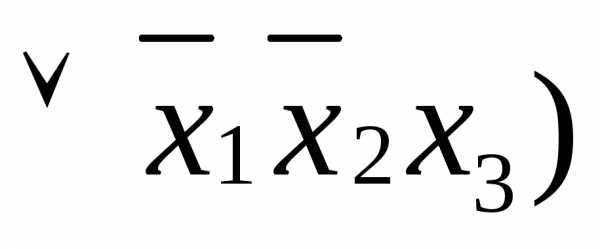
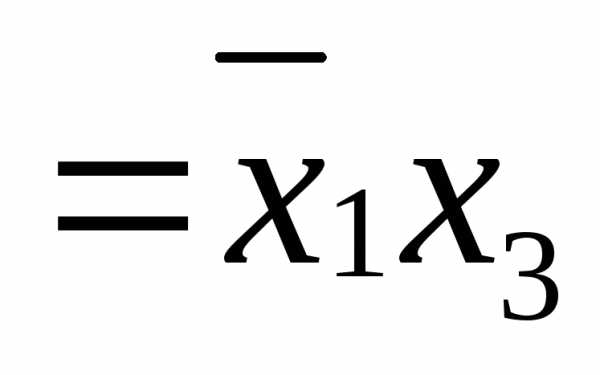
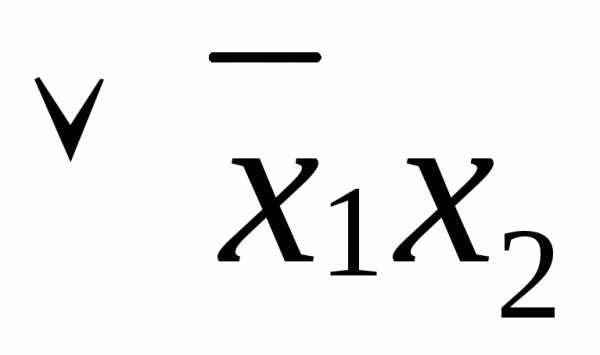
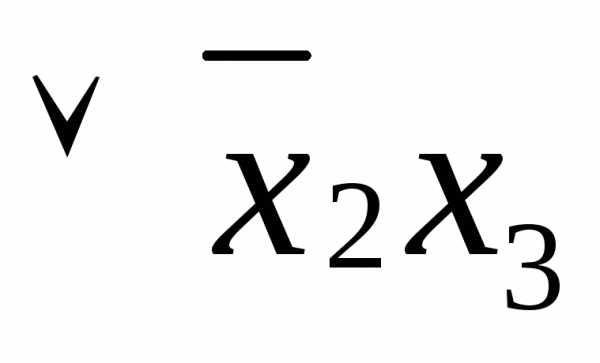 .
.

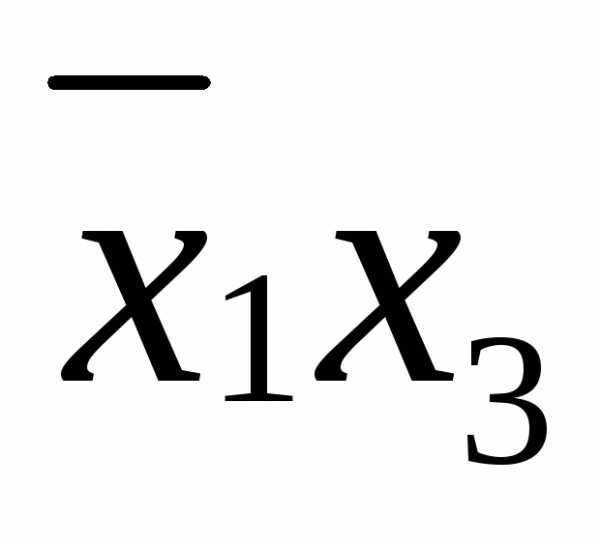
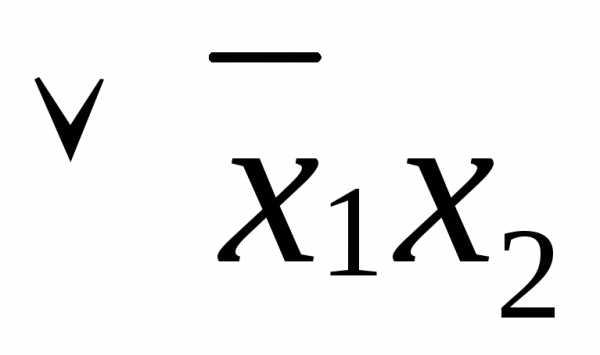
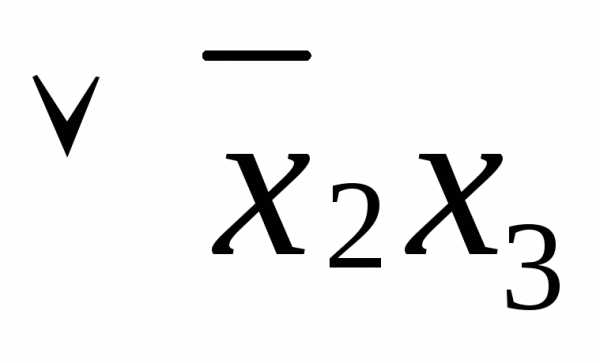 .
.
2 .
Функциязадана списком единичного набора:
(1,3,6,7,8,9,12,13,14). Переведя эти числа в
двоичную систему, отметим в карте Карно
для функции четырех аргументов клетки,
соответствующие единичному значению
функции
.
Функциязадана списком единичного набора:
(1,3,6,7,8,9,12,13,14). Переведя эти числа в
двоичную систему, отметим в карте Карно
для функции четырех аргументов клетки,
соответствующие единичному значению
функции .
.
Объединим пары и четверки рядом стоящих отмеченных клеток. Оставляя в объединенных клетках лишь одинаковые переменные, запишем сокращенную дизъюнктивную форму функции :
.
Таблица Куайна.
Полученная в примере 2 формула может
быть дополнительно сокращена с помощью
таблицы Куайна. Рассмотрим, как это
делается. В таблице Куайна столбцы
соответствуют элементарным конъюнкциям
СДНФ( ),
а строки – конъюнкциям сокращенной
формулы. В каждой строке знаком «*»
отмечены те клетки, в которых элементарная
конъюнкция сокращенной формулыпокрывает конъюнкции СДНФ.
),
а строки – конъюнкциям сокращенной
формулы. В каждой строке знаком «*»
отмечены те клетки, в которых элементарная
конъюнкция сокращенной формулыпокрывает конъюнкции СДНФ.
Конъюнкции сокращенной формулы | Векторы единичного набора (1,3,6,7,8,9,12,13,14) функции и
соответствующие им элементарные
конъюнкции СДНФ( | ||||||||
0001
| 0011
| 0110
| 0111
| 1000
| 1001
| 1100
| 1101
| 1110
| |
1. | * | * | * | * | |||||
2. | * | * | |||||||
3. | * | * | |||||||
4. | * | * | * | ||||||
5. | * | * | |||||||
6. | * | * | |||||||
Формальным признаком покрытия является
вхождение в состав элементарной
конъюнкции СДНФ соответствующей
конъюнкции сокращенной формулы.
Например, 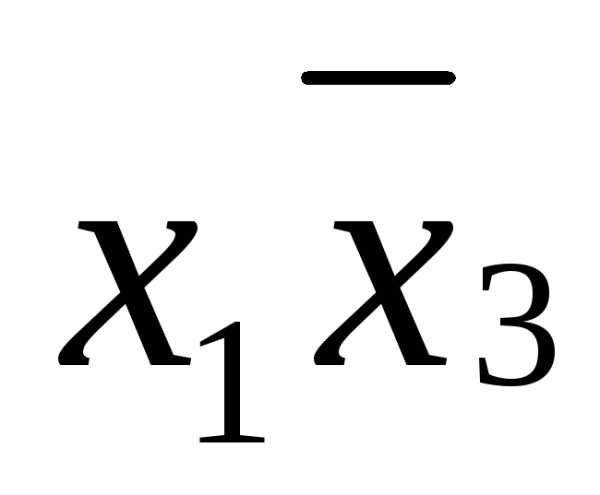 покрывает
покрывает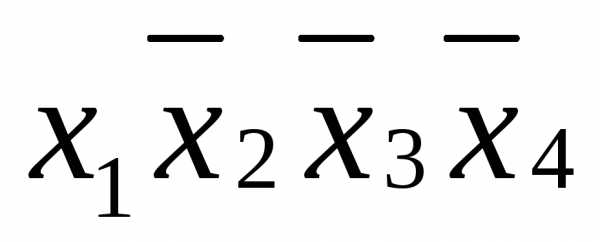 ,
,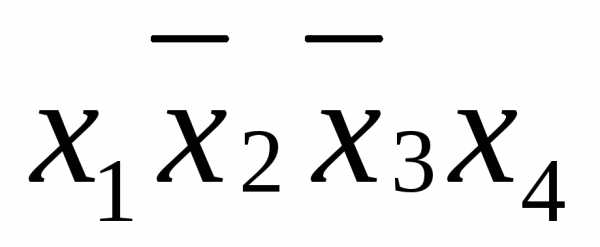 ,
,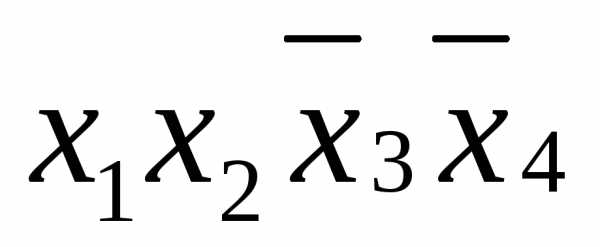 ,
, ,
так как входит в каждую из этих конъюнкций.
,
так как входит в каждую из этих конъюнкций.
Смысл покрытия состоит в том, что
конъюнкция сокращенной формулы не
меньше элементарных конъюнкций СДНФ,
которые она покрывает. В самом деле, из
выполнения равенства: 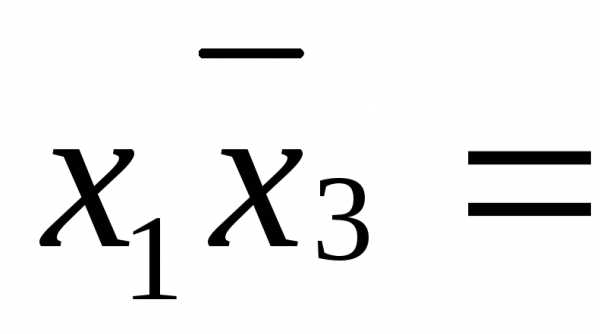
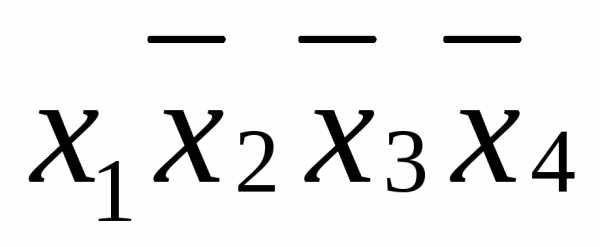

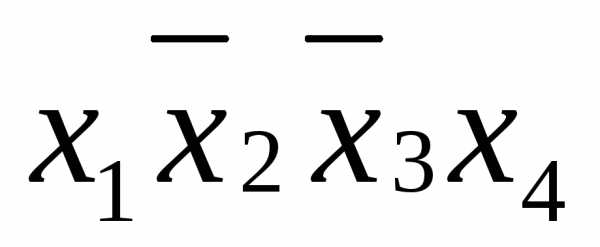

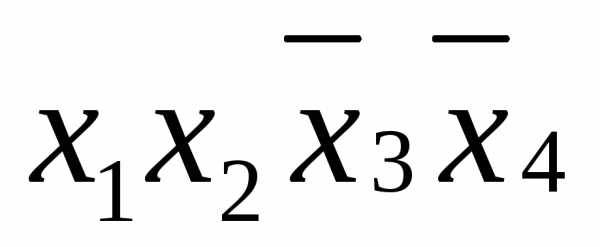

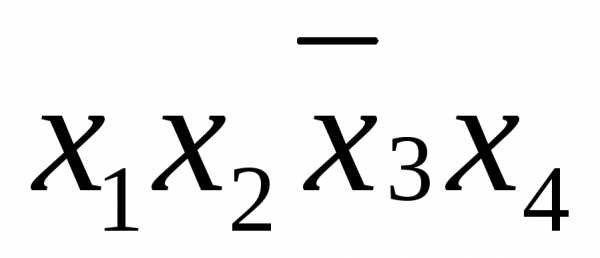 ,
в силу свойства порядка операций булевой
алгебры (см. табл. 4.1), оказываются
справедливыми неравенства:
,
в силу свойства порядка операций булевой
алгебры (см. табл. 4.1), оказываются
справедливыми неравенства: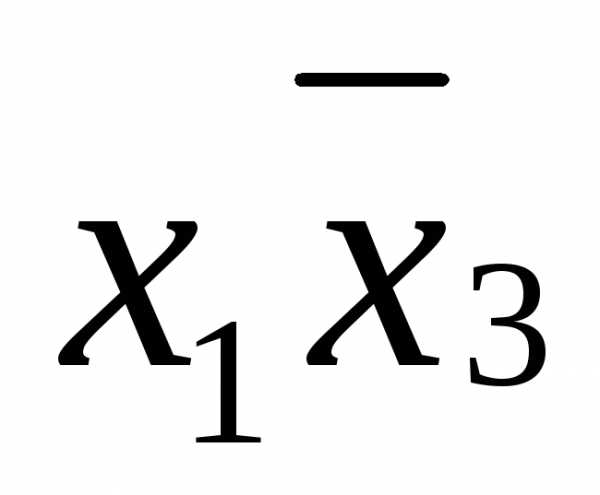 ;
;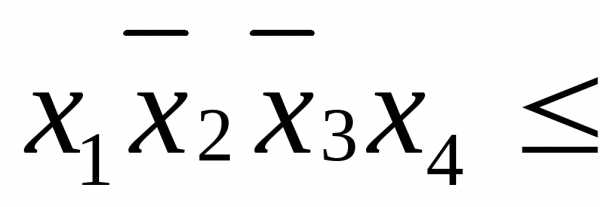
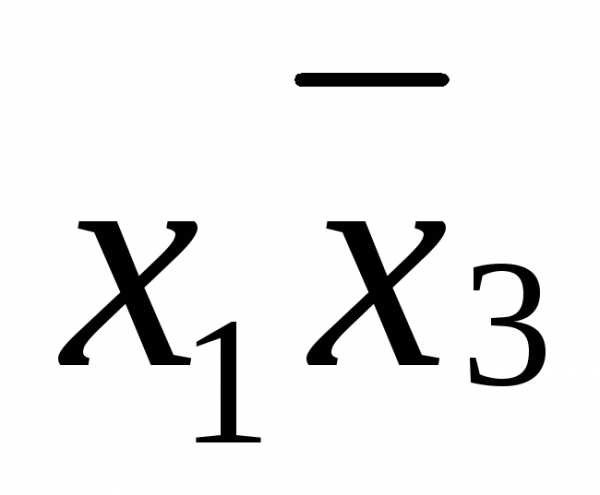 ,
,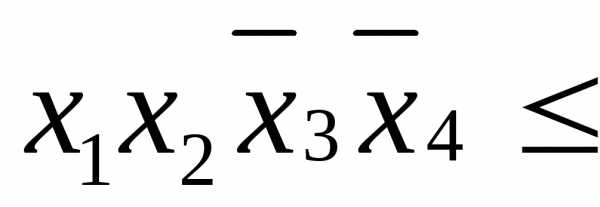
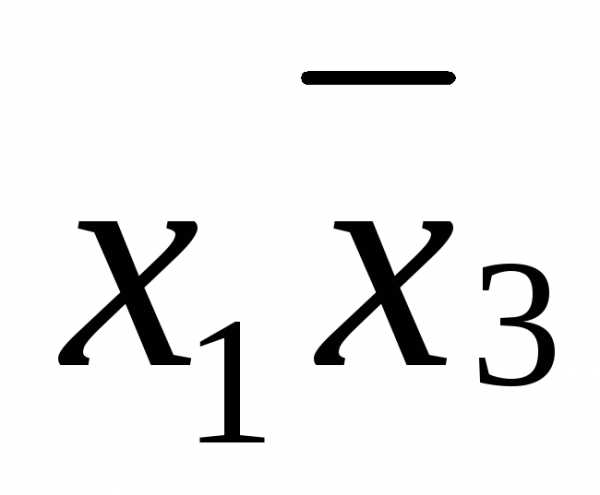 ,
,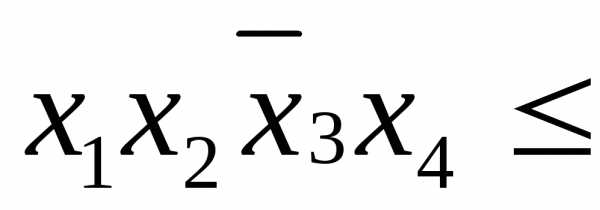
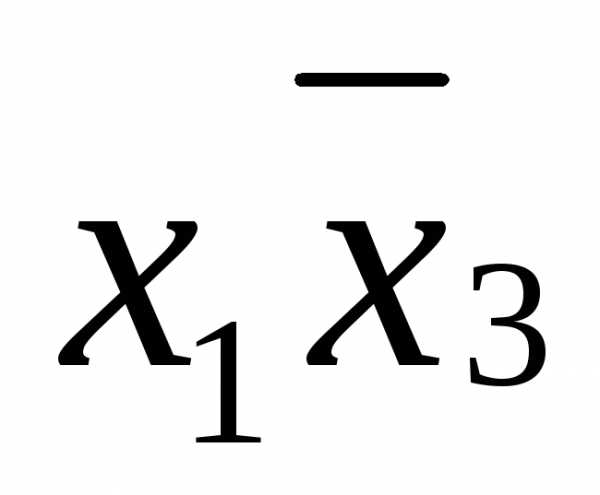 .
.
Отметив покрытия в строках таблицы,
выделяем повторяющиеся знаки покрытий
в столбцах (в таблице отмечено цветом).
Если в строке все знаки покрытий
оказываются выделенными, значит эта
строка лишняя, и соответствующая этой
строке конъюнкция может быть удалена
из сокращенной формулы. Например, лишней
оказывается конъюнкция 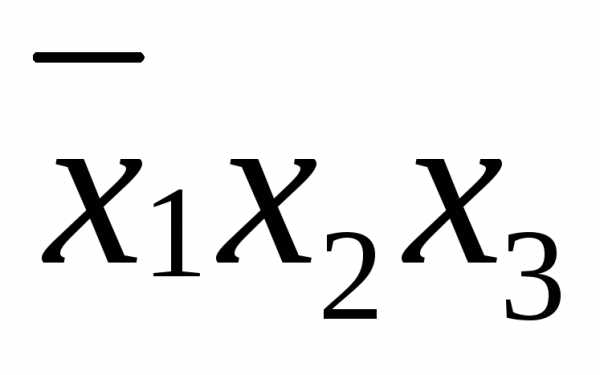 ,
поскольку
,
поскольку и
и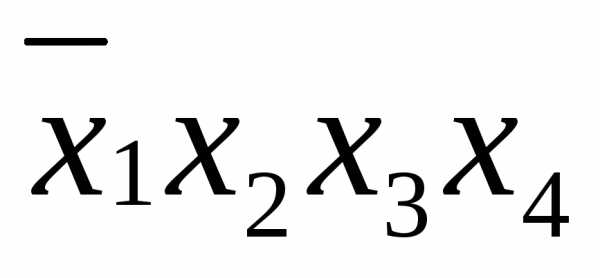 покрываются второй и четвертой строками.
Лишней оказывается и
покрываются второй и четвертой строками.
Лишней оказывается и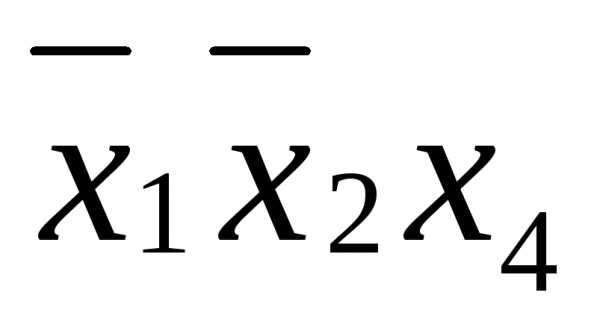 ,
так как
,
так как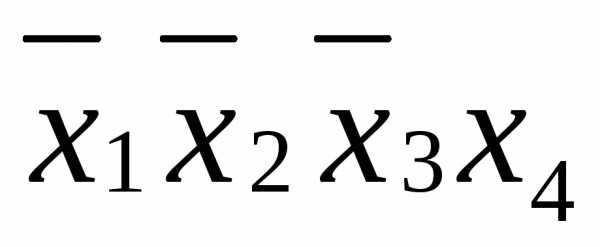 и
и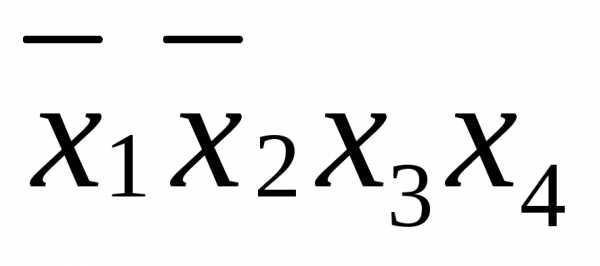 покрываются четвертой и шестой строками.
После вычеркивания лишних конъюнкций,
сокращенная формула принимает вид:
покрываются четвертой и шестой строками.
После вычеркивания лишних конъюнкций,
сокращенная формула принимает вид:
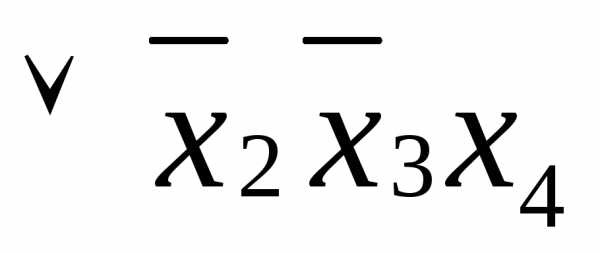 .
.
67
studfiles.net
Дискретная математика, комбинаторика, теория чисел
Доброго времени суток.Прошу совета — верно ли я всё делаю.
Имею задание по Схемотехнике, составить по таблице истинности СДНФ и СКНФ и упростить их.
В дальнейшем по этому необходимо строить цифровые схемы, поэтому желательно не использовать «Исключающее ИЛИ»/»Сложение по модулю 2».
Таблица истинности:
1. Составим СДНФ. Берем те строки, где функция равна 1 и пишем в виде дизъюнкции полных совершенных конъюнкций (тобишь в виде сложения произведений).
СДНФ:
2. Упростим СДНФ.
равно
Далее
равно
И наконец
равно
Проверяем программой Logisim:
Всё правильно, всё совпало.
3. Составим СКНФ. Берем те строки, где функция равна 0 и пишем в виде произведения сумм, инвертируя переменные. Если 0 — то обычная, если 1 то отрицание.
СКНФ:
4. Упростим СКНФ
равно
и это равно
Где ошибка? Мне сказали, что они должны сойтись, но они не сходятся. В получении и упрощении СДНФ я уверен, в получении СКФН тоже, а вот в упрощении СКНФ — большие сомнения.
Карты Карно не изучались.
Для проверки использую программу Logisim (построение цифровых схем).
Судя по всему, она считает СДНФ и СКНФ по Карно.
Но как добиться того же чисто аналитически? Используя формулы.
СДНФ совпало полностью, а вот СКНФ частично — только первые две скобки совпали.
Как аналитически получить СКНФ, как в программе Logisim? и должны ли СДНФ и СКНФ после упрощения «совпасть»?
Или я может чего не так понял? Как бы вы получили и упростили СКНФ?
dxdy.ru
СДНФ. Теорема о представлении в виде СДНФ. Построение СДНФ по таблице / Алгебра логики [Ф.Г. Кораблёв] / 3dstroyproekt.ru
ДНФ
Простой конъюнкцией или конъюнктом называется конъюнкция одной или нескольких переменных или их отрицаний, причём каждая переменная встречается не более одного раза.
Простая конъюнкция
- полная, если в неё каждая переменная { или её отрицание } входит ровно 1 раз;
- монотонная, если она не содержит отрицаний переменных.
ДНФ { Дизъюнктивная Нормальная Форма } — нормальная форма, в которой булева функция имеет вид дизъюнкции нескольких простых конъюнктов.
Пример ДНФ: $f(x,y,z) = (x \land y) \lor (y \land \neg { z } )$
СДНФ
СДНФ { Совершенная Дизъюнктивная Нормальная Форма } — это такая ДНФ, которая удовлетворяет условиям:
- в ней нет одинаковых простых конъюнкций
- каждая простая конъюнкция полная
Пример СДНФ: $f(x,y,z) = (x \land \neg { y } \land z) \lor (x \land y \land \neg { z } )$
Теорема: Для любой булевой функции $f(\vec { x } )$, не равной тождественному нулю (), существует СДНФ, ее задающая.
Доказательство:
Для любой булевой функции выполняется следующее соотношение, называемое разложением Шеннона.
$f(\vec { x } ) = \neg x_i \wedge f(x_1, \dots ,x_ { i-1 } ,0,x_ { i+1 } , \dots ,x_n) \vee x_i \wedge f(x_1, \dots ,x_ { i-1 } ,1,x_ { i+1 } , \dots ,x_n)$
Данное соотношение легко проверить подстановкой всевозможных значений $x_i$ { $0$ и $1$ } . Эта формула позволяет выносить $x_i$ за знак функции. Последовательно вынося $x_1$, $x_2$,.., $x_n$ за знак $f(\vec { x } )$, получаем следующую формулу :
$ f(\vec { x } ) = \neg x_1 \wedge \neg x_2 \wedge …\wedge \neg x_ { n-1 } \wedge \neg x_n \wedge f(0,0,…,0,0)~\vee~$
$\neg x_1 \wedge \neg x_2 \wedge … \wedge \neg x_ { n-1 } \wedge x_n \wedge f(0,0,…,0,1) ~\vee~ $ $\dots $ $~\vee~ x_1 \wedge x_2 \wedge … \wedge x_ { n-1 } \wedge \neg x_n \wedge f(1,1,…,1,0) ~\vee~ $ $x_1 \wedge x_2 \wedge … \wedge x_ { n-1 } \wedge x_n \wedge f(1,1,…,1) $
Так как применение данного соотношения к каждой из переменных увеличивает количество конъюнктов в два раза, то для функции от $n$ переменных мы имеем { { { $2^ { n } $ } } } конъюнктов. Каждый из них соответствует значению функции на одном из { { { $2^ { n } $ } } } возможных наборов значений $n$ переменных. Если на некотором наборе $f(\vec { x } )=0$, то весь соответствующий конъюнкт также равен нулю и из представления данной функции его можно исключить. Если же $ f(\vec { x } )=1$, то в соответствующем конъюнкте само значение функции можно опустить. В результате для произвольной функции была построена СДНФ.
Алгоритм построения СДНФ по таблице истинности
- В таблице истинности отмечаем те наборы переменных, на которых значение функции равно 1.
- Для каждого отмеченного набора записываем конъюнкцию всех переменных по следующему правилу: если значение некоторой переменной есть 1, то в конъюнкцию включаем саму переменную, иначе ее отрицание.
- Все полученные конъюнкции связываем операциями дизъюнкции.
Пример построения СДНФ для медианы
В таблице истинности отмечаем те наборы переменных, на которых значение функции равно 1.
x y z $\langle x,y,z \rangle$ 0 0 0 0 0 0 1 0 0 1 1 0 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 1 - Для каждого отмеченного набора записываем конъюнкцию всех переменных по следующему правилу: если значение некоторой переменной есть 1, то в конъюнкцию включаем саму переменную, иначе ее отрицание.
x y z $ \langle x,y,z \rangle $ 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 $(\neg { x } \land y \land z)$ 1 0 0 0 1 0 1 1 $(x \land \neg { y } \land z)$ 1 1 0 1 $(x \land y \land \neg { z } )$ 1 1 1 1 $(x \land y \land z)$ - Все полученные конъюнкции связываем операциями дизъюнкции. $ \langle x,y,z \rangle = (x \land y \land z) \lor (\neg { x } \land y \land z) \lor (x \land \neg { y } \land z) \lor (x \land y \land \neg { z } )$
Примеры СДНФ для некоторых функций
Стрелка Пирса: $x \downarrow y = (\neg { x } \land \neg { y } )$
Исключающее или: $x \oplus y \oplus z = (\overline { x } \land \overline { y } \land z) \lor (\overline { x } \land y \land \overline { z } ) \lor (x \land \overline { y } \land \overline { z } ) \lor (x \land y \land z)$
Совершенной дизъюнктивной нормальной формой формулы $A(x_1,x_2,…,x_n)$ называется ДНФ, обладающая следующими свойствами:
а } в ней нет одинаковых дизъюнктивных элементов;
б } ни одна элементарная конъюнкция не содержит двух одинаковых высказываний;
в } ни какая элементарная конъюнкция не содержит высказывание вместе с ее отрицанием;
г } в каждой элементарной конъюнкции содержится либо $X_i$, либо $\overline { X } _i$, где $i = 1, n$.
Условие а } – г } являются необходимыми и достаточными для того, чтобы ДНФ стала СДНФ. В свою очередь эти условия дают возможность составить алгоритм получения СДНФ из ДНФ:
1) если какая-нибудь элементарная конъюнкция не содержит высказывание $X_i$, то заменим выражением $B\wedge (X_i\vee \overline { X } _i) \equiv (B\wedge X_i)\vee (B\wedge \overline { X } _i)$;
2) если в полученном выражении окажутся одинаковые элементарные конъюнкции, то лишние опускаются;
3) если в некоторых элементарных конъюнкциях окажутся одинаковые высказывания, то лишние опускаются;
4) удаляем элементарные конъюнкции, в которых содержатся высказывания вместе с их отрицанием.
Если все элементарные конъюнкции окажутся таковыми, т.е. вся формула будет ложной, то она не будет иметь СДНФ.
Если все элементарные конъюнкции окажутся таковыми, т.е. вся формула будет ложной, то она не будет иметь СДНФ.
Формула называется дизъюнктивной нормальной формой { ДНФ } , если она является дизъюнкцией неповторяющихся элементарных конъюнкций. ДНФ записываются в виде: $A_1\vee A_2\vee …\vee A_n$ , где каждое $A_n$ — элементарная конъюнкция.
Формула $A$ от $k$ переменных называется совершенной дизъюнктивной нормальной формой { СДНФ } , если:
$A$ является ДНФ, в которой каждая элементарная конъюнкция есть конъюнкция $k$ переменных $x_1,x_2,…,x_k$, причем на $i$-м месте этой конъюнкции стоит либо переменная $x_i$ либо ее отрицание;
- Все элементарные конъюнкции в такой ДНФ попарно различны.
Например: $A = x_1 \wedge$ НЕ $x_2 \vee x_1 \wedge x_2$
Совершенная дизъюнктивная нормальная форма представляет собой формулу, построенную по строго определенным правилам с точностью до порядка следования элементарных конъюнкций { дизъюнктивных членов } в ней.
Она является примером однозначного представления булевой функции в виде формульной { алгебраической } записи.
Теорема о СДНФ: Пусть $f(x_1 x_2, …, x_n)$ – булева функция от n переменных, не равная тождественно нулю. Тогда существует совершенная дизъюнктивная нормальная форма, выражающая функцию $f$.
Алгоритм построения СДНФ по таблице истинности:
- В таблице истинности отмечаем наборы переменных, на которых значение функции $f = 1$.
- Записываем для каждого отмеченного набора конъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 1, то в конъюнкцию включаем саму переменную, в противном случае – ее отрицание.
- Все полученные конъюнкции связываем операциями дизъюнкции.
3dstroyproekt.ru
Дискретная математика, комбинаторика, теория чисел
Доброго времени суток.Прошу совета — верно ли я всё делаю.
Имею задание по Схемотехнике, составить по таблице истинности СДНФ и СКНФ и упростить их.
В дальнейшем по этому необходимо строить цифровые схемы, поэтому желательно не использовать «Исключающее ИЛИ»/»Сложение по модулю 2».
Таблица истинности:
1. Составим СДНФ. Берем те строки, где функция равна 1 и пишем в виде дизъюнкции полных совершенных конъюнкций (тобишь в виде сложения произведений).
СДНФ:
2. Упростим СДНФ.
равно
Далее
равно
И наконец
равно
Проверяем программой Logisim:
Всё правильно, всё совпало.
3. Составим СКНФ. Берем те строки, где функция равна 0 и пишем в виде произведения сумм, инвертируя переменные. Если 0 — то обычная, если 1 то отрицание.
СКНФ:
4. Упростим СКНФ
равно
и это равно
Где ошибка? Мне сказали, что они должны сойтись, но они не сходятся. В получении и упрощении СДНФ я уверен, в получении СКФН тоже, а вот в упрощении СКНФ — большие сомнения.
Карты Карно не изучались.
Для проверки использую программу Logisim (построение цифровых схем).
Судя по всему, она считает СДНФ и СКНФ по Карно.
Но как добиться того же чисто аналитически? Используя формулы.
СДНФ совпало полностью, а вот СКНФ частично — только первые две скобки совпали.
Как аналитически получить СКНФ, как в программе Logisim? и должны ли СДНФ и СКНФ после упрощения «совпасть»?
Или я может чего не так понял? Как бы вы получили и упростили СКНФ?
dxdy.ru
скнф и сднф — что это?
СКНФ — совершенно конъюнктивная нормальная формаСДНФ — совершенная дизъюнктивная нормальная форма
Что значит нормальна форма:
Нормальная форма логической формулы не содержит знаков импликации, эквиваленции и отрицания неэлементарных формул.
Существует два вида нормальной формы: конъюнктивная нормальная форма, т. е. конъюнкция нескольких дизъюнкций (КНФ) и дизъюнктивная нормальная форма, т. е. дизъюнкция нескольких конъюнкций (ДНФ), пример:
КНФ: \(\left (x\vee \bar{y}\vee z \right )\wedge \left (y\vee z \right )\)
ДНФ: \( \left (x\wedge \bar{y}\wedge z \right )\vee \left (y\wedge z \right )\)
Совершенно конъюнктивная НФ — конъюнкция дизъюнкций, причём в каждой дизъюнкции (в каждой скобке) присутствуют все переменные, входящие в формулу, либо их отрицание, нет одинаковых дизъюнкций, в каждой дизъюнкции нет одинаковых слагаемых, пример:
СКНФ: \( (x\vee y\vee \bar{z})\wedge ( x\vee \bar{y}\vee z )\)
Совершенно дизьюнктивная НФ — дизьюнкция коньюнкций , причём в каждой коньюнкции (в каждой скобке) присутствуют все переменные, входящие в формулу, либо их отрицание, нет одинаковых коньюнкций, в каждой коньюнкции нет одинаковых слагаемых, пример:
СДНФ: \( ( x\wedge y\wedge \bar{z}) \vee ( x\wedge \bar{y} \wedge z ) \)
Взаимозаменяемые обозначения:
логика | булева алгебра |
∨ | + |
∧ | ∙ |
Правила построения СДНФ и СКНФ по таблице истинности
Пример: Восстановите логическую функцию по ее таблице истинности:
x | y | z | F |
0 | 0 | 0 | 1 |
0 | 0 | 1 | 1 |
0 | 1 | 0 | 0 |
0 | 1 | 1 | 0 |
1 | 0 | 0 | 1 |
1 | 0 | 1 | 1 |
1 | 1 | 0 | 0 |
1 | 1 | 1 | 1 |
РЕШЕНИЕ
СДНФ составляется на основе таблицы истинности по следующему правилу:
для каждого набора переменных, при котором функция равна 1, записывается произведение, в котором с отрицанием берутся переменные, имеющие значение «0».
x | y | z | F |
0 | 0 | 0 | 1 |
0 | 0 | 1 | 1 |
1 | 0 | 0 | 1 |
1 | 0 | 1 | 1 |
1 | 1 | 1 | 1 |
Получаем СДНФ:
\(F(x,y,z)=\bar{x}\bar{y}\bar{z}+\bar{x}\bar{y} z+x\bar{y} \bar{z}+x\bar{y}z+xyz\)
СКНФ составляется на основе таблицы истинности по правилу:
для каждого набора переменных, при котором функция равна 0, записывается сумма, в которой с отрицанием берутся переменные, имеющие значение 1.
x | y | z | F |
0 | 1 | 0 | 0 |
0 | 1 | 1 | 0 |
1 | 1 | 0 | 0 |
www.reshim.su
Минимизация скнф сднф
Часть 11. Минимизация СКНФ, СДНФ.
Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ, является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:
Аналогично для КНФ:
Возможность поглощения следует из очевидных равенств
Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск термов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей.
Карты Карно.
Как известно, булевы функции N переменных, представленные в виде СДНФ или СКНФ, могут иметь в своём составе 2N различных термов. Все эти члены составляют некоторую структуру, топологически эквивалентную N–мерному кубу, причём любые два терма, соединённые ребром, пригодны для склейки и поглощения.
На рисунке изображена простая таблица истинности для функции из двух переменных, соответствующий этой таблице 2-мерный куб (квадрат), а также 2-мерный куб с обозначением членов СДНФ и эквивалентная таблица для группировки термов:
Часть 12. Полином Жегалкина.
Метод неопределенных коэффициентов
Построение полинома Жегалкина
Существует несколько способов построения полинома Жегалкина.
[править]
По таблице истинности
Пусть для функции задана таблица истинности. Запишем сначала данную функцию в виде полинома Жегалкина с неопределёнными коэффициентами. Затем по очереди подставляем всевозможные наборы в порядке увеличения количества единиц и находим коэффициенты с учётом того, что, а. За каждую подстановку находим только один коэффициент.
Пример: Дана функция и её таблица истинности:
0 | 0 | 0 | 0 | 0 |
0 | 0 | 0 | 1 | 0 |
0 | 0 | 1 | 0 | 0 |
0 | 0 | 1 | 1 | 0 |
0 | 1 | 0 | 0 | 0 |
0 | 1 | 0 | 1 | 0 |
0 | 1 | 1 | 0 | 1 |
0 | 1 | 1 | 1 | 0 |
1 | 0 | 0 | 0 | 1 |
1 | 0 | 0 | 1 | 0 |
1 | 0 | 1 | 0 | 0 |
1 | 0 | 1 | 1 | 1 |
1 | 1 | 0 | 0 | 1 |
1 | 1 | 0 | 1 | 0 |
1 | 1 | 1 | 0 | 1 |
1 | 1 | 1 | 1 | 0 |
Построим для неё полином Жегалкина:
Так как , то. Далее подставляем все остальные наборы в порядке возрастания числа единиц, подставляя вновь полученные значения в следующие формулы:
Таким образом, полином Жегалкина выглядит так:
Преобразование дизъюнктивной нормальной формы
Этот способ основан на том, что . Если функция задана в виде ДНФ, то можно сначала убрать дизъюнкцию, используя правило Де-Моргана, а все отрицания заменить прибавлением единицы по модулю два, после чего раскрыть скобки по обычным правилам, при этом учитывая, что четное число одинаковых слагаемых равно нулю (так как), а нечетное число одинаковых слагаемых равно одному такому слагаемому. Либо же можно заменить дизъюнкцию по следующему правилу:
.
Если функция задана в СДНФ, то так как при любых значениях входных переменных в единицу обращается не более одного члена выражения, то достаточно просто заменить все дизъюнкции исключающим ИЛИ.
Пример: Дана функция в ДНФ , построим полином Жегалкина.
Запишем функцию так:
;
Сгруппируем слагаемые и воспользуемся преобразованием (1):
Воспользуемся свойствами конъюнкции и, а также тем, что, и упростим выражение:
Ещё раз воспользуемся преобразованием (1):
Раскроем скобку по алгебраическим правилам:
Снова воспользуемся свойствами конъюнкции и исключающего ИЛИ:
Заменим отрицание на прибавление :
Раскроем скобки:
Выкинем парные слагаемые и получим окончательную формулу:
studfiles.net
3. Днф, сднф, кнф, скнф
Простой конъюнкцией называется конъюнкция одной или нескольких переменных, при этом каждая переменная встречается не более одного раза (либо сама, либо ее отрицание).
Например, является простой конъюнкцией,
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция простых конъюнкций.
Например, выражение является ДНФ.
Совершенной дизъюнктивной нормальной формой (СДНФ) называется такая дизъюнктивная нормальная форма, у которой в каждую конъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одном и том же порядке.
Например, выражение является ДНФ, но не СДНФ. Выражениеявляется СДНФ.
Аналогичные определения (с заменой конъюнкции на дизъюнкцию и наоборот) верны для КНФ и СКНФ. Приведем точные формулировки.
Простой дизъюнкцией называется дизъюнкция одной или нескольких переменных, при этом каждая переменная входит не более одного раза (либо сама, либо ее отрицание).Например, выражение – простая дизъюнкция,
Конъюнктивной нормальной формой (КНФ) называется конъюнкция простых дизъюнкций (например выражение – КНФ).
Совершенной конъюнктивной нормальной формой (СКНФ) называется такая КНФ, у которой в каждую простую дизъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одинаковом порядке.
Например, выражение является СКНФ.
Приведем алгоритмы переходов от одной формы к другой. Естественно, что в конкретных случаях (при определенном творческом подходе) применение алгоритмов бывает более трудоемким, чем простые преобразования, использующие конкретный вид данной формы:
а) переход от ДНФ к КНФ
Алгоритм этого перехода следующий: ставим над ДНФ два отрицания и с помощью правил де Моргана (не трогая верхнее отрицание) приводим отрицание ДНФ снова к ДНФ. При этом приходится раскрывать скобки с использованием правила поглощения (или правила Блейка). Отрицание (верхнее) полученной ДНФ (снова по правилу де Моргана) сразу дает нам КНФ:
Заметим, что КНФ можно получить и из первоначального выражения, если вынести у за скобки;
б) переход от КНФ к ДНФ
Этот переход осуществляется простым раскрытием скобок (при этом опять-таки используется правило поглощения)
Таким образом, получили ДНФ.
Обратный переход (от СДНФ к ДНФ) связан с проблемой минимизации ДНФ. Подробнее об этом будет рассказано в разд. 5, здесь же мы покажем, как упростить ДНФ (или СДНФ) по правилу Блейка. Такая ДНФ называется сокращенной ДНФ;
в) сокращение ДНФ (или СДНФ) по правилу Блейка
Применение этого правила состоит из двух частей:
— если среди дизъюнктных слагаемых в ДНФ имеются слагаемые , то ко всей дизъюнкции добавляем слагаемоеК1К2. Проделываем эту операцию несколько раз (можно последовательно, можно одновременно) для всех возможных пар слагаемых, а затем, применяем обычное поглощение;
— если добавляемое слагаемое уже содержалось в ДНФ, то его можно отбросить совсем, например,
или
Разумеется, сокращенная ДНФ не определяется единственным образом, но все они содержат одинаковое число букв (например, имеется ДНФ , после применения к ней правила Блейка можно прийти к ДНФ, равносильной данной):
в) переход от ДНФ к СДНФ
Если в какой-то простой конъюнкции недостает переменной, например, z, вставляем в нее выражение ,после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем). Например:
г) переход от КНФ к СКНФ
Этот переход осуществляется способом, аналогичным предыдущему: если в простой дизъюнкции не хватает какой-то переменной (например, z, то добавляем в нее выражение (это не меняет самой дизъюнкции), после чего раскрываем скобки с использованием распределительного закона):
Таким образом, из КНФ получена СКНФ.
Заметим, что минимальную или сокращенную КНФ обычно получают из соответствующей ДНФ.
studfiles.net


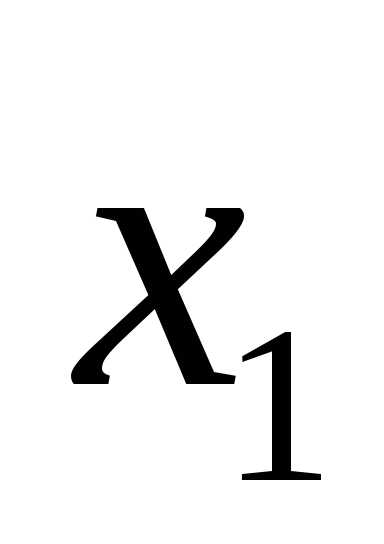
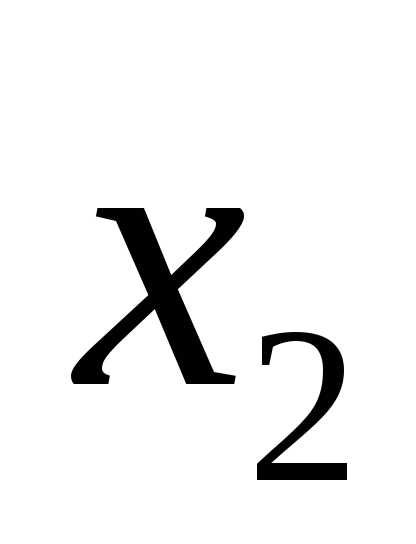
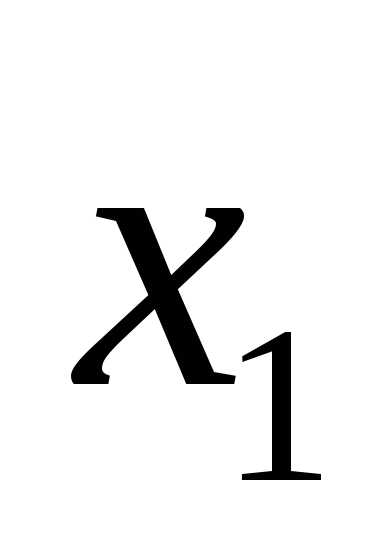
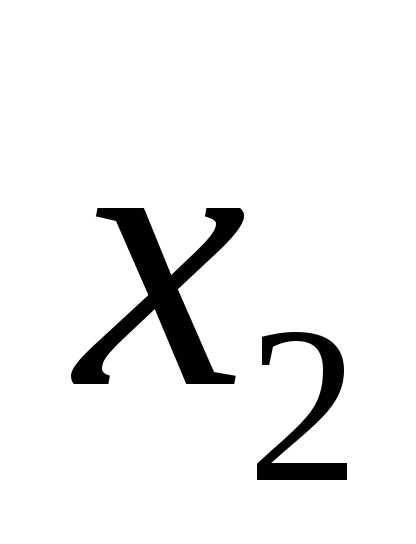
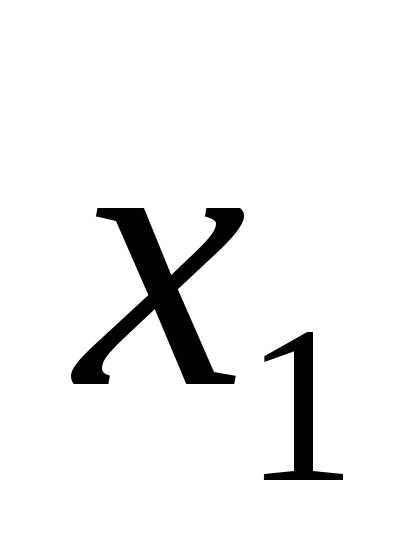
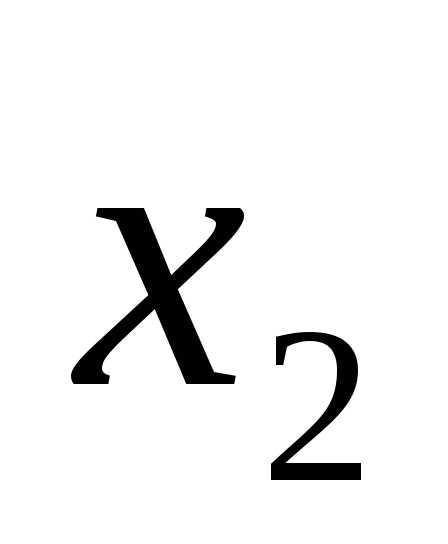
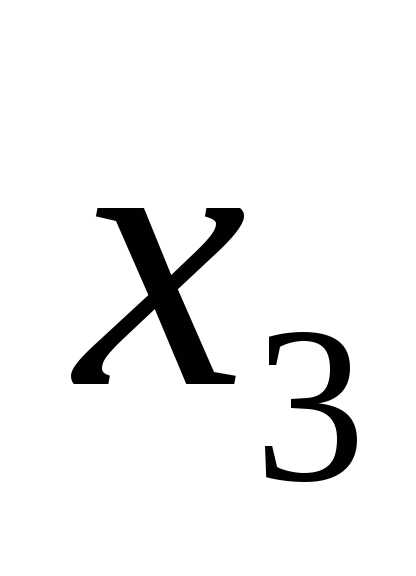

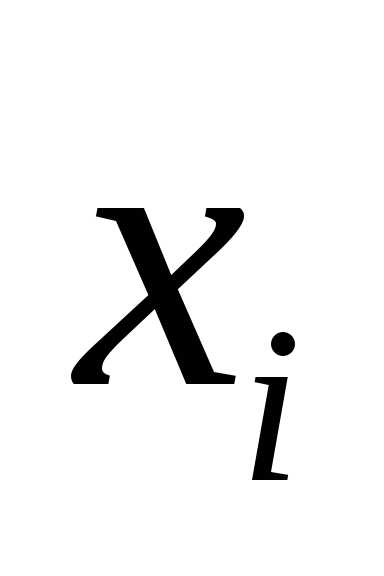 в данной строке представлена единицей,
то в элементарную конъюнкцию включаем
в данной строке представлена единицей,
то в элементарную конъюнкцию включаем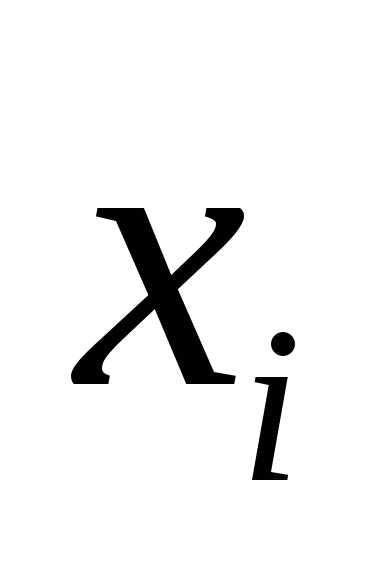 ,
если нулем, то –
,
если нулем, то –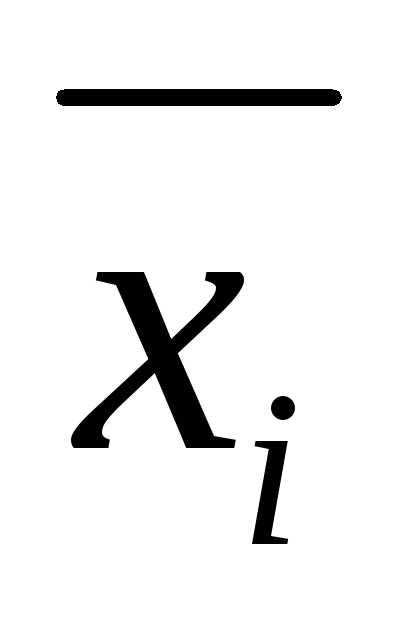 .
.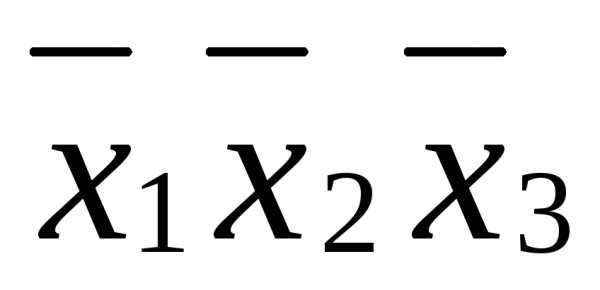

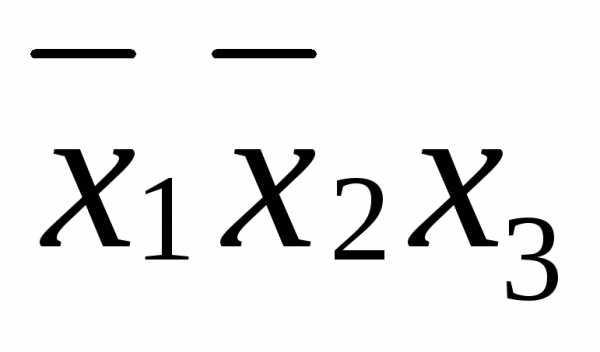

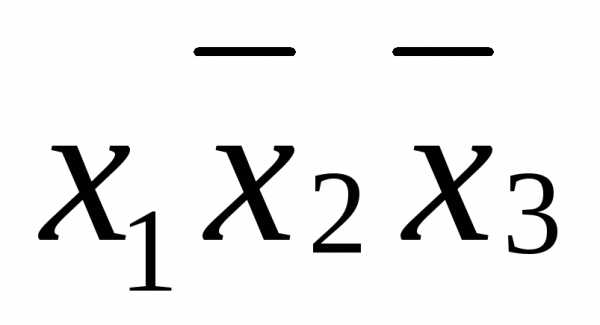

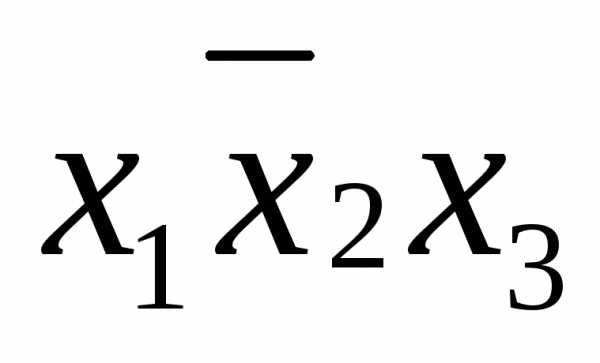

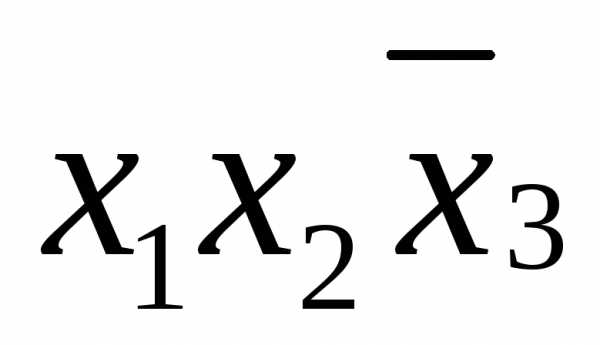 .
.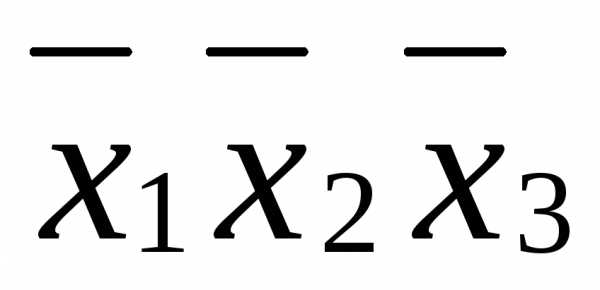
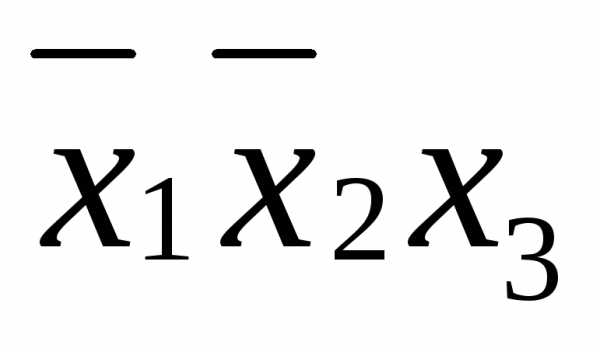
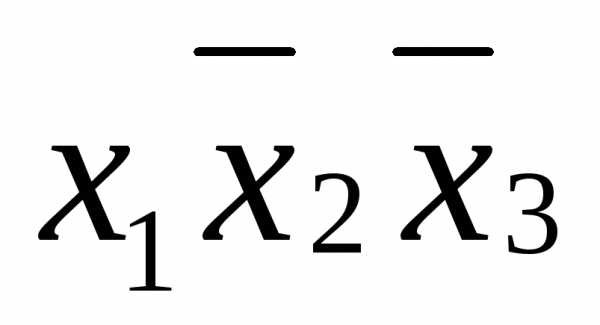
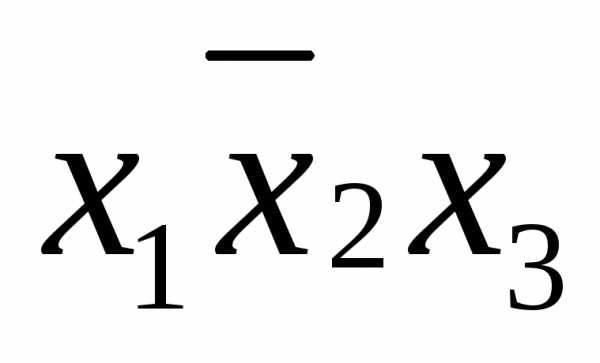
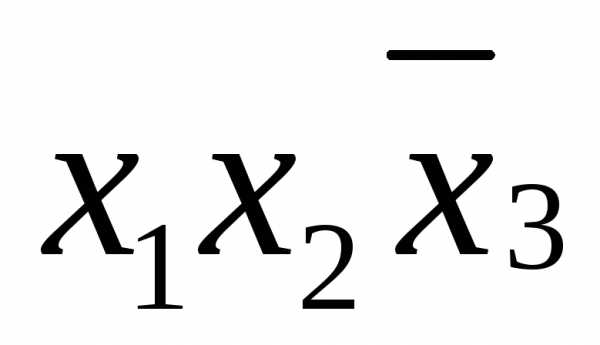
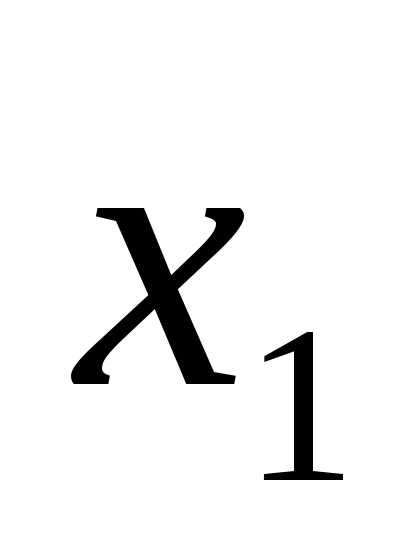
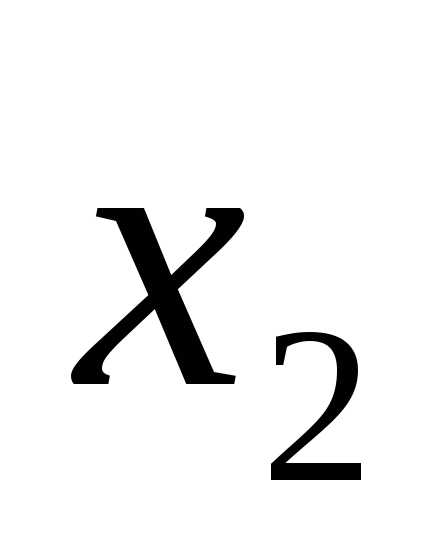
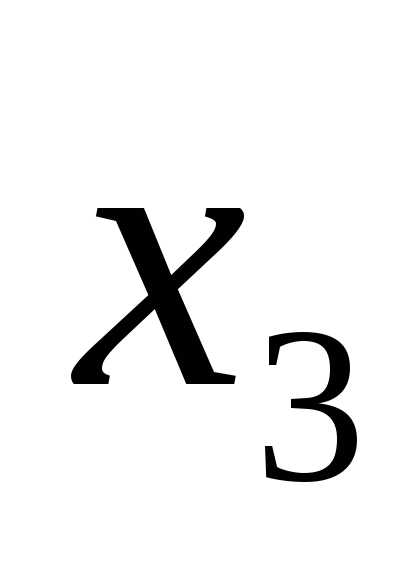

 и очень компактен в записи. В следующем
примере функция от четырех аргументов
будет задана именно списком единичного
набора.
и очень компактен в записи. В следующем
примере функция от четырех аргументов
будет задана именно списком единичного
набора. )=
)=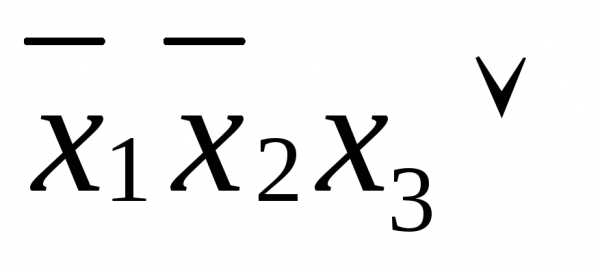
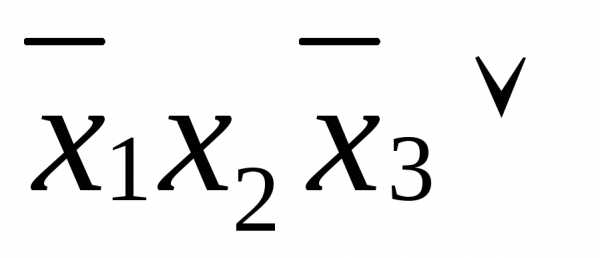
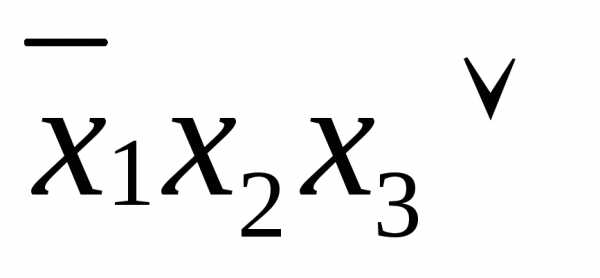
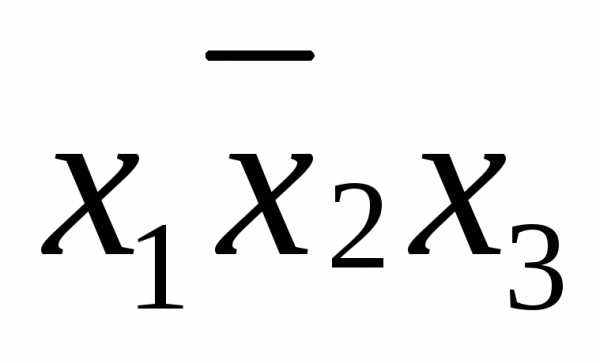 .
.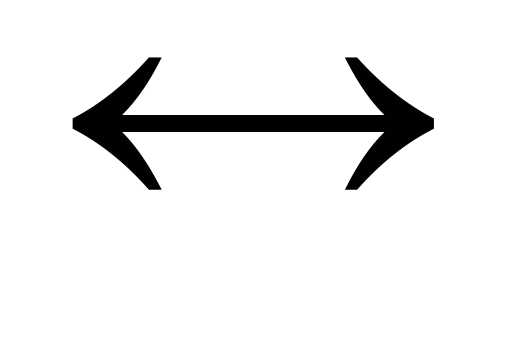
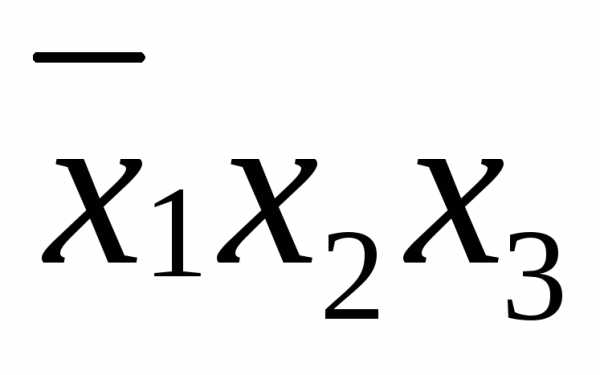
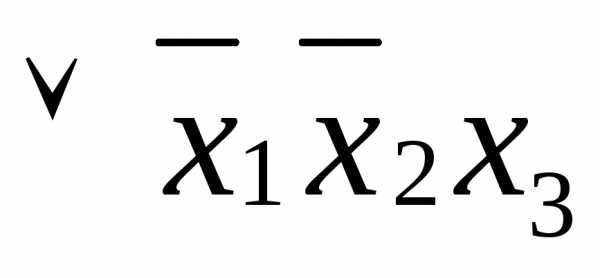 ,
,
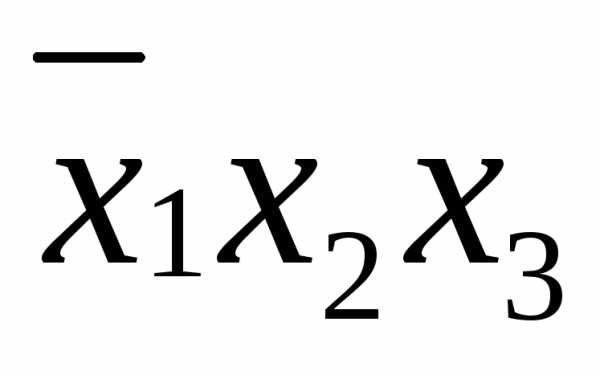
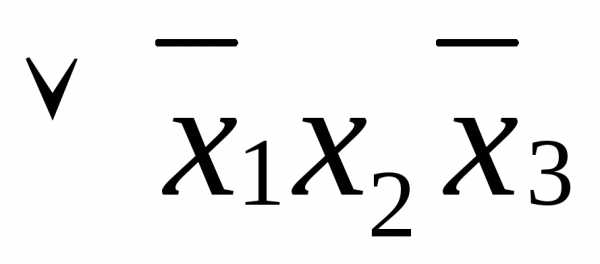 ,
,
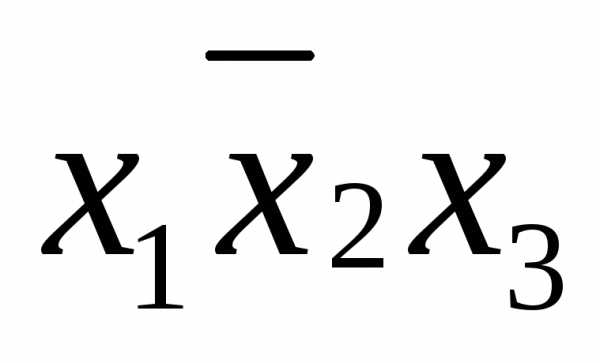
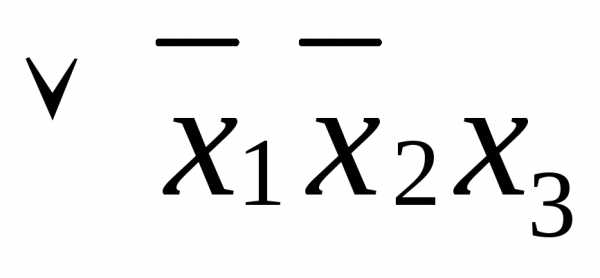 .
.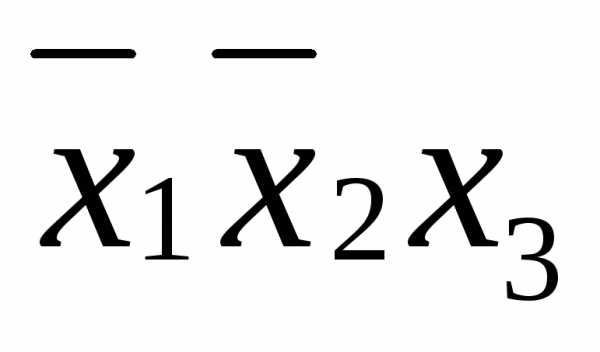
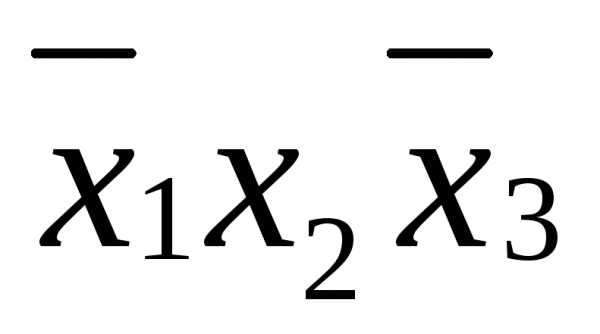
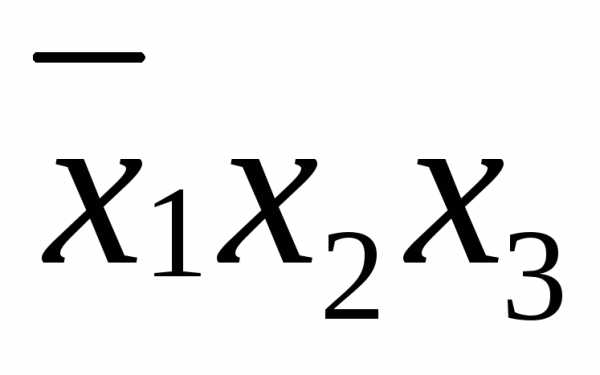
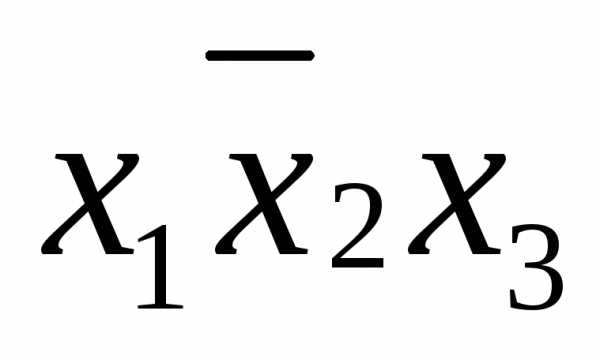
 )
)