Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости онлайн
С помощю этого онлайн калькулятора можно построить уравнение прямой, проходящей через данную точку и перпендикуляной данной плоскости. Дается подробное решение с пояснениями. Для построения уравнения прямой введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости
Наша цель построить уравнение прямой, проходящей через данную точку M0 и перпендикулярной к данной плоскости Ax+By+Cz+D=0.
Общее уравнение плоскости имеет вид:
где n(A,B,C
Уравнение прямой, проходящей через точку M0(x0, y0, z0) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:
Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .
Таким образом, уравнение прямой, проходящей через точку M0(x0, y0, z0) и ортогональный плоскости (1) имеет следующий вид:
Пример 1. Построить прямую, проходящую через точку M0(5, -4, 4) и перпендикулярной плоскости
Решение.
Общее уравнение плоскости имеет вид (1), где :
Подставляя координаты точки M0(5, -4, 4) и координаты нормального вектора плоскости (4) в (3), получим:
Ответ:
matworld.ru
Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.
Найдем уравнение прямой, проходящей через заданную точку М0(х0,у0) перпендикулярно данному ненулевому вектору .
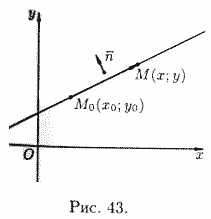Возьмем на прямой произвольную точку М(х;у) и рассмотрим вектор .Поскольку векторы n и М0М перпендикулярны, то их скалярное произведение равно нулю: ,то есть Уравнение (10.8) называется уравнением прямой, проходящей через заданную точку перпендикулярно заданному вектору.
Любая прямая на плоскости может быть задана уравнением первого порядка
Ах + Ву + С = 0.
Угол между прямыми. Условия параллельности и перпендикулярности прямых.
Условия параллельности двух прямых:
а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:
k1 = k2.
б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.
5. Условия перпендикулярности двух прямых:
а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.
б) Если уравнения прямых заданы в общем виде (6), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства A1A2 + B1B2 = 0.
Вычисление расстояния от точки до прямой.
Расстояние от точки до прямой определяется длиной перпендикуляра, опущенного из точки на прямую.
Уравнение плоскости, проходящей через три точки.
| x — x1 y — y1 z — z1 |
| x2 — x1 y2 — y1 z2 — z1 | = 0
| x3 — x1 y3 — y1 z3 — z1 |
Уравнение плоскости проходящей через данную точку перпендикулярно данному вектору.
Пусть в трехмерном пространстве задана прямоугольная декартова система координат. Сформулируем следующую задачу:
Составить уравнение плоскости, проходящей через данную точку
M(x0, y0, z0) перпендикулярно данному вектору →n = {A, B, C} .
Решение. Пусть P(x, y, z) — произвольная точка пространства. Точка P принадлежит плоскости тогда и только тогда, когда вектор
MP = {x − x0, y − y0, z − z0} ортогонален вектору →n = {A, B, C} (рис.1).
Написав условие ортогональности этих векторов (→n, MP) = 0 в координатной форме, получим:
A(x − x0) + B(y − y0) + C(z − z0) = 0 (1)
Это и есть искомое уравнение. Вектор →n = {A, B, C} называется нормальным вектором плоскости.
Таким образом, чтобы написать уравнение плоскости, нужно знать нормальный вектор плоскости и какую–нибудь точку, принаждежащую плоскости.
Если теперь в уравнении (1) раскрыть скобки и привести подобные члены, получим общее уравнение плоскости:
Ax + By + Cz + D = 0 ,
где D = −Ax0 − By0 − Cz0 .
Уравнение прямой, проходящей через две точки в пространстве.
Уравнение прямой, проходящей через данную точку параллельно данному вектору(в пространстве).
Уравнение прямой, проходящей через данную точку A(x1, y1) параллельно данному вектору a(m, n):
Условия параллельности и перпендикулярности прямой и плоскости.
Для того, чтобы прямая и плоскость были параллельны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были перпендикулярны. Для этого необходимо, чтобы их скалярное произведение было равно нулю.
Для того, чтобы прямая и плоскость были перпендикулярны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были коллинеарные. Это условие выполняется, если векторное произведение этих векторов было равно нулю.
Вычисление расстояния от данной точки до данной плоскости.
Пусть Pa = (xa, ya, za) точка, расстояние от которой необходимо подсчитать.
Плоскость можно задать нормалью n = (A, B, C) и одной точкой Pb = (xb, yb, zb)
Произвольная точка P = (x,y,z) лежит на плоскости тогда и только тогда, когда Ax+By+Cz+D=0
Наименьшее расстояние между Pa и плоскостью будет равно абсолютной величине выражения (A xa + B ya + C za + D) / sqrt(A2 + B2 + C2)
Знак самого выражения дает расположение точки относительно плоскости: с какой она стороны.
Уравнение окружности.
или .
Эллипс.
Эллипсом называется множество всех таких точек плоскости, для которых сумма расстояний до двух фиксированных точек постоянна.
Гипербола.
Гиперболой называется множество всех таких точек плоскости, для которых модуль разности расстояний до двух фиксированных точек есть постоянная положительная величина.
Парабола.
Параболой называется множество всех таких точек плоскости, для которых расстояние до фиксированной точки равно расстоянию до фиксированной прямой, не проходящей через эту точку.
Рекомендуемые страницы:
lektsia.com
№1. а Написать уравнение прямой, проходящей через точку, перпендикулярно вектору, и привести его к общему виду
с. 1
КОНТРОЛЬНАЯ РАБОТА №2
Вариант 20
№1. а) Написать уравнение прямой, проходящей через точку , перпендикулярно вектору , и привести его к общему виду;
б) Привести общее уравнение к нормальному виду и указать расстояние от начала координат до прямой.
Решение:
а) Уравнение прямой, проходящей через точку , перпендикулярно вектору , имеет вид:
б) Общее уравнение прямой приводится к нормальному (нормированному) виду умножением обеих частей уравнения на нормирующий множитель , где знак должен быть противоположным знаку .
Свободный член нормированного уравнения с противоположным знаком численно равен расстоянию от начала координат до прямой.
Ответ: а) ;
б) ;
№2. а) Написать уравнение прямой, проходящей через точку , параллельно вектору , в каноническом виде и привести его к общему виду;
б) Записать параметрические уравнения прямой, показать, что точка принадлежит этой прямой и найти соответствующее этой точке значение параметра.
Решение:
а) Уравнение прямой проходящей через точку , параллельно вектору , имеет вид:
б) Параметрические уравнения прямой получаются из канонического уравнения , где – параметр (переменная величина, принимающая значения от до )
Точка принадлежит прямой, если координаты этой точки удовлетворяют уравнению прямой
Следовательно, точка принадлежит прямой , а соответствующее этой точке значение параметра .
Ответ: а) ;
;
б) ;
№3. а) Составить уравнение прямой, которая проходит через точку перпендикулярно заданной прямой ; б) Составить уравнение прямой, которая проходит через точку параллельно заданной прямой и найти расстояние между ними.
Решение:
а) Уравнение прямой, которая проходит через точку перпендикулярно прямой имеет вид:
б) Уравнение прямой, которая проходит через точку перпендикулярно прямой имеет вид:
Расстояние между найденной прямой и прямой равно расстоянию от точки до прямой , которое определяется по формуле:
Ответ: а) ;
б) ; .
№4. Найти уравнение прямой, проходящей через точку под углом к данной прямой .
Решение:
Уравнение пучка прямых с центром в точке имеет вид:
Из множества прямых этого пучка следует выбрать те, которые составляют с данной прямой угол , т. е. определить угловые коэффициенты этих прямых. Т. к. , то задача имеет 2 решения. Угол между двумя прямыми определяется по формуле:
В данном случае, , а для определения коэффициента данной прямой представим уравнение в виде уравнения с угловым коэффициентом:
Таким образом,
Уравнения прямых, проходящих через точку под углом к данной прямой имеют вид:
Ответ:
№5. а) Написать уравнение плоскости, проходящей через точку , перпендикулярно вектору , и привести его к общему виду;
б) Привести общее уравнение к нормальному виду и указать расстояние от начала координат до плоскости.
Решение:
а) Уравнение плоскости, проходящей через точку , перпендикулярно вектору , имеет вид:
б) Общее уравнение плоскости приводится к нормальному (нормированному) виду умножением обеих частей уравнения на нормирующий множитель , где знак должен быть противоположным знаку .
Свободный член нормированного уравнения с противоположным знаком численно равен расстоянию от начала координат до прямой.
Ответ: а) ;
;
б) ;
№6. а) Составить уравнение плоскости, проходящей через три данные точки , и найти расстояние от точки до этой плоскости;
б) Составить уравнение плоскости, проходящей через точки перпендикулярно первой плоскости.
Решение:
Уравнение плоскости, проходящей через три данные точки имеет вид:
Расстояние от точки до плоскости определяется по формуле:
б) Уравнение плоскости, проходящей через точки перпендикулярно плоскости имеет вид:
Ответ: а) ;;
б) .
№7. а) Написать канонические и параметрические уравнения прямой, проходящей через точку параллельно вектору ;
б) Составить уравнение плоскости, проходящей через точку перпендикулярно прямой ;
в) Составить уравнение плоскости, проходящей через прямую и точку .
Решение:
а) Канонические уравнения прямой, проходящей через точку параллельно вектору имеют вид:
Параметрические уравнения прямой, проходящей через точку параллельно вектору имеют вид:
б) Уравнение плоскости, проходящей через точку перпендикулярно прямой имеет вид:
в) Плоскость, проходящая через прямую и точку проходит через точки , и параллельна вектору . Поэтому ее уравнение имеет вид:
Ответ: а) ;;
б) ;
в)
№8. а) Найти угол между данными плоскостями и ;
б) Составить уравнение плоскости, которая проходит через прямую пересечения плоскостей и и точку ;
в) Написать канонические уравнения прямой, заданной общими уравнениями , , и составить уравнение прямой, проходящей через точку параллельно данной прямой.
Решение:
а) Угол между данными плоскостями и
б) Две пересекающиеся плоскости задают пучок плоскостей, уравнение которого имеет вид:
Из множества этого пучка выберем ту, которая проходит через точку , т. е определим значение параметра :
Таким образом, уравнение искомой плоскости имеет вид:
в) Система, составленная из уравнений плоскостей , называется общими уравнениями прямой пересечения этих плоскостей:
Чтобы определить канонические уравнения прямой необходимо определить две точки, принадлежащих этой прямой:
Канонические уравнения прямой, проходящей через две точки и , имеют вид:
Канонические уравнения прямой, проходящей через точку параллельно прямой , имеют вид:
Ответ: а) ;
б) ;
в) ;
№9. а) Вычислить угол между плоскостью и прямой ;
б) Найти точку пересечения прямой и плоскости ;
в) Составить уравнение прямой, проходящей через эту точку перпендикулярно плоскости
Решение:
а) Угол между плоскостью и прямой вычисляется по формуле:
б) Координаты точки пересечения прямой и плоскости определяются из системы, составленной из их уравнений:
в) Уравнение прямой, проходящей через точку перпендикулярно плоскости имеет вид:
Ответ: а) ;
б) ;
в)
№10. Исследовать кривую второго порядка и построить ее график.
Дано:
Решение:
Любое уравнение кривой второго порядка путем поворота системы координат на определенный угол α может быть приведено к уравнению, в котором не будет содержаться слагаемого с произведением переменных.
Формулы преобразования координат при повороте системы вокруг начала координат на угол α (в направлении против часовой стрелки) имеют вид:
Таким образом,
Сделаем замену переменных:
Замена переменных означает параллельный перенос системы в точку . В системе координат уравнение кривой есть каноническое уравнение гиперболы с действительной осью , действительная полуось , мнимая .
с. 1
www.prerek.ru
№1. а Написать уравнение прямой, проходящей через точку, перпендикулярно вектору, и привести его к общему виду
с. 1
КОНТРОЛЬНАЯ РАБОТА №2
Вариант 20
№1. а) Написать уравнение прямой, проходящей через точку , перпендикулярно вектору , и привести его к общему виду;
б) Привести общее уравнение к нормальному виду и указать расстояние от начала координат до прямой.
Решение:
а) Уравнение прямой, проходящей через точку , перпендикулярно вектору , имеет вид:
б) Общее уравнение прямой приводится к нормальному (нормированному) виду умножением обеих частей уравнения на нормирующий множитель , где знак должен быть противоположным знаку .
Свободный член нормированного уравнения с противоположным знаком численно равен расстоянию от начала координат до прямой.
Ответ: а) ;
б) ;
№2. а) Написать уравнение прямой, проходящей через точку , параллельно вектору , в каноническом виде и привести его к общему виду;
б) Записать параметрические уравнения прямой, показать, что точка принадлежит этой прямой и найти соответствующее этой точке значение параметра.
Решение:
а) Уравнение прямой проходящей через точку , параллельно вектору , имеет вид:
б) Параметрические уравнения прямой получаются из канонического уравнения , где – параметр (переменная величина, принимающая значения от до )
Точка принадлежит прямой, если координаты этой точки удовлетворяют уравнению прямой
Следовательно, точка принадлежит прямой , а соответствующее этой точке значение параметра .
Ответ: а) ;
;
б) ;
№3. а) Составить уравнение прямой, которая проходит через точку перпендикулярно заданной прямой ;
б) Составить уравнение прямой, которая проходит через точку параллельно заданной прямой и найти расстояние между ними.
Решение:
а) Уравнение прямой, которая проходит через точку перпендикулярно прямой имеет вид:
б) Уравнение прямой, которая проходит через точку перпендикулярно прямой имеет вид:
Расстояние между найденной прямой и прямой равно расстоянию от точки до прямой , которое определяется по формуле:
Ответ: а) ;
б) ; .
№4. Найти уравнение прямой, проходящей через точку под углом к данной прямой .
Решение:
Уравнение пучка прямых с центром в точке имеет вид:
Из множества прямых этого пучка следует выбрать те, которые составляют с данной прямой угол , т. е. определить угловые коэффициенты этих прямых. Т. к. , то задача имеет 2 решения. Угол между двумя прямыми определяется по формуле:
В данном случае, , а для определения коэффициента данной прямой представим уравнение в виде уравнения с угловым коэффициентом:
Таким образом,
Уравнения прямых, проходящих через точку под углом к данной прямой имеют вид:
Ответ:
№5. а) Написать уравнение плоскости, проходящей через точку , перпендикулярно вектору , и привести его к общему виду;
б) Привести общее уравнение к нормальному виду и указать расстояние от начала координат до плоскости.
Решение:
а) Уравнение плоскости, проходящей через точку , перпендикулярно вектору , имеет вид:
б) Общее уравнение плоскости приводится к нормальному (нормированному) виду умножением обеих частей уравнения на нормирующий множитель , где знак должен быть противоположным знаку .
Свободный член нормированного уравнения с противоположным знаком численно равен расстоянию от начала координат до прямой.
Ответ: а) ;
;
б) ;
№6. а) Составить уравнение плоскости, проходящей через три данные точки , и найти расстояние от точки до этой плоскости;
б) Составить уравнение плоскости, проходящей через точки перпендикулярно первой плоскости.
Решение:
Уравнение плоскости, проходящей через три данные точки имеет вид:
Расстояние от точки до плоскости определяется по формуле:
б) Уравнение плоскости, проходящей через точки перпендикулярно плоскости имеет вид:
Ответ: а) ;;
б) .
№7. а) Написать канонические и параметрические уравнения прямой, проходящей через точку параллельно вектору ;
б) Составить уравнение плоскости, проходящей через точку перпендикулярно прямой ;
в) Составить уравнение плоскости, проходящей через прямую и точку .
Решение:
а) Канонические уравнения прямой, проходящей через точку параллельно вектору имеют вид:
Параметрические уравнения прямой, проходящей через точку параллельно вектору имеют вид:
б) Уравнение плоскости, проходящей через точку перпендикулярно прямой имеет вид:
в) Плоскость, проходящая через прямую и точку проходит через точки , и параллельна вектору . Поэтому ее уравнение имеет вид:
Ответ: а) ;;
б) ;
в)
№8. а) Найти угол между данными плоскостями и ;
б) Составить уравнение плоскости, которая проходит через прямую пересечения плоскостей и и точку ;
в) Написать канонические уравнения прямой, заданной общими уравнениями , , и составить уравнение прямой, проходящей через точку параллельно данной прямой.
Решение:
а) Угол между данными плоскостями и
б) Две пересекающиеся плоскости задают пучок плоскостей, уравнение которого имеет вид:
Из множества этого пучка выберем ту, которая проходит через точку , т. е определим значение параметра :
Таким образом, уравнение искомой плоскости имеет вид:
в) Система, составленная из уравнений плоскостей , называется общими уравнениями прямой пересечения этих плоскостей:
Чтобы определить канонические уравнения прямой необходимо определить две точки, принадлежащих этой прямой:
Канонические уравнения прямой, проходящей через две точки и , имеют вид:
Канонические уравнения прямой, проходящей через точку параллельно прямой , имеют вид:
Ответ: а) ;
б) ;
в) ;
№9. а) Вычислить угол между плоскостью и прямой ;
б) Найти точку пересечения прямой и плоскости ;
в) Составить уравнение прямой, проходящей через эту точку перпендикулярно плоскости
Решение:
а) Угол между плоскостью и прямой вычисляется по формуле:
б) Координаты точки пересечения прямой и плоскости определяются из системы, составленной из их уравнений:
в) Уравнение прямой, проходящей через точку перпендикулярно плоскости имеет вид:
Ответ: а) ;
б) ;
в)
№10. Исследовать кривую второго порядка и построить ее график.
Дано:
Решение:
Любое уравнение кривой второго порядка путем поворота системы координат на определенный угол α может быть приведено к уравнению, в котором не будет содержаться слагаемого с произведением переменных.
Формулы преобразования координат при повороте системы вокруг начала координат на угол α (в направлении против часовой стрелки) имеют вид:
Таким образом,
Сделаем замену переменных:
Замена переменных означает параллельный перенос системы в точку . В системе координат уравнение кривой есть каноническое уравнение гиперболы с действительной осью , действительная полуось , мнимая .
с. 1
prerek.ru
Уравнение плоскости, проходящей через данную точку и перпендикулярной данной прямой онлайн
С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через данную точку и перпендикуляной данной прямой. Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямой (канонический или параметрический) введите координаты точки и коэффициенты уравнения прямой в ячейки и нажимайте на кнопку «Решить».
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Уравнение плоскости, проходящей через данную точку и перпендикулярной данной прямой − теория, примеры и решения
Задана точка M0(x0, y0, z0) и прямая L:
Построить уравнение плоскости α, проходящей через точку M0 и перпендинулярной прямой L.
Решение. Уравнение плоскости, проходящей через точку M0 и имеющий нормальный вектор n={A, B, C} имеет следующий вид:
Направляющий вектор прямой L имеет вид q={m, p, l}. Поскольку прямая L и плоскость α перпендикулярны друг другу, следовательно нормальный вектор плоскостти и направляющий вектор прямой должны быть коллинеарны (Рис.1). Тогда вместо координат нормального вектора плоскости нужно подставить координаты направляющего вектора прямой L. Получим следующее уравнение плоскости:
Упростим уравнение (3):
где D=−mx0−px0−lx0.
Таким образом уравнение (4) определяет плоскость, проходящей через точку M0(x0, y0, z0) и перпендикулярной прямой (1).
Ответ. Уравнение плоскости прпоходящей через точку M0(x0, y0, z0) и перпендикулярной прямой (1) имеет вид (4).
Пример 1. Найти уравнение плоскости α, проходящую через точку M0(3, −1, 2) и перпендикулярной прямой L:
Решение. Уравнение плоскости α, проходящей через точку M0(x0, y0, z0) и имеющий нормальный вектор n={A, B, C} представляется формулой (2).
Направляющий вектор прямой L имеет следующий вид: :
Для того, чтобы прямая L была перпендикулярна плоскости α, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L, т.е. уравнение плоскости (2) примет следующий вид:
Подставляя координаты точки M0 и направляющего вектора q в (8), получим:
Упростим уравнение (9):
Ответ: Уравнение плоскости, проходящей через точку M0(3, −1, 2) и перпендикулярной прямой (7) имеет вид (10).
Пример 2. Найти уравнение плоскости α, проходящую через точку M0(4, 3, −6) и перпендикулярной прямой L, заданной параметрическим уравнением:
Решение. Приведем параметрическое уравнение (11) к каноническому виду:
Уравнение плоскости α, проходящей через точку M0(x0, y0, z0) и имеющий нормальный вектор n={A, B, C} представляется формулой:
Направляющий вектор прямой L имеет следующий вид:
Для того, чтобы прямая L была перпендикулярна плоскости α, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L, т.е. уравнение плоскости (12) примет следующий вид:
Подставляя координаты точки M0 и направляющего вектора q в (13), получим:
Упростим уравнение (13):
Ответ. Уравнение плоскости, проходящей через точку M0(4, 3, −6) и перпендикулярной прямой (11) имеет вид (14).
matworld.ru
Как найти уравнение перпендикулярной прямой
В декартовой системе координат всякая прямая может быть записана в виде линейного уравнения. Различают общий, канонический и параметрический способы задания прямой, каждый из которых предполагает свои условия перпендикулярности.Инструкция
- Пусть две прямые в пространстве заданы каноническими уравнениями:(x-x1)/q1 = (y-y1)/w1 = (z-z1)/e1;(x-x2)/q2 = (y-y2)/w2 = (z-z2)/e2.
- Числа q, w и e, представленные в знаменателях, являются координатами направляющих векторов к этим прямым. Направляющим называют такой ненулевой вектор, который лежит на данной прямой либо параллелен ей.
- Косинус угла между прямыми имеет формулу:cosλ = ± (q1·q2 + w1·w2 + e1·e2) / √ [(q1)² + (w1)² + (e1)²] · [(q2)² + (w2)² + (e2)²].
- Прямые, заданные каноническими уравнениями, взаимно перпендикулярны тогда и только тогда, когда их направляющие векторы ортогональны. То есть, угол между прямыми (он же – угол между направляющими векторами) равен 90°. Косинус угла в этом случае обращается в ноль. Поскольку косинус выражен дробью, то его равенство нулю эквивалентно нулевому знаменателю. В координатах это запишется так:q1·q2 + w1·w2 + e1·e2 = 0.
- Для прямых на плоскости цепочка рассуждений выглядит аналогично, но условие перпендикулярности запишется чуть более упрощенно: q1·q2 + w1·w2 = 0, т.к. третья координата отсутствует.
- Пусть теперь прямые заданы общими уравнениями:J1 · x + K1 · y + L1 · z = 0;J2 · x + K2 · y + L2 · z = 0.
- Здесь коэффициенты J, K, L – это координаты нормальных векторов. Нормаль – это единичный вектор, перпендикулярный к прямой.
- Косинус угла между прямыми теперь запишется в таком виде:cosλ = (J1·J2 + K1·K2 + L1·L2) / √ [(J1)² + (K1)² + (L1)²] · [(J2)² + (K2)² + (L2)²].
- Прямые взаимно перпендикулярны в том случае, если нормальные векторы ортогональны. В векторном виде, соответственно, это условие выглядит так:J1·J2 + K1·K2 + L1·L2 = 0.
- Прямые на плоскости, заданные общими уравнениями, перпендикулярны, когда J1·J2 + K1·K2 = 0.
completerepair.ru
Составить уравнение прямой проходящей через точку
Для того, чтобы разобраться как составить уравнение прямой, проходящей через точку перпендикулярно конкретной прямой, необходимо понимать, что это возможно только для решения на плоскости. В пространстве таких прямых можно построить бесконечное множество.
Поскольку заданы координаты точки, которая будет принадлежать прямой, необходимо знать еще один из параметров:
- координаты направляющего вектора прямой, перпендикулярно которой будет проходить полученная прямая;
- координаты вектора нормали прямой;
- угловой коэффициент заданной прямой.
Все эти параметры можно получить из уравнения прямой, которое данной в условии задачи.
Рассмотрим пример.
Пример 1.
Составим уравнение прямой на плоскости, которая проходит через точку (17; —19) перпендикулярно прямой .
Решение.
Определим направляющий вектор заданной прямой:
Прямая, уравнение которой мы ищем, и прямая, которая задана по условию, — перпендикулярны. Соответственно, направляющий вектор прямой будет вектором нормали искомой прямой.
Составим уравнение прямой, если известны координаты точки и вектора нормали:
Ответ. .
ru.solverbook.com