Уравнение перпендикулярной прямой | Треугольники
Как составить уравнение прямой перпендикулярной данной прямой и проходящей через данную точку?
Пусть y=k1x+b1— данная прямая. С учётом условия перпендикулярности прямых уравнение прямой, перпендикулярной данной, имеет вид
Если эта прямая проходит через точку M(xo; yo), то её координаты удовлетворяют уравнению прямой. Подставив в уравнение xo и yo, мы найдем b.
Примеры.
1) Написать уравнение прямой, проходящей через точку A(-10;3), перпендикулярной прямой y=5x-11.
Решение:
Так как прямые перпендикулярны, если их угловые коэффициенты обратны по абсолютной величине и противоположны по знаку, то
Значит уравнение прямой, перпендикулярной прямой y=5x-11, имеет вид
Так как прямая проходит через точку A(-10;3), то координаты A удовлетворяют уравнению прямой:
откуда b=1.
Итак, уравнение прямой, перпендикулярной прямой y=5x-11 и проходящей через точку A(-10;3)
Ответ: y= -0,2x+1.
2) Написать уравнение прямой, перпендикулярной прямой x= -2, проходящей через точку M(-5;9).
Решение:
Прямая x= -2 перпендикулярна оси абсцисс. Значит, прямая, уравнение которой мы ищем, параллельна оси абсцисс, то есть ищем уравнение прямой в виде y=b.
Так как искомая прямая проходит через точку M(-5;9), то координаты M удовлетворяют уравнению прямой: y=9.
Ответ: y=9.
3) Написать уравнение прямой, перпендикулярной прямой y=4, проходящей через точку F(7;-5).
Решение:
Прямая y=4 перпендикулярна оси ординат. Следовательно, прямая, уравнение которой мы ищем, параллельна оси ординат, а значит, её уравнение имеет вид x=a.
Так как эта прямая проходит через точку F(7;-5), то координаты F удовлетворяют уравнению прямой: x=7.
Ответ: x=7.
www.treugolniki.ru
Перпендикулярные прямые, условие перпендикулярности прямых
В статье рассматривается вопрос о перпендикулярных прямых на плоскости и трехмерном пространстве. Определение перпендикулярных прямых и их обозначения с приведенными примерами подробно разберем. Рассмотрим условия применения необходимого и достаточного условия перпендикулярности двух прямых и подробно рассмотрим на примере.
Yandex.RTB R-A-339285-1Перпендикулярные прямые – основные сведения
Угол между пересекающимися прямыми в пространстве может быть прямым. Тогда говорят, что данные прямые перпендикулярные. Когда угол между скрещивающимися прямыми прямой, тогда прямые также являются перпендикулярными. Отсюда следует, что перпендикулярные прямые на плоскости пересекающиеся, а перпендикулярные прямые пространства могут быть пересекающимися и скрещивающимися.
То есть понятия «прямые a и b перпендикулярны» и «прямые b и a перпендикулярны» считаются равноправными. Отсюда и взялось понятие взаимно перпендикулярные прямые. Обобщив вышесказанное, рассмотрим определение.
Две прямые называют перпендикулярными, если угол при их пересечении дает 90 градусов.
Перпендикулярность обозначается «⊥», а запись принимает вид a⊥b, что значит, прямая a перпендикулярна прямой b.
Например, перпендикулярными прямыми на плоскости могут быть стороны квадрата с общей вершиной. В трехмерном пространстве прямые Ox, Oz, Oy перпендикулярны попарно: Ox и Oz, Ox и Oy, Oy и Oz.
Перпендикулярность прямых – условия перпендикулярности
Свойства перпендикулярности необходимо знать, так как большинство задач сводится к его проверке для последующего решения. Бывают случаи, когда о перпендикулярности идет речь еще в условии задания или когда необходимо пользоваться доказательством. Для того, чтобы доказать перпендикулярность достаточно, чтобы угол между прямыми был прямым.
Для того, чтобы определить их перпендикулярность при известных уравнениях прямоугольной системы координат, необходимо применить необходимое и достаточное условие перпендикулярности прямых. Рассмотрим формулировку.
Теорема 1Для того, чтобы прямые a и b были перпендикулярными, необходимо и достаточно, чтобы направляющий вектор прямой обладал перпендикулярностью относительно направляющего вектора заданной прямой b.
Само доказательство основывается на определении направляющего вектора прямой и на определении перпендикулярности прямых.
Доказательство 1Пусть введена прямоугольная декартова система координат Оху с заданными уравнениями прямой на плоскости, которые определяют прямые a и b. Направляющие векторы прямых a и b обозначим
zaochnik.com
Условие перпендикулярности прямых | Треугольники
I. Выясним условие перпендикулярности двух прямых y=k1x+b1 и y=k2x+b2.
Пусть прямые y=k1x+b1 и y=k2x+b2 образуют с положительным направлением оси Ox углы α
Обозначим точки пересечения прямых с осью абсцисс через A и B, точку пересечения прямых — C.
Так как α2 — внешний угол при вершине B треугольника ABC, то
Отсюда угловой коэффициент второй прямой
Итак,
условие перпендикулярности прямых:
прямые, заданные уравнениями y=k1x+b1 и y=k2x+b2 перпендикулярны, если их угловые коэффициенты обратны по абсолютной величине и противоположны по знаку:
II. Для общего уравнения прямой
угловые коэффициенты
Отсюда
и условие перпендикулярности прямых в этом случае имеет вид:
Уравнение прямой
www.treugolniki.ru
Перпендикулярность прямых — условия перпендикулярности. — КиберПедия
Перпендикулярные прямые фигурируют чуть ли не в каждой геометрической задаче. Иногда перпендикулярность прямых известна из условия, а в других случаях перпендикулярность прямых приходится доказывать. Для доказательства перпендикулярности двух прямых достаточно показать, используя любые геометрические методы, что угол между прямыми равен девяноста градусам.
А как ответить на вопрос «перпендикулярны ли прямые», если известны уравнения, задающие эти прямые в прямоугольной системе координат на плоскости или в трехмерном пространстве?
Для этого следует воспользоваться необходимым и достаточным условием перпендикулярности двух прямых. Сформулируем его в виде теоремы.
Теорема.
Для перпендикулярности прямых a и b необходимо и достаточно, чтобы направляющий вектор прямой a был перпендикулярен направляющему вектору прямой b.
Доказательство этого условия перпендикулярности прямых основано на определении направляющего вектора прямой и на определении перпендикулярных прямых.
Добавим конкретики.
Пусть на плоскости введена прямоугольная декартова система координат Oxy и заданыуравнения прямой на плоскости некоторого вида, определяющие прямые a и b. Обозначим направляющие векторы прямых а и b как и соответственно. По уравнениям прямых a и bможно определить координаты направляющих векторов этих прямых – получаем и . Тогда, для перпендикулярности прямых a и b необходимо и достаточно, чтобы выполнялось условие перпендикулярности векторов и , то есть, чтобы скалярное произведение векторов и равнялось нулю: .
Итак, необходимое и достаточное условие перпендикулярности прямых a и b в прямоугольной системе координат Oxy на плоскости имеет вид , где и — направляющие векторы прямых a и b соответственно.
Это условие удобно использовать, когда легко находятся координаты направляющих векторов прямых, а также когда прямым a и b соответствуют канонические уравнения прямой на плоскости или параметрические уравнения прямой на плоскости.
Пример.
В прямоугольной системе координат Oxy заданы три точки . Перпендикулярны ли прямые АВ и АС?
Решение.
Векторы и являются направляющими векторами прямых АВ и АС. Обратившись к статье координаты вектора по координатам точек его начала и конца, вычисляем . Векторы и перпендикулярны, так как . Таким образом, выполняется необходимое и достаточное условие перпендикулярности прямых АВ и АС. Следовательно, прямые АВи АС перпендикулярны.
Ответ:
да, прямые перпендикулярны.
Пример.
Решение.
— направляющий вектор прямой , а — направляющий вектор прямой . Вычислим скалярное произведение векторов и : . Оно отлично от нуля, следовательно, направляющие векторы прямых не перпендикулярны. То есть, не выполняется условие перпендикулярности прямых, поэтому, исходные прямые не перпендикулярны.
Ответ:
нет, прямые не перпендикулярны.
Аналогично, необходимое и достаточное условие перпендикулярности прямых a и b в прямоугольной системе координат Oxyz в трехмерном пространстве имеет вид , где и — направляющие векторы прямых a и b соответственно.
Пример.
Перпендикулярны ли прямые, заданные в прямоугольной системе координат Oxyz в трехмерном пространстве уравнениями и ?
Решение.
Числа, стоящие в знаменателях канонических уравнений прямой в пространстве, являются соответствующими координатами направляющего вектора прямой. А координатами направляющего вектора прямой, которая задана параметрическими уравнениями прямой в пространстве, являются коэффициенты при параметре. Таким образом, и — направляющие векторы заданных прямых. Выясним, перпендикулярны ли они: . Так как скалярное произведение равно нулю, то эти векторы перпендикулярны. Значит, выполняется условие перпендикулярности заданных прямых.
Ответ:
прямые перпендикулярны.
Для проверки перпендикулярности двух прямых на плоскости существуют другие необходимые и достаточные условия перпендикулярности.
Теорема.
Для перпендикулярности прямых a и b на плоскости необходимо и достаточно, чтобы нормальный вектор прямой a был перпендикулярен нормальному вектору прямой b.
Озвученное условие перпендикулярности прямых удобно использовать, если по заданным уравнениям прямых легко находятся координаты нормальных векторов прямых. Этому утверждению отвечает общее уравнение прямой вида , уравнение прямой в отрезках и уравнение прямой с угловым коэффициентом .
Пример.
Убедитесь, что прямые и перпендикулярны.
Решение.
По заданным уравнениям прямых легко найти координаты нормальных векторов этих прямых. – нормальный вектор прямой . Перепишем уравнение в виде , откуда видны координаты нормального вектора этой прямой: .
Векторы и перпендикулярны, так как их скалярное произведение равно нулю: . Таким образом, выполняется необходимое и достаточное условие перпендикулярности заданных прямых, то есть, они действительно перпендикулярны.
В частности, если прямую a на плоскости определяет уравнение прямой с угловым коэффициентом вида , а прямую b – вида , то нормальные векторы этих прямых имеют координаты и соответственно, а условие перпендикулярности этих прямых сводится к следующему соотношению между угловыми коэффициентами .
Пример.
Перпендикулярны ли прямые и ?
Решение.
Угловой коэффициент прямой равен , а угловой коэффициент прямой равен . Произведение угловых коэффициентов равно минус единице , следовательно, прямые перпендикулярны.
Ответ:
заданные прямые перпендикулярны.
Можно озвучить еще одно условие перпендикулярности прямых на плоскости.
Теорема.
Для перпендикулярности прямых a и b на плоскости необходимо и достаточно, чтобы направляющий вектор одной прямой и нормальный вектор второй прямой были коллинеарны.
Этим условием, очевидно, удобно пользоваться, когда легко находятся координаты направляющего вектора одной прямой и координаты нормального вектора второй прямой, то есть, когда одна прямая задана каноническим уравнением или параметрическими уравнениями прямой на плоскости, а вторая – или общим уравнением прямой, или уравнением прямой в отрезках, или уравнением прямой с угловым коэффициентом.
Пример.
Являются ли прямые и перпендикулярными?
Решение.
Очевидно, — нормальный вектор прямой , а — направляющий вектор прямой . Векторы и не коллинеарны, так как для них не выполняется условие коллинеарности двух векторов(не существует такого действительного числа t, при котором ). Следовательно, заданные прямые не перпендикулярны.
Ответ:
прямые не перпендикулярны.
21. Расстояние от точки до прямой.
Расстояние от точки до прямой определяется через расстояние от точки до точки. Покажем как это делается.
Пусть на плоскости или в трехмерном пространстве задана прямая a и точка M1, не лежащая на прямой a. Проведем через точку M1 прямую b, перпендикулярную прямой a. Обозначим точку пересечения прямых a и b как H1. Отрезок M1H1 называется перпендикуляром, проведенным из точки M1 к прямой a.
Определение.
Расстоянием от точки M1 до прямой a называют расстояние между точками M1 и H1.
Однако чаще встречается определение расстояния от точки до прямой, в котором фигурирует длина перпендикуляра.
Определение.
Расстояние от точки до прямой – это длина перпендикуляра, проведенного из данной точки к данной прямой.
Это определение эквивалентно первому определению расстояния от точки до прямой.
Обратите внимание на то, что расстояние от точки до прямой – это наименьшее из расстояний от этой точки до точек заданной прямой. Покажем это.
Возьмем на прямой a точку Q, не совпадающую с точкой M1. Отрезок M1Q называютнаклонной, проведенной из точки M1 к прямой a. Нам нужно показать, что перпендикуляр, проведенный из точки M1 к прямой a, меньше любой наклонной, проведенной из точки M1 к прямой a. Это действительно так: треугольник M1QH1 прямоугольный с гипотенузой M1Q, а длина гипотенузы всегда больше длины любого из катетов, следовательно, .
22. Плоскость в пространстве R3. Уравнение плоскости.
Плоскость в декартовой прямоугольной системе координат может быть задана уравнением, которое называется общим уравнениемплоскости.
Определение.Вектор перпендикулярен плоскости и называется ее нормальным вектором.
Если в прямоугольной системе координат известны координаты трех точек , не лежащих на одной прямой, то уравнение плоскости записывается в виде: .
Вычислив данный определитель, получим общее уравнение плоскости.
Пример.Написать уравнение плоскости, проходящей через точки .
Решение:
Уравнение плоскости: .
23. Исследование общего уравнения плоскости.
| О п р е д е л е н и е 1. Общим уравнением плоскости называется линейное уравнение первой степени относительно трех переменных: х, у и z, т.е. уравнение вида Ax + By + Cz + D = 0. (3.21) Коэффициенты при х, у и z являются координатами вектора, который перпендикулярен плоскости (рис. 57). | 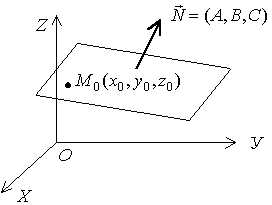 Рис. 57
Рис. 57
|
О п р е д е л е н и е 2. Всякий вектор, перпендикулярный плоскости, называется нормальным вектором этой плоскости.
Если известна фиксированная точка M0 (x0, y0, z0), лежащая в данной плоскости, и вектор , перпендикулярный данной плоскости, то уравнение плоскости, проходящей через точкуM0 (x0, y0, z0), перпендикулярно вектору , имеет вид
A(x-x0)+ B(y-y0) + C(z-z0)= 0. (3.22)
Покажем, что уравнение (3.22) является общим уравнением плоскости (3.21). Для этого раскроем скобки и соберем в скобки свободный член:
.Ax + By+ Cz + (-Ax0 — By -Cz0)= 0
ОбозначивD = -Ax0 — By -Cz0 , получим уравнение Ax + By + Cz + D = 0.
Задача 1. Составить уравнение плоскости, проходящей через точку А, перпендикулярно вектору , если A(4, -3, 1), B(1, 2, 3).
Решение. Найдем нормальный вектор плоскости :
.
Для нахождения уравнения плоскости используем уравнение (3.22):
Ответ: -3x + 5y + 2z + 25 = 0.
Задача 2. Составить уравнение плоскости, проходящей через точку M0 (-1, 2, -1), перпендикулярно оси OZ.
Решение. В качестве нормального вектора искомой плоскости можно взять любой вектор, лежащий на оси OZ, например, , тогда уравнение плоскости
Ответ: z + 1 = 0.
24. Расстояние от точки до плоскости.
Расстояние от точки до плоскости определяется через расстояние от точки до точки, одна из которых заданная точка, а другая – проекция заданной точки на заданную плоскость.
Пусть в трехмерном пространстве задана точка М1 и плоскость . Проведем через точку М1прямую a, перпендикулярную к плоскости . Обозначим точку пересечения прямой a и плоскости как H1. Отрезок M1H1 называют перпендикуляром, опущенным из точки М1 на плоскость , а точку H1 – основанием перпендикуляра.
Определение.
Расстояние от точки до плоскости – это расстояние от данной точки до основания перпендикуляра, проведенного из заданной точки к заданной плоскости.
Чаще встречается определение расстояние от точки до плоскости в следующем виде.
Определение.
Расстояние от точки до плоскости – это длина перпендикуляра, опущенного из заданной точки к заданной плоскости.
Следует отметить, что расстояние от точки М1 до плоскости , определенное таким образом, является наименьшим из расстояний от заданной точки М1 до любой точки плоскости . Действительно, пусть точка H2 лежит в плоскости и отлична от точки H1. Очевидно, треугольник М2H1H2 является прямоугольным, в нем М1H1 – катет, а M1H2 – гипотенуза, следовательно, . Кстати, отрезок M1H2 называется наклонной, проведенной из точки М1 к плоскости . Итак, перпендикуляр, опущенный из заданной точки на заданную плоскость, всегда меньше наклонной, проведенной из этой же точки к заданной плоскости.
25. Прямая в пространстве R3.
Если прямая проходит через две заданные точки ,то ее уравнениезаписывают в виде: .
Определение. Вектор называется направляющим вектором прямой, если он параллелен или принадлежит ей.
Пример.Написать уравнение прямой, проходящей через две заданные точки .
Решение: Используем общую формулу прямой, проходящей через две заданные точки: — каноническое уравнение прямой, проходящей через точки и . Вектор — направляющий вектор прямой.
26. Взаимное расположение прямых в пространстве R3.
Перейдем к вариантам взаимного расположения двух прямых в пространстве.
Во-первых, две прямые могут совпадать, то есть, иметь бесконечно много общих точек (по крайней мере две общие точки).
Во-вторых, две прямые в пространстве могут пересекаться, то есть, иметь одну общую точку. В этом случае эти две прямые лежат в некоторой плоскости трехмерного пространства. Если две прямые в пространстве пересекаются, то мы приходим к понятию угла между пересекающимися прямыми.
В-третьих, две прямые в пространстве могут быть параллельными. В этом случае они лежат в одной плоскости и не имеют общих точек. Рекомендуем к изучению статью параллельные прямые, параллельность прямых.
После того как мы дали определение параллельных прямых в пространстве, следует сказать онаправляющих векторах прямой линии в силу их важности. Любой ненулевой вектор, лежащий на этой прямой или на прямой, которая параллельна данной, будем называть направляющим вектором прямой. Направляющий вектор прямой очень часто используется при решении задач, связанных с прямой линией в пространстве.
Наконец, две прямые в трехмерном пространстве могут быть скрещивающимися. Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости. Такое взаимное расположение двух прямых в пространстве приводит нас к понятию угла между скрещивающимися прямыми.
Особое практическое значение имеет случай, когда угол между пересекающимися или скрещивающимися прямыми в трехмерном пространстве равен девяноста градусам. Такие прямые называют перпендикулярными (смотрите статью перпендикулярные прямые, перпендикулярность прямых).
27. Взаимное расположение прямой и плоскости в пространстве R3.
Прямая может лежать на данной плоскости, быть параллельна данной плоскости или пересекать ее в одной точке, см. следующие рисунки.
рис.6.
рис.7.
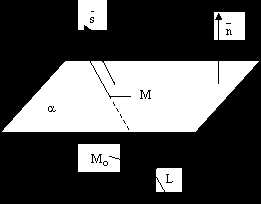
рис.8.
Теорема. Пусть плоскость задана общим уравнением
,
а прямая L задана каноническими уравнениями
или параметрическими уравнениями
, ,
в которых – координаты нормального вектора плоскости , – координаты произвольной фиксированной точки прямой L, –
координаты направляющего вектора прямой L. Тогда:
1) если , то прямая L пересекает плоскость в точке,координаты которой можно найти из системы уравнений
; (7)
2) если и , то прямая лежит на плоскости;
3) если и , то прямая параллельна плоскости.
Доказательство. Условие говорит о том, что вектроры и не ортогональны, а значит прямая не параллельна плоскости и не лежит в плоскости, а значит пересекает ее в некоторой точке М. Координаты точки М удовлетворяют как уравнению плоскости, так и уравнениям прямой, т.е. системе (7). Решаем первое уравнение системы (7) относительно неизвестной t и затем, подставляя найденное значение t в остальныеуравнения системы, находим координаты искомой точки.
Если , то это означает, что . А такое возможно лишь тогда, когда прямая лежит на плоскости или параллельна ей. Если прямая лежит на плоскости, то любая точка прямой является точкой плоскости икоординаты любой точки прямой удовлетворяют уравнению плоскости. Поэтому достаточно проверить, лежит ли на плоскости точка . Если , то точка – лежит на плоскости, а это означает, что и сама прямая лежит на плоскости.
Если , а , то точка на прямой не лежит на плоскости, а это означает, что прямая параллельна плоскости.
Теорема доказана.
cyberpedia.su
Уравнение прямой, проходящей через заданную точку перпендикулярно заданной прямой
В данной статье научимся составлять уравнения прямой, проходящей через заданную точку на плоскости перпендикулярно заданной прямой. Изучим теоретические сведения, приведем наглядные примеры, где необходимо записать такое уравнение.
Yandex.RTB R-A-339285-1Принцип составления уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой
Перед нахождением уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой. Теорема рассматривается в средней школе. Через заданную точку, лежащую на плоскости, можно провести единственную прямую, перпендикулярную данной. Если имеется трехмерное пространство, то количество таких прямых увеличится до бесконечности.
Определение 1Если плоскость α проходит через заданную точку М1 перпендикулярно к заданной прямой b, то прямые, лежащие в этой плоскости, в том числе и проходящая через М1 являются перпендикулярными заданной прямой b.
Отсюда можно прийти к выводу, что составление уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой применимо только для случая на плоскости.
Задачи с трехмерным пространством подразумевают поиск уравнения плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.
Если на плоскости с системой координат Охуz имеем прямую b, то ей соответствует уравнение прямой на плоскости, задается точка с координатами M1(x1, y1), а необходимо составить уравнение прямой a, которая проходит через точку М1 , причем перпендикулярно прямой b.
По условию имеем координаты точки М1. Для написания уравнения прямой необходимо иметь координаты направляющего вектора прямой a, или координаты нормального вектора прямой a, или угловой коэффициент прямой a.
Необходимо получить данные из заданного уравнения прямой b. По условию прямые a и b перпендикулярные, значит, направляющий вектор пр
zaochnik.com
2.6. Условия параллельности и перпендикулярности прямых
Прямые, заданные
общими уравнениями:
ивзаимно перпендикулярны тогда и только
тогда, когдаДанные прямые параллельны тогда и только
тогда, когда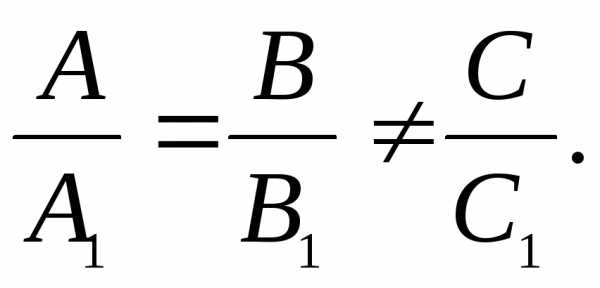
Прямые на плоскости,
заданные в виде:
иперпендикулярны только том случае,
когда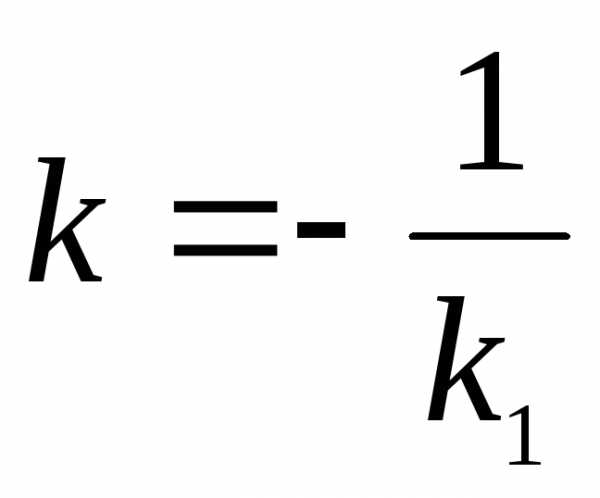 (при
(при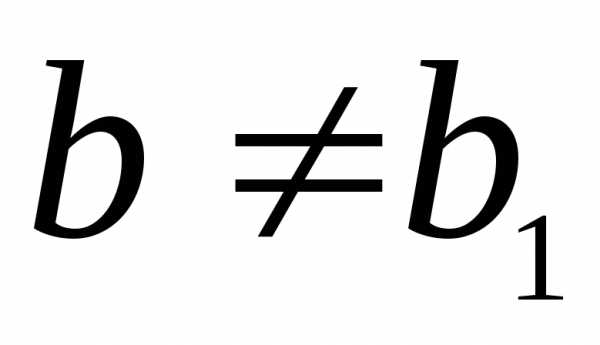 ).
Данные прямые параллельны тогда и только
тогда, когда их угловые коэффициенты
равны, т. е.
).
Данные прямые параллельны тогда и только
тогда, когда их угловые коэффициенты
равны, т. е.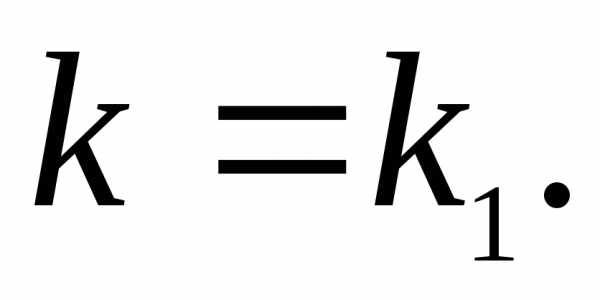
Прямые, заданные
своими каноническими уравнениями: 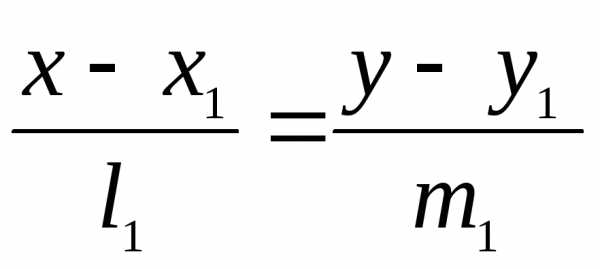 и
и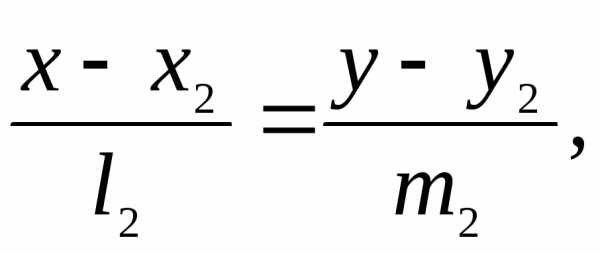 взаимно перпендикулярны тогда и только
тогда, когдаДанные прямые параллельны, если только
выполнено условие:
взаимно перпендикулярны тогда и только
тогда, когдаДанные прямые параллельны, если только
выполнено условие: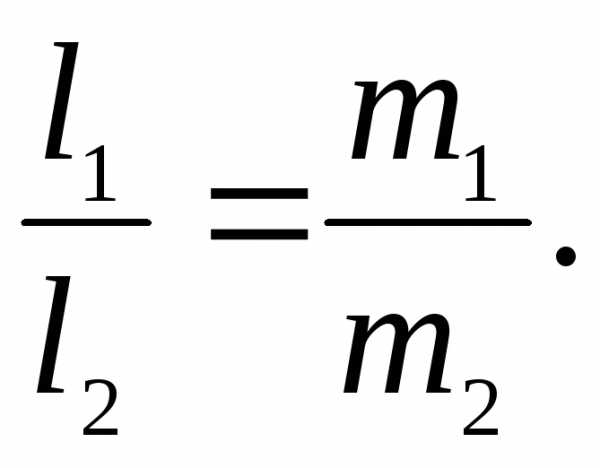
2.7. Точка пересечения непараллельных прямых
Если на плоскости
заданы две прямые:
и,
то согласно утверждению 2 координаты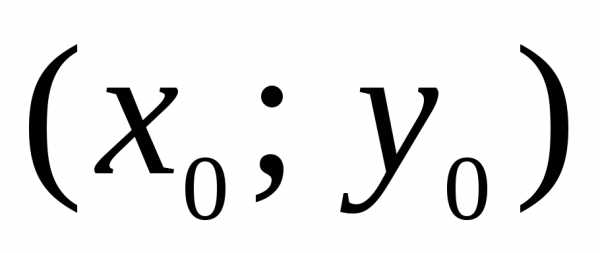 точки пересечения этих прямых можно
вычислить по формулам:
точки пересечения этих прямых можно
вычислить по формулам:
| (21) |
| (22) |
Лекция 10. Прямая в пространстве
Общее уравнение прямой
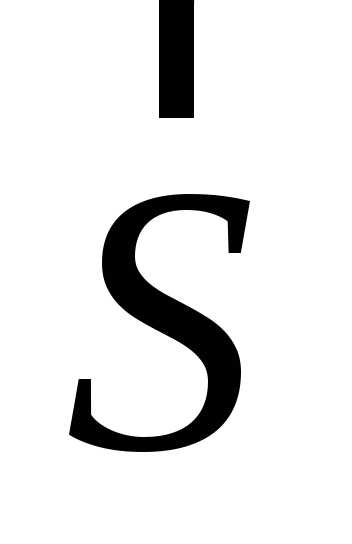 направляющий вектор прямой
направляющий вектор прямой
Каноническое уравнение прямой
Параметрические уравнения прямой
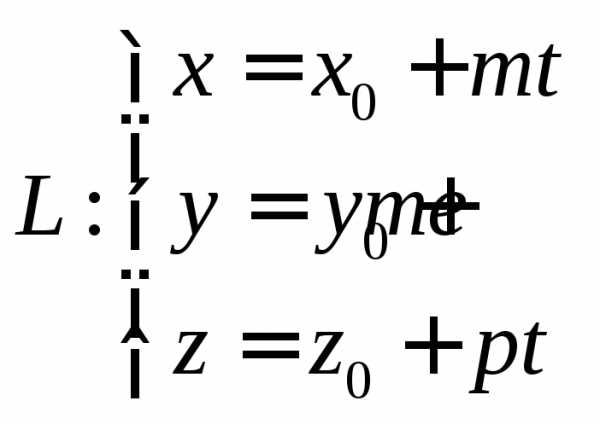
Уравнение прямой проходящей через 2 данные точки
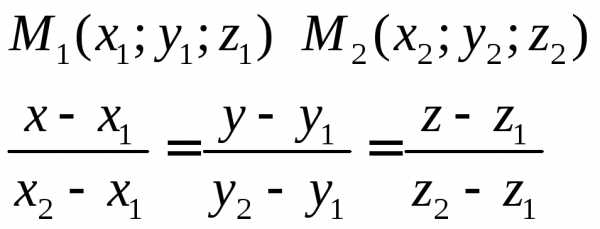
Угол между прямыми
 и
и
6.
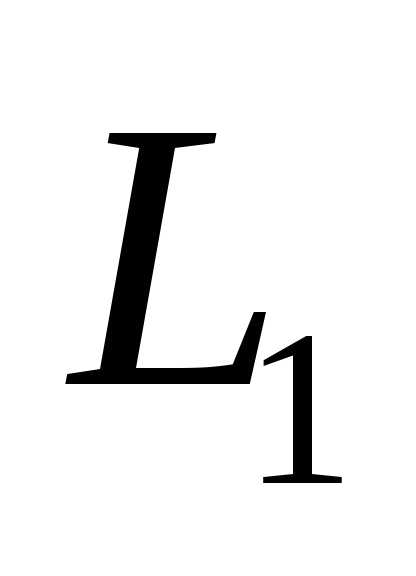 и
и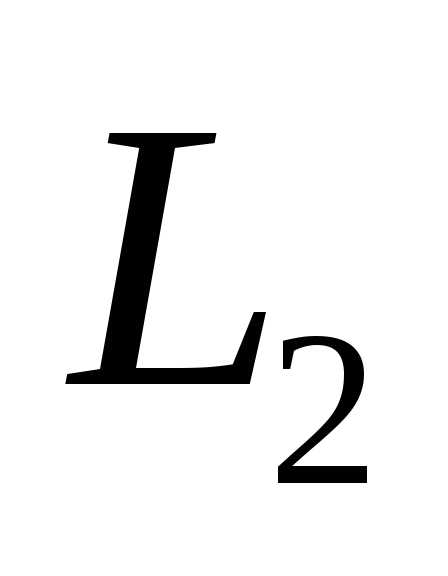 лежат в одной плоскости
лежат в одной плоскости
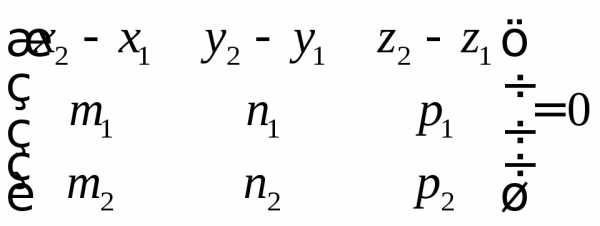
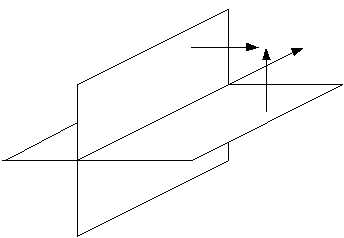
Прямая и плоскость в пространстве
Угол между прямой L и плоскостью

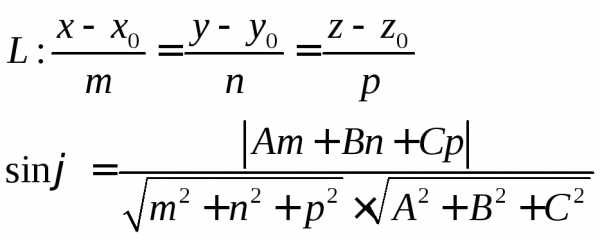
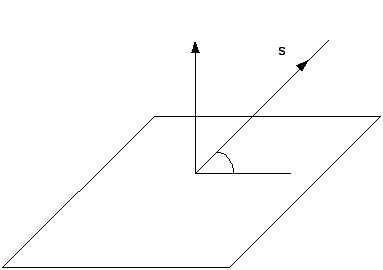
2.
L-
лежит в
плоскости 
3. 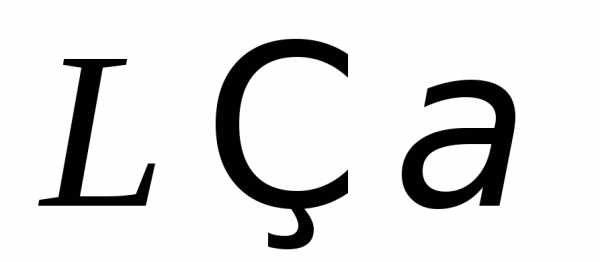 если
если
4.
Лекция 11. Кривые второго порядка
Кривой второго порядка называется геометрическое место точек, задаваемых уравнением: . В зависимости от вида этой кривой уравнение можно привести к одному из канонических, задающему кривую, принадлежащую одному из классов.
Классификация кривых второго порядка
Невырожденные Вырожденные
Эллипс | Гипербола | Парабола | Точка (0;0) | Пара пересекающихся прямых | Пара совпадающих прямых | Пара параллельных прямых |
Каноническое
уравнение | Каноническое
уравнение | Каноническое
уравнение | Каноническое
уравнение | Каноническое
уравнение | Каноническое
уравнение
| Каноническое
уравнение |
Признак вырожденности кривой: уравнение можно представить в виде произведения двух сомножителей.
Эллипс
Кривая второго
порядка, заданная каноническим уравнением 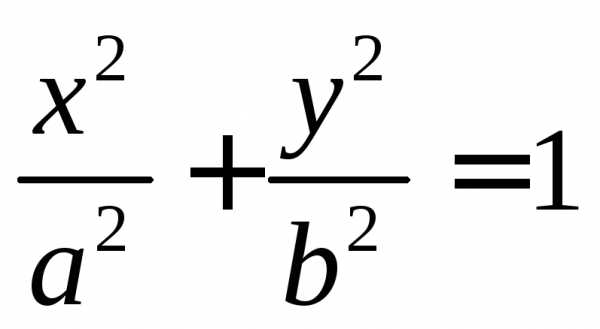 ,
называется эллипсом.a,b – полуоси
эллипса. Если
,
называется эллипсом.a,b – полуоси
эллипса. Если 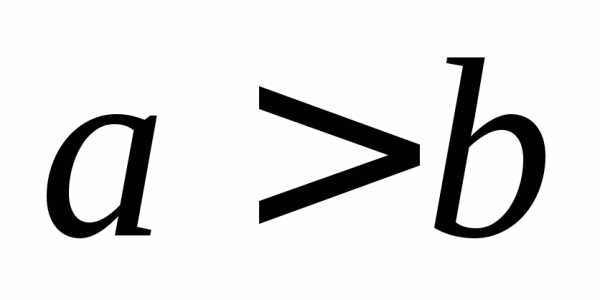 ,
то a—
большая полуось, b—
малая полуось.
,
то a—
большая полуось, b—
малая полуось.
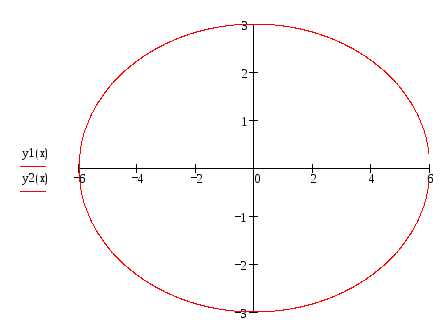
Построение эллипса,
заданного каноническим уравнением 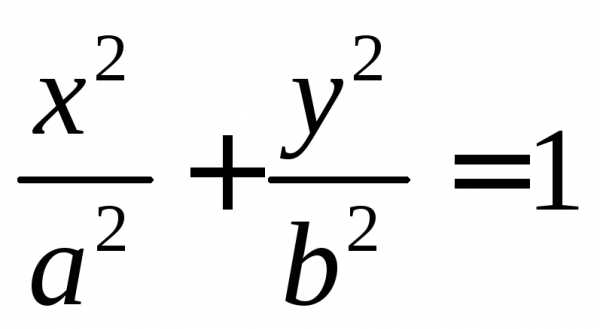 .
Пусть уравнение эллипса имеет вид
.
Пусть уравнение эллипса имеет вид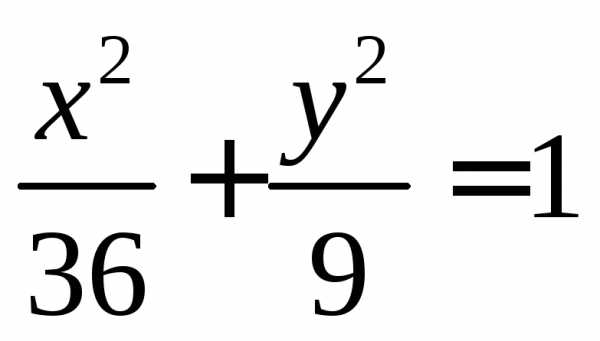 .
Построим прямыеx=6 и y=3.
Точки пересечения данных прямых с осями
координат принадлежат эллипсу. Соединим
их плавной кривой, получим искомый
график. Обычно эллипс
определяется как геометрическое место
точек, сумма расстояний от которых до
фокусов эллипса является величиной
постоянной и равной 2a.
Координаты фокуса из уравнения эллипса
находятся по формулам
если в уравнении
.
Построим прямыеx=6 и y=3.
Точки пересечения данных прямых с осями
координат принадлежат эллипсу. Соединим
их плавной кривой, получим искомый
график. Обычно эллипс
определяется как геометрическое место
точек, сумма расстояний от которых до
фокусов эллипса является величиной
постоянной и равной 2a.
Координаты фокуса из уравнения эллипса
находятся по формулам
если в уравнении 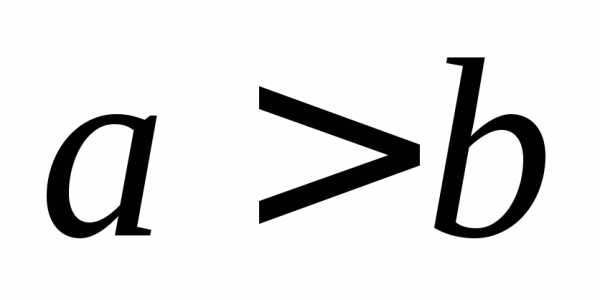 .
Если
.
Если 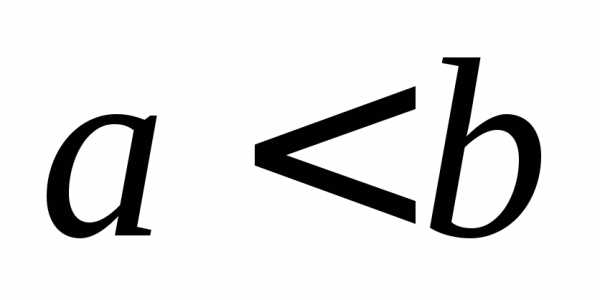 ,
то фокусы имеют координаты
(эллипс ориентирован вертикально).
,
то фокусы имеют координаты
(эллипс ориентирован вертикально).
Оптическое свойство эллипса состоит в том, что если точечный источник света поместить в один фокус эллипса, то в другом фокусе появится его изображение.
Эксцентриситет
эллипса – степень его вытянутости
— отношение расстояния от центра эллипса
до фокуса к его большой полуоси,
вычисляется по формуле 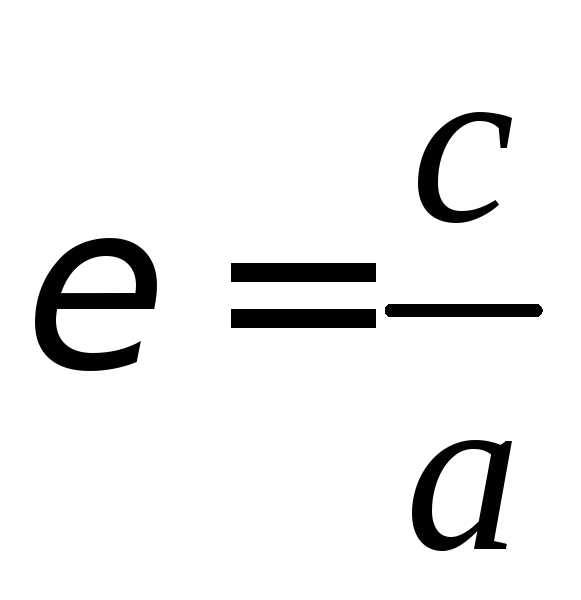 .
Для эллипса в общем случае>1,
если ,
то эллипс превращается в окружность.
Для эллипса, задаваемого уравнением
.
Для эллипса в общем случае>1,
если ,
то эллипс превращается в окружность.
Для эллипса, задаваемого уравнением 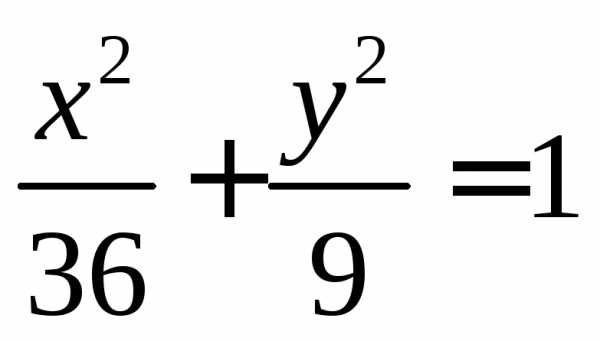 эксцентриситет,
а фокусы находятся в точках
эксцентриситет,
а фокусы находятся в точках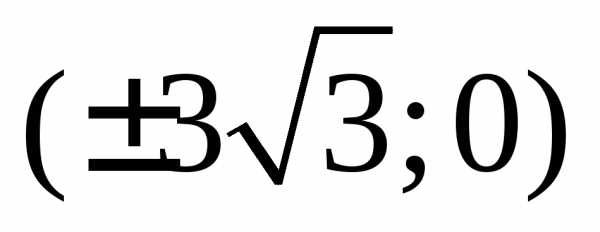 .
.
Окружность – частный случай эллипса, задается уравнением , гдеR – радиус окружности. У окружности 0, а фокусы совпадают с центром ( началом координат).
Гипербола
Гипербола
– кривая, задаваемая каноническим
уравнением 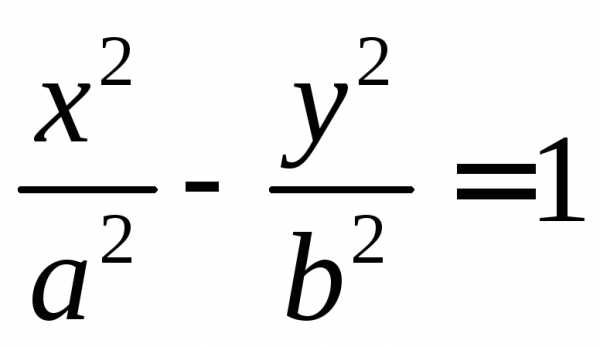 или
или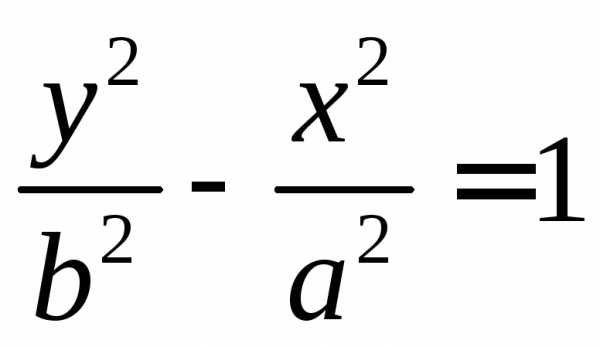 .a,b – полуоси
гиперболы. Действительной называется
та полуось, около которой в уравнении
стоит знак «+». Прямые
.a,b – полуоси
гиперболы. Действительной называется
та полуось, около которой в уравнении
стоит знак «+». Прямые 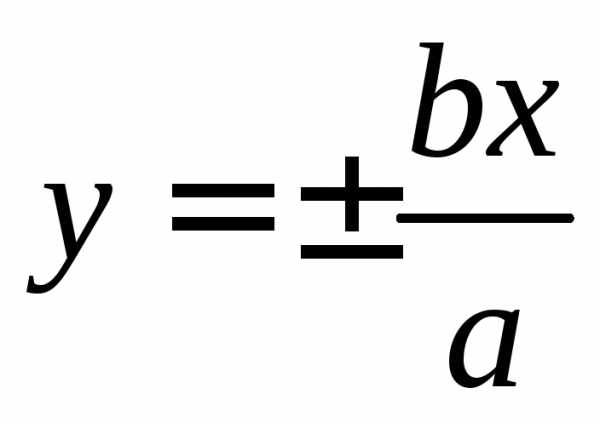 — асимптоты гиперболы (график стремится
к ним, но никогда не достигает).
— асимптоты гиперболы (график стремится
к ним, но никогда не достигает).
Построение гиперболы
Построение
гиперболы, заданной уравнением начинаем
с отложения по оси Ox
отрезка длиной a единиц, а по
оси Oy
– длиной b единиц.
Строим прямые 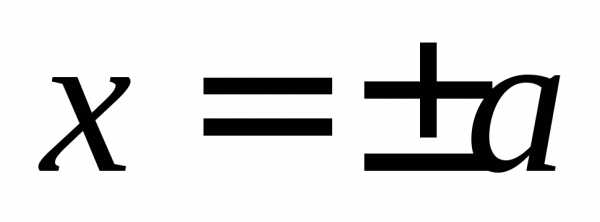 и
и 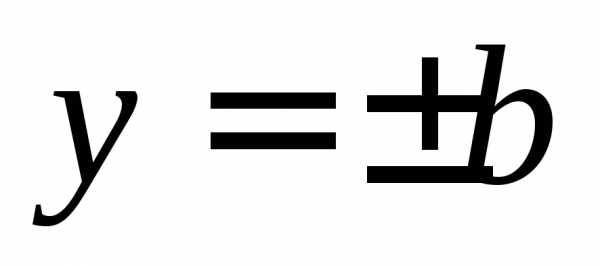 .
Гипербола будет касаться полученного
прямоугольника в двух точках
.
Гипербола будет касаться полученного
прямоугольника в двух точках 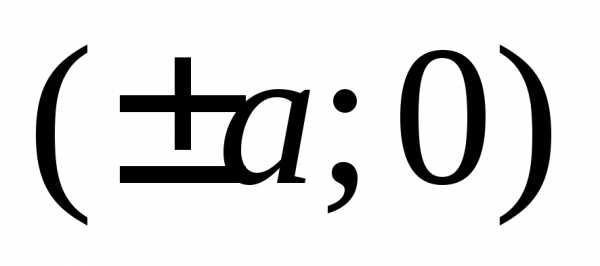 .
Проведем прямые
.
Проведем прямые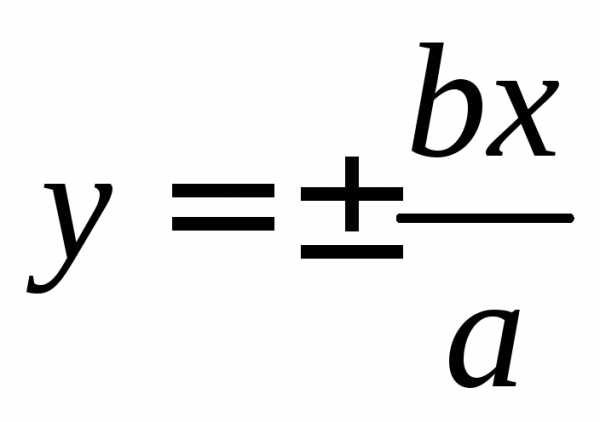 — асимптоты гиперболы. Возьмем еще пару
точек для более точного выяснения формы
кривой (чем больше точек, тем лучше). Вид
кривой (для примера взята гипербола,
заданная уравнением
— асимптоты гиперболы. Возьмем еще пару
точек для более точного выяснения формы
кривой (чем больше точек, тем лучше). Вид
кривой (для примера взята гипербола,
заданная уравнением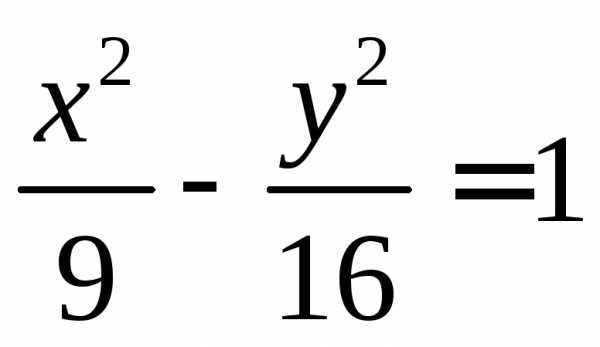 )
представлен на рисунке. Если в уравнении
гиперболы
)
представлен на рисунке. Если в уравнении
гиперболы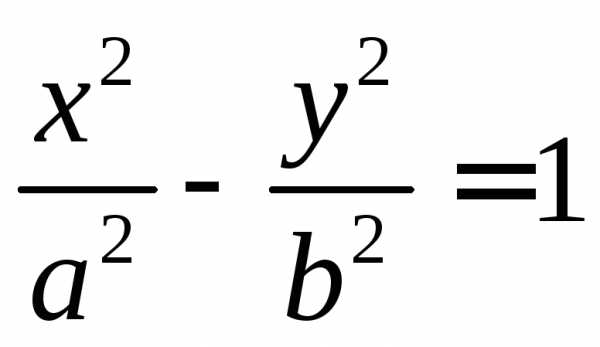 поменять знаки передx
и y,
то получим сопряженную ей гиперболу
поменять знаки передx
и y,
то получим сопряженную ей гиперболу 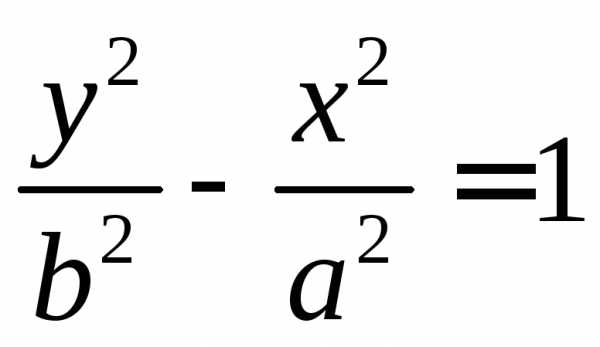 ,
которая имеет те же асимптоты.
,
которая имеет те же асимптоты.
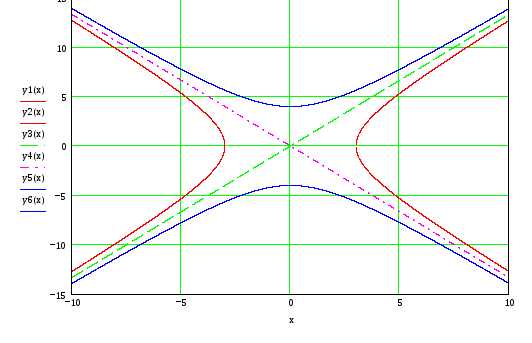
Так же как и эллипс,
гиперболу можно определить как
геометрическое
место точек, разность расстояний которых
от фокусов постоянна.
Фокусы гиперболы имеют координаты 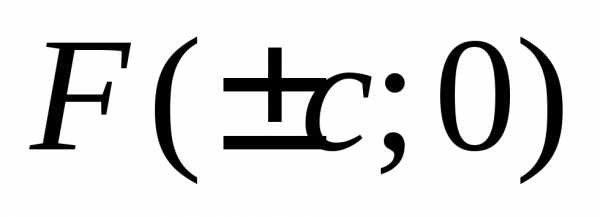 ,
где
(значенияa,b берутся из
уравнения гиперболы). Гипербола,
сопряженная данной, будет иметь фокусы
в точках
,
где
(значенияa,b берутся из
уравнения гиперболы). Гипербола,
сопряженная данной, будет иметь фокусы
в точках 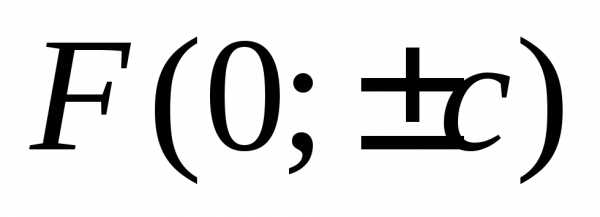 .
.
Оптическое свойство гиперболы состоит в том, что если источник света поместить в один фокус гиперболы, то из бесконечно удаленной точки он будет виден так, как будто он находится во втором фокусе.
Эксцентриситет
гиперболы – степень ее вытянутости.
Для гиперболы
(в общем случае >1)
, задаваемой
уравнением 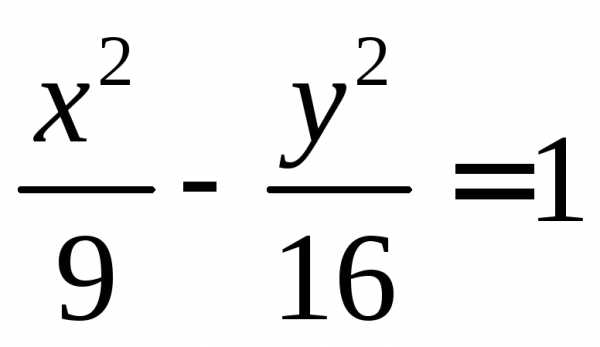 эксцентриситет
эксцентриситет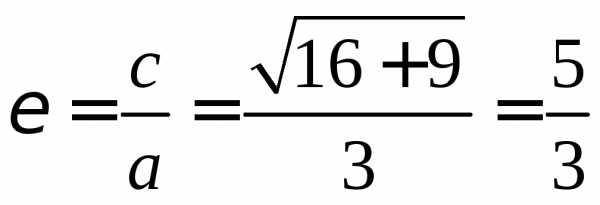 ,
а фокусы находятся в точках
,
а фокусы находятся в точках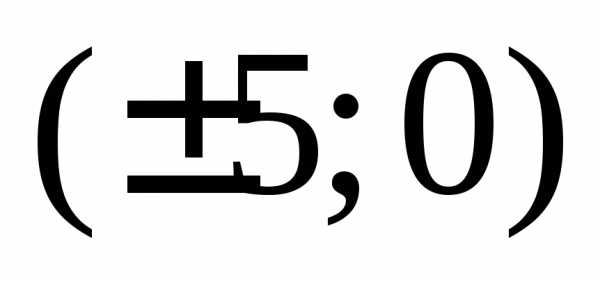 .
.
Парабола
Параболой
называется
кривая второго порядка, задаваемая
каноническим уравнением вида 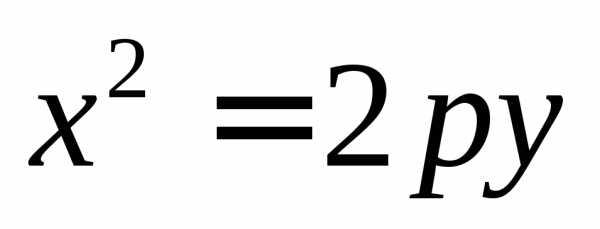 или
или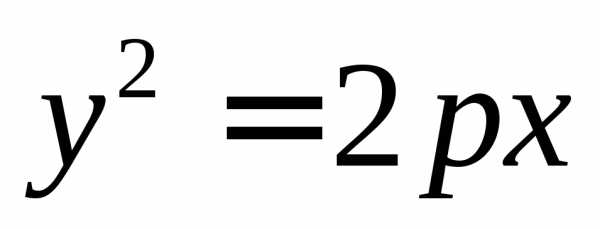 ,
гдеp – параметр параболы. В зависимости от
вида уравнения и значения параметра
ветви параболы могут быть направлены:
,
гдеp – параметр параболы. В зависимости от
вида уравнения и значения параметра
ветви параболы могут быть направлены:
Вверх, в случае если уравнение имеет вид
 приp>0.
приp>0.Вниз, в случае если уравнение имеет вид
 приp<0.
приp<0.Вправо, в случае если уравнение имеет вид
 приp>0.
приp>0.Влево, в случае если уравнение имеет вид
 приp<0.
приp<0.
Параболу можно
определить как геометрическое место
точек, равноудаленных от точки 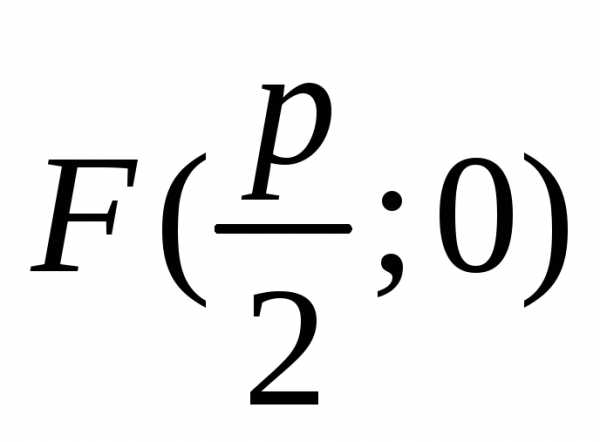 — фокуса — и прямой
— фокуса — и прямой 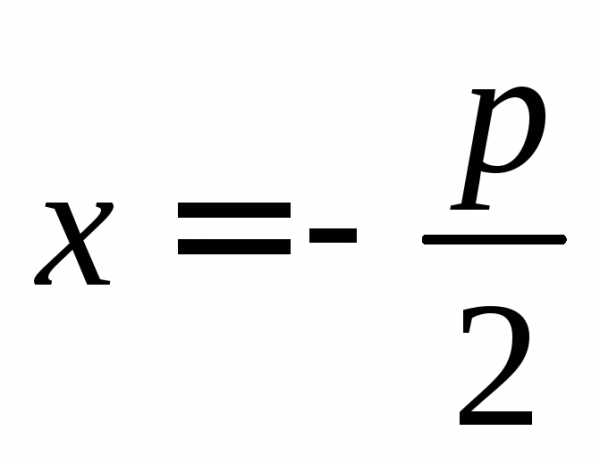 — директрисы.
— директрисы.
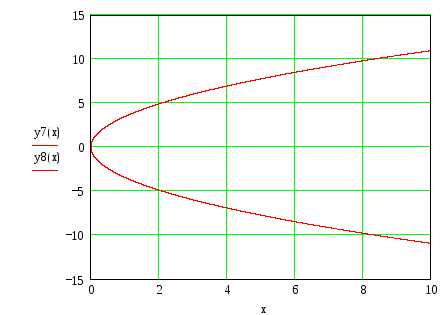
Оптическое свойство параболы состоит в том, что если в фокус параболы поместить точечный источник света, то из нее будет выходить параллельный пучок лучей.
Приведение уравнений кривых второго порядка к каноническому виду.
Общее уравнение кривой , причем примем ( для упрощения расчетов)B=0. Существуют два метода преобразования уравнения общего вида к каноническому:
Выделение полного квадрата
Замена переменной
Для данного уравнения замену удобно ввести замену в виде:
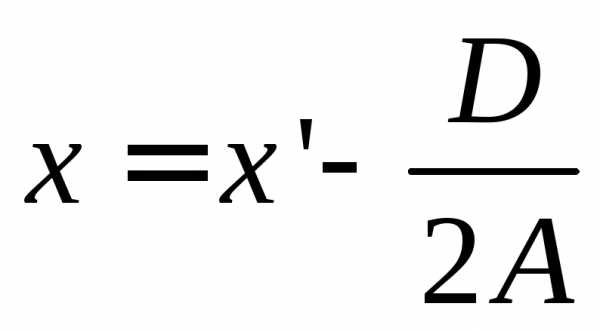
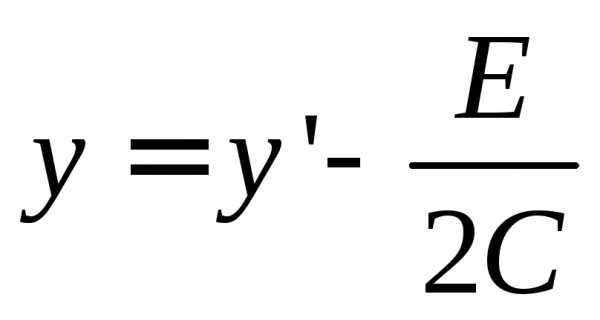 ,
где x’ и y’ – новые переменные.
,
где x’ и y’ – новые переменные.
Если
A
и C
не равны 0, то 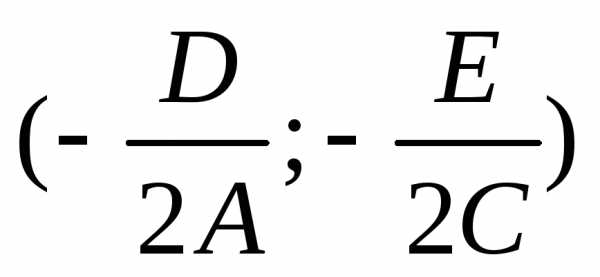 — новый центр кривой второго порядка, аx’ и y’ — новые оси.
— новый центр кривой второго порядка, аx’ и y’ — новые оси.
Пример:
1. Кривая второго порядка задана уравнением . Выяснить, чему оно соответствует.
Данному уравнению соответствует окружность со смещенным центром, имеющая каноническое уравнение , где (x0;y0) – координаты центра окружности, а R – ее радиус. Воспользуемся методом выделения полного квадрата для нахождения канонического вида уравнения.
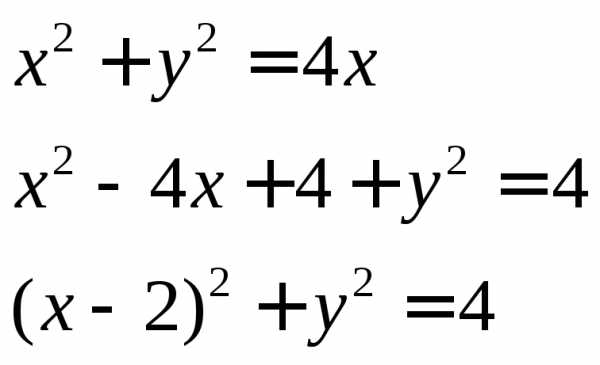
Итак, данное уравнение соответствует окружности радиуса 2 ед. с центром в точке (2;0).
Привести уравнение к каноническому виду и построить кривую:
Воспользуемся методом замены переменных. Имеем:
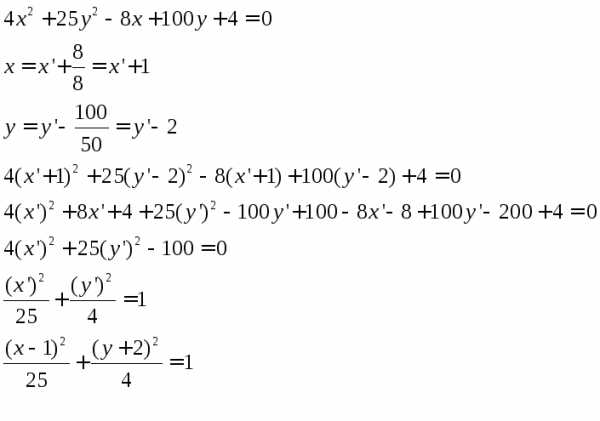
Получилось каноническое уравнение эллипса с центром в точке (1;-2). Строим его по вышеописанному алгоритму.
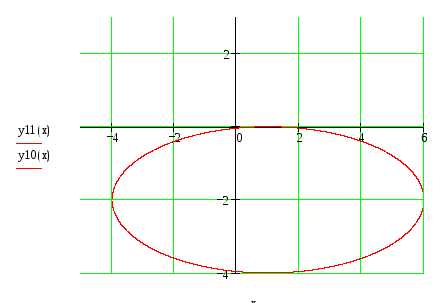
Привести к каноническому виду уравнение . Построить кривую, заданную вышеописанным уравнением.
Используем метод выделения полного квадрата и замены переменной.
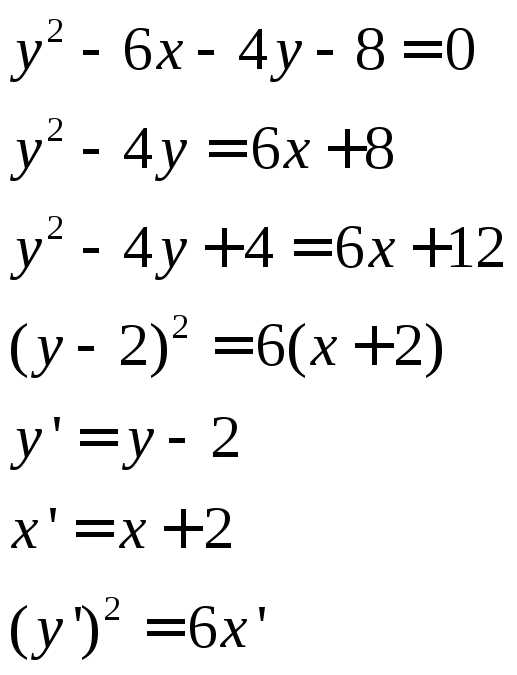
Получилось уравнение параболы с центром в точке (-2;2)
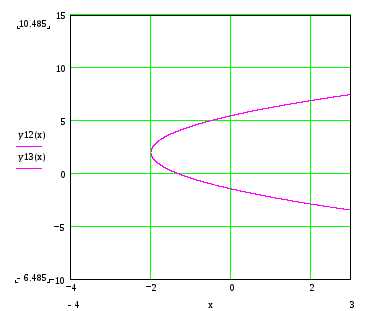
studfiles.net
3.3. Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых
Способ задания прямых | Угол между двумя прямыми | Условия параллельности | Условия перпендику-лярности |
Прямые заданы общими уравнениями: , . |
| ||
Прямые
заданы каноническими уравнениями:
|
| ||
Прямые заданы уравнениями с угловым коэффициентом: , |
|
|
3.4. Задание плоскости в пространстве
Плоскость в пространстве может быть задана:
тремя точками плоскости;
точкой и нормальным вектором плоскости, тогда множество точек М плоскости, проходящей через точку М0 ортогонально вектору
 ,
будет удовлетворять условию.
,
будет удовлетворять условию.точкой и двумя неколлинеарным векторам
 ,
, ,
тогда множество точекМ плоскости
будет удовлетворять условию, что векторы
,
тогда множество точекМ плоскости
будет удовлетворять условию, что векторы  ,
, ,
, компланарны
компланарны
3.5. Виды уравнений плоскости
Общее уравнение плоскости:
Ах+By+Cz+D=0,
где  (A;B;C)
– нормальный вектор плоскости.
(A;B;C)
– нормальный вектор плоскости.
2) Уравнение плоскости, проходящей через точку М0 параллельно
двум неколлинеарным векторам 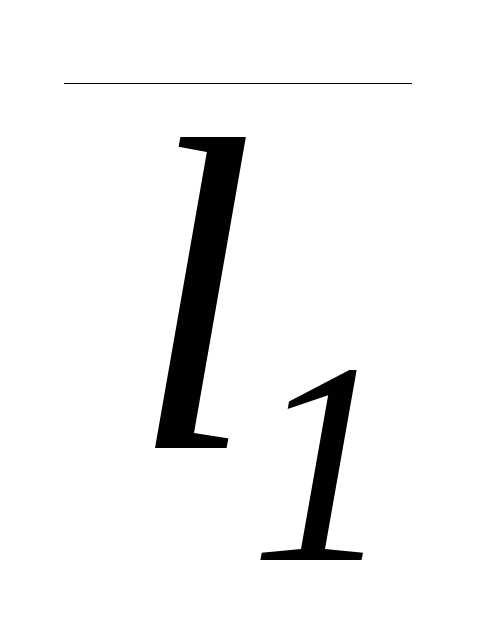 (m1;n1;p1),
(m1;n1;p1), 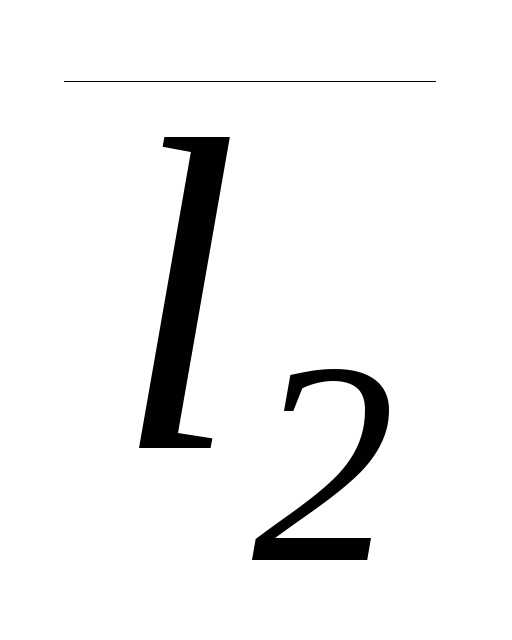 (m2;n2;p2).
(m2;n2;p2).
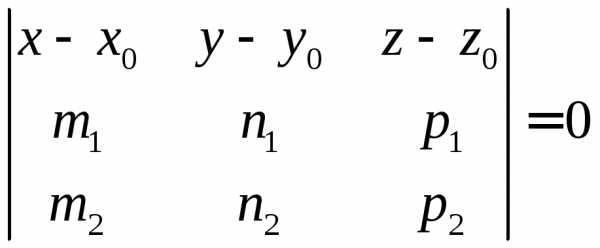 .
.
Уравнение плоскости, проходящей через три точки
М1(x1;y1;z1), M2(x2;y2;z2), M3(x3,y3,z3):
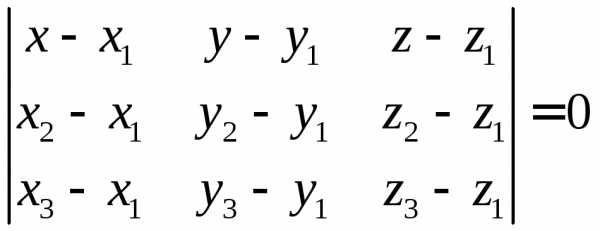 .
.
Это уравнение есть условие компланарности трех векторов .
3.6. Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей
Пусть две плоскости 1 и 2 заданы общими уравнениями:
1: A1x+B1y+C1z+D=0;
2: A2x+B2y+C2z+D=0.
Вопрос об определении
угла между указанными плоскостями
сводится к определению угла
между их нормальными векторами  (А1,В1,С1)
и
(А1,В1,С1)
и  (А2,В2,С2).
(А2,В2,С2).
Из определения скалярного произведения и записи его в координатной форме, получим:
.
Условие параллельности плоскостей 1 и 2,
эквивалентное условию коллинеарности
векторов  (А1,В1,С1)
и
(А1,В1,С1)
и  (А2,В2,С2),
заключается в пропорциональности
координат этих векторов, т.е. имеет вид:
(А2,В2,С2),
заключается в пропорциональности
координат этих векторов, т.е. имеет вид:
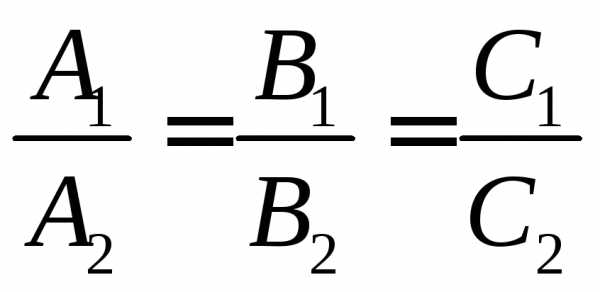 .
.
Условие перпендикулярности плоскостей 1 и 2 выражается равенством нулю скалярного
произведения векторов  (А1,В1,С1)
и
(А1,В1,С1)
и  (А2,В2,С2).
Оно имеет вид:
(А2,В2,С2).
Оно имеет вид:
А1А2+В1В2+С1С2=0.
3.7. Определение прямой в пространстве
Прямая в пространстве может быть задана как линия пересечения двух плоскостей; либо точкой и направляющим вектором прямой.
Прямая в пространствене определяется через нормальный вектор, т.к. любая прямая имеет в каждой своей точке бесконечное множество нормальных векторов.
3.8. Виды уравнений прямой в пространстве
1) Каноническое уравнение прямой:
,
где 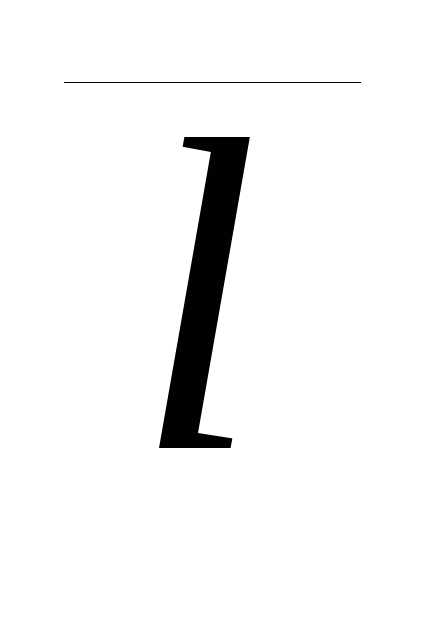 (m;n;p)
– направляющий вектор прямой;
(m;n;p)
– направляющий вектор прямой; 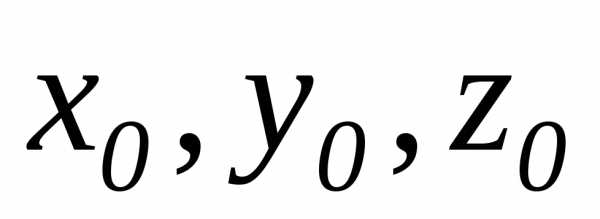 —
координаты заданной точки прямой.
—
координаты заданной точки прямой.
2) Уравнение прямой, проходящей через две точки М1(х1;у1;z1) и М2(х2;у2;z2):
.
3) Общее уравнение прямой в пространстве:
Каждое из уравнений системы является уравнением плоскости, прямая – линия пересечения двух плоскостей.
4) Параметрическое уравнение прямой:
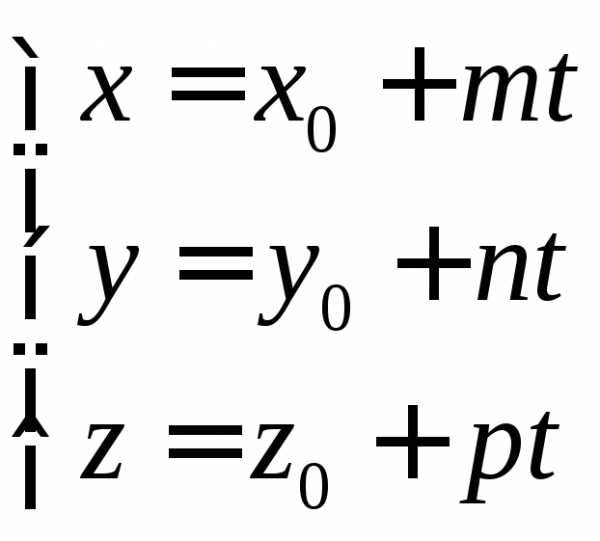 ,
,
где m, n, p – координаты направляющего вектора 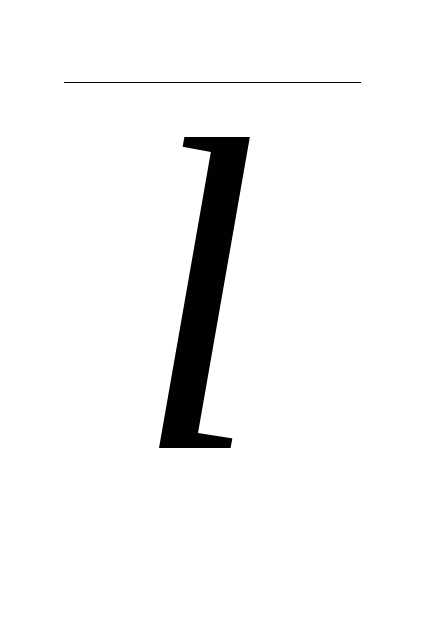 прямой;
прямой;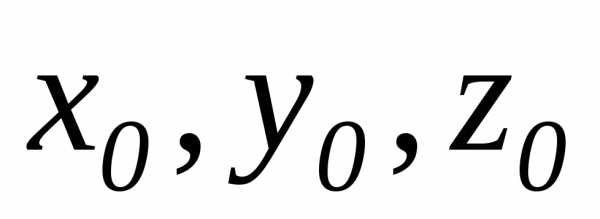 —
координаты заданной точки прямой,t – параметр,
-t+.
—
координаты заданной точки прямой,t – параметр,
-t+.
3.9. Угол между прямыми в пространстве. Условия параллельности и перпендикулярности прямых
Пусть две прямые в пространстве заданы своими каноническими уравнениями:
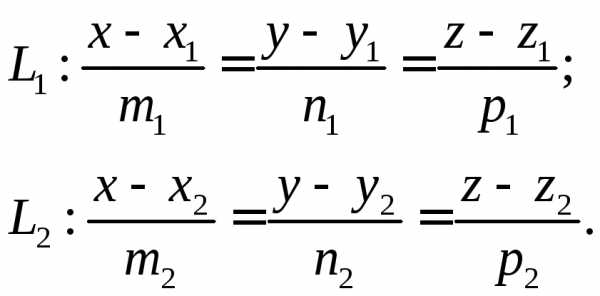
Задача
определения угла между этими
прямыми сводится к определению угла
между их направляющими векторами 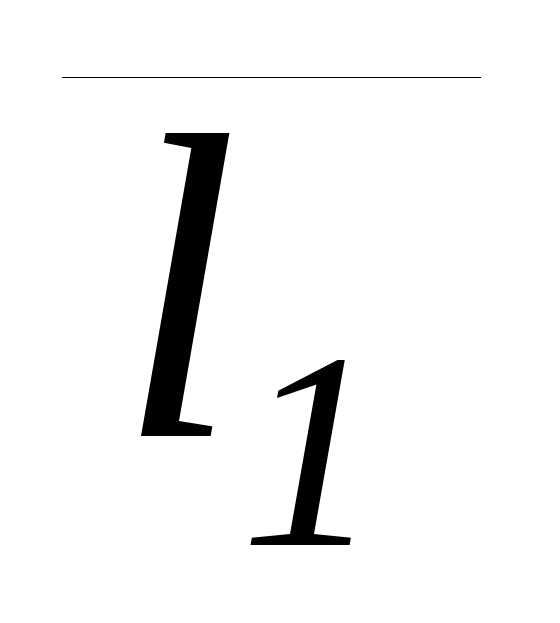 (m1;n1;p1)
и
(m1;n1;p1)
и 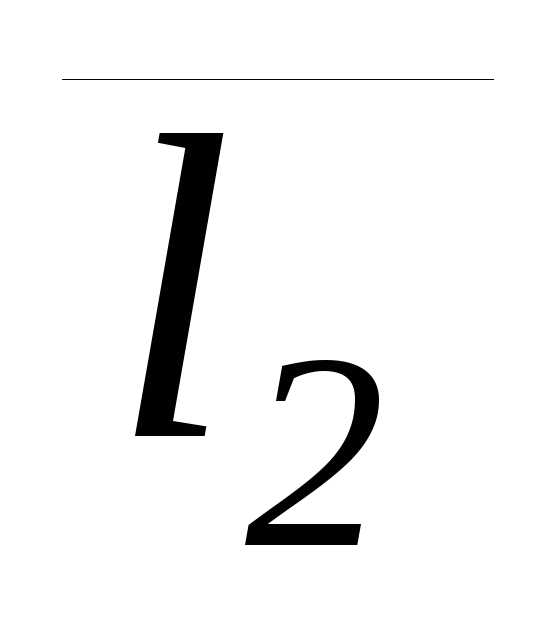 (m2;n2;p2).
По определению скалярного произведения:
(m2;n2;p2).
По определению скалярного произведения:
Условие
параллельности прямых L1 и L2,
эквивалентное условию коллинарности
векторов 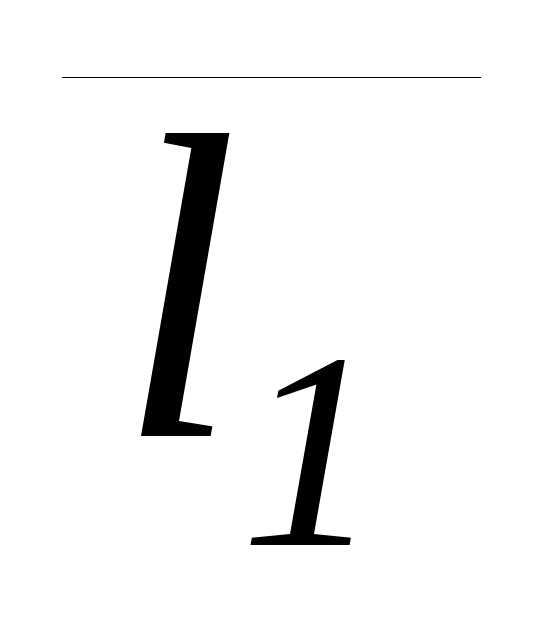 (m1;n1;p1)
и
(m1;n1;p1)
и 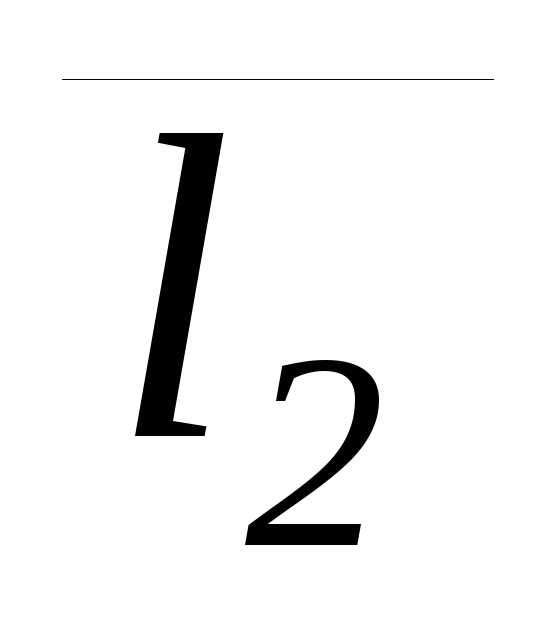 (m2;n2;p2),
заключается в пропорциональности
координат их направляющих векторов:
(m2;n2;p2),
заключается в пропорциональности
координат их направляющих векторов:
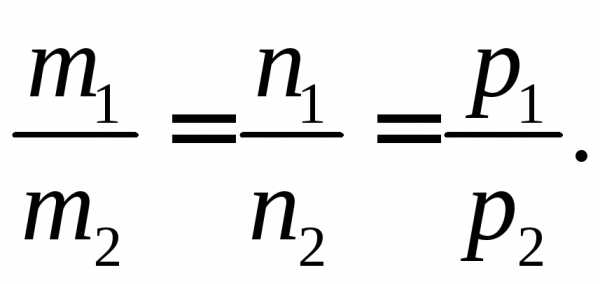
Условие
перпендикулярности прямых L1 и L2 выражается равенством нулю скалярного
произведения векторов 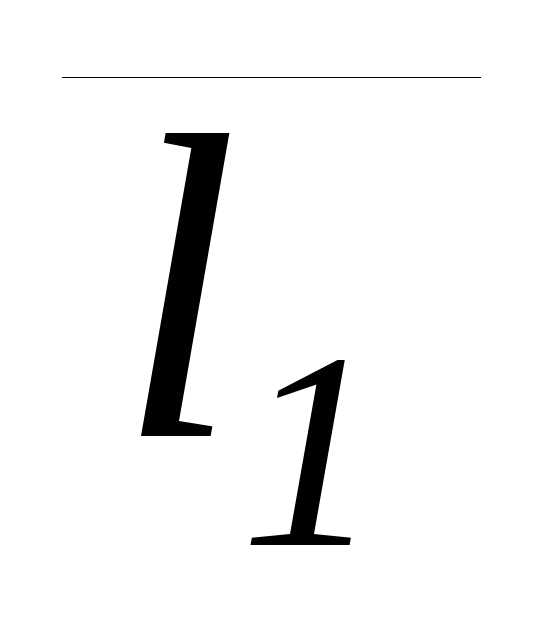 и
и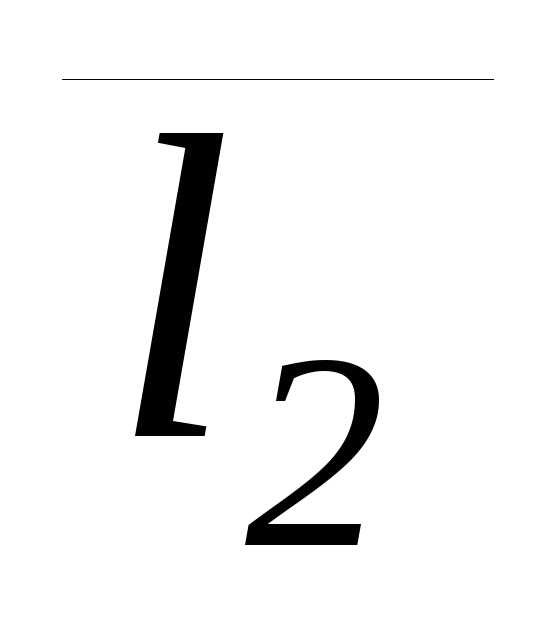 :
:
m1m2+n1n2+p1p2=0.
studfiles.net

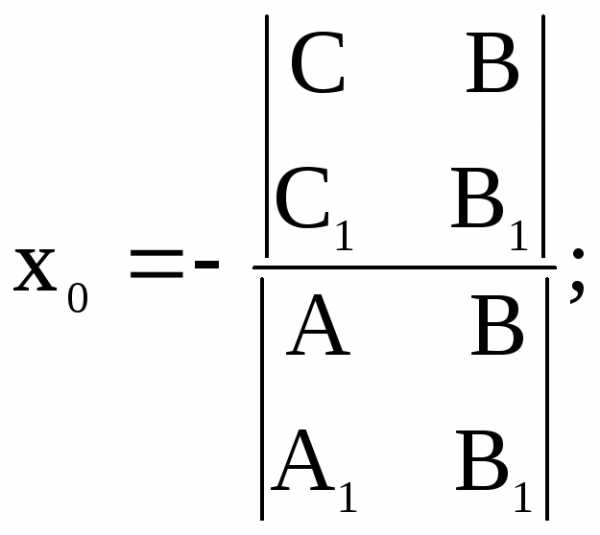
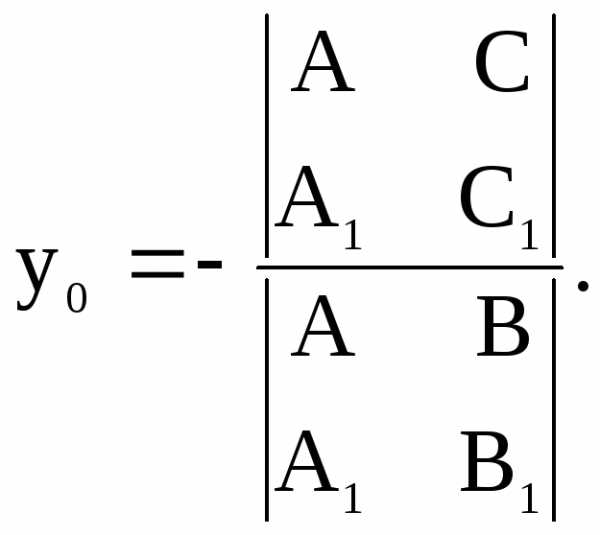
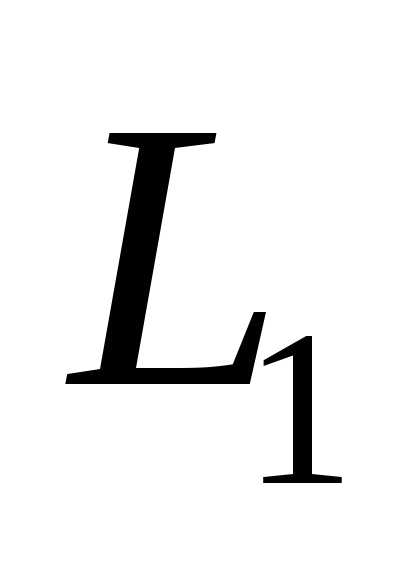 и
и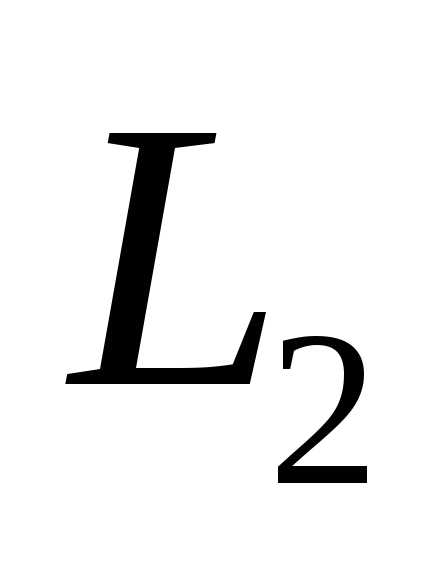

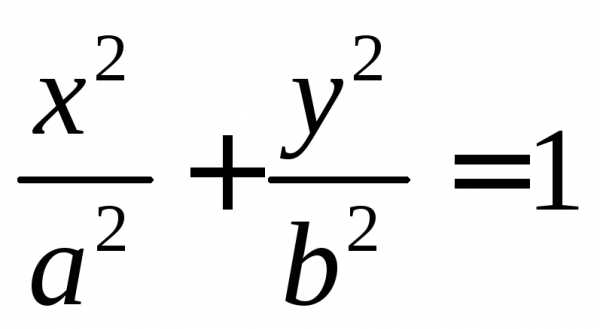
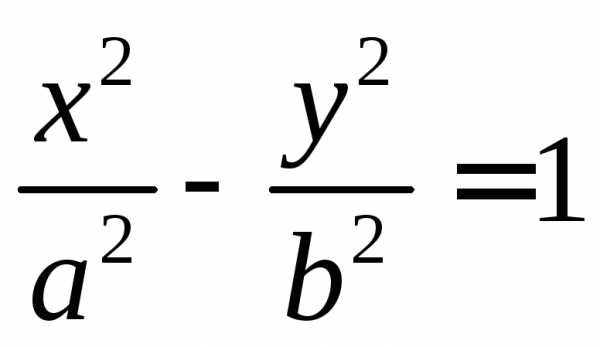
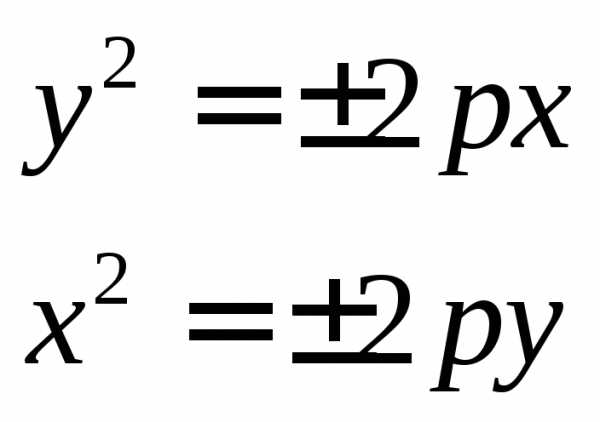
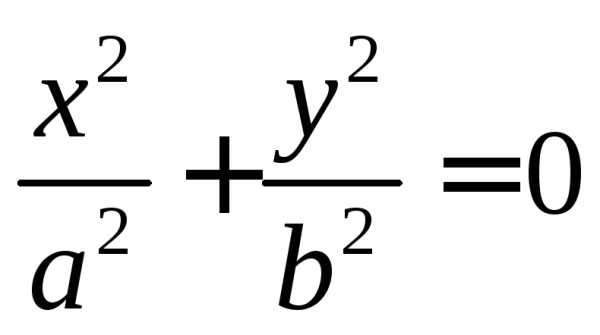
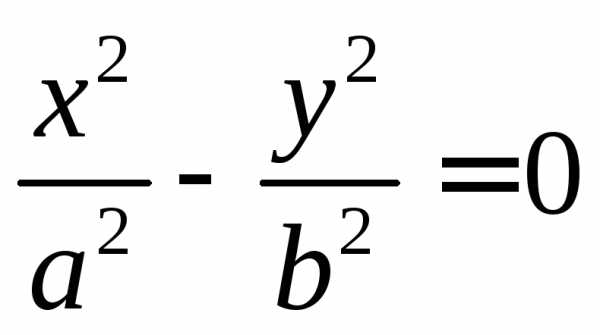
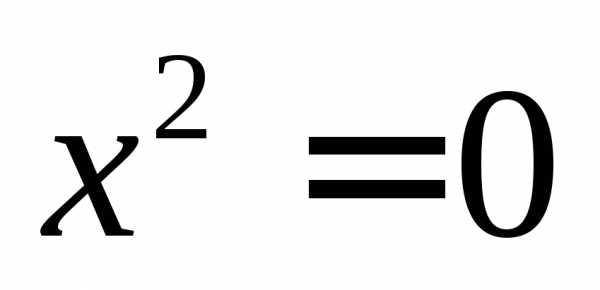 или
или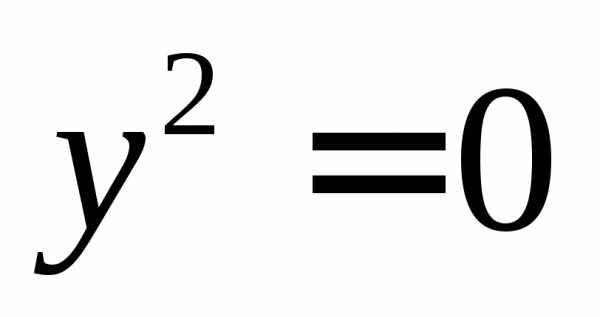
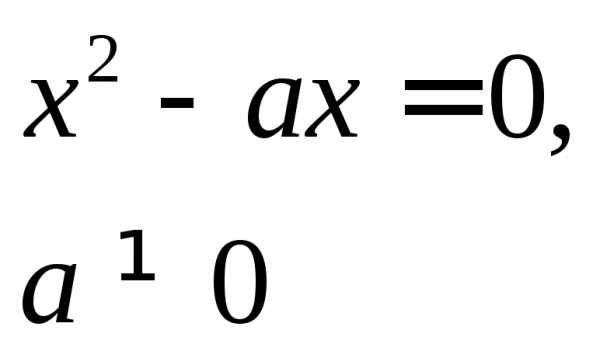
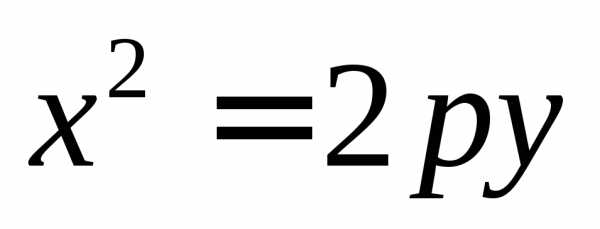 приp>0.
приp>0.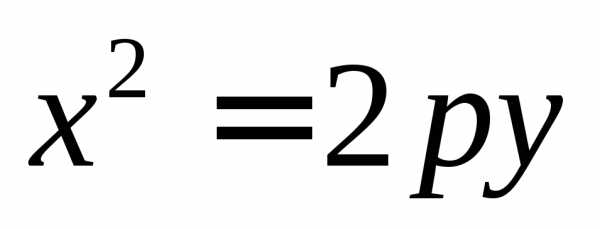 приp<0.
приp<0.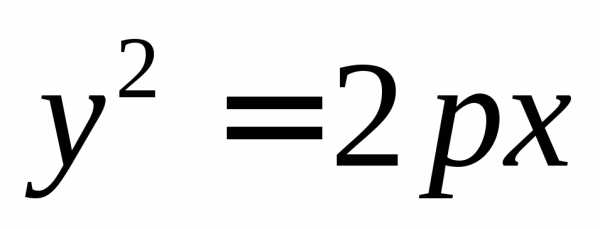 приp>0.
приp>0.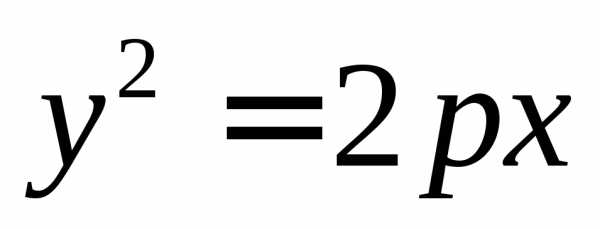 приp<0.
приp<0.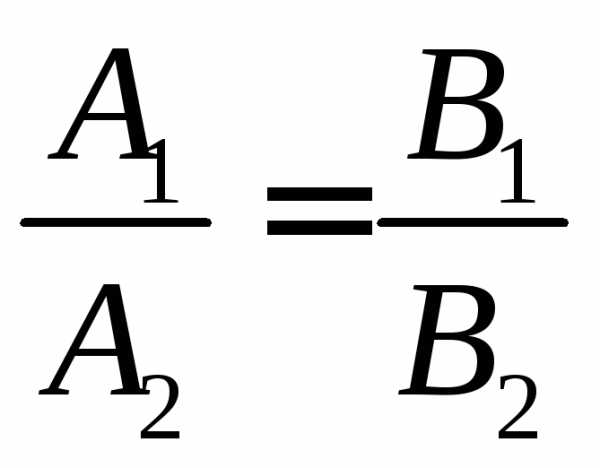
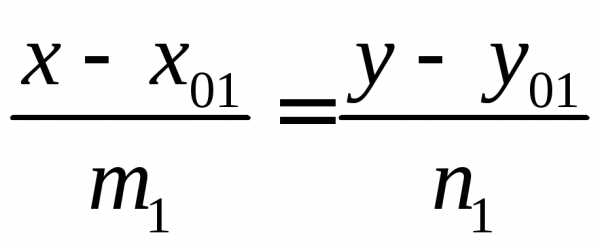 ,
,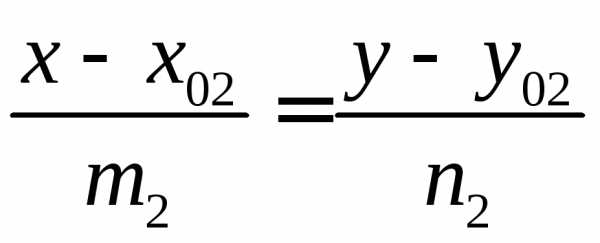 .
.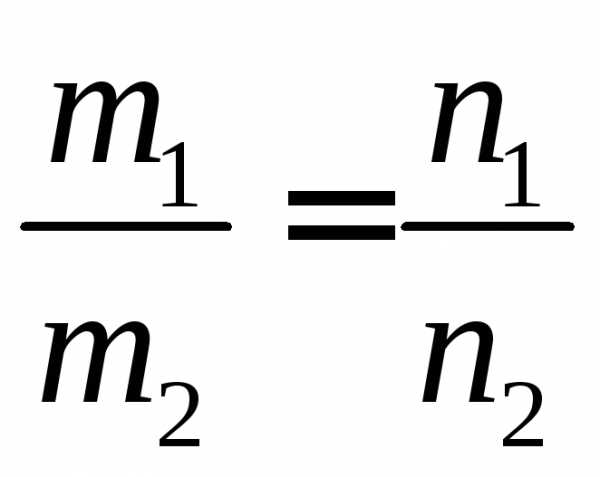
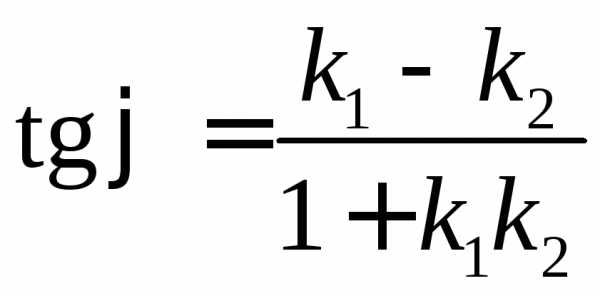
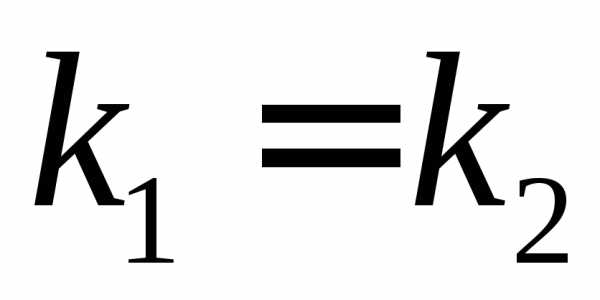
 ,
будет удовлетворять условию.
,
будет удовлетворять условию.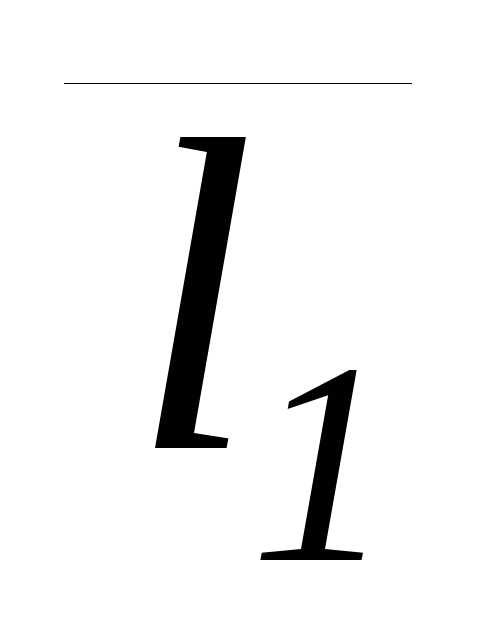 ,
,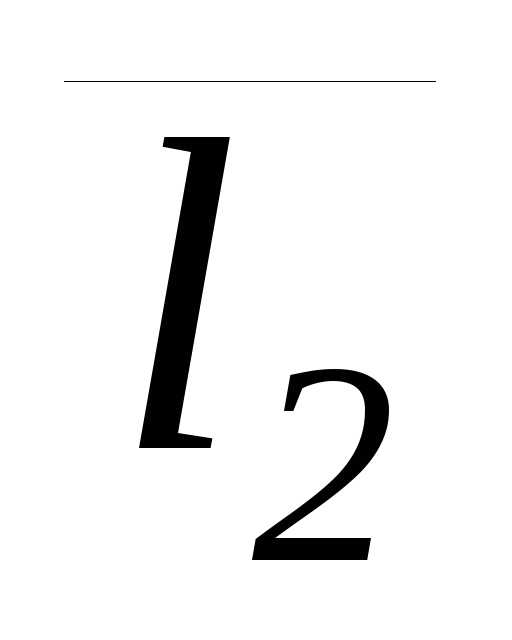 ,
тогда множество точекМ плоскости
будет удовлетворять условию, что векторы
,
тогда множество точекМ плоскости
будет удовлетворять условию, что векторы 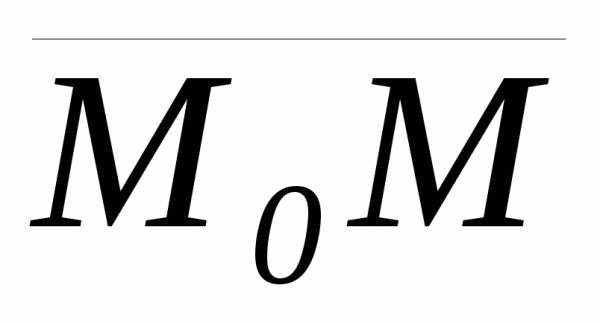 ,
,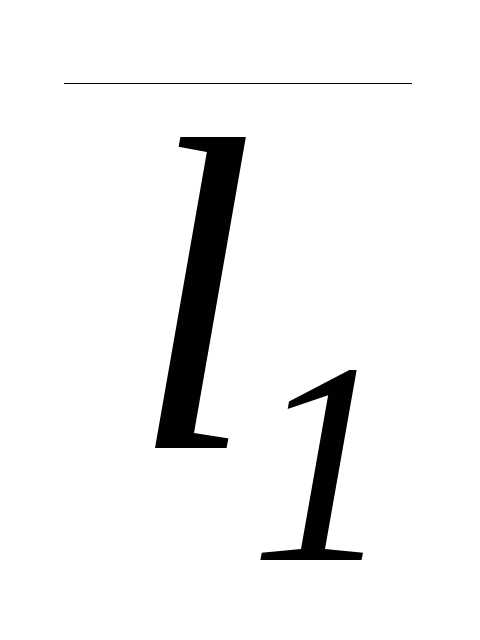 ,
, компланарны
компланарны