Учитель Сообщение темы урока «Применение основного свойства пропорции при решении уравнений»; Цели урока сообщают учащиеся Ход урока: 1. Устная работа (слайд 1) На доске: Заполните пропуски 1 м= см= мм, 1 км= м= см 1 ц= кг, 1 кг= г 1 ч= мин, 1 мин= с Найдите отношение величин (слайд 2) Ответить на вопросы: Что такое пропорция? Что такое отношение? Как называются члены пропорции? Сформулируйте основное свойство пропорции. Как можно проверить, верна ли пропорция? Проверить, верна ли пропорция (слайд 2) Решение задачи на определение масштаба карты Чтобы вычислить масштаб карты, мы должны, найти какое отношение? Определить масштаб карты Решение задачи на отношение Задание на составление пропорции из предложенных чисел Историческая справка Решение уравнений 6 человек работают на обычной доске, 1 работает на интерактивной доске. Остальные ученики решают уравнения с листов, выбирая для себя уровень сложности, тот, кто справится у доски быстрее, так же может сесть и решать уравнения с листа. Когда решили все уравнения на доске, определяем ключевое слово, используя ключ. Ученики, которые решали уравнения с листов проверяют по таблице свои ответы и ставят плюсы, где правильный ответ (тетради после урока должны быть сданы для выставления оценок). Приступаем к выполнению теста. (презентация – тест) Работа проходит в парах – пульт один на парту Тест состоит из 7 вопросов, в каждом вопросе предложены 4 варианта ответа, среди них только один правильный. После того, как ответили на вопрос, объяснить какой ответ правильный и показать диаграмму кто как ответил, чтобы ученики смогли увидеть допустили ли они ошибку или нет. Подведение итогов урока: Что мы делали сегодня на уроке? Как мы решали уравнения, чем пользовались для решения уравнения? Домашнее задание: номера из учебника. | Ученик 1м=100см=1000мм 1км=1000м=100000см 1ц=100кг, 1кг=1000г 1ч=60мин, 1мин=60с Равенство двух отношений Частное двух чисел Средние и крайние члены В верной пропорции произведение крайних членов равно произведению средних членов. Если произвед. крайних чл. равно произвед. средних членов, то пропорция верна. По определению пропорции, по основному свойству Отношение длины отрезка на карте к длине на местности Лейбниц 1-В, 2-Д, 3-А, 4-В, 5-С, 6-С, 7-С. |
pedsovet.su
Пропорции и отношения, прямая и обратная пропорциональность
Определение: Пропорцией называется равенство двух отношений.
или .
Основное свойство пропорций
Произведение крайность членов членов пропорции равно произведению ее средних членов: если, то
Свойства пропорций
- Произведение крайность членов членов пропорции равно произведению ее средних членов: .
- Каждый крайний член пропорции равен произведению ее средних членов, деленному на другой крайний член.
- В каждой пропорции можно поменять местами или только средние члены или крайние, или и те, и другие одновременно.
Пример нахождения пропорции в математике
Если , то
В пропорции изменим местами средние члены или крайние члены, тогда получим опять правильные равенства:
и
Производные пропорции
Если заданная пропорция , то , что называется производной пропорцией.
Наиболее часто употребляемые производные пропорции
Масштаб
Определение: Масштаб — отношение расстояния на карте к соответствующему расстоянию на реальной местности.
Прямо пропорциональные величины
Определение: Две величины называются
Задачи на прямо пропорциональные величины
Сторона квадрата равна 3 дм. Как изменится периметр квадрата, если его сторону увеличить в 3 раза, в 4 раза, в 5 раз?
Сторона квадрата 3 дм, периметр 12 дм
Сторона квадрата 9 дм, периметр 36 дм
Сторона квадрата 12 дм, периметр 48 дм
Сторона квадрата 15 дм, периметр 60 дм
При увеличении стороны квадрата в 3 раза (была 3 дм, стала — 9 дм), периметр увеличился также в 3 раза (был 9 дм, стал — 36 дм).
Аналогично, при увеличении стороны квадрата в 4 раза (была 3 дм, стала — 12 дм), периметр увеличился также в 4 раза (был 12 дм, стал — 48 дм).
Вывод: при увеличении стороны квадрата в несколько раз, периметр увеличивается во столько же раз.
Сторона квадрата прямо пропорциональна его периметру.
Обратно пропорциональные величины
Определение: Две величины называются обенено пропорциональными, если с увеличением значений одной из них в несколько раз значение другой уменьшается во столько же раз.
Задачи на обратно пропорциональные величины
Расстояние между двумя поселками равно 160 км. За какое время можно доехать из одного поселка в другой, если скорость 10 км/ч увеличить в 2 раза, 4 раза, в 8 раз?
Скорость, км/ч 10 время, ч 16
Скорость, км/ч 20 время, ч 8
Скорость, км/ч 40 время, ч 4
Скорость, км/ч 80 время, ч 2
При увеличении скорости в 2 раза (была 10 км/ч, стала — 20 км/ч), время сократился (уменьшился) в 2 раза (было 16 ч, стало — 8 ч).
Аналогично, при увеличении скорости в 4 раза (была 10 км/ч, стала — 40 км/ч), время сократился (уменьшился) в 4 раза (было 16 ч, стало — 4 ч).
Вывод: при увеличении скорости в несколько раз, время уменьшается во столько же раз.
Скорость обратно пропорциональна времени.
Числа пропорциональные числам , если — коэффициент пропорциональности
cubens.com
Пропорции | Математика
51. Пропорции. Рассмотрим особый вид равенства, а именно:
a/b = c/d;
это равенство показывает, что частное от деления числа a на число b равно частному от деления числа c на число d. Вместо «частно от деления числа a на число b» говорят «отношение числа a к числу b». Поэтому наше равенство мы можем прочесть: отношение числа a к числу b равно отношению числа c к числу d. Иногда еще читают и так: «число a относится к числу b, как число c к числу d». Подобные равенства называются пропорциями. Итак, пропорция есть равенство двух отношений. То число, которое является делимым каждого частного, называют предыдущим членом отношения: a есть предыдущий член 1-го отношения, c есть предыдущий член 2-го. Каждое из тех чисел, которое служит делителем, называется последующим членом отношения: b есть последующий член 1-го отношения и d есть последующий член 2-го отношения. Еще называют a и d крайними членами пропорции, а b и c — средними. Эти названия особенно ясны, если знак деления взять знак : и написать пропорцию в виде:
a : b = c : d.
Мы можем также рассматривать пропорцию:
a/b = c/d,
как равенство двух дробей, а именно: дроби a/b и дроби c/d.
Уничтожим в этом равенстве дроби. Для этой цели надо обе части равенства умножить на общего знаменателя, т. е. на bd. Получим:
abd/b = cbd/d
Сократив каждую дробь, получим:
ad = cb.
Это равенство можно прочесть словами: произведение крайних членов пропорции равно произведению ее средних членов.
Это свойство членов пропорции принимают за ее основное свойство.
Мы можем из этого равенства получить и еще следующие:
1. Разделим обе части равенства
ad = cb
на d (или на a), получим
a = cb/d (или d = cb/a),
т. е. один из крайних членов пропорции равен произведению средних, деленному на другой крайний.
2. Напишем наше равенство в обратном порядке:
cb = ad
и разделим обе части его на b (или на c), получим:
c = ad/b (или b = ad/c),
т. е. средний член пропорции равен произведению крайних, деленному на дрогой средний.
Пользуясь основным свойством пропорции, мы можем иногда освобождать те уравнения, какие имеют форму пропорции, от дробей без отыскания общего знаменателя.
Например, возьмем уравнение:
(x – 7) / (3x – 1) = 2/5.
Это уравнение имеет форму пропорции: отношение числа x – 7 к числу 3x – 1 равно отношению числа 2 к числу 5. Воспользуемся основным свойством пропорции, т. е. произведение крайних членов равно произведению средних; получим:
(x – 7 ) · 5 = (3x – 1) · 2
(ибо в нашей пропорции крайние члены суть x – 7 и 5, а средние — 3x – 1 и 2). Теперь уравнение без труда может быть решено.
maths-public.ru
Решение уравнений с использованием пропорций
Тема:
Решение уравнений с использованием пропорций.
Организационный момент.
П
Проверить устно составленные пропорции и ответы
роверка Д/З:
№1311
№1312
№
Письменно на доске
1341 (г-е)№1342(ж-и)
Актуализация знаний:
Перенести все слагаемые с неизвестным влево, без неизвестного – вправо.
а)
;б)
;в)
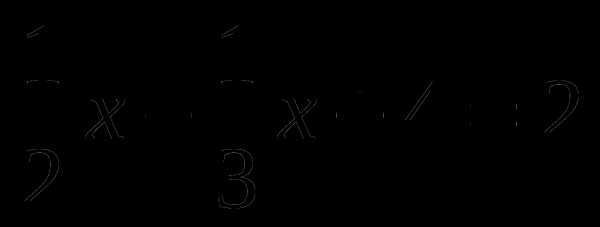 ;
;г)
;д)
;е)
.Решить уравнение:
а
№1318(в,г)
) ;б)
Новый материал:
Вспомним основное свойство пропорции:
Произведение крайних членов пропорции равно произведению средних членов пропорции
Р
ешим такое уравнение: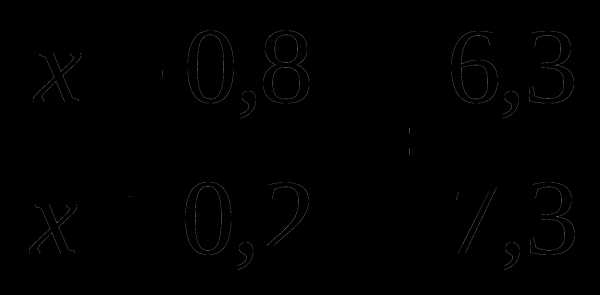
Средние члены пропорции
Средние члены пропорции
Приравняем теперь эти произведения и решим получившееся уравнение:
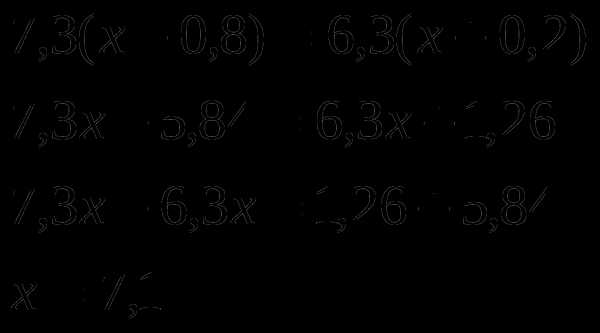
Закрепление:
№1320
В каждом примере назвать: крайние члены, средние члены, произведение крайних членов, произведение средних членов.
Проверка знаний(самостоятельная работа на 15 мин.)
Итог урока: как мы уже говорили, упрощение выражений – это инструмент, который нужен в том числе и для решения уравнений. Уравнения же – это тоже инструмент для решения многих задач. Именно этим мы и займемся на следующем уроке.
Домашнее задание: №1342(к-м), №1348, 1369
globuss24.ru
