Уравнения пуассона решение – 2.4.2. Решения уравнения Пуассона

2.4.2. Решения уравнения Пуассона

Пример. Найти функцию 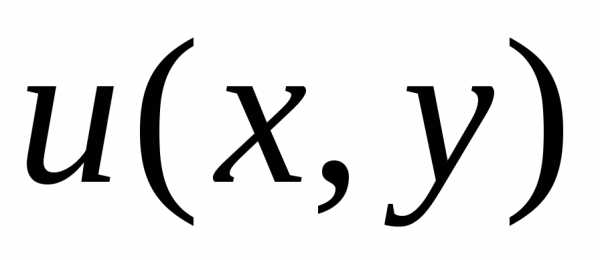, удовлетворяющую неоднородному уравнению Лапласа – уравнению Пуассона

(2.107)

и однородным граничным условиям на прямоугольном контуре (см. рис.2.2)

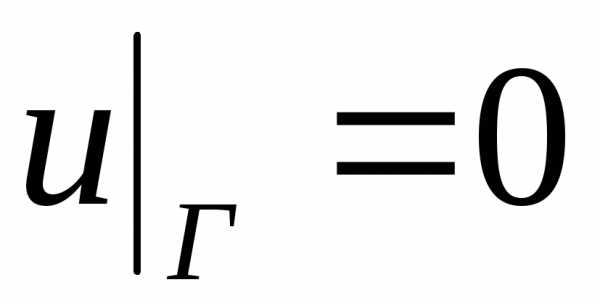. (2.108)

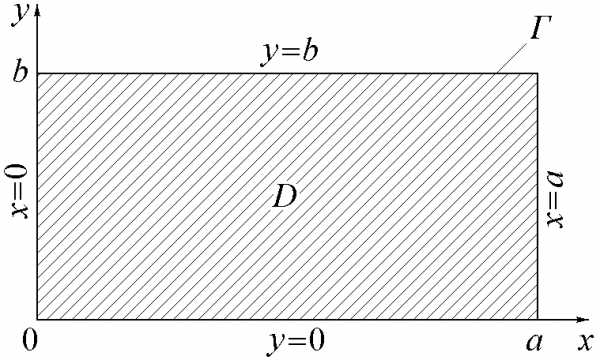
Рис.2.2.

Решение. Будем искать решение задачи (2.107–2.108) в виде разложения в ряд по собственным функциям однородной задачи

. (2.109)

При этом удовлетворяются граничные условия на вертикальных сторонах области

x = 0 и x = a. Функцию Y_n(y) следует определить так, чтобы функция u(x, y) удовлетворяла уравнению (2.107) и граничным условиям на горизонтальных границах y = 0 и y = b. Для этого подставляем (2.109) в уравнение (2.107). Тогда получим

. (2.110)

В левой части уравнения имеем ряд Фурье по синусам на промежутке [0, a]. Разложим функцию в правой части (2.110) также в ряд Фурье по синусам на том же промежутке:

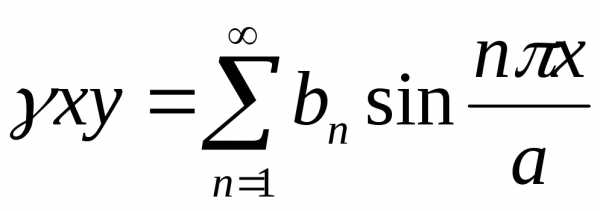, (2.111)

. (2.112)

Подставляем выражение (2.111) с учётом (2.112) в правую часть уравнения (2.110):

.

В результате для определения функции Y_n(y) приходим к обыкновенному линейному неоднородному дифференциальному уравнению второго по­ряд­ка с постоянными коэффициентами:

. (2.113)

Однородное уравнение, соответствующее уравнению (2.113), совпадает с (2.90), и его общее решение согласно (2.91) имеет вид

.

Частное решение 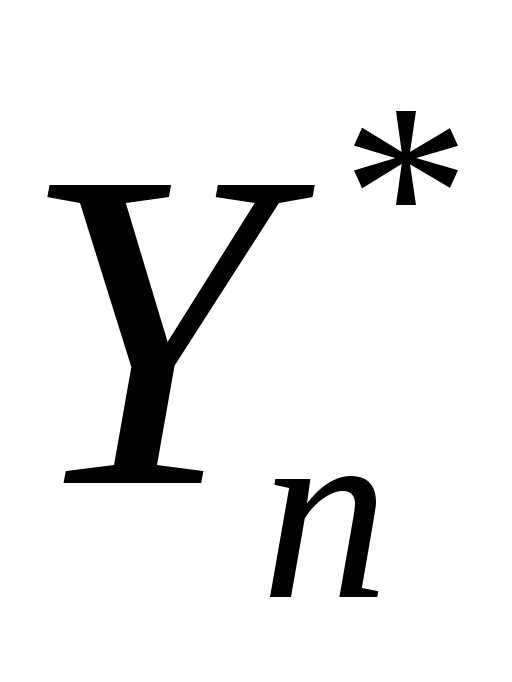неоднородного уравнения (2.113) легко находится методом подбора:

.

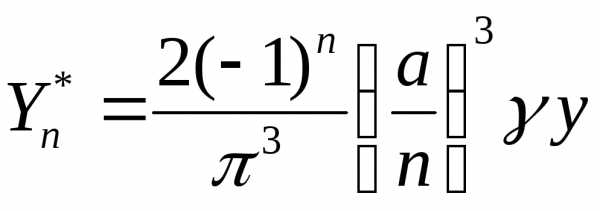В результате общее решение уравнения (2.113) примет вид

. (2.114)

После подстановки (2.114) в равенство (2.109) получаем

. (2.115)

Функция u(x, y) в выражении (2.115) удовлетворяет уравнению (2.107) и граничным условиям на сторонах x = 0 и x =

a. Константы α_n и β_n найдём из условия удовлетворения граничным условиям на горизонтальных сторонах области y = 0 и y = b.

При y = 0 из условия u(x, 0) = 0 имеем

,

откуда в силу произвольности функции следует

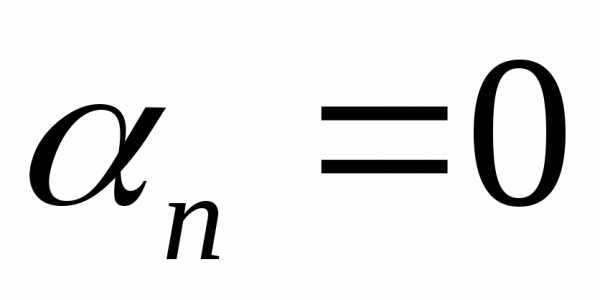. (2.116)

При y = b из условия u(x, b) = 0 с учетом α_n = 0 находим

,

и, следовательно

.

Из последнего равенства находим

. (2.117)

Подставляя (2.116) и (2.117) в (2.115), окончательно получим решение поставленной задачи в виде

.

Пример. Две стороны AC и BC прямоугольного однородного бруса 0ACB покрыты тепловой изоляцией (на рисунке 2.3 они выделены жирными линиями), а две другие поддерживаются при температуре, равной нулю. Найти стационарное распределение температуры при условии, что в брусе выделяется тепло с плотностью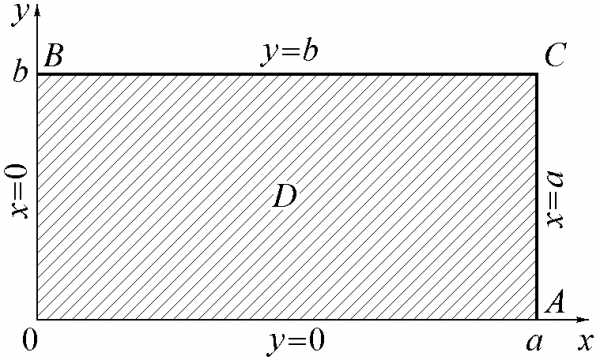

Рис.2.3.

Решение. Задача сводится к решению уравнения

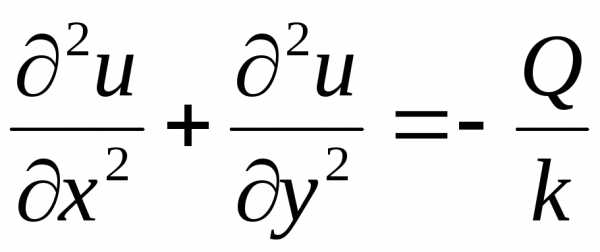, (2.118)

при краевых условиях

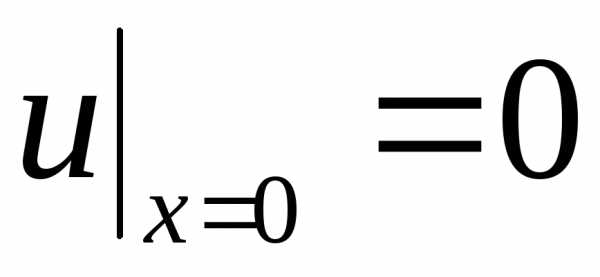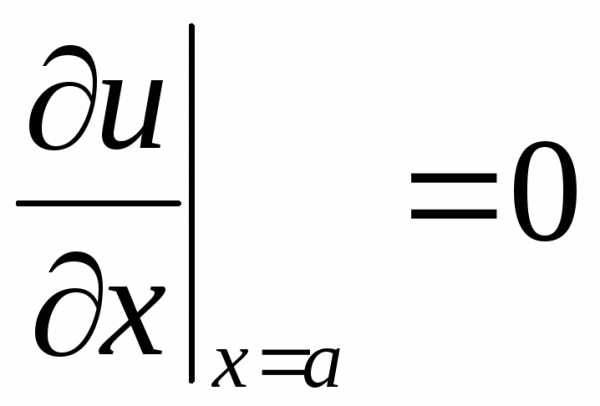, , (2.119)

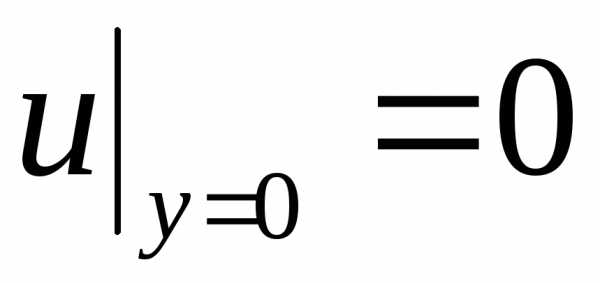
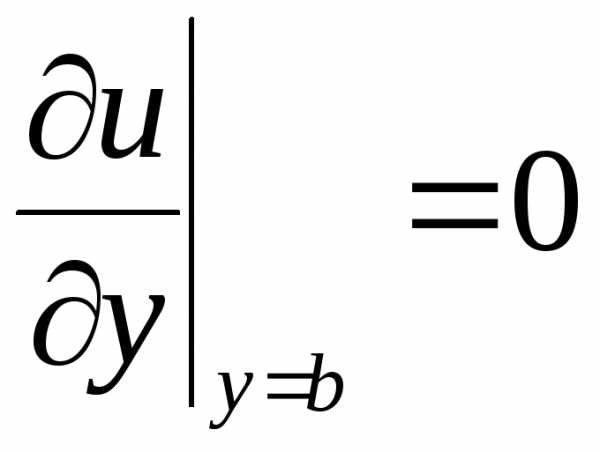, . (2.120)

Здесь k – коэффициент внутренней теплопроводности.

Сначала находим решение однородного уравнения Лапласа (2.80) методом разделения переменных, принимая, как обычно, согласно (2.84)

.

Тогда после обычных преобразований, характерных для метода разделения переменных, получаем для функций X(x) и Y(y) независимые обыкновенные линейные однородные уравнения (2.86), (2.87). Подставляя далее (2.84) в граничные условия (2.119), получим

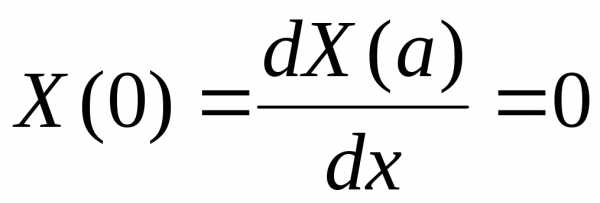. (2.121)

Таким образом, для определения функции X(x) приходим к задаче на собственные значения (2.86), (2.121). Собственные значения этой задачи будут

, (2.122)

а соответствующие собственные функции с точностью до множителя будут равны

. (2.123)

Раскладываем далее искомую функцию u(x, y) и правую часть в уравнении (2.118) в обобщённые ряды Фурье по системе ортогональных на [0, a] функций (2.123):

, (2.124)

. (2.125)

При этом коэффициенты C_n определяются по формуле (1.24):

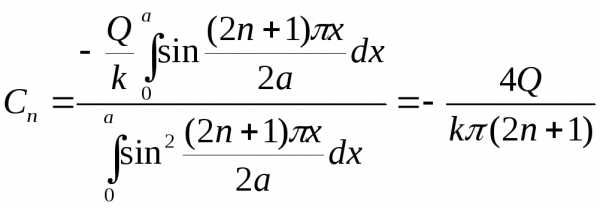. (2.126)

Подставляя (2.124) и (2.125) в уравнение (2.118), получим обык­новенное линейное неоднородное дифференциальное уравнение второго порядка относительно функции Y_n(y)

. (2.127)

Общее решение однородного уравнения (2.127) находим, как и для уравнения (2.90), в виде

.

Частное решение неоднородного уравнения (2.127) при постоянной правой части, как легко видеть, будет равно

.

Поэтому общее решение уравнения (2.127) запишется в виде

. (2.128)

Подставляя (2.128) в (2.124), получим

. (2.129)

Произвольные постоянные α_n и β_n в общем решении (2.129) находим из граничных условий (2.120) на горизонтальных сторонах области.

При y = 0 имеем

,

откуда в силу произвольности функции следует:

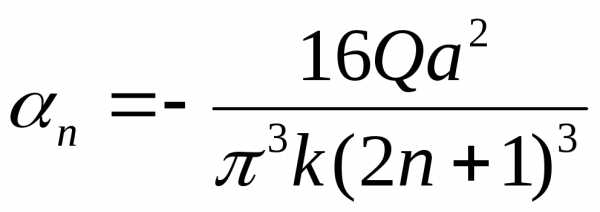. (2.130)

Из второго граничного условия (2.120) с учетом (2.130) получим

. (2.131)

Подставляя (2.130) и (2.131) в (2.129) и используя формулу сложения для гиперболических функций

,

после несложных преобразований получим окончательное решение задачи в виде

.

Пример. Найти решение уравнения Пуассона

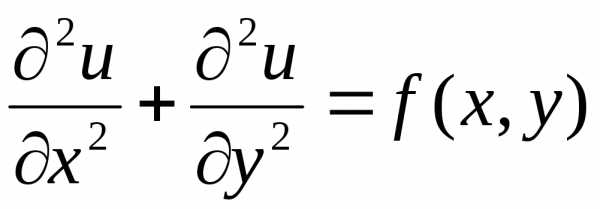(2.132)

в прямоуголь­ной области при следующих граничных условиях

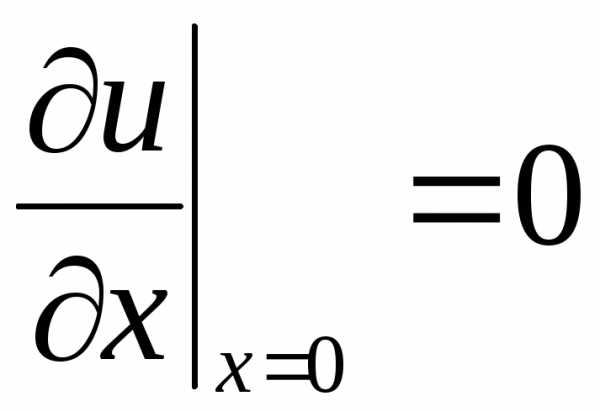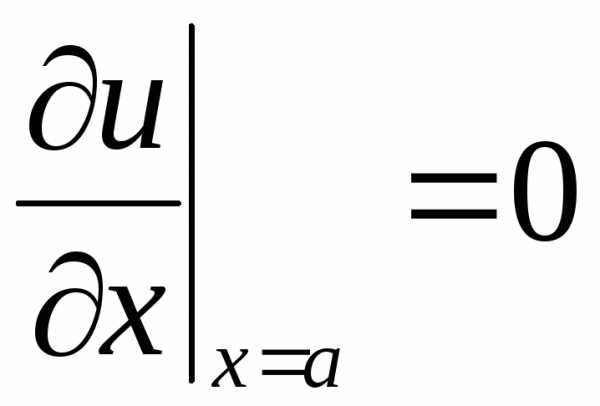, , (2.133)

,

. (2.134)

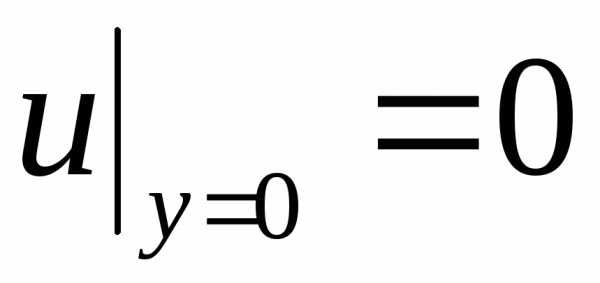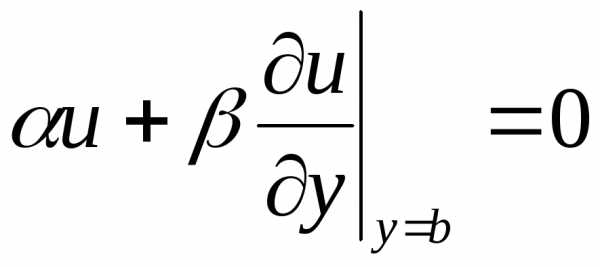
Решение. Решая сначала, как и в предыдущем примере, однородное уравнение Лапласа (2.80) методом разделения переменных и используя представление (2.84)

,

с учетом граничных условий (2.133) на вертикальных сторонах области для определения функции X(x) приходим к задаче на собственные значения

. (2.135)

Собственные значения этой задачи будут

(2.136)

а соответствующие собственные функции с точностью до множителя

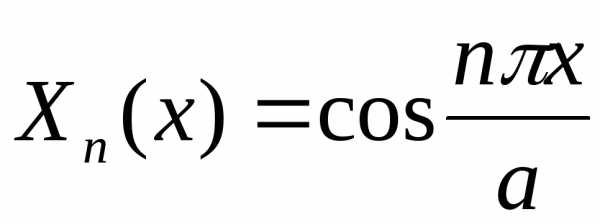. (2.137)

Далее раскладываем в ряды Фурье по собственным функциям однородной задачи искомую функцию u(x, y) и правую часть уравнения (2.132):

, (2.138)

, (2.139)

при этом

. (2.140)

Подставляя (2.138) и (2.139) в (2.132), после обычной процедуры приходим к обыкновенным линейным неоднородным уравнениям второго порядка относительно функций Y_n(y) (n = 0, 1, 2,…):

, (2.141)

. (2.142)

Подставляя (2.138) в граничные условия (2.134), в силу линейности задачи (2.132–2.134) представим граничные условия для функций Y₀(y) и Y_n(y) в виде

, (2.143)

, (n = 1, 2,…). (2.144)

Таким образом, для определения функций Y₀(y) и Y_n(y) приходим к краевым задачам (2.141) и (2.143) и соответственно (2.142) и (2.144). Общее решение однородного уравнения (2.141) будет

,

а общее решение однородного уравнения (2.142), как было показано выше, имеет вид

(n = 1, 2,…).

Частные решения 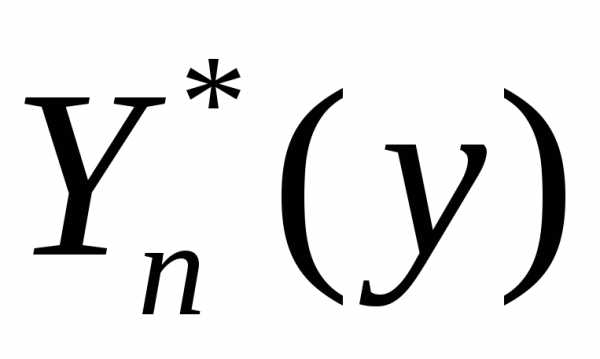уравнений (2.141–2.142) находятся методом подбора или методом вариации произвольных постоянных. Далее должны быть определены произвольные постоянные в общих решениях уравнений (2.141–2.142)

, (2.145)

(n = 1, 2,…). (2.146)

из граничных условий (2.143), (2.144).

Окончательное решение поставленной задачи запишется после подстановки (2.145) и (2.146) с учётом найденных значений произвольных постоянных в (2.138).

studfiles.net

Уравнение Пуассона и математическая постановка задач электростатики

Существует большое количество случаев, когда самым удобным методом нахождения напряженности поля считается решение дифференциального уравнения для потенциала. После его получения применим в качестве основы теорему Остроградского-Гаусса в дифференциальной форме:

где ρ является плотностью распределения заряда, ε0 — электрической постоянной, div E→=∇→E→=∂Ex∂x+∂Ey∂y+∂Ez∂z — дивергенцией вектора напряженности и выражением, связывающим напряженность поля и потенциал.

Произведем подстановку (2) в (1):

Учитывая, что divgrad φ=∇2φ=∂2φ∂x2+∂2φ∂y2+∂2φ∂z2, где ∆=∇2 — это оператор Лапласа, равенство (3) принимает вид:

Выражение (4) получило название уравнения Пуассона для вакуума. При отсутствующих зарядах запишется как уравнение Лапласа:

После нахождения потенциала переходим к вычислению напряженности, используя (2). Решения уравнения Пуассона должны удовлетворять требованиям:

• значение потенциала как непрерывная функция;
• потенциал должен быть конечной функцией;
• производные потенциала как функции по координатам должны быть конечными.

При наличии сосредоточенных зарядов в объеме V, решение уравнения (4) будет выражаться для потенциала вида:

Определение 1

Общая задача электростатики сводится к нахождению решения дифференциального уравнения, то есть уравнения Пуассона, удовлетворяющего вышеперечисленным требованиям. Теоретические вычисления известны для небольшого количества частных случаев. Если возможно подобрать функцию φ, удовлетворяющую условиям, то она является единственным решением.

В таких задачах не всегда необходимо задавать заряды или потенциалы во всем пространстве. Для нахождения электрического поля в полости, окруженной проводящей оболочкой, достаточно вычислить поле тел, находящихся внутри нее.

Любое решение уравнения Пуассона ограниченной области может быть определено краевыми условиями, накладывающимися на поведение решения. Границы перехода из одной среды в другую имеют условия, которые должны быть выполнены:

E2n-E1n=4πσ, или ∂φ1∂n-∂φ2∂n=0.

E1τ=E2τ.

φ1=φ2,

где σ — это по

zaochnik.com

Задание №5 Численное решение уравнения Пуассона

Задание № 5

ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЯ ПУАССОНА

В ПРЯМОУГОЛЬНИКЕ

Цель работы — изучение разностных схем для уравнений эллиптического типа, численное решение уравнения Пуассона в прямоугольнике методами Зейделя или последо­вательной верхней релаксации.

ПОСТАНОВКА ЗАДАЧИ

Типичным уравнением в частных производных эллиптического типа является уравнение вида

–u + u = f.

При   0, f  0 уравнение представляет собой неоднородное уравнение Гельмгольца, при   0, f = 0 – однородное уравнение

Гельмгольца, при  = 0 и f  0  — уравнение Пуассона

u = –f

и, наконец, при  = 0 и f = 0 — уравнение Лапласа.

Так, однородным уравнением Гельмгольца

описывается стационарное распределение в резонаторе электрического поля 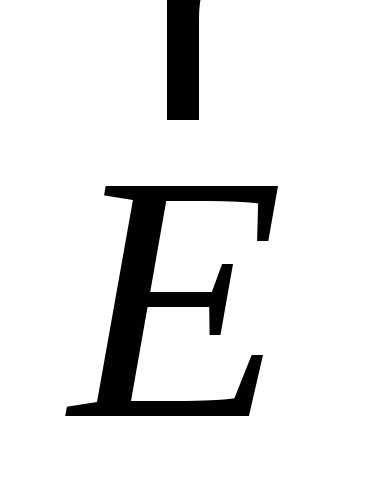с волновым числомk; уравнение Пуассона

u = –/

описывает распределение электрического потенциала u в среде с плотностью заряда  и электрической проницаемостью  и т. п.

Установившееся распределение температуры (или плотности газа) также описывается уравнением Пуассона, которое получается из уравнения теплопроводности (диффузии) при u/t = 0.

Поскольку уравнения эллиптического типа часто встречаются в важных физических приложениях, для их решения разработано много численных методов, которые можно разделить на конечно-разностные и проекционные.

В дальнейшем ограничимся так называемой задачей Дирихле, или первой краевой задачей для уравнения Пуассона

в прямоугольнике с границей Г, используя равномерную сетку.

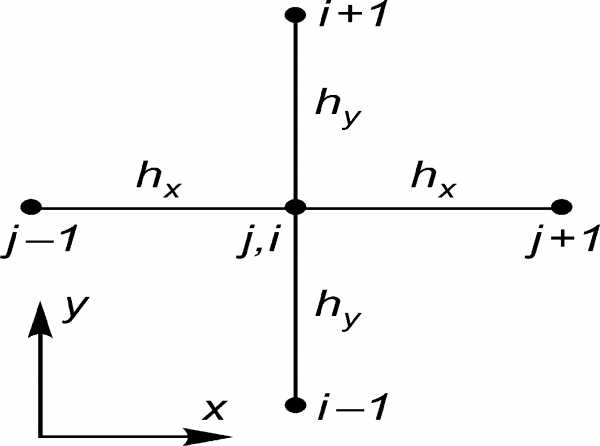
Рис. 1. Расположение узлов

пространственной сетки

для двумерного уравнения

эллиптического типа

Вводя в прямоугольнике G равномерную сетку, имеющую N шагов но х и М шагов по у, аппроксимируем вторые производные в операторе  = ²/x² + ²/y² конечно-разностными формулами на пятиточечном шаблоне «крест» (рис. 1) и построим разностную схему

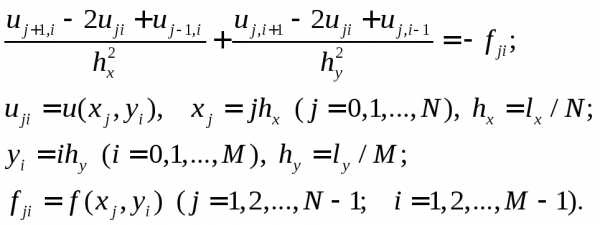
Приведём её к виду

Здесь h_x— шаг сетки по х, h_y— шаг по у, (x_j y_i) — узлы сетки.

Схема имеет погрешность аппроксимации O(h²_x, h²_y), т. е. это схема второго порядка; значения u_ji при j = 0, N и i = 0, M задаются краевыми условиями. Уравнения представляют собой систему (N — 1) (М — 1) линейных алгебраических уравнений, которую можно записать в виде

Au = b.

Здесь u — вектор значений u_ji во всех внутренних узлах сетки, имеющий (N – 1) (M – 1) элементов; b — вектор правой части, включающий как значения f_ji во внутренних узлах сетки, так и краевые значения; А — симметричная редкая матрица размерности

(N – l) (M – 1)  (N – 1) (М – 1).

Для решения полученной системы можно использовать рассмотренный ранее в задании № 5 второго семестра метод Зейделя или же применить метод последовательной верхней релаксации, ускорение сходимости с использованием Чебышевского набора итерационных параметров и др.

Решим уравнение итерационным методом Зейделя:

(1)

где k=l,2,…— номер итерации. Этот метод называют также схемой Либмана.

В качестве начального приближения можно принять любые значения, например:

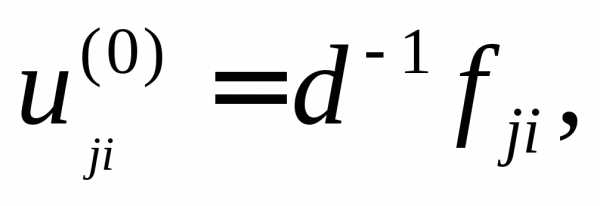
или даже

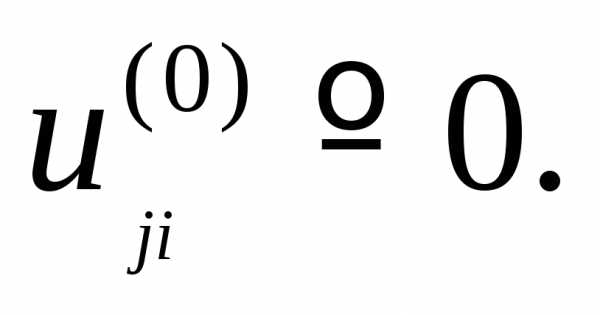
Одним из более эффективных методов решения уравнения (1) является предложенный Янгом и Франкелом итерацион­ный метод последовательной верхней релаксации. В этом методе каждая итерация в узлах (j,i) складывается из двух этапов.

Первый этап — вычисление предварительного значения методом Зейделя:

где k =1,2… — номер итерации.

Второй этап — вычисление окончательного значения в узле (j, i) по релаксационной формуле:

где 0< ω <2 — релаксационный параметр.

Объединяя эти два этапа получаем расчетную формулу:

Максимальная скорость сходимости итераций достигается при оптимальном значении релаксационного параметра

где λ_max — модуль максимального собственного значения матрицы метода простой итерации в правой части исходного уравнения, т. е. λ — это решение проблемы собственных значений

Отыскивая решение уравнения в прямоугольнике G в виде

находим собственные значения

Максимальное значение λ достигается при п = т =1:

В частности, в случае квадратной области G при N = M:

В качестве начального приближения можно по-прежнему принять приведенные ранее значения.

И

(2)

терации прекращаются при выполнении условия

где ε — заданная малая величина.

ВАРИАНТЫ ЗАДАНИЙ

ВАРИАНТЫ ПРАВОЙ ЧАСТИ f(x,у) УРАВНЕНИЯ

ВАРИАНТЫ КРАЕВЫХ УСЛОВИЙ

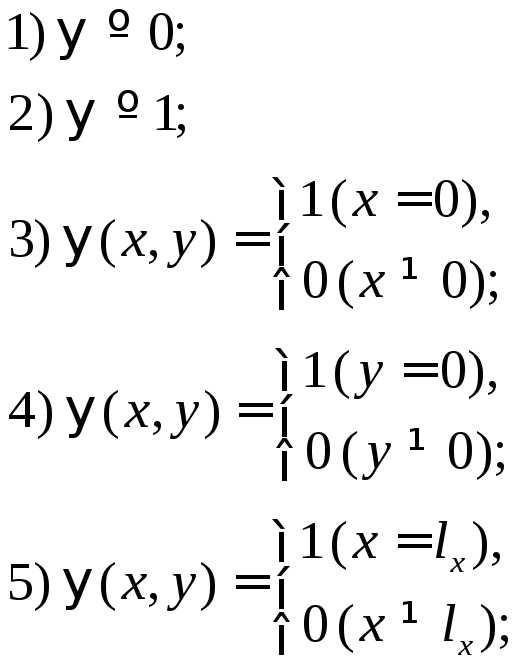
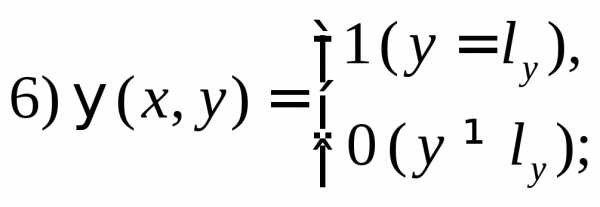
ПРОГРАММИРОВАНИЕ

Для хранения правой части f_ji и текущей итерации следует описать двумерные массивы. Правую часть удобно оформить в виде подпрограммы-функции. Норма (2) вы­числяется на этапе релаксации перед тем, как новое значение посылается на место прежнего.

Значения N, М достаточно взять небольшими в диапазоне 10 ÷50 для ускорения расчетов. Чтобы избежать зацикливания из-за ошибок в программе, следует задать максимальное число итераций k _max порядка нескольких сотен, по достижении которого итерации прерываются.

Блок-схема решения уравнения Пуассона методом последовательной верхней релаксации приведена на рис. 2.

Для проверки программы можно предварительно решить тестовую задачу при

и исследовать сходимость итераций к тривиальному решению

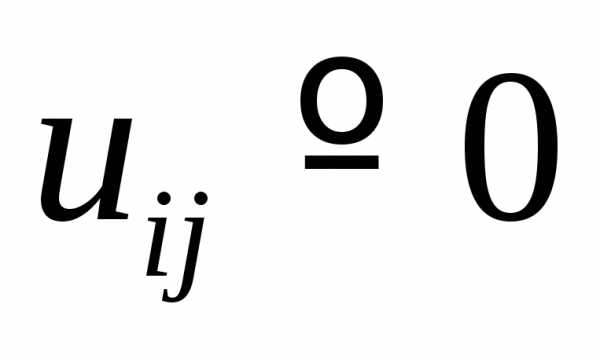
СОДЕРЖАНИЕ ОТЧЕТА

Отчет должен содержать:

• формулы и параметры для конкретного варианта;

• текст программы;

• результаты решения, число итераций и графики распределения потенциала в области.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какова погрешность конечно-разностного уравнения, по-

строенного на шаблоне «крест»?

2. Как строится численное решение уравнения Пуассона методом Зейделя?

3. Как строится численное решение уравнения Пуассона методом последовательной верхней релаксации?

4. Получите формулу для собственного значения матрицы исходной системы уравнений.

1. Какие еще существуют методы решения уравнения Пуассона?

5. Как определить скорость сходимости итераций?

6. Что такое невязка и погрешность численного решения?

9

studfiles.net

4. Уравнение Пуассона и Лапласа. Теорема единственности решения

Расчет электростатических полей с использованием уравнени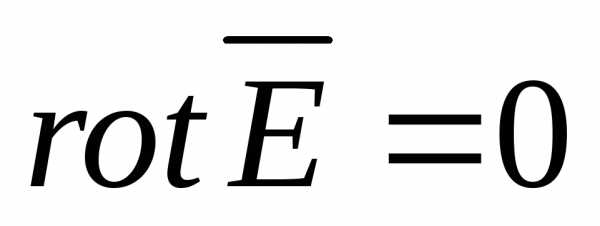й и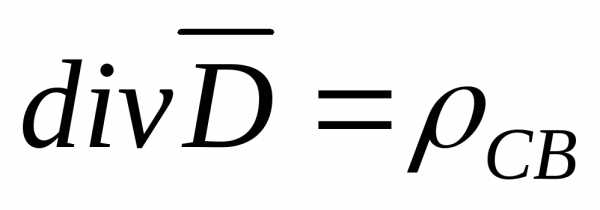возможен только в простейших случаях. Наиболее общим методом является расчет электро­статических полей на основе решения уравнений Пуас­сона и Лапласа. Выве­дем эти уравне­ния.

Ранее было получено . Подставим это выражение в уравнение ди­вергенции:

, откуда следует:

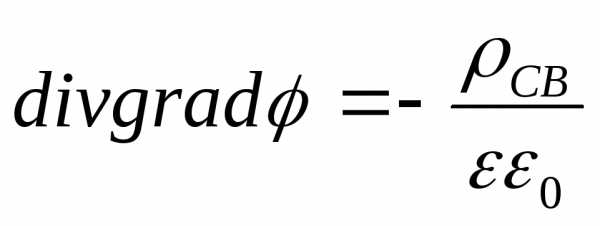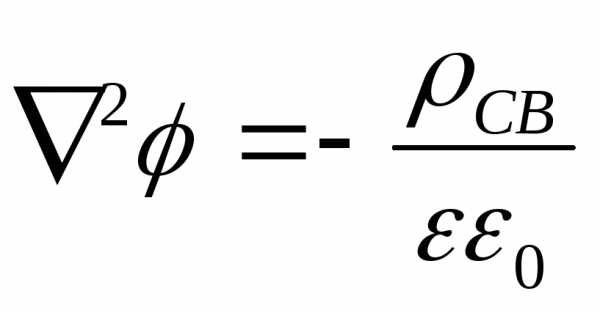или ― уравнение Пуассона.

Уравнение Пуассона справедливо для тех точек среды, где существуют объемные за­ряды .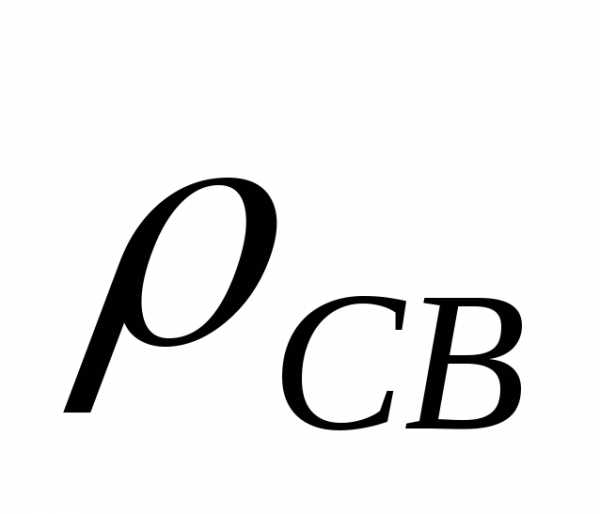

В реальных условиях свободные заряды располагаются на поверхности проводников бесконечно тонким слоем. Объемная плотность таких зарядов равна бесконечности и уравне­ние Пуассона применительно к ним теряет свой смысл.

В диэлектриках, которыми разделены заряженные проводники, объемные заряды от­сутствуют (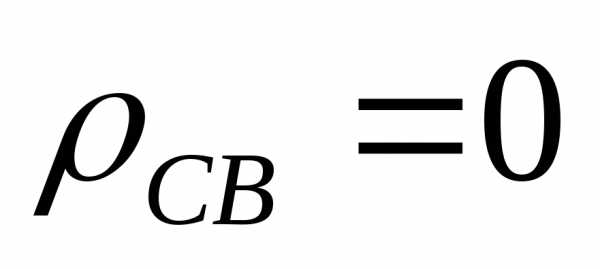), уравнение Пуассона превращается в уравнение Лапласа:

или 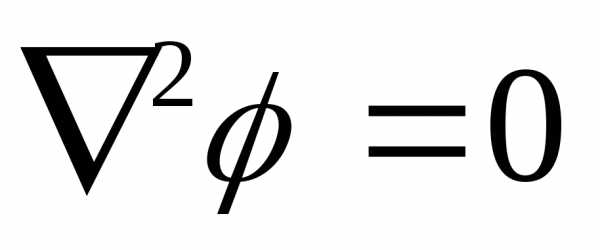― уравнение Лапласа.

Таким образом, электростатическое поле в диэлектрике описывается уравнением Лап­ласа, внутри проводников поле отсутствует вообще, а на гра­нице раздела диэлектрика с про­водником вступают в силу граничные усло­вия,.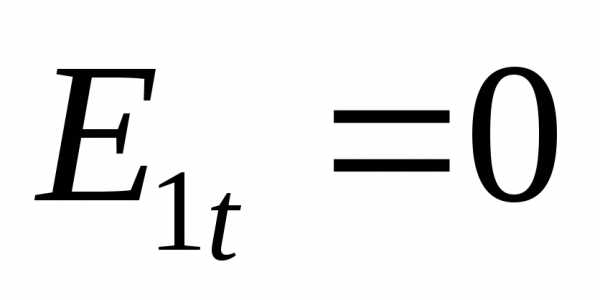

В декартовой системе координат операцию двойного дифференцирова­ниязаписы­вают так:

.

Уравнение Лапласа в электростатике имеет исключительно важное значе­ние.

Уравнения Пуассона и Лапласа, как уравнения в частных производных, допускают множество линейно независимых частных решений. Однако в реаль­ных условиях каждой конкретной задаче соответствует только одно определен­ное решение.

Теорема единственности решения гласит, что найденное любым способом решение уравнений Пуассона или Лапласа, является единственно верным реше­нием, если оно удовле­творяет граничным условиям данной задачи.

Предположим, что существует два решения для вектора напряженности поля 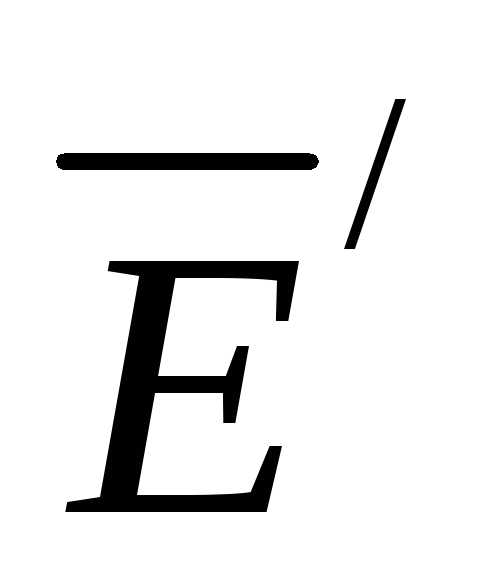и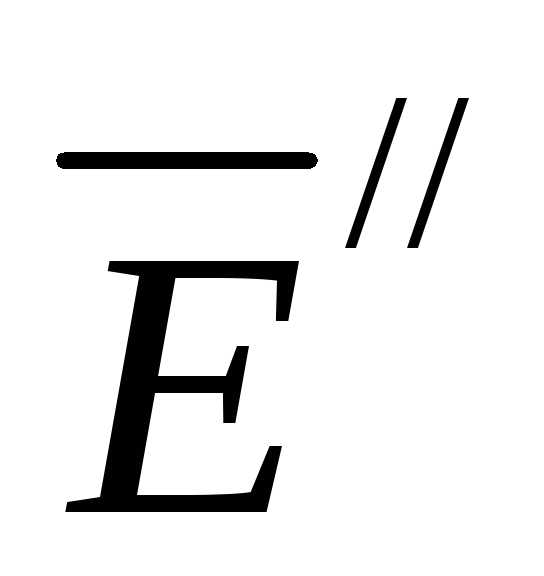, оба удовлетворяющие граничным условиям задачи. Тогда полу­чим:

.

Если rot и div от вектора равны нулю, то сам вектор тождественно равен нулю, следо­вательно , или, что требовалось доказать.

Из теоремы единственности решения вытекают два следствия, имеющее важное прак­тическое значение:

1. электростатическое поле в некотором объеме, ограниченном экви­потенциаль­ной поверхностью, не изменится, если эту поверхность заменить бесконечно тонким прово­дящим слоем;

2. электростатическое поле по одну сторону некоторой поверхности S не изме­нится, если по другую сторону поверхности изменить параметры среды (например, заменить поводящую среду диэлектриком) и изменить расположе­ние свободных зарядов так, чтобы на этой поверхности сохранились прежние граничные условия.

Второе следствие лежит в основе так называемого метода зеркальных отображений, применяемого на практике для расчета электростатических полей.

5. Электростатическое поле осевых зарядов

Ниже будет рассмотрено несколько примеров электростатических полей, создаваемых осевыми зарядами.

1. Поле уединенной равномерно заряженной оси (рис. 257а).

Pасчет параметров поля в произвольной точке n выполним с помощью теоремы Гаусса в интегральной форме. Окружим ось цилиндром с произволь­ным радиусом r и длиной обра­зующей l =1. Вектор электрического смещения 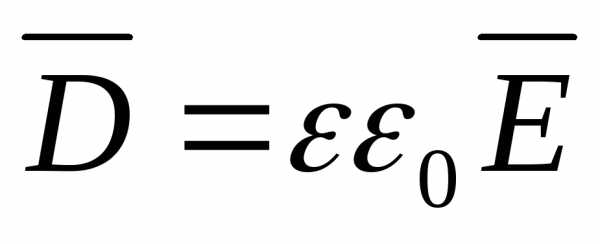в силу симметрии во всех точках на боковой поверхности цилиндра (r=const) имеет одно и то же значение и направление по ра­диусу, т.е. нормально к этой поверхности.

По теореме Гаусса получим:

.

Откуда следует, что .

Поток вектора 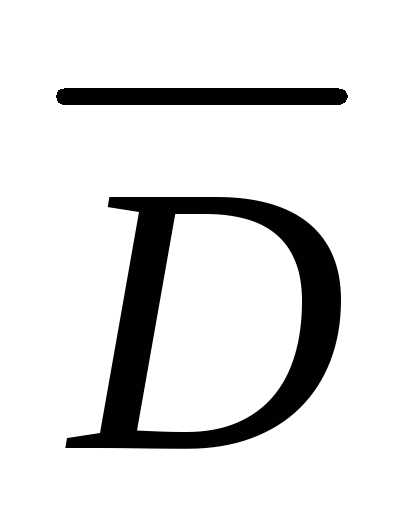через торцевые поверхности цилиндра равен нулю, так как линии вектора здесь направлены по касательной к поверхности.

В цилиндрической системе координат потенциал поля будет зависеть только от ра­диусаr: , откуда

.

Если принять на некоторой поверхности радиуса 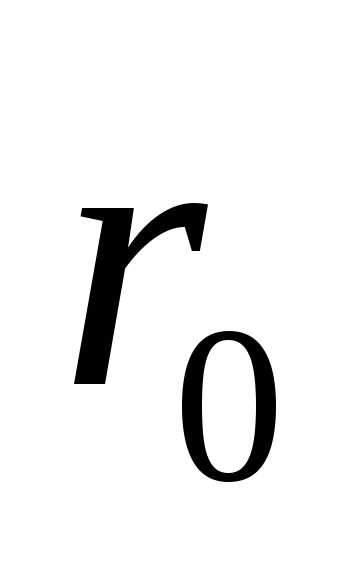значение потенциала равным нулю, то 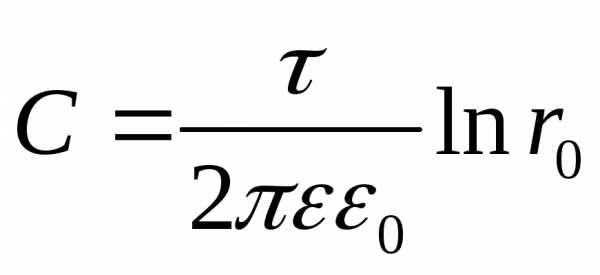и значение потенциала на поверхности произ­вольного радиуса бу­дет равна:

.

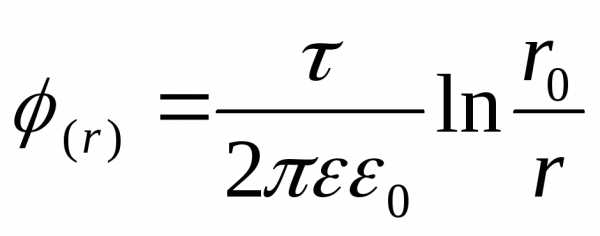2). Поле коаксиального кабеля (рис. 257б).

Конструктивно коаксиальный кабель состоит из внутреннего провода ра­диуса r₁ (прямой провод) и наружного провода в виде трубы или металличе­ского чехла радиуса r₂ (обратный провод), разделенных между собой диэлек­триком с относительной проницаемо­стью .

Реальные заряды в коаксиальном кабеле расположены равномерно по по­верхности внутреннего провода (жиле) и на внутренней поверхности внешней оболочки. В соответствии со вторым следствием из теоремы единственности заменим поверхностные заряды внутрен­него провода осевым зарядом с линей­ной плотностью , после чего к расчету параметров поля можно применить по­ложения и выводы, полученные ранее для заряженной оси:

.

Напряжение между внутренней жилой и оболочкой:

.

Емкость кабеля на единицу длины:

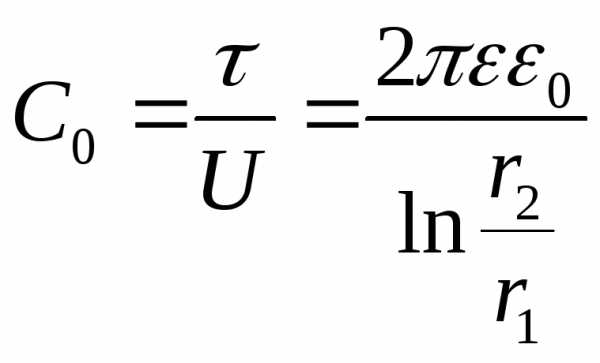, откуда следует, что .

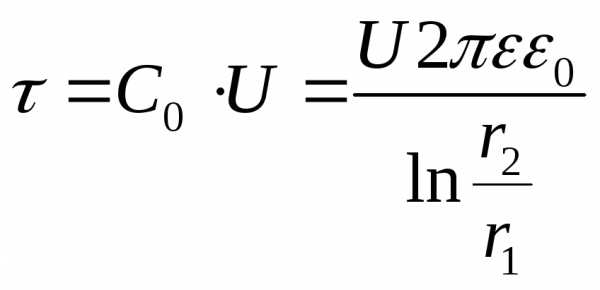Наибольшее значение напряженности поля имеет место на поверхности внутреннего провода при :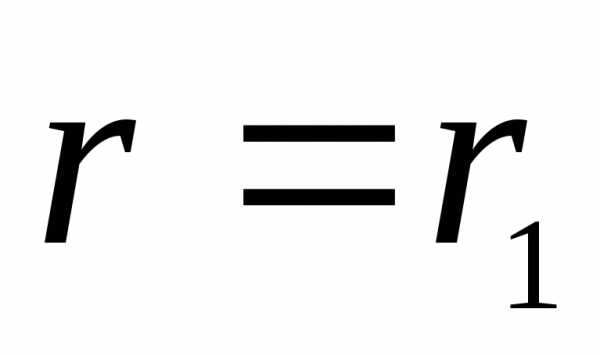

.

3). Поле двух разноименно заряженных параллельных осей (рис. 258). Две двух разно­именно заряженные оси расположены параллельно на расстоянии 2а в ди­электрическом пространстве.

E₁ E

n E₂

R r₁ r₂

₁= ₂= 

0 1 2

s-a a a

d

Рис. 258

Параметры поля в произвольной точке пространства n могут быть опреде­лены по ме­тоду наложения. Результирующий вектор напряженности поля ра­вен геометрической сумме составляющих, а результирующий потенциал – ал­гебраической сумме составляющих от каж­дого провода:

.

Если принять 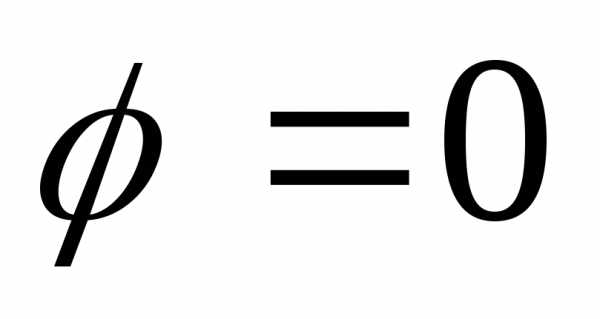в точках равноудалённых от обеих осей (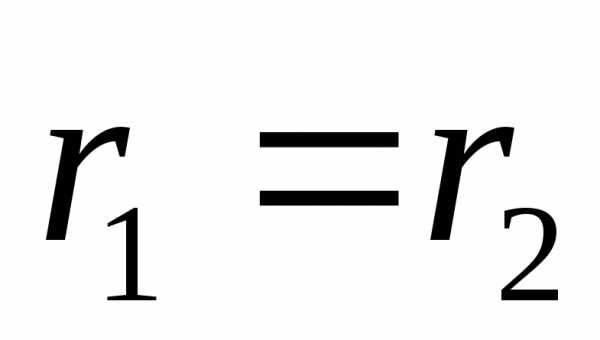), то постоянная интегрирования будет равна нулю (С=0), тогда получим:

.

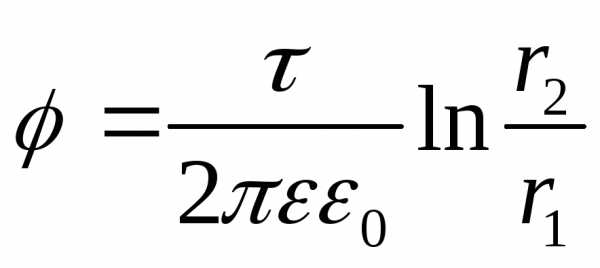Эквипотенциальные поверхности должны удовлетворять усло­вию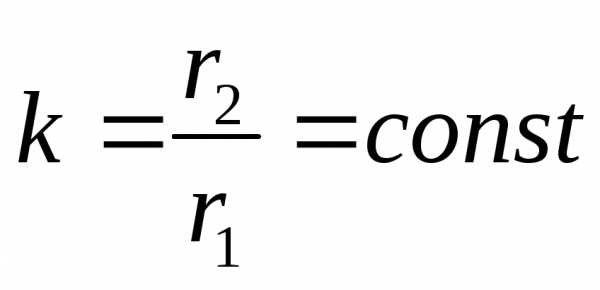. В геометрии есть малоизвестная теорема Аполония, которая гласит, что гео­метрическим местом точек, отношение расстояний от которых до заданной пары точек по­стоянно, является окружность, центр которой лежит на линии, соединяющей заданную пару точек. Эта окружность должна удовлетво­рять следующему условию:

или .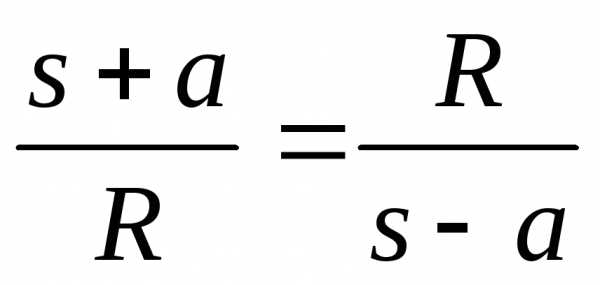

Анализ геометрии рис. 2 показывает, что треугольник 20n подобен тре­угольнику n01 (общий угол с вершиной 0 и прилежащие к углу стороны про­порциональны). Из подобия треугольников следует:

.

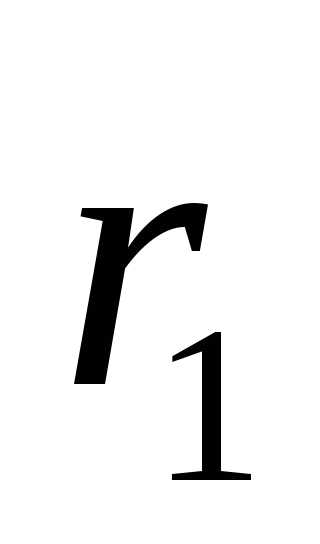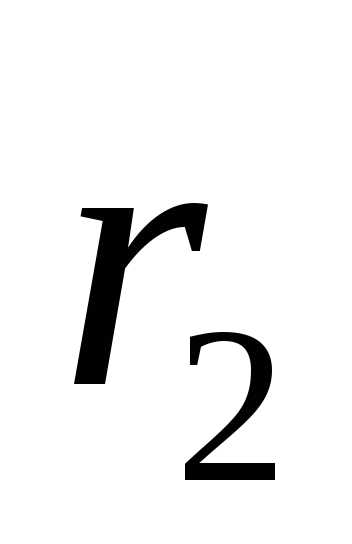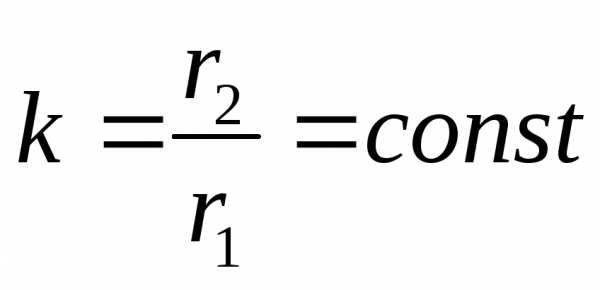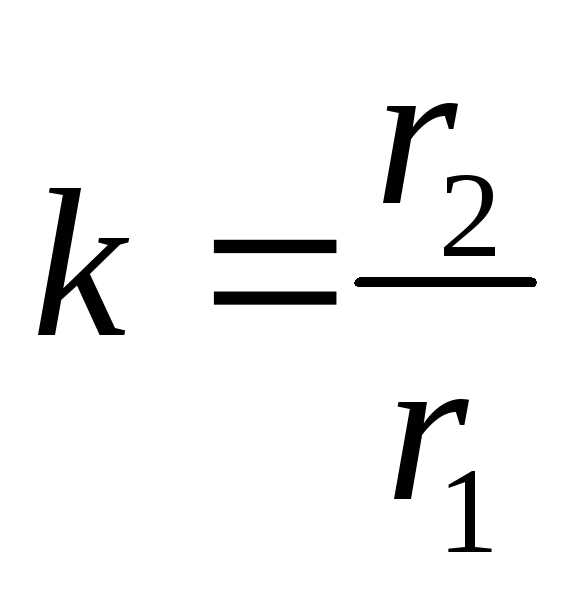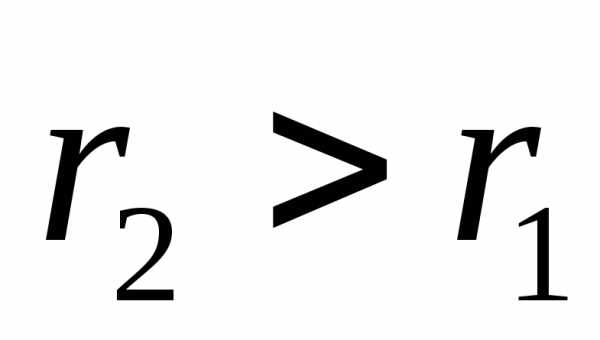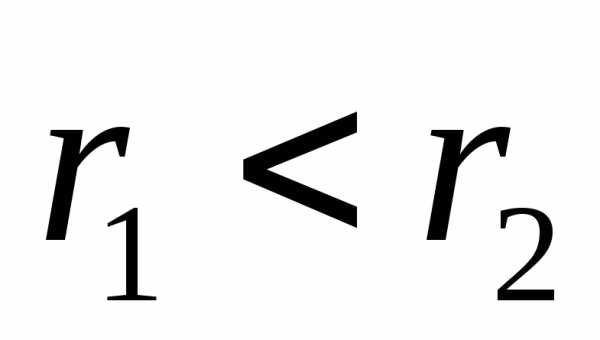При перемещении точки n вдоль окружности изменяются расстояния и так, что их отношение остается постоянным . При изменении отношенияцентр окружности перемещается вдоль линии, соединяю­щую заданную пару точек 1 и 2. Приk>1, и центр окружности нахо­диться в левой полуобласти, приk<1, и центр ок­ружно­сти находится в правой полуобласти, a приk=1, 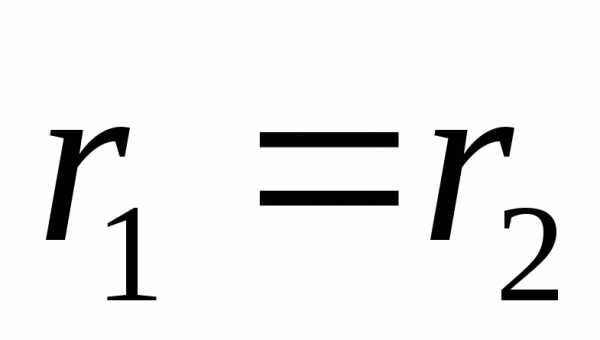, центр окружности смещается в беско­нечность, а сама окружность превращается в прямую линию, совпадающую с верти­кальной осью симметрии.

Линии вектора напряженности поля также является дугами окружно­сти, но с цен­трами, расположенными на вертикальной оси симметрии.

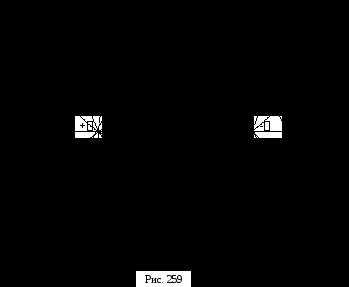
Графической диаграммой или сеткой поля называется совокупность сле­дов эквипо­тенциальных поверхностей с заданными значениями потенциалов, построенная совместно с совокупностью следов линии вектора напряженности поля . Графическая диаграмма поля двух разноименно заряженных осей имеет вид рис. 259.

По графической диаграмме поля можно определить его параметры (,) в любой точке.

studfiles.net

Решение — уравнение — пуассон

Решение — уравнение — пуассон

Cтраница 1

Решение уравнения Пуассона в случае больших значений начальных скоростей ( равных для всех электронов) представляет большой интерес при расчете тока и распределения потенциалов в области между экранирующей сеткой и анодом лампы.  [1]

Решение уравнений Пуассона или Лапласа в конечном объеме У, если на ограничивающей поверхности 5 заданы граничные условия Дирихле или Неймана, можно получить с помощью теоремы Грина (1.35) и так называемых функций Грина.  [2]

Решение уравнения Пуассона относительно потенциала Ut очевидно, может быть получено лишь тогда, когда объемный заряд р и диэлектрическая постоянная заданы как функции координат точек во всем пространстве. Однако этого недостаточно для однозначности решения. В простейшем случае распределения объемного заряда в безграничной однородной диэлектрической среде необходимым дополнительным условием является задание поведения функции U на бесконечности, которое в данном случае оказывается и достаточным для однозначности решения. Если диэлектрическая среда кусочно-однородная и в ней присутствуют проводники, то должны выполняться определенные условия на поверхностях разделов между соприкасающимися друг с другом диэлектриками и на поверхностях проводников. Так например, на поверхности проводника значение потенциала принимает постоянное значение поскольку электростатическое поле внутри проводника отсутствует.  [3]

Решение уравнения Пуассона внутри моделируемого объема приравнивается на границе вакуумному решению, которое не расходится при у — юо.  [4]

Обычно решение уравнения Пуассона — Больцмана проводят применительно к конкретным граничным условиям.  [5]

Для решения уравнения Пуассона Mathcad предлагает функции multigrid и relax. Эти функции решают уравнение Пуассона методом сеток и только для квадратной области.  [6]

Матрица решения уравнения Пуассона, у которого решение равно нулю на границах.  [7]

Формула (6.20) дает решение уравнения Пуассона в конечном объеме пространства V при определенных граничных условиях на поверхности 5, ограничивающей данный объем.  [8]

Интересно найти такие решения уравнения Пуассона, которые определяются вполне интегрируемой системой уравнений Пфаффа.  [9]

Можно показать, что решение уравнения Пуассона при заданных граничных условиях является единственным. Однако это доказательство выходит за рамки данной книги.  [10]

В данном примере рассматривается решение уравнения Пуассона методом конечных элементов для областей произвольной формы и произвольной разбивки на элементы.  [11]

Полученная задача — найти решение уравнения Пуассона с граничным условием u f ( s) на L — называется задачей Дирихле для этого уравнения.  [12]

Можно показать, что решение уравнения Пуассона при заданных граничных условиях является единственным. Однако это доказательство выходит за рамки данной книги.  [13]

R) определяется из решения уравнения Пуассона Ду / — 4тгд /, где qf — найденная известная функция.  [14]

Последняя формула аналогична представлению решения уравнения Пуассона в виде суммы гармонической функции и плоского логарифмического потенциала.  [15]

Страницы:      1    2    3    4

www.ngpedia.ru

Уравнение Пуассона и математическая постановка задач электростатики

Решение уравнения Пуассона

В достаточно большом количестве случаев наиболее удобным методом поиска напряженности поля является решение дифференциального уравнения для потенциала. Получим его, используя в качестве основы теорему Остроградского — Гаусса в дифференциальной форме:

где $\rho $ — плотность распределения заряда, ${\varepsilon }_0$ — электрическая постоянная, $div\overrightarrow{E}=\overrightarrow{\nabla }\overrightarrow{E}=\frac{\partial E_x}{\partial x}+\frac{\partial E_y}{\partial y}+\frac{\partial E_z}{\partial z}$) — дивергенция вектора напряженности и выражение связывающее напряженность поля и потенциал:

Подставим (2) в (1), получим:

Учитываем, что $divgrad\varphi ={\nabla }^2\varphi =\frac{{\partial }^2\varphi }{\partial x^2}+\frac{{\partial }^2\varphi }{\partial y^2}+\frac{{\partial }^2\varphi }{\partial z^2}$, где $\triangle ={\nabla }^2$- оператор Лапласа, тогда равенство (3) запишем как:

Уравнение (4) называется уравнением Пуассона (для вакуума) в системе СИ. Если заряды отсутствуют, то уравнение (4) преобразуется в уравнение Лапласа:

После того, как найден потенциал из уравнения Пуассона, обычно вычисляется напряженность по формуле (2). Решения уравнения Пуассона должны удовлетворять таким требованиям:

1. Потенциал должен быть непрерывной функцией.
2. Потенциал должен быть конечной функцией.
3. Производные от потенциала как функции по координатам должны быть конечными.

Если заряды сосредоточены в объеме V, то решением уравнения (4) будет выражение для потенциала вида:

Итак, общая задача электростатики сводится к нахождению решения дифференциального уравнения (уравнения Пуассона), которое удовлетворяет выше перечисленным требованиям. Нахождение решения — задача весьма сложная. Теоретические решения известны для небольшого количества частных случаев. Если удалось подобрать функцию $\varphi $, которая удовлетворяет всем условиям задачи, то она единственная.

Не всегда есть необходимости задавать заряды или потенциалы во всем пространстве. Например, если необходимо найти электрическое поле в полости, которая окружена проводящей оболочкой, то можно найти поле только для тел внутри самой полости.

Каждое решение уравнения Пуассона в ограниченной области однозначно определяется краевыми условиями, которые накладывают на поведение решения. На границе перехода из одной среды в другую выполняются граничные условия:

\[E_{2n}-E_{1n}=4\pi \sigma ,\ или\ \frac{\partial {\varphi }_1}{\partial n}-\frac{\partial {\varphi }_2}{\partial n}=0.\] \[E_{1\tau }=E_{2\tau }.\] \[{\varphi }_1=ц_{2\ }\]

где $\sigma $- поверхностная плотность свободных зарядов, n- единичный вектор нормали к границе раздела, проведенный из среды 1 в 2, $\tau -\ $единичный вектор, касательный к границе.

Данные уравнения выражают скачок нормальных составляющих вектора напряженности и непрерывность касательной составляющей вектора напряженностей электрического поля при переходе через любую заряженную поверхность не зависимо от формы этой поверхности и наличия и отсутствия зарядов вне ее.

Уравнение Пуассона в сферических, полярных и цилиндрических координатах

Уравнение Пуассона может быть записано не только в декартовых координатах, но также в сферических и цилиндрических, полярных.

В сферических координатах ($r,\theta ,\vartheta)$ уравнение Пуассона имеет следующий вид:

\[\frac{1}{r^2}\cdot \frac{\partial }{\partial r}\left(r^2\frac{\partial \varphi }{\partial r}\right)+\frac{1}{r^2sin\theta \partial \theta }\left(sin\theta \cdot \frac{\partial \varphi }{\partial \theta }\right)+\frac{{\partial }^2\varphi }{r^2{sin}^2\theta \partial {\varphi }^2}=-\frac{1}{{\varepsilon }_0}\rho \left(7\right).\]

В полярных координатах ($r,\theta )$ система координат уравнение имеет вид:

\[\frac{1}{r}\cdot \frac{\partial }{\partial r}\left(r\frac{\partial \varphi }{\partial r}\right)+\frac{{\partial }^2\varphi }{r^2\partial {\theta }^2}=-\frac{1}{{\varepsilon }_0}\rho \left(8\right).\]

В цилиндрических координатах ($r,\vartheta,z)$ уравнение имеет вид:

\[\frac{1}{r}\cdot \frac{\partial }{\partial r}\left(r\frac{\partial \varphi }{\partial r}\right)+\frac{{\partial }^2\varphi }{\partial z^2}+\frac{{\partial }^2\varphi }{r^2\partial \vartheta^2}=-\frac{1}{{\varepsilon }_0}\rho \left(9\right).\]

Пример 1

Задание: Найдите поле между двумя коаксиальными цилиндрами с радиусами $r_1$ и $r_2$, разность потенциалов между которыми равна $\triangle U={\varphi }_1-{\varphi }_2.$

Рис. 1

Решение:

Запишем уравнение Лапласа в цилиндрических координатах с учетом аксиальной симметрии:

$\frac{1}{r}\cdot \frac{\partial }{\partial r}\left(r\frac{\partial \varphi }{\partial r}\right)=0$(1.1)

Оно имеет решение $\varphi =-Aln(r)$+B. Выберем нулевой потенциал на наружном цилиндре, найдем, получим:

$\varphi \left(r_2\right)=0=-Alnr_2+B,$ следовательно

\[B=Alnr_2.\ \] $\varphi \left(r_1\right)=\triangle U=-Alnr_1+B$, получим: \[A=\frac{\triangle U}{{ln \left(\frac{r_2}{r_1}\right)\ }}.\]

В результате имеем: $\varphi (r)=-\frac{\triangle U}{{ln \left(\frac{r_2}{r_1}\right)\ }}ln\left(r\right)+\frac{\triangle U}{{ln \left(\frac{r_2}{r_1}\right)\ }}lnr_2$

Ответ: Поле между двумя коаксиальными цилиндрами задается функцией $\varphi (r)=-\frac{\triangle U}{{ln \left(\frac{r_2}{r_1}\right)\ }}ln\left(r\right)+\frac{\triangle U}{{ln \left(\frac{r_2}{r_1}\right)\ }}lnr_2$

Пример 2

Задание: Найти, используя уравнение Пуассона потенциал поля, которое создает бесконечно длинный круглый цилиндр радиуса R с объемной плотностью заряда $\rho $.

Решение:

Ось Z направим по оси цилиндра. Так как цилиндрическое распределение заряда аксиально симметрично, то потенциал обладает той же симметрией, то есть он является функцией $\varphi \left(r\right),\ $где r — расстояние от оси цилиндра. Поэтому используем цилиндрическую систему координат. Запишем уравнение Пуассона в ней с учетом симметрии:

\[\frac{1}{r} \cdot \frac{\partial}{\partial r} \left(r\frac{\partial {\varphi }_1}{\partial r}\right)=- \frac{1}{ \varepsilon_0} \rho \ \left(0 Общие решения уравнений (2.1) (2.2) имеют вид: \[{\varphi }_1=-\frac{1}{4}\frac{\rho }{{\varepsilon }_0}r^2+C_1lnr+{C’}_1\left(2.3\right),\] \[{\varphi }_2=C_2lnr+{C’}_2\left(2.4\right),\]

где $C_1$,$\ {C’}_1,C_2$,$\ {C’}_2$ — постоянные интегрирования. Так как потенциал во всех точках должен быть конечным, а ${\mathop{lim}_{r\to 0} lnr\ }=\infty $, следовательно, $C_1=0.$ Пронормируем потенциал условием:${\varphi }_1\left(0\right)=0$, тогда: ${C’}_1=0.$

Так как поверхностных зарядов нет, то напряженность электрического поля на поверхности шара непрерывна, то есть непрерывна производная от потенциала при r=R. И непрерывен сам потенциал. Эти условия дают два алгебраических уравнения для того, чтобы найти постоянные $C_2$,$\ {C’}_2:$

\[C_2lnR+{C’}_2=-\frac{1}{4}\frac{\rho }{{\varepsilon }_0}R^2(2.5)\] \[\frac{C_2}{R}=-\frac{1}{2}\frac{\rho }{{\varepsilon }_0}R\left(2.6\right).\]

Следовательно, получаем выражения для потенциалов:

\[{\varphi }_1\left(r\right)=-\frac{1}{4}\frac{\rho }{{\varepsilon }_0} r ^ 2 \left(0 Ответ: Потенциал поля равен: $$ \varphi_1 \left(r \right)=-\frac{1}{4}\frac{\rho }{\varepsilon_0} r^2 \left (0

spravochnick.ru

Алгоритм поиска приближенных решений уравнения Пуассона

Численное решение уравнения Пуассона является важным элементом многих задач вычислительной физики.

В данной работе опишем новую вычислительную модель для поиска приближенного решения смешанной краевой задачи для уравнения Пуассона. Данная модель использует нестационарные регуляризации, метод прямых, идеи схем без насыщения, сплайн-интерполяцию, метод прогонки и метод установления (рис. 1).

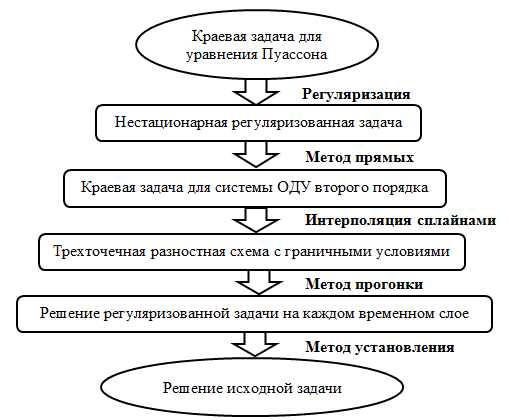
Рис. 1.Алгоритм поиска приближенных решений краевой задачи для уравнения Пуассона

 

Рассмотрим в прямоугольной области  (см. рис. 2) уравнение Пуассона для функции :

                                                                       (1)

со смешанными краевыми условиями:

                                                                                                         (2)

Здесь  ‒ известная правая часть, ,  ‒ часть границы  ,  ‒ единичный вектор внешней нормали к границе ,  ‒ некоторые постоянные.

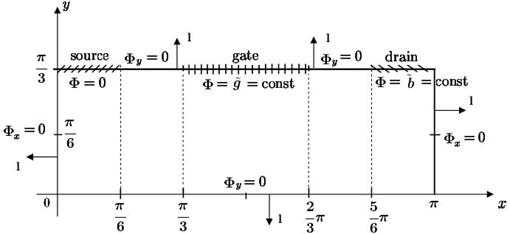
Рис. 2. Область и граница  для модельной задачи

 

Замечание. Сделав в задаче (1), (2) замену зависимой переменной :

,

где функция  изображена на рис. 3, мы получаем для новой зависимой переменной  следующую смешанную краевую задачу:

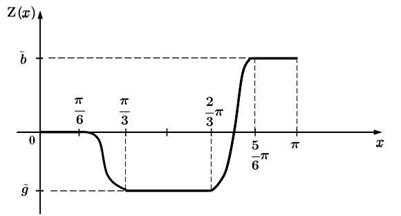
Рис. 3. График вспомогательной достаточно гладкой функции

 

Следовательно, не нарушая общности, будем полагать далее, что в (2) функция  удовлетворяет на  однородному условию .

При конструировании численного алгоритма для нахождения приближенных решений задачи (1), (2) мы воспользуемся методом установления. С этой целью вместо уравнения Пуассона (1) рассмотрим три его нестационарные регуляризации:

1.параболическая регуляризация

,                                                                                                          (3)

2. регуляризация Соболева

,                                                                                                 (4)

3.гиперболическая регуляризация

.                                                                                                (5)

Здесь  ‒ новая неизвестная функция,  ‒ постоянная, ‒ временная переменная. Краевые условия (2) для уравнений (3 ‒ 5) перепишутся так

.                                                                             (6)

Добавляя начальные условия

,                                                                                            (7)

стационарное решение исходной смешанной краевой задачи ищется как предел  при .

Для каждого из трех видов регуляризаций получены априорные оценки на нормы решений резуляризованных задач, из которых следует сходимость , а также однозначная разрешимость и устойчивость стационарного решения.

Для нахождения приближенного решения смешанной задачи (3), (6), (7) или (4), (6), (7) или (5), (6), (7) предложена дифференциально-разностная модель, основанная на методе прямых и принципах схем без насыщения. При этом производную  в уравнениях (3) — (5) мы заменим не разностным отношением, а используем для аппроксимации ее интерполяционный многочлен [1]

с узлами в нулях многочлена Чебышева

В итоге для каждой из регуляризаций будем иметь:

,                                                                                                       (8)

,                                                                                  (9)

,                                                                                            (10)

где , , , , , , ,   .

Далее в системах (8) ‒ (10) проведем дискретизацию по переменной . С этой целью вводим обозначения: , , , , ‒ шаг разностной сетки по времени.

Заменяя ,  получаем систему ОДУ второго порядка:

                                                                                                               (11)

Выражения для элементов матрицы  и компонент вектора  зависят от вида примененной регуляризации:

,

,

 ‒ единичная матрица порядка N.

К системе (11) добавляем граничные краевые условия (см. (6)):

                                                                             (12)

-диагональные матрицы порядка N(диагональные элементы равны либо 0, либо 1), причем:

Учитывая определенные трудности, возникающие при практическом использовании формулы для нахождения приближенного решения краевой задачи (11), (12), мы предложим следующую технологию построения приближенного решения этой краевой задачи. Будем искать приближенное решение в виде интерполяционного кубического сплайна класса (см. [2]):

                                   (13)

     

С учетом (13) из (11), (12) получаем трехточечную разностную схему:

                                        (11)

Здесь   ‒ диагональная матрица порядка N (диагональные элементы равны либо 0, либо 1). Систему алгебраических уравнений (11) можно решить методом матричной прогонки. Из неравенства  следуют условия хорошей обусловленности разностной краевой задачи (11).

Данный алгоритм был запрограммирован на языке Object Pascal (среда Delphi 6). Были проведены тестовые расчеты, которые показали хорошую работоспособность, приведенного выше алгоритма.

Данный алгоритм хорошо зарекомендовал себя при поиске решения 1D задачи о баллистическом диоде и 2D задачах о переносе заряда в транзисторе MESFET и MOSFET.

 

Литература:

 

1.                  Бабенко К. И. Основы численного анализа. Москва-Ижевск: НИЦ » Регулярная и хаотическая динамика», 2002.

2.                  Завьялов Ю. С., Квасов Б. И., Мирошниченко В. Л. Методы сплайн ‒ функций. М.: Наука, 1980.

moluch.ru

No related posts.