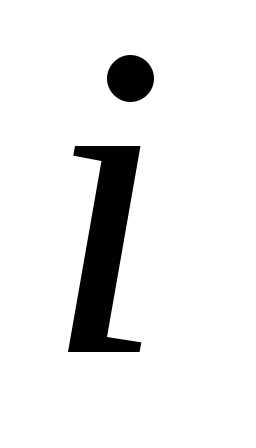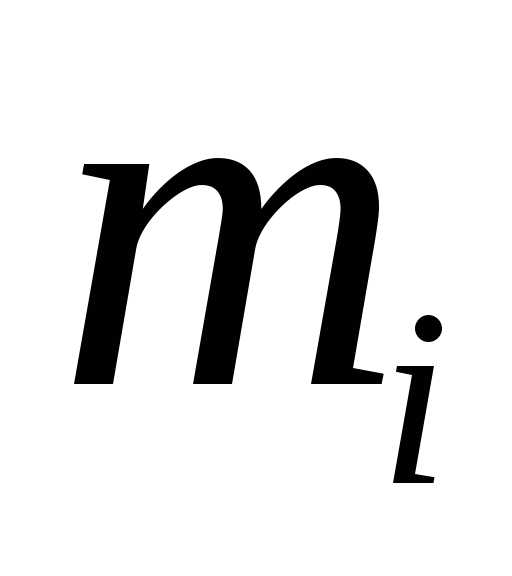3. Формулы полной вероятности и Байеса.
Задача 3. В магазин поступают однотипные изделия с трех заводов, причем i-й завод поставляет mi % изделий (i = 1, 2, 3). Среди изделий i -го завода ni % первосортных. Определить вероятность того, что купленное изделие выпущено j-м заводом, если оно оказалось первого сорта.
Решение (для
нулевого варианта: m1 =20, m2 =30, m3 =50, n1 =70, n2 =70, n3=90, j=1). Введем
обозначения. Событие А –
куплено первосортное изделие. События,
заключающиеся в том, что купленное
изделие выпущено первым, вторым или
третьим заводом — Н1,
Н
В задаче требуется найти — вероятность того, что купленное изделие изготовленоj-тым заводом, если оно оказалось первого сорта.
Воспользуемся формулой Байеса. .
По условию задачи Р(Н1) = =,
Р(Н2) = =0,3;Р(Н3) = = 0,5.
= 0,7 (70%), = 0,7 (70%),= 0,9 (90%).
Подставляя эти значения в формулу Байеса, получим:
=≈0,175.
Ответ: ≈ 0,175
4. Приближенные вычисления в схеме Бернулли. Локальная и интегральная теоремы Лапласа.
Задача 4. Вероятность получения кредита для одного потенциального заемщика равна р. В течение недели в банк обращаются за получением кредита n человек. Найти: а) наивероятнейшее число лиц, получивших одобрение на получение кредита; б) соответствующую вероятность.Решение (для нулевого варианта: p=0,3; n=13). Наивероятнейшее число лиц, получивших одобрение на получение кредита k0 определяется из двойного неравенства np–q ≤ k0 < np+p, где (q=1–p).
Вероятность того, что из 13 обратившихся в банк, получивших кредит окажется ровно k0 находится по локальной теореме Лапласа (т.к. n ≥ 10): ,где x=. Подставив значения n
а). np–q ≤ k0 < np+p, => 3,9-0,7 ≤ k0 < 3,9+0,3 => k0 = 4.
б). ,где =, х==.
Значения функции для вычисленного значения х находятся по специальным справочным таблицам учебников, пособий и справочников по теории вероятности.
Для х=0,06 находим =0,3982. А искомая вероятность =0,24
Ответ: k0 = 4, Р13(4)=0,24.
Задача 5. Вероятность досрочного погашения ипотечного кредита для каждого из n заемщиков равна р. Определить вероятность того, что число m заемщиков, досрочно погасивших кредит, удовлетворяет следующему неравенству:
Варианты 0-11- k1≤m≤ k2; варианты 12-21- m≤ k2; варианты 22-31- m≥k1.
Решение (для нулевого варианта: n=400, p=0,8, k1=300. k2=350). Вероятность того, что число появлений события А в n независимых испытаниях попадет в некоторый интервал [k1,k2] определяется интегральной теоремой Лапласа: Рn(k1,k2)= ½(Ф(X«) – Ф(X‘)), где Ф(X)=— функция Лапласа, X‘=,X
X‘==; Ф(-2,5)= -0,9876;X«==; Ф(1,25)= 0,7888
Рn(k1,k2)= ½(Ф(X«) – Ф(X‘))= ½(0,7888 – (-0,9876))= 0,8882
studfiles.net
Решения-2
Задача 1. Бросаются две игральные кости. Определить вероятность того, что:
а) сумма числа очков не превосходит N;
б) произведение числа очков не превосходит N;
в) произведение числа очков делится на N.
N=12
Решение:
а)

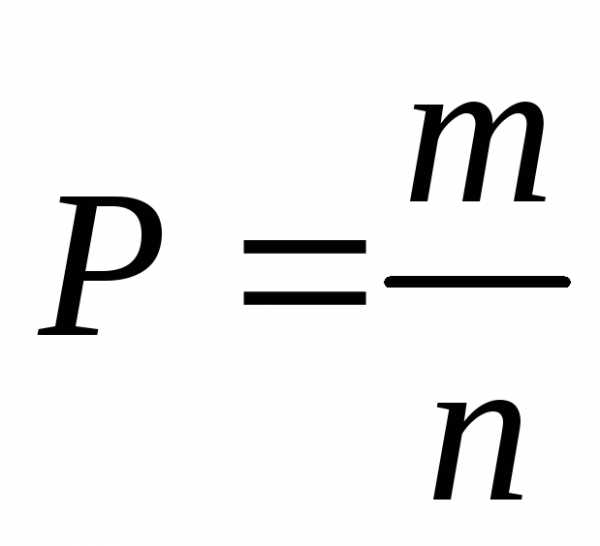
 -количество
возможных исходов.
-количество
возможных исходов.
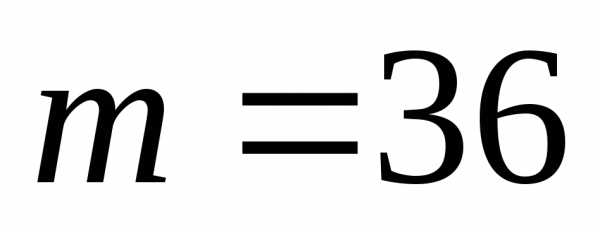 -количество
благоприятных исходов.
-количество
благоприятных исходов.

б)
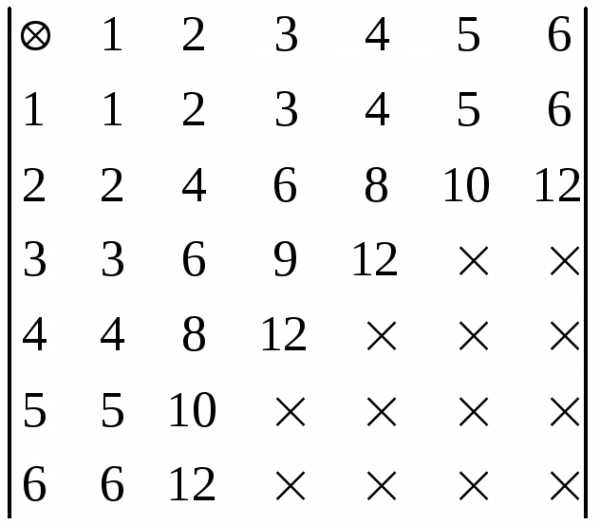
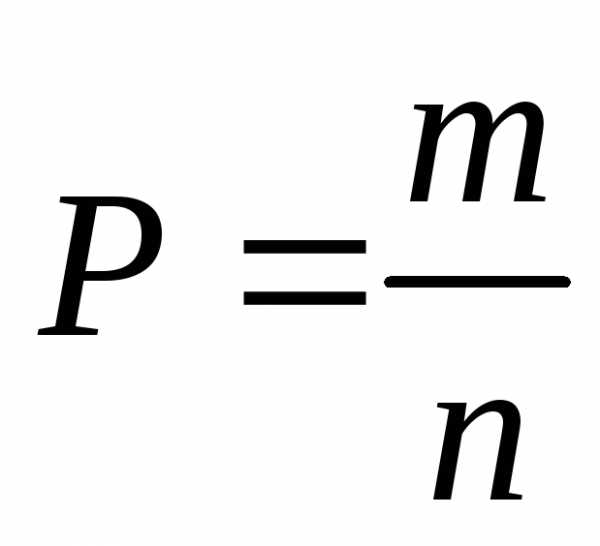
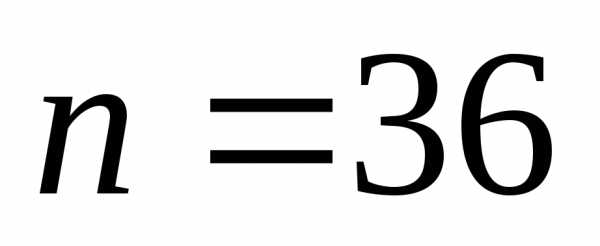 -количество
возможных исходов
-количество
возможных исходов
 -количество
благополучных исходов
-количество
благополучных исходов
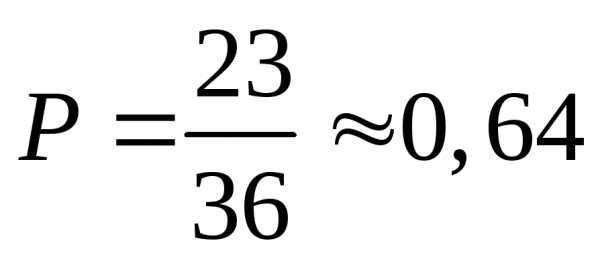
в)
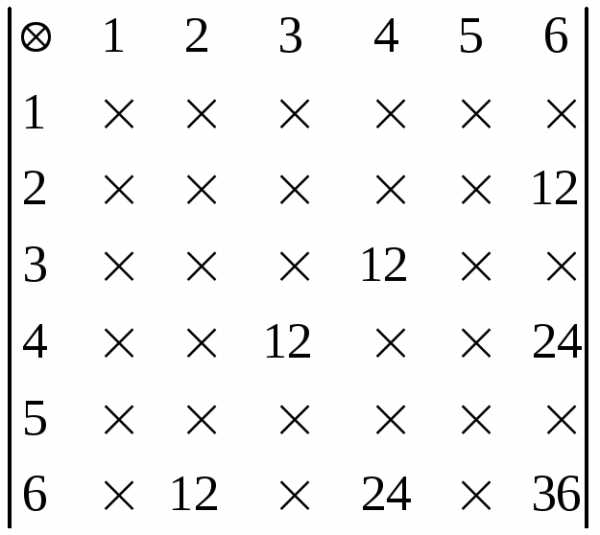
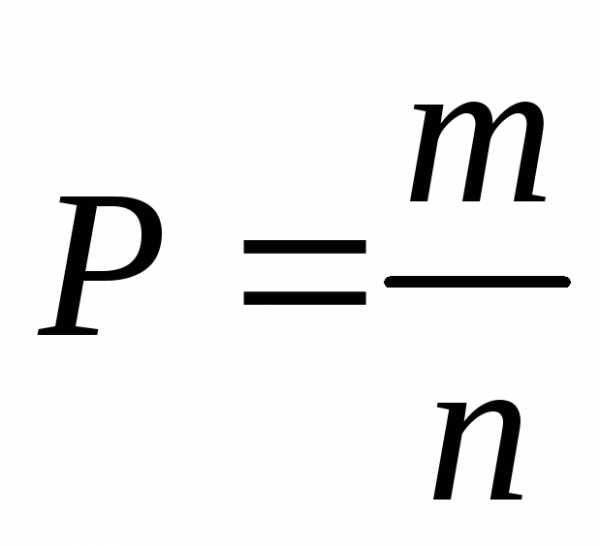
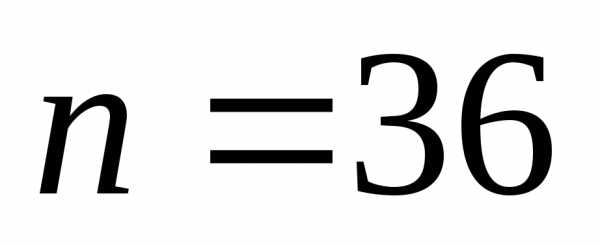
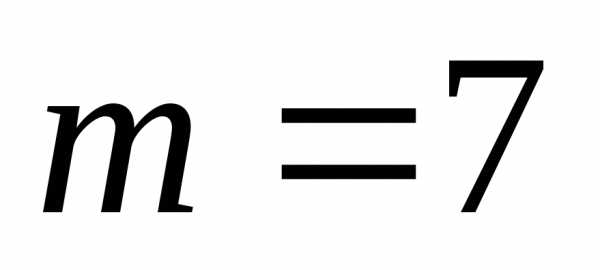
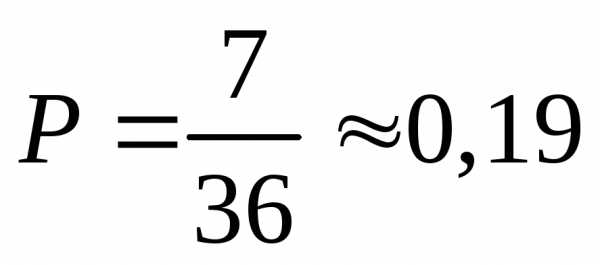
Ответ: 1; 0,64; 0,19.
Задача
3. Среди п лотерейных
билетов k
выигрышных. Наудачу взяли т билетов.
Определить вероятность того, что среди
них 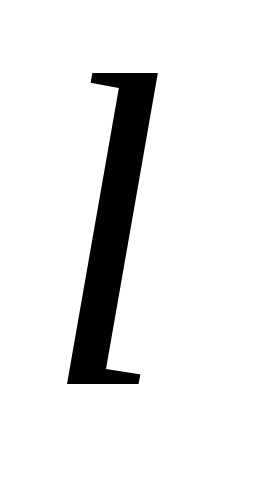 выигрышных.
выигрышных.
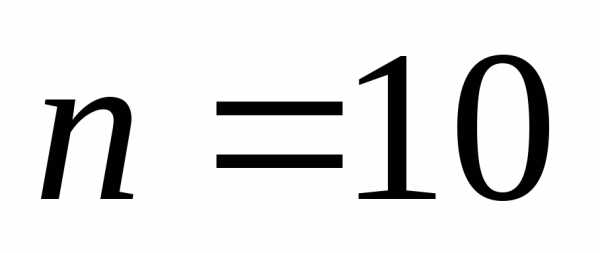 ,
, 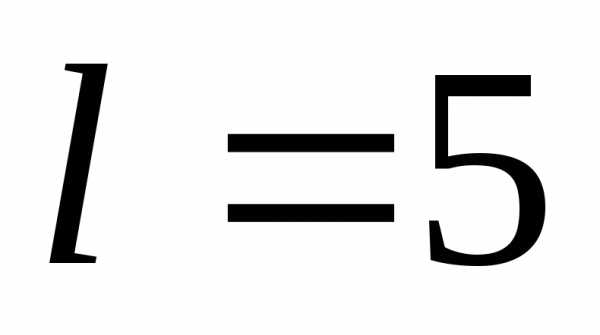 ,
,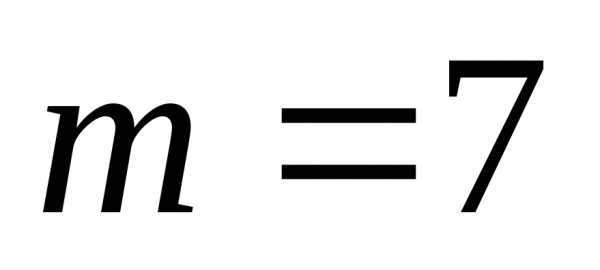 ,
,
Решение:
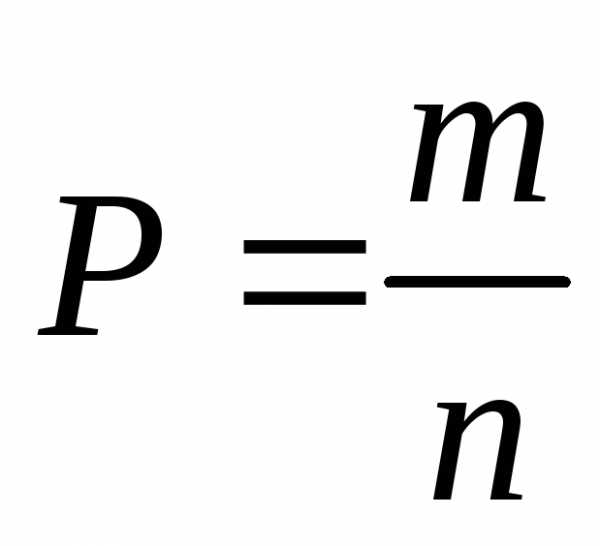
Число возможных исходов:
Число благоприятных исходов:
5
выигрышных из 7 можно взять 
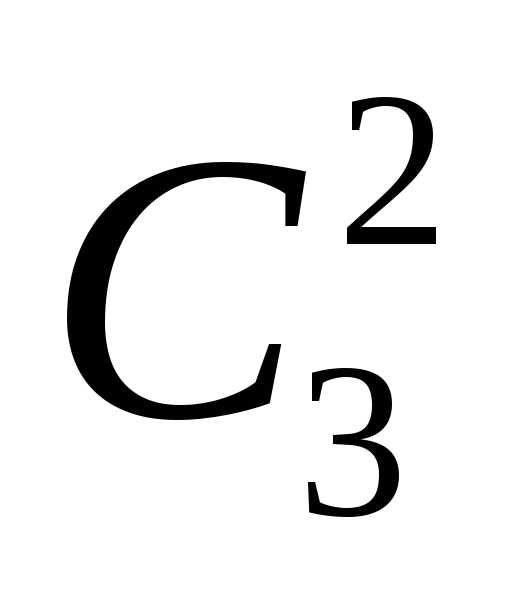 способами.
способами. 
Ответ:
Задача 4. В лифт k — этажного дома сели n пассажиров (n<k). Каждый независимо от других с одинаковой вероятностью может выйти на любом (начиная со второго) этаже. Определить вероятность того, что:
а) все вышли на разных этажах;
б) по крайней мере, двое сошли на одном этаже.
а) Количество возможных исходов:
Количество благоприятных исходов:
б) В задаче речь идёт про событие противоположное первому, значит
Ответ:  ,.
,.
Задача
5. В отрезке единичной длины на удачу
появляется точка. Определить вероятность
того, что расстояние от точки до обоих
концов отрезка превосходит величину 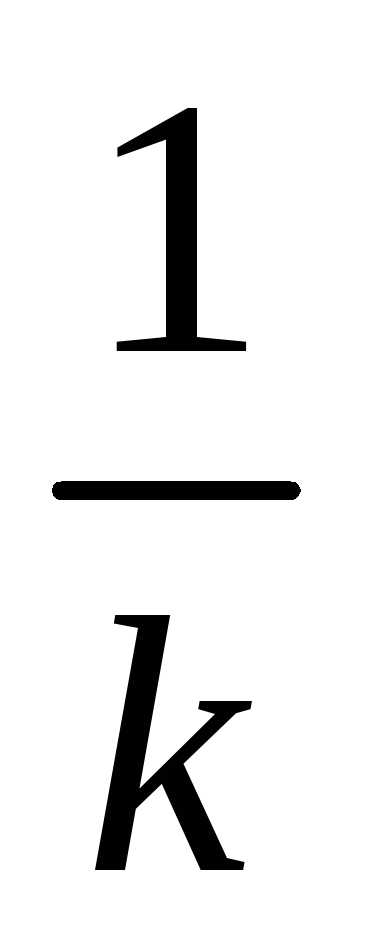
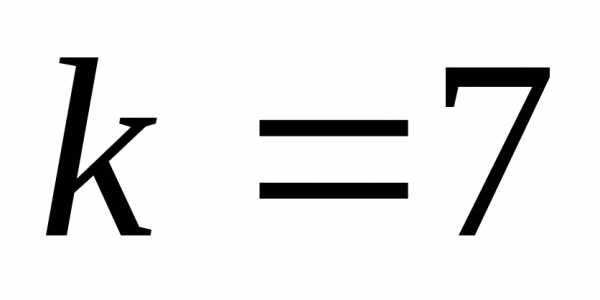 )
)Решение:
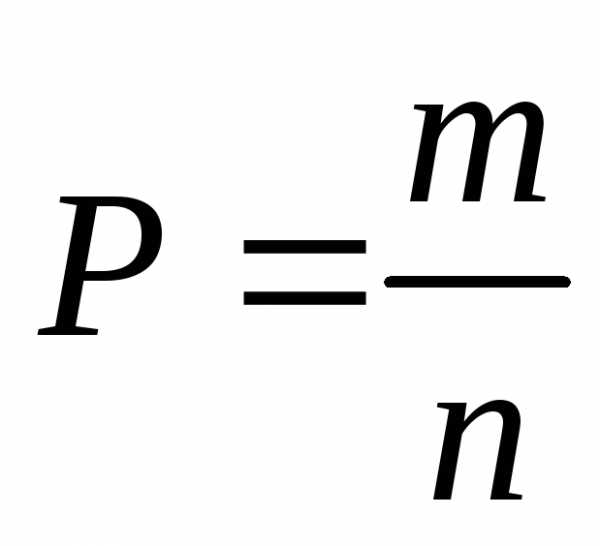
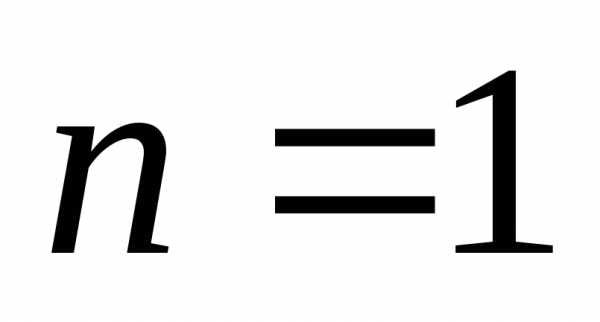 -длина
отрезка, где появится точка.
-длина
отрезка, где появится точка.
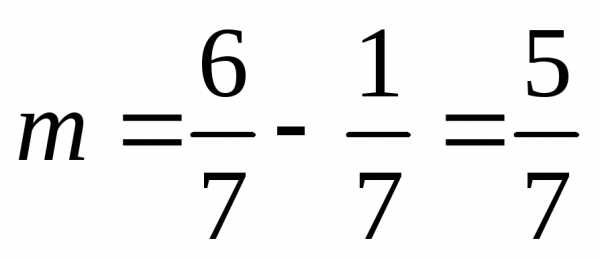 -длина
отрезка «благоприятного исхода»
-длина
отрезка «благоприятного исхода»
Ответ: 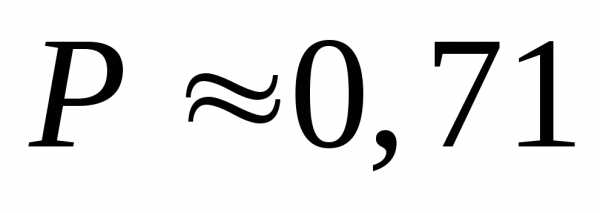
Задача
7. В круге радиуса R
наудачу появляется точка. Определить
вероятность того, что она попадает в
одну из двух непересекающихся фигур,
площади которых равны 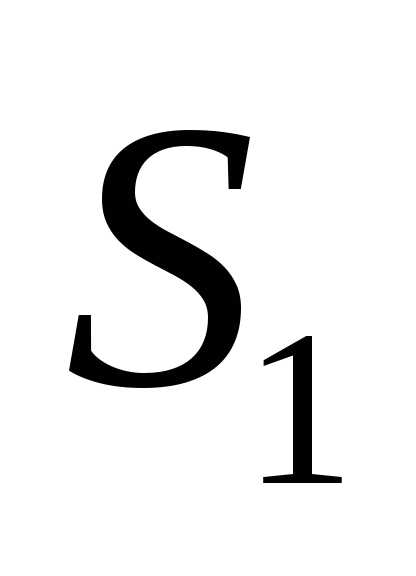
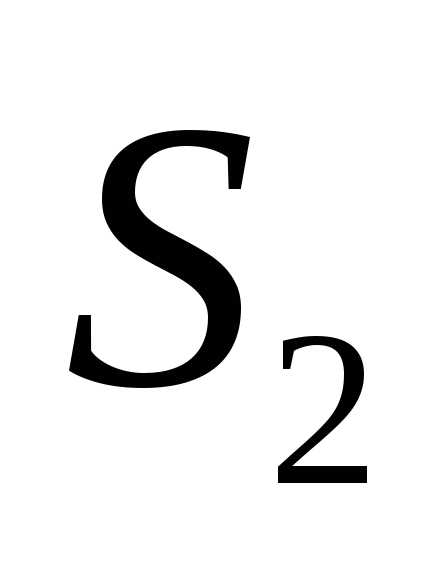 .
.Решение:
Мера вероятности — площадь.
Все варианты попадания точки — в круг.
Благоприятные
— в фигурах 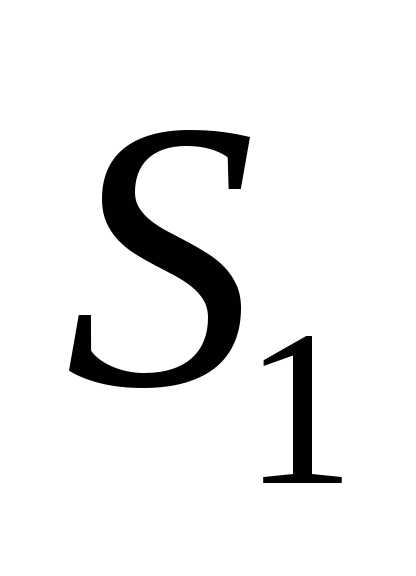 и
и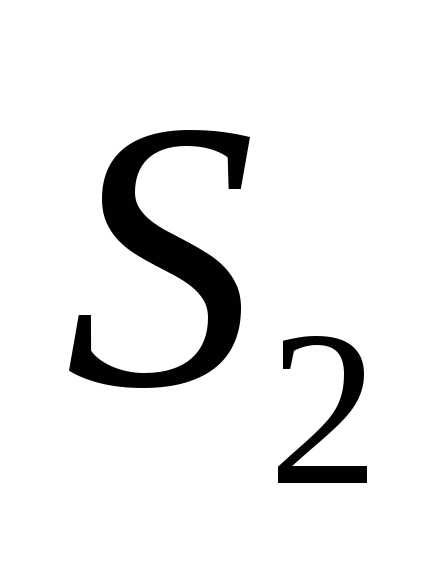
Ответ:
Задача
8. В двух партиях 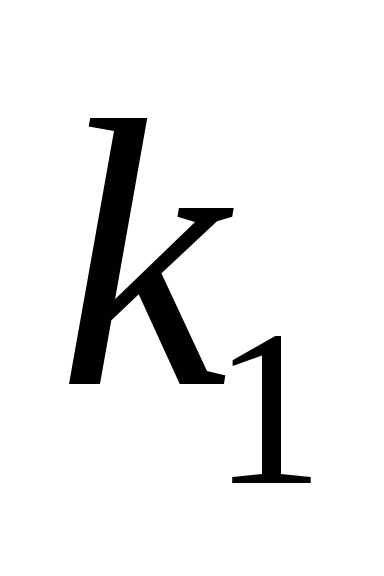 и
и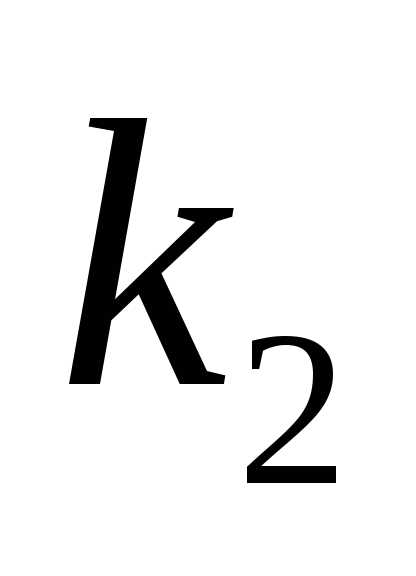 %
доброкачественных изделий соответственно.
Наудачу выбирают по одному изделию из
каждой партии. Какова вероятность
обнаружить среди них:
%
доброкачественных изделий соответственно.
Наудачу выбирают по одному изделию из
каждой партии. Какова вероятность
обнаружить среди них:
а) хотя бы одно бракованное;
б) два бракованных;
в) одно доброкачественное и одно бракованное?
События:
А-из первой партии достали бракованное.
В-из второй партии достали бракованное.
а) С-хотя бы одно бракованное.
б) D-оба бракованных:
в) Е-одно бракованное и одно качественное.
Ответ:
Задача
9. Вероятность того, что цель поражена
при одном выстреле первым стрелком 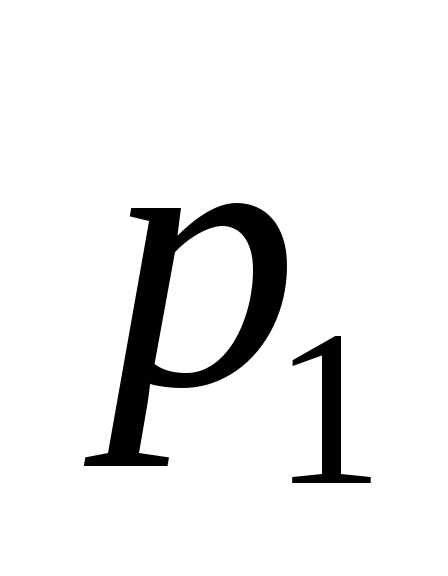 ,
вторым —
,
вторым —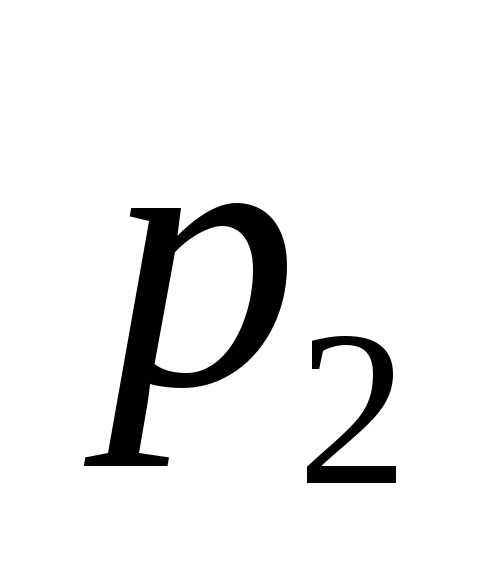 .
Первый сделал
.
Первый сделал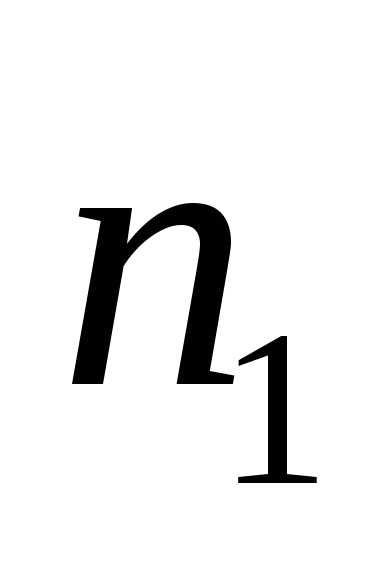 ,
второй —
,
второй —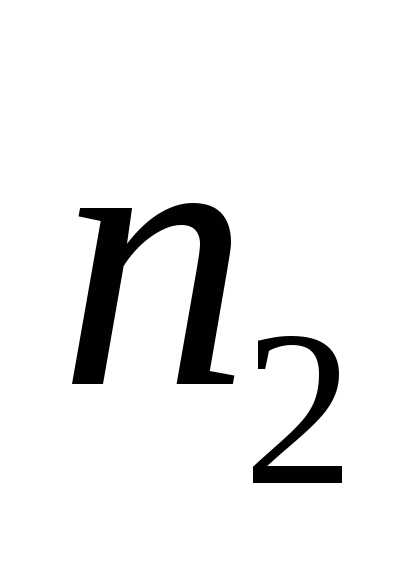 выстрелов. Определить вероятность того,
что цель не поражена.
выстрелов. Определить вероятность того,
что цель не поражена.
Решение:
События:
Цель не поражена
А — первый стрелок промахнулся 3 раза
В — второй стрелок промахнулся 2 раза
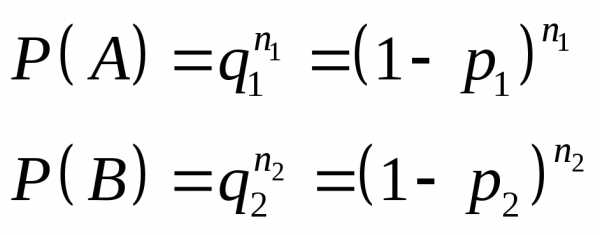
Ответ: 
Задача
12. Из 1000 ламп 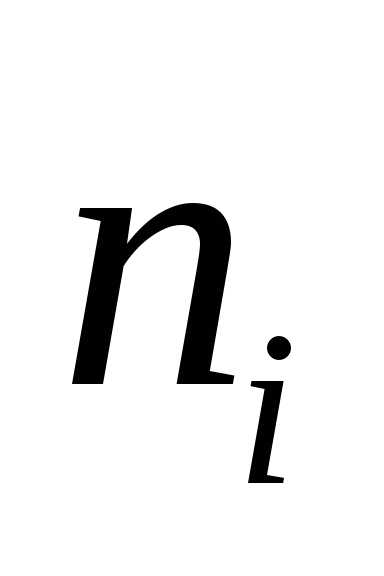 принадлежат
принадлежат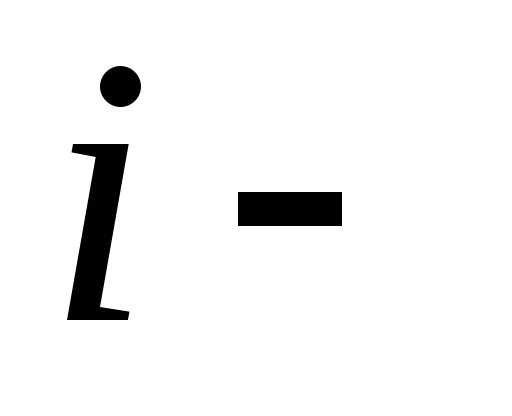 й
партии,
й
партии,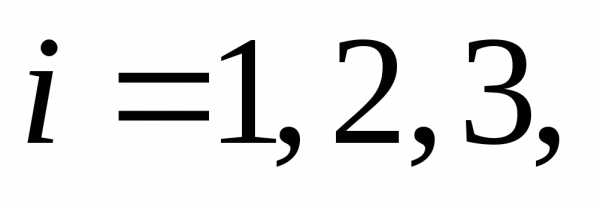
 В первой партии 6%, во второй 5%, в третьей
4% бракованных ламп. Наудачу выбирается
одна лампа. Определить вероятность
того, что выбранная лампа — бракованная.
В первой партии 6%, во второй 5%, в третьей
4% бракованных ламп. Наудачу выбирается
одна лампа. Определить вероятность
того, что выбранная лампа — бракованная.
Решение:
Количество брака в первой партии:
Количество брака во второй партии:
Количество брака в третьей партии:
Ответ:
Задача
15. В магазин поступают однотипные изделия
с трёх заводов, причём 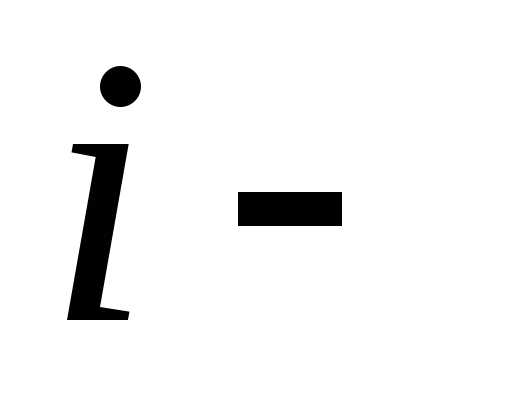 й
завод поставляет
й
завод поставляет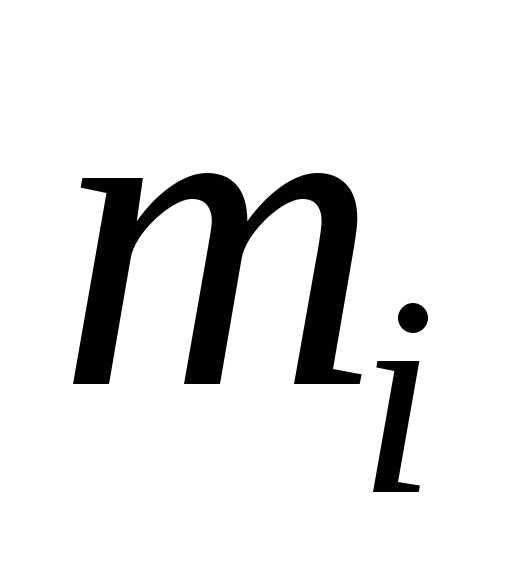 %
изделий
%
изделий .
Среди изделий
.
Среди изделий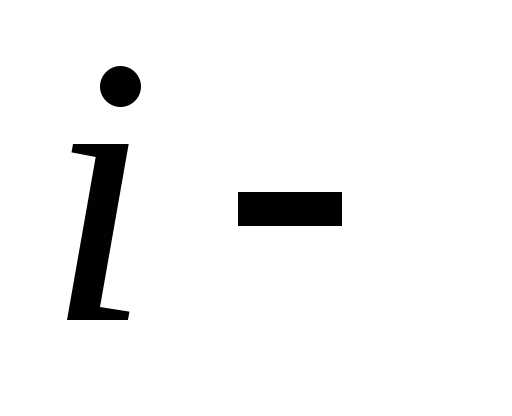 го
завода
го
завода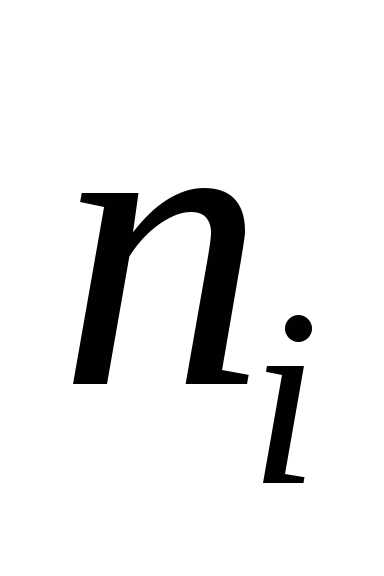 %
первосортных. Куплено одно изделие. Оно
оказалось первосортным. Определить
вероятность того, что купленное изделие
выпущено третьим заводом.
%
первосортных. Куплено одно изделие. Оно
оказалось первосортным. Определить
вероятность того, что купленное изделие
выпущено третьим заводом.
Решение:
Ответ: 59%
Задача
17. Вероятность выигрыша в лотерею на
один билет равна  .
Куплено
.
Куплено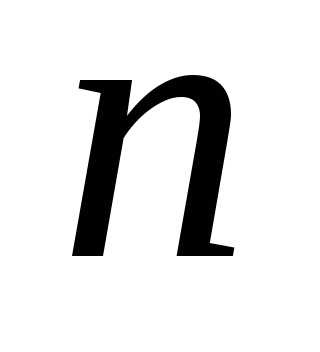 билетов. Найти наивероятнейшее число
выигравших билетов и соответствующую
вероятность.
билетов. Найти наивероятнейшее число
выигравших билетов и соответствующую
вероятность.
Решение:
Найдём наивероятнейшее число выигравших билетов из неравенства:
Значит, есть два наивероятнейших числа 7 и 8.
Применима формула Бернулли:
Ответ: 
Задача
19. Вероятность «сбоя» в работе телефонной
станции при каждом вызове равна 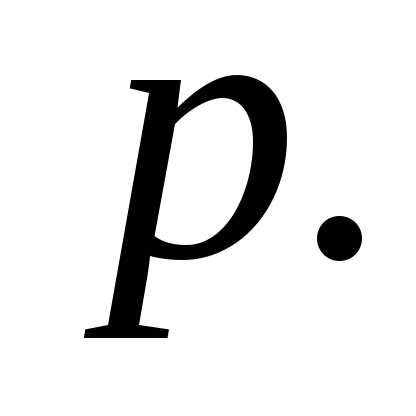 Поступило
Поступило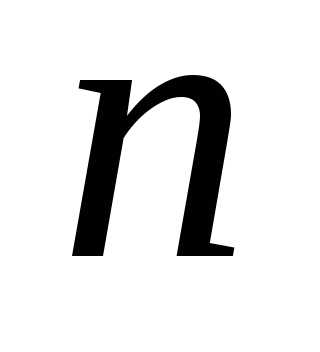 вызовов. Определить вероятность
вызовов. Определить вероятность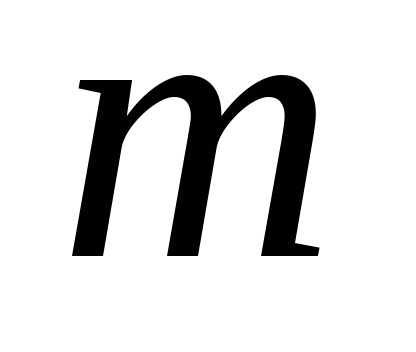 «сбоев».
«сбоев».
Так
как 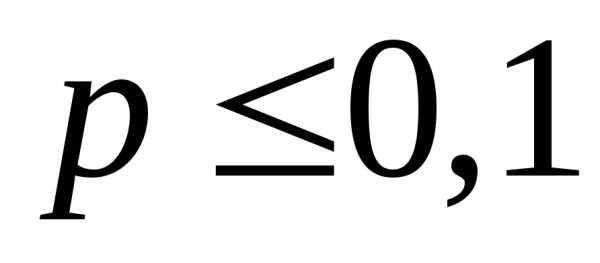 и
и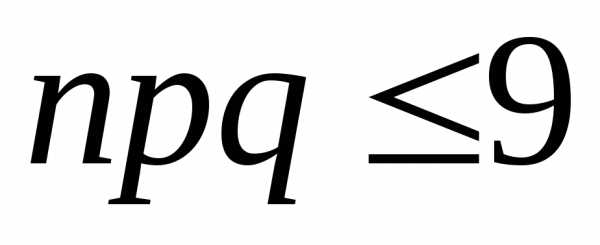 ,
то применима формула Пуассона.
,
то применима формула Пуассона.
Ответ: 13,2%
Задача
20. Вероятность наступления некоторого
события в каждом из 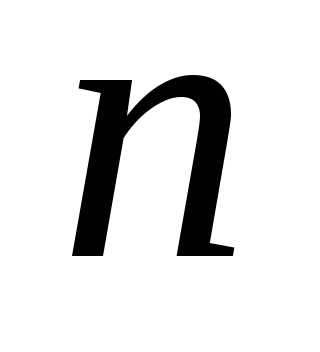 независимых испытаний равна
независимых испытаний равна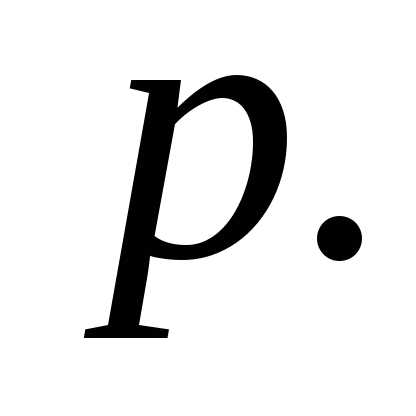 Определить вероятность того, что число
Определить вероятность того, что число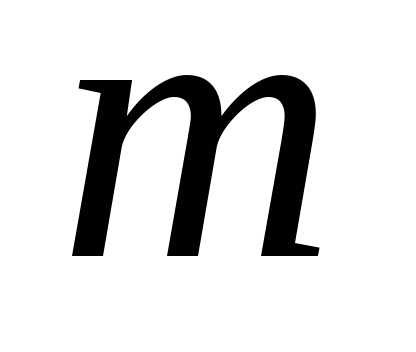 наступлений события удовлетворяют
следующему неравенству:
наступлений события удовлетворяют
следующему неравенству: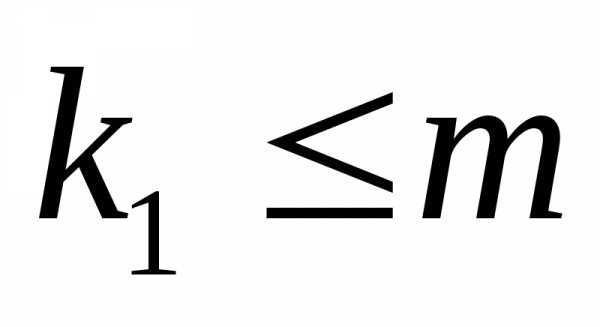 .
.
Решение:
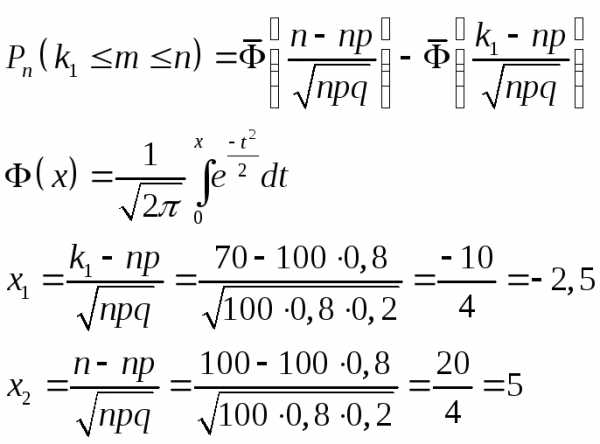
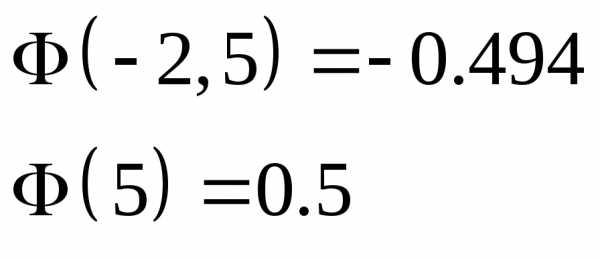
Ответ: 0,994.
Задача
21. Дана плотность распределения 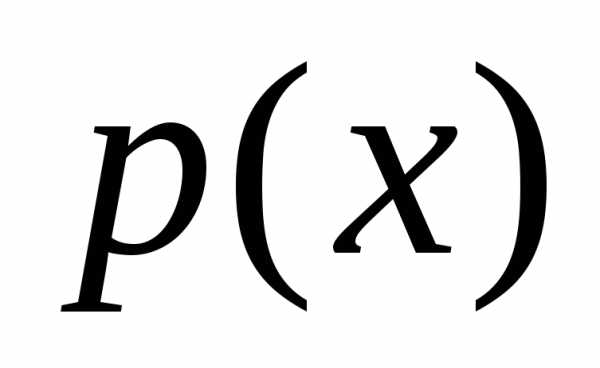 случайной величины
случайной величины .
Найти параметр
.
Найти параметр ,
математическое ожидание
,
математическое ожидание ,
дисперсию
,
дисперсию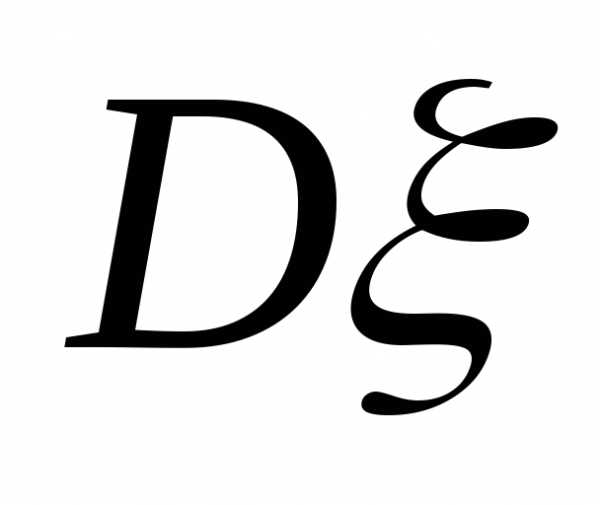 ,
функцию распределения случайной величины
,
функцию распределения случайной величины ,
вероятность выполнения неравенства
,
вероятность выполнения неравенства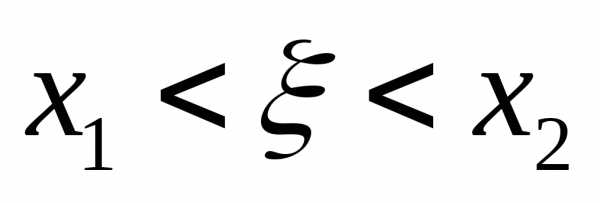
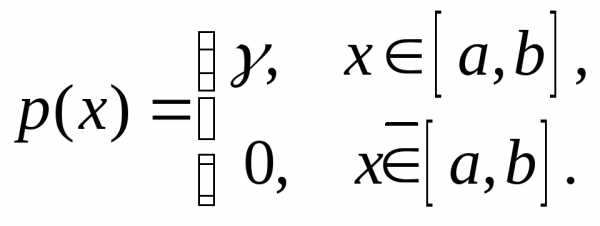
Решение:
а)
найдём параметр 
б)
найдём математическое ожидание 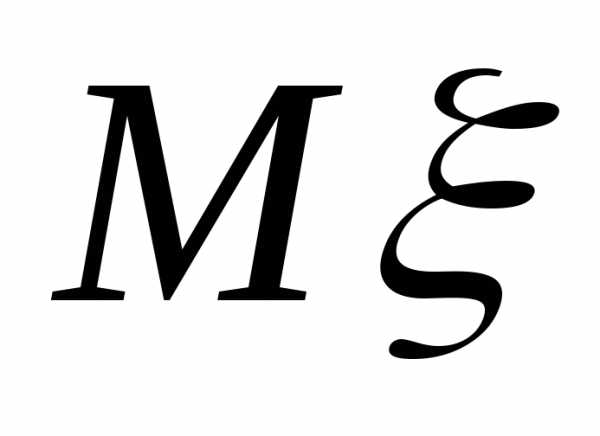 :
:
в)
найдём дисперсию 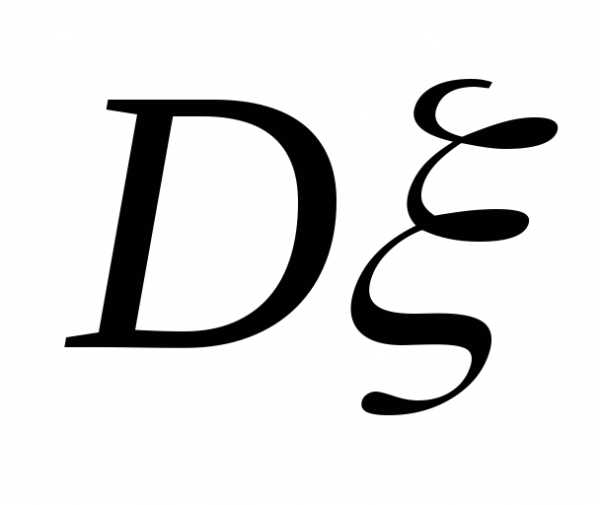 :
:
г)
Найдём функцию распределения случайной
величины  :
:
При 
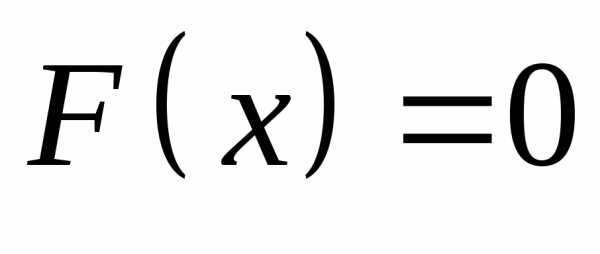
При 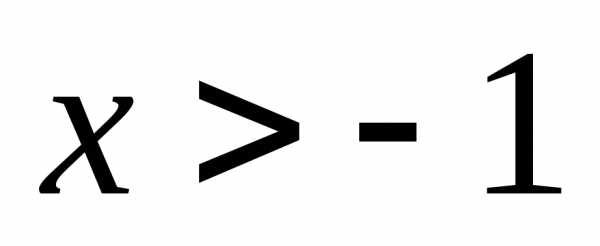

При
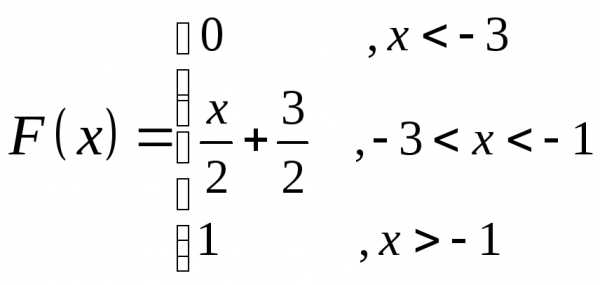
д)Найдём вероятность выполнения неравенства
Задача
27. Случайная величина  имеет плотность распределения вероятностей
имеет плотность распределения вероятностей .
Найти плотность распределения вероятностей
.
Найти плотность распределения вероятностей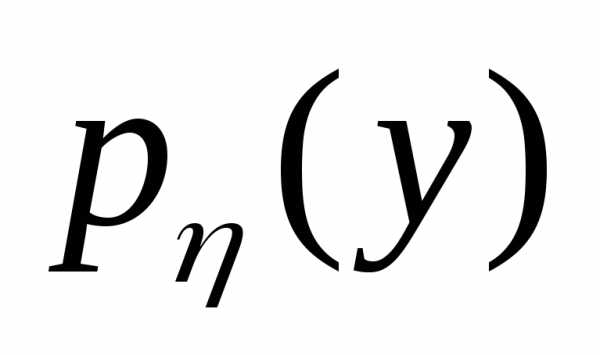 случайной величины
случайной величины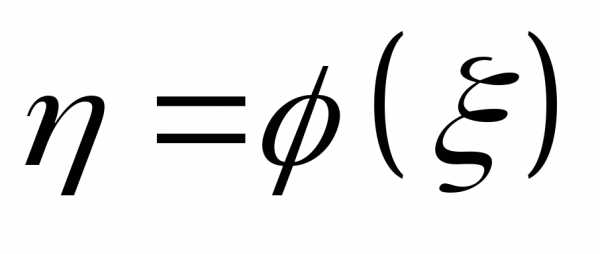
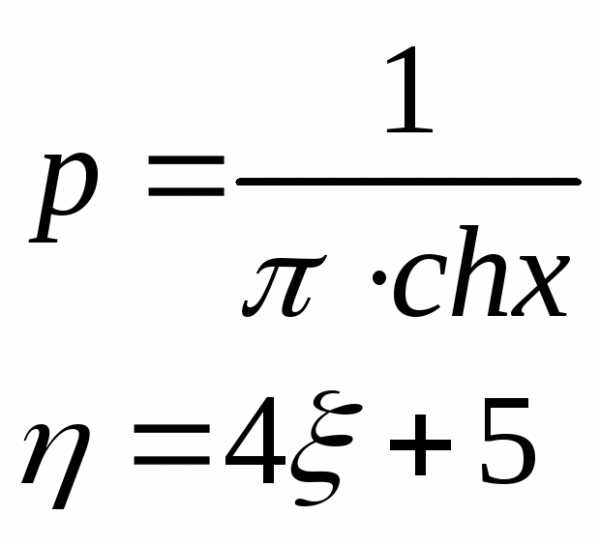
Так как функция монотонная, то:
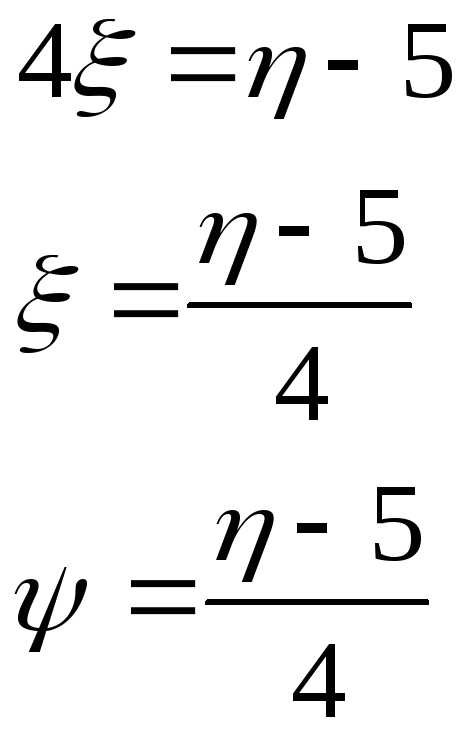
Найдём производную:

Найдём
интервал для 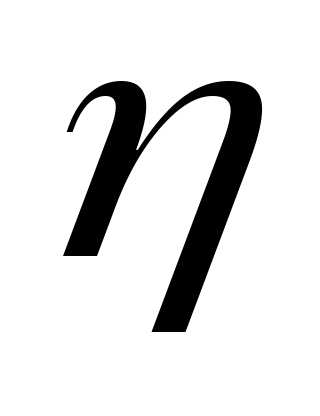
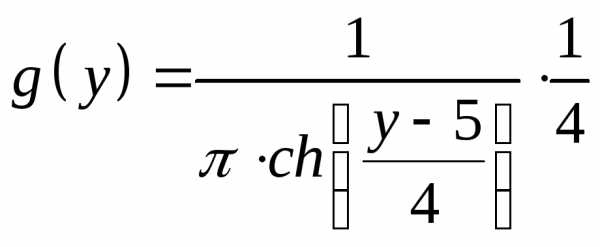
Проверка в системе MathCAD:
Задача
33. На отрезке 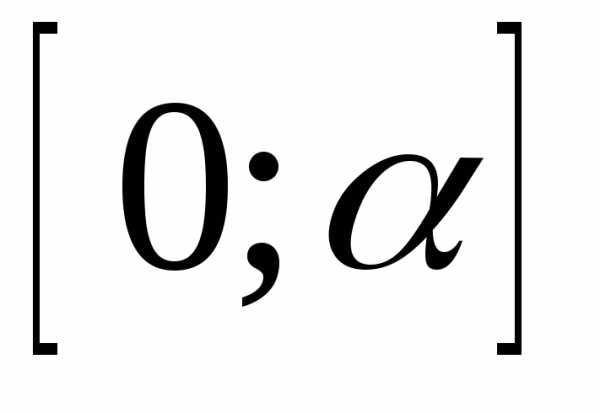 случайным образом выбрано
случайным образом выбрано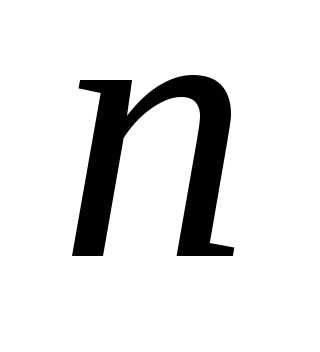 чисел, точнее, рассматриваются
чисел, точнее, рассматриваются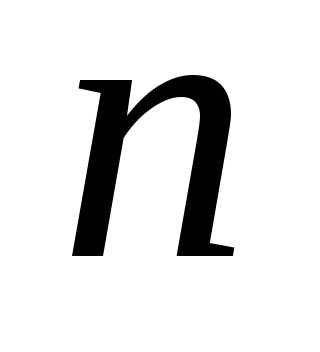 независимых случайных величинравномерно распределённых на отрезке
независимых случайных величинравномерно распределённых на отрезке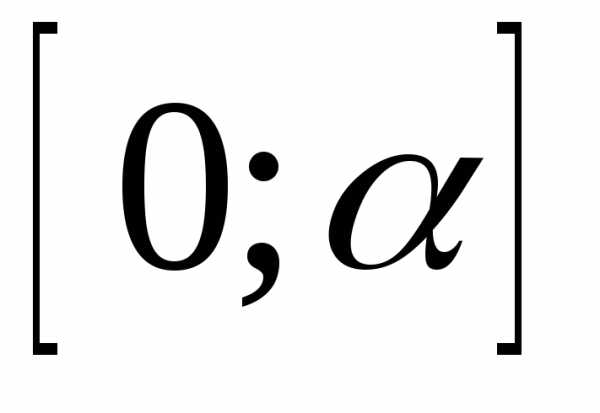 .
Найти вероятность того, что их сумма
заключена между
.
Найти вероятность того, что их сумма
заключена между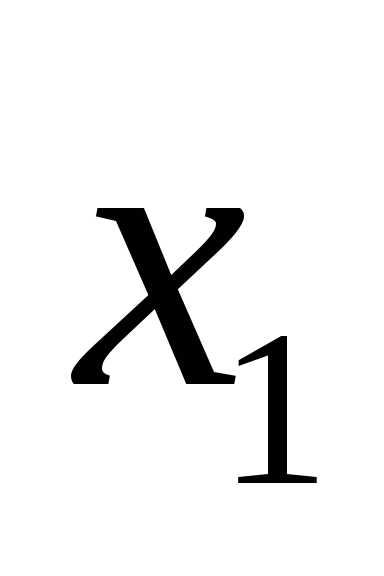 и
и т.е.
т.е.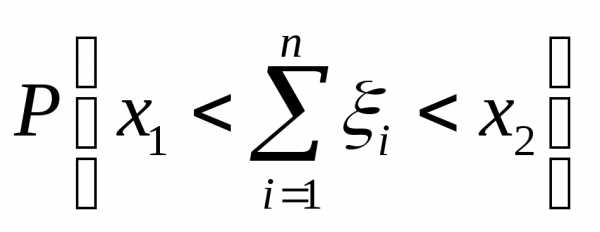
 ,
, 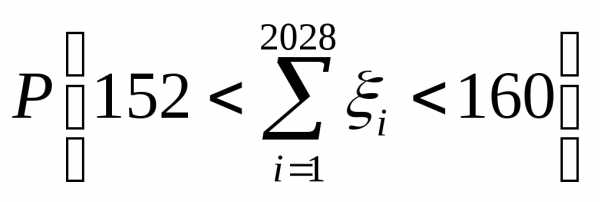
Решение:
Так как распределение равномерное, то
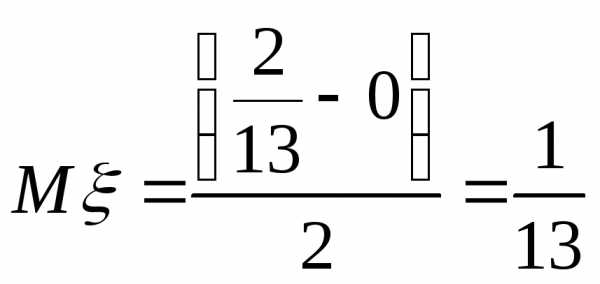
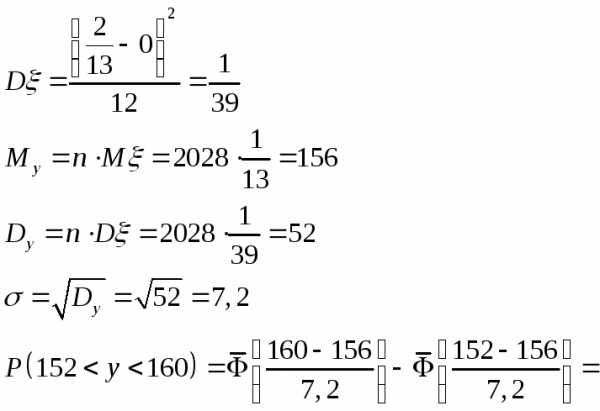
Ответ: 0,43 или 43%
Задача
34. Известно, что случайная величина  имеет распределение Пуассона,
неизвестным является параметр а.
Используя указанный ниже метод получения
точечных оценок, найти по реализации
выборкизначения оценки
имеет распределение Пуассона,
неизвестным является параметр а.
Используя указанный ниже метод получения
точечных оценок, найти по реализации
выборкизначения оценки неизвестного параметра а (метод
максимального правдоподобия)
неизвестного параметра а (метод
максимального правдоподобия)
Находим
производную  по а :
по а :
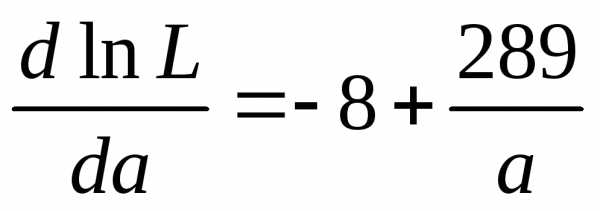
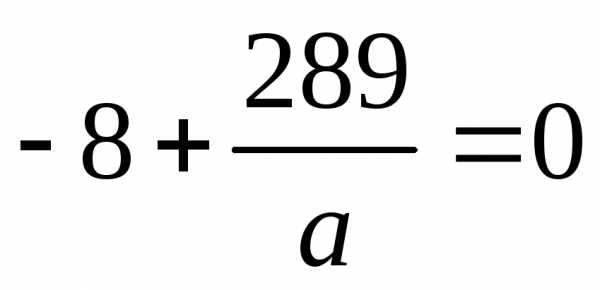
Находим
вторую производную 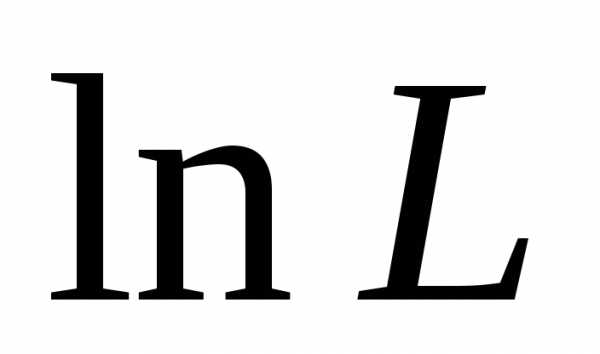 по а:
по а:

При  максимум исходной функции. Значит
максимум исходной функции. Значит
Ответ: 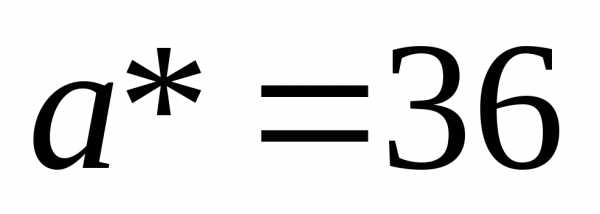
Задача
36. Случайная величина  имеет нормальное распределение с
неизвестным математическим ожиданием
а и неизвестной дисперсией
имеет нормальное распределение с
неизвестным математическим ожиданием
а и неизвестной дисперсией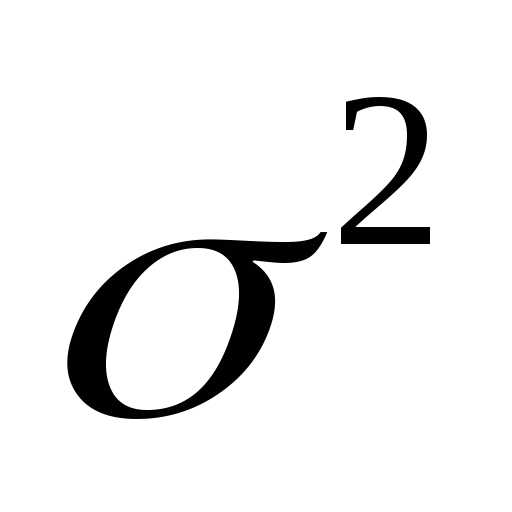 .
По выборкеобъёма
.
По выборкеобъёма вычислено выборочное среднее
вычислено выборочное среднее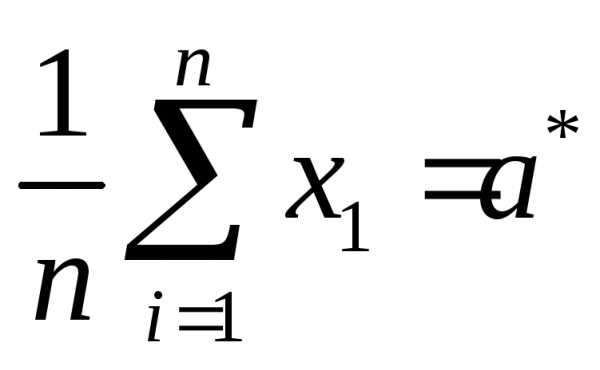 .
Определить доверительный интервал для
неизвестного параметра распределения
.
Определить доверительный интервал для
неизвестного параметра распределения ,
отвечающий заданной доверительной
вероятности
,
отвечающий заданной доверительной
вероятности .
.
Решение:

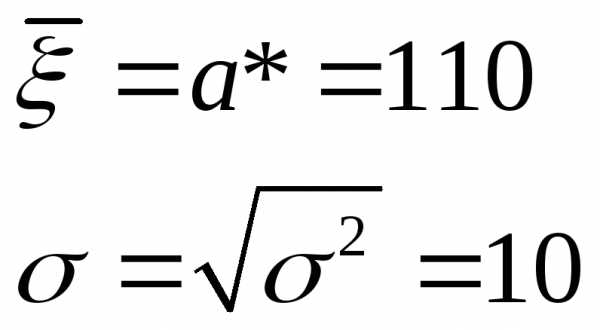
Ответ:
studfiles.net
Типовой расчёт №1
КГТА
18 Вариант
Студент гр У-103
Проверил: Юлина
Задача 1. Бросаются две игральные кости. Определить вероятность того, что:
а) сумма числа очков не превосходит N;
б) произведение числа очков не превосходит N;
в) произведение числа очков делится на N.
N=12
Решение:
а)

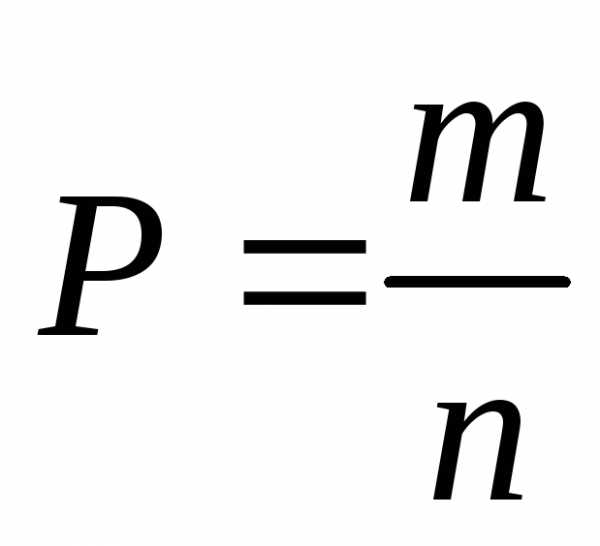
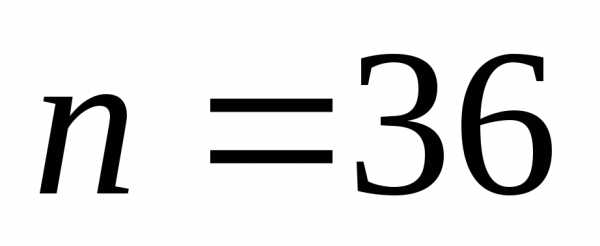 -количество
возможных исходов.
-количество
возможных исходов.
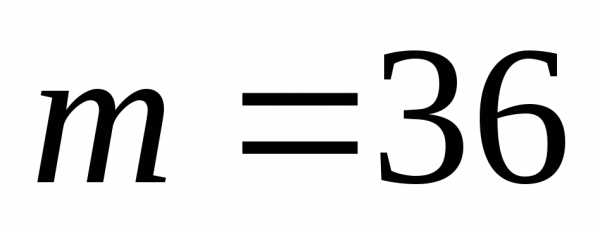 -количество
благоприятных исходов.
-количество
благоприятных исходов.
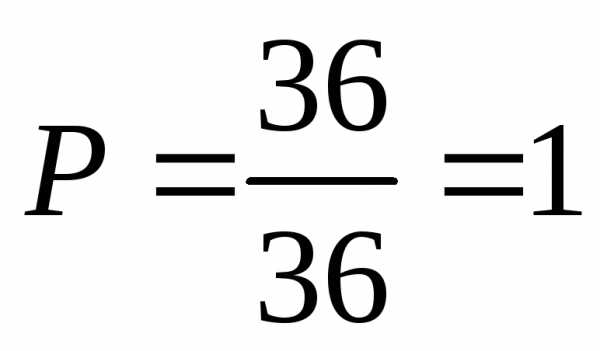
б)

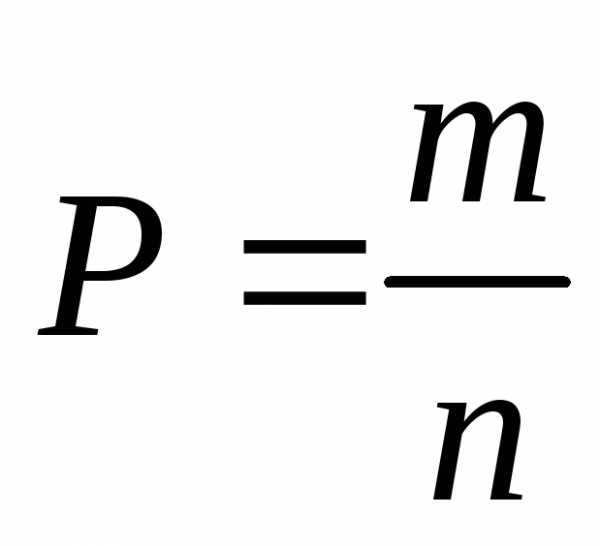
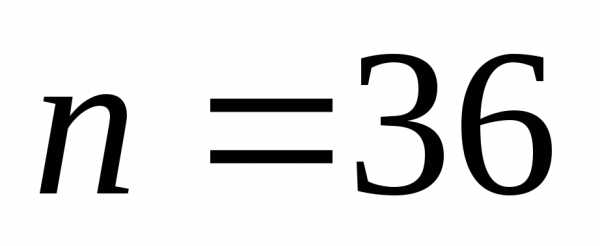 -количество
возможных исходов
-количество
возможных исходов
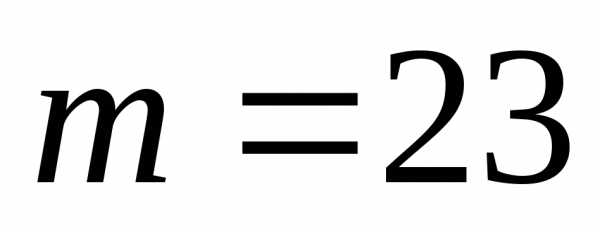 -количество
благополучных исходов
-количество
благополучных исходов
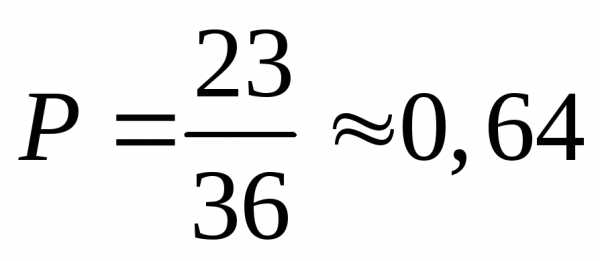
в)
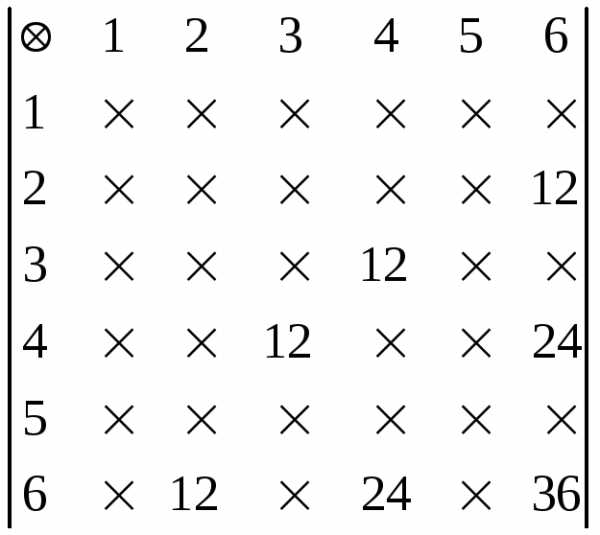
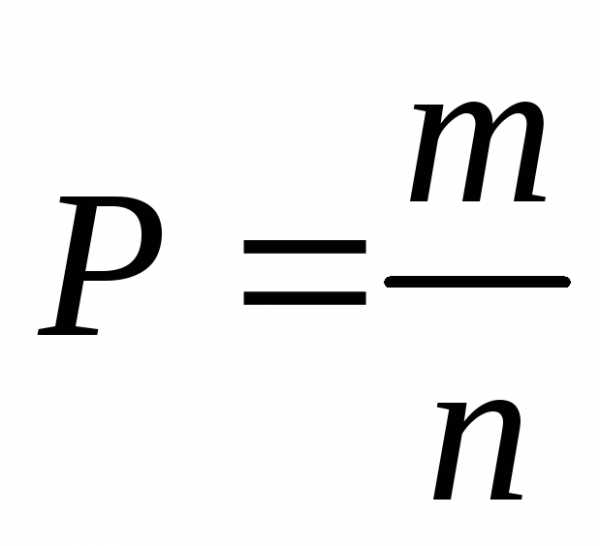
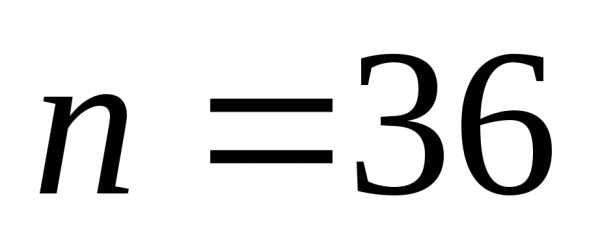
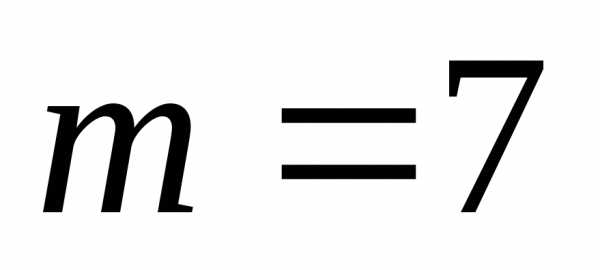

Ответ: 1; 0,64; 0,19.
Задача
3. Среди п лотерейных
билетов k
выигрышных. Наудачу взяли т билетов.
Определить вероятность того, что среди
них 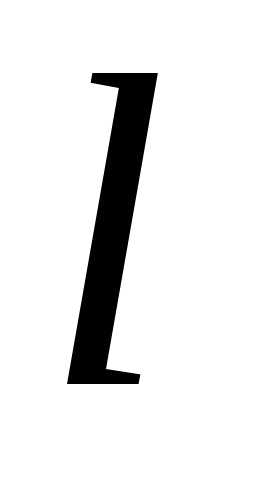 выигрышных.
выигрышных.
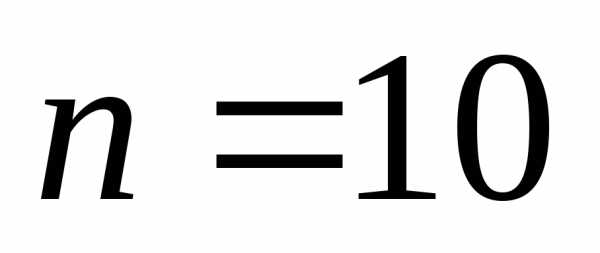 ,
, 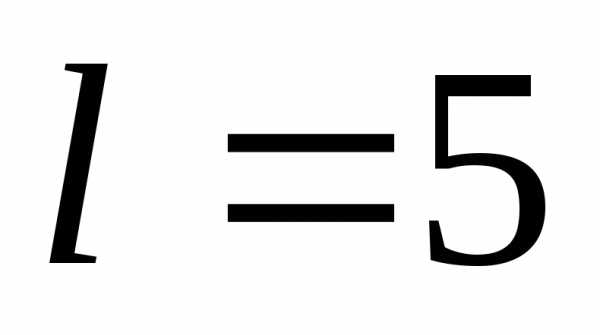 ,
,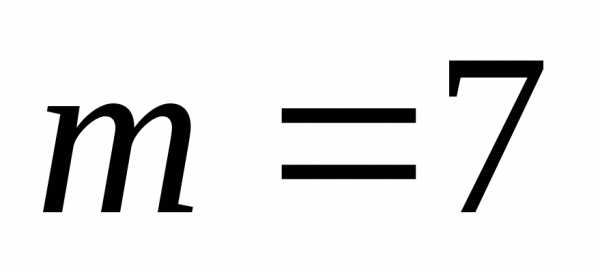 ,
,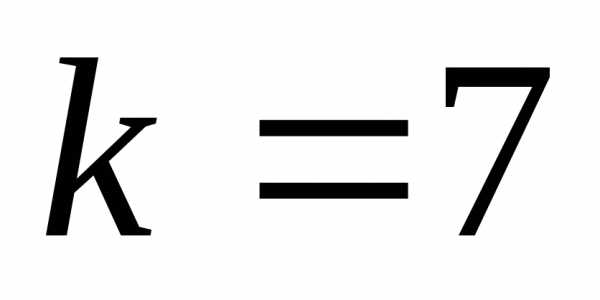
Решение:
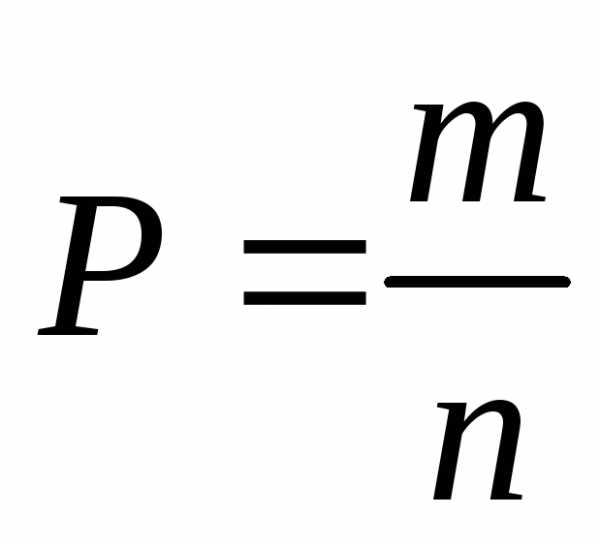
Число возможных исходов:
Число благоприятных исходов:
5
выигрышных из 7 можно взять  способами, а ещё 2 невыигрышных из 3 можно
выбрать
способами, а ещё 2 невыигрышных из 3 можно
выбрать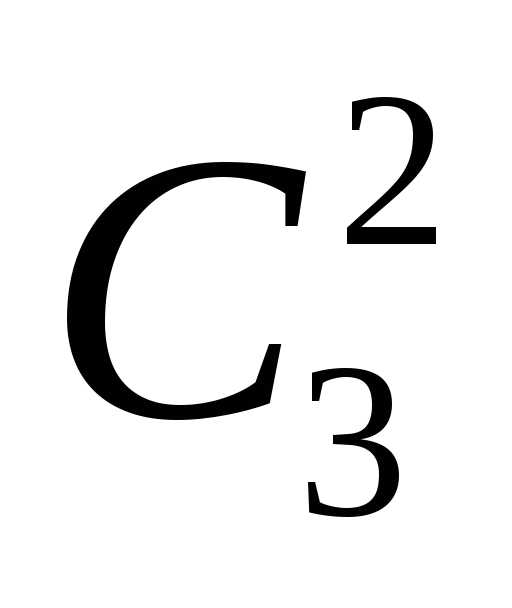 способами.
способами.
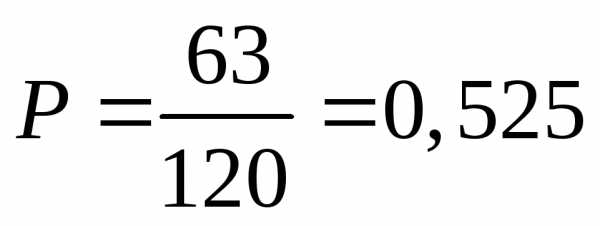
Ответ:
Задача 4. В лифт k — этажного дома сели n пассажиров (n<k). Каждый независимо от других с одинаковой вероятностью может выйти на любом (начиная со второго) этаже. Определить вероятность того, что:
а) все вышли на разных этажах;
б) по крайней мере, двое сошли на одном этаже.
а) Количество возможных исходов:
Количество благоприятных исходов:
б) В задаче речь идёт про событие противоположное первому, значит
Ответ: 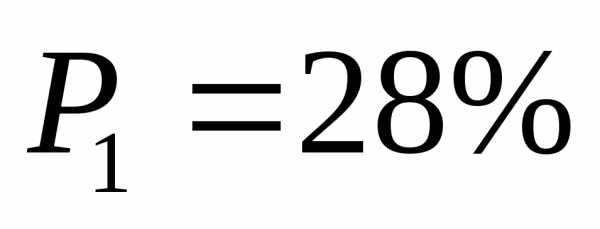 ,.
,.
Задача
5. В отрезке единичной длины на удачу
появляется точка. Определить вероятность
того, что расстояние от точки до обоих
концов отрезка превосходит величину 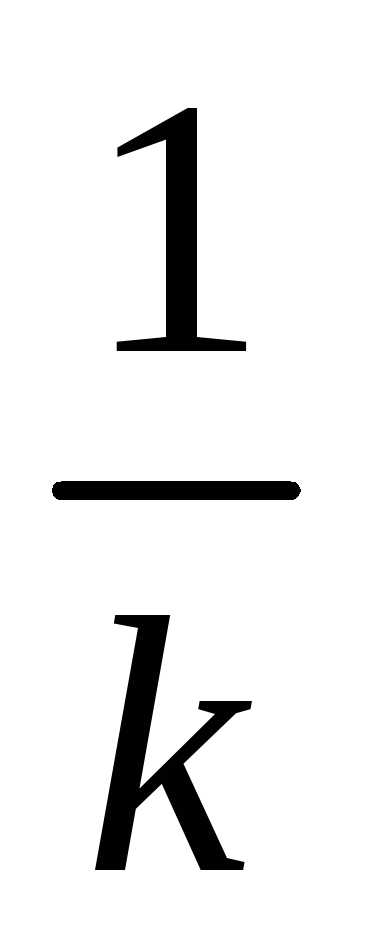 .
(
.
(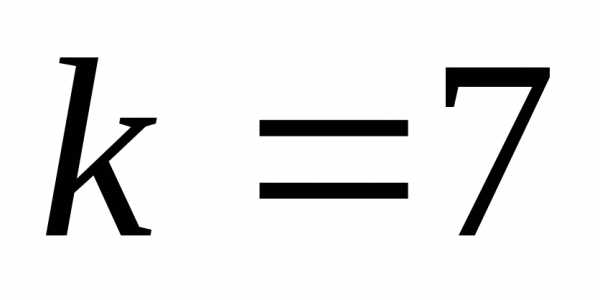 )
)
Решение:
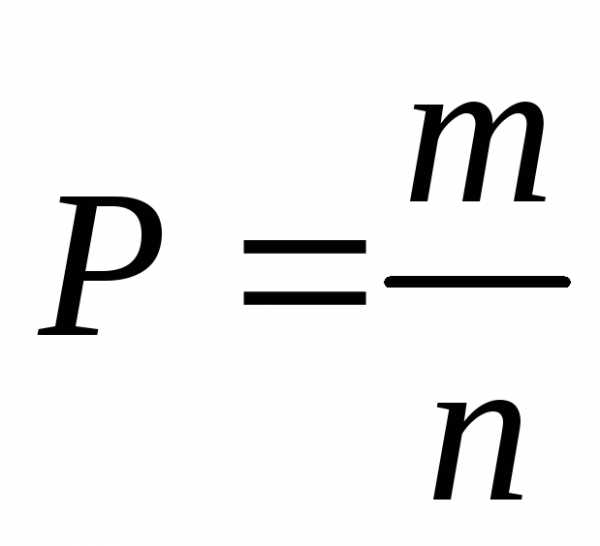
 -длина
отрезка, где появится точка.
-длина
отрезка, где появится точка.
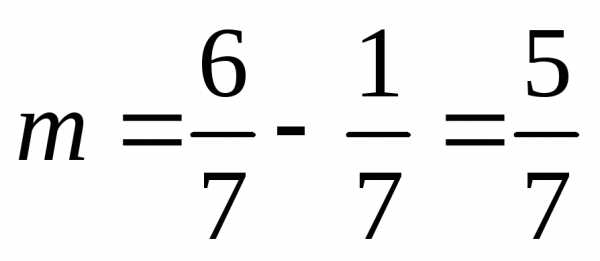 -длина
отрезка «благоприятного исхода»
-длина
отрезка «благоприятного исхода»
Ответ: 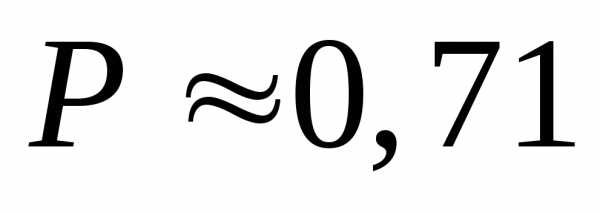
Задача
7. В круге радиуса R
наудачу появляется точка. Определить
вероятность того, что она попадает в
одну из двух непересекающихся фигур,
площади которых равны 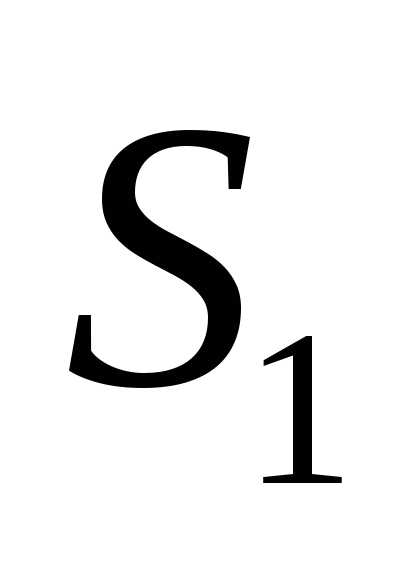 и
и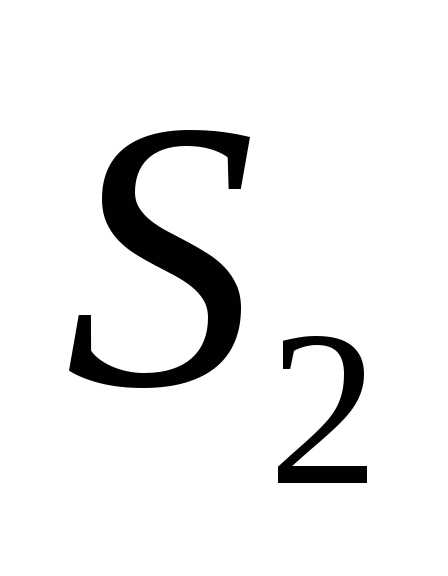 .
.
Решение:
Мера вероятности — площадь.
Все варианты попадания точки — в круг.
Благоприятные
— в фигурах  и
и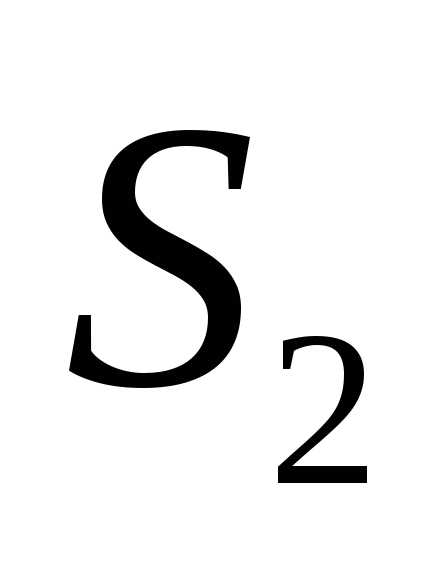
Ответ:
Задача
8. В двух партиях 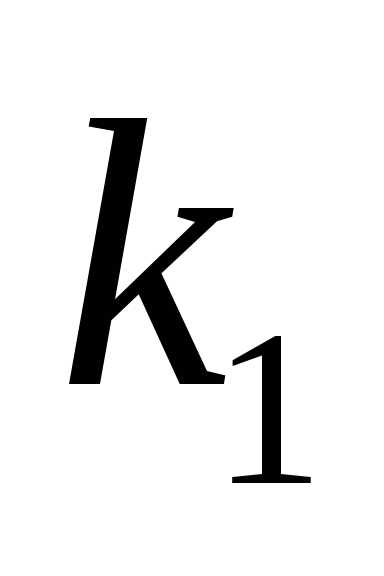 и
и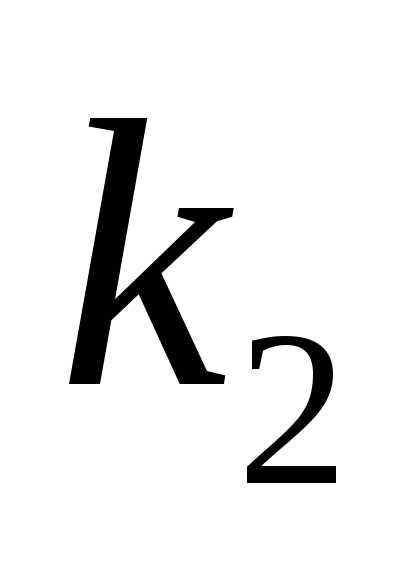 %
доброкачественных изделий соответственно.
Наудачу выбирают по одному изделию из
каждой партии. Какова вероятность
обнаружить среди них:
%
доброкачественных изделий соответственно.
Наудачу выбирают по одному изделию из
каждой партии. Какова вероятность
обнаружить среди них:
а) хотя бы одно бракованное;
б) два бракованных;
в) одно доброкачественное и одно бракованное?
События:
А-из первой партии достали бракованное.
В-из второй партии достали бракованное.
а) С-хотя бы одно бракованное.
б) D-оба бракованных:
в) Е-одно бракованное и одно качественное.
Ответ:
Задача
9. Вероятность того, что цель поражена
при одном выстреле первым стрелком  ,
вторым —
,
вторым —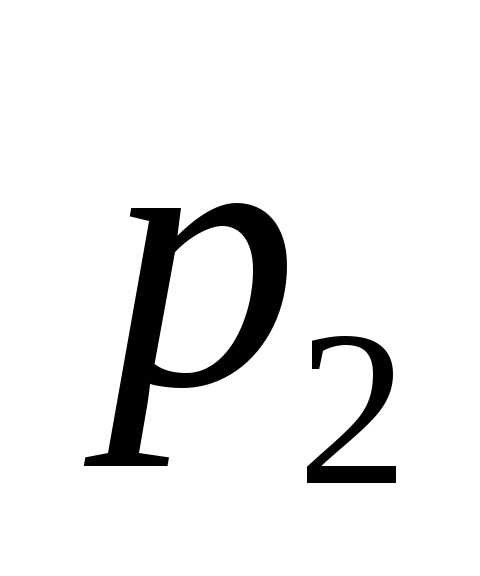 .
Первый сделал
.
Первый сделал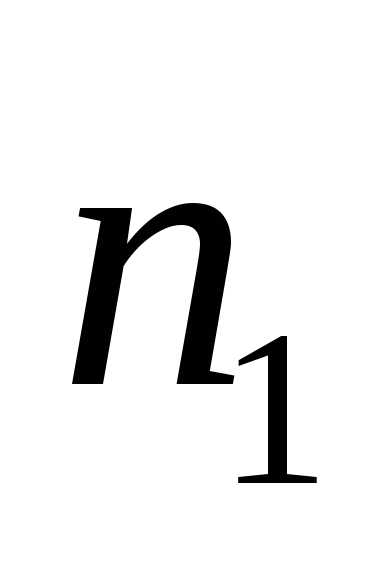 ,
второй —
,
второй —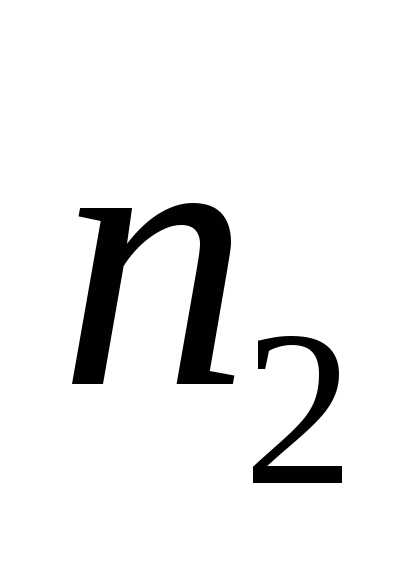 выстрелов. Определить вероятность того,
что цель не поражена.
выстрелов. Определить вероятность того,
что цель не поражена.
Решение:
События:
Цель не поражена
А — первый стрелок промахнулся 3 раза
В — второй стрелок промахнулся 2 раза
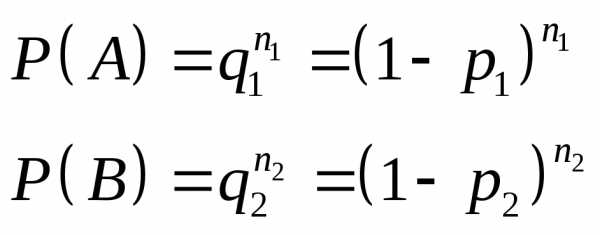
Ответ: 
Задача
12. Из 1000 ламп 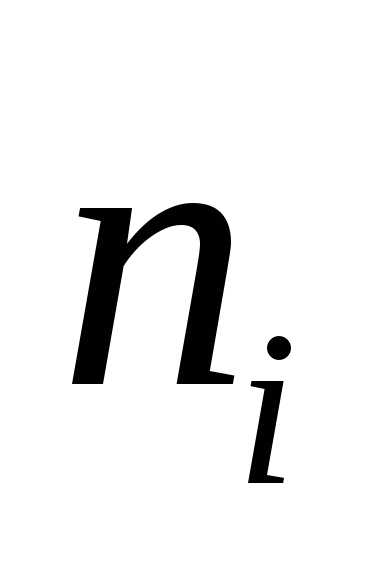 принадлежат
принадлежат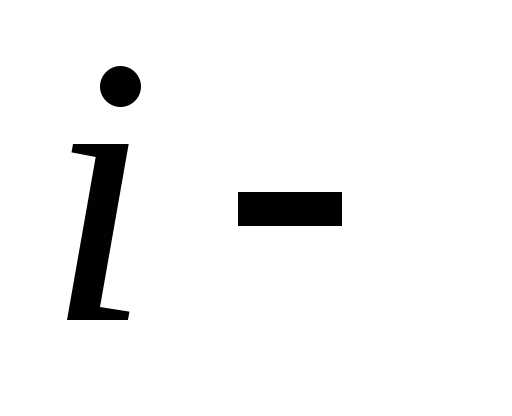 й
партии,
й
партии,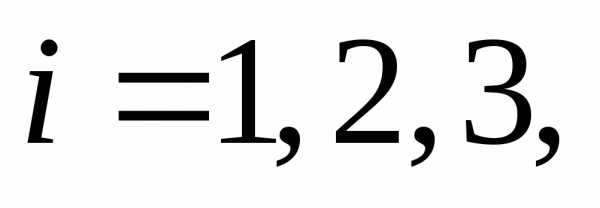
 В первой партии 6%, во второй 5%, в третьей
4% бракованных ламп. Наудачу выбирается
одна лампа. Определить вероятность
того, что выбранная лампа — бракованная.
В первой партии 6%, во второй 5%, в третьей
4% бракованных ламп. Наудачу выбирается
одна лампа. Определить вероятность
того, что выбранная лампа — бракованная.
Решение:
Количество брака в первой партии:
Количество брака во второй партии:
Количество брака в третьей партии:
Ответ:
Задача
15. В магазин поступают однотипные изделия
с трёх заводов, причём 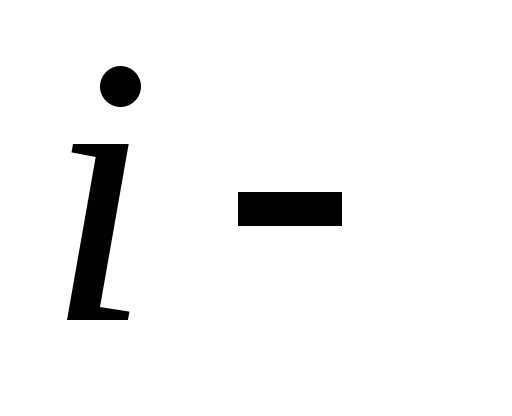 й
завод поставляет
й
завод поставляет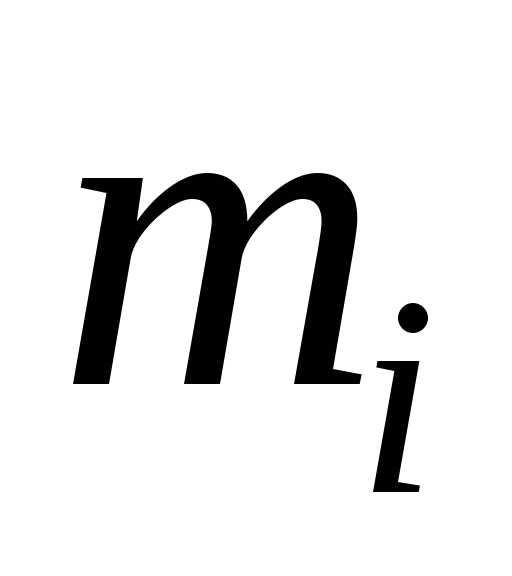 %
изделий
%
изделий .
Среди изделий
.
Среди изделий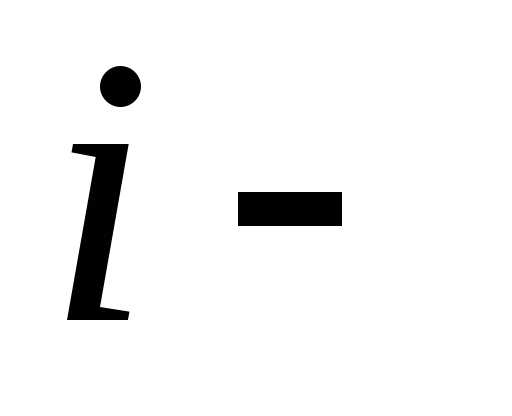 го
завода
го
завода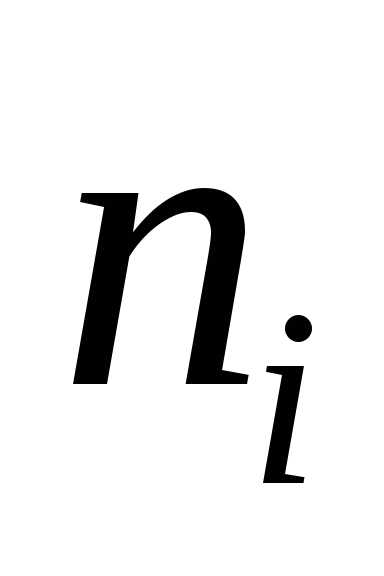 %
первосортных. Куплено одно изделие. Оно
оказалось первосортным. Определить
вероятность того, что купленное изделие
выпущено третьим заводом.
%
первосортных. Куплено одно изделие. Оно
оказалось первосортным. Определить
вероятность того, что купленное изделие
выпущено третьим заводом.
Решение:
Ответ: 59%
Задача
17. Вероятность выигрыша в лотерею на
один билет равна 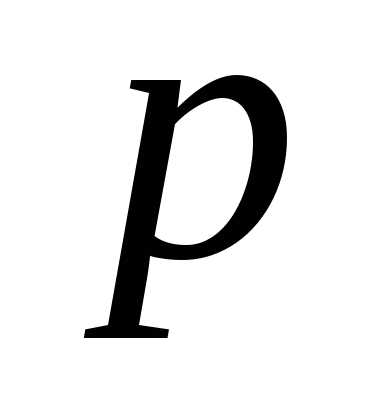 .
Куплено
.
Куплено билетов. Найти наивероятнейшее число
выигравших билетов и соответствующую
вероятность.
билетов. Найти наивероятнейшее число
выигравших билетов и соответствующую
вероятность.
Решение:
Найдём наивероятнейшее число выигравших билетов из неравенства:
Значит, есть два наивероятнейших числа 7 и 8.
Применима формула Бернулли:
Ответ: 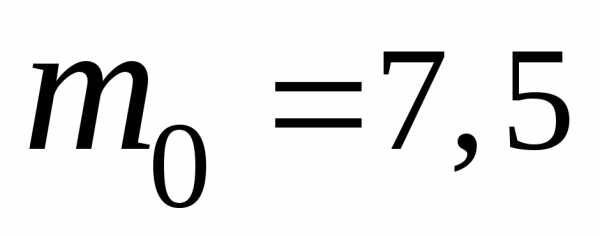
Задача
19. Вероятность «сбоя» в работе телефонной
станции при каждом вызове равна 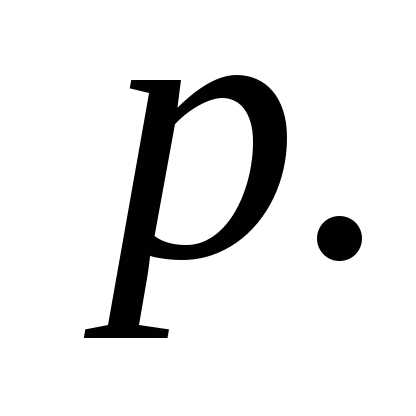 Поступило
Поступило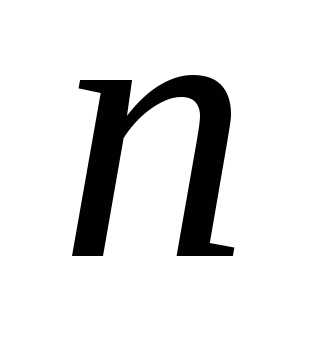 вызовов. Определить вероятность
вызовов. Определить вероятность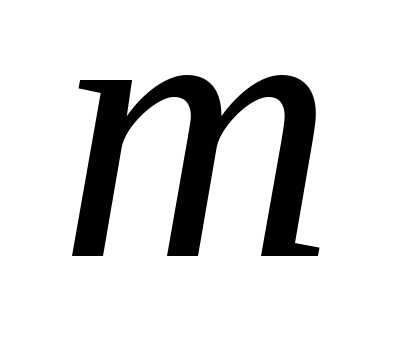 «сбоев».
«сбоев».
Так
как 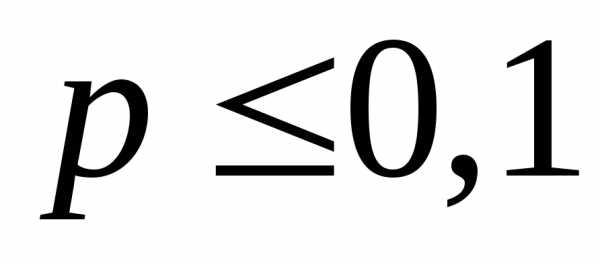 и
и ,
то применима формула Пуассона.
,
то применима формула Пуассона.
Ответ: 13,2%
Задача
20. Вероятность наступления некоторого
события в каждом из 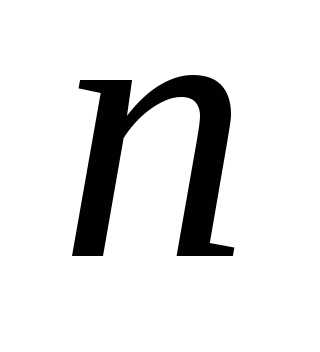 независимых испытаний равна
независимых испытаний равна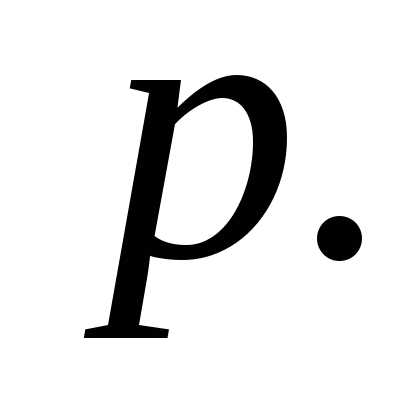 Определить вероятность того, что числонаступлений события удовлетворяют
следующему неравенству:
Определить вероятность того, что числонаступлений события удовлетворяют
следующему неравенству: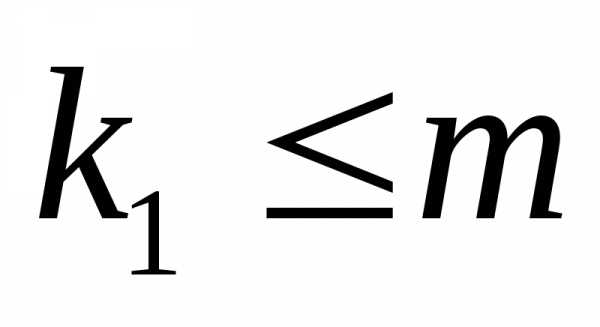 .
.
Решение:
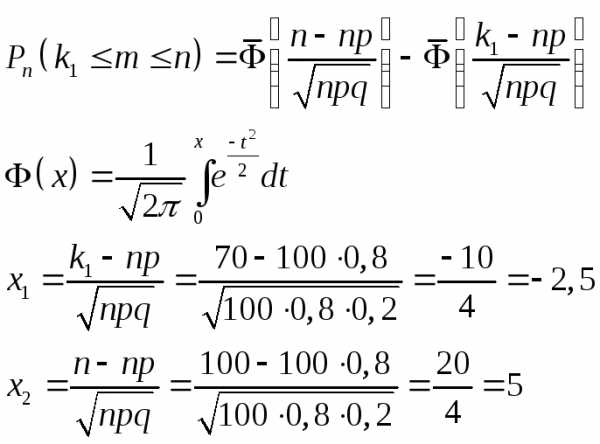
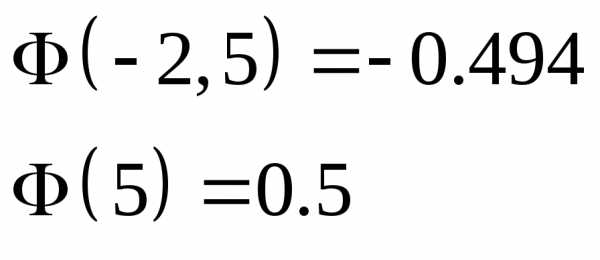
Ответ: 0,994.
Задача
21. Дана плотность распределения 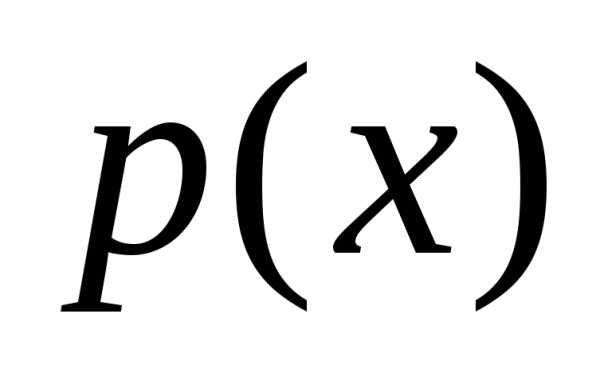 случайной величины
случайной величины .
Найти параметр
.
Найти параметр ,
математическое ожидание
,
математическое ожидание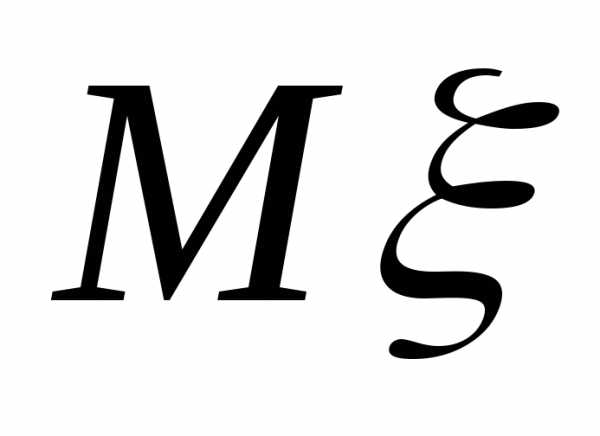 ,
дисперсию
,
дисперсию ,
функцию распределения случайной величины
,
функцию распределения случайной величины ,
вероятность выполнения неравенства
,
вероятность выполнения неравенства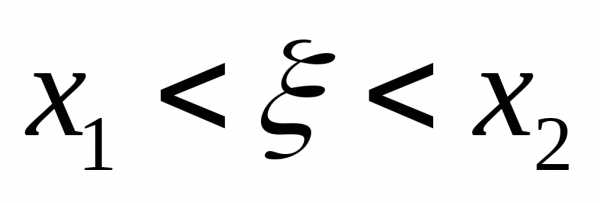
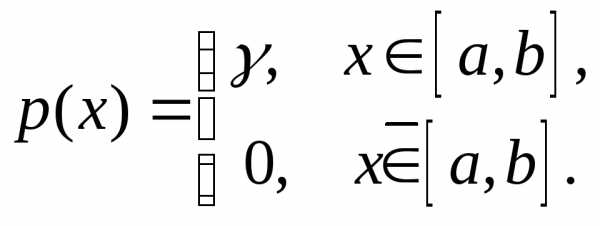
Решение:
а)
найдём параметр 
б)
найдём математическое ожидание  :
:
в)
найдём дисперсию 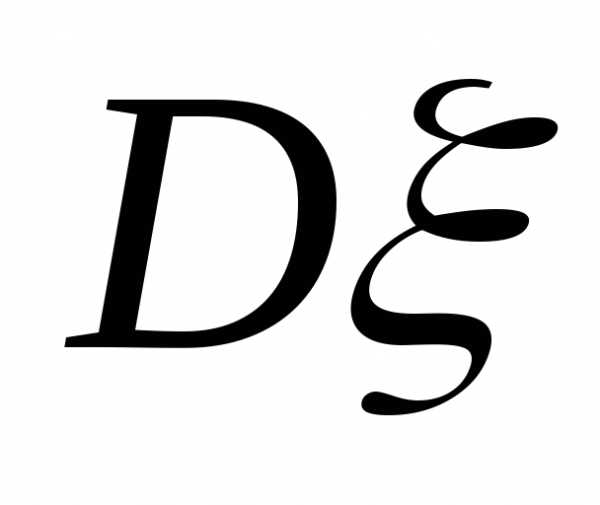 :
:
г)
Найдём функцию распределения случайной
величины  :
:
При 
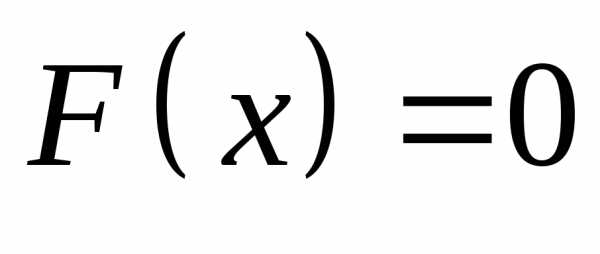
При 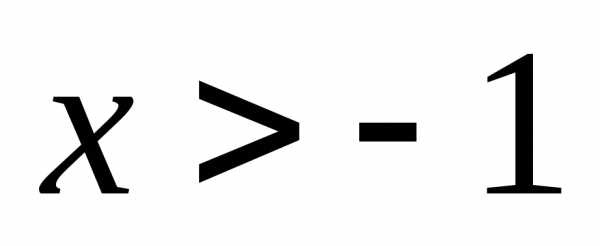
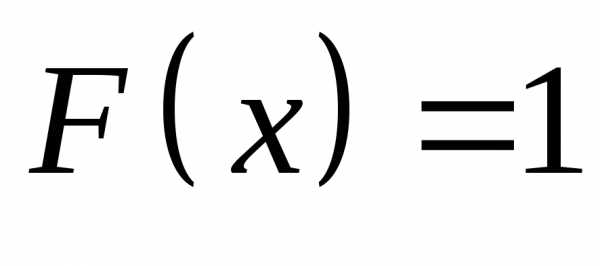
При
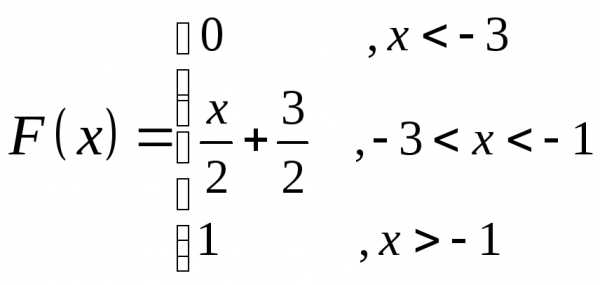
д)Найдём вероятность выполнения неравенства
Задача
27. Случайная величина  имеет плотность распределения вероятностей
имеет плотность распределения вероятностей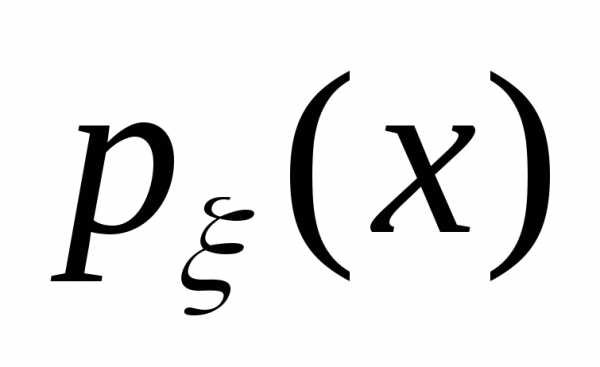 .
Найти плотность распределения вероятностей
.
Найти плотность распределения вероятностей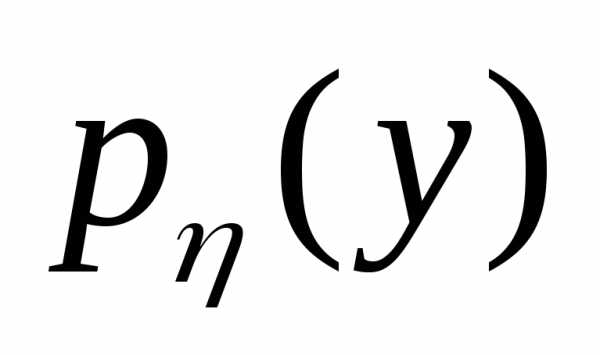 случайной величины
случайной величины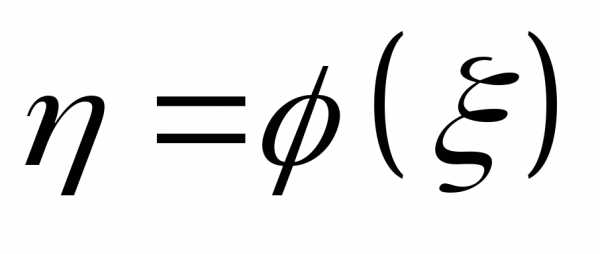
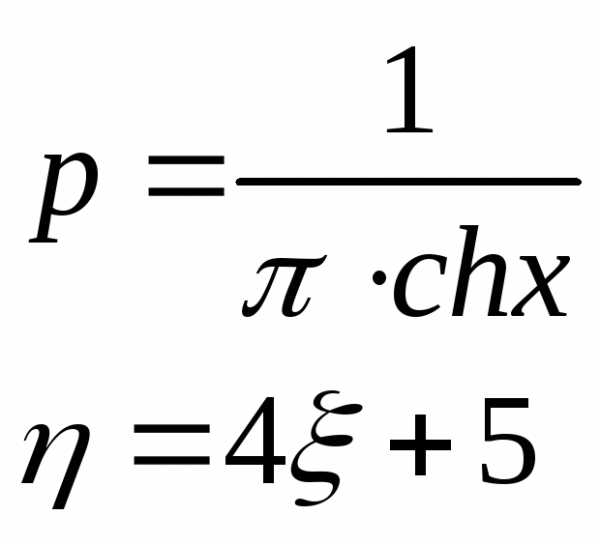
Так как функция монотонная, то:
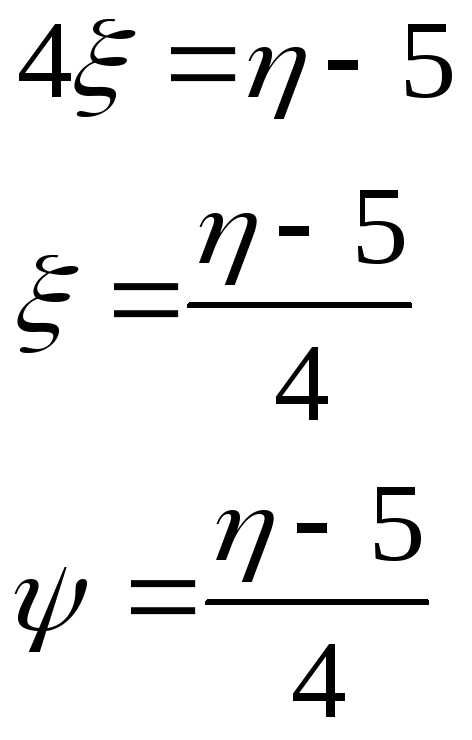
Найдём производную:
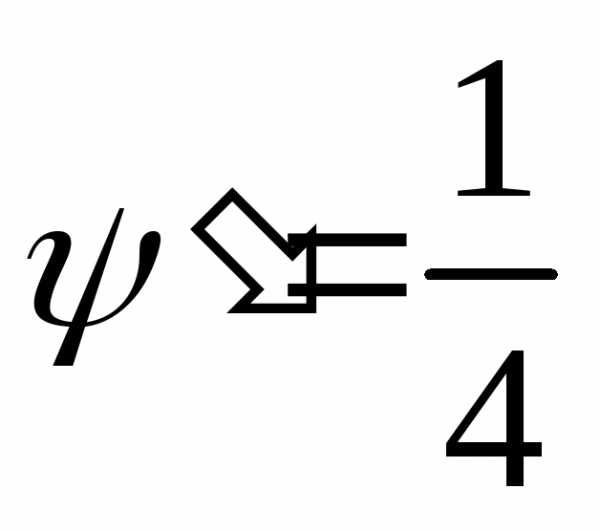
Найдём
интервал для 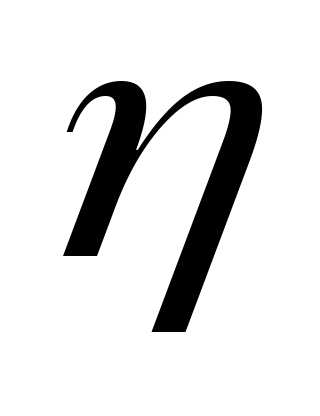
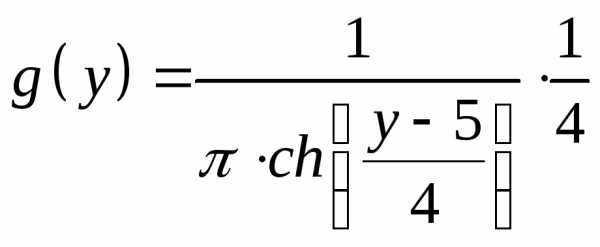
Проверка в системе MathCAD:
Задача
33. На отрезке 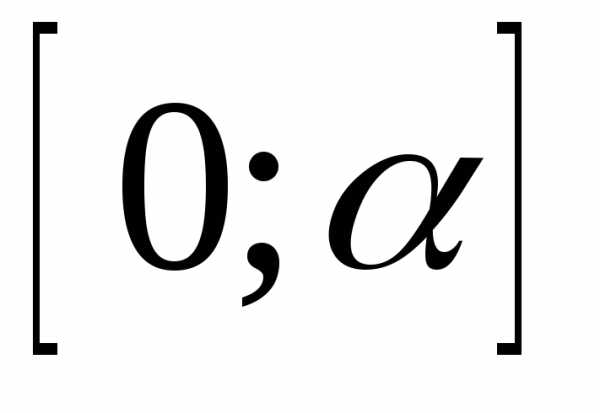 случайным образом выбрано
случайным образом выбрано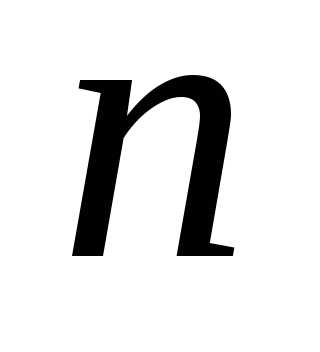 чисел, точнее, рассматриваются
чисел, точнее, рассматриваются независимых случайных величинравномерно распределённых на отрезке
независимых случайных величинравномерно распределённых на отрезке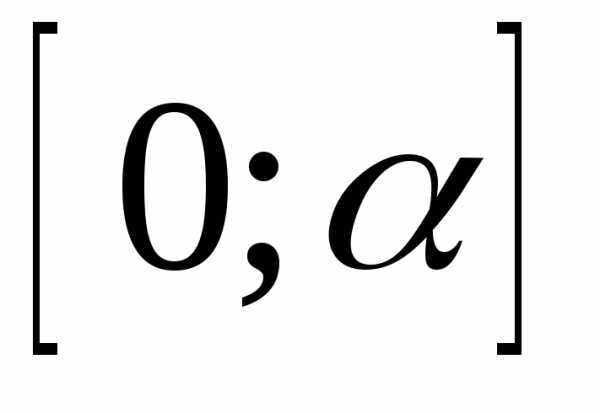 .
Найти вероятность того, что их сумма
заключена между
.
Найти вероятность того, что их сумма
заключена между и
и т.е.
т.е.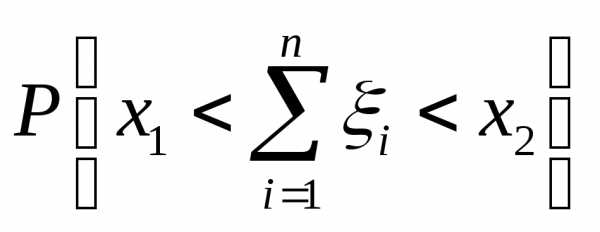
 ,
, 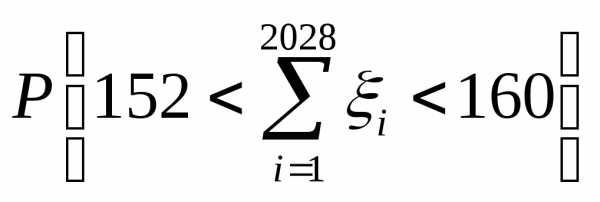
Решение:
Так как распределение равномерное, то
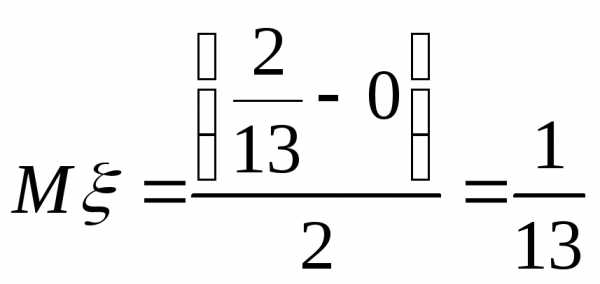
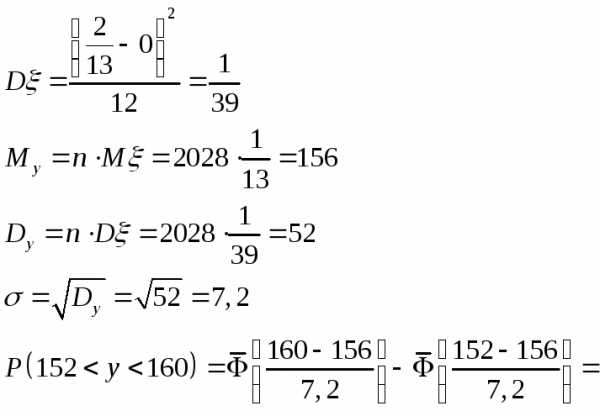
Ответ: 0,43 или 43%
Задача
34. Известно, что случайная величина  имеет распределение Пуассона,
неизвестным является параметр а.
Используя указанный ниже метод получения
точечных оценок, найти по реализации
выборкизначения оценки
имеет распределение Пуассона,
неизвестным является параметр а.
Используя указанный ниже метод получения
точечных оценок, найти по реализации
выборкизначения оценки неизвестного параметра а (метод
максимального правдоподобия)
неизвестного параметра а (метод
максимального правдоподобия)
Находим
производную 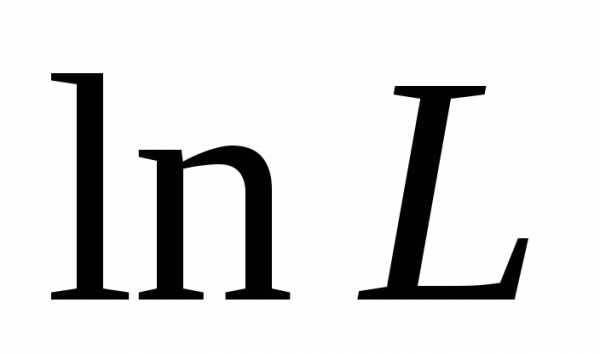 по а :
по а :
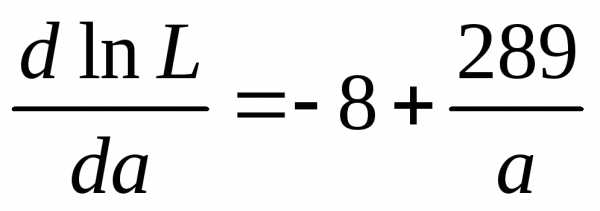
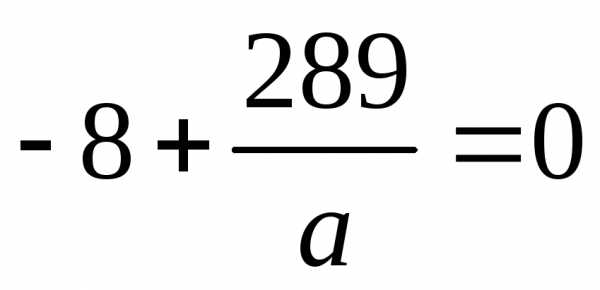
Находим
вторую производную  по а:
по а:
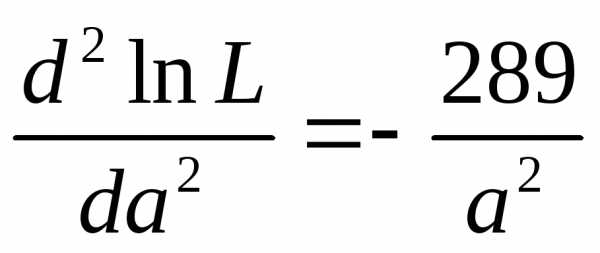
При  максимум исходной функции. Значит
максимум исходной функции. Значит
Ответ: 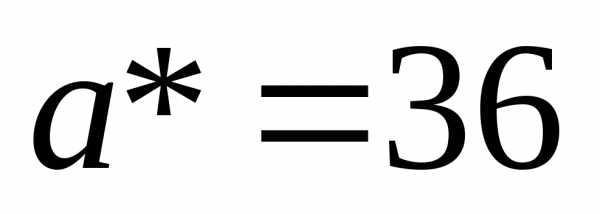
Задача
36. Случайная величина  имеет нормальное распределение с
неизвестным математическим ожиданием
а и неизвестной дисперсией
имеет нормальное распределение с
неизвестным математическим ожиданием
а и неизвестной дисперсией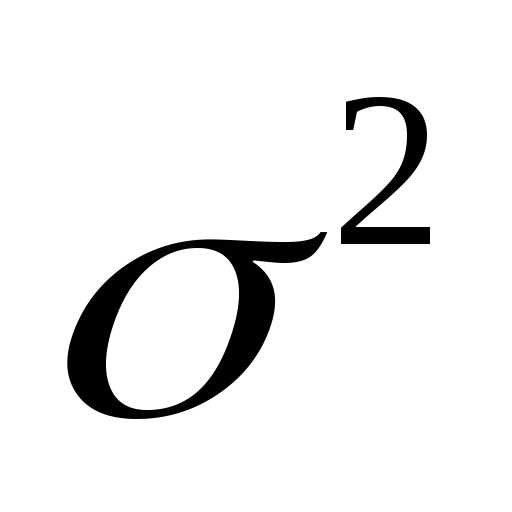 .
По выборкеобъёма
.
По выборкеобъёма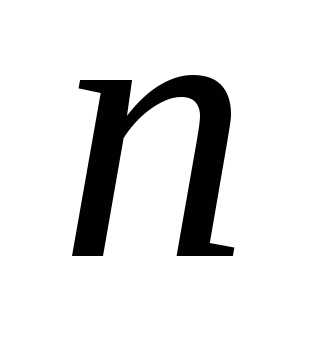 вычислено выборочное среднее
вычислено выборочное среднее .
Определить доверительный интервал для
неизвестного параметра распределения
.
Определить доверительный интервал для
неизвестного параметра распределения ,
отвечающий заданной доверительной
вероятности
,
отвечающий заданной доверительной
вероятности .
.
Решение:
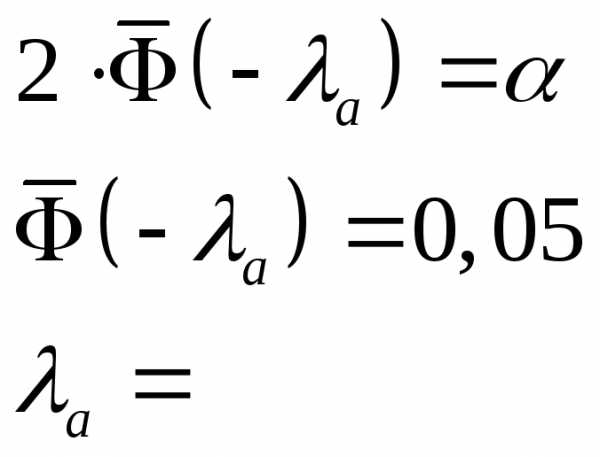
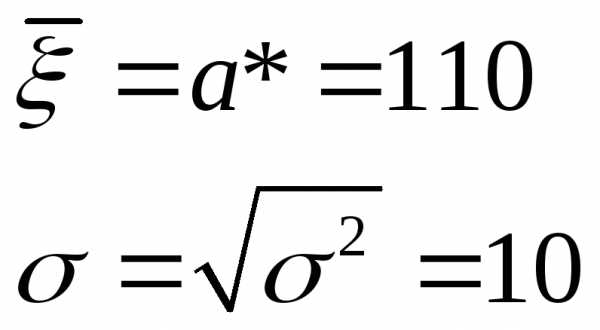
Ответ:
Задача
37. Случайная величина  имеет нормальное распределение с
неизвестным математическим ожиданием
имеет нормальное распределение с
неизвестным математическим ожиданием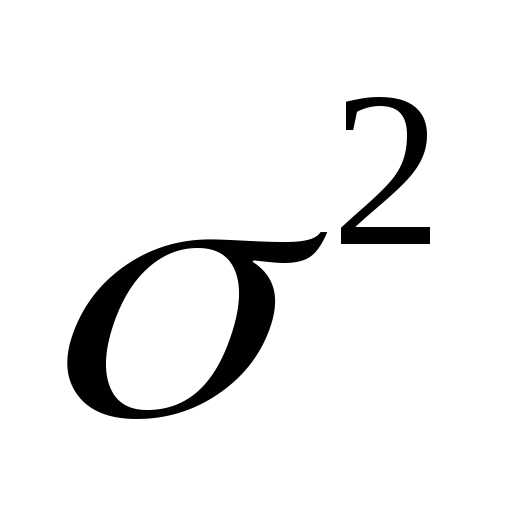 .
По выборкеобъёма
.
По выборкеобъёма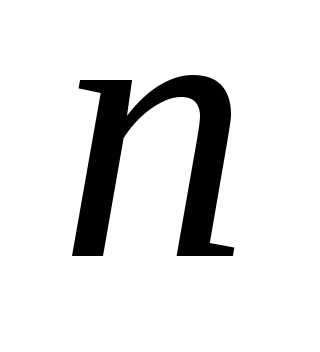 вычислены оценки:
вычислены оценки:
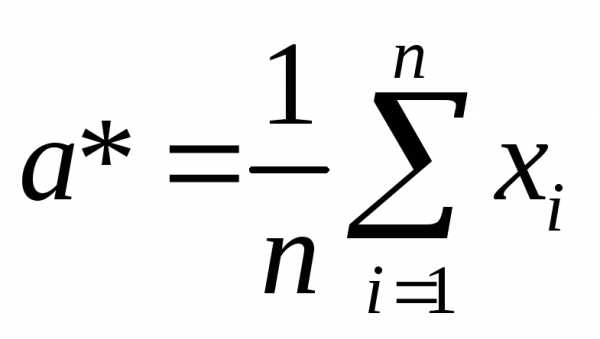 и
и
неизвестных
параметров. Найти доверительный интервал
для математического ожидания а, отвечающей
доверительной вероятности  .
.
Решение:
Задача
41. Для контроля взяты 200 узлов, собранных
на ученическом конвейере. Число узлов  ,
при сборке которых пропущено
,
при сборке которых пропущено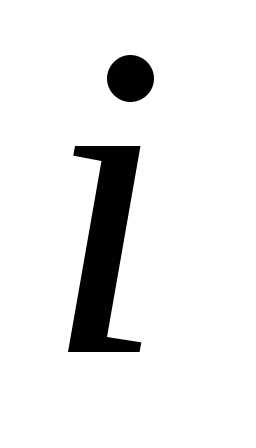 операций, сведено в таблицу.
операций, сведено в таблицу.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | >7 |
| 41 | 62 | 45 | 22 | 16 | 8 | 4 | 0 |
Согласуются
ли полученные результаты с распределением
Пуассона (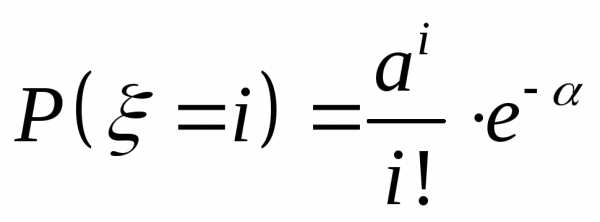 ,
где
,
где случайное число пропущенных операций)
по критерию
случайное число пропущенных операций)
по критерию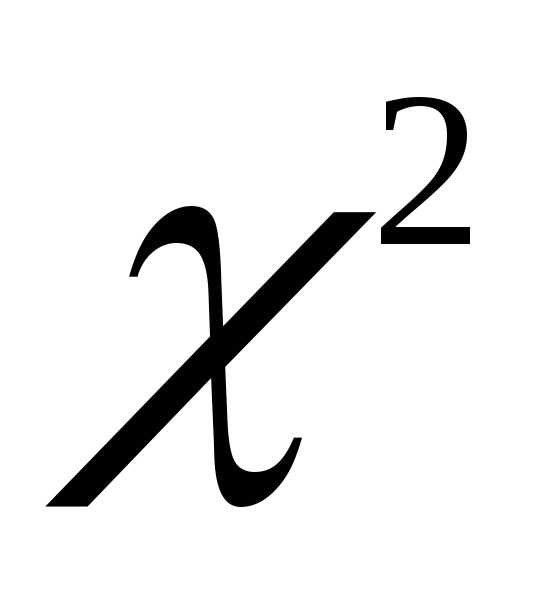 при уровне значимости
при уровне значимости ?
Решить задачу для заданного значения
параметра а, и для случая когда параметр
а оценивается по выборке.
?
Решить задачу для заданного значения
параметра а, и для случая когда параметр
а оценивается по выборке.
Решение:
studfiles.net