§ 2. Операции над векторами
1. Сложение. Пусть а и b – два вектора. От произвольной точки О отложим вектор ОА = а, а от получившейся точки А – вектор АВ = b. Вектор ОВ называется суммой a+b векторов а и b (рис.6), а операция нахождения суммы векторов – их сложением.
П
Прямо из определения суммы двух векторов вытекает правило треугольника:
(2.1) для любых трех точек О, А и В ОА + АВ = ОВ.
Кроме того, как известно из школьного курса геометрии, для любых трех точек О, А и В длина отрезка ОВ не превосходит суммы длин отрезков ОА и АВ, причем равенство |ОВ| = |ОА| + |АВ| достигается только тогда, когда точка А лежит на отрезке [ОВ]. Это неравенство часто называют неравенством треугольника. Определение суммы векторов позволяет записать его в векторной форме:
(2.2) |а + b| |a| + |b| .
Равенство в (2.2) достигается тогда и только тогда, когда векторы а и b сонаправлены, а в остальных случаях неравенство является строгим. Записывать равенство |а+b| = |a|+|b| для произвольных векторов – грубая ошибка.
2. Основные свойства сложения векторов. К ним относят:
(C1) Для любых трех векторов a, b и c (a+b)+c = a+(b+c) (ассоциативность).
(С2) Для любых двух векторов a и b a+b = b+a (коммутативность).
(С3) Для любого вектора а а+0 = а.
(С4) Для любых двух точек А и В АВ+ВА = 0.
В
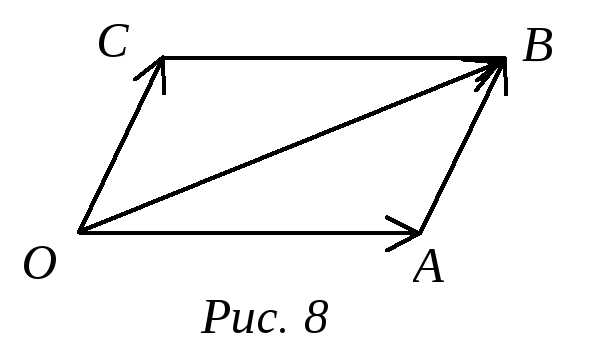
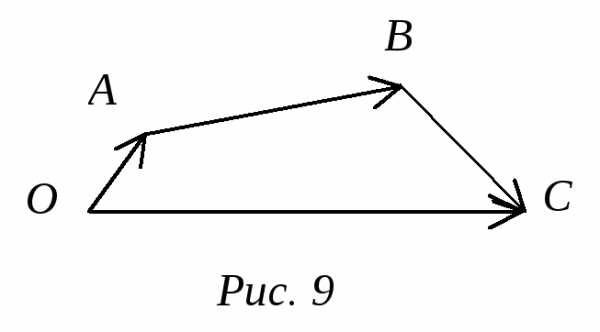
Докажем свойство (С1). Для этого последовательно отложим векторы ОА = а , АВ = b и ВС = с. По определению сложения векторов (a+b)+c = ОВ+ВС, а a+(b+c) = ОА+АС. Но ОВ+ВС = ОА+АС = ОС (рис.9).
Заметим, что на рис.8 OC = AB. Поэтому справедливо
(2.3) Правило параллелограмма: Сумма неколлинеарных векторов а и b равна диагонали ОВ параллелограмма ОАВС, построенного на векторах2 ОА = а и ОС = b.
Кроме того, из проведенного выше доказательства ассоциативности получается
(2.4) Правило многоугольника. Чтобы сложить несколько векторов, взятых в определенном порядке, надо отложить их друг за другом так, чтобы конец каждого вектора служил началом следующего, а затем соединить начало первого с концом последнего.
Мы доказали это правило только для случая трех векторов, но проведенное рассуждение без труда переносится на любое число слагаемых.
П
(2.5) Правило замкнутой цепочки. Сумма нескольких векторов равна нулю тогда и только тогда, когда при последовательном их откладывании они образуют замкнутую цепочку, т.е. конец последнего совпадает с началом первого.
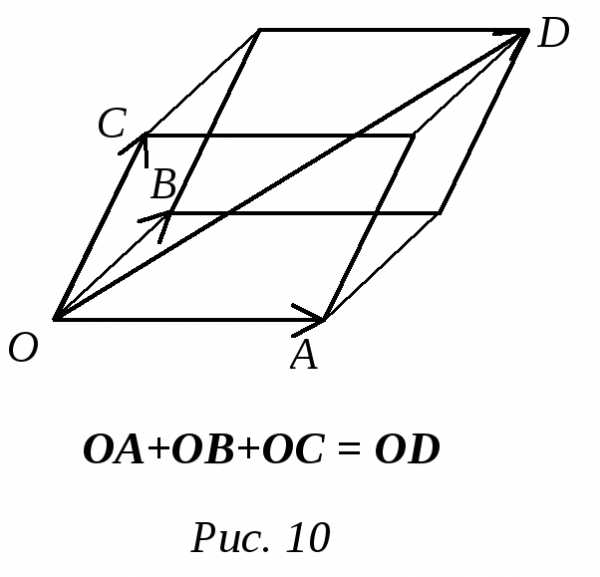
(2.6) Упражнение. Докажите правило параллелепипеда: чтобы сложить три вектора, не параллельные одной плоскости, надо отложить их из одной точки О, достроить три получившихся отрезка до параллелепипеда и провести из точки О диагональ этого параллелепипеда, которая и будет искомой суммой (рис.10).
Ассоциативность сложения векторов показывает, что сумма трех векторов, взятых в определенном порядке, не зависит от того, сложим ли мы сначала два первых вектора, а потом прибавим к ним третий, или сначала найдем сумму второго и третьего векторов, а потом прибавим ее к первому. Это означает, что мы можем записывать сумму трех векторов как а+b+с, не задумываясь, каким образом расставлять в ней скобки. В курсе алгебры будет показано, что если это свойство выполняется для трех слагаемых, то оно выполняется и для любого их числа, то есть мы можем, не заботясь о способе расстановки скобок, записывать любую векторную сумму а+b+с+…+d. А свойство коммутативности (С2) показывает, что мы можем также, не меняя этой суммы, произвольным образом переставлять в ней слагаемые. В этом и состоит смысл ассоциативности и коммутативности.
3
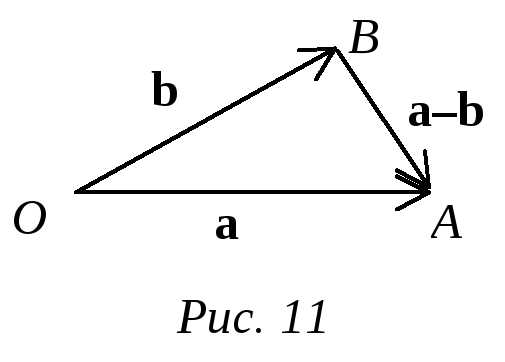
Отложим от произвольной точки О векторы ОА= а и ОВ=b. Очевидно, единственным вектором, который в сумме с ОВ дает ОА, является вектор ВА. Таким образом,
(2.7) у любых двух векторов есть разность, и только одна. Чтобы построить ее, надо отложить векторы от одной точки и соединить конец второго с концом первого (рис.11).
З
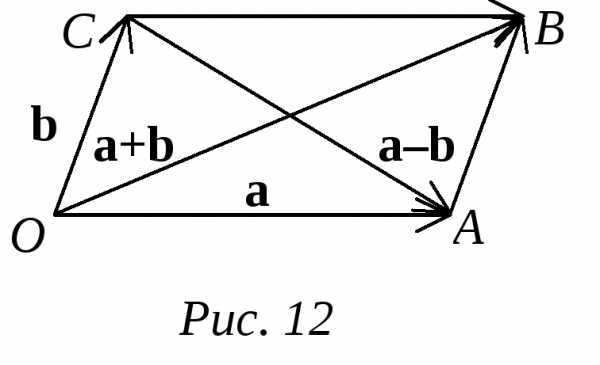
a–b = a+(–b).
Иными словами, вычесть один вектор из другого – это все равно, что сложить первый вектор с вектором, противоположным второму.
Пусть
векторы а и b неколлинеарны. Тогда точки
О, А и В образуют треугольник. Если
достроить его до параллелограмма ОАСВ,
то в нем диагональ 
будет изображать сумму а+b, а диагональ
– разность а–b (рис.12). Это полезное
дополнение к правилу параллелограмма.
Равенство (2.8) можно было доказать и чисто алгебраически. В самом деле, если x = a+(–b) , то x+b = a+(–b)+b = а+0 = a. Также алгебраически можно показать, что других значений у разности а–b нет: x+b = a (x+b)+(–b) = a+(–b) x+(b+(–b)) = a+(–b) x+0=a+(–b) x = a+(–b). Мы намеренно записали все эти преобразования подробно, чтобы показать, что все они опираются только на основные свойства сложения (С1)-(С4) (проверьте!). В общей теории векторных пространств, с которой вы познакомитесь в курсе алгебры, эти свойства принимаются за аксиомы сложения векторов, а все остальные свойства сложения выводятся из них.
4. Умножение вектора на число. Умножением вектора на число называется операция нахождения произведения вектора на число. Произведение ненулевого вектора а на число х – это вектор, обозначаемый «ха» и удовлетворяющий следующим двум условиям:
(П1) | ха | = |х||а| ; (П2) хаа, если х0, и хаа, если х<0.
Произведение нулевого вектора на любое число по определению считается равным 0.
Условие (П1) остается справедливым и при x = 0, но условие (П2) в этом случает нарушается при х<0 (из-за чего случай нулевого вектора и приходится рассматривать отдельно). Однако, при любых а и х векторы а и ха коллинеарны (почему?).
Заметим, что ха = 0 |ха| = 0 |х||а| = 0 |х| = 0 или |а| = 0 х = 0 или а = 0. Значит,
(2.9) произведение вектора на число равно нулю тогда и только тогда, когда либо число, либо вектор равны нулю.
Пусть
даны не равные нулю число х и вектор а.
От произвольной точки О отложим вектор
ОА=а и попробуем построить вектор OX = ха. Так как векторы а и ха должны быть
коллинеарными, отрезок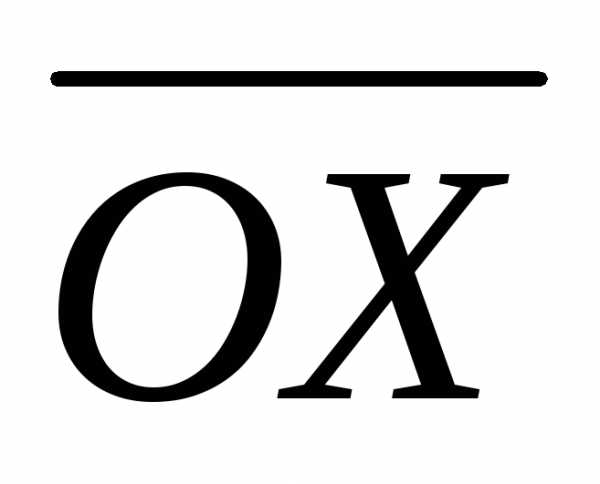 
обязан лежать на прямой (ОА), а его длина
по условию (П1) должна равняться |х||а|.
Таких отрезков ровно два, причем один
из них (назовем его
)
сонаправлен с
,
а другой (назовем его
)
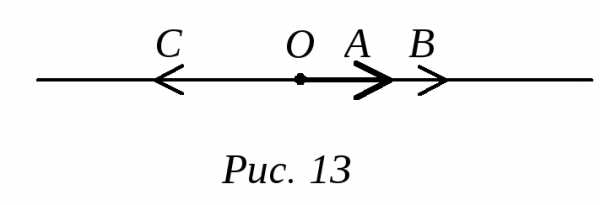
направлен противоположно
(рис.13). Возвращаясь к условию (П2), видим,
что
=
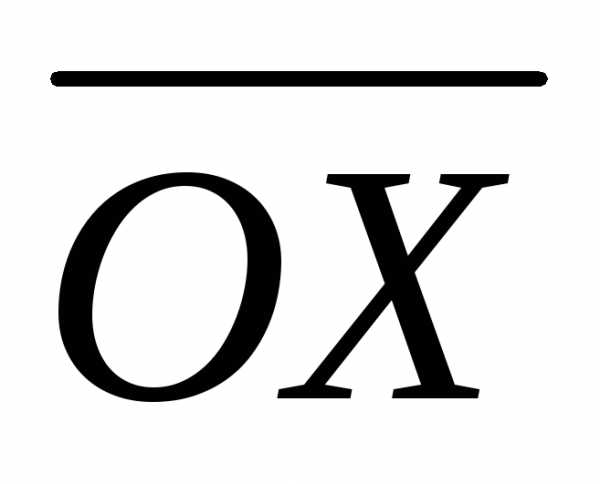при x > 0, и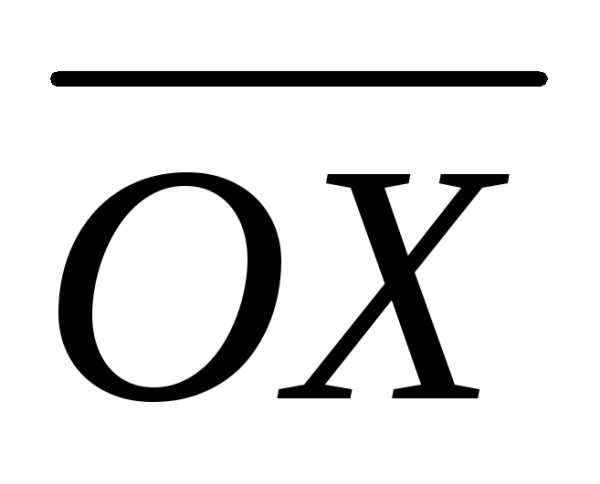
=
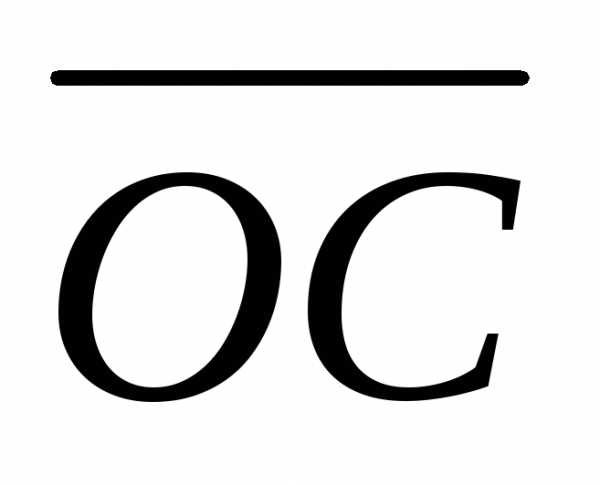при х < 0.
Т
К основным свойствам умножения векторов на числа относят следующие:
(У1) Для любого вектора а 1а=а (т.е., умножение на 1 не изменяет вектора).
(У2) Для любых чисел х, у и вектора а х(уа) = (ху)а (ассоциативность).
(У3) Для любых чисел х, у и вектора а (х+у)а = ха+уа (дистрибутивность умножения относительно сложения чисел).
(У4) Для любых числа х и векторов а и b х(a+b) = xa + xb (дистрибутивность умножения относительно сложения векторов).
Первое из этих свойств вытекает непосредственно из определения (проверьте!). Доказательства остальных можно найти на стр. 14-16 учебника Л.С. Атанасяна и В.Т. Базылева “Геометрия” (ч.1).
Отметим еще такие свойства умножения вектора на число:
(2.10) Если вектор а – ненулевой, то а/|a| – сонаправленный с вектором а единичный вектор.3
В самом деле, векторы а и а/|a| сонаправлены (ибо 1/|а| > 0) и |а/|a|| = |а|/|а| = 1.
(2.11) (–1)а = –а.
Действительно, по определению умножения вектора на число векторы (–1)а и а противоположно направлены, а их длины равны.
5. Признаки коллинеарности.
(2.12) Признак коллинеарности вектора ненулевому вектору. Вектор b коллинеарен ненулевому вектору а тогда и только тогда, когда существует такое число t, что b = tа. При этом если векторы а и b сонаправлены, то t = |b| / |a|, а если они противоположно направлены, то t = – |b| / |a|.
Мы уже отмечали, что векторы а и tа всегда коллинеарны. Обратно, возьмем ненулевой вектор а и коллинеарный ему вектор b. Если они сонаправлены, положим t = |b|/|a|. Тогда |tа| = |t||а| = (|b|/|a|)|а| = |b|, и вектор tа сонаправлен с а, а, значит, и с b. Стало быть, tа = b по признаку 1.7. Если же аb, положим t = –|b|/|a|. И снова |tа| = |t||а| = (|b|/|a|)|а| = |b|, а векторы tа и b, направленные противоположно вектору а, по (Н5) сонаправлены между собой. Значит, и в этом случае tа = b.
Оговорка насчет того, что вектор а – ненулевой, иногда бывает неудобна. Тогда можно использовать такой
(2.13) Признак коллинеарности двух векторов. Два вектора коллинеарны тогда и только тогда, когда один из них можно выразить через другой с помощью умножения на число.
Для случая, когда хотя бы один из двух данных векторов не равен нулю, это доказано выше. Если же оба вектора нулевые, то, во-первых, они коллинеарны, а, во-вторых, любой из них можно получить из другого умножением на любое число, так что и в этом случае все в порядке.
6. Сохранение параллельности при операциях над векторами.
(2.14) Лемма о параллельности. Если два вектора параллельны некоторой прямой (плоскости), то той же прямой (плоскости) параллельна и их сумма. Если вектор параллелен прямой (плоскости), то той же прямой (плоскости) параллельно и его произведение на любое число.
Пусть векторы а и b параллельны данной прямой (плоскости). Отложим от произвольной её точки О векторы ОА = а и АВ = b. Тогда точки А и В тоже будут лежать на этой прямой (плоскости). Значит, там будет лежать и отрезок ОВ, изображающий сумму а+b, что и означает ее параллельность данной прямой (плоскости).
Возьмем теперь любое число х, и отложим от той же точки О вектор ОС = ха. Если а = 0, то и ха = 0, а нулевой вектор параллелен любой прямой и плоскости. Если же нет, то отрезок ОС, изображающий вектор ха, будет целиком лежать на прямой ОА, а, значит, и на данной прямой (плоскости). Тем самым вектор ха будет параллелен этой прямой (плоскости).
studfiles.net
Векторы. Линейные операции над векторами
ТЕМА 6. ВЕКТОРЫ. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ.
1.Основные определения
Из курса элементарной физики известно, что некоторые физические величины, как, например, температура, масса, время, плотность, работа, являются скалярными. Некоторые другие величины, такие как сила, скорость, ускорение, напряженность магнитного поля, являются векторными. Скалярная величина может быть охарактеризована одним числом. Векторная величина характеризуется числом и направлением.
Определение 1. Вектором называется направленный отрезок. Если начало вектора находится в точке A , конец в точке B , то вектор обозначается символом AB . Начало вектора называют также точкой его приложения.
Другое обозначение вектора a (a = AB) .
Модулем вектора a называется его длина, т. е. расстояние между его началом и концом, он обозначается через |a| . Модуль вектора скалярная неотрицательная величина.
Нулевым вектором называется вектор, начало и конец которого совпадают. Нулевой вектор обозначается символом 0 . Его модуль равен нулю, а направление не определено.
Единичным вектором называется вектор, длина которого равна единице.
Определение 2. Два вектора a и b называются коллинеарными, если они лежат на одной или на параллельных прямых. Три вектора a, b, c называются компланарными, если они лежат в одной или в параллельных плоскостях.
Определение 3. Коллинеарные векторы, имеющие одинаковые направления и равные длины, называются равными. Векторы, противоположно направленные и имеющие равные длины, называются противоположными.
Вектор, противоположный вектору a, обозначается через −a , а вектору AB через
BA .
|
|
|
|
|
| * |
|
|
|
|
|
|
|
|
| * |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
| a |
|
|
|
|
|
|
|
|
| c |
| |
|
|
|
|
|
|
|
|
| ||||||||
| b |
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
| e |
|
|
|
|
| |
| d * |
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
| Рис. 1 |
|
|
|
|
| ||
На рис. 1 все векторы попарно коллинеарны; a и c равные векторы, a и b противоположные векторы.
Для каждого вектора точка приложения может быть выбрана произвольно. Соответственно этому в геометрии векторы рассматривают с точностью до их положения (т. е. не различают равных векторов, получающихся друг из друга параллельным переносом). В этом смысле векторы называют свободными.
studfiles.net
! вектор с, представляющий собой разность a-b, причём этот вектор с=a+b’, где b’
Из свойств 1-4c+b=(a+b’)+b=a+(b’+b)=a+0=a
c=a-b
! П d: d+b=a
Тогда , с одной стороны (d+b)+b’=a+b’=c
C другой, (d+b)+b’=d+(b+b’)=d+0=dc=d
Правило построения разности
Разность a-b,приведенных к общему началу векторовa иb представляет собой вектор, идущий из конца вычитаемогоb в конец уменьшаемого вектораa.
Правило построения разности
Разность a-b,приведенных к общему началу векторовa иb представляет собой вектор, идущий из конца вычитаемогоb в конец уменьшаемого вектораa.
a
b
O
Правило построения разности
Разность a-b,приведенных к общему началу векторовa иb представляет собой вектор, идущий из конца вычитаемогоb в конец уменьшаемого вектораa.
Операция умножения вектора на вещественное число
Операция умножения вектора на вещественное число
Произведение а (илиа ) вектораа на вещественное число называется векторb, коллинеарный векторуа и имеющий длину, равную | ||а| и имеющий направление, совпадающее с направлением вектораа в случае >0 и противоположное направлению вектораа в случае <0.
Операция умножения вектора на вещественное число
Произведение а (илиа ) вектораа на вещественное число называется векторb, коллинеарный векторуа и имеющий длину, равную | |·|а| и имеющий направление, совпадающее с направлением вектораа в случае >0 и противоположное направлению вектораа в случае <0.
ЗАМЕЧАНИЕ: В случае =0 илиа=0, произведениеа=0
Геометрический смысл : при умножении вектора а на число вектор а «растягивается», в раз , при >1; при
0< <1 происходит сжатие, а при <0 происходит, кроме растяжения или сжатия, изменение направления на противоположное.
studfiles.net
! вектор с, представляющий собой разность a-b, причём этот вектор с=a+b’, где b’
Из свойств 1-4c+b=(a+b’)+b=a+(b’+b)=a+0=a
c=a-b
! вектор с, представляющий собой разностьa-b, причём этот векторс=a+b’, гдеb’ – вектор, противоположныйb
Из свойств 1-4c+b=(a+b’)+b=a+(b’+b)=a+0=a
c=a-b
! вектор с, представляющий собой разностьa-b, причём этот векторс=a+b’, гдеb’ – вектор, противоположныйb
Из свойств 1-4c+b=(a+b’)+b=a+(b’+b)=a+0=a
c=a-b
!
! вектор с, представляющий собой разностьa-b, причём этот векторс=a+b’, гдеb’ – вектор, противоположныйb
Из свойств 1-4c+b=(a+b’)+b=a+(b’+b)=a+0=a
c=a-b
! П
! вектор с, представляющий собой разностьa-b, причём этот векторс=a+b’, гдеb’ – вектор, противоположныйb
Из свойств 1-4c+b=(a+b’)+b=a+(b’+b)=a+0=a
c=a-b
! П d:
! вектор с, представляющий собой разностьa-b, причём этот векторс=a+b’, гдеb’ – вектор, противоположныйb
Из свойств 1-4c+b=(a+b’)+b=a+(b’+b)=a+0=a
c=a-b
! П d: d+b=a
! вектор с, представляющий собой разностьa-b, причём этот векторс=a+b’, гдеb’ – вектор, противоположныйb
Из свойств 1-4c+b=(a+b’)+b=a+(b’+b)=a+0=a
c=a-b
! П d: d+b=a
Тогда , с одной стороны
! вектор с, представляющий собой разностьa-b, причём этот векторс=a+b’, гдеb’ – вектор, противоположныйb
Из свойств 1-4c+b=(a+b’)+b=a+(b’+b)=a+0=a
c=a-b
! П d: d+b=a
Тогда , с одной стороны (d+b)+b’=a+b’=c
! вектор с, представляющий собой разностьa-b, причём этот векторс=a+b’, гдеb’ – вектор, противоположныйb
Из свойств 1-4c+b=(a+b’)+b=a+(b’+b)=a+0=a
c=a-b
! П d: d+b=a
Тогда , с одной стороны (d+b)+b’=a+b’=c C другой,
! вектор с, представляющий собой разностьa-b, причём этот векторс=a+b’, гдеb’ – вектор, противоположныйb
Из свойств 1-4c+b=(a+b’)+b=a+(b’+b)=a+0=a
c=a-b
! П d: d+b=a
Тогда , с одной стороны (d+b)+b’=a+b’=c
C другой, (d+b)+b’=d+(b+b’)=d+0=d
studfiles.net
1. Векторы. Действия над векторами.
Вектором наз. упорядоченная совокупность чисел Х={X1,X2,…Xn} вектор дан в n-мерном пространстве. Т(X1,X2,X3). n=1,2,3. Геометрический вектор — направленный отрезок. |AB|=|a| — длинна. 2 вектора наз. коллинеарными, если они лежат на 1 прямой или ||-ных прямых. Векторы наз. компланарными, если они лежат в 1-ой плоскости или в ||-ных плоскостях. 2 вектора равны, когда они коллинеарны, сонаправленны, и имеют одинак-ую длинну.
1.умножение на число: произведение вектора А на число наз. такой вектор В, который обладает след. св-ми: а) А||В. б) >0, то АВ, <0, то АВ. в)>1, то А<В, )<1, то А>В. 2. Разделить вектор на число n значит умножить его на число, обратное n: а/n=a*(1/n).
3.Суммой неск-их векторов а и в наз. соединяющий начало 1-го и конец последнего вектора. 4. Разностью векторов а и в наз-ся вектор c, который, будучи сложенным с вектором в даст вектор а.
2.3. Декартова прямоугольная система координат. Базис.
Базисом на плоскости называется совокупность фиксированной точки и 2х неколлинеарных векторов, проведенных к ней.
Базисом в пространстве наз. совокупность фиксированной точки в пространстве и 3х некомпланарных векторов.
Любой вектор на плоскости может быть разложен по векторам базиса на плоскости. Любой вектор в пространстве может быть разложен по векторам базиса в пространстве.
ОС=OA+OB, OA=x*i, OB=j*y, OC=xi+yj. Числа х,у наз-ся координатами вектора ОС в данном базисе
4. Действия над векторами.
а=х1i+y1j+z1k; b=х2i+y2j+z2k
*a=(х1i+y1j+z1k)= (х1)i+ (y1)j+(z1)k
ab=(x1x2)i+(y1y2)j+(z1z2)k
ab=x1x2ii+y1x2ij+x2z1ki+x1y2ij+y1y2jj+ z1y2kj+x1z1ik+y1z2jk+z1z2kk=x1x2+y1y2+z1z2
ii=1; ij=0; и т.д.
скалярное произведение 2х векторов равно сумме произведений соответствующих координат этих векторов.
аа=x2+y2+z2=|a|2 a{x,y,z}, aa=|a|*|a|, то a2=|a|2
ab=|a|*|b|*cos
а)ав=0,<=>ав, x1x2+y1y2+z1z2=0
б)а||в — коллинеарны, если , x1/x2=y1/y2=z1/z2
5. Скалярное произведение векторов и его свойства.
-(“skala”-шкала) 2х векторов а и в наз. число, равное произведению длин этих векторов на cos угла между ними. (а,в)- скалярное произведение. а*в=|а|*|в|*cos, =/2, cos/2=0, ab=>ab=0. Равенство “0” скаляргного произведения необходимое и достаточное условие их перпендикулярности (ортогональности).
6. Векторное произведение 2х векторов.
левая —— правая
Тройка векторов а,в,с наз. правоориентированной (правой), если с конца 3го вектора с кратчайший поворот от 1го ко 2му вектору мы будем видеть против час. стрелки. Если кратчайший поворот от 1го ко 2му по час. стрелки — левая. Векторным произведением 2х векторов а и в наз. такой вектор с, который удовлетворяет условиям: 1. |c|=|a|*|b|*sin. 2. ca и cb. 3. тройка а,в,с-правая.
7. Смешанное произведение векторов и его свойства.
Смешанным произведением векторов наз. векторно-скалярное произведение, являющееся числом: a*b*c=[a*b]*c=a*[b*c], где
a={ax,ay,az}
b={bx,by,bz}
c={cx,cy,cz}
Св-ва:1. При перестановке 2х сомножителей:
a*b*c=-b*c*a
2. не меняется при перестановке циклических сомножителей:
a*b*c=c*a*b=b*c*a
3.а)(Геометрич. смысл) необходимым и достаточным условием компланарности 3х векторов явл. равенство a*b*c=0
б)если некомпланарные вектора a,b,c привести к 1 началу, то |a*b*c|=Vпараллепипеда, построенного на этих векторах
если a*b*c>0, то тройка a,b,c — правая
если a*b*c<0, то тройка a,b,c — левая
studfiles.net