Примеры решения задач с векторами
Примеры решения задач с векторами
Вектора применяются во многих науках, таких как: математика, физика, геометрия и многих других прикладных науках. На практике, они позволяют не делать лишних операций и сократить время выполнения задач. Поэтому, будущим специалистам очень важно понять теорию векторов и научиться решать задачи с ними.
Перед изучением примеров решения задач советуем изучить теоретический материал по векторам, прочитать все определения и свойства. Список тем находится в правом меню.
Координаты вектора
Теоретический материал по теме — координаты вектора.
Пример
Запись означает, что векторимеет следующие координаты: абсцисса равна 5, ордината равна -2.
Пример
Задание.
Решение.
Пример
Задание. Вектор . Найти координаты вектора
Решение.
Пример
Задание. Найти координаты вектора , если
Решение.
Длина (модуль) вектора
Теоретический материал по теме — длина вектора.
Пример
Задание. Найти длину вектора
Решение. Используя формулу, получаем:
Пример
Задание. Найти длину вектора
Решение. Используя формулу, получаем:
Угол между векторами
Теоретический материал по теме — угол между векторами.
Пример
Задание. Известно, что скалярное произведение двух векторов , а их длины. Найти угол между векторамии.
Решение. Косинус искомого угла:
Пример
Задание. Найти угол между векторами и
Решение. Косинус искомого угла
Пример
Задание. Найти угол между векторами и
Решение. Косинус искомого угла:
Разложение вектора по ортам координатных осей
Теоретический материал по теме — разложение вектора по ортам.
Пример
Задание. Зная разложения вектора по базисной системе векторов:, записать координаты этого вектора в пространстве.
Решение. Коэффициенты при ортах и есть координатами вектора, поэтому из того, что , получаем, что
Задание. Вектор задан своими координатами:. Записать разложение данного вектора по ортам осей координат.
Решение. Координаты вектора — это коэффициенты при ортах координатных осей в разложении вектора по базисной системе векторов, поэтому искомое разложение:
Скалярное произведение векторов
Теоретический материал по теме — скалярное произведение векторов.
Пример
Задание. Вычислить скалярное произведение векторов и, если их длины соответственно равны 2 и 3, а угол между ними 60°.
Решение. Так как из условия ,, а, то
Пример
Задание. Найти скалярное произведение векторов и
Решение. Скалярное произведение
Векторное произведение векторов
Теоретический материал по теме — векторное произведение векторов.Пример
Задание. Найти векторное произведение векторов и
Решение. Составляем определитель и вычисляем его:
Смешанное произведение векторов
Теоретический материал по теме — смешанное произведение векторов.
Пример
Задание. Вычислить объем пирамиды, построенной на векторах ,,
Решение. Найдем смешанное произведение заданных векторов, для это составим определитель, по строкам которого запишем координаты векторов ,и:
studfiles.net
Примеры решения задач с векторами — энциклопедический справочник и словарь для студента от А до Я
Векторы используются во многих науках, таких как: математика, физика, геометрия и многие другие прикладные науки. На практике они позволяют не выполнять ненужных операций и сокращают время на выполнение задач. Поэтому для будущих специалистов очень важно понять теорию векторов и научиться решать с ними проблемы.
Прежде чем изучать примеры решения проблем, советуем вам изучить теоретический материал по векторам, прочитать все определения и свойства. Список тем находится в правом меню.
Векторные координаты пример Запись \(\
\overline{a}=(5 ;-2)
\) означает, что вектор \(\
\overline{a}
\) имеет следующие координаты: абсцисса равна 5, ордината равна -2. пример Векторы и дан \(\
\overline{a}=(-3 ; 5)
\) и \(\
\overline{b}=(0 ;-1)
\) . Найти векторные координаты \(\
\overline{c}=\overline{a}+\overline{b}
\) \(\
\overline{c}=\overline{a}+\overline{b}=(-3 ; 5)+(0 ;-1)=(-3+0 ; 5+(-1))=(-3 ; 4)
\) Пример Вектор \(\
\overline{a}=(3 ;-2)
\) Найти векторные координаты \(\
2 \overline{a}
\) \(\
2 \overline{a}=2 \cdot(3 ;-2)=(2 \cdot 3 ; 2 \cdot(-2))=(6 ;-4)
\) Пример Найти координаты вектора \(\
\overline{A B}
\), если \(\
A(-4 ; 2), B(1 ;-3)
\) \(\
\overline{A B}=(1-(-4) ;-3-2)=(5 ;-5)
\) Длина (модуль) вектора пример Найти длину вектора \(\
\overline{a}=(-4 ; 3)
\) Используя формулу, получаем: \(\
|\overline{a}|=\sqrt{(-4)^{2}+3^{2}}=\sqrt{16+9}=\sqrt{25}=5
\) Пример Найти длину вектора\(\
\overline{a}=(1 ; 0 ;-4)
\) Используя формулу, получаем: \(\
|\overline{a}|=\sqrt{1^{2}+0^{2}+(-4)^{2}}=\sqrt{1+0+16}=\sqrt{17}
\) Угол между векторами пример Известно, что скалярное произведение двух векторов \(\
(\overline{a} ; \overline{b})=2
\) и их длины \(\
|\overline{a}|=2,|\overline{b}|=2
\). Найти угол между векторами \(\
\overline{a}
\) и \(\
\overline{b}
\). Косинус необходимого угла: \(\
\cos (\overline{a}, \overline{b})=\frac{(\overline{a} ; \overline{b})}{|\overline{a}| \cdot|\overline{b}|}=\frac{2}{2 \cdot 2}=\frac{1}{2} \Rightarrow(\overline{a}, \overline{b})=60^{\circ}
\) Пример Найти угол между векторами \(\
\overline{a}=(1 ; \sqrt{3})
\) и \(\
\overline{b}=(1 ; 0)
\) Косинус желаемого угла \(\
\cos (\overline{a}, \tilde{b})=\frac{1 \cdot 1+\sqrt{3} \cdot 0}{\sqrt{1^{2}+(\sqrt{3})^{2}} \cdot \sqrt{1^{2}+0^{2}}}=\frac{1}{2}
\) \(\
(\overline{a}, \overline{b})=\arccos \frac{1}{2}=60^{\circ}
\) Разложение вектора по ортам координатных осей пример Зная разложение вектора \(\
\overline{a}
\) на базисной системе векторов: \(\
\overline{a}=3 \overline{i}-\overline{k}
\)запишите координаты этого вектора в пространстве. Коэффициенты ортов являются координатами вектора, поэтому из того, что \(\
\overline{a}=3 \overline{i}-0 \cdot \overline{j}-\overline{k}
\) мы получаем \(\
\overline{a}=(3 ; 0 ;-1)
\) Пример Вектор \(\
\overline{a}
\) определяется его координатами: \(\
\overline{a}=(2 ;-1 ; 5)
\) запишите разложение этого вектора по осям осей. Координаты вектора представляют собой коэффициенты по осям координатных осей при разложении вектора в основную систему векторов, поэтому требуется разложение: \(\
\overline{a}=2 \overline{i}-\overline{j}+5 \overline{k}
\) Скалярное произведение векторов Пример Рассчитайте скалярное произведение векторов \(\
\overline{a}
\) и \(\
\overline{b}
\) , если их длины равны 2 и 3 соответственно, а угол между ними равен 60 °. С условием \(\
|\overline{a}|=2,|\overline{b}|=3
\), а \(\
(\widehat{a}, \overline{b})=60^{\circ}
\) затем \(\
\overline{a} \cdot \overline{b}=(\overline{a}, \overline{b})=2 \cdot 3 \cdot \cos 60^{\circ}=6 \cdot \frac{1}{2}=3
\) Пример Найти скалярное произведение векторов \(\
\overline{a}=(3 ;-1)
\) и \(\
\overline{b}=(-2 ; 7)
\) Скалярное произведение \(\
\overline{a} \overline{b}=3 \cdot(-2)+(-1) \cdot 7=-6-7=-13
\)
Векторное произведение векторов
пример Найти векторное произведение векторов \(\
\overline{a}=(6 ; 7 ; 10)
\) и \(\
\overline{b}=(8 ; 5 ; 9)
\) Составляем определитель и вычисляем его: \(\
\overline{a} \times \overline{b}=\left| \begin{array}{ccc}{\overline{i}} & {\overline{j}} & {\overline{k}} \\ {6} & {7} & {10} \\ {8} & {5} & {9}\end{array}\right|=\overline{i} \left| \begin{array}{cc}{7} & {10} \\ {5} & {9}\end{array}\right|-\overline{j} \left| \begin{array}{cc}{6} & {10} \\ {8} & {9}\end{array}\right|+\overline{k} \left| \begin{array}{cc}{6} & {7} \\ {8} & {5}\end{array}\right|=
\) \(\
=\overline{i}(7 \cdot 9-5 \cdot 10)-\overline{j}(6 \cdot 9-8 \cdot 10)+\overline{k}(6 \cdot 5-8 \cdot 7)=
\) \(\
=13 \overline{i}+26 \overline{j}-26 \overline{k}=(13 ; 26 ;-26)
\) Смешанное произведение векторов Пример Рассчитать объем пирамиды, построенной на векторах \(\
\overline{a}=(2 ; 3 ; 5), \overline{b}=(1 ; 4 ; 4), c=(3 ; 5 ; 7)
\) Мы находим смешанное произведение указанных векторов, для этого составляем определитель, в строки которого записываем координаты векторов \(\
\overline{a}, \overline{b}
\) и \(\
\overline{c}
\): \(\
(\overline{a}, \overline{b}, \overline{c})=\left| \begin{array}{ccc}{2} & {3} & {5} \\ {1} & {4} & {4} \\ {3} & {5} & {7}\end{array}\right|=2 \cdot 4 \cdot 7+1 \cdot 5 \cdot 5+3 \cdot 4 \cdot 3-
\) \(\
-3 \cdot 4 \cdot 5-5 \cdot 4 \cdot 2-1 \cdot 3 \cdot 7=-4
\) \(\
V_{\mathrm{пир}}=\frac{1}{6}|(\overline{a}, \overline{b}, \overline{c})|=\frac{1}{6} \cdot 4=\frac{2}{3}(\mathrm{куб} . \mathrm{ед.})
\)
sciterm.ru
В5. Вектора. Подготовка к егэ по математике
В этой статье работаем с Задачами №3 ЕГЭ по математике, которые связаны с векторами.
Смотрите в других статьях разбор Задач №3, в которых фигурирует:
– треугольник;
– прямоугольник;
– ромб;
– параллелограмм;
– произвольный четырехугольник;
– трапеция;
– многоугольник;
– круг;
– координатная плоскость;
Видеоразбор задач
Задача 1. Найдите длину вектора .
Решение: + показать
Задача 2. Найдите квадрат длины вектора .
Решение: + показать
Длина вектора – есть длина отрезка, его изображающего.
Квадрат длины отрезка несложно найти по т. Пифагора:
Ответ: 40.
Задача 3. Стороны правильного треугольника ABC равны . Найдите длину вектора .
Решение: + показать
Задача 4. Стороны правильного треугольника равны 35. Найдите скалярное произведение векторов и .
Решение: + показать
Скалярное произведение векторов есть произведение длин векторов на косинус угла между ними.
В нашем случае длины векторов равны 35, а угол между ними (так как треугольник правильный)
Ответ: 612,5.
Задача 5. Вектор с началом в точке имеет координаты . Найдите абсциссу точки .
Решение: + показать
Координаты вектора равны разности координат конца вектора и его начала. Пусть координаты точки . Тогда и
Нас интересует только абсцисса точки. Она равна
Ответ: 12.
Задача 6. Найдите сумму координат вектора .
Решение: + показать
Задача 7. Найдите квадрат длины вектора .
Решение: + показать
Задача 8. Найдите скалярное произведение векторов и .
Решение: + показать
Задача 9. Найдите угол между векторами и . Ответ дайте в градусах.
Решение: + показать
Переменка –>+ показать
А вам доводилось встречать такого водителя маршрутного такси?
Вы можете пройти тест по Задачам №3, вектора.
egemaximum.ru
1. Основные понятия векторной алгебры; примеры решения задач.
Основные понятия включают в себя: понятие вектора, разложение вектора по другим векторам, модуль вектора, скалярное произведение, векторное произведение и смешанное произведение, а также их приложения для решения задач.
Пример 1. Задание. Разложить вектор по векторам
Прежде чем привести решение задачи напомним понятие линейной зависимости системы векторов.
Рассмотрим систему векторов и составим равенство вида:
–постоянные величины.
Если это равенство выполняется только
при одновременном равенстве нулю всех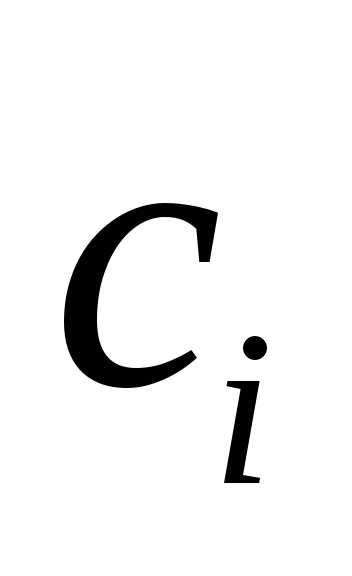 
,
, тогда система векторов называется линейно независимой , в противном случае – система векторов линейно зависима, то есть один вектор можно представить в виде линейной комбинации других векторов.
.
Разделим левую и правую части равенства
на 
,
получим:
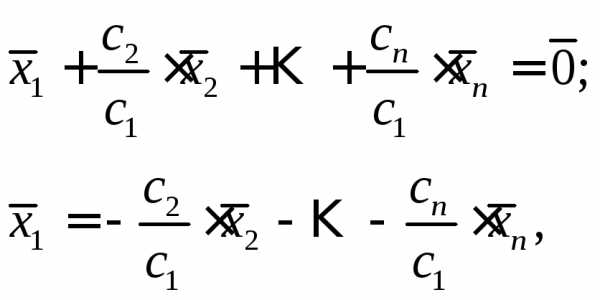
то есть вектор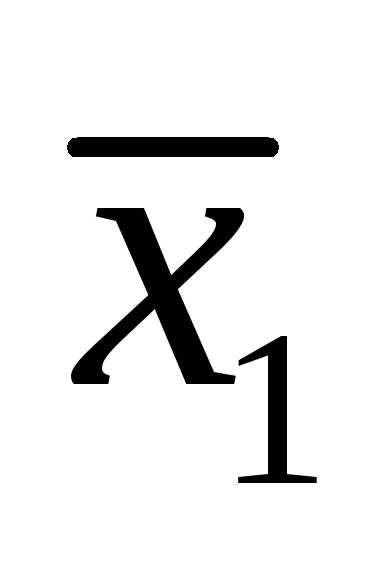 
представлен в виде линейной комбинации.
Решение.
Разложить вектор 
по векторам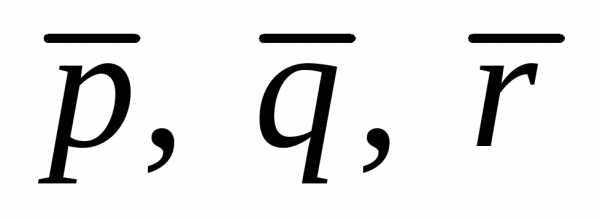
это значит представить его в виде
линейной комбинации– искомые числа.
Представим линейную комбинацию в координатной форме
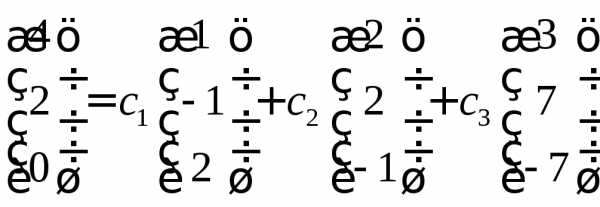
И получим систему линейных уравнений
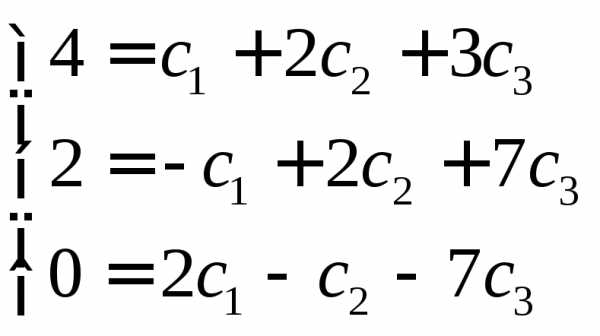
Решение системы имеет вид:
Следовательно:
Пример 2.
Напомним понятие длины вектора (модуля вектора)
Если , то
–называется длиной вектора.
Рассмотрим свойство
скалярного произведения:
,
то есть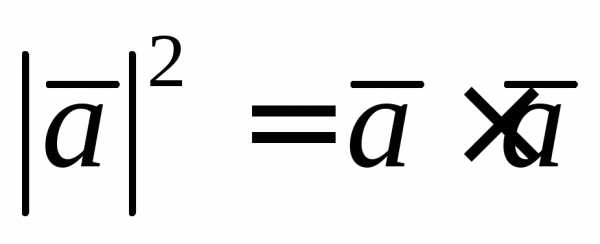
Задание.
Найти длину вектора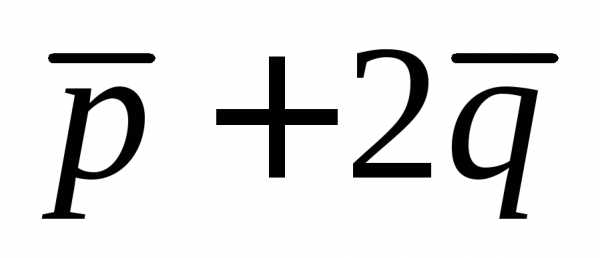 
,
если
Решение. Имеем
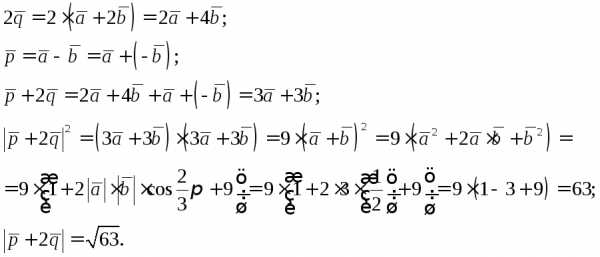
Пример 3.
Напомним определение
коллинеарности двух векторов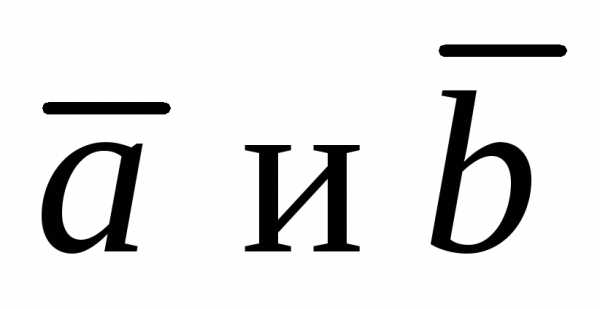 
отличных от нуля: два вектора
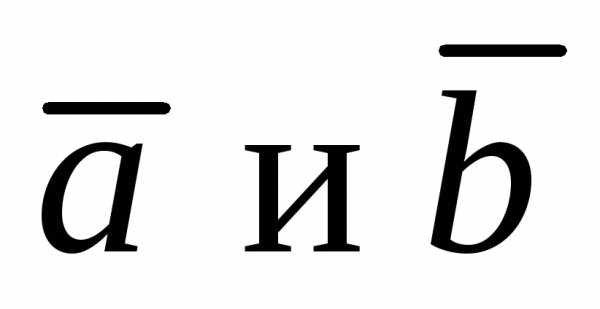называются коллинеарными, если
,
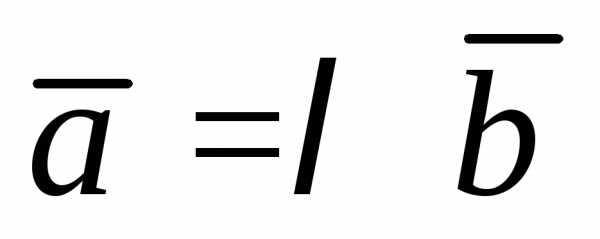где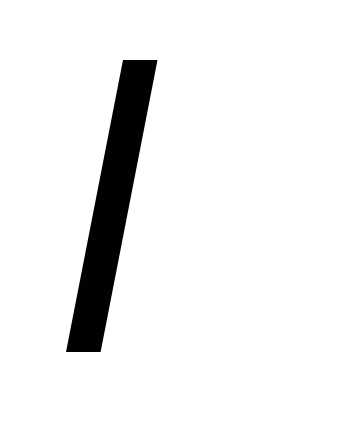
– некоторый постоянный множитель.
Задание.
Найти вектор 
,
коллинеарный векторуи
удовлетворяющий условию: скалярное
произведение векторов.
Решение.
Запишем условие
коллинеарности двух векторов
и полученный вектор
Следовательно .
Пример 4.
Напомним определение скалярного произведения векторов:
.
Задание.
Вычислить проекцию
вектора 
на направление вектора
,
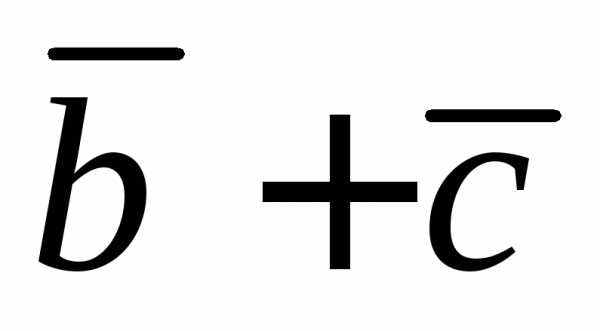если
Решение.
Обозначим , тогда
, отсюда
Ответ: 
Пример 5.
Пусть
.
Напомним, что векторное произведение
двух векторов
и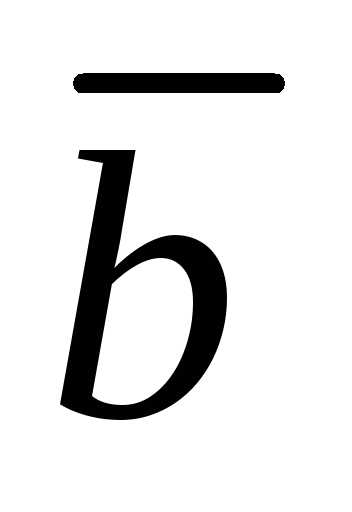
равно: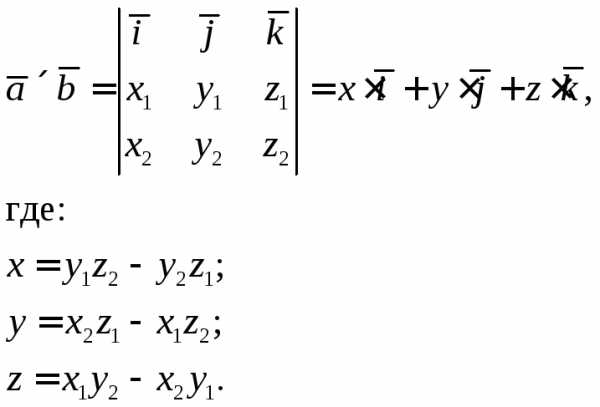
Модуль векторного произведения равен площади параллелограмма, построенного на этих векторах.
Задание.
Найти площадь треугольника
Решение.
Построим
параллелограмм 
на векторах(рис. 1):
рис. 1 
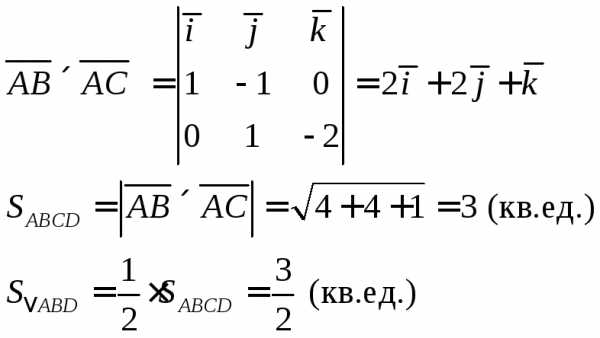
Пример 6.
Задание.
Найти вектор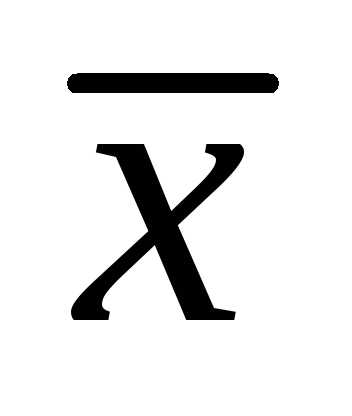 
,
перпендикулярный векторами образующий с осью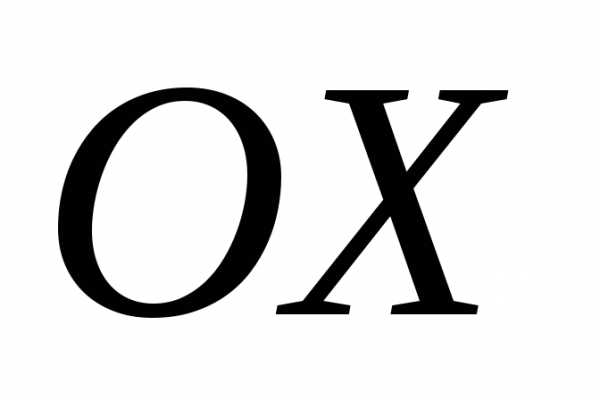
тупой угол, если
.
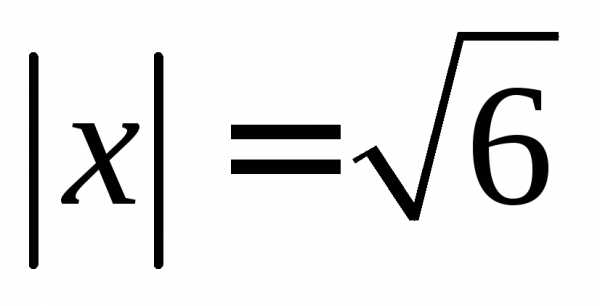Решение.
Если
,
тогда вектор
перпендикулярен векторам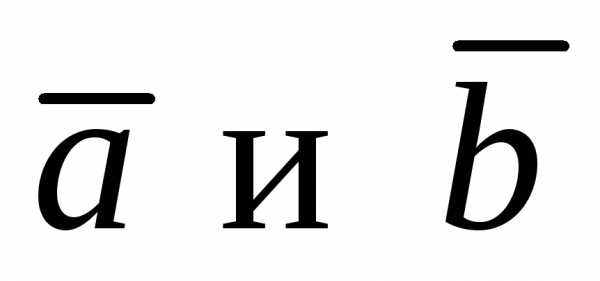
.
Найдем вектор 
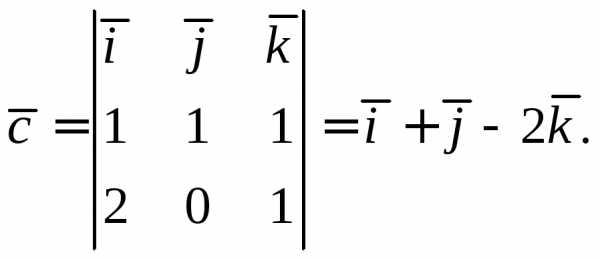
Так как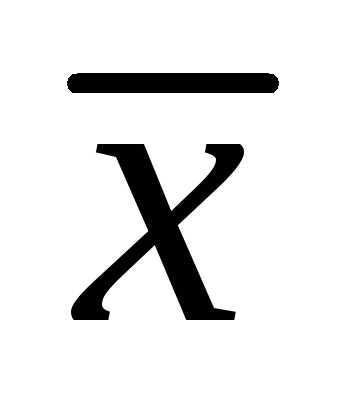 
тоже перпендикулярен
,
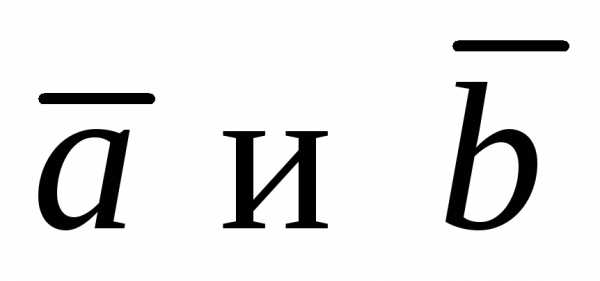следовательно вектора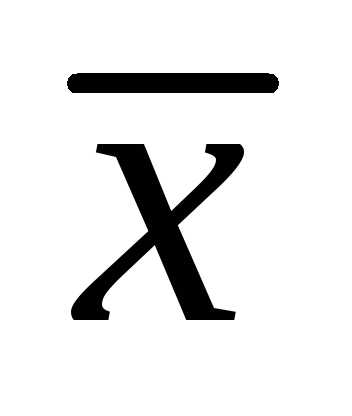
и
— коллинеарны. Запишем условие
коллинеарности векторов: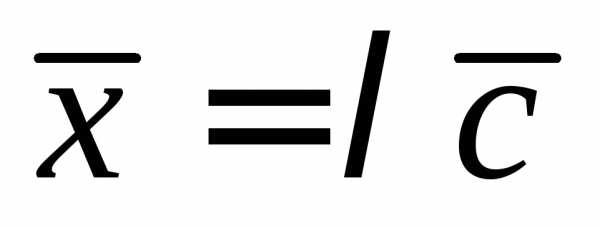
,
По условию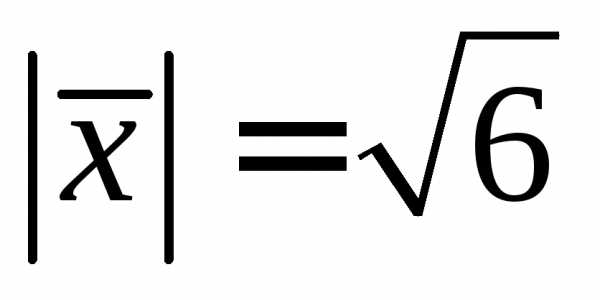 
,
то есть
Так как вектор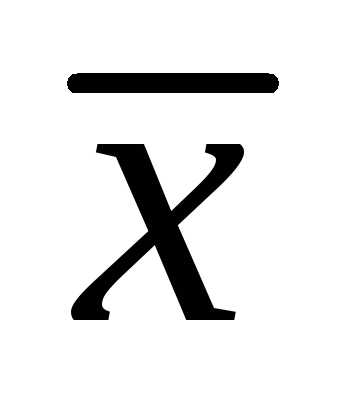 
образует с осью
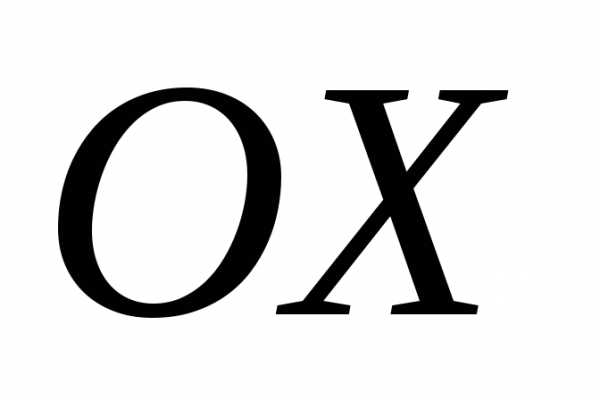тупой угол, то его проекция на ось
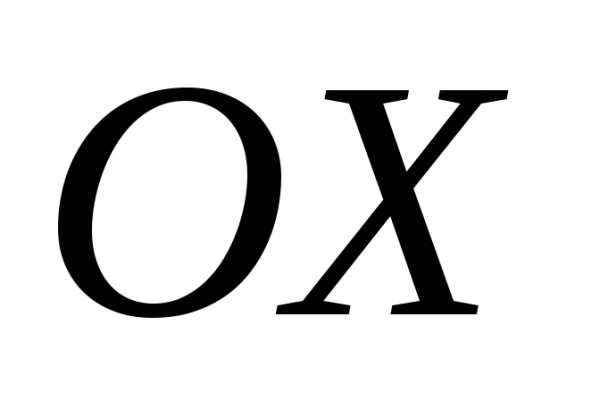должна быть отрицательной.
Отсюда
Пример 7.
Рассмотрим вектор
.
Вектор
,
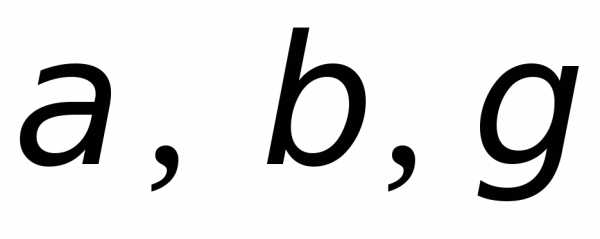аназываются направляющими косинусами,
при этомЗадание.
Найти направляющие
косинусы вектора силы
,
приложенной в точке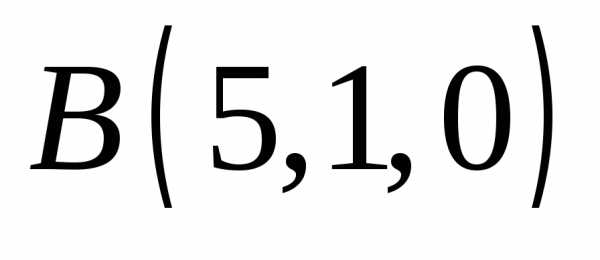
,
и момент этой силы относительно точки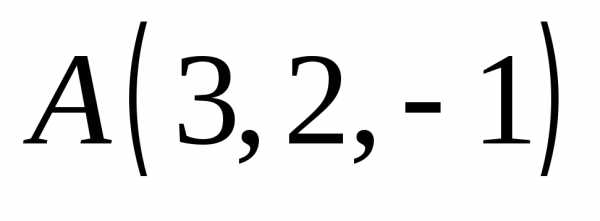
.
Решение.
Найдем направляющие косинусы вектора силы:
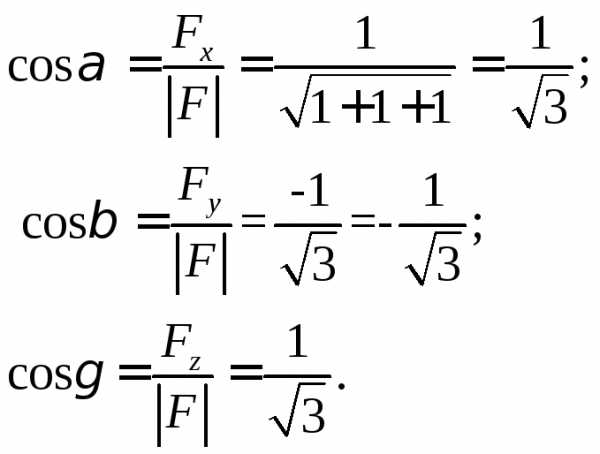
Момент силы
определим как векторное произведение
вектора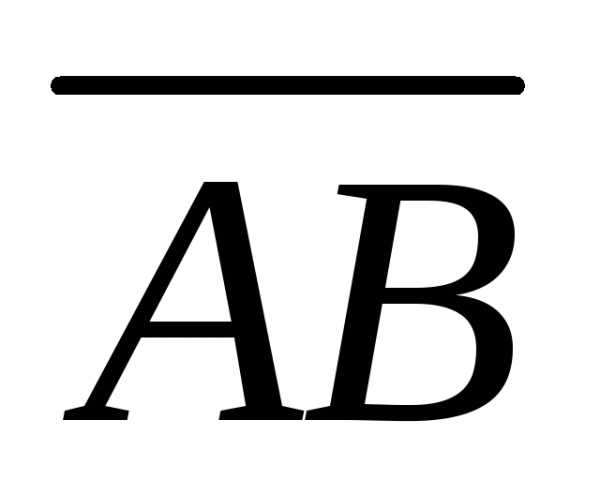 
на вектор
.
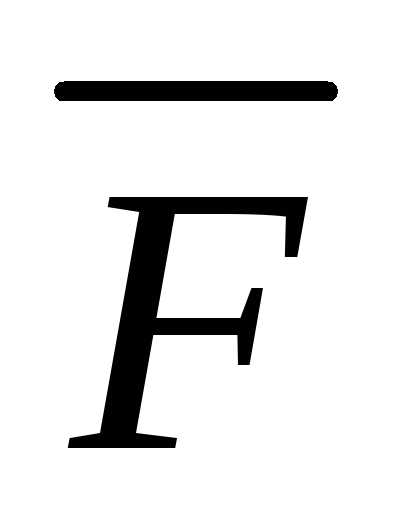Имеем
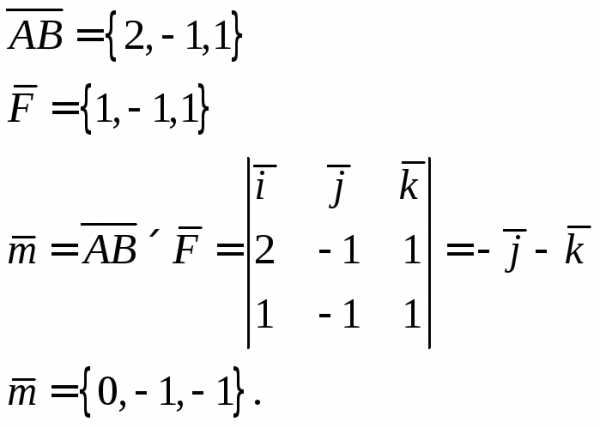
Пример 8.
Напомним формулу смешанного произведения трех векторов
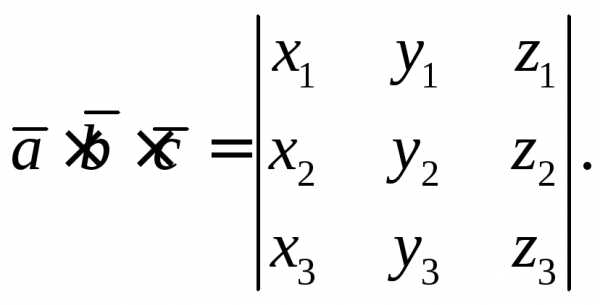
Известно, что
модуль смешанного произведения 
равен объему параллелепипеда, построенного
на этих векторах.
Задача.
Найти длину высоты
пирамиды, опущенной из вершины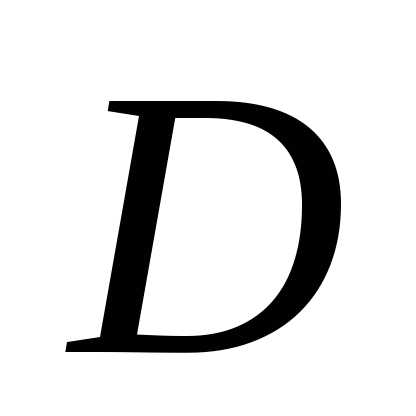 
(рис. 2), если ее вершины
Решение.
рис. 2
Найдем векторы:
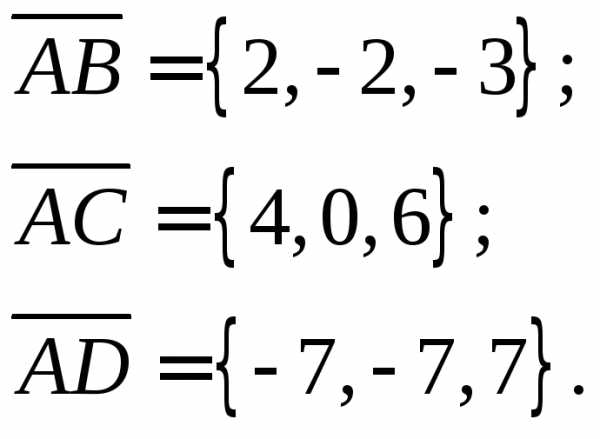
Объем пирамиды, построенной на векторах , равен одной шестой модуля смешанного произведения этих векторов.
, где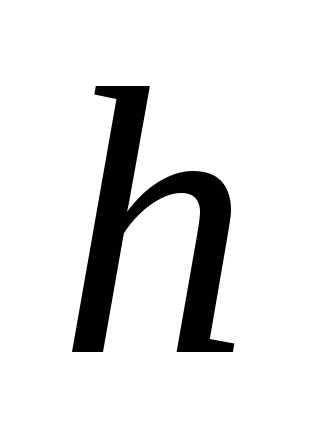 
– высота пирамиды, а площадь прямоугольника,
построенного на векторах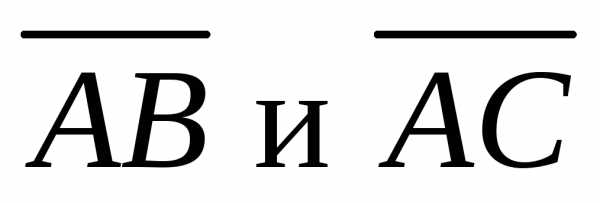
равна одной второй векторного произведения.
Вычислим смешанное произведение векторов
Отсюда 
пирамиды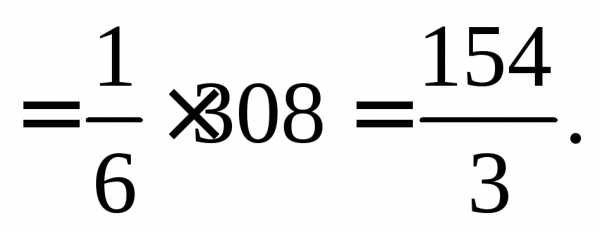
Вычислим векторное произведение векторов:
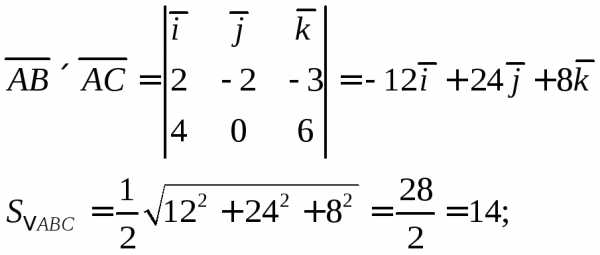
Найдем высоту пирамиды:
studfiles.net
Решение задач с применением векторов. Видеоурок. Геометрия 10 Класс
На данном уроке мы решим достаточно сложную задачу двумя способами – геометрически и при помощи векторов. Мы покажем возможности того и другого способов, а также вспомним важные геометрические факты и свойства векторов.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Векторы и координаты»
Тема: Векторы в пространстве
Урок: Решение задач с применением векторов (продолжение)
В тетраэдре ABCD M и N – точки пересечения медиан граней ADB и BDC. Доказать, что . Найти отношение
Решение:
Рис. 1. Иллюстрация к задаче 1
Решим задачу векторным методом. Для начала вводим тройку некомпланарных векторов, пусть . Мы знаем, что теперь любые векторы в пространстве можно выразить через три выбранных вектора, при чем единственным образом. Выразим вектор
Мы применили свойство точки пересечения медиан треугольника – она делит каждую медиану в отношении два к одному, считая от вершины.
Выразим векторы и .
Аналогичным образом
Имеем:
Теперь выразим вектор :
Очевидна связь между векторами: или
Очевиден ответ на поставленный вопрос: прямые MN и АС параллельны, т. к. векторы и коллинеарны; отношение составляет .
Теперь решим эту же задачу геометрическим способом, опираясь на свойства точки пересечения медиан треугольника.
Рассмотрим треугольники и . Эти треугольники подобны. В них:
Мы применили свойство точки пересечения медиан треугольника – она делит каждую медиану в отношении два к одному, считая от вершины.
Кроме того, треугольники имеют общий угол .
Из подобия треугольников вытекает параллельность соответствующих сторон:
Кроме того:
Рассмотрим треугольник , в нем – средняя линия, т. к. точки и основания медиан граней ADB и BDC. Согласно свойству средней линии:
Имеем:
Ответ получен такой же, как и при решении векторным методом.
Итак, была рассмотрена и решена задача о тетраэдре. Решена двумя методами – с помощью векторов, что позволило повторить известную нам теорию о векторах, и геометрически – основываясь на свойствах основных элементов треугольника.
Список литературы
- И. М. Смирнова, В. А. Смирнов. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е изд., испр. и доп. – М.: Мнемозина, 2008. – 288 с.: ил.
- Шарыгин И. Ф. Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений / Шарыгин И. Ф. – М.: Дрофа, 1999. – 208 с.: ил.
- Е. В. Потоскуев, Л. И. Звалич. Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики /Е. В. Потоскуев, Л. И. Звалич. – 6-е изд., стереотип. – М.: Дрофа, 2008. – 233 с.: ил.
Домашнее задание
- докажите, что треугольник, вершинами которого являются точки пересечения медиан боковых граней тетраэдра, подобен основанию тетраэдра.
- высоты АМ и DN правильного тетраэдра ABCD пересекаются в точке К. Разложите векторы по векторам
- в тетраэдре ABCD медианы грани BCD пересекаются в точке О. Докажите, что длина отрезка АО меньше одной трети суммы длин ребер с общей вершиной А.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал Cleverstudents.ru (Источник).
- Интернет-портал Ppt4web.ru (Источник).
- Математическая интернет-энциклопедия (Источник).
interneturok.ru
8 класс. Геометрия. Векторы. Применение векторов к решению задач. — Векторы. Повторение теории. Решение задач с применением векторов.
Комментарии преподавателя
Повторение теории. Задачи
Напомним, что существуют такие физические величины, для которых важна не только величина, но и направление. Такие величины называются векторными, или векторами, и обозначаются они направленным отрезком, то есть таким отрезком, у которого отмечены начало и конец. Введено было понятие коллинеарных векторов, то есть таких, которые лежат либо на одной прямой, либо на параллельных прямых.
Мы рассматриваем вектор, который можно отложить от любой точки, заданный вектор от произвольно выбранной точки можно отложить единственным образом.
Было введено понятие равных векторов – это такие сонаправленные векторы, длины которых равны. Сонаправленными называются коллинеарные векторы, направленные в одну сторону.
Были введены правила треугольника и параллелограмма – правила сложения векторов.
Заданы два вектора – векторы и . Найдем сумму этих двух векторов . Для этого отложим из некоторой точки А вектор . – направленный отрезок, точка А – его начало, а точка В – конец. Из точки В отложим вектор . Тогда вектор называют суммой заданных векторов: – правило треугольника (см. Рис. 1).
Рис. 1
Задано два вектора – векторы и . Найдем сумму этих двух векторов по правилу параллелограмма.
Откладываем из точки А вектор и вектор (см. Рис. 2). На отложенных векторах можно построить параллелограмм. Из точки В откладываем вектор , векторы и равны, стороны ВС и
Рис. 2
АВ1 параллельны. Аналогично параллельны и стороны АВ и В1С, таким образом, мы получили параллелограмм. АС – диагональ параллелограмма.
Для сложения нескольких векторов применяют правило многоугольника (см. Рис. 3). Нужно из произвольной точки отложить первый вектор, из его конца отложить второй вектор, из конца второго вектора отложить третий и так далее, когда все векторы отложены – соединить начальную точку с концом последнего вектора, в итоге получится сумма нескольких векторов.
Рис. 3
Кроме того, мы рассмотрели понятие обратного вектора – вектора, имеющего такую же длину, как заданный, но ему противонаправленного.
Пример 1 – задача 747: выпишите пары коллинеарных сонаправленных векторов, которые определяются сторонами параллелограмма; укажите противоположно направленные векторы;
Задан параллелограмм MNPQ (см. Рис. 4). Выпишем пары коллинеарных векторов. В первую очередь это векторы и . Они не только коллинеарные, но и равные, т.к. они сонаправлены, и длины их равны по свойству параллелограмма (в параллелограмме противоположные стороны равны). Следующая пара . Аналогично
Рис. 4
выпишем коллинеарные векторы второй пары сторон:
www.kursoteka.ru
8 класс. Геометрия. Векторы. Применение векторов к решению задач. — Векторы. Повторение теории. Решение задач с применением векторов.
Комментарии преподавателя
Повторение теории. Задачи
Напомним, что существуют такие физические величины, для которых важна не только величина, но и направление. Такие величины называются векторными, или векторами, и обозначаются они направленным отрезком, то есть таким отрезком, у которого отмечены начало и конец. Введено было понятие коллинеарных векторов, то есть таких, которые лежат либо на одной прямой, либо на параллельных прямых.
Мы рассматриваем вектор, который можно отложить от любой точки, заданный вектор от произвольно выбранной точки можно отложить единственным образом.
Было введено понятие равных векторов – это такие сонаправленные векторы, длины которых равны. Сонаправленными называются коллинеарные векторы, направленные в одну сторону.
Были введены правила треугольника и параллелограмма – правила сложения векторов.
Заданы два вектора – векторы и . Найдем сумму этих двух векторов . Для этого отложим из некоторой точки А вектор . – направленный отрезок, точка А – его начало, а точка В – конец. Из точки В отложим вектор . Тогда вектор называют суммой заданных векторов: – правило треугольника (см. Рис. 1).
Рис. 1
Задано два вектора – векторы и . Найдем сумму этих двух векторов по правилу параллелограмма.
Откладываем из точки А вектор и вектор (см. Рис. 2). На отложенных векторах можно построить параллелограмм. Из точки В откладываем вектор , векторы и равны, стороны ВС и
Рис. 2
АВ1 параллельны. Аналогично параллельны и стороны АВ и В1С, таким образом, мы получили параллелограмм. АС – диагональ параллелограмма.
Для сложения нескольких векторов применяют правило многоугольника (см. Рис. 3). Нужно из произвольной точки отложить первый вектор, из его конца отложить второй вектор, из конца второго вектора отложить третий и так далее, когда все векторы отложены – соединить начальную точку с концом последнего вектора, в итоге получится сумма нескольких векторов.
Рис. 3
Кроме того, мы рассмотрели понятие обратного вектора – вектора, имеющего такую же длину, как заданный, но ему противонаправленного.
Пример 1 – задача 747: выпишите пары коллинеарных сонаправленных векторов, которые определяются сторонами параллелограмма; укажите противоположно направленные векторы;
Задан параллелограмм MNPQ (см. Рис. 4). Выпишем пары коллинеарных векторов. В первую очередь это векторы и . Они не только коллинеарные, но и равные, т.к. они сонаправлены, и длины их равны по свойству параллелограмма (в параллелограмме противоположные стороны равны). Следующая пара . Аналогично
Рис. 4
выпишем коллинеарные векторы второй пары сторон: ; .
Противоположно направленные векторы: , , , .
Пример 2 – задача 756: начертите попарно неколлинеарные векторы , и . Постройте векторы ;; ;.
Для выполнения данного за
www.kursoteka.ru