Презентация «Множества на кругах «Эйлера-Венна»

МНОЖЕСТВА
на кругах
Эйлера-Венна
Государственное автономное профессиональное образовательное учреждение
«Елабужский колледж культуры и искусств»
преподаватель математики и информатики
Лопанова Любовь Александровна
2016 год

Понятие множества является одним из наиболее Общих и наиболее важных математических понятий.
Оно было введено в математику немецким ученым
Георгом кантором (1845-1918).
Следуя кантору множество можно определить так:
Множество – совокупность объектов,
обладающих определенным свойством,
объединенных в единое целое.

МНОЖЕСТВО
ОБЩИМ СВОЙСТВОМ
2, 4, 6, 8
Множество
четных однозначных чисел
Множество
геометрических фигур
ПРЕДМЕТ, ВХОДЯЩИЙ ВО МНОЖЕСТВО НАЗЫВАЕТСЯ ЭЛЕМЕНТОМ МНОЖЕСТВА
— элемент множества геометрических фигур
4
— элемент множества четных однозначных чисел
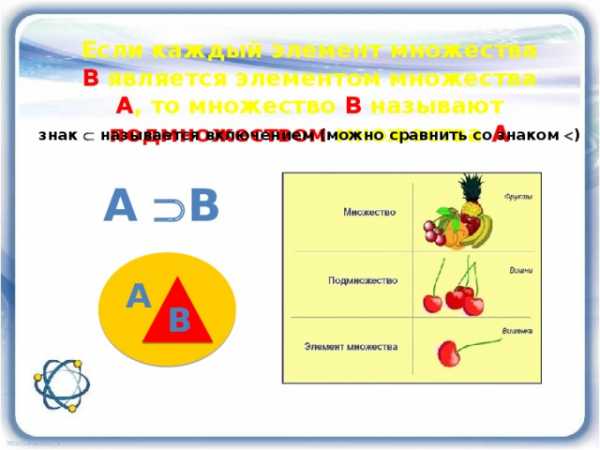
Если каждый элемент множества В является элементом множества А , то множество В называют подмножеством множества А
знак называется включением (можно сравнить со знаком )
A B
A
A
B

Два способа записи множеств:
Первый способ: перечислительный
A={1; 2; 3; 4; 5}
Второй способ: описательный – множество выделяется из всевозможных других тем или иным свойством
A={Х/ — первые пять натуральных чисел}
А
В
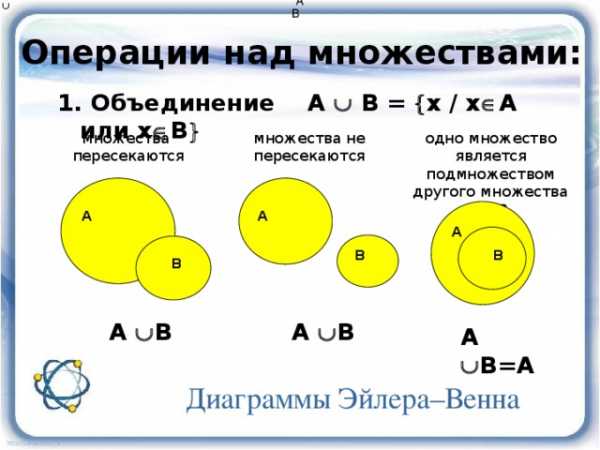
Операции над множествами:
1. Объединение A B = х / х А или х В
множества
пересекаются
множества не пересекаются
одно множество является подмножеством другого множества A B
A
A
A
B
B
B
А В
А В
А В=А
Диаграммы Эйлера–Венна
А
В
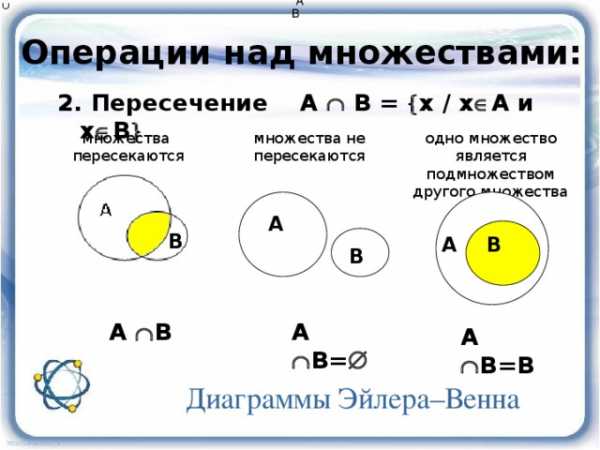
Операции над множествами:
2. Пересечение A B = х / х
множества
пересекаются
множества не пересекаются
одно множество является подмножеством другого множества A B
А
В
А
В
В
А В=
А В
А В=В
Диаграммы Эйлера–Венна
А
В
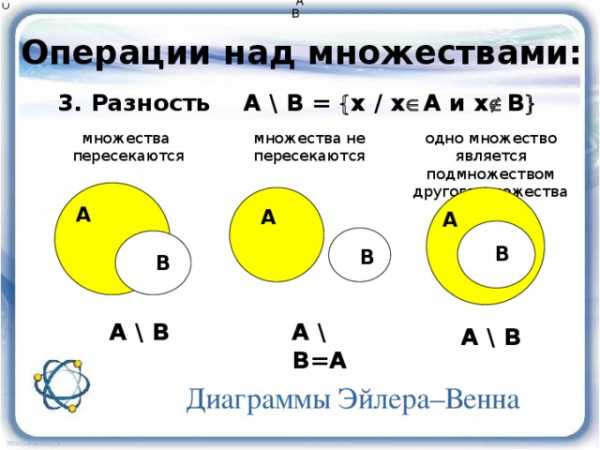
Операции над множествами:
3. Разность A \ B = х / х А и х В
множества
пересекаются
множества не пересекаются
одно множество является подмножеством другого множества A B
А
А
А
В
В
В
А \ В
А \ В=А
А \ В
Диаграммы Эйлера–Венна

Леонард Эйлер, крупнейший математик XVIII века, родился в Швейцарии. Эйлер принадлежит к числу гениев, чьё творчество стало достоянием всего человечества. До сих пор во всех странах изучают тригонометрию и логарифмы в том виде, какой придал им Эйлер.
Он оставил важнейшие труды по самым различным отраслям математики, механики, физики, астрономии и по ряду прикладных наук.
Трудно даже перечислить все отрасли, в которых трудился великий учёный.
Леонард Эйлер
(1707 — 1783)
Леонард Эйлер написал более 850 научных работ. В одной из них и появились круги. А впервые он их использовал в письмах к немецкой принцессе. Эйлер писал тогда, что «круги очень подходят для того, чтобы облегчить наши размышления».

Позднее аналогичный прием использовал ученый Джон Венн — британский логик и философ; основные труды в области логики классов; и этот приём назвали «диаграммы Венна», который используется во многих областях: теория множеств, теория вероятностей, логика, статистика, компьютерные науки.
Джон Венн (1834 — 1923)
При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов, и они получили название «круги Эйлера».
Этот метод даёт более наглядное представление о возможном способе изображения условий, зависимости, отношений в логических задачах.
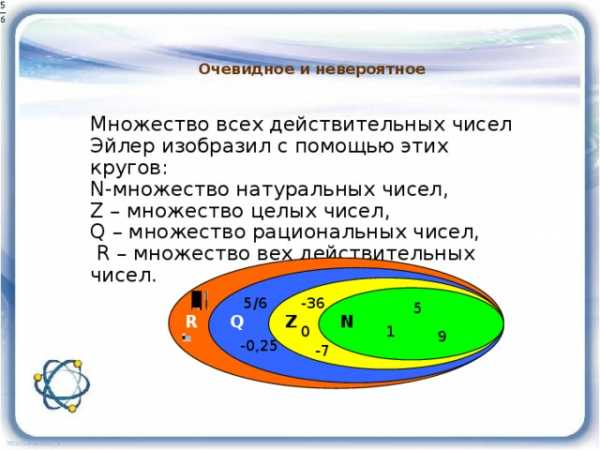
Очевидное и невероятное
Множество всех действительных чисел Эйлер изобразил с помощью этих кругов:
N-множество натуральных чисел,
Z – множество целых чисел,
Q – множество рациональных чисел,
R – множество вех действительных чисел.
5/6
-36
5
N
Z
R
Q
1
0
9
-0,25
-7
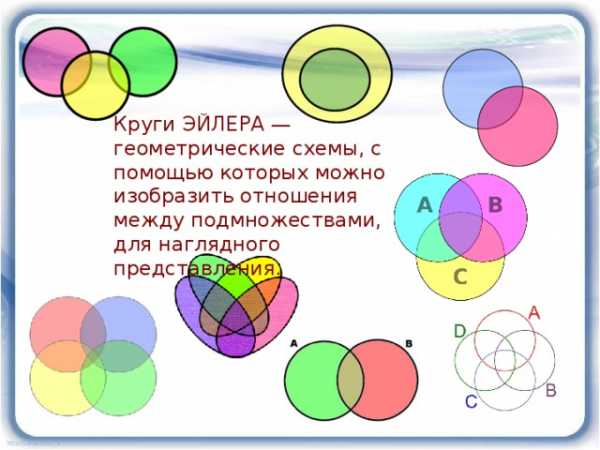
Круги ЭЙЛЕРА — геометрические схемы, с помощью которых можно изобразить отношения между подмножествами, для наглядного представления.

Наряду с кругами в подобных задачах применяют прямоугольники и другие фигуры.
А В-?
Натуральные числа
А
Четные числа
Простые числа
2
В
А В-?
C
D

Система наук
на кругах Эйлера-венна
естественные
социальные
технические
гуманитарные
философия
Примеры кругов Эйлера-Венна
Игрушка
Пистолет
Заводная
игрушка
Кукла
Заводной
автомобиль
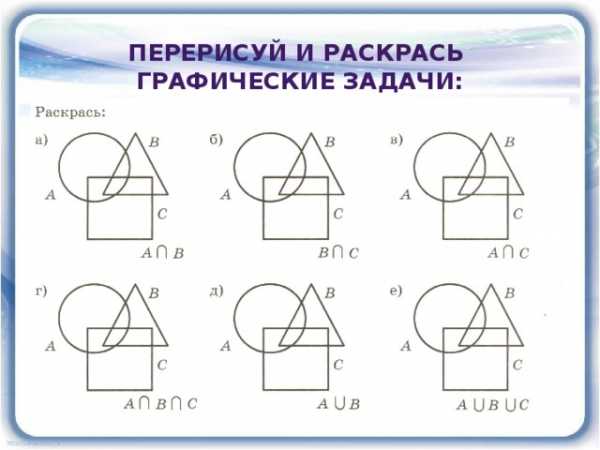
Перерисуй и раскрась
графические задачи:

Задача на числовые множества
Даны множества A={1; 3; 6; 8}, В={2; 4; 6; 8}.
Найти объединение, пересечение и разность множеств А и В: AB, AB, AB, B ∖ A — ?
Решение:
Очевидно, что объединение двух данных множеств AB={1; 2; 3; 4; 6; 8}, их пересечение AB={6; 8}, а разности AB={1; 3} и ВА={2; 4}
Так эти множества можно представить на кругах.
А
В
2
6
3
1
8
4

Задача «Мир музыки»
В магазин «Мир музыки» пришло 35 покупателей. Из них 20 человек купили новый диск певицы Максим, 11 – диск Земфиры, 10 человек не купили ни одного диска. Сколько человек купили диски и Максим, и Земфиры?
Решение:
Изобразим эти множества
на кругах Эйлера .
11
20
35
диски
диски Земфиры
Максим

Теперь посчитаем: Всего внутри большого круга 35 покупателей, внутри двух меньших 35–10=25 покупателей. По условию задачи 20 покупателей купили новый диск певицы Максим, следовательно, 25 – 20 = 5 покупателей купили только диск Земфиры. А в задаче сказано, что 11 покупателей купили диск Земфиры, значит 11 – 5 = 6 покупателей купили диски и Максим, и Земфиры:
не купили диски
5
6
10
диски
диски Земфиры
Максим
Ответ: 6 покупателей купили диски и Максим, и Земфиры

Задача «Занятия в кружках»

Решение:
По рисунку (М) помещены все математики, а в (Б) – все биологи, те ребята, которые не ходят на кружки и помещены они в самый большой круг. Теперь посчитаем:
Внутри большого круга 27 ребят.
Внутри 2-х меньших 27-8=19 ребят.
Внутри М находятся 10 ребят.
Внутри Б находятся 19-10=9 биологов (не посещающих математический кружок)
Внутри МБ находятся 11-9=2 биологов увлекающиеся математикой.
М
МБ
Б
Ответ: 2 биологов посещают математический кружок
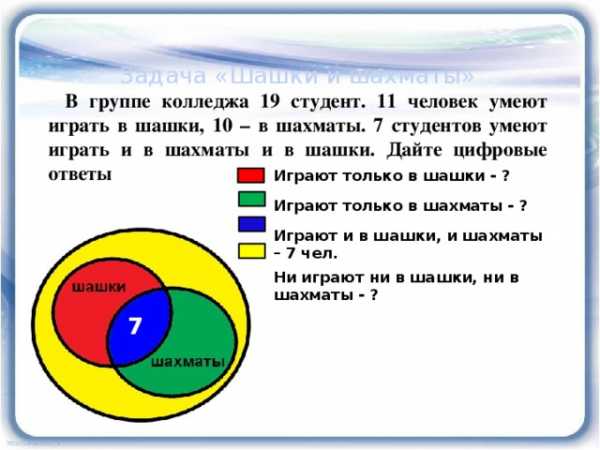
Задача «Шашки и шахматы»
В группе колледжа 19 студент. 11 человек умеют играть в шашки, 10 – в шахматы. 7 студентов умеют играть и в шахматы и в шашки. Дайте цифровые ответы
Играют только в шашки — ?
Играют только в шахматы — ?
Играют и в шашки, и шахматы – 7 чел.
Ни играют ни в шашки, ни в шахматы — ?
7
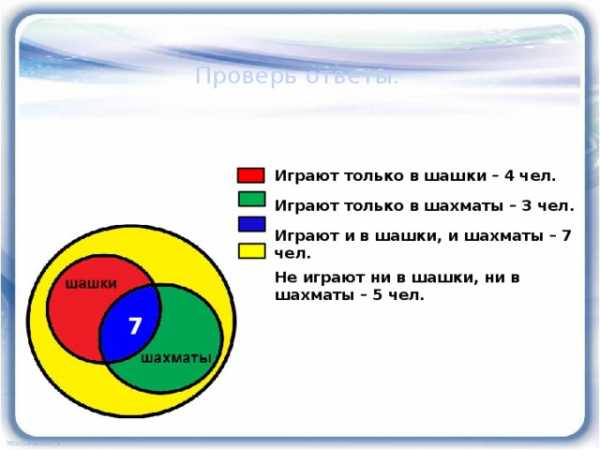
Проверь ответы:
Играют только в шашки – 4 чел.
Играют только в шахматы – 3 чел.
Играют и в шашки, и шахматы – 7 чел.
Не играют ни в шашки, ни в шахматы – 5 чел.
7

Задача «Знание языков»
Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским – 28, французским – 42. Английским и немецким одновременно владеют 8 человек, английским и французским -10 , немецким и французским – 5, всеми тремя языками – 3.
Сколько туристов не владеют ни одним языком?
Решение:
Выразим условие задачи графически. Обозначим кругом тех, кто знает английский, другим кругом – тех, кто знает французский, и третьим кругом – тех, кто знают немецкий.
французский
немецкий
английский

французский
Немецким и французским языками владеют 5 человек, а 3 из них владеют ещё и английским. Значит, немецким и французским владеют 5-3=2 человека.
немецкий
20
2
30
3
7
5
13
В общую часть немецкого и французского кругов вписываем цифру 2 .
английский
Известно, что немецким языком владеют 30 человек, но 5+3+2=10 из них владеют и другими языками, значит, только немецкий знают 20 человек.
Английский язык знают 28 человек, но 5+3+7=15 человек владеют и другими языками, значит, только английский знают 13 человек.
Французский язык знают 42 человека, но 2+3+7=12 человек владеют и другими языками, значит, только французский знают 30 человек.
По условию задачи всего 100 туристов. 20+30+13 +5+2+3+7=80 туристов знают хотя бы один язык, следовательно, 20 человек не владеют ни одним языком.
Ответ: 20 человек
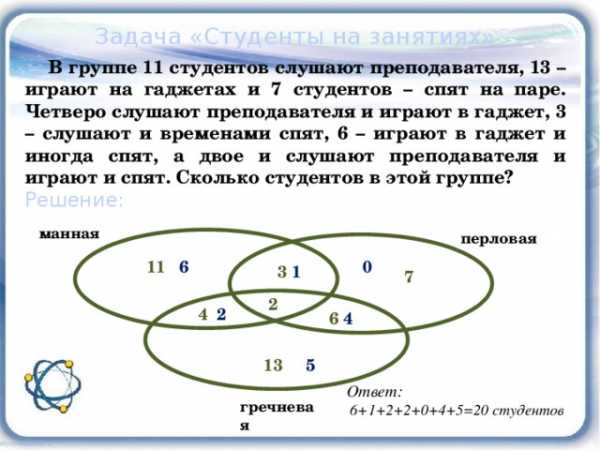
Задача «Студенты на занятиях»
В группе 11 студентов слушают преподавателя, 13 – играют на гаджетах и 7 студентов – спят на паре. Четверо слушают преподавателя и играют в гаджет, 3 – слушают и временами спят, 6 – играют в гаджет и иногда спят, а двое и слушают преподавателя и играют и спят. Сколько студентов в этой группе?
Решение:
манная
перловая
0
11
6
3
1
7
2
4
2
6
4
5
13
Ответ:
6+1+2+2+0+4+5=20 студентов
гречневая

Задача «Многодетная семья»
В одной семье было много детей. 7 из них любили капусту, 6 – морковь, 5 – горох, 4 – капусту и морковь, 3 – капусту и горох, 2 – морковь и горох, 1 – и капусту, и морковь, и горох. Сколько детей было в семье?
Решение:
капуста
морковь
1
4
7
3
6
1
1
3
2
2
1
1
5
горох
Ответ: 10 человек

Задача «Студенты и музыка»
В группе 29 студентов. Среди них 14 любителей классической музыки, 15-джаза, 14 – народной музыки. Классическую музыку и джаз слушают 6 студентов, народную музыку и джаз – 7, классику и народную – 9. Пятеро студентов слушают всякую музыку, а остальные не любят никакой музыки. Сколько их?
Решение:
классическая музыка
джаз
7
1
6
15
14
4
5
9
4
2
7
14
3
народная музыка
Ответ:
29-7-2-1-5-3-4-4=3 (человека)
– не любят никакую музыку

Задача «Домашние любимцы»
У всех моих подруг есть домашние питомцы. Шестеро из них любят и держат кошек, а пятеро — собак. И только у двоих есть и те и другие.
Угадайте, сколько у меня подруг? : Изобразим два круга, так как у нас два вида питом цев.
В одном будем фиксировать владелиц кошек, в другом — собак.
Поскольку у некоторых подруг есть и те, и другие животные, то круги нарисуем так, чтобы у них была общая часть.
В этой общей части ставим цифру 2 так как кошки и собаки есть у двоих.
В оставшейся части «кошачьего» круга ставим цифру 4 (6 — 2 = 4).
В свободной части «собачьего» круга ставим цифру 3 (5 — 2 = 3).
А теперь рисунок сам подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг.

Решение:
Изобразим два круга, так как у нас два вида питомцев.
В одном будем фиксировать владелиц кошек, в другом — собак.
Поскольку у некоторых подруг есть и те, и другие животные, то круги нарисуем так, чтобы у них была общая часть.
В этой общей части ставим цифру 2 так как кошки и собаки есть у двоих.
В оставшейся части «кошачьего» круга ставим цифру 4 (6 — 2 = 4).
В свободной части «собачьего» круга ставим цифру 3 (5 — 2 = 3).
А теперь рисунок сам подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг.
С
К
2
3
4
Ответ: 9 подруг

Задача «Хобби»
Из 24 учеников 5 класса музыкальную школу посещают 10 человек, художественную школу — 8 человек, спортивную школу — 12 человек, музыкальную и художественную школу — 3, художественную и спортивную школу — 2, музыкальную и спортивную школу — 2, все три школы посещает 1 человек.
Сколько учеников посещают только одну школу?
Сколько учащихся ни в чем себя не развивают?

Решение:
В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Только музыкальную школу посещают 10-3-2-1=4 учащихся. Только художественную школу посещают 8-3-2-1=2 учащихся. Только спортивную школу посещают 12-2-2-1=7 учащихся.
Только одну школу посещают 4+2+7=13 учеников.
Ни в чем себя не развивают 24-(4+2+7+3+2+2+1)=3 учащихся.
Ответ: 13 учеников посещают только одну школу, 3 учащихся себя не развивают
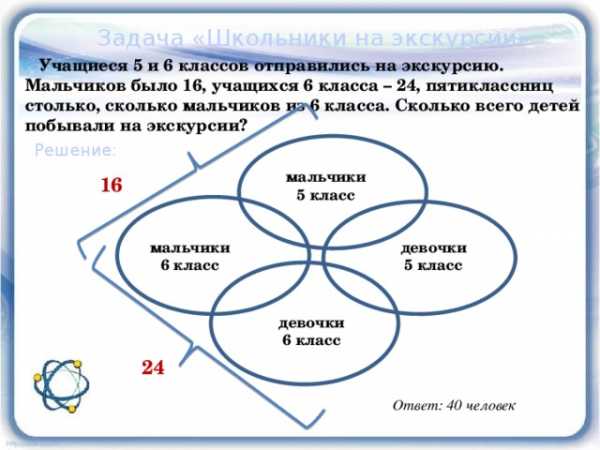
Задача «Школьники на экскурсии»
Учащиеся 5 и 6 классов отправились на экскурсию. Мальчиков было 16, учащихся 6 класса – 24, пятиклассниц столько, сколько мальчиков из 6 класса. Сколько всего детей побывали на экскурсии?
Решение:
мальчики
5 класс
16
мальчики
девочки
6 класс
5 класс
девочки
6 класс
24
Ответ: 40 человек
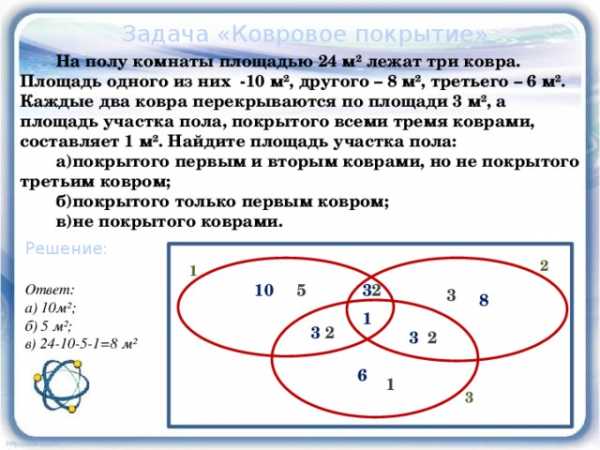
Задача «Ковровое покрытие»
На полу комнаты площадью 24 м² лежат три ковра. Площадь одного из них -10 м², другого – 8 м², третьего – 6 м². Каждые два ковра перекрываются по площади 3 м², а площадь участка пола, покрытого всеми тремя коврами, составляет 1 м². Найдите площадь участка пола:
а)покрытого первым и вторым коврами, но не покрытого третьим ковром;
б)покрытого только первым ковром;
в)не покрытого коврами.
Решение:
2
1
5
10
Ответ:
2
3
а) 10м²;
б) 5 м²;
в) 24-10-5-1=8 м²
3
8
1
3
2
3
2
6
1
3

Задача «Туристы»
Из 100 приехавших туристов 75 знали немецкий язык и 83 знали французский. 10 человек не знали ни немецкого, ни французского. Сколько туристов знали оба эти языка?
Решение:
немецкий
французский
75
83
х
Получим уравнение: 75+83-х=90
158-х=90
х=68
100-10=90
Ответ: 68 человек знали оба языка

Задача для самостоятельного решения:
1. Из 40 опрошенных человек 32 любят молоко, 21 – лимонад, а 15 – и молоко, и лимонад. Сколько человек не любят ни молоко, ни лимонад?
Ответ: 2 человека
30

Задача для самостоятельного решения:
2. В воскресенье 19 учеников класса побывали в планетарии, 10 – в цирке и 6 – в музее. Планетарий и цирк посетили 5 учеников; планетарий и музей – трое, в цирке и музее был один человек. Сколько учеников в классе, если никто не успел посетить все три места, а трое вообще никуда не ходили?
Ответ: 29 человек

Задача для самостоятельного решения:
3. В детском лагере отдыхало 70 ребят. Из них 20 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов, а 3 спортсмена посещают и драмкружок, и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты спортом?
Ответ: 17 ребят, 11 спортсменов

Задача для самостоятельного решения:
4. Из сотрудников фирмы 16 побывали во Франции, 10 – в Италии, 6 – в Англии. В Англии и Италии – пятеро, в Англии и Франции – 6, во всех трёх странах – 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работает 19 человек, и каждый их них побывал хотя бы в одной из названных стран?
Ответ: 7 сотрудников

Придумайте задачи по картинкам
Использованные Интернет-ресурсы:
- http :// mat .1 september . ru Газета «Математика» Издательского дома «Первое сентября»
- http :// www . math . ru Math.ru: Математика и образование
- http://festival.1september.ru/articles/635933 /
- https://znanija.com/task/3231925
- https:// yandex.ru/images/search?textstype=image&lr=43&noreask=1&parent-reqid=1483952074037160-1110803268472871449321762-sas1-3418&source=wiz
multiurok.ru
Диаграмма Венна — это… Что такое Диаграмма Венна?

Диаграмма Венна — схематичное изображение всех возможных пересечений нескольких (часто — трёх) множеств. Если пересечения позволяется указывать не все, получается более общий случай — круги Эйлера.
Диаграммы Эйлера — Венна (как их ещё называют) изображают все комбинаций свойств, то есть конечную булеву алгебру. При диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.
Пример получения произвольных кругов Эйлера из диаграмм Венна с пустыми (чёрными) множествами.Они появились в сочинениях английского логика Джона Венна (1834—1923), подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году.
Ссылки
| Логика | |
|---|---|
| Формальная | Логические операции с понятиями Изменение содержания понятия: отрицание • ограничение • обобщение • деление |
| Математическая (теоретическая, символическая) | Логические связки (операции) над высказываниями Высказывание — построение над множеством {B, , , , 0, 1} |
dic.academic.ru
Круги Эйлера — Википедия
Пример кругов Эйлера. Буквами обозначены, например, свойства: — живое существо, — человек, — неживая вещьКруги́ Э́йлера[1] — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.
Важный частный случай кругов Эйлера — диаграммы Эйлера — Венна, изображающие все комбинаций свойств, то есть конечную булеву алгебру. При диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.
При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов. Однако этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц. Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но при этом всё же предпочитал использовать линейные схемы.[2]
Пример получения произвольных кругов Эйлера из диаграмм Венна с пустыми (чёрными) множествамиНо достаточно основательно развил этот метод сам Л. Эйлер. Методом кругов Эйлера пользовались и немецкие математики Алекс ван Сивцео и Эрнст Шрёдер в книге «Алгебра логики». Особенного расцвета графические методы достигли в сочинениях английского логика Джона Венна, подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году. Поэтому такие схемы иногда называют Диаграммы Эйлера — Венна.
- ↑ «Круги…» — это условный термин, вместо кругов могут быть любые многомерные фигуры, иерархически расположенные в пространстве, то есть одни фигуры поглощают либо часть других фигур, либо полностью.
- ↑ Leibniz G. W. Opuscules et fragments inédits de Leibniz. — Paris, 1903. — p. 293—321.
| Логика | |
|---|---|
| Формальная | Логические операции с понятиями Изменение содержания понятия: отрицание • ограничение • обобщение • деление |
| Математическая (теоретическая, символическая) | Логические связки (операции) над высказываниями Высказывание — построение над множеством {B, , , , 0, 1} |
| См. также | импликация () • Круги Эйлера/Диаграмма Венна • Теория множеств |
www.wikiznanie.ru
