Комплексные числа Википедия
Запросы «Re», «Im» и «Мнимая величина» перенаправляются сюда; см. также другие значения терминов Re, Im и Мнимая величина.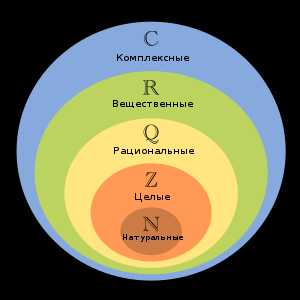
Иерархия чисел
Ко́мпле́ксные чи́сла (от лат. complex — совокупный, тесно связанный[1]; о двойном ударении см. примечание[K 1]) — числа вида a+bi{\displaystyle a+bi}, где a,b{\displaystyle a,b} — вещественные числа, i{\displaystyle i} — мнимая единица[2], то есть число, для которого выполняется равенство: i2=−1.{\displaystyle i^{2}=-1.} Множество комплексных чисел обычно обозначается символом C.{\displaystyle \mathbb {C} .} Вещественные числа можно рассматривать как частный случай комплексных, они имеют вид a+0i{\displaystyle a+0i}. Главное свойство C{\displaystyle \mathbb {C} } — в нём выполняется
ru-wiki.ru
Комплексное число Википедия
Запросы «Re», «Im» и «Мнимая величина» перенаправляются сюда; см. также другие значения терминов Re, Im и Мнимая величина.
Иерархия чисел
Ко́мпле́ксные чи́сла (от лат. complex — совокупный, тесно связанный[1]; о двойном ударении см. примечание[K 1]) — числа вида a+bi{\displaystyle a+bi}, где a,b{\displaystyle a,b} — вещественные числа, i{\displaystyle i} — мнимая единица[2], то есть число, для которого выполняется равенство: i2=−1.{\displaystyle i^{2}=-1.} Множество комплексных чисел обычно обозначается символом C.{\displaystyle \mathbb {C} .} Вещественные числа можно рассматривать как частный случай комплексных, они имеют вид a+0i{\displaystyle a+0i}. Главное свойство C{\displaystyle \mathbb {C} } — в нём выполняется основная теорема алгебры, то есть любой многочлен
ru-wiki.ru
Чисто комплексные числа Википедия
Запросы «Re», «Im» и «Мнимая величина» перенаправляются сюда; см. также другие значения терминов Re, Im и Мнимая величина.
Иерархия чисел
Ко́мпле́ксные чи́сла (от лат. complex — совокупный, тесно связанный[1]; о двойном ударении см. примечание[K 1]) — числа вида a+bi{\displaystyle a+bi}, где a,b{\displaystyle a,b} — вещественные числа, i{\displaystyle i} — мнимая единица[2], то есть число, для которого выполняется равенство: i2=−1.{\displaystyle i^{2}=-1.} Множество комплексных чисел обычно обозначается символом C.{\displaystyle \mathbb {C} .} Вещественные числа можно рассматривать как частный случай комплексных, они имеют вид a+0i{\displaystyle a+0i}. Главное свойство C{\displaystyle \mathbb {C} } — в нём выполняется основная теорема алгебры, то есть любой многочлен n{\displaystyle n}-й степени (n⩾1
ru-wiki.ru
Показательная форма комплексного числа Википедия
Запросы «Re», «Im» и «Мнимая величина» перенаправляются сюда; см. также другие значения терминов Re, Im и Мнимая величина.
Иерархия чисел
Ко́мпле́ксные чи́сла (от лат. complex — совокупный, тесно связанный[1]; о двойном ударении см. примечание[K 1]) — числа вида a+bi{\displaystyle a+bi}, где a,b{\displaystyle a,b} — вещественные числа, i{\displaystyle i} — мнимая единица[2], то есть число, для которого выполняется равенство: i2=−1.{\displaystyle i^{2}=-1.} Множество комплексных чисел обычно обозначается символом C.{\displaystyle \mathbb {C} .} Вещественные числа можно рассматривать как частный случай комплексных, они имеют вид a+0i{\displaystyle a+0i}. Главное свойство C{\displaystyle \mathbb {C} }
ru-wiki.ru
Комплексные числа — Википедия
Материал из Википедии — свободной энциклопедии
Запросы «Re», «Im» и «Мнимая величина» перенаправляются сюда; см. также другие значения терминов Re, Im и Мнимая величина.
Иерархия чисел
Ко́мпле́ксные[K 1] чи́сла (от лат. complex — совокупный, тесно связанный[1]) — числа вида a+bi{\displaystyle a+bi}, где a,b{\displaystyle a,b} — вещественные числа, i{\displaystyle i} — мнимая единица[2], то есть число, для которого выполняется равенство: i2=−1.{\displaystyle i^{2}=-1.} Множество комплексных чисел обычно обозначается символом C.{\displaystyle \mathbb {C} .} Вещественные числа можно рассматривать как частный случай комплексных, они имеют вид a+0i{\displaystyle a+0i}. Главное свойство C{\displaystyle \mathbb {C} } — в нём выполняется основная теорема алгебры, то есть любой многочлен n{\displaystyle n}-й степени (n⩾1{\displaystyle n\geqslant 1}) имеет n{\displaystyle n} корней. Доказано[⇨], что система комплексных чисел логически непротиворечива[K 2].
Так же как и для вещественных чисел, для комплексных чисел определены операции сложения, вычитания[⇨], умножения[⇨] и деления[⇨]. Однако многие свойства комплексных чисел отличаются от свойств вещественных чисел; например, нельзя указать, какое из двух комплексных чисел больше или меньше[⇨]. Удобно представлять комплексные числа a+bi{\displaystyle a+bi} точками на комплексной плоскости[⇨]; например, для изображения сопряжённых чисел используется операция отражения относительно горизонтальной оси
encyclopaedia.bid
Поле комплексных чисел Википедия
Запросы «Re», «Im» и «Мнимая величина» перенаправляются сюда; см. также другие значения терминов Re, Im и Мнимая величина.
Иерархия чисел
Ко́мпле́ксные чи́сла (от лат. complex — совокупный, тесно связанный[1]; о двойном ударении см. примечание[K 1]) — числа вида a+bi{\displaystyle a+bi}, где a,b{\displaystyle a,b} — вещественные числа, i{\displaystyle i} — мнимая единица[2], то есть число, для которого выполняется равенство: i2=−1.{\displaystyle i^{2}=-1.} Множество комплексных чисел обычно обозначается символом C.{\displaystyle \mathbb {C} .} Вещественные числа можно рассматривать как частный случай комплексных, они имеют вид a+0i{\displaystyle a+0i}. Главное свойство C{\displaystyle \mathbb {C} } — в нём выполняется основная теорема алгебры, то есть любой многочлен
ru-wiki.ru
Модуль комплексного числа Википедия
Запросы «Re», «Im» и «Мнимая величина» перенаправляются сюда; см. также другие значения терминов Re, Im и Мнимая величина.
Иерархия чисел
Ко́мпле́ксные чи́сла (от лат. complex — совокупный, тесно связанный[1]; о двойном ударении см. примечание[K 1]) — числа вида a+bi{\displaystyle a+bi}, где a,b{\displaystyle a,b} — вещественные числа, i{\displaystyle i} — мнимая единица[2], то есть число, для которого выполняется равенство: i2=−1.{\displaystyle i^{2}=-1.} Множество комплексных чисел обычно обозначается символом C.{\displaystyle \mathbb {C} .} Вещественные числа можно рассматривать как частный случай комплексных, они имеют вид a+0i{\displaystyle a+0i}. Главное свойство C{\displaystyle \mathbb {C} } — в нём выполняется основная теорема алгебры, то есть любой многочлен
ru-wiki.ru
