§2. Методы вычисления определенных интегралов
Так как формула Ньютона–Лейбница сводит задачу вычисления определенного интеграла от непрерывной функции к нахождению первообразной, то все основные методы вычисления неопределенных интегралов переносятся и на задачу вычисления определенных интегралов. Сформулируем эти методы с учетом специфики определенных интегралов.
1. Непосредственное интегрирование
Типовой пример
Вычислить
определенный интеграл 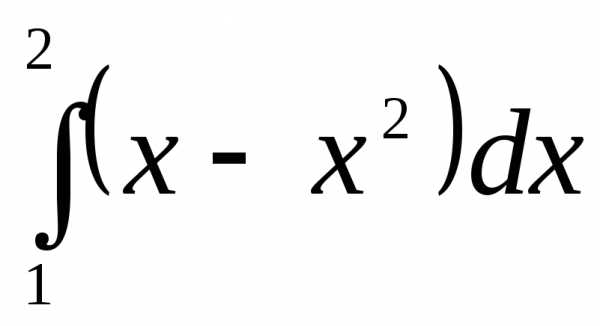 .
.
►Используя формулу Ньютона–Лейбница, получим:
.◄
2. Замена переменной в определённом интеграле
ТЕОРЕМА
Пусть:
для ;
.
Тогда .
При решении задач нельзя забывать о том, что при переходе к новой переменной надо обязательно вычислить новые пределы интеграла.
Типовые примеры
Вычислить интегралы.
1. 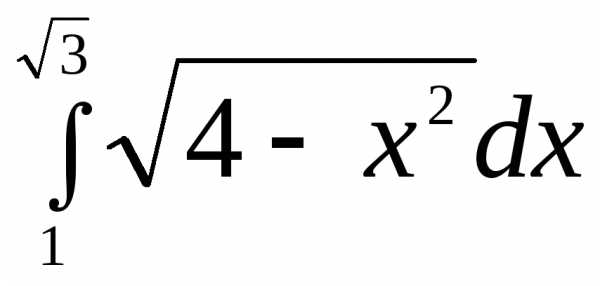 .
.
►
.◄
2.  .
.
►
.◄
3. 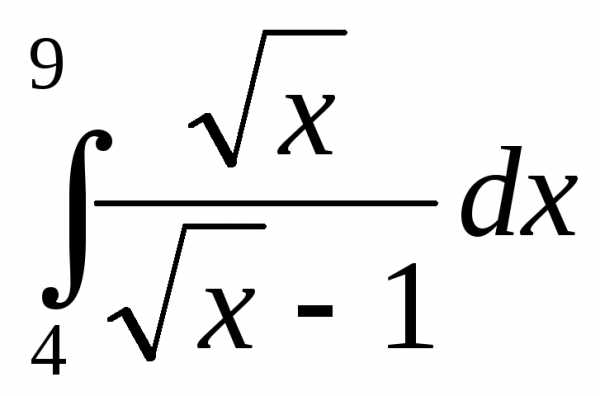 .
.
►Воспользуемся формулой замены переменной в определенном интеграле:
и
применим подстановку 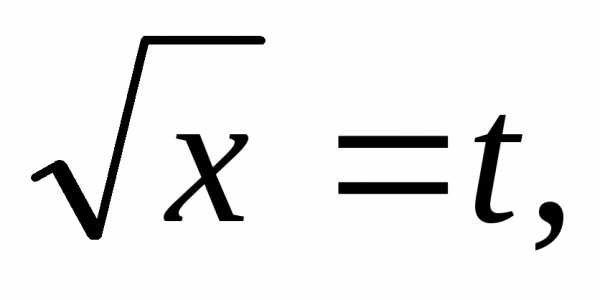 т.е.x =
т.е.x =
◄
3. Формула интегрирования по частям для определённого интеграла
ТЕОРЕМА
Пусть .Тогда
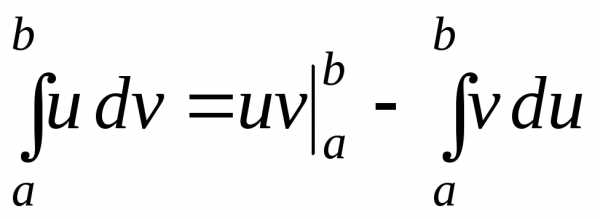 .
.
Типовые примеры
Вычислить интегралы.
1. 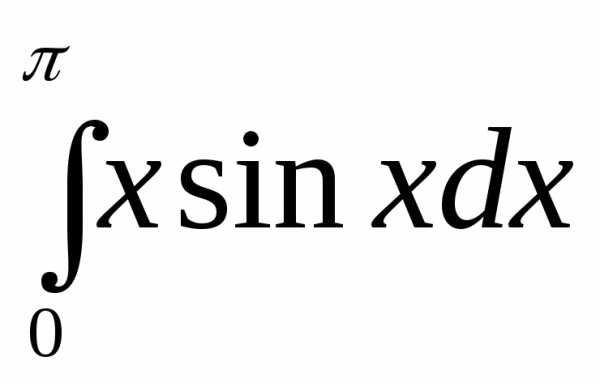 .
.
►Воспользуемся формулой интегрирования по частям в определенном интеграле. Имеем
. ◄
2. 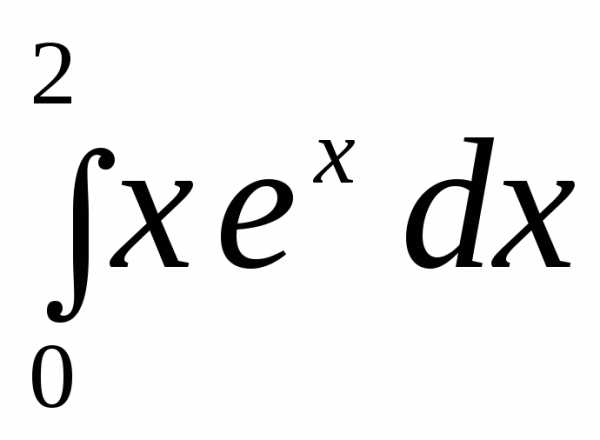 .
.
►
.◄
3. 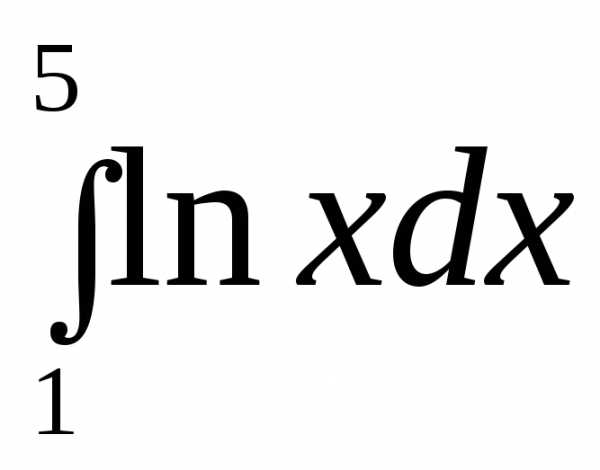
►.◄
§3. Геометрические приложения определенного интеграла
1. Площадь плоской области
1.1. Декартовы координаты
Если 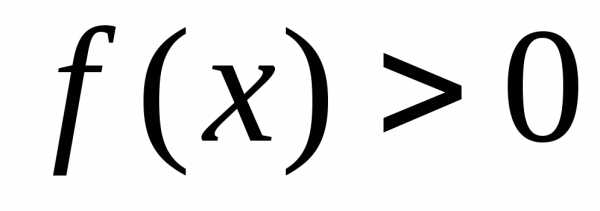 на отрезке
на отрезке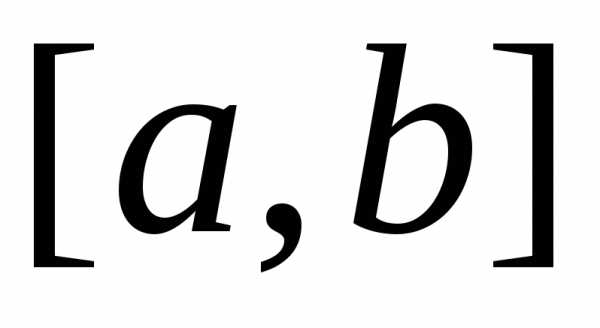 ,
то
,
то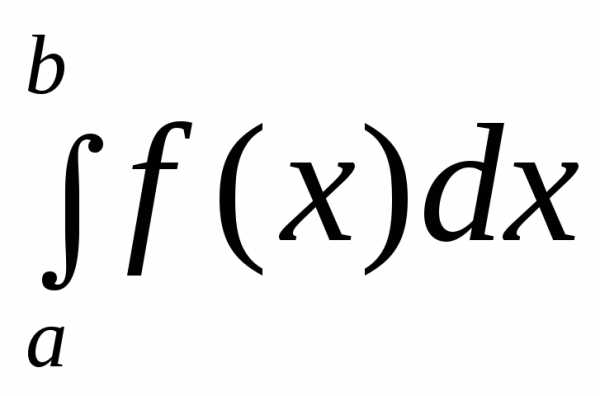 равен площади криволинейной трапеции
равен площади криволинейной трапеции ,
ограниченной снизу отрезком
,
ограниченной снизу отрезком ,
слева и справа – прямыми
,
слева и справа – прямыми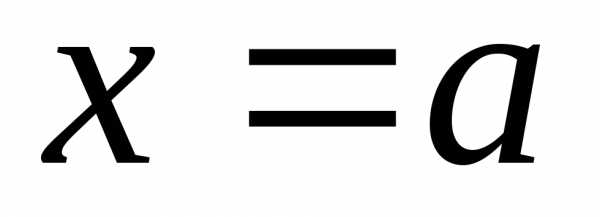 и
и ,
сверху – функцией
,
сверху – функцией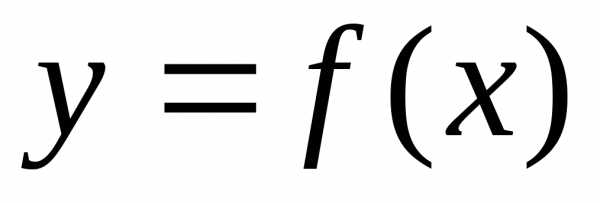
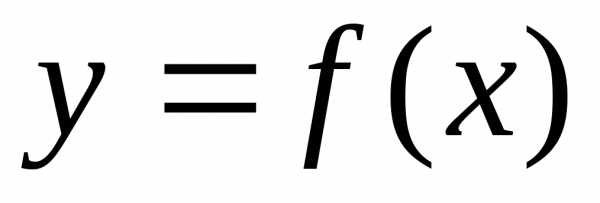 ,
снизу – кривой
,
снизу – кривой ,
слева и справа – отрезками прямых
,
слева и справа – отрезками прямых и
и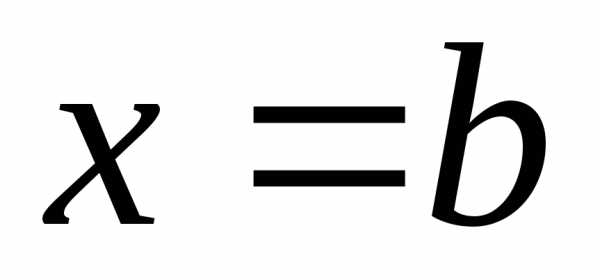 ,
то её площадь равна
,
то её площадь равна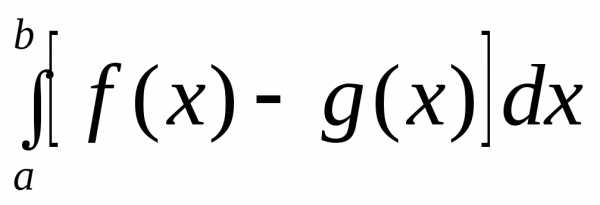 .
.Типовые примеры
1)
Найти площадь области  ,
ограниченной кривымипри
условии, что
,
ограниченной кривымипри
условии, что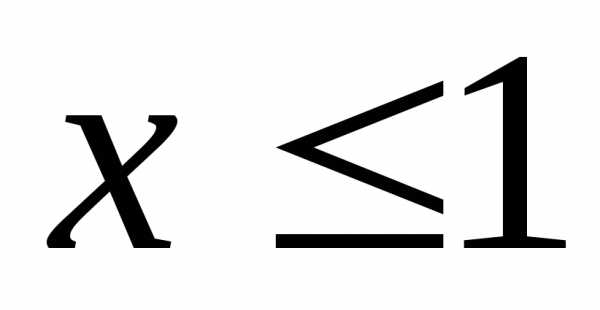 (дальше мы будем писать так:
(дальше мы будем писать так: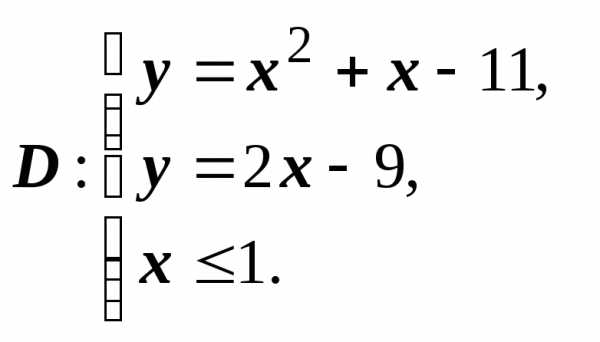 ).
).
►При
решении таких задач следует обязательно
изобразить исследуемый геометрический
объект. Для определения нижнего предела
интегрирования надо найти точку
пересечения кривых, уравнение
имеет два корня: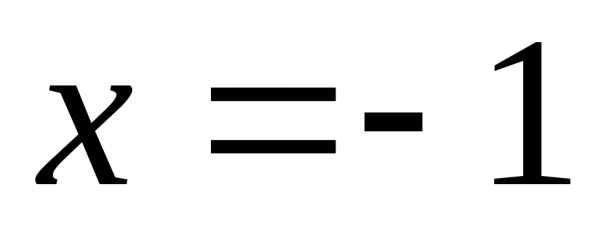
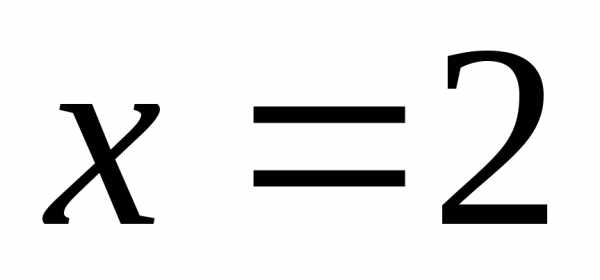 ;
; Подходящий
корень – 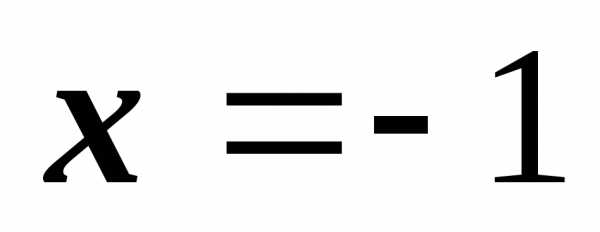 .
Область ограничена сверху параболой,
снизу – прямой, справа – прямой
.
Область ограничена сверху параболой,
снизу – прямой, справа – прямой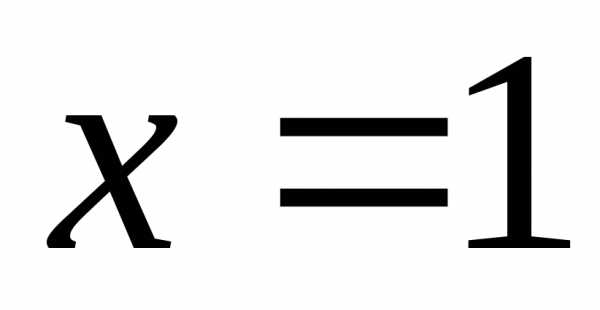 ,
крайняя левая точка –
,
крайняя левая точка –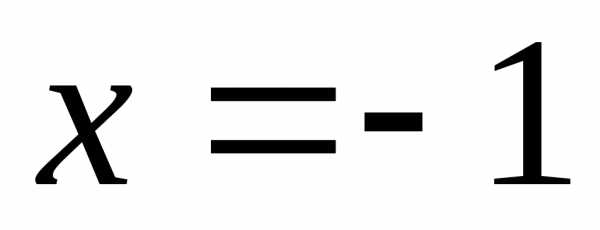 ,
поэтомуЕсли
область имеет более сложную структуру,
её следует разбить на простые части. ◄
,
поэтомуЕсли
область имеет более сложную структуру,
её следует разбить на простые части. ◄
2)
Вычислить площадь фигуры, ограниченной
графиками функций  и
и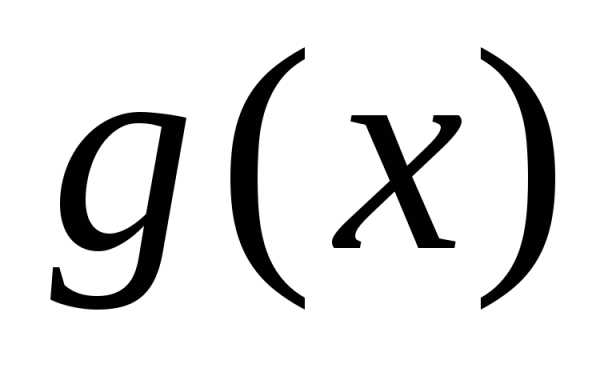 :
:
 ◄
◄
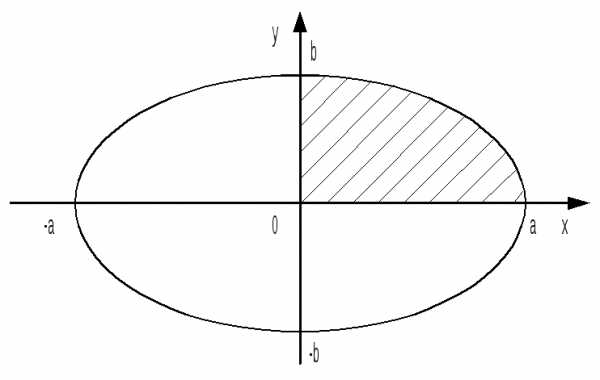
3)
Найти площадь фигуры, ограниченной
эллипсом 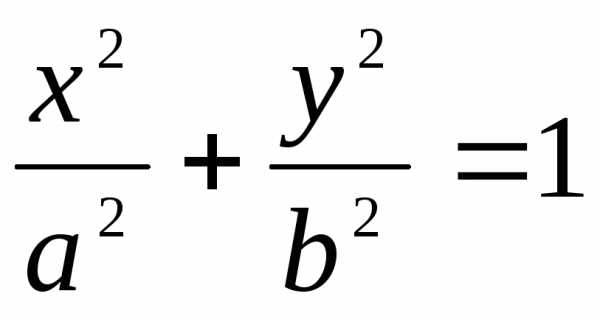 .
.
►Эллипс
имеет две оси симметрии: координатные
оси 0х и 0у. Поэтому площадь S
фигуры равна учетверённой площади S1 части (D1)
фигуры, расположенной в первой четверти
(заштриховано). Фигура (D1)
ограничена сверху линией 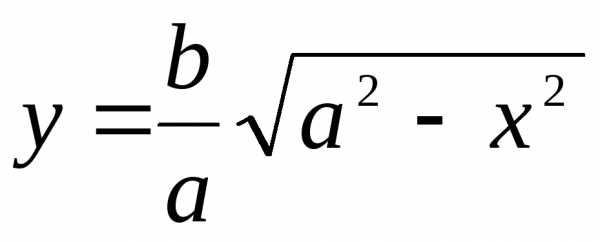 , снизу – осью 0х, слева – осью 0у. Поэтому
, снизу – осью 0х, слева – осью 0у. Поэтому
. Отсюда находим S = 4S1 = ab. ◄
1.2. Область задана в полярных координатах
Если
область 
 ,
,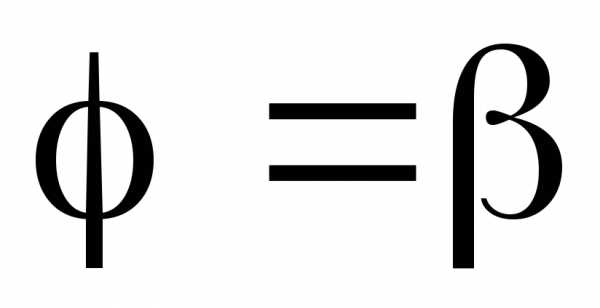 и кривой
и кривой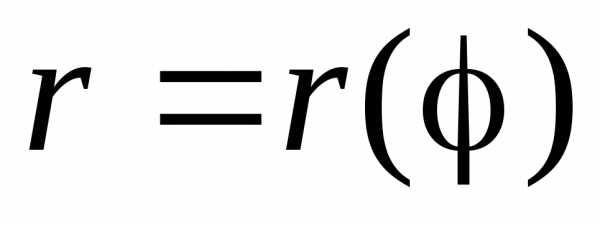 .
В Этом случае
.
В Этом случае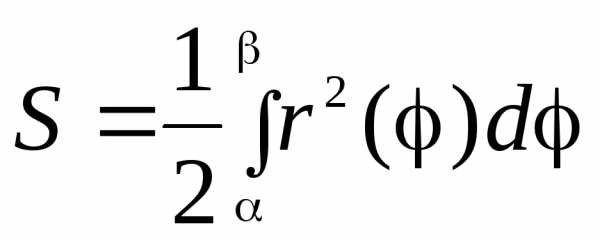 .
.Типовые примеры
1. Найти площадь, ограниченную лемнискатой .
►Точки
лемнискаты расположены в секторах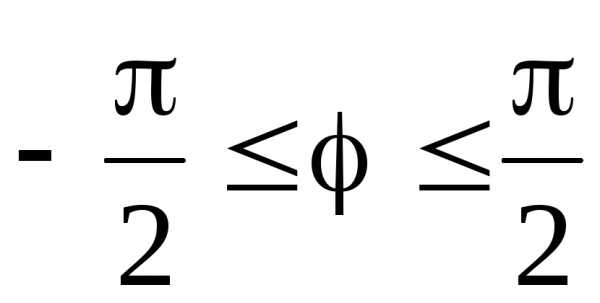 и
и ;
кроме того, при решении таких задаче
целесообразно использовать симметрию
фигуры, поэтому мы найдём площадь части,
расположенной в секторе
;
кроме того, при решении таких задаче
целесообразно использовать симметрию
фигуры, поэтому мы найдём площадь части,
расположенной в секторе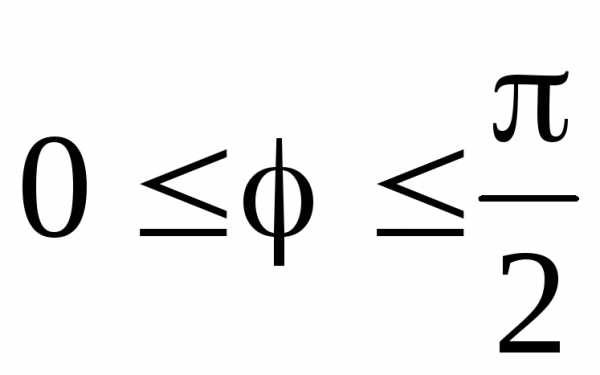 и учетверим её:
и учетверим её:
◄
2. Найти площадь, лежащую внутри кардиоиды вне окружности.
►Найдём разность площадей, лежащих внутри кардиоиды и окружности. Для верхней части кардиоиды ; для верхней части окружности, поэтому◄
1.3.
Область ограничена кривыми, заданными
параметрически Если кривая, ограничивающая криволинейную
трапецию  задана в параметрическом виде,
то переход в интеграле
задана в параметрическом виде,
то переход в интеграле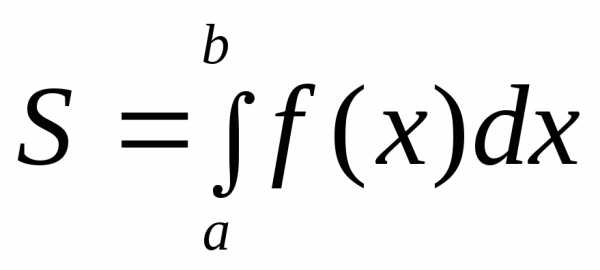 к переменной
к переменной приводит к формуле
приводит к формуле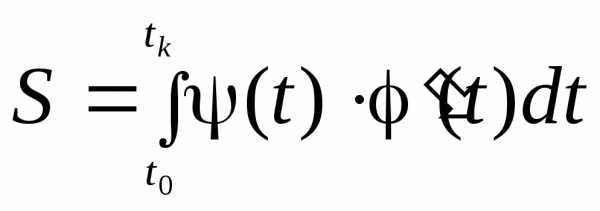 .
.
Типовой пример
Найти
площадь, ограниченную астроидой 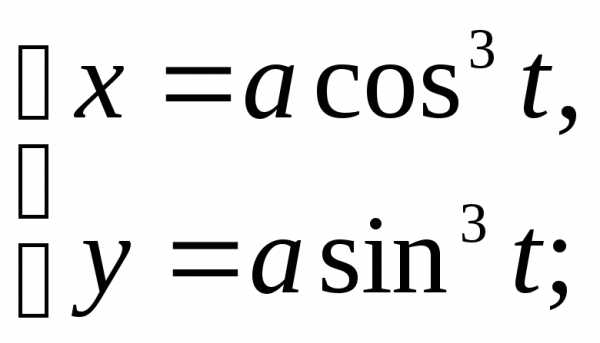 ().
().
►Используем
симметрию фигуры. Мы найдём площадь
части фигуры, расположенной в первом
квадранте (),
и учетверим её. Точка
 – при
– при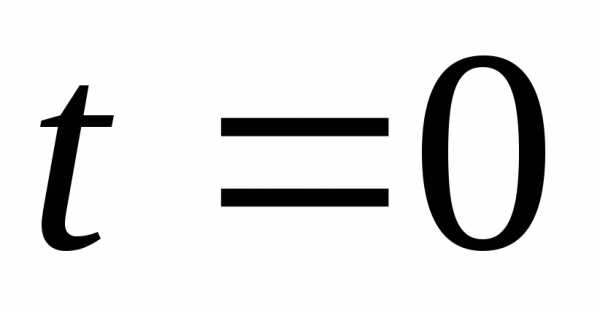 ,
поэтому◄
,
поэтому◄studfiles.net
Вычисление определенных интегралов. Формула Ньютона-Лейбница
Если для подынтегральной функции можно найти первообразную, то определенный интеграл можно вычислить по формуле Ньютона-Лейбница.
—Формула Ньютона-Лейбница позволяет вычислить определенный интеграл как разность первообразных на верхнем и нижнем пределах интегрирования, не вычисляя предела интегральной суммы
.
Можно выделить два этапавычисления определенного интеграла.
Одним из методов интегрирования (см. тему 6) находят первообразную F(x) для функцииf(x ).
Вычисляют разность значений первообразной функции на верхнем и нижнем пределах интегрирования.
Примеры вычисления определенных интегралов можно найти в разделеПримеры выполнения обязательных заданий по теме 7 cучетом некоторых особенностей, сведенных в схему.
Особенности вычисления определенного интеграла
При замене переменных (подстановках) | При интегрировании по частям |
Замена переменных, в отличие от неопределенного интеграла, предполагает не только замену подынтегрального выражения, но и замену пределов интегрирования | Не следует забывать, что определенный интеграл – это |
, где новые пределы интегрирования находят как корни уравнений: ; . | . |
Вычисление площадей криволинейных фигур
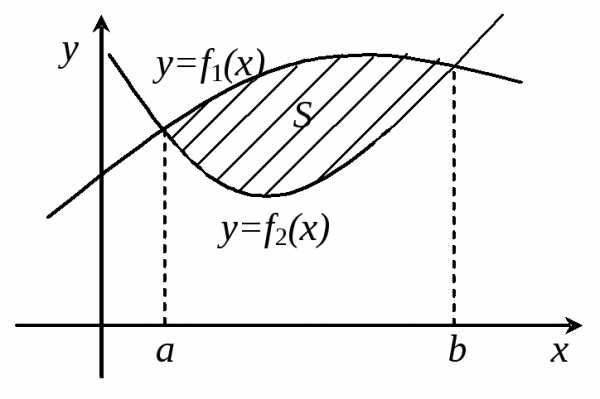
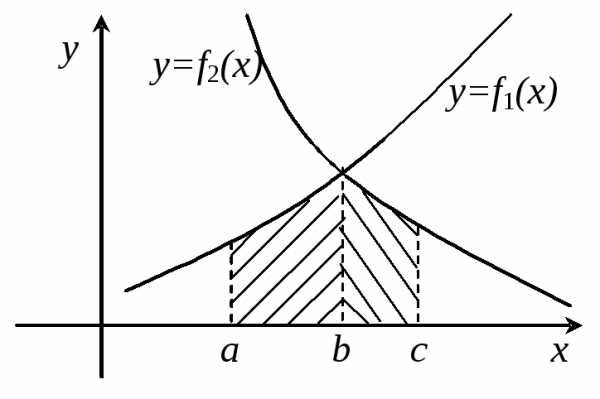
Из задачи о площади криволинейной трапеции ясно, что с помощью определенного интеграла можно вычислять площади плоских криволинейных фигур. При этом следует различать два случая.
Площадь заключена между заданными кривыми. | Площадь лежит под (над) заданными линиями (между линиями и осью ОХ). |
|
|
Тогда, определив точки пересечения линий, т.е. пределы интегрирования, можно найти площадь как разность площадей под вышележащей и нижележащей кривой. | По
рисунку видно, что в данном случае
общая площадь складывается из площадей
под линией |
; по свойству линейности |
Среди геометрических приложений определенного интеграла можно еще отметить :
| Вычисление
длины дуги кривой от точки А до точки В : |
Вычисление
объемов тел вращения:
|
Применение определенного интеграла в экономических задачах
Пусть
функция z = f(t) описывает изменение производительности
некоторого производства с течением
времени. Найдем объем продукции  ,
произведенной за промежуток времени
[0; Т].
,
произведенной за промежуток времени
[0; Т].
Если
производительность не изменяется с
течением времени ( f(t) – постоянная функция), то объем продукции 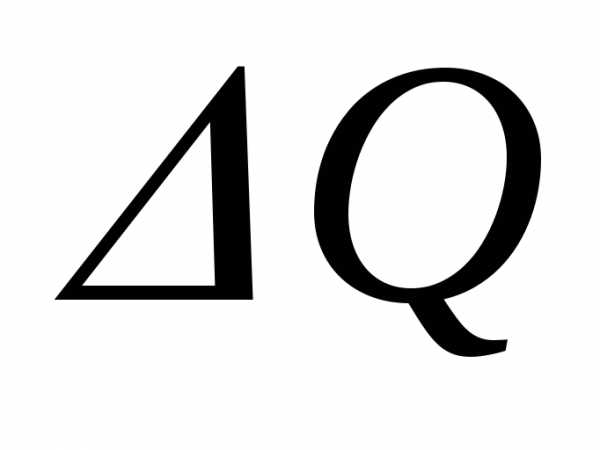 ,
произведенной за некоторый промежуток
времени [t, t +t], находится по формуле:
,
произведенной за некоторый промежуток
времени [t, t +t], находится по формуле: 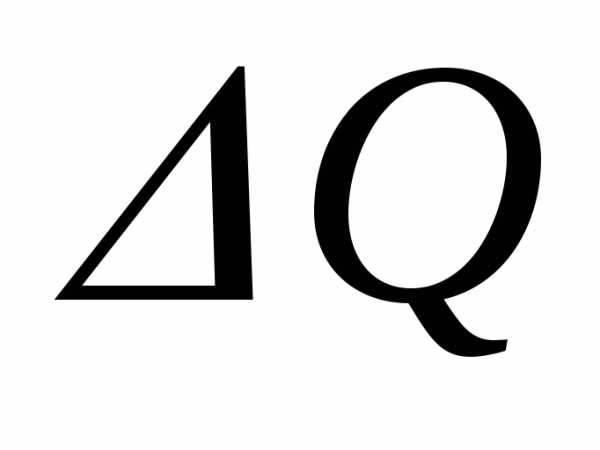 = f(t) t.
= f(t) t.
В
общем случае справедливо приближенное
равенство 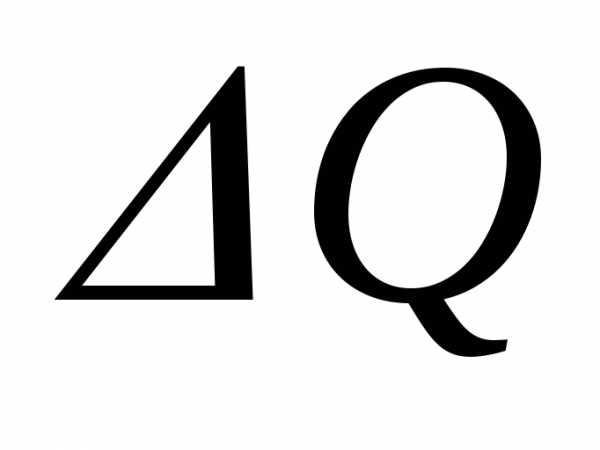
 f()t,
где [t, t+t],
которое оказывается тем более точным,
чем меньше t.
f()t,
где [t, t+t],
которое оказывается тем более точным,
чем меньше t.
Разобьем отрезок [0; T] на промежутки времени точками:
0 = t0 < t1 < t2 << tn = T.
Для величины объема продукции 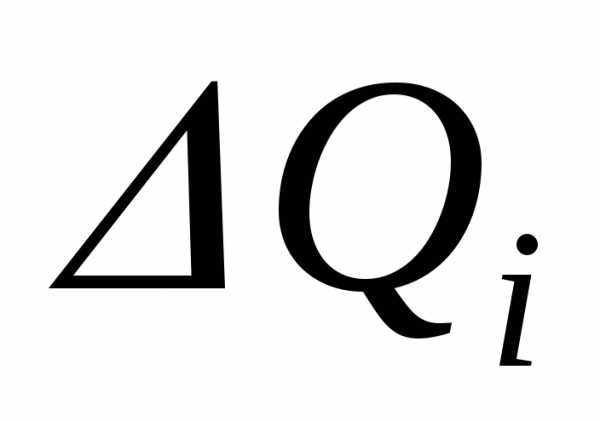 ,
произведенной за промежуток времени
[ti—1, ti],
имеем
,
произведенной за промежуток времени
[ti—1, ti],
имеем 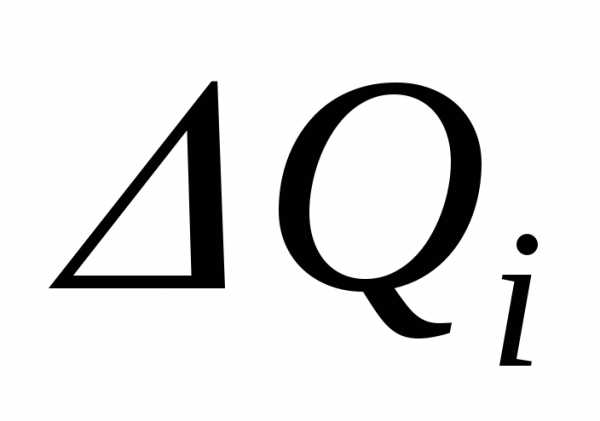 = f(i) ti, где i[ti—1, ti], ti = ti — ti—1, i = 1, 2,,n.
Тогда
= f(i) ti, где i[ti—1, ti], ti = ti — ti—1, i = 1, 2,,n.
Тогда
При
стремлении 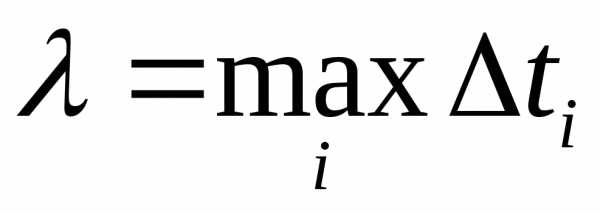 к нулю каждое из использованных
приближенных равенств становится все
более точным, поэтому
к нулю каждое из использованных
приближенных равенств становится все
более точным, поэтому
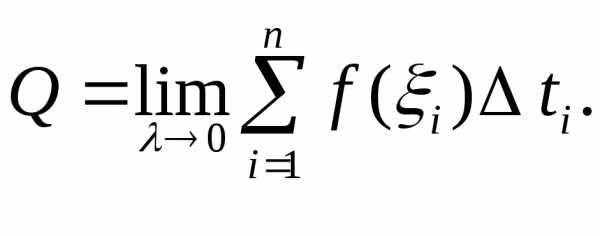
По определению определенного интеграла, окончательно получаем:
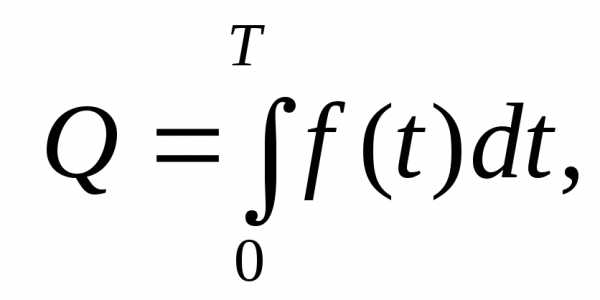
т.е. если f(t) – производительность труда в моментt, то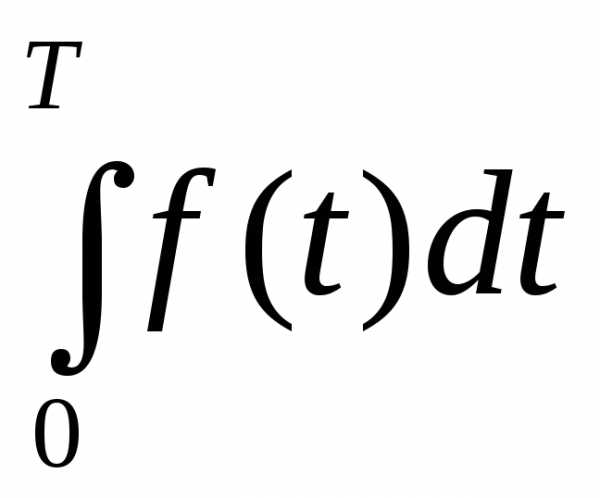 есть объем выпускаемой продукции за
промежуток [0; T].
есть объем выпускаемой продукции за
промежуток [0; T].
Сравнение данной задачи с задачей о площади криволинейной трапеции показывает, что величина и объем продукции, произведенной за промежуток времени [0; T], численно равен площади под графиком функции z = f(t), описывающей изменение производительности труда с течением времени, на промежутке [0; T].
Экономический смысл определенного интеграла — объем произведенной продукции при известной функции производительности труда.
Рассмотрим другие примеры использования интеграла в экономике.
1. Если в
функции Кобба-Дугласа считать, что затраты труда линейно
зависят от времени, а затраты капитала
неизменны, то она примет вид
.
Тогда объем выпускаемой продукции за Т лет составит 
Найдем объем продукции, произведенной за 4 года, если функция Кобба-Дугласа имеет вид .
= | Объем произведенной продукции Q. Интегрируем по частям. |
(у.ед.) | |
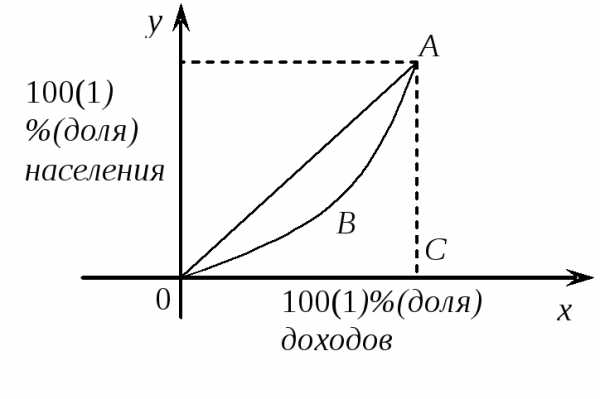 2. Исследуя
кривую Лоренца – зависимость процента
доходов от процента имеющего их населения
(кривую ОВА), мы можем оценить степень
неравенства в распределении доходов
населения. При равномерном распределении
доходов кривая Лоренца вырождается в
прямую – биссектрису ОА, поэтому площадь
фигуры ОАВ между биссектрисой ОА и
кривой Лоренца, отнесенная к площади
треугольника ОАС (коэффициент Джини),
характеризует степень неравенства в
распределении доходов населения. Высокое
значение этого коэффициента показывает
существенно неравномерное распределение
доходов среди населения в рассматриваемой
стране.
2. Исследуя
кривую Лоренца – зависимость процента
доходов от процента имеющего их населения
(кривую ОВА), мы можем оценить степень
неравенства в распределении доходов
населения. При равномерном распределении
доходов кривая Лоренца вырождается в
прямую – биссектрису ОА, поэтому площадь
фигуры ОАВ между биссектрисой ОА и
кривой Лоренца, отнесенная к площади
треугольника ОАС (коэффициент Джини),
характеризует степень неравенства в
распределении доходов населения. Высокое
значение этого коэффициента показывает
существенно неравномерное распределение
доходов среди населения в рассматриваемой
стране.
По данным исследований в распределении доходов в одной из стран кривая Лоренца ОВА может быть описана уравнением , гдех – доля населения, у – доля доходов населения. Вычислить коэффициент Джини .
так
как 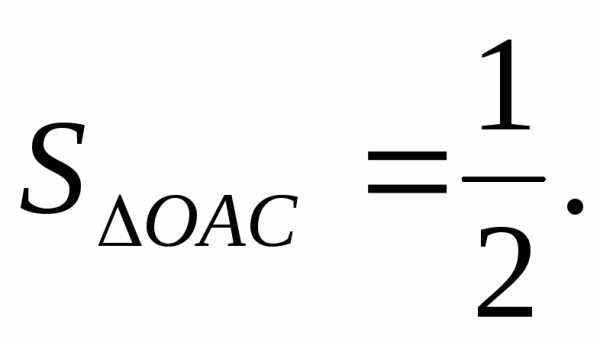
Поэтому
С помощью замены, x=sin t можно вычислить
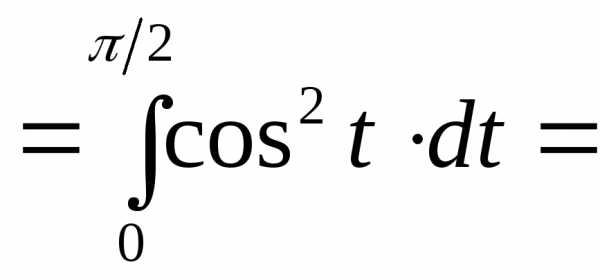
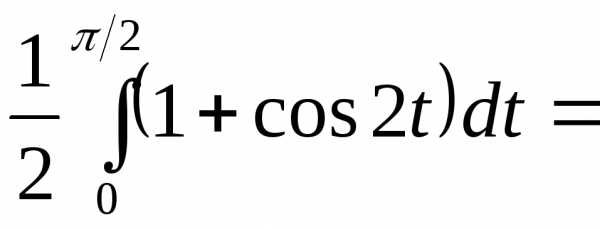
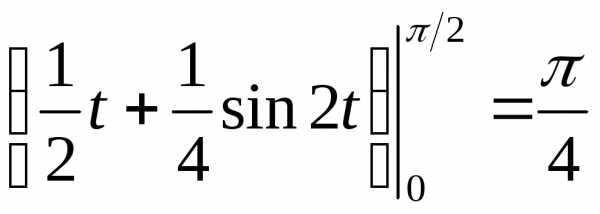 .
.
Интеграл от квадрата косинуса вычисляется по формуле понижения степени. При подстановке пределов в первообразную учтено, что и.
Итак, коэффициент Джини
Достаточно
высокое значение 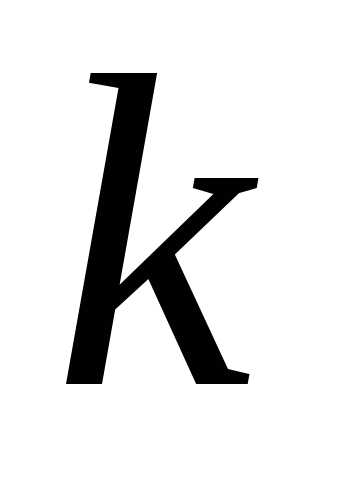 показывает существенно неравномерное
распределение доходов среди населения
в рассматриваемой стране.
показывает существенно неравномерное
распределение доходов среди населения
в рассматриваемой стране.
3. Определение начальной суммы по ее конечной величине, полученной через время t (лет) при годовом проценте (процентной ставке) q, называется дисконтированием (см. тему 4). Задачи такого рода встречаются при определении экономической эффективности капитальных вложений.
Пусть Аt – конечная сумма, полученная за t лет, и А – дисконтируемая (начальная) сумма, которую в финансовом анализе называют также современной суммой.
Если проценты простые, то At = A×(1 + r t), где r = q / 100 – удельная процентная ставка. Тогда A = At / (1 + r t). В случае сложных процентов At = A×(1 + r t)t и потому A = At / (1 + r t)t.
Пусть поступающий ежегодно доход изменяется во времени и описывается функцией f(t) и при удельной норме процента, равной r, процент начисляется непрерывно. Можно показать, что в этом случае дисконтированный доход A за время Т вычисляется по формуле
4.Пусть известна функцияt = t(x),описывающая изменение затрат времениtна изготовление изделия в зависимости от степени освоения производства, гдеx– порядковый номер изделия в партии. Тогда среднее времяtср, затраченное на изготовление одного изделия в период освоения отх1дох2изделий, вычисляется по теореме о среднем:
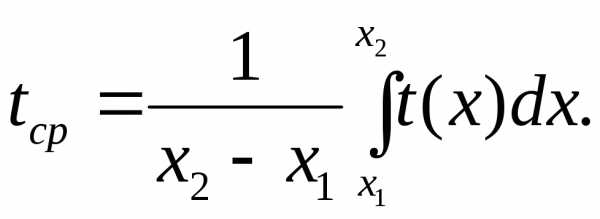
Что касается функции изменения затрат времени на изготовление изделий t = t(x), то часто она имеет вид
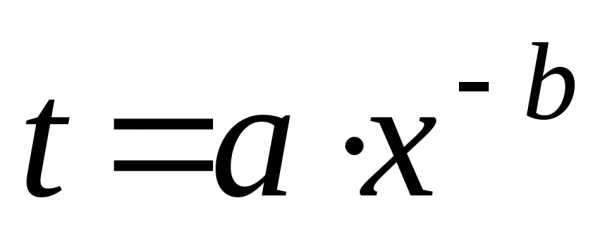 ,
,
где а – затраты времени на первое изделие, b – показатель производственного процесса.
Найдем среднее время, затраченное на освоение одного изделия в период освоения от х1 = 100 до х2 = 121 изделий, полагая в формуле а = 600 (мин.), b= 0,5.
Используя формулу, получаем
(мин.).
studfiles.net
Приближённое вычисление определённых интегралов
Рассмотрим задачу о приближённом нахождении значения определённого интеграла
Относительно подынтегральной функции f(x) мы будем предполагать, что она непрерывна на отрезке интегрирования, а также, когда это понадобится, что она имеет на этом отрезке производные до некоторого порядка. Вычислять значение интеграла мы будем по значениям функцииf(x) в некоторых точках отрезка xi. Эти значения yi=f(xi.) мы будем предполагать известными, то есть предполагать, что у нас есть некоторый эффективный способ вычисления значений функции с любой требуемой точностью. Формулы, позволяющие по известным значениям yiприближённо определить значение , называютсяквадратурными формулами.
Для наглядности
мы будем прибегать к геометрической
интерпретации смысла определённого
интеграла, как площади некоторой
криволинейной трапеции, в случае функции
f(x) .
Следует, однако, иметь в виду, что
квадратурные формулы, которые мы будем
получать, имеют смысл для функций,
принимающих значения произвольного
знака.
.
Следует, однако, иметь в виду, что
квадратурные формулы, которые мы будем
получать, имеют смысл для функций,
принимающих значения произвольного
знака.
При f(x) вычислить интегралзначит
найти площадь под графикомy=f(x),
расположенную над отрезком
вычислить интегралзначит
найти площадь под графикомy=f(x),
расположенную над отрезком 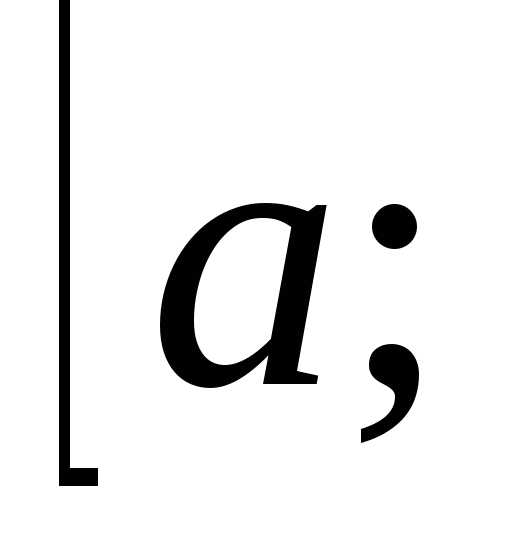 .
.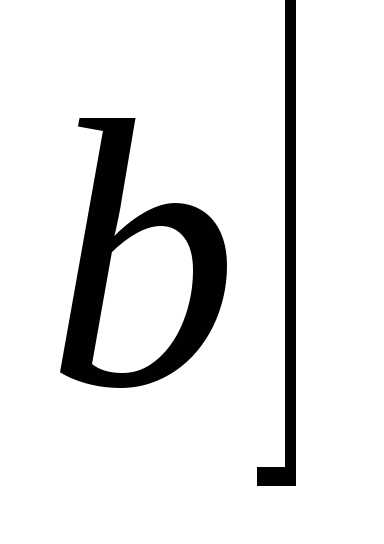 .
Естественной идеей является следующее
построение: разобьём отрезок на части
точками деленияx1,
x2,
… xn-1 и положим
x0=a
и xn=b
(см. определение значения определённого
интеграла). Тогда разбиение отрезка
.
Естественной идеей является следующее
построение: разобьём отрезок на части
точками деленияx1,
x2,
… xn-1 и положим
x0=a
и xn=b
(см. определение значения определённого
интеграла). Тогда разбиение отрезка 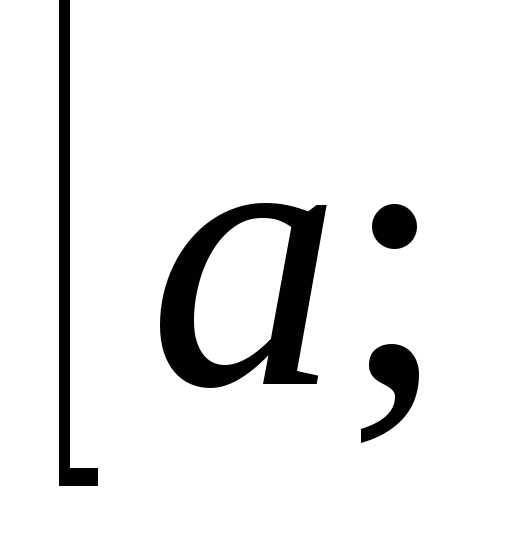 .
.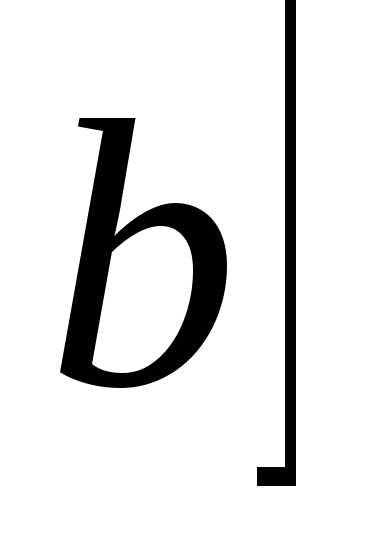 состоит из отрезков
состоит из отрезков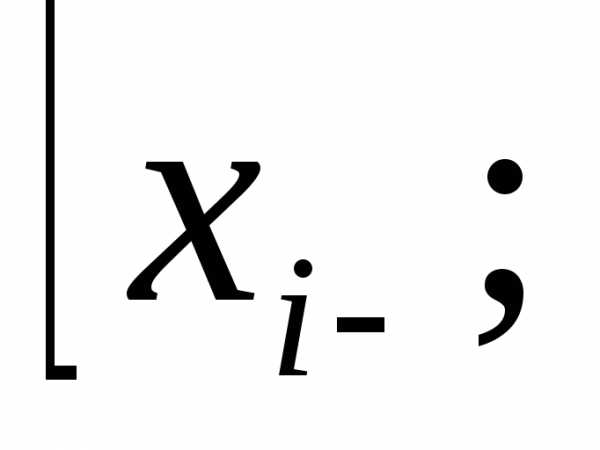
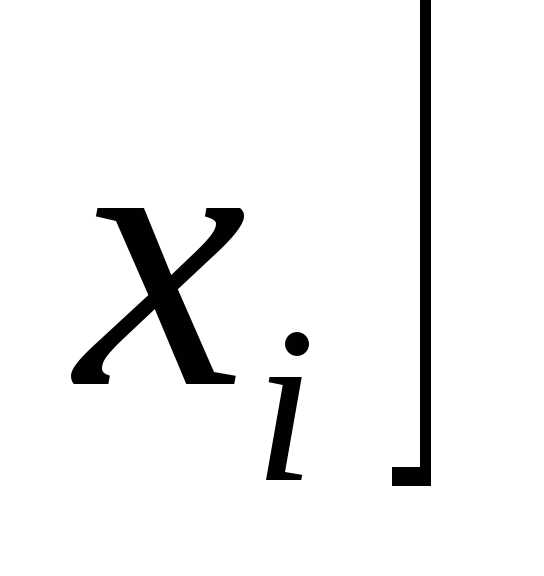 приi=1,2…n.
Вместо площади под графиком, равной
,
будем приближённо находить суммарную
площадь узких полосок, лежащих над
отрезками разбиения
приi=1,2…n.
Вместо площади под графиком, равной
,
будем приближённо находить суммарную
площадь узких полосок, лежащих над
отрезками разбиения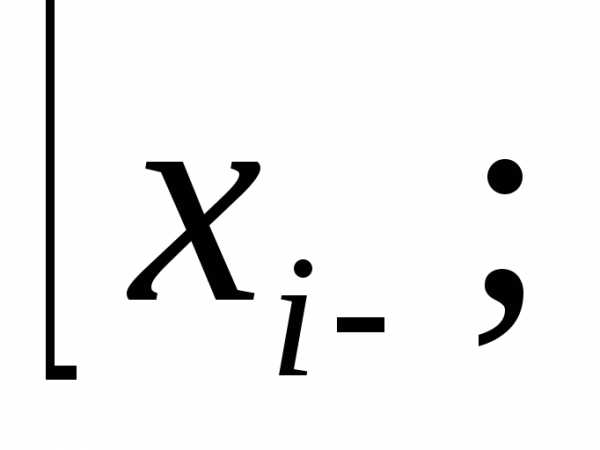
 (см. рис.1).
(см. рис.1).
Рис.1.
Квадратурные формулы левых и правых прямоугольников
Самый простой
метод приближённого вычисления площадей
узких полосок — заменить их площадями
Siпрямоугольников,
основанием которых служит отрезок 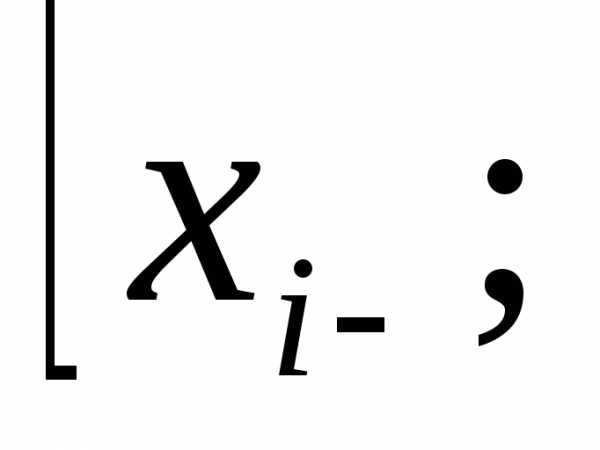
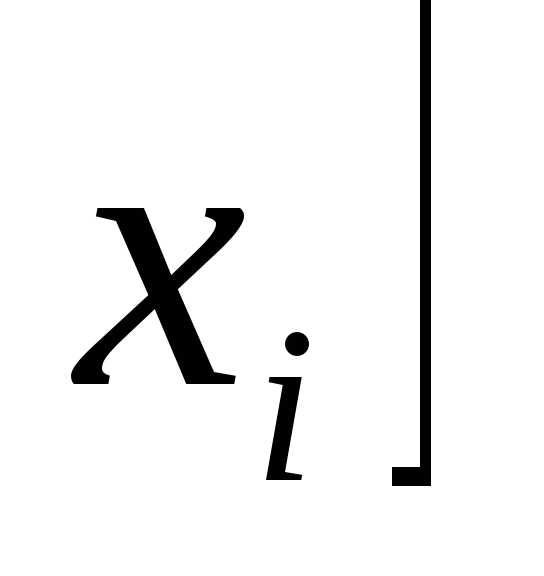 на оси,
а высотой — отрезок, задающий значение
функции в одном из концов основания, то
есть либо в точкеxi-1,
либо в точке xi.
Тогда в первом случае площадь Si
равняется f(xi-1)(
xi—
xi-1),
а во втором
на оси,
а высотой — отрезок, задающий значение
функции в одном из концов основания, то
есть либо в точкеxi-1,
либо в точке xi.
Тогда в первом случае площадь Si
равняется f(xi-1)(
xi—
xi-1),
а во втором
Si= f(xi)( xi— xi-1).
Суммируя по всем отрезкам разбиения, то есть по отдо, получаем в первом случаеквадратурную формулу левых прямоугольников:
а во втором случае квадратурную формулу левых прямоугольников:
Рис.2.
Из приведённого
чертежа ясно, что ошибки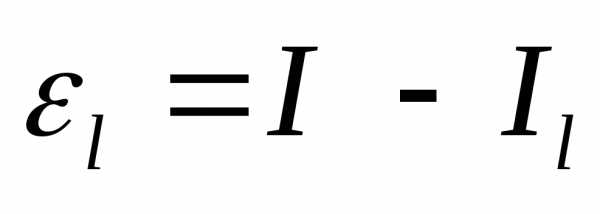 и
и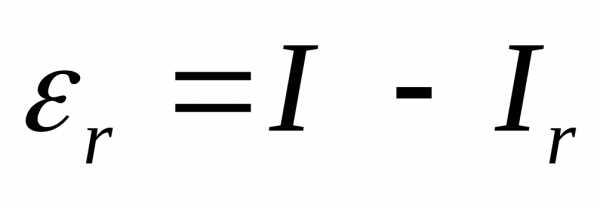 ,
которые возникают при замене точного
значения интегралана
его приближённое значениеIlили Ir соответственно, обладают такими
свойствами:
,
которые возникают при замене точного
значения интегралана
его приближённое значениеIlили Ir соответственно, обладают такими
свойствами:
если
функция f(x)
возрастает на 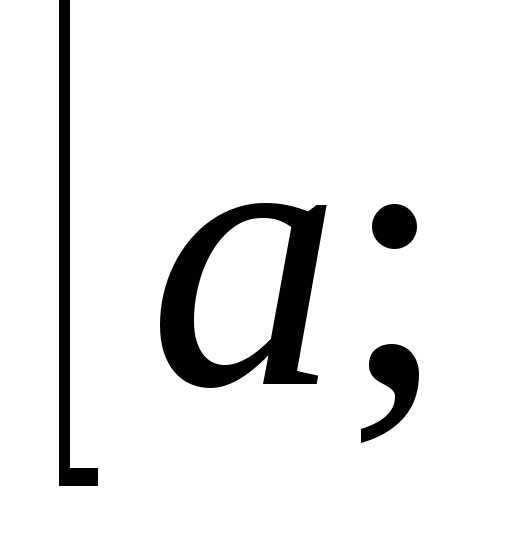 .
.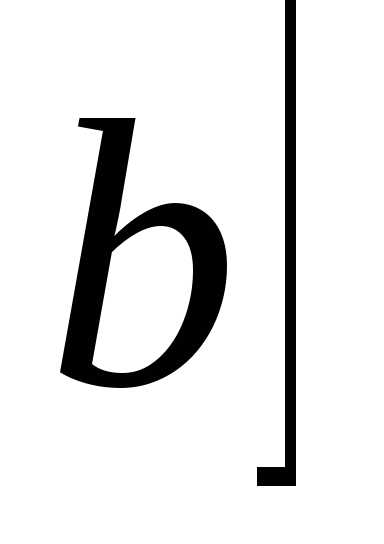 ,
то
,
то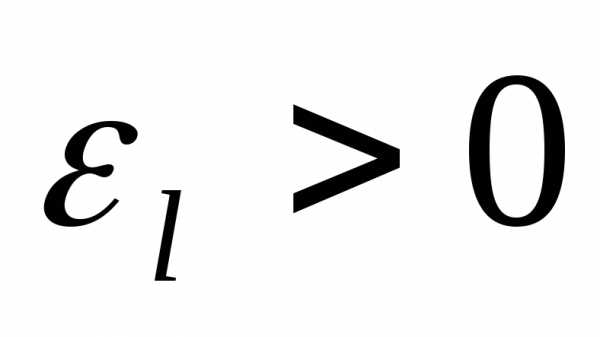 ,
посколькуI>Il;
,
посколькуI>Il;
если
функция f(x)
убывает на 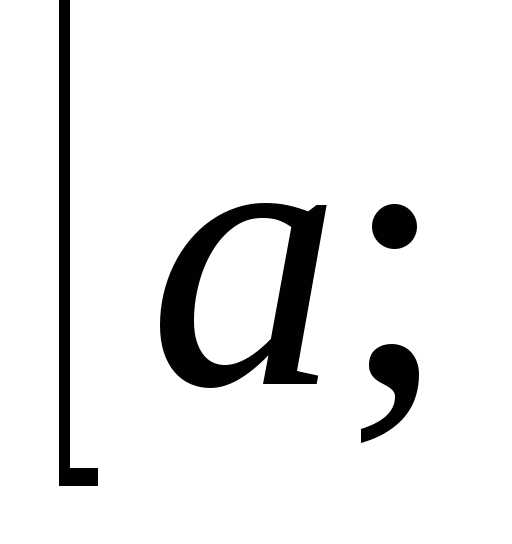 .
.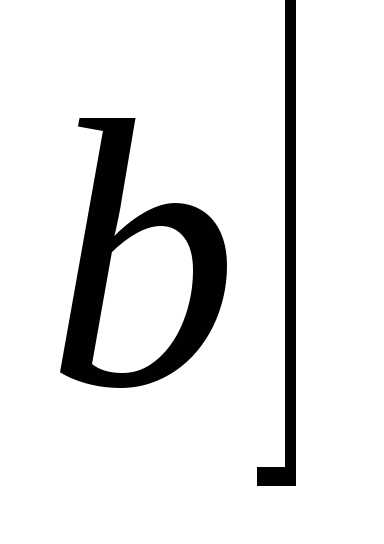 ,
то
,
то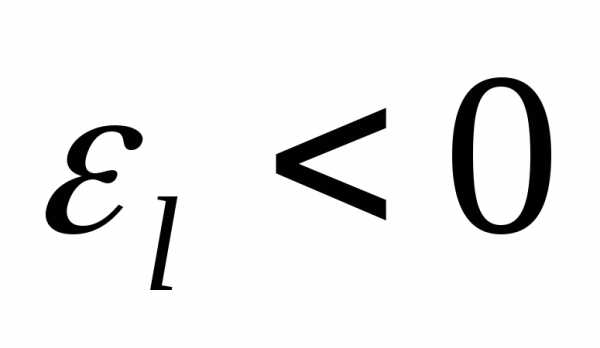 ,
посколькуI<Il;
,
посколькуI<Il;
если
функция f(x)
возрастает на  .
.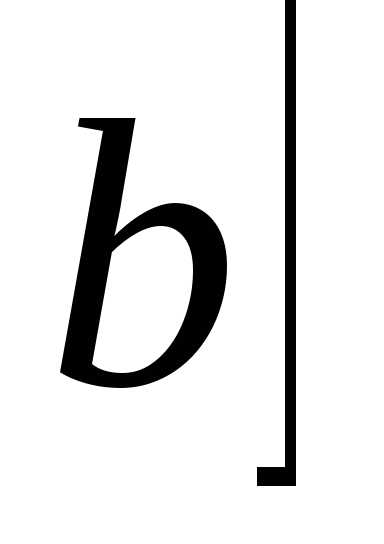 ,
то
,
то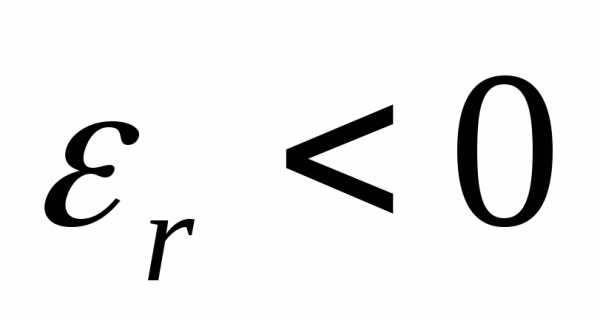 ,
посколькуI<Ir ;
,
посколькуI<Ir ;
если
функция f(x)
убывает на 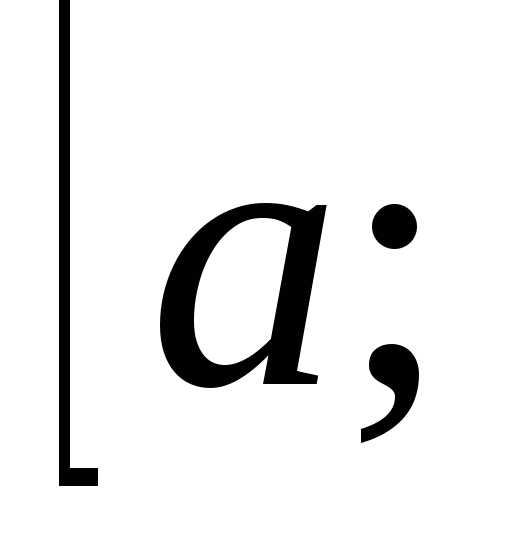 .
.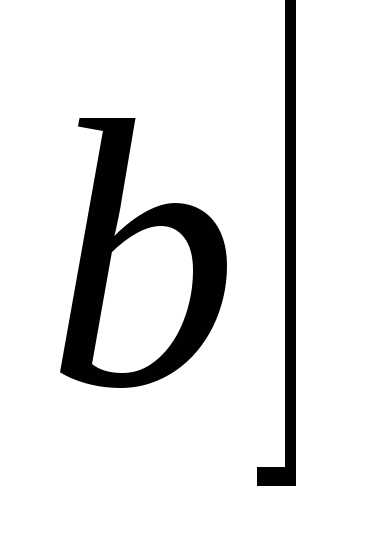 ,
то
,
то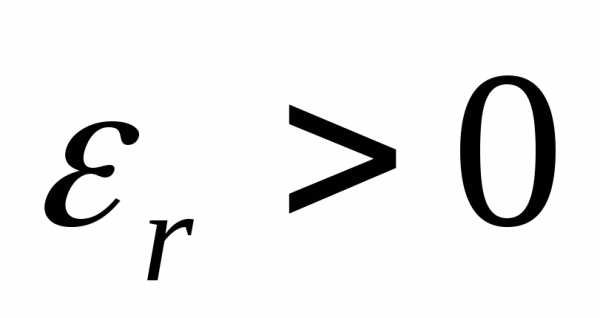 ,
посколькуI>Ir.
,
посколькуI>Ir.
Таким
образом, в случае монотонной функции f
ошибки 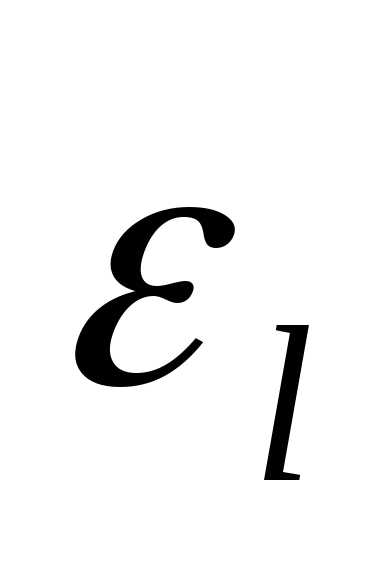 и
и имеют
разные знаки. Возникает желание взаимно
скомпенсировать эти ошибки (хотя бы
частично), взяв полусумму чиселIlи Ir за приближённое значение интеграла.
Получаем при этом такую квадратурную
формулу:
имеют
разные знаки. Возникает желание взаимно
скомпенсировать эти ошибки (хотя бы
частично), взяв полусумму чиселIlи Ir за приближённое значение интеграла.
Получаем при этом такую квадратурную
формулу:
Как мы впоследствии
увидим, полученная квадратурная формула
в точности совпадает с формулой
трапеций.
Она часто применяется на практике для
вычисления интеграла благодаря своей
простоте. Сами же формулы для Ilи Ir , из которых она возникла, на практике
применяются чрезвычайно редко ввиду
своей малой точности: ошибки 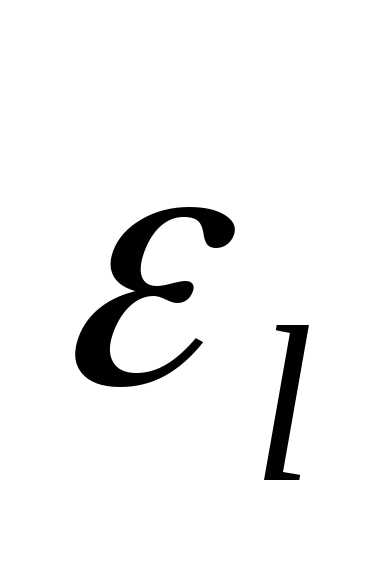 и
и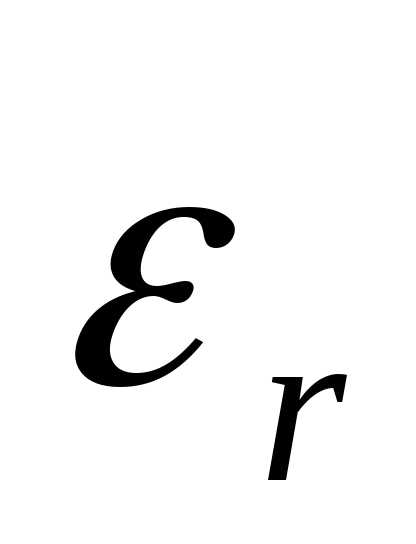 слишком значительны даже при достаточно
мелких разбиениях. Большую точность
обеспечивает следующий метод, применение
которого ничуть не сложнее.
слишком значительны даже при достаточно
мелких разбиениях. Большую точность
обеспечивает следующий метод, применение
которого ничуть не сложнее.
studfiles.net
Приближенное вычисление определенных интегралов
Данный способ называется методом наискорейшего спуска. На каждом шаге необходимо решать задачу одномерной оптимизации, для чего можно использовать описанный выше метод золотого сечения. Несмотря на кажущуюся огромную трудоемкость метода, он обычно сходится намного быстрее описанных выше двух, компенсируя затраты на решение задачи одномерной оптимизации.
Рассмотрим функцию ( , ) = | (1 − )2 + 100( −2)2 и найдем локальный минимум в | ||
окрестности точки (0, 0) с точностью = 10−5. Найдем градиент функции: | |||
grad = ( ∂ , | ∂ ) | = (2(200 3 − 200 + − 1), 200( −2)). | |
| ∂ | ∂ |
|
При использовании постоянного шага = 10−5 метод сходится относительно медленно, но зато к верному решению (1, 1). Если же применить метод наискорейшего спуска, причем ограничить 0 6 6 10 и использовать теперь метод золотого сечения, то метод сходится мгновенно. Заметим однако, что если, например, ограничить 6 104, то метод золотого сечения не пригоден для нахождения минимума, и градиентный спуск не находит искомое решение. Поэтому применять наискорейший спуск следует с большой осторожностью. Точнее говоря, нужно аккуратно искать минимум в одномерном случае.
|
|
Рассмотрим задачу вычисления определенного интеграла ∫ | ( ) . В простейших случаях |
данный интеграл можно вычислить по формуле Ньютона-Лейбница,но на практике, в реальных задачах, чаще всего она не используется. Дело в том, что найти первообразную ( ) зачастую очень сложно, нередко она и вовсе не выражается через элементарные функции. Однако вычислять интегралыкаким-тообразом все же нужно, и тут на помощь приходит геометрический смысл определенного интеграла.
Вспомним, как именно вычисляется определенный интеграл. Мы разбиваем отрезок [ , ] на частей, на каждой из которых берем некоторую точку и прибавляем к общей сумме величину ( )Δ . Устремляя размеры частей к 0, мы получаем искомую сумму. Понятно, что если размер каждой части не стремится к 0, то «площадь» (а это и есть геометрический смысл определенного интеграла) будет посчитана неточно. Чем меньше (а соответственно, чем больше размер каждой части), тем менее точной оказывается посчитанная площадь.
Суть всех описанных здесь методов заключается в том, что теперь размер каждой части не стремится к 0. Мы выбираем достаточно большим (чтобы минимизировать получившуюся ошибку), но в пределах разумного. Разница лишь в том, как именно мы теперь оцениваем величину ( )Δ для каждого . Наиболее подробно мы рассмотрим метод прямоугольников — самый простой из описанных ниже. Но несколько слов скажем и о двух других.
studfiles.net
Способы вычисления определенного интеграла Интегрирование по частям
Пусть  и
и — дифференцируемая функция от
— дифференцируемая функция от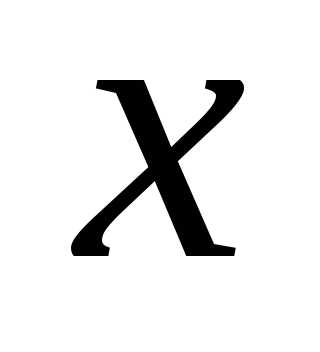 .
Тогда
.
Тогда
(8.21)
Проинтегруем
тождество (8.21) в границах от  до
до ,
получим
,
получим
(8.22)
Поскольку
,
то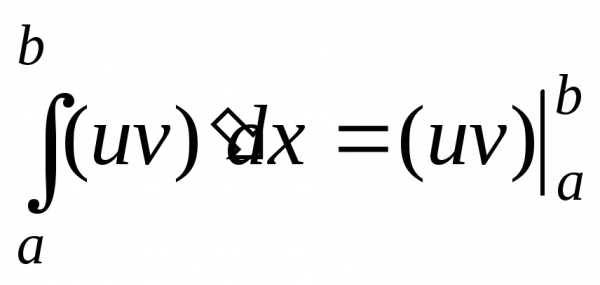 и равенство (8.22) приобретает вид
и равенство (8.22) приобретает вид
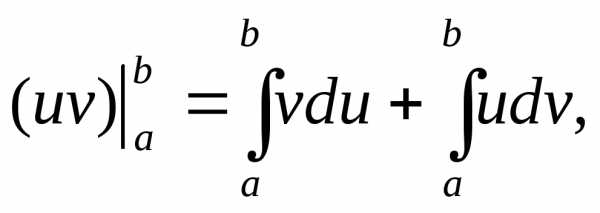
или
окончательно 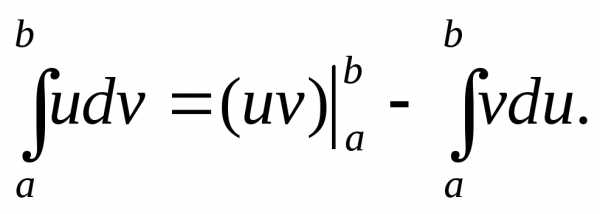 (8.23)
(8.23)
Формула (8.23) и выражает способ интегрирования по частям определенного интеграла. Видно, что она подобна формуле (7.12) интегрирования по частям неопределенного интеграла.
Пример.1. Вычислить 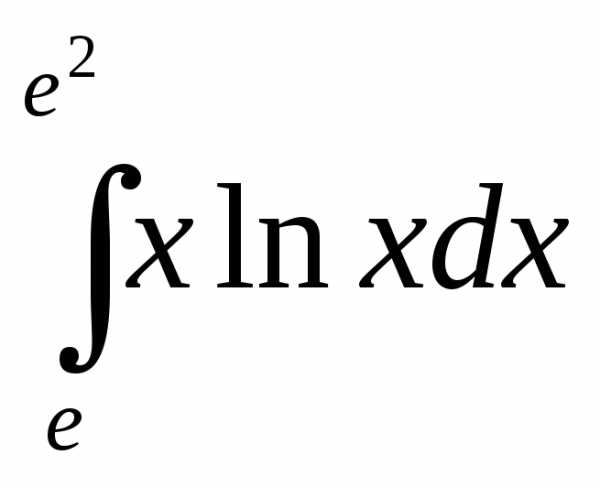 .
.
Решение
Пример 2. Вычислить  .
.
Решение.
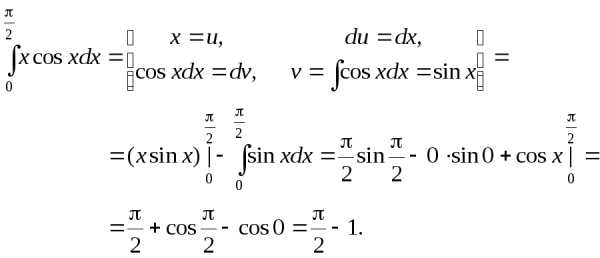
Интегрирование подстановкой
Пусть
надо вычислить определенный интеграл 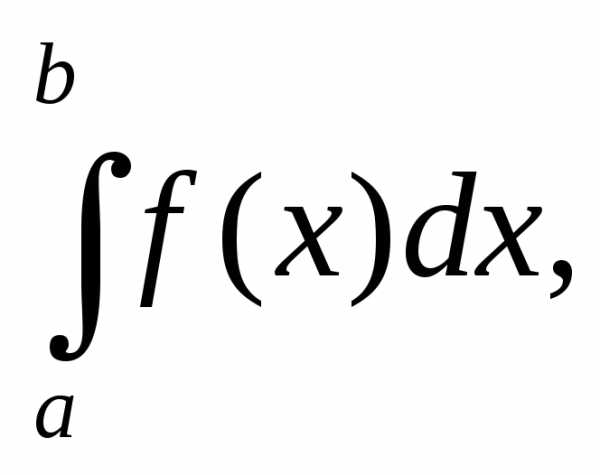
где 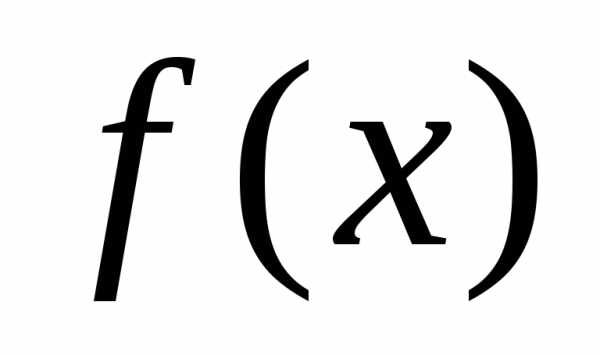 — непрерывная на
— непрерывная на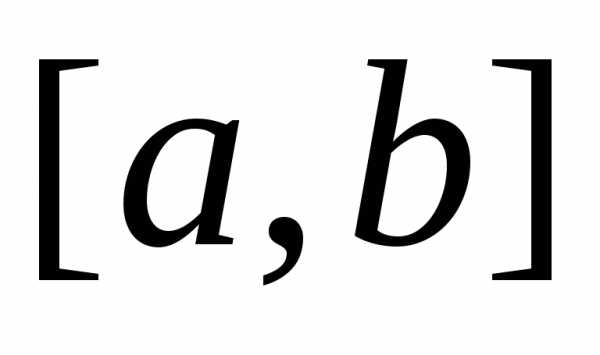 функция, а первообразной для нее нет в
таблице простейших интегралов. Тогда
произведем замену переменной, а именно,
введем новую переменную
функция, а первообразной для нее нет в
таблице простейших интегралов. Тогда
произведем замену переменной, а именно,
введем новую переменную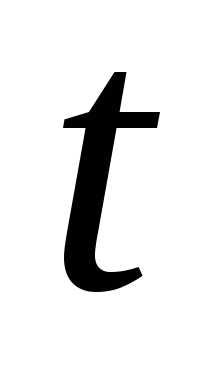 таким образом:,
где
таким образом:,
где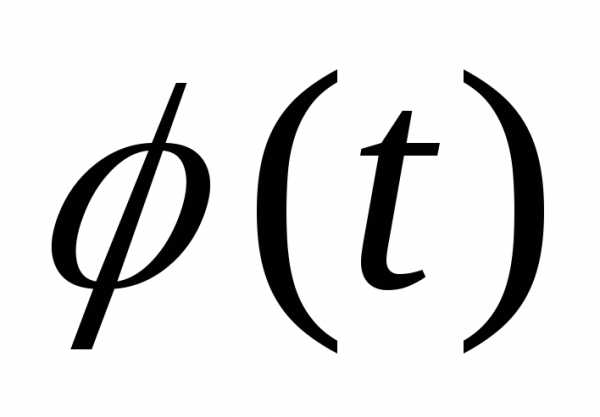 — непрерывно дифференцируема на
— непрерывно дифференцируема на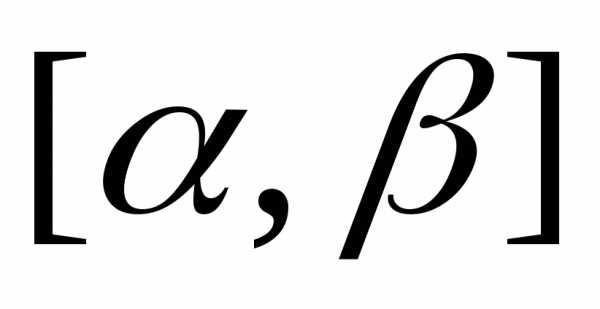 функция.
функция.
Если при этом будут выполняться такие условия:
при изменении
 от
от до
до переменная
переменная изменяется от
изменяется от до
до ,
то есть
,
то есть
. (8.24)
сложная функция
 определена и непрерывна на отрезке
определена и непрерывна на отрезке ,
то справедлива такая формула
,
то справедлива такая формула
(8.25)
Формула (8.25) и выражает собою суть метода подстановки.
Замечание. При вычислении определенного интеграла с помощью замены переменной нет необходимости возвращаться к старой переменной (как это нужно было делать при вычислении неопределенного интеграла) достаточно лишь учесть границы интегрирования соответственно (8.24).
Пример 8.3. Вычислить 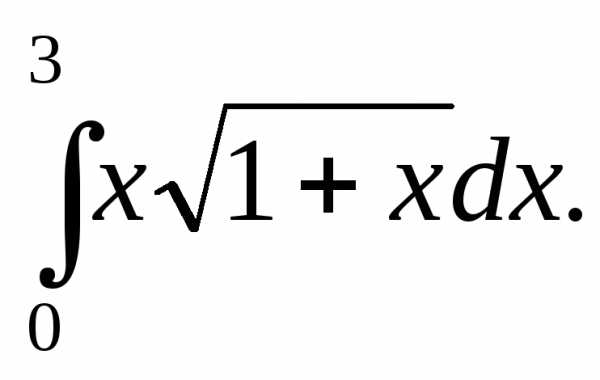
Решение
Введем
новую переменную 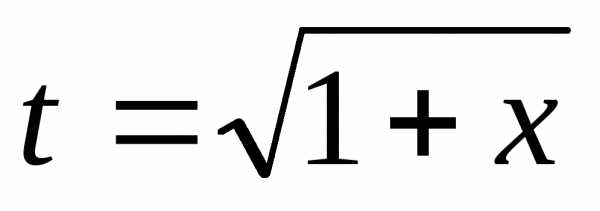 .
Тогда
.
Тогда
. Вычислим границы интегрирования и результат представим в виде табл. 1. Таблица 1
из
которой видно, что при
,
а при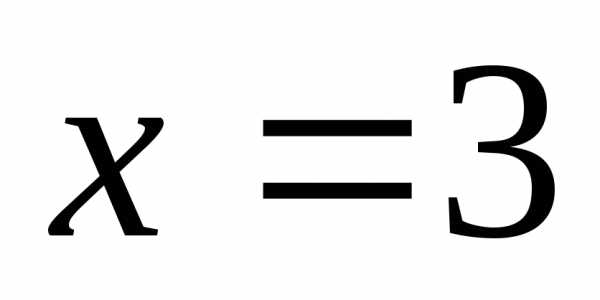 .
Итак, после введении новой переменной
получим
.
Итак, после введении новой переменной
получим
Пример 4.Вычислить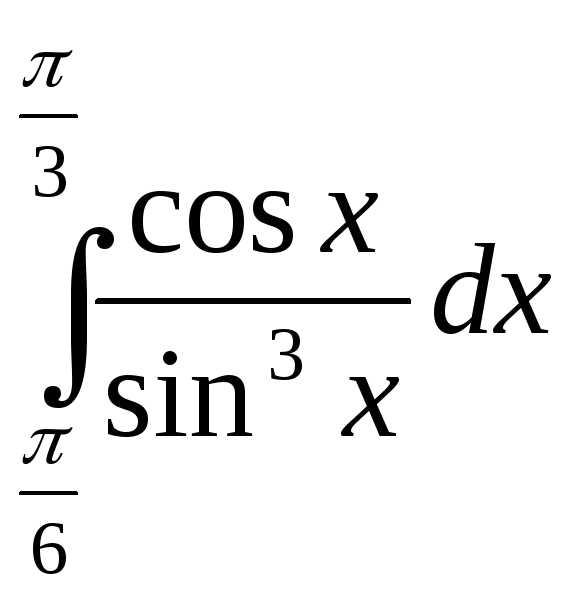 .
.
Решение.
Произведем замену переменной: . Тогда, а границы интегрирования приобретают значения: при
при
Итак, получаем
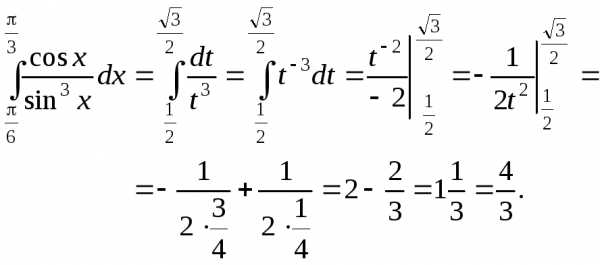
Таким образом, видим, что различие в применении метода замены переменной в неопределенном и определенном интеграле состоит в том, что в втором случае не надо возвращаться к старой переменной, поскольку при замене переменной изменяются также и границы интегрирования.
Приближенное вычисление определенного интеграла
Пусть
надо вычислить 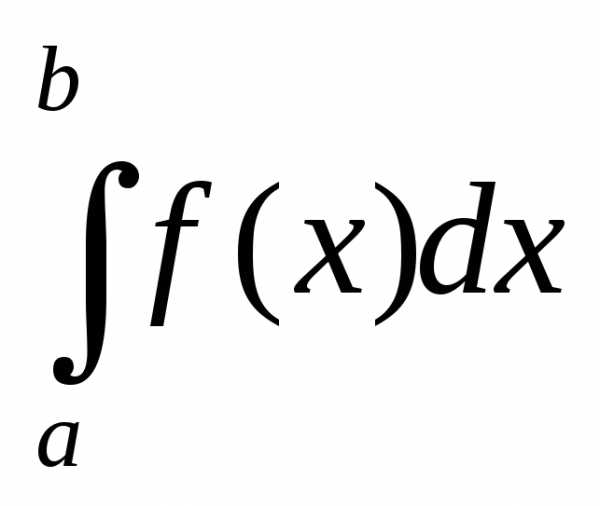 ,
но первообразная для функции
,
но первообразная для функции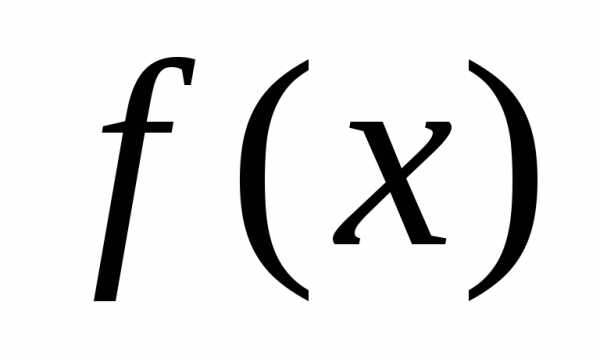 не выражается через элементарные
функции. Тогда применить формулу
Ньютона-Лейбница невозможно. В таких
случаях применяются методы приближенного
вычисления определенных интегралов.
Рассмотрим их, используя определение
интеграла как границы интегральной
суммы. Разделим отрезок
не выражается через элементарные
функции. Тогда применить формулу
Ньютона-Лейбница невозможно. В таких
случаях применяются методы приближенного
вычисления определенных интегралов.
Рассмотрим их, используя определение
интеграла как границы интегральной
суммы. Разделим отрезок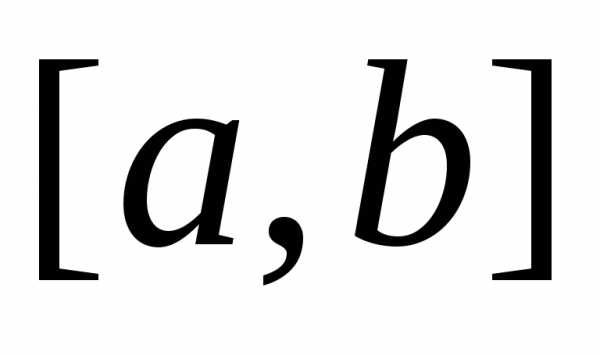 точкамина
точкамина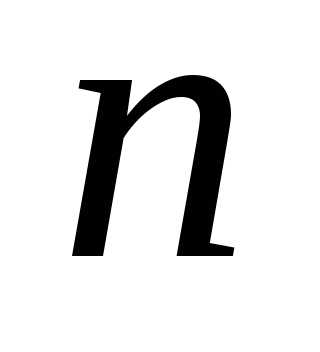 частичных отрезков равной длины.
Обозначим длину каждый из них через
частичных отрезков равной длины.
Обозначим длину каждый из них через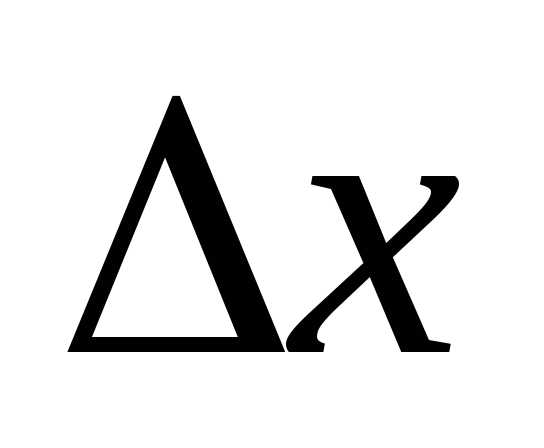 .
Тогда
.
Тогда
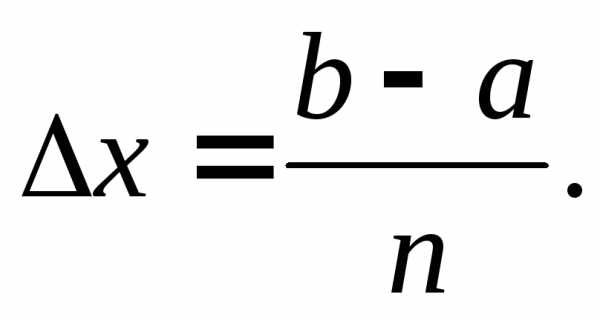
Обозначим
через
значения функции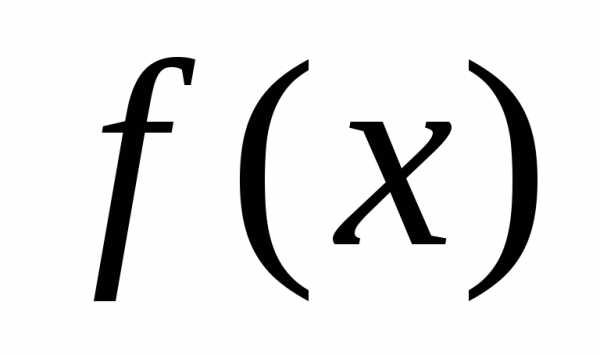 в точках,
то есть
в точках,
то есть
.
Составим суммы:
,
.
Каждая
из этих сумм представляет собой
интегральную сумму для 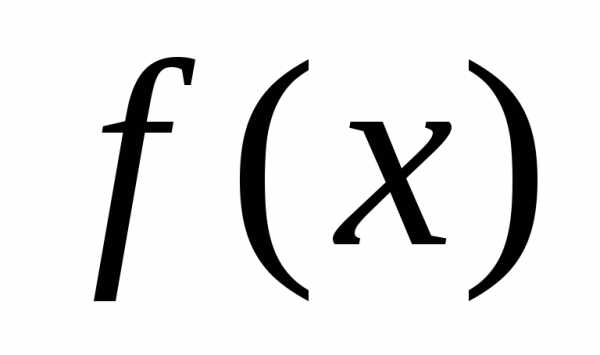 на отрезке
на отрезке и поэтому приближенно выражает интеграл
и поэтому приближенно выражает интеграл
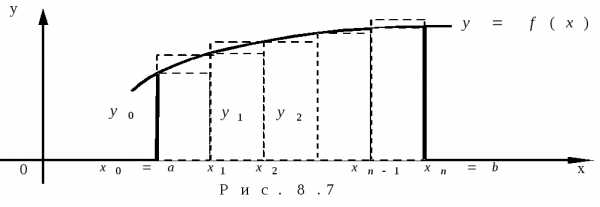 , (8.26)
, (8.26)
. (8.27)
Из
рис. 8.7 видно, что формула (8.26) выражает
площадь ступенчатой фигуры, составленной
из прямоугольников, вписанных в
криволинейную трапецию, а формула (8.27)
выражает площадь ступенчатой фигуры,
составленной из прямоугольников,
описанных вокруг криволинейной трапеции.
Поэтому формулы (8.26; 8.27) называются
формулами прямоугольников. Погрешность
при вычислении интегралов за формулами
прямоугольников будет тем меньше, чем
больше число n. Она выражается формулой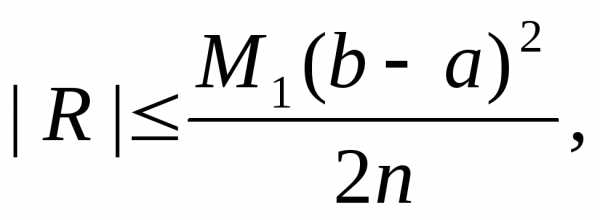
где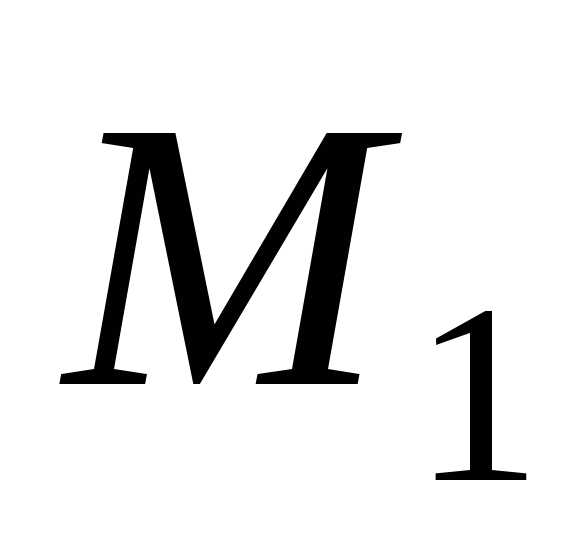 -максимальное значение
абсолютной величиныпроизводной
-максимальное значение
абсолютной величиныпроизводной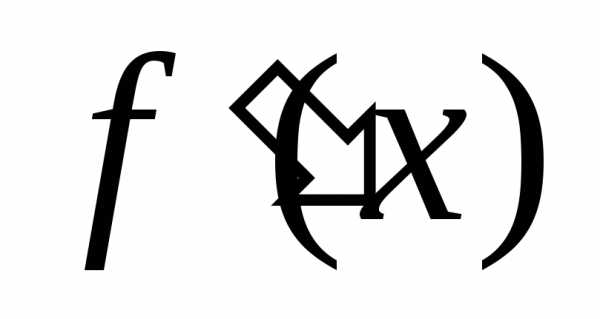 на
на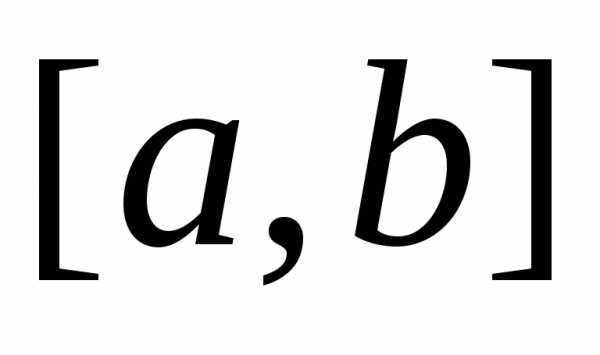 .
.
Более точное значение определенного интеграла получим, если данную кривую заменим не ступенчатой линией, как это делается в формуле прямоугольников, а вписанной ломаной (рис. 8.8).
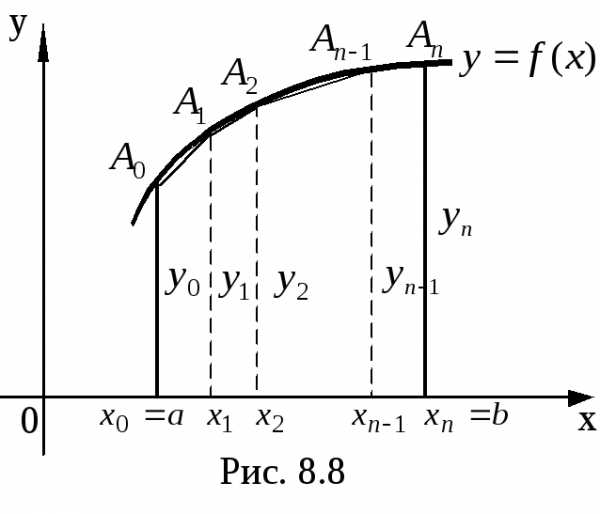 Тогда
площадь криволинейной трапеции
Тогда
площадь криволинейной трапеции  заменится суммой площадей прямолинейных
трапеций, ограниченных сверху хордами
заменится суммой площадей прямолинейных
трапеций, ограниченных сверху хордами
Поскольку площадь первой из
этих трапеций равна 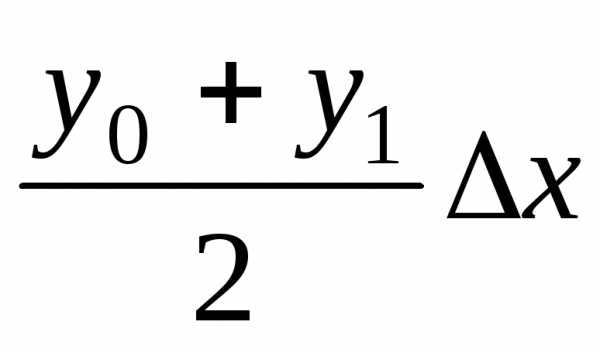 ,
площадь второй равняется
,
площадь второй равняется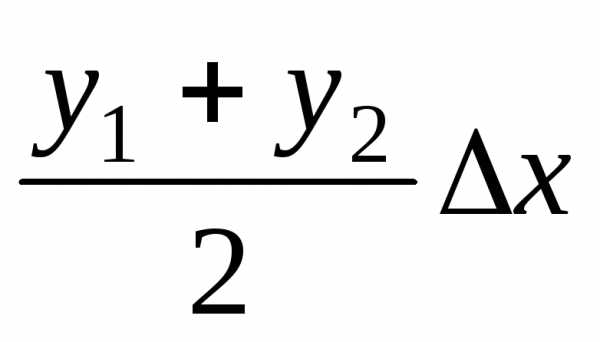 ,
то
,
то
или
. (8.28)
Легко
видеть, что она дает среднее арифметическое
из формул (8.26 и 8.27). Формула (8.28) называется
формулой трапеций. В этом случае
погрешность вычисляется по формуле 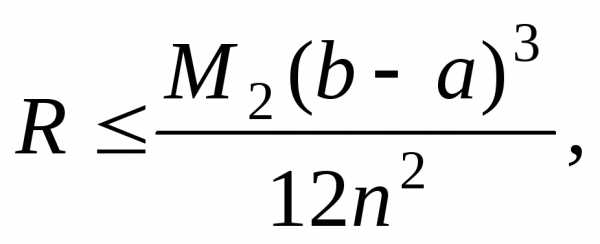
где 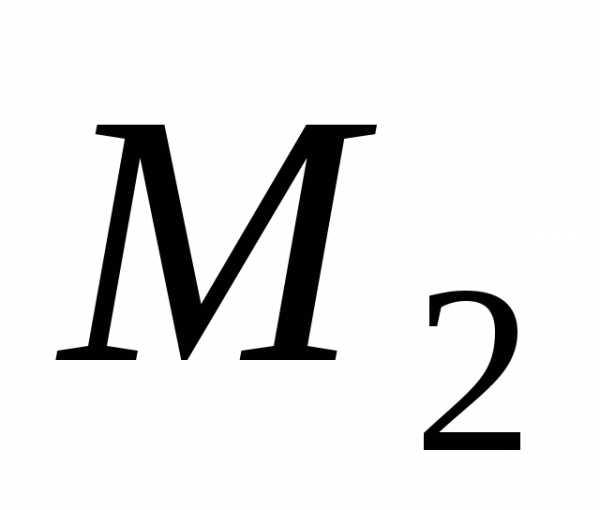 — минимальное значение абсолютной
величины второй производной
— минимальное значение абсолютной
величины второй производной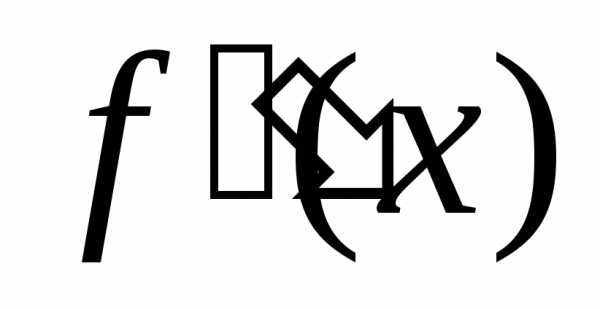 на
на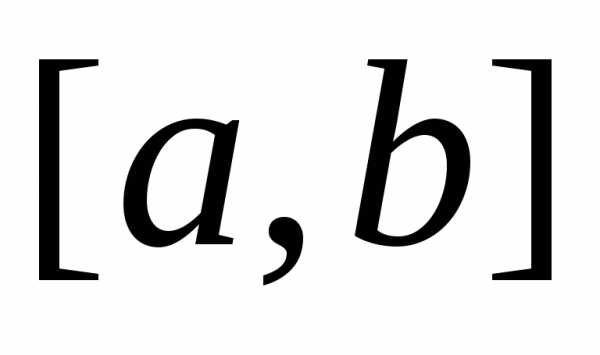 .
.
Более точные результаты можно получить по формуле Симпсона (или формуле парабол), которая имеет вид:
(8.29)
При
этому надо обратить внимание на то, что
число  частичных отрезков, на которые разбивается
отрезок
частичных отрезков, на которые разбивается
отрезок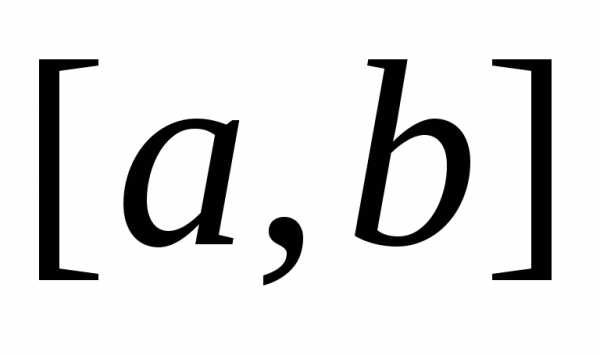 ,
должно быть обязательно четным, то есть
,
должно быть обязательно четным, то есть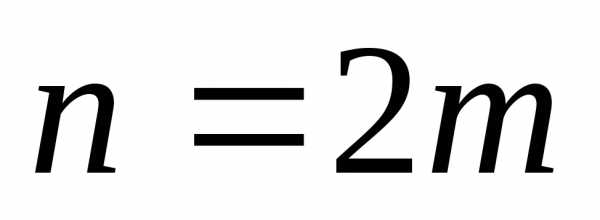 .
Тогда каждые две соседних криволинейных
трапеции, на которые разбилась вся
криволинейная трапеция
.
Тогда каждые две соседних криволинейных
трапеции, на которые разбилась вся
криволинейная трапеция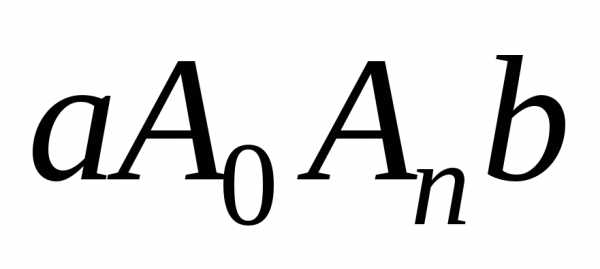 (рис. 8.8), заменяютсяпараболической
трапецией, площадь
которой исчисляется по формуле
,
(рис. 8.8), заменяютсяпараболической
трапецией, площадь
которой исчисляется по формуле
,
гдеи —
крайние ординаты,
—
крайние ординаты,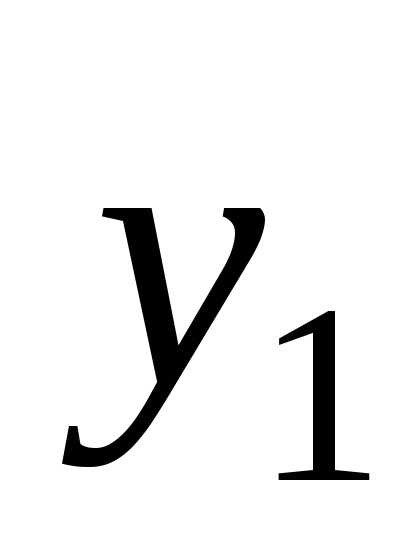 —
ордината кривой в середине отрезка, а
—
ордината кривой в середине отрезка, а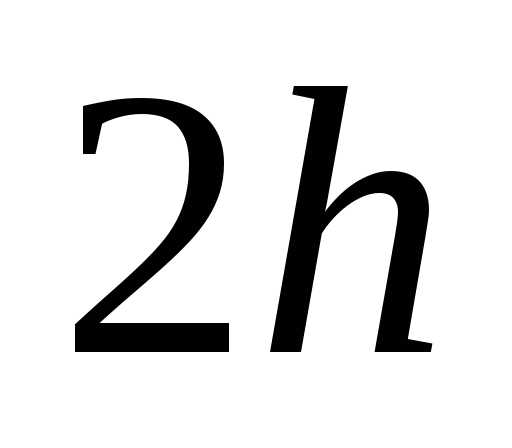 — расстояние между ординатами
— расстояние между ординатами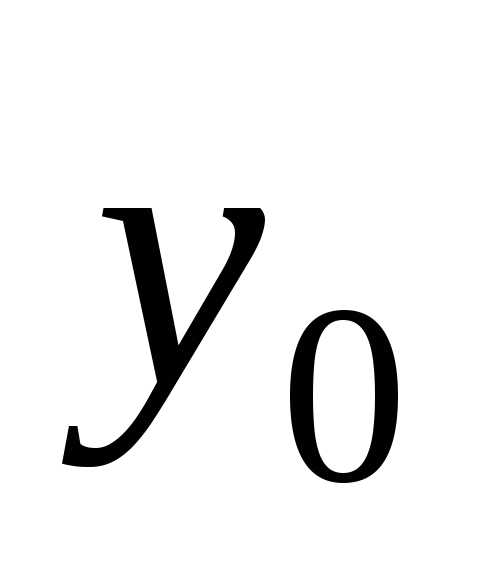 и
и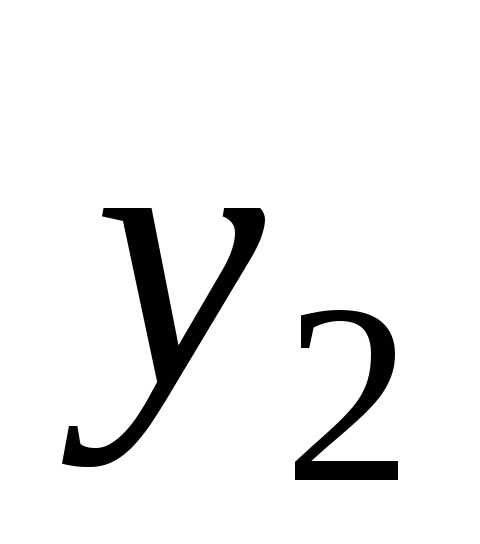 (рис. 8.9).
(рис. 8.9).
Погрешность при этом может быть вычислена по формуле
где 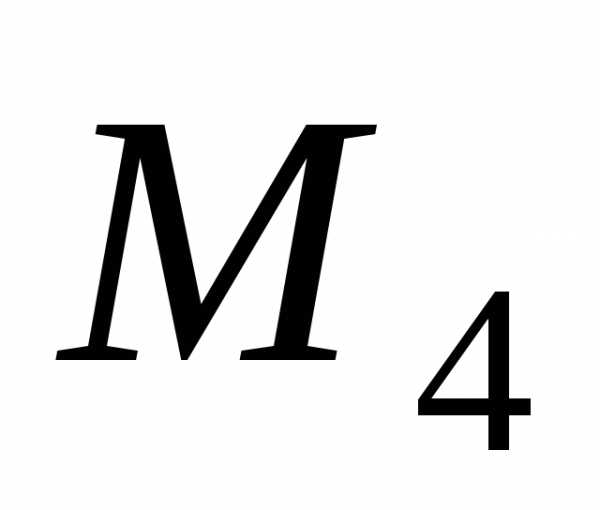 — максимальное значение абсолютной
величины производной
— максимальное значение абсолютной
величины производной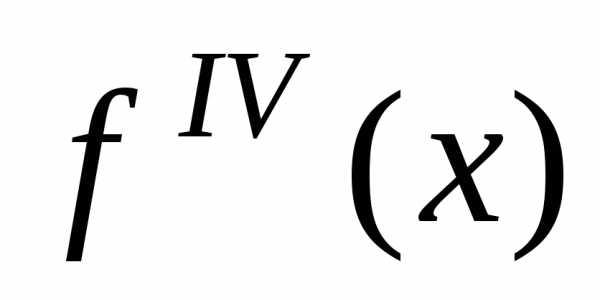 на отрезке
на отрезке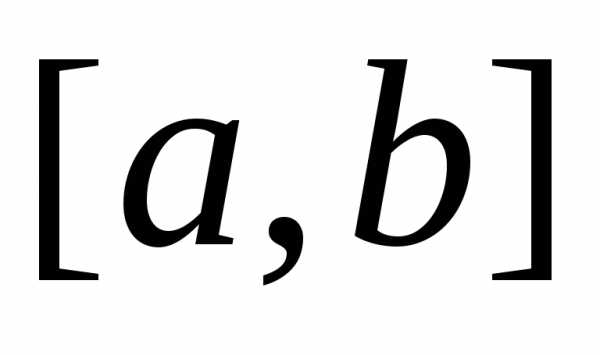 .
.
Пример.5. Вычислить приближенно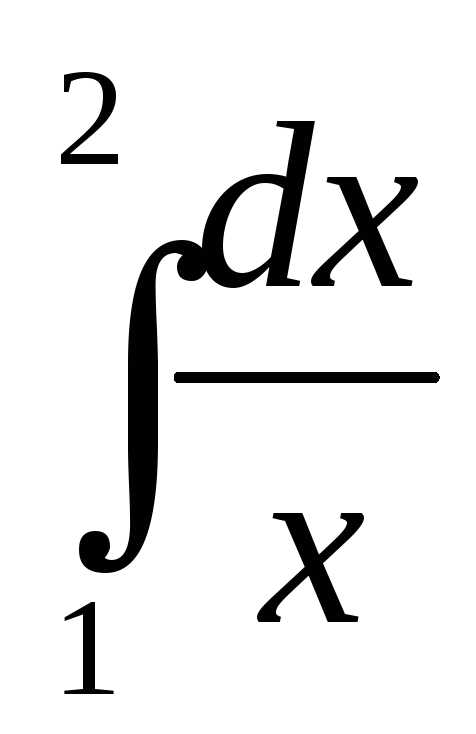 .
.
Точное
значение его  .
З точностью до седьмого знака.
Вычислим теперь его значение, пользуясь
формулами (8.26-8.29). Для этого разделим
отрезок
.
З точностью до седьмого знака.
Вычислим теперь его значение, пользуясь
формулами (8.26-8.29). Для этого разделим
отрезок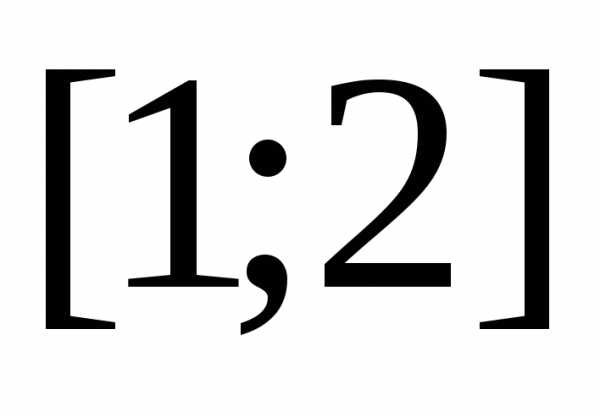 на 10 равных отрезков. Тогда длина каждого
из них будет
на 10 равных отрезков. Тогда длина каждого
из них будет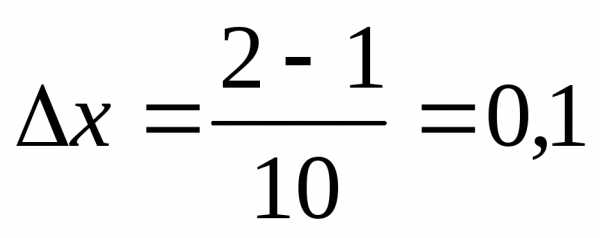 .
.
Составим табл. 2 значений подынтегральной функции в точках разбиения .
Таблица 2
Тогда по формуле (8.26) получим.
По формуле (8.27) .
По формуле (8.28) .
По формуле Симпсона (8.29)
Таким
образом, по формуле Симпсона при 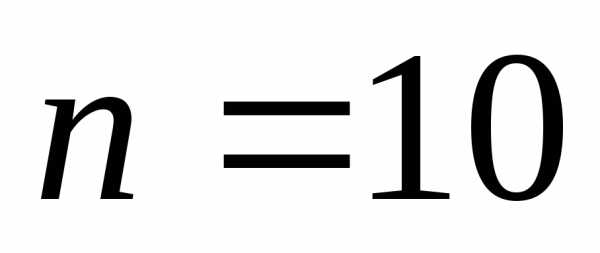 получили 5 верных знаков, по формуле
трапеций — лишь три верных знака, за
формулами прямоугольников мы можем
быть уверены только в одном знаке.
получили 5 верных знаков, по формуле
трапеций — лишь три верных знака, за
формулами прямоугольников мы можем
быть уверены только в одном знаке.
studfiles.net
Тема 7. Теория
Тема 7. Определенные и несобственные интегралы Определенный интеграл
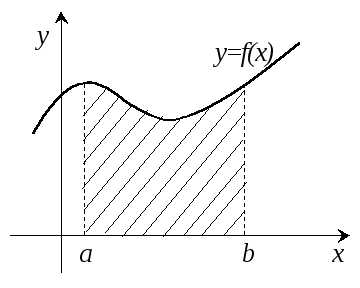
Задача, приводящая к понятию определенного интеграла – задача о вычислении площади криволинейной трапеции.
Пусть
на отрезке 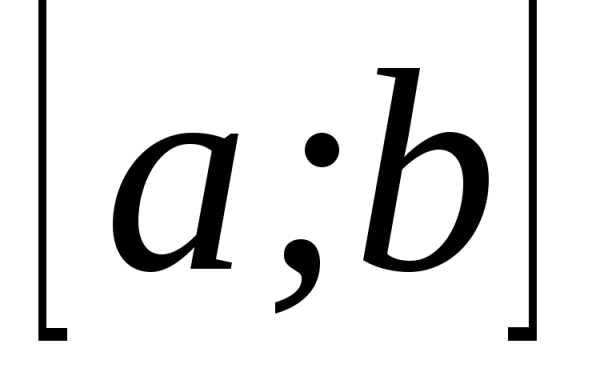 задана непрерывная функция
задана непрерывная функция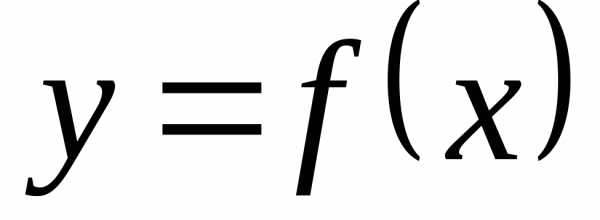 ,
для определенности
,
для определенности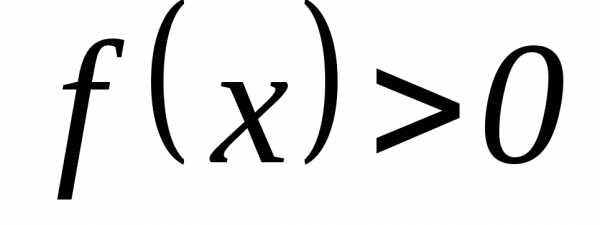 .
Найдем площадь, ограниченную осьюОХ,
прямыми
и линией
.
Найдем площадь, ограниченную осьюОХ,
прямыми
и линией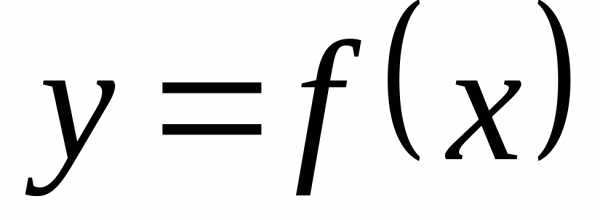 .
Можно также говорить о площадипод кривой
.
Можно также говорить о площадипод кривой  или о площади криволинейной трапеции.
или о площади криволинейной трапеции.
Для
этого разобьем трапецию произвольным
образом на частичные трапеции линиями, параллельными ОУ:
,
а затем заменим каждую прямоугольником
со сторонойи высотой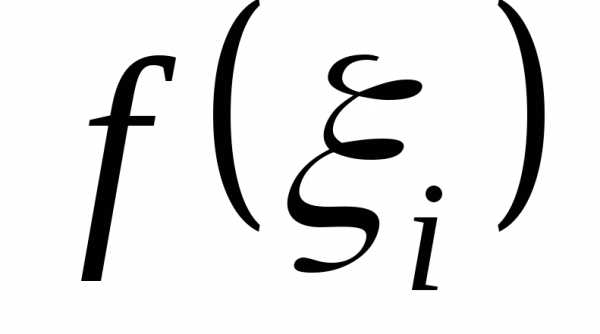 ,
где-произвольно
выбранная на
частичном отрезке точка.
,
где-произвольно
выбранная на
частичном отрезке точка.
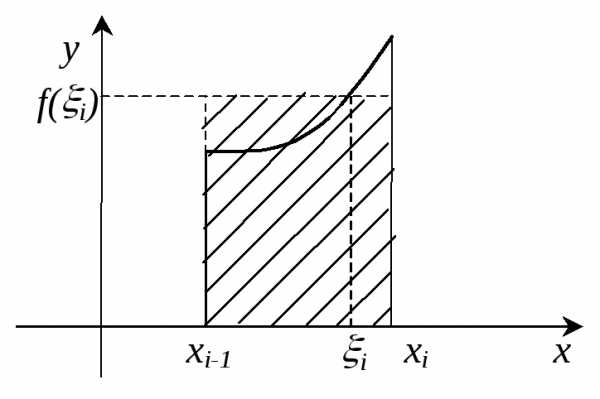
Составим
сумму площадей всех прямоугольников,
она будет приближенно равна площади
всей криволинейной трапеции: 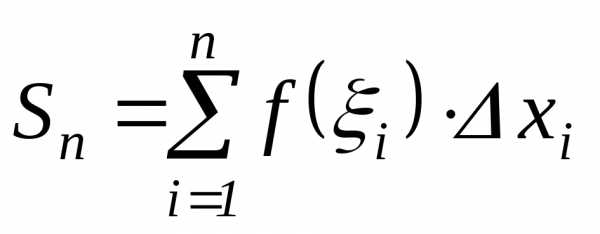 .
Такая сумма называетсяинтегральной.
Очевидно,
.
Такая сумма называетсяинтегральной.
Очевидно, 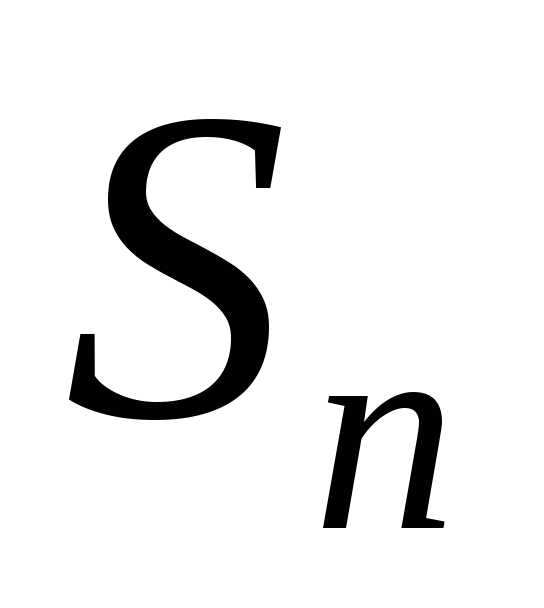 будет тем более точно определять площадь
криволинейной трапеции, чем на большее
число частичных трапеций будет разбита
исходная криволинейная трапеция. А при
будет тем более точно определять площадь
криволинейной трапеции, чем на большее
число частичных трапеций будет разбита
исходная криволинейная трапеция. А при или, что то же самое,эти площади совпадут.
или, что то же самое,эти площади совпадут.
Если
существует конечный предел интегральной
суммы 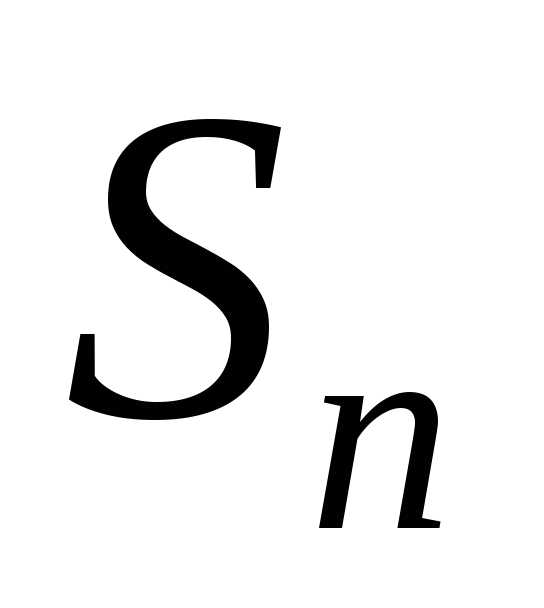 ,
при,
который не зависит от способа разбиения
области на частичные отрезки и выбора
точек
,
при,
который не зависит от способа разбиения
области на частичные отрезки и выбора
точек ,
то он называетсяопределенным
интегралом функции
,
то он называетсяопределенным
интегралом функции 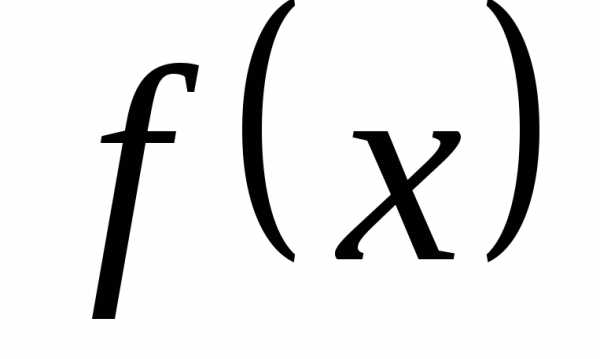 на отрезке
на отрезке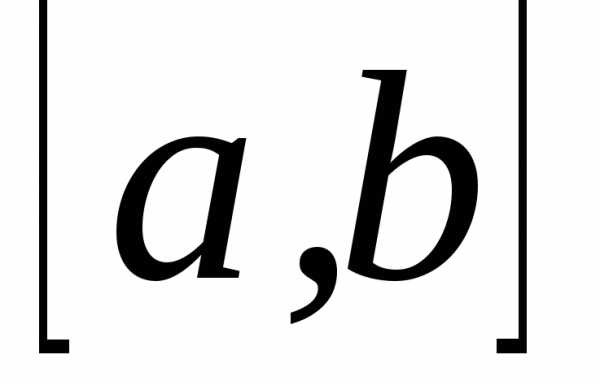 и обозначается
и обозначается
.
Здесь  – нижний ,
– нижний ,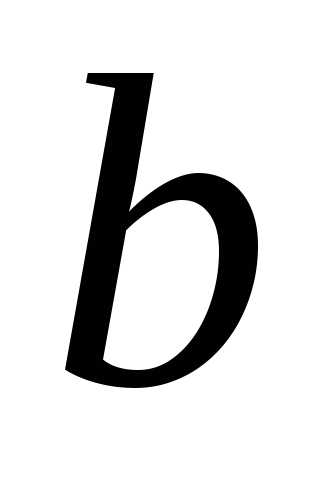 – верхний пределы интегрирования.
– верхний пределы интегрирования.
— Несмотря на
сходство в обозначениях и терминологии,
определенный и неопределенный интегралы
существенно различные понятия: если
— представляет семейство функций, то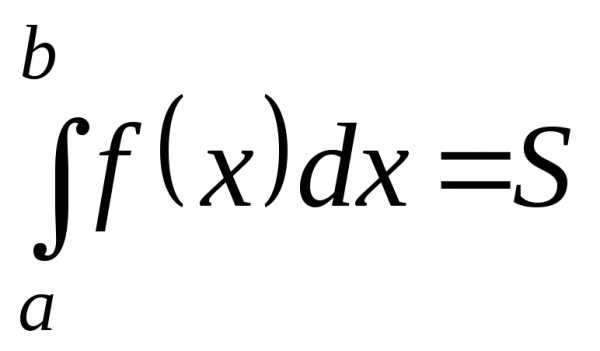 —
—
— определенное число.
— Заметим, что не имеет значения, какой буквой обозначена переменная интегрирования, т.к. смена обозначений не влияет на интегральную сумму.
Свойства определенного интеграла.
1 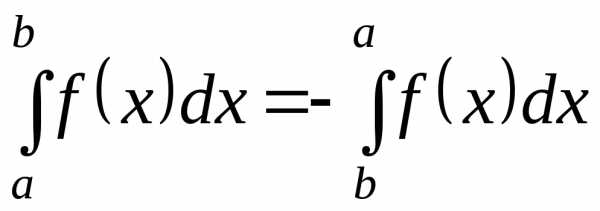 — если
поменять местами верхний и нижний
пределы интегрирования, определенный
интеграл поменяет знак.
— если
поменять местами верхний и нижний
пределы интегрирования, определенный
интеграл поменяет знак.
2 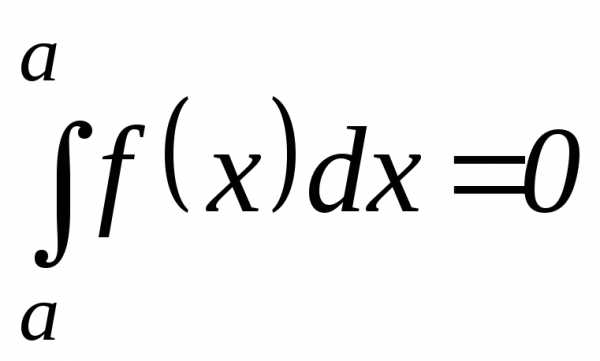 — интеграл с одинаковыми пределами
интегрирования равен нулю по определению.
— интеграл с одинаковыми пределами
интегрирования равен нулю по определению.
3 ;
.
Аналогичные свойства есть и у неопределенного интеграла. Они показывают, что интегрирование – линейная операция и может быть распространена на любое конечное число слагаемых: .
4
Свойство аддитивности.
Если  — функция, интегрируемая на
— функция, интегрируемая на
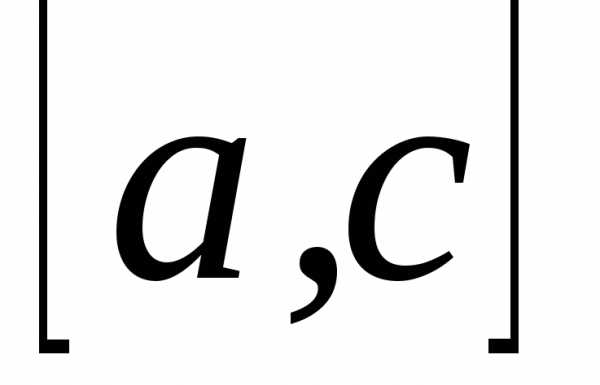 и
и 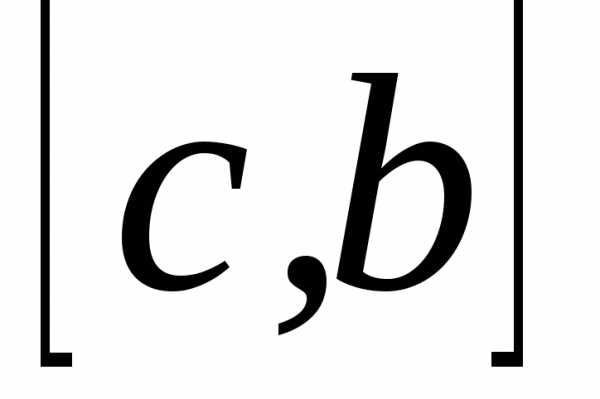 ,
где
,
где ,
то она интегрируема на
,
то она интегрируема на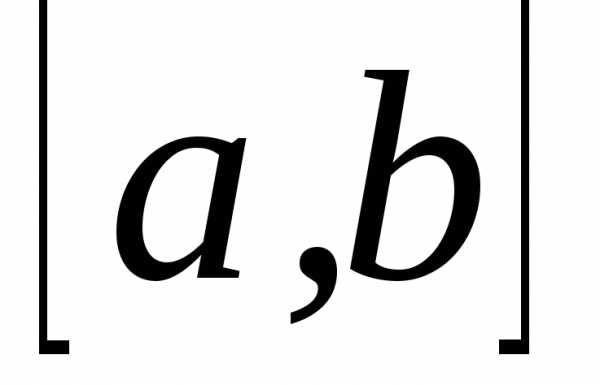 и
и
Иными словами, отрезок интегрирования можно разделить на части какой-либо точкой и интеграл по всему отрезку заменить суммой интегралов по двум полученным отрезкам.
5 Свойство алгебраической площади. Определенный интеграл есть число того же знака, что и подынтегральная функция. То есть при вычислении площадей с помощью определенного интеграла можно получить отрицательную площадь.
Теорема— о среднем значении функции на отрезке.
Если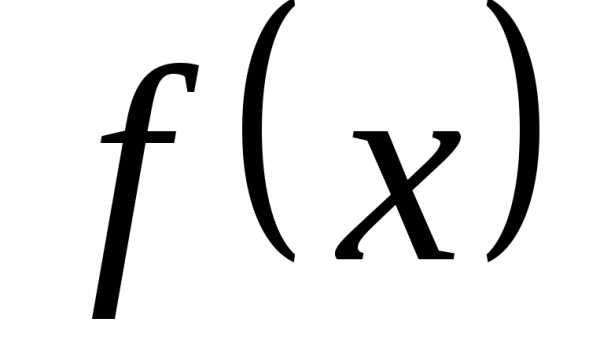 непрерывна на отрезке (),
то на этом отрезке существует хотя бы
одна точка (),
такая, что функция принимает в ней свое
непрерывна на отрезке (),
то на этом отрезке существует хотя бы
одна точка (),
такая, что функция принимает в ней свое
среднее значение: .
.
Г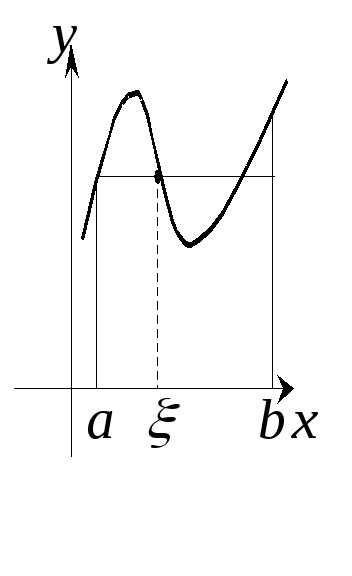 еометрический
смысл теоремы: пусть
еометрический
смысл теоремы: пусть ,
тогда существует по крайней мере одна
точка
,
тогда существует по крайней мере одна
точка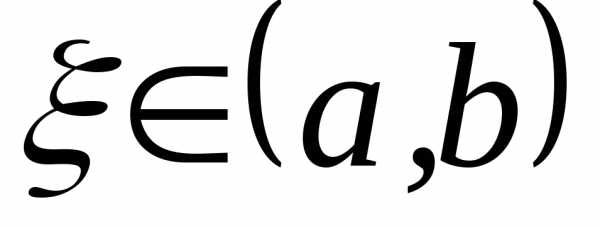 ,
такая, что площадь криволинейной
трапеции, ограниченной сверху непрерывной
кривойбудет равна площади прямоугольника с
тем же основанием и высотой, равной
,
такая, что площадь криволинейной
трапеции, ограниченной сверху непрерывной
кривойбудет равна площади прямоугольника с
тем же основанием и высотой, равной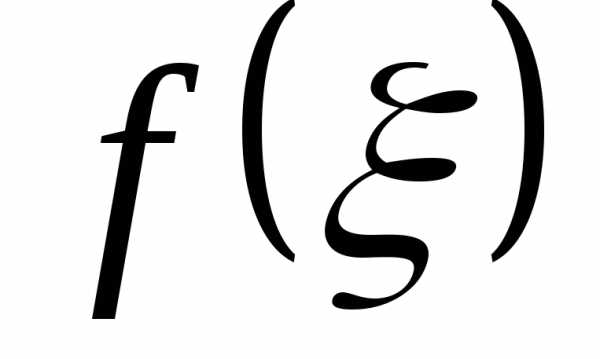 :
: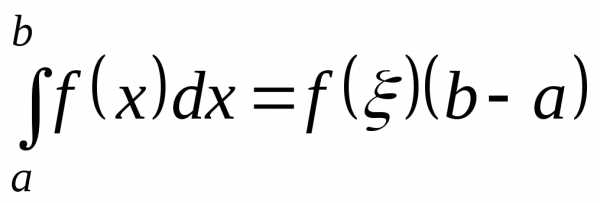 .
.
Вычисление определенных интегралов. Формула Ньютона-Лейбница
Если для подынтегральной функции можно найти первообразную, то определенный интеграл можно вычислить по формуле Ньютона-Лейбница.
—Формула Ньютона-Лейбница позволяет вычислить определенный интеграл как разность первообразных на верхнем и нижнем пределах интегрирования, не вычисляя предела интегральной суммы.
Можно выделить два этапа вычисления определенного интеграла.
Одним из методов интегрирования (см. тему 6) находят первообразную.
Вычисляют разность значений первообразной функции на верхнем и нижнем пределах интегрирования.
— Сначала в первообразную подставляют верхний предел.
studfiles.net
Тема_19_ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
153
ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
I. Теорема о производной интеграла по верхнему пределу.
Пусть
в определенном интеграле 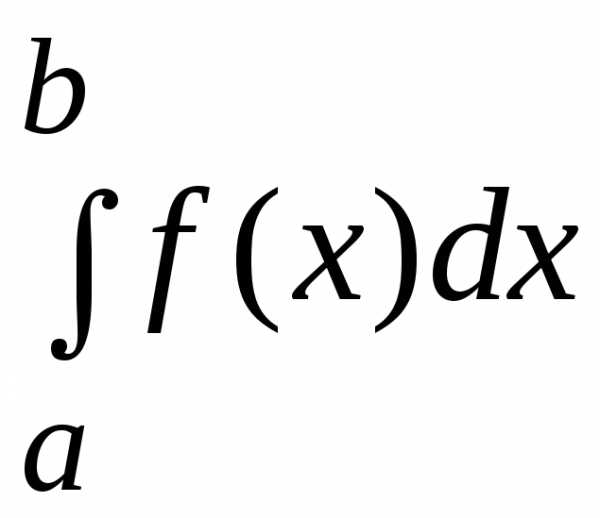 нижний пределa закреплен, а верхний предел меняется.
Тогда будет меняться значение определенного
интеграла, т.е. интеграл
нижний пределa закреплен, а верхний предел меняется.
Тогда будет меняться значение определенного
интеграла, т.е. интеграл 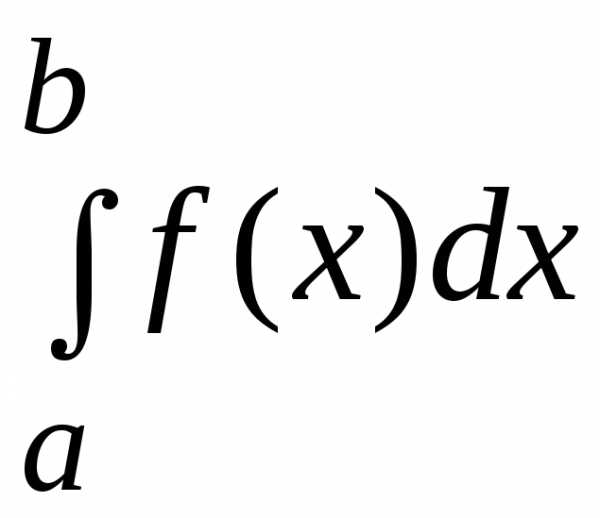 можно рассматривать как функцию верхнего
предела.
можно рассматривать как функцию верхнего
предела.
Обозначим верхний предел через x , а переменную интегрирования через t , тогда функция
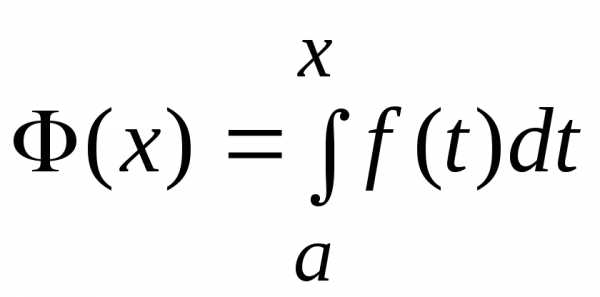 (1)
(1)
численно
равна площади криволинейной трапеции  ,
изображенн
,
изображенн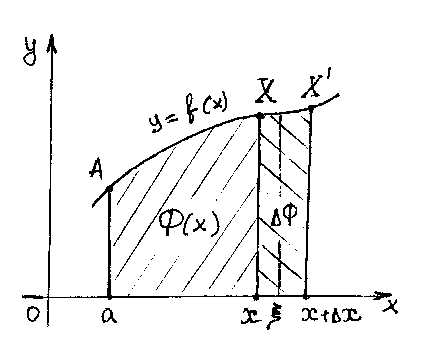 ой
на рисунке.
ой
на рисунке.
Пусть x получит приращение ∆x , тогда функция Ф(x) получит приращение ∆x , равное площади криволинейной трапеции :
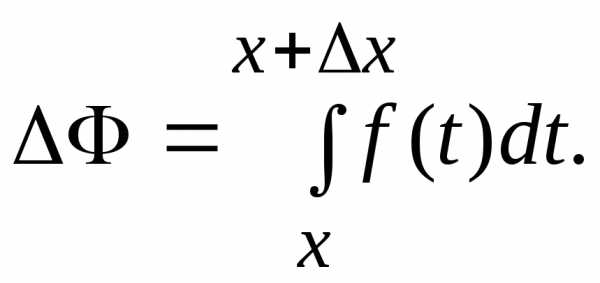
Применим к последнему интегралу теорему о среднем, выбрав
:
Найдем производную функции Ф(x) как
, т.к.
при 
Нами доказана следующая _теорема.:
если f(x) непрерывная функция и 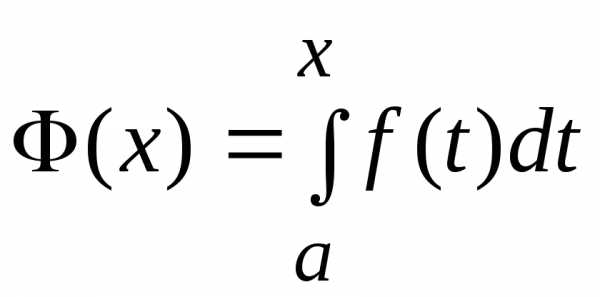 , то
, то
имеет место равенство
, т.е. (2)
производная от определенного интеграла по верхнему пределу равна подынтегральной функции:

в которую вместо переменной интегрирования подставлено значение верхнего предела.
II. Формула Ньютона- Лейбница.
На основе доказанной теоремы получим простой способ вычисления
определенного интеграла.
Пусть 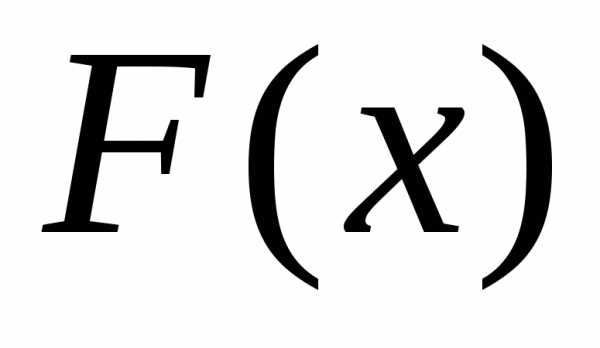 — некоторая первообразная функции f(x) .
— некоторая первообразная функции f(x) .
В
соответствии с доказанной теоремой 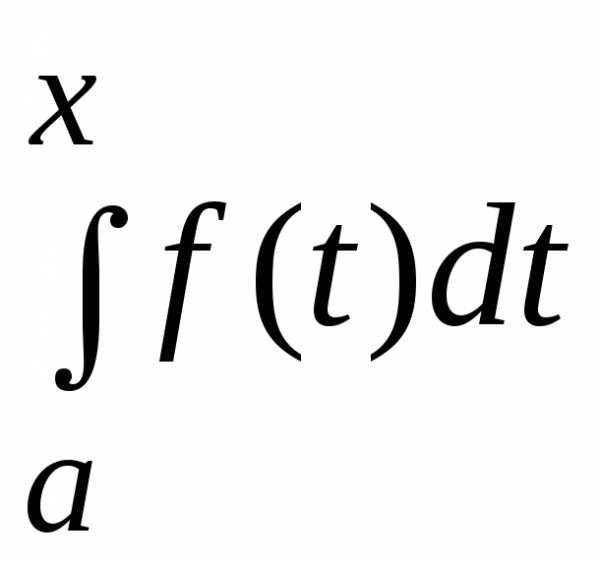 также является первообразной функции.
Поскольку любые две первообразные
отличаются только на постоянную величинуC , можно записать
также является первообразной функции.
Поскольку любые две первообразные
отличаются только на постоянную величинуC , можно записать
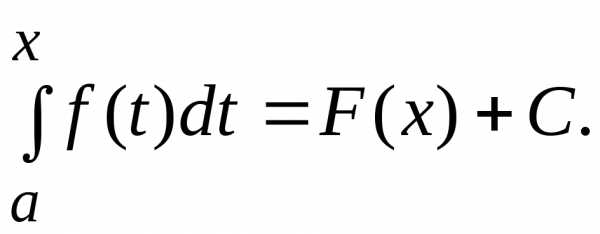 (3)
(3)
Положим x=a и учитывая свойства определенного интеграла, получим
Откуда
Обозначая x через b и t через x и подставляя в (3) найденное значение, приходим к формуле, известной под названием формулы Ньютона-Лейбница:
(4)
или
Формула Ньютона-Лейбница дает практически удобный способ вычисления определенных интегралов в отличие от вычисления их как пределов интегральных сумм.
_Примеры.: вычислить определенные интегралы
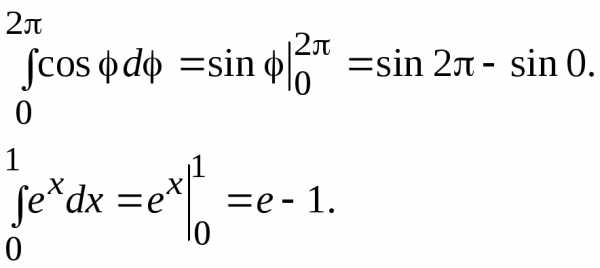
Таким образом, вычисление определенного интеграла сводится к нахождению первообразной подынтегральной функции и вычислению разности ее значений в верхнем и нижнем пределах интегрирования. При этом методы нахождения первообразной рассматривались при изучении неопределенных интегралов.
III. Замена переменной в определенном интеграле.
Реализация метода замены переменной в определенном интеграле производится по следующим правилам.
Пусть дан интеграл от непрерывной на отрезке [a,b] функции f(x).
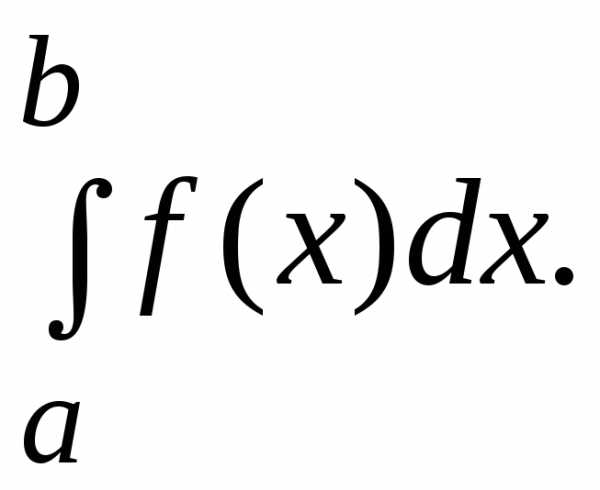
Введем
новую переменную t по формуле 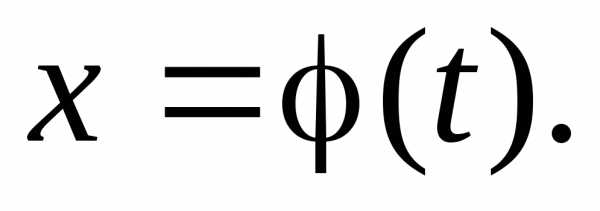 Если
Если ,
, , функции
, функции и
и непрерывны на отрезке [α‚β]
и функция
непрерывны на отрезке [α‚β]
и функция 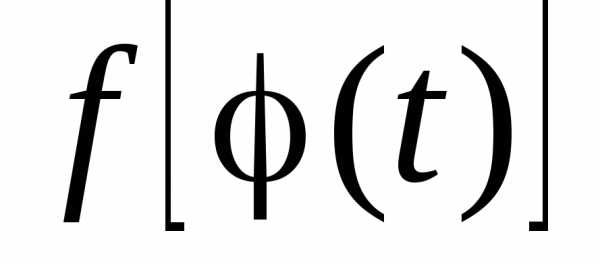 определена и непрерывна на отрезке
определена и непрерывна на отрезке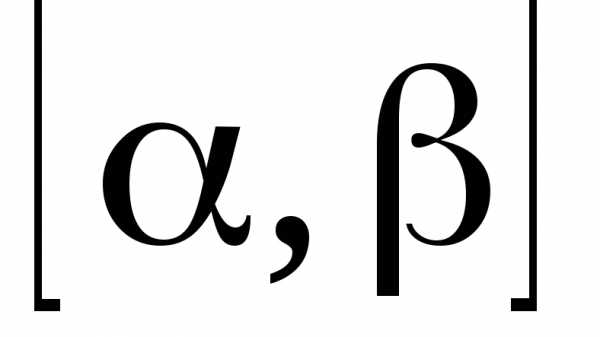 , то
, то
(5)
При вычислении определенного интеграла по этой формуле можно не возвращаться к старой переменной x, так как для переменной определены соответствующие пределы интегрирования α и β .
_Пример.. Вычислить интеграл
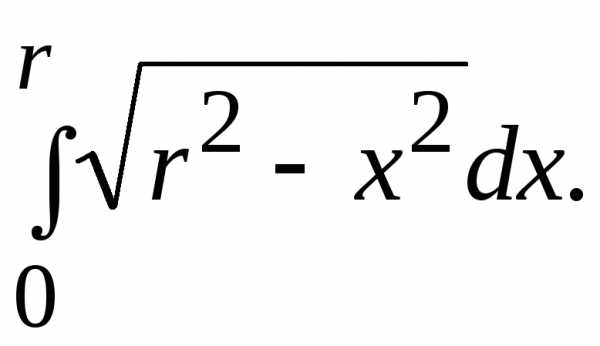
Введем новую переменную t по формуле , тогда
Определим новые пределы интегрирования:
x=0
при  ; x=r при
; x=r при  .
.
Следовательно,
IV. Интегрирование по частям.
Получим формулу интегрирования по частям в определенном интеграле. Для этого воспользуемся формулой производной произведения двух функций u(x) и v(x) :
откуда
и
Тогда 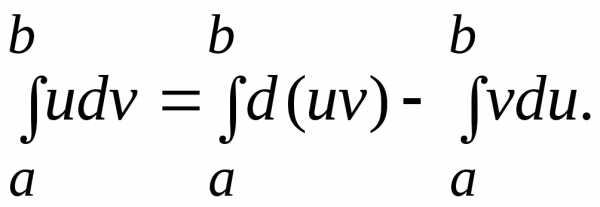
Вычислим 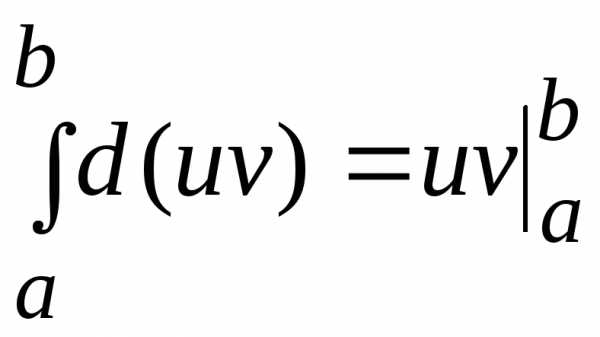 ,
тогда окончательно формула интегрирования
по частям имеет вид:
,
тогда окончательно формула интегрирования
по частям имеет вид:
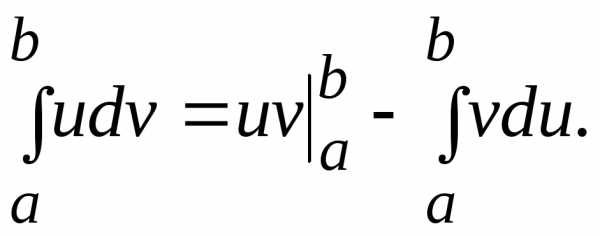 (6)
(6)
_Пример.. Вычислить интеграл
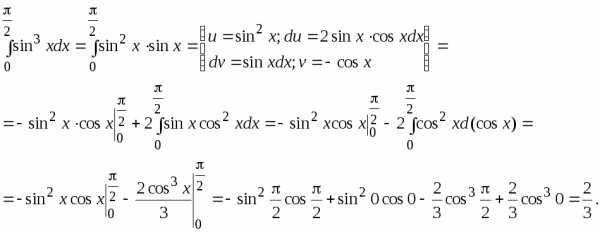
V. Приближенные вычисления определенного интеграла.
Методы приближенного вычисления определенных интегралов используются в тех случаях, когда первообразная подынтегральной функции не выражается через элементарные функции или ее нахождение вызывает значительные трудности. При этом не удается использовать формулу Ньютона-Лейбница. Существует несколько способов приближенного интегрирования. Все они основаны на понятии об определенном интеграле как пределе интегральных сумм.
Любой метод приближенного интегрирования включает следующие основные этапы:
1) отрезок интегрирования [a,b] разбивается точками
на n равных частей длиной ∆x ;
2)
в точках  вычисляются
вычисляются
значения интегрируемой функции f(x) , которые обозначим через
3) на каждом из отрезков функция f(x) заменяется на некоторую более простую функцию (постоянную, линейную, квадратичную
или
другую), проходящую через точки
и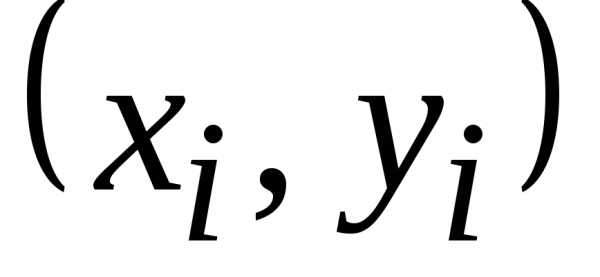 ;
;
4)
при этом рассматриваемая криволинейная
трапеция заменяется на некоторую близкую
к ней фигуру, состоящую из суммы n криволинейных трапеций с легко
вычисляемыми площадями 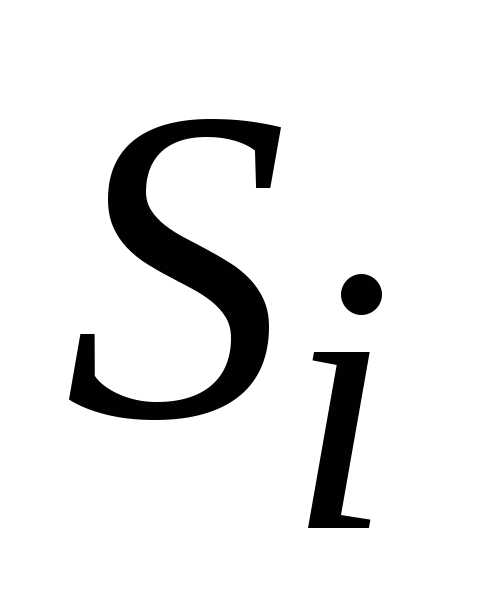 .
.
5)
определенный интеграл (площадь
криволинейной трапеции) 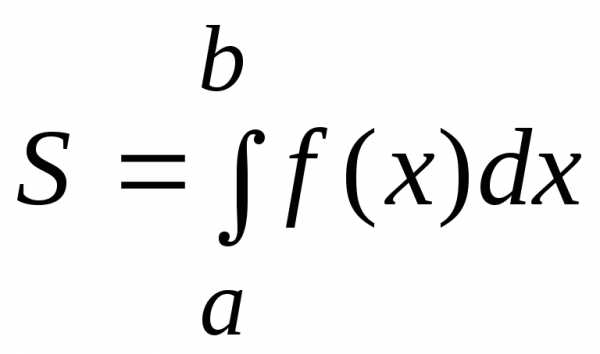 может быть найден как сумма конечного
числа площадей
может быть найден как сумма конечного
числа площадей ,
вычисляемых по известным формулам:
,
вычисляемых по известным формулам:
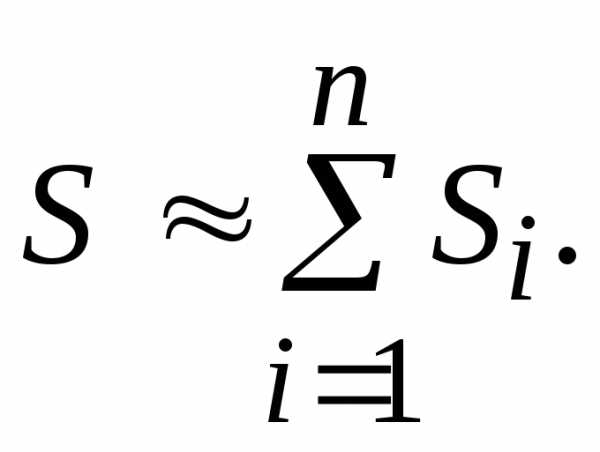
В зависимости от того, на какую фигуру заменяется криволинейная трапеция, различают следующие методы приближенного интегрирования:
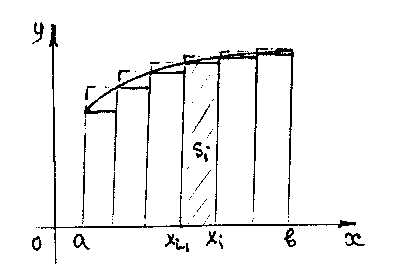 1)
метод прямоугольников: криволинейная
трапеция заменяется на вписанную или
описанную ступенчатую фигуру. В первом
случае площадь i -го прямоугольника определяется
1)
метод прямоугольников: криволинейная
трапеция заменяется на вписанную или
описанную ступенчатую фигуру. В первом
случае площадь i -го прямоугольника определяется
во втором случае
Учитывая,
что 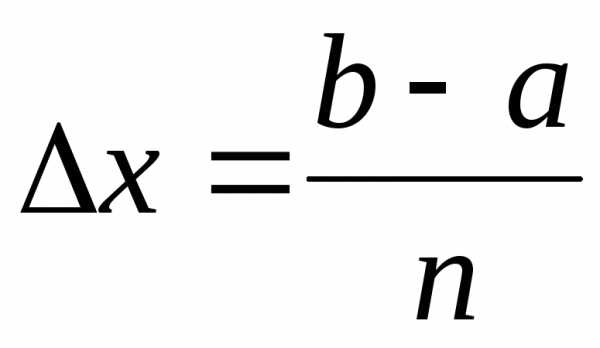 ,
получим формулу прямоугольников:
,
получим формулу прямоугольников:
или
Тогда
(7)
или

Первая из формул дает приближенное значение определенного интеграла меньшее точного, вторая — большее точного.
2)
метод хорд: на каждом отрезке 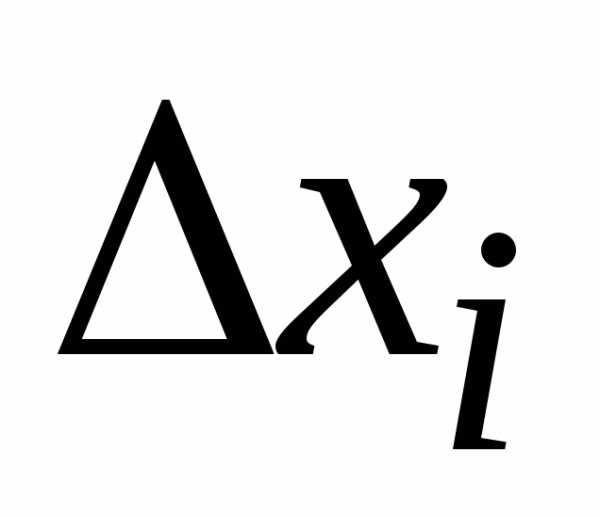 функция f(x) заменяется линейной функцией
функция f(x) заменяется линейной функцией
В этом случае площадь криволинейной трапеции можно представить как
сумму трапеций с площадями
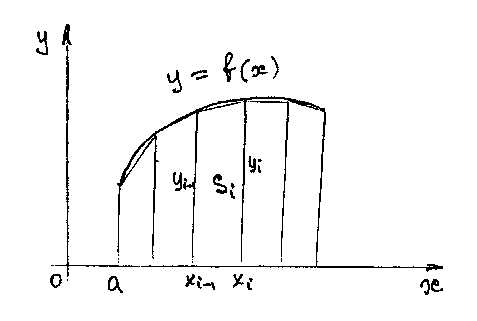
Тогда
Тогда — (8)
формула трапеций.
3) метод парабол (Симпсона): через каждые три точки на кривой
проводят параболу и вычисляют площади получающихся криволинейных
трапеций.
Точность методов вычисления определенных интегралов определяет-
ся, во-первых, мелкостью разбиения отрезка [a,b] , во-вторых,
степенью приближения функции f(x) на i -ом интервале. Точ-
ность вычислений по каждому из перечисленных методов возрастает с
уменьшением
величины 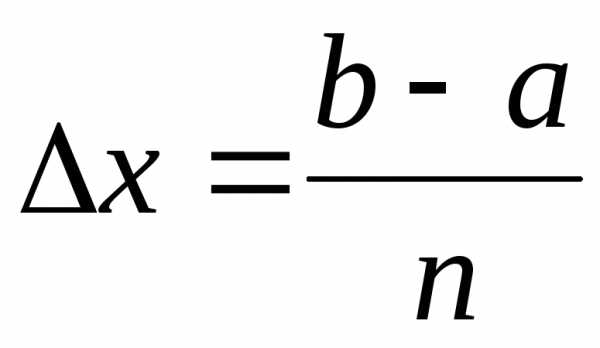 , т.е. с возрастанием числаn
, т.е. с возрастанием числаn
Второй критерий показывает, что точность вычислений методом
хорд выше, чем методом прямоугольников, а методом Симпсона выше, чем
методом хорд.
studfiles.net

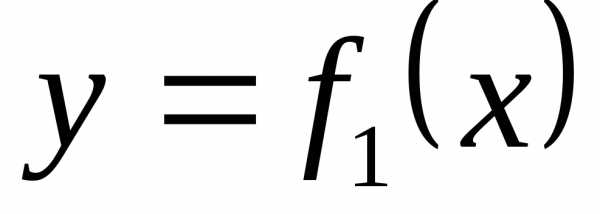 и
и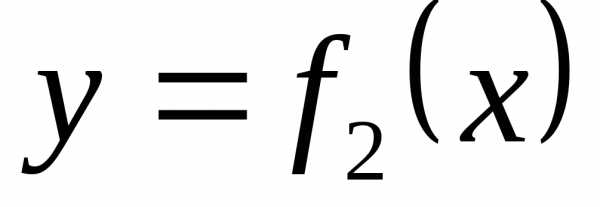
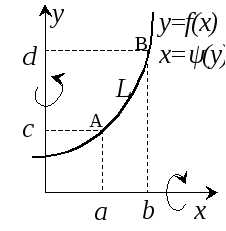
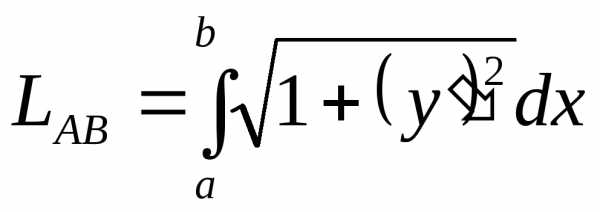 .
.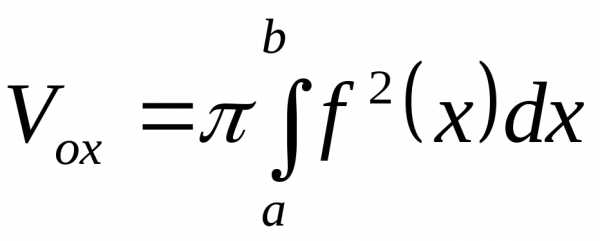 ,
если вращение части дуги функции
,
если вращение части дуги функции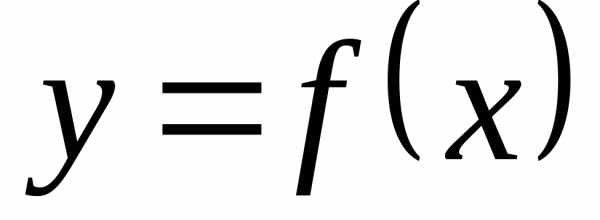 происходит относительно оси 0Х,
происходит относительно оси 0Х,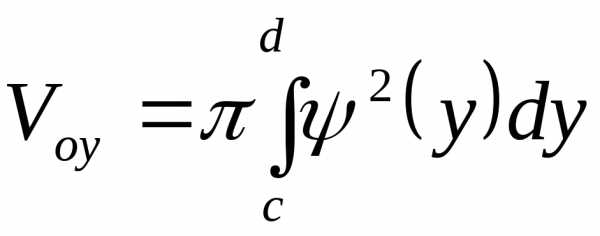 ,
если вращение происходит относительно
оси 0У ,
,
если вращение происходит относительно
оси 0У , 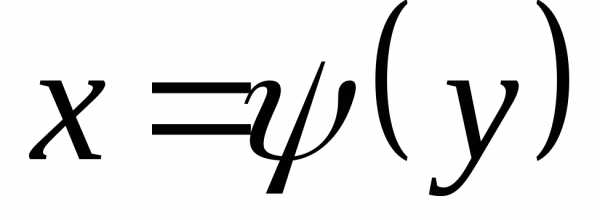 .
.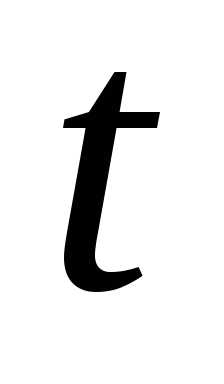 от
от до
до переменная
переменная изменяется от
изменяется от до
до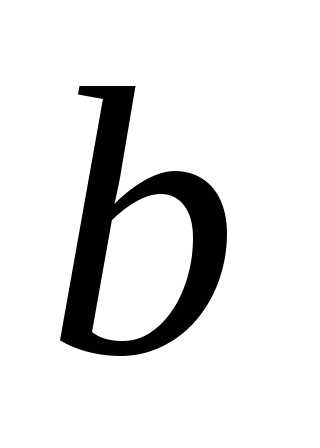 ,
то есть
,
то есть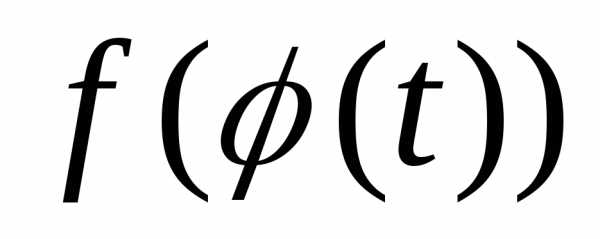 определена и непрерывна на отрезке
определена и непрерывна на отрезке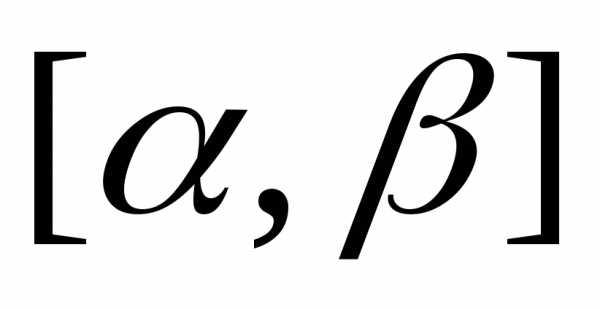 ,
то справедлива такая формула
,
то справедлива такая формула